Содержание:
- Определение и формула силы тяги
- Единицы измерения силы тяги
- Примеры решения задач
В том случае, если тело при перемещении имеет ускорение, то на него кроме всех прочих обязательно действует некоторая сила, которая является
силой тяги в рассматриваемый момент времени. В действительности, если тело движется прямолинейно и с постоянной скоростью, то сила тяги также
действует, так как тело должно преодолевать силы сопротивления. Обычно силу тяги находят, рассматривая силы, действующие на тело, находя
равнодействующую и применяя второй закон Ньютона. Жестко определенной формулы для силы тяги не существует.
Не следует считать, что сила тяги, например, транспортного средства действует со стороны двигателя, так как внутренние силы не могут менять
скорость системы как единого целого, что входило бы в противоречие с законом сохранения импульса. Однако следует отметить, что для получения у
силы трения покоя необходимого направления, мотор вращает колеса, колеса «цепляются за дорогу» и порождается сила тяги. Теоретически было бы
возможно не использовать понятие «сила тяги», а говорить о силе трения покоя или силе реакции воздуха. Но удобнее внешние силы, которые действуют
на транспорт делить на две части, при этом одни силы называть силами тяги
$(/bar{F}_T)$, а другие – силами сопротивления
$bar{F}_S$ . Это делается для того,
чтобы уравнения движения не потеряли свой универсальный вид и полезная механическая мощность (P) имела простое выражение:
$$P=bar{F}_{T} bar{v}(1)$$
Определение и формула силы тяги
Определение
Исходя из формулы (1) силу тяги можно определить через полезную мощность, и скорость транспортного средства (v):
$$F_{T}=frac{P}{v}(2)$$
Для автомобиля, поднимающегося в горку, которая имеет уклон
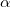 , масса автомобиля m сила тяги (FT) войдет в уравнение:
, масса автомобиля m сила тяги (FT) войдет в уравнение:
$$F_{T}-F_{s}-m g sin alpha=m a(3)$$
где a – ускорение, с которым движется автомобиль.
Единицы измерения силы тяги
Основной единицей измерения силы в системе СИ является: [FT]=Н
В СГС: [FT]=дин
Примеры решения задач
Пример
Задание. На автомобиль имеющий массу 1 т при его движении по горизонтальной поверхности, действует сила трения,
которая равна $mu$=0,1 от силы тяжести.
Какой будет сила тяги, если автомобиль движется с ускорением 2 м/с?
Решение. Сделаем рисунок.
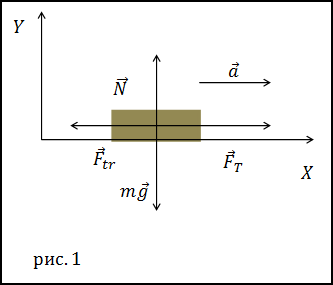
В качестве основы для решения задачи используем второй закон Ньютона:
$$bar{N}+m bar{g}+bar{F}_{t r}+bar{F}_{T}=m bar{a}(1.1)$$
Спроектируем уравнение (1.1) на оси X и Y:
$$
begin{array}{c}
X: F_{T}-F_{t r}=m a(1.2) \
Y: m g=N(1.3)
end{array}
$$
По условию задачи:
$$
F_{t r}=mu cdot m g (1.4)
$$
Подставим правую часть выражения (1.4) вместо силы трения в (1.2), получим:
$$F_{T}=m a+mu cdot m g$$
Переведем массу в систему СИ m=1т=103 кг, проведем вычисления:
$$F_{T}=10^{3}(2+0,1 cdot 9,8)=2,98 cdot 10^{3}(H)$$
Ответ. FT=2,98 кН

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. На гладкой горизонтальной поверхности лежит доска массой M. На доске находится тело массы m.
Коэффициент трения тела о доску равен $mu$ . К доске
приложена сила горизонтальная сила тяги, которая зависит от времени как: F=At (где A=const). В какой момент
времени доска начнет выскальзывать из-под тела?
Решение. Сделаем рисунок.
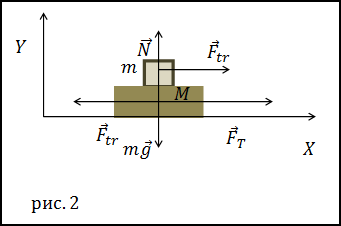
Для решения задачи нам потребуются проекции сил на осиX и Y, которые отличны от нуля. Для тела массы m:
$$
begin{array}{c}
X: m a_{1}=F_{t r}(2.1) \
Y: m g=N(2.2) \
F_{t r}=mu N=mu m g rightarrow m a_{1}=mu m g rightarrow a_{1}=mu g(2.3)
end{array}
$$
Для тела массы M:
$$M a_{2}=F-F_{t r} rightarrow M a_{2}=A t-F_{t r} rightarrow a_{2}=frac{A t-F_{t r}}{M}(2.2)$$
Обозначим момент времени, в который доска начнет выскальзывать из-под тела t0, тогда
$$mu g=frac{A t_{0}-mu m g}{M} rightarrow t_{0}=frac{m+M}{A} mu g$$
Ответ. $t_{0}=frac{m+M}{A} mu g$
Читать дальше: Формула силы упругости.
Что такое сила тяги
Сила тяги — сила, прикладываемая к телу для поддержания его в постоянном движении.
Действие силы тяги
Множество сил, действующих на движущийся объект, для упрощения вычислений делят на две группы: силу тяги и силы сопротивления.
Её прекращение
Когда действие силы тяги прекращается, движущееся тело замедляется и постепенно останавливается, так как на него воздействуют силы, мешающие продолжать двигаться, например, трение.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
1 закон Ньютона о действии
Согласно этому закону в формулировке самого Ньютона, любое тело остается в покое или равномерно движется по прямой, пока на него не воздействуют силы, заставляющие его изменить это состояние.
В современной физике в формулировку внесены уточнения:
- закон применим только в системах отсчета, называемых инерциальными;
- тело может вращаться на месте, не находясь под воздействием внешних сил, поэтому вместо термина «тело» следует использовать термин «материальная точка».
Чтобы переместить неподвижный предмет, на него должна воздействовать некая сила. Чтобы изменить скорость движения предмета, также необходимо воздействие силы, замедляющей его или ускоряющей. Так как предметы обладают разной массой и соответственно разной инертностью, силы, достаточные для эффективного воздействия, тоже будут различаться.
Состояние ускорения после воздействия силы тяги
Когда движение равномерное, сила тяги и сила трения совершают одинаковую работу, уравновешивая друг друга. Воздействие силы на тело в направлении движения придает ему ускорение. Если направить ту же силу в противоположном направлении, она замедлит движение тела, что можно назвать отрицательным ускорением.
Формулы для определения силы тяги
Согласно второму закону Ньютона, сумма сил, воздействующих на движущееся тело, равна массе (m), умноженной на ускорение (a). Универсальной формулы, подходящей для любого сочетания сил, не существует. Чаще всего силу тяги находят с помощью общей формулы( F_т-;F_{с}=m;times;a), где (F_т) — сила тяги, (F_{с}) — силы сопротивления.
При решении конкретной задачи силы, воздействующие на тело, схематически изображают в виде векторов. На схеме:
- сила тяжести mg;
- сила реакции опоры (N);
- сила трения( F_{тр});
- сила тяги (F).
При нахождении тела на горизонтальной поверхности сила тяжести и сила реакции опоры уравновесят друг друга. Но если транспортное средство движется в гору или под гору, придется учесть влияние уклона. Тогда формула может выглядеть так: (F_т-;F_с-;mg;times;sinalpha=m;times;a.)
Работа A, которую должна совершить сила тяги, сдвигая тело, связана с ней соотношением (A;=;F;times;s). (s) здесь — расстояние, на которое тело переместилось.
Какое условие должно соблюдаться
Сила тяги всегда должна быть больше противодействующих ей сил.
Формула через мощность
Полезную механическую мощность (N) можно вычислить по формуле (N=F_т;times;v), где (v) — скорость. Для определения силы тяги нужно разделить мощность на скорость: (F_т;=;frac N v.)
Измерение и обозначение силы тяги
Силу тяги обозначают (F_т) или (F). Единица измерения — ньютон ((Н)).
Для решения задач недостаточно измерить усилие, приложенное к объекту, и выразить его конкретным числом, так как сила обладает еще и направлением. Чтобы подчеркнуть, что сила — векторная величина, к буквенному обозначению добавляют стрелку.
Как определить силу тяги двигателя. Примеры решения задач
Задача 1
Автомобиль может разгоняться до 216 км/ч. Максимальная мощность двигателя равна 96 кВт. Определите максимальную силу тяги двигателя.
Решение
Переведем киловатты в ватты, а километры в час — в метры в секунду:
(96;times;1000=96000;Вт)
(frac{216times1000}{3600}=60frac мс)
(F_т;=;frac N v = frac{96000}{60} = 1600 Н)
Задача 2
Троллейбус весом 12 тонн за 5 секунд проезжает по горизонтальной дороге 10 метров. Сила трения равна 2,4 кН. Определите силу тяги, которую развивает двигатель.
Решение
Переведем тонны в килограммы, а килоньютоны в ньютоны:
(12;times;1000=12000;кг)
(2,4;times;1000=2400;Н)
(F_т-;F_{тр}=m;times;a), следовательно, (F_т=mtimes a;+;F_{тр})
Чтобы определить ускорение а, воспользуемся формулой (s;=;frac{at^2}2)
Подставив численные значения величин, получаем:
(a;=;frac{2s}{t^2}^{}=frac{20}{25};=;0,8)
(F_т=;12000times0,8;+;2400;=;12000;Н;=;12;кН)
Задача 3
Транспорт, весящий 4 тонны, едет в гору. Уклон — 1 метр на каждые 25 метров пути. (mu) — 0,1 от силы тяжести, (а = 0). Определите силу тяги.
Решение
Начертим схему:
(mtimes g;+;N;+;F_{тр;}+;F_т;=;mtimes a)
Сделаем проекции на координатные оси:
(OX: -;mg;times;sinalpha;-;F_{тр;}+;F_т;=;0)
(OY: N;-;mg;times;cosalpha;=;0 => N;=;mg;times;cosalpha;)
(F_{тр};=;mu N;=;mu mg;times;cosalpha)
Подставим значение (F_{тр}) в уравнение (OX) и определим (F_т):
(-mg;times;sinalpha;-;mu)
(mg;times;cosalpha;+;F_т;=;0)
(=> F;=;mg;left(sinalpha;+;mu;times;cosalpharight))
Найдем синус и косинус (alpha), подставим их в общую формулу:
(sinalpha;=;frac hl;=;frac1{25})
(cosalpha;=;frac{sqrt{l^{2;}-;h^2}}l;)
(F;=;frac{4;times;10^{3;};times;9,8;timesleft(1;+;0,1;sqrt{l^{2;}-;h^2}right)}{25};=;5,5;times;10^3;Н;=;5,5;кН)
Разберёмся в вопросе, что такое сила тяги. Как следует из самого названия – это сила, которую необходимо прикладывать к телу, чтобы оно находилось в состоянии постоянного движения.

Если её убрать, то тело, будь то автомобиль, электровоз, космическая ракета или санки, со временем остановится. Это произойдёт потому, что на тело всегда действуют силы, которые заставляют его стремиться к состоянию покоя:
- силы трения (покоя, качения, скольжения),
- сопротивления воздуха (газа),
- сопротивления воды и др.
Содержание:
- Первый и второй законы Ньютона
- Примеры из жизни
- Насколько вы сильны?
- Насколько силён ваш автомобиль?
Первый и второй законы Ньютона
Обратимся к законам Ньютона, которые хорошо описывают механическое движение тел. Из школьной программы мы знаем, что есть первый закон Ньютона, который описывает закон инерции. Он гласит, что любое тело, если на него не действуют силы, или если их равнодействующая равна нулю, движется прямолинейно и равномерно, или же находится в состоянии покоя. Это означает, что тело, пока на него ничто не действует, будет двигаться с постоянной скоростью v=const или пребывать в состоянии покоя сколько угодно долго, пока какое-то внешнее воздействие не выведет тело из этого состояния. Это и есть движение по инерции.
Надо сказать, что этот закон справедлив лишь в так называемых инерциальных системах отсчёта. В неинерциальных системах отсчёта этот закон не действует и нужно использовать второй закон Ньютона. В таких системах отсчёта тело тоже будет двигаться по инерции, но оно будет двигаться с ускорением, стремясь сохранять своё движение, т.е. на него также не будут действовать никакие внешние силы, кроме силы инерции, стремящейся двигать тело в том направлении, в каком оно двигалось до воздействия. Тут мы приходим к рассмотрению второго закона Ньютона, который также справедлив в инерциальных системах отсчёта, т. е. в таких системах отсчёта, в которых тело движется с постоянной скоростью либо находится в покое.
Этот закон утверждает, что для того, чтобы вывести тело из состояния покоя или равномерного движения, к нему необходимо приложить силу, равную F=m•a, где m — это масса тела, a — ускорение, сообщаемое телу. Зная эти законы, можно рассчитать силу тяги (двигателя автомобиля, ракетного двигателя или, например, лошади, тянущей нагруженную повозку).

Примеры из жизни
Насколько вы сильны?
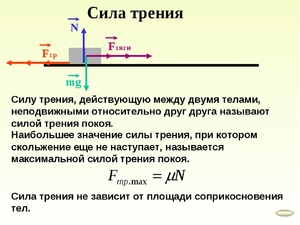
Рассмотрим простейший пример. Ваш ребёнок сел на санки и просит вас его покатать. С какой силой вам нужно тянуть эти санки, чтобы ребёнок остался доволен быстрой ездой ? Пока санки с ребёнком остаются в состоянии покоя, все силы, действующие на них, уравновешены. Состояние покоя — это частный случай инерции. Здесь на санки действуют две силы: тяжести Fт = m•g, направленная вертикально вниз, и нормального давления N, направленная вертикально вверх. Поскольку санки не движутся, то N – m•g = 0. Тогда из этого равенства следует, что N = m•g.
Когда вы решили покатать своего ребёнка, вы прикладываете силу тяги (Fтяги) к санкам с ребёнком. Когда вы начинаете тянуть санки, возникает сопротивление движению, вызванное силой трения (Fтр.), направленной в противоположную сторону. Это так называемая сила трения покоя. Когда тело не движется, она равна нулю. Стоит потянуть за санки — и появляется сила трения покоя, которая меняется от нуля до некоторого максимального значения (Fтр. max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.
Чтобы найти Fтяги, применим второй закон Ньютона: Fтяги – Fтр.max = m•a, где a – ускорение, с которым вы тянете санки, m – масса санок с ребёнком. Допустим, вы разогнали санки до определённой скорости, которая не изменяется. Тогда a = 0 и вышеприведённое уравнение запишется в виде: Fтяги – Fтр. max = 0, или Fтяги = Fтр.max. Есть известный закон из физики, который устанавливает определённую зависимость для Fтр.max и N. Эта зависимость имеет вид: Fтр.max = fmax • N, где fmax – максимальный коэффициент трения покоя.
Если в эту формулу подставить выражение для N, то мы получим Fтр.max = fmax•m•g. Тогда формула искомой силы тяги примет вид: Fтяги = fmax•m•g = fск•m•g, где fск = fmax – коэффициент трения скольжения, g – ускорение свободного падения. Допустим, fск = 0,7, m = 30 кг, g = 9,81 м/с², тогда Fтяги = 0,7 • 30 кг • 9,81 м/с² = 206,01 Н (Ньютона).
Насколько силён ваш автомобиль?
Рассмотрим ещё пример. У вас есть автомобиль, мощность двигателя которого N. вы едете со скоростью v. Как в этом случае узнать силу тяги двигателя вашего автомобиля ? Поскольку скорость автомобиля не меняется, то Fтяги уравновешена силами трения качения, лобового сопротивления, трения в подшипниках и т. д. (первый закон Ньютона). По второму закону Ньютона она будет равна Fтяги = m•a. Чтобы её вычислить, достаточно знать массу автомобиля m и ускорение a.
Допустим, вы разогнали свой автомобиль до скорости v за какое-то время t, проехав расстояние s. Тогда Fтяги будет легко рассчитана по формуле: Fтяги = m•v/t. Как и в примере с санками, справедлива также такая формула: Fтяги = f•m•g, где f – коэффициент трения качения, который зависит от скорости автомобиля (чем больше скорость, тем меньше этот коэффициент).
Но что делать, если масса автомобиля m, коэффициент трения качения f и время разгона t неизвестны ? Тогда можно поступить по-другому. Двигатель вашего автомобиля при разгоне совершил работу A = Fтяги • s. Поскольку формула расстояния имеет вид s = v•t, то выражение для работы будет таким: A = Fтяги • v • t. Разделив обе части этого равенства на t, получим A/t = Fтяги • v. Но A/t = N – это мощность двигателя вашего автомобиля, поэтому N = Fтяги • v. Отсюда уже получим искомую формулу: Fтяги =N/v.
Допустим, вы разогнали свой автомобиль до скорости v = 180 км/ч, а мощность его двигателя N = 200 л. с. (лошадиных сил). Чтобы вычислить Fтяги двигателя, необходимо прежде перевести указанные единицы измерения в единицы СИ, т. е. международной системы измерения. Здесь 1 л. с. = 735,499 Вт, поэтому мощность двигателя составит N = 200 л. с. • 735,499 Вт/л. с. = 147099,8 Вт. Скорость в системе СИ будет равна v = 180 км/ч = 180 • 1000 м/3600 с = 50 м/с. Тогда искомое значение будет равно Fтяги = 147099,8 Вт/50 (м/с) = 2941,996 Н ~ 2,94 кН (килоньютона).
Около 3 килоньютонов. Много это или мало ? Допустим, вы жмёте 100 килограммовую штангу. Чтобы её поднять, вам нужно преодолеть её вес, равный P = m•g = 100 кг • 9,81 м/с² = 981 Н (ньютон)~0,98 кН. Полученное для автомобиля значение Fтяги больше веса штанги в 2,94/0,98 = 3 раза. Это равносильно тому, что вы будете поднимать штангу массой в 300 кг. Такова сила тяги двигателя вашего автомобиля (на скорости 180 км/ч).
Таким образом, зная школьный курс физики, мы можем с лёгкостью вычислить силу тяги:
- человека,
- лошади,
- паровоза,
- автомобиля,
- космической ракеты и всех прочих видов техники.
Видео
В нашем видео вы найдете интересные опыты, поясняющие, что такое сила тяги и сила сопростивления.
Основное понятие силы тяги в физике
Определение 1
Сила тяги — это показатель силы, которую прикладывают к некоторому телу.
Она служит для обеспечения нахождения данного тела в состоянии равновесия.
Когда сила тяги прекращает свое действие — это может привести к следующим последствиям:
- остановка, которая связана с силой трения;
- состояние вязкости окружающей среды;
- множество других сопутствующих факторов и сил.
Для тела, на которое оказывает свое воздействие сила тяги, характерно постоянное движение. И обозначается следующим значение, а именно: [(v=operatorname{cons} t)]
Особым, частным случаем данного движения является состояние покоя.
При котором, скорость равна нулевому значению.
Определение 2
Состояние инерции — характер движения, при котором соблюдается постоянная скорость движения тела.
Чтобы тело поменяло свое состояние, и изменило скорость своего движения, необходимо приложить к нему силу тяги. При данных условиях скорость тела будет изменяться, причиной этого является получаемое ускорение. Также ускорение может быть отрицательным, в таком случае будет наблюдаться замедление скорости.
Показатель величины ускорения по закону физики обратно пропорционален массе тела.
Из состояния инерции труднее всего вывести тело более массивное и тяжелое.
Также величина ускорения прямо пропорциональна значению интенсивности силы, которая оказывает воздействие на тело.
Данное утверждение можно преобразовать и вывести в виде формулы:
Формула
[mathrm{F}=mathrm{m} cdot mathrm{a}]
Где: F — сила тяги, m — масса тела, которая оказывает воздействие на тело, a — ускорение.
Данная формула наглядно характеризует второй закон Ньютона.
Основные формулы для расчета силы тяги
Наглядно силу тяги можно рассмотреть на примере спортсмена штангиста.
Именно на данном примере можно подробно понять, как приложенная сила, может вывести тело из состояния равновесия.
Распишем все операции, выполняемые спортсменам поэтапно:
- первоначально штанга находится в состоянии инерции, иными словами имеет состояние покоя;
- при отрыве от поверхности земли штанги, все мышцы спортсмена имеют способность сокращаться, с силой которая не превышает вес самой штанги (иначе это звучит как: величина силы с которой ее к себе притягивает гравитация Земли);
- при отрыве от пола, штанги на определенную высоту, происходит процесс ускорения;
Силой тяги для снаряда, который осуществляет движение будет являться величина силы с которой сокращаются мышцы спортсмена.
Для данного случая, обязательно должно соблюдаться следующее условие:
[F_{M}>F_{T} text {. то есть } F_{M}>m times g]
Где:
- [F_{m}] — сила, с которой происходит сокращение мышечной массы (сила тяги для данного случая);
- [F_{т}] сила тяжести или гравитационная;
- m — масса, которая оказывает воздействие на тело;
- g — показатель ускорение свободного падения.
Характер движения тела по инерции всегда нужно уметь отличать от движения, которое совершается равномерно. Следовательно, в случае, когда сила тяги имеет способность уравновешиваться сторонними силами (противодействующими).
Например:
Автомобиль совершает движение и его двигатель находится в состоянии работы. Работающий двигатель придает силу на колеса, через трансмиссию, проделывая следующие операции:
- преодолевает силу трения, которая возникает внутри всего механизма;
- сопротивление воздуха;
- процесс трения колес о любую поверхность.
Для определения силы тяги, необходимо знать следующие данные:
- t — время, за которое происходит разгон транспортного средства;
- [v] — необходимая скорость;
- m — непосредственная масса автомобиля.
Сила определяется по формуле:
[F=m times frac{V}{t}]
Из формулы видно, что ускорение выражено как: деление скорости на время разгона транспортного средства:
[a=frac{V}{t}]
Через мощность можно выразить силу.
Определение 3
Мощность — это совершенная работа, любым источником энергии.
Если высокая мощность, то следует что, время за которое источник развивает силу будет уменьшаться. А именно: способность разогнать тело определенной массы равной m до необходимой величины скорости движения.
Значение совершаемой работы прямо пропорционально силе и вычисляется по формуле:
[A=F times s]
Где: S — расстояние, на которое при помощи силы, перемещается тело;
Расстояние можно определить по формуле, выразив его через скорость тела и время движения:
[s=v cdot t]
Затем определяется мощность, которая должна выполнять в единицу времени и выражается следующей формулой:
[mathrm{N}=frac{d}{t}]
Окончательное уравнение выражает так:
[frac{A}{t}=frac{F cdot V cdot t}{t} Rightarrow N=F cdot V Rightarrow F=frac{N}{V}]
Нет времени решать самому?
Наши эксперты помогут!
Пример решения задачи на определение силы тяги
Нужно определить показатель силы тяги транспортного средства. Оно движется с ускорением равным a. Масса автомобиля равна 1,5 тонны и сила трения составляет 10 процентов от всей силы тяжести.
Сила тяги будет определяться как сумма двух основных сил:
- Автомобиль, который разгоняется с заданным значением ускорения: [F_{1}=m cdot a]
Где: m — масса автомобиля, a — показатель ускорения.
- Преодоление силы трения:
[F_{2}=mu cdot m cdot g]
Где: [mu] — коэффициент, который характеризует силу трения, g — значение ускорения свободного падения.
Все числовые известные значения подставим в формулу, и вычислим нужное нам значение силы. В процессе вычисления все единицы измерения переводятся в единицы системы СИ, а именно: килограммы.
[F=F_{1}+F_{2}=m cdot a+mu cdot m cdot g]
[mathrm{F}=1500 cdot 3+0.1 cdot 9.8 cdot 1500=1500 cdot(3+0.98)=5970]
Ответ: 5970.
Наталья Николаевна Пушкина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Сила тяги: определение
Определение 1
Силой тяги называют силу, прикладываемую к телу для поддержании его в постоянном движении.
Прекращение действия силы тяги приводит к остановке вследствие трения, вязкости окружающей среды и других противодействующих движению сил.
Тело, на которое не действуют силы, движется с постоянной скоростью $v = const$ (первый закон Ньютона). Частным случаем такого движения является состояние покоя ($v = 0$). Движение с постоянной скоростью называют состоянием инерции. Чтобы вывести тело из такого состояния, нужно приложить к нему силу. Скорость тела в этом случае изменится, т.е. оно получит ускорение (либо замедление, которое можно считать отрицательным ускорением).
Величина ускорения обратнопропорциональна массе тела (чем оно массивнее, тем труднее его вывести из состояния инерции) и прямопропорциональна интенсивности приложенной силы. Таким образом:
$F = m cdot a$,
где:
- $F$ – сила,
- $m$ – масса,
- $a$ – ускорение.
Замечание 1
Эта формула отражает Второй закон Ньютона.
Формулы для расчета
В качестве примера силы тяги, выводящей тело из состояния покоя, можно рассмотреть спортсмена, поднимающего штангу. В исходном состоянии штанга находится в состоянии инерции (остается неподвижной). Когда спортсмен отрывает ее от земли, его мышцы должны сокращаться с такой силой, чтобы она превысила вес штанги, т.е. силу, с которой ее притягивает гравитационное поле Земли. Если штангисту удастся оторвать штангу от пола – значит она переместится вверх на некоторое расстояние, т.е. получит ускорение. Т.е. силой тяги, двигающей данный снаряд, является сила сокращающихся мышц спортсмена. При этом должно соблюдаться условие:
«Сила тяги» 👇
$F_м$ > $F_т$, т.е. $F_м$ >$ m cdot g$,
где $F_м$ – сила мышц (в данном случае сила тяги), $F_т$ – сила тяжести (гравитация), $m$ – масса, $g$ – ускорение свободного падения.
Состояние движения по инерции следует отличать от равномерного движения, когда сила тяги уравновешивается противодействующими силами. Например, при движении автомобиля работающий двигатель через систему трансмиссии передает на колеса силу, преодолевающую силы трения внутри механизмов автомобиля, трения колес о поверхность дороги, сопротивления воздуха и т.д. Силу тяги можно в этом случае вычислить зная время разгона $t$ до нужной скорости $v$ и массу автомобиля $m$:
$F = m cdot frac{v}{t}$
Здесь ускорение выражено как частное от деления скорости на время разгона.
Силу тяги можно также выразить через мощность – способность некоторого источника энергии совершать работу. Чем мощность выше – тем за меньшее время этот источник разовьет силу, способную разогнать тело массой $m$ до требуемой скорости $v$. Работа же прямопропорциональна силе, которая ее совершила:
$A = F cdot s$,
где $s$ – расстояние, на которое сила переместила данное тело.
Поскольку расстояние можно выразить через скорость и время,
$s = v cdot t$,
а мощность есть работа, выполняемая в единицу времени
$N = frac{A}{t}$
можно составить уравнения:
$frac{A}{t} = frac{F cdot v cdot t}{t} implies N = F cdot v implies F = frac{N}{v}$
Пример 1
Вычислить силу тяги автомобиля, движущегося с ускорением $3 м/с^2$, если его масса составляет 1,5 тонны, а сила трения – 10% от силы тяжести.
Рассмотрим силу тяги как сумму двух сил:
- разгоняющей автомобиль с заданным ускорением: $F_1 = m cdot a$, где $m$ – масса, $a$ – ускорение;
- преодолевающей силу трения: $F_2 = mu cdot m cdot g$, где $mu$ – коэффициент силы трения, $g$ – ускорение свободного падения.
Подставив числовые значения в формулу
$F = F_1 + F_2 = m cdot a + mu cdot m cdot g$
получим, попутно переведя тонны в единицы СИ килограммы,
$F = 1500 cdot 3 + 0,1 cdot 9,8 cdot 1500 = 1500 cdot (3 + 0,98) = 5970$
Ответ: 5970 ньютонов.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

