Как найти силу тяги двигателя ракеты

Сила тяги реактивного (ракетного) двигателя

Тяга
– равнодействующая всех реактивных
сил, создаваемых агрегатами двигателя,
определяется по формуле:

где
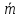– массовый секундный расход топлива
реактивного двигателя;W_a
– скорость газовой струи на срезе сопла;
F_a
– площадь среза сопла; р_а
– давление на срезе сопла; р_h
– давление
окружающей среды.

Первый
член данного уравнения характеризует
тягу, создаваемую за счет отбрасывания
от сопла газов и эта часть – реактивная
сила (статическая составляющая).

Второй
член характеризует тягу, которая
определяется разностью давлений на
срезе сопла и давления окружающей среды
и эта часть – переменная составляющая
реактивной тяги (зависит от высоты
полета).

Реактивный момент

Пусть
есть ракета с однокамерной двигательной
установкой (ДУ) рис.29: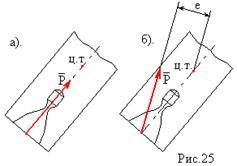

а) Если
вектор тяги двигателя Р
направлена вдоль оси, то реактивный
момент отсутствует (рис. 29,а).

б) Если
вектор тяги (и результирующий вектор
тяги для многокамерной ДУ) действует с
некоторым эксцентриситетом относительно
центра тяжести (рис. 29,б),
то в этом случае действует реактивный
момент
.

Рис.29

Аэродинамические схемы ла

Планером
называется конструкция, объединяющая
корпус, крылья, органы управления и
стабилизации в единую аэродинамическую
схему. Он предназначен для создания
управляющих сил и размещения всей
аппаратуры ракеты. Корпус планера обычно
цилиндрической формы, за исключением
ракеты типа «несущий конус», с конической
(сферической) головной частью. Форма
корпуса и головной части выбирается в
целях получения наименьшей силы лобового
сопротивления ракеты при полете.
Материалом для корпуса служат легкие
прочные металлы и сплавы

Аэродинамические
поверхности планера служат для создания
подъемной и управляющих сил. Подъемная
сила, которая возникает при взаимодействии
ракеты с воздухом во время ее полета,
обеспечивает удержание ЛА в воздухе.
Управляющие силы необходимы для изменения
направления полета ракеты.

Различают
подвижные и неподвижные аэродинамические
поверхности (АП). Подвижные АП,
предназначенные для управления полетом
и стабилизацией ЛА, называются рулями,
поворотными крыльями. Свои функции они
выполняют путем поворота вокруг осей,
перпендикулярных продольной оси корпуса
ракеты, либо при выдвижении из корпуса
на определенное время и в определенной
последовательности.

Неподвижные
АП служат для стабилизации полета ЛА
(стабилизаторы) и для создания подъемной
силы (несущие крылья, поверхности). По
взаимному расположению рулей и неподвижных
аэродинамических поверхностей можно
выделить следующие аэродинамические
схемы ракет (рис.30):

–
нормальная или обычная;

–
«утка»;

–
«бесхвостка»;

–
«поворотное крыло»;

В
нормальной схеме рули и стабилизатор
располагаются позади крыльев в хвостовой
части ракеты.

Схема
«бесхвостка». Данная схема является
разновидностью нормальной схемы. Здесь
крылья выполняют одновременно функции
крыльев и стабилизаторов и отличаются
большей стреловидностью и малым размахом.
С целью увеличения подъемной силы в
этой схеме увеличена площадь крыльев.
При этом рули оказываются расположенными
непосредственно за крыльями и связываются
с ними конструктивно.

В
аэродинамической схеме «утка» рули
находятся в головной части ракеты
(впереди центра масс), а крылья, выполняющие
и функцию стабилизатора, расположены
в хвостовой части корпуса ракеты. Эта
схема удобна с точки зре­ния компоновки
ракеты, так как рулевые машинки могут
быть расположены близко к рулям. При
такой компоновке ракеты подъемная сила
рулей совпадает по направлению с
подъемной силой крыльев и корпуса.
Однако расположение рулей в носовой
части ракеты и возникновение скоса
воздушного потока при отклонении рулей
приводит к потере подъемной силы на
крыльях и возникновению значительных
моментов крена. Чтобы избежать «момента
косой обдувки» крыльевой блок делается
вращающимся вокруг оси ракеты, что
позволяет избежать воздействия скоса
воздушного потока на них.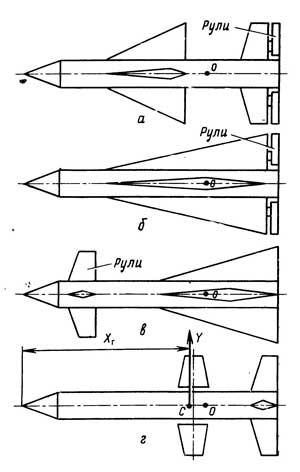

В схеме
«поворотное крыло» подвижные поверхности
(поворотные крылья) располагаются в
районе центра тяжести и наряду с функцией
крыла выполняют функцию рулей, а
неподвижные стабилизаторы расположены
в хвостовой части корпуса.

Рис.
30 Аэродинамические схемы: а)Нормальная;
б)”Бесхвостка”; в)”Утка”;
г)”Поворотное крыло”.

Принципиально
не существует наилучшей аэродинамической
схемы. Выбор схемы аэродинамической
компоновки определяется требуемыми
высотами и дальностями полета ракеты,
маневренностью и составом бортовой
аппаратуры.

Таблица

Соседние файлы в папке 02-12-2014_07-07-59

• #
• #

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 августа 2021 года; проверки требуют 3 правки.

Реактивная тяга — сила, возникающая в результате взаимодействия реактивной двигательной установки с истекающей из сопла струёй расширяющейся жидкости или газа, обладающих кинетической энергией^[1].

В основу возникновения реактивной тяги положен закон сохранения импульса. Реактивная тяга обычно рассматривается как сила реакции отделяющихся частиц. Точкой приложения её считают центр истечения — центр среза сопла двигателя, а направление — противоположное вектору скорости истечения продуктов сгорания (или рабочего тела, в случае не химического двигателя). То есть, реактивная тяга:

• приложена непосредственно к корпусу реактивного двигателя;
• обеспечивает передвижение реактивного двигателя и связанного с ним объекта в сторону, противоположную направлению реактивной струи^[2].

Реактивное движение в природе[править | править код]

Среди растений реактивное движение встречается у созревших плодов бешеного огурца. При созревании растения его плод отцепляется от плодоножки. Под большим давлением из плода выбрасывается жидкость с семенами, которая направлена противоположно движению плода^[3].

Среди животного мира реактивное движение встречается у кальмаров, осьминогов, медуз, каракатиц, морских гребешков и других. Перечисленные животные передвигаются, выбрасывая вбираемую ими воду.

Величина реактивной тяги[править | править код]

Формула при отсутствии внешних сил[править | править код]

Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени.

, где

 — масса ракеты

 — её ускорение

 — скорость истечения газов

 — расход массы топлива в единицу времени

Поскольку скорость истечения продуктов сгорания (рабочего тела) определяется физико-химическими свойствами компонентов топлива и конструктивными особенностями двигателя, являясь постоянной величиной при не очень больших изменениях режима работы реактивного двигателя, то величина реактивной силы определяется в основном массовым секундным расходом топлива^[1].

Доказательство[править | править код]

До начала работы двигателей импульс ракеты и топлива был равен нулю, следовательно, и после включения сумма изменений векторов импульса ракеты и импульса истекающих газов равна нулю:
, где

 — изменение скорости ракеты

Разделим обе части равенства на интервал времени t, в течение которого работали двигатели ракеты:

Произведение массы ракеты m на ускорение её движения a по определению равно силе, вызывающей это ускорение:

Уравнение Мещерского[править | править код]

Если же на ракету, кроме реактивной силы , действует внешняя сила , то уравнение динамики движения примет вид:

Формула Мещерского представляет собой обобщение второго закона Ньютона для движения тел переменной массы. Ускорение тела переменной массы определяется не только внешними силами , действующими на тело, но и реактивной силой , обусловленной изменением массы движущегося тела:

Формула Циолковского[править | править код]

Применив уравнение Мещерского к движению ракеты, на которую не действуют внешние силы, и проинтегрировав уравнение, получим формулу Циолковского^[4]:

Релятивистское обобщение этой формулы имеет вид:

, где  — скорость света.

См. также[править | править код]

• Тяга (авиация)
• Ракетный двигатель
• Ракета
• Парадокс силы тяги реактивного двигателя

Примечания[править | править код]

Ссылки[править | править код]

• Реактивное движение
• Реактивное движение

Разработка проекта действующей модели ракеты тесно связана с вопросом о двигателе. Какой двигатель лучше поставить на модель? Какие из его характеристик являются главными? В чем их сущность? Разбираться в этих вопросах моделисту необходимо.

В этой главе по возможности элементарно рассказывается о характеристиках двигателя, т. е. тех факторах, которые определяют его особенности. Ясное представление о значении тяги двигателя, времени его работы, суммарном и удельном импульсе и их влиянии на качество полета модели ракеты поможет модели-сту-конструктору правильно выбрать двигатель для модели ракеты, а значит, обеспечит успех в соревнованиях.

Основными характеристиками ракетного двигателя являются:

• 1. Тяга двигателя Р (кг)
• 2. Время работы t (сек)
• 3. Удельная тяга Р_уд (кг·сек/кг)
• 4. Суммарный (общий) импульс J_∑ (10 н·сек ≈ 1 кг·сек)
• 5. Вес топлива G_T (кг)
• 6. Секундный расход топлива ω (кг)
• 7. Скорость истечения газов W (м/сек)
• 8. Вес двигателя G_дв (кг)
• 9. Размеры двигателя l, d (мм)

1. Тяга двигателя

Рассмотрим схему возникновения тяги в ракетном двигателе.

В процессе работы двигателя в камере сгорания непрерывно образуются газы, являющиеся продуктами сгорания топлива. Допустим, что камера, в которой находятся под давлением газы, представляет собой замкнутый сосуд (рис. 11, а), тогда легко понять, что никакой тяги в этой камере возникнуть не может, так как давление распределяется одинаково по всей внутренней поверхности замкнутого сосуда и все силы давления взаимно уравновешены.

В случае же открытого сопла (рис. 11, б) газы, находящиеся в камере сгорания под давлением, устремляются с большой скоростью через сопло. При этом часть камеры напротив сопла оказывается неуравновешенной. Силы давления, действующие на ту часть площади дна камеры, которая находится против отверстия сопла, тоже неуравновешены, в результате чего и возникает тяга.

Если рассматривать только поступательное движение газов вдоль камеры сгорания и сопла, то распределение скорости газов на этом пути можно охарактеризовать кривой (рис. 12, а). Давление на элементы поверхности камеры и сопла распределяются так, как показано на рис. 12, б.

Величина нескомпенсированной площади дна камеры сгорания равна площади наименьшего сечения сопла. Очевидно, чем больше площадь этого сечения, тем большее количество газов сможет покинуть камеру сгорания в единицу времени.

Таким образом, можно сделать вывод: тяга двигателя зависит от количества газов, покидающих камеру сгорания в единицу времени в результате нескомпенсированной площади и скорости истечения газов, обусловленной неуравновешенностью давлений.

Для получения количественной зависимости рассмотрим изменение количества движения газов при их истечении из камеры сгорания. Допустим, что в течение времени t камеру сгорания двигателя покидает некоторое количество газа, массу которого обозначим т. Если предположить, что поступательная скорость газов в камере сгорания равна нулю, а на выходе из сопла достигает значения W м/сек, то изменение скорости газа будет равно W м/сек. В этом случае изменение количества движения упомянутой массы газа запишется в виде равенства:

Однако изменение количества движения газов может произойти только в том случае, если на газ будет действовать некоторая сила Р на протяжении некоторого времени t, тогда

где J_∑=P·t — импульс силы, действующий на газ.

Заменив в формуле (1) значение ΔQ на равное J_∑=P·t, получим:

отсюда

Мы получили выражение силы, с которой стенки камеры сгорания и сопла действуют на газ, вызывая изменение его скорости от 0 до W м/сек.

В соответствии с законами механики сила, с которой стенки камеры и сопла действуют на газ, равна по величине силе Р, с которой в свою очередь газ действует на стенки камеры и сопла. Эта сила Р и есть тяга двигателя.

Известно, что масса любого тела связана с его весом (в данном случае с весом топлива в двигателе) соотношением:

где G_T — вес топлива;

g — ускорение силы земного тяготения.

Подставив в формулу (5) вместо массы газа m ее аналогичное значение из формулы (6), получим:

Величина G_T/t представляет собой весовое количество топлива (газа), покидающего камеру сгорания двигателя за единицу времени (1 сек). Эту величину называют весовым секундным расходом и обозначают ω. Тогда

Итак, мы вывели формулу тяги двигателя. Необходимо заметить, что такой вид формула может иметь лишь в том случае, когда давление газа в момент прохождения его через выходной срез сопла равно окружающему давлению. В противном случае в правую часть формулы добавляется еще один член:

где f — площадь выходного сечения сопла (см²);

р_к — давление газа в выходном сечении сопла (кг/см²);

р_о — окружающее (атмосферное) давление (кг/см²).

Таким образом, окончательно формула тяги ракетного двигателя имеет вид:

Первый член правой части ω/g·W носит название динамической составляющей тяги, а второй f(р_к—р_о) — статической составляющей. Последняя составляет около 15% от общей тяги, поэтому для простоты изложения в расчет приниматься не будет.

Для расчета тяги можно использовать формулу, имеющую аналогичное значение с формулой (5), при Р=const:

где Р_ср — средняя тяга двигателя (кг);

J_∑ — суммарный импульс двигателя (кг·сек);

t — время действия двигателя (сек).

При постоянном значении тяги часто используется формула

где Р_уд — удельная тяга двигателя (кг·сек/кг);

Υ — удельный вес топлива (г/см³);

U — скорость горения топлива (см/сек);

F — площадь горения (см²);

Р — тяга двигателя (кг).

В случаях непостоянной тяги, например при определении начальной, максимальной, средней тяги и тяги в любой момент времени действия двигателя, в эту формулу необходимо вводить истинные значения U и F данного двигателя.

Итак, тяга является произведением эффективной скорости истечения газов W на массовый секундный расход топлива ω/g.

Задача 1. Определить тягу ракетного двигателя типа ДБ-З-СМ-10, имея следующие данные: Р_уд=45,5 кг·сек/кг; G_T=0,022 кг; t=4 сек.

Решение. Эффективная скорость истечения газов из сопла:

Секундный расход топлива:

Тяга двигателя:

Примечание. Для двигателя ДБ-З-СМ-10 — это средняя тяга.

Задача 2. Определить тягу ракетного двигателя типа ДБ-З-СМ-10, имея следующие данные: 1 кг·сек; G_T=0,022 кг; t=4 сек.

Решение. Используем формулу (11):

2. Скорость истечения газов

Скорость истечения газов из сопла двигателя, так же как и секундный расход топлива, имеет непосредственное влияние на величину тяги. Тяга двигателя, как усматривается из формулы (8), прямо пропорциональна скорости истечения газов. Таким образом, скорость истечения является важнейшим параметром ракетного двигателя.

Скорость истечения газов зависит от разных факторов. Важнейшим параметром, характеризующим состояние газов в камере сгорания, является температура (Т°К). Скорость истечения прямо пропорциональна квадратному корню из температуры газов в камере. Температура в свою очередь зависит от количества тепла, выделяемого при сгорании топлива. Таким образом, скорость истечения зависит прежде всего от качества топлива, его энергетического ресурса.

3. Удельная тяга и удельный импульс

Совершенство двигателя и эффективность его работы характеризуются удельной тягой. Удельной тягой называют отношение силы тяги к секундно-весовому расходу топлива.

Размерность удельной тяги будет (кг силы·сек/кг расхода) или кг·сек/кг. В зарубежной печати размерность Руд часто записывают в виде (сек). Но физический смысл значения при такой размерности теряется.

Современные модельные РДТТ имеют низкие значения удельной тяги: от 28 до 50 кг·сек/кг. Имеются и новые двигатели с удельной тягой 160 кг·сек/кг и выше, с нижним пределом давления не выше 3 кг/см² и сравнительно высоким удельным весом топлива — более 2 г/см³.

Удельная тяга показывает эффективность использования одного килограмма топлива в данном двигателе. Чем выше удельная тяга двигателя, тем меньше топлива затрачивается для получения одного и того же суммарного импульса двигателя. Значит, при одинаковом весе топлива и размерах двигателей предпочтительнее будет тот, у которого удельная тяга выше.

Задача 3. Определить вес топлива в каждом из четырех двигателей с суммарным импульсом 1 кг·сек, но с разными удельными тягами: а) Р_уд=28 кг-сек/кг; б) Р_уд=45,5 кг·сек/кг; в) Р_уд=70 кг·сек/кг; г) Р_уд=160 кг·сек/кг.

Решение. Вес топлива определим из формулы:

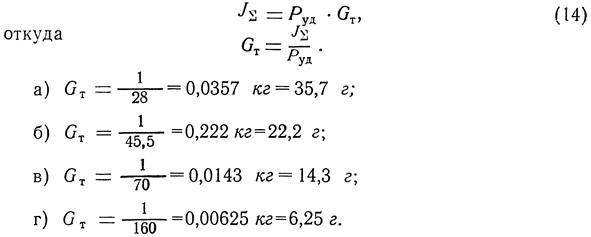
Полученные результаты наглядно показывают, что для моделей ракет выгоднее применять двигатели с более высокой удельной тягой (с целью уменьшения стартового веса модели).

Под удельным импульсом J_уд понимают отношение полного импульса тяги за время t работы двигателя к весу израсходованного за это время топлива G_T.

При постоянной тяге, т. е. при постоянном давлении в камере сгорания и работе двигателя на земле, J_уд=Р_уд.

4. Расчет характеристик двигателя ДБ-1-СМ-6

Для расчета двигателей применяется коэффициент, характерный для данного топлива и определяющий оптимальный режим в камере сгорания:

где К — постоянный коэффициент для данного топлива;

F_макс — максимальная площадь горения в камере сгорания;

f_кр — критическое сечение сопла.

Задача 4. Подсчитать основные характеристики двигателя ДБ-1-СМ-6, у которого корпусом является бумажная охотничья гильза 12-го калибра. Топливом служит смесь № 1 (селитра калиевая — 75, сера — 12 и древесный уголь — 26 частей). Плотность прессования (удельный вес топлива) γ=1,3—1,35 г/см², Р_уд=30 кг·сек/кг, К=100. Задаемся максимальным давлением в камере сгорания в пределах 8 кг/см². Скорость горения данного топлива в зависимости от давления при нормальной температуре окружающей среды представлена на графике рис. 13.

Решение. Прежде всего необходимо вычертить корпус двигателя, т. е. гильзу 12-го калибра (Жевело), что дает возможность наглядно проследить за ходом расчетов (рис. 14). Корпус двигателя (гильза) имеет уже готовое сопло (отверстие для пистона Жевело). Диаметр отверстия 5,5 мм, длина гильзы 70 мм, ее внутренний диаметр 18,5 мм, внешний — 20,5 мм, длина сопла 9 мм. Топливная шашка двигателя должна иметь свободное пространство — продольный канал, благодаря которому имеется возможность довести площадь горения топлива в двигателе до максимальной величины. Форма канала — усеченный конус, нижнее основание которого соответствует размеру отверстия в гильзе (5,5 мм), а при калибровке может быть равным 6 мм. Диаметр верхнего основания — 4 мм. Верхнее основание делается несколько меньше из-за технологических соображений и техники безопасности при удалении металлического конуса из пороховой массы. Для определения длины конуса (стержня) необходимы исходные данные, которые получают в следующем порядке.

Используя формулу (15), определяют возможную максимальную площадь горения:

Максимальная площадь горения топлива (рис. 15) образуется в результате выгорания топлива по каналу радиально до внутренней стенки камеры сгорания (гильзы) и вперед на толщину свода топливной шашки до ее полной длины h, т. е.

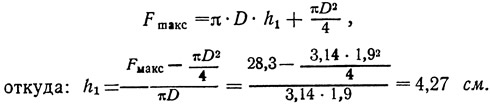
Внутренний диаметр гильзы 18,5 мм, однако надо помнить, что в процессе прессования топлива гильза несколько деформируется, ее диаметр увеличивается до 19 мм (1,9 см), высота цоколя уменьшается до 7 мм. Толщину свода топлива находим из выражения:

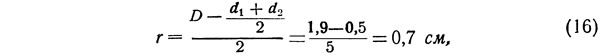
где г — средняя толщина свода топлива (см);

d₁ — диаметр канала у сопла (см);

d₂ — диаметр канала в конце (см).

Длина канала l=h₁—r=4,27—0,7=3,57 см. Полученные размеры сразу же нанесем на чертеж (рис. 15). Длина стержня для запрессовки: 3,57+0,7=4,27 см (0,7 см — высота цоколя гильзы).

Перейдем к определению высоты маршевой части топливной шашки. Эта часть топливной шашки не имеет канала, т. е. запрессована всплошную. Назначение ее в том, чтобы после достижения наибольшего значения тяги получить маршевый участок желательно с постоянной тягой. Высота маршевой части шашки должна быть строго определенной. Горение маршевой части ракетного топлива протекает в двигателе с незначительным давлением 0,07—0,02 кг/см². Исходя из этого, по графику рис. 13 определяем скорость горения маршевой части топлива: U=0,9 см/сек.

Высота маршевой части h₂ для времени горения t=1,58 сек. составит:

Полная длина камеры сгорания h слагается из полной длины топливной шашки h₁ и длины маршевой части h₂:

Перейдем к определению веса топлива.

Для этого подсчитаем объем камеры сгорания и объем свободного пространства. Разница этих объемов даст объем топлива. Зная удельный вес топлива, определим его полный вес.

Объем камеры сгорания:

Объем свободного пространства:

Объем топлива:

Вес топлива:

По формуле (12) подсчитаем начальную и максимальную тягу двигателя:

где F_нач — площадь свободного пространства.

Начальная тяга практически будет несколько меньше из-за небольшого начального давления в камере сгорания, а следовательно, и скорости горения. В данном случае значение для G=0,9 м/сек намеренно сохраняется, чтобы пока не усложнять расчет.

Скорость горения топлива U=2 см/сек определена по графику рис. 13. Эта скорость соответствует давлению в камере сгорания 8 кг/см2, которое дано по условиям задачи.

Время работы двигателя t слагается из основного времени t₁ и дополнительного времени t₂ (маршевого):

По формуле (14) найдем суммарный импульс ракетного двигателя:

По формуле (11) подсчитаем среднюю тягу двигателя:

Приближенное значение максимального давления в камере сгорания найдем по формуле

Узнав примерное максимальное давление в камере сгорания, необходимо проверить прочность стенки гильзы, чтобы определить надежность камеры сгорания. Нужно обеспечить также некоторый запас прочности на случай повышения давления в очень жаркие дни, когда скорость горения топлива увеличивается против расчетной. Возьмем запас прочности — 2, обозначим его через n.

Толщину стенки гильзы определяют по формуле

где δ — толщина стенки гильзы (см);

Р_макс — максимальное давление в камере сгорания (кг/см²);

D — внутренний диаметр гильзы (см);

n — коэффициент запаса прочности;

σ_в — временное сопротивление данного материала (кг/см²).

Временное сопротивление бумаги, из которой изготовлена папковая гильза 12-го калибра, в среднем равно 490 кг/см². Такое сопротивление имеют также хорошие сорта крафт-бумаги.

Подставив данные в формулу (18), получим:

Папковая гильза с наружным диаметром 20,5 мм и внутренним после запрессовки топлива 19 мм имеет толщину стенки:

Фактический запас прочности n_факт=2,4, т. е. выше расчетного.

Днище у модельных двигателей данного типа круглое с двумя отверстиями диаметром 2 мм. Впрессовывают его одновременно с топливом. Делается оно из прочных сортов картона, толщиной не менее 2 мм.

Эта формула позволяет определить величину тяги реактивного двигателя любого типа. Формула получается на основе закона механики (следствие второго закона Ньютона), по которому изменение количества движения тела равно действующей на него силе (в единицу времени).

Для ракетного двигателя

R = M·C

где R — сила тяги в кг;

М — масса газов, вытекших из двигателя за секунду (масса равна секундному весовому количеству газов, деленному на ускорение земного тяготения, то есть где G_сек — в кг/сек

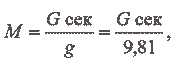
С — скорость истечения газов в м/сек.

Для воздушно-реактивных двигателей формула для тяги иная, так как изменение скорости воздуха, проходящего через двигатель, равно

C–V,

где V — скорость полета; добавкой топлива к воздуху обычно пренебрегают, так как она относительно невелика. Поэтому в случае воздушно-реактивного двигателя

R = М (С — V)

Примеры использования формул

1. В пороховой ракете сгорает 1 кг пороха в секунду. Газы вытекают со скоростью 1200 м/сек. Какую тягу развивает двигатель?

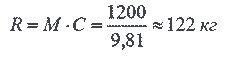
2. На реактивном истребителе установлен турбореактивный двигатель, через который в полете со скоростью 1440 км/час протекает 120 кг воздуха в секунду. С какой скоростью вытекают при этом газы из двигателя, если его тяга равна 6 т?

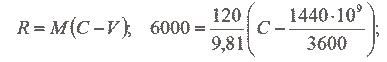
С ? 900 м/сек.