Сила тяги, теория и онлайн калькуляторы
Сила тяги
Понятие сила тяги
Определение
Понятие «сила тяги» часто встречается в задачах по физике, когда речь идеи о механической мощности или движении транспорта.
Вообще говоря, это гипотетическая сила, которая вводится для удобства при решении задач.
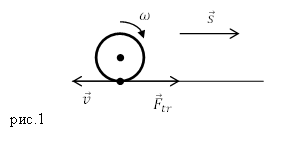
Поясним эту мысль. Рассмотрим движение автобуса. Сила тяги (обозначим ее как ${overline{F}}_t$) в этом случае является силой трения покоя, которая действует на нижние точки колес со стороны поверхности шоссе. Для реализации движения автобуса по дороге колеса транспортного средства вращает двигатель так, чтобы сила трения была направлена в сторону перемещения (рис.1). В этом случае силу тяги определим как силу трения, которая возникает между ведущими колесами и поверхностью, по которой колеса катятся. Если сила трения отсутствует (колесо находится на льду), то автобус не двигается с места, так как колеса проскальзывают. Трение, которое появляется между колесами и поверхностью дороги создает поступательное перемещение.
Так как сила тяги зависит от силы трения, то для увеличения величины $F_t $ следует увеличить трение. Трение увеличивается при росте коэффициента трения и (или) с увеличением силы нормального давления, которое зависит от массы тела.
Возникает вопрос о необходимости введения некоей силы тяги вместо того, чтобы использовать привычную силу трения. При выделении из внешних сил, которые действуют на наш автобус силы тяги и силы сопротивления движению уравнения движения имеют универсальный вид, и, используя силу тяги, просто выражается полезная механическая мощность ($N$):
[N={overline{F}}_tcdot overline{v}left(1right),]
где $overline{v}$ – скорость движения тела (у нас автобуса).
Отметим, что у силы тяги нет четко определенной формулы, как, например, у гравитационной силы или силы Архимеда и других сил. Ее часто вычисляют, используя второй закон Ньютона и рассматривая все силы, которые действуют на тело.
Реактивная сила тяги
Уравнения движения тел переменной массы и формулу для вычисления реактивной силы получил первым И.В. Мещерский в 1897 г. Формула реактивной силы является основой для расчета силы тяги ракетных и турборакетных двигателей всех систем.
Пусть ракета перемещается со скоростью $overline{v}$ относительно Земли. Вместе с ней с такой же скоростью движется часть топлива, которая сгорает в ближайшую секунду. При сгорании продукты горения этой части топлива получают дополнительную скорость $overline{u}$ относительно ракеты. Относительно Земли они имеют скорость $overline{v}-overline{u}$. При этом сама ракета увеличивает скорость. После выброса продукты горения не взаимодействуют с ракетой. Поэтому систему ракета плюс продукты горения топлива рассматривают как систему из двух тел, которые взаимодействуют при горении по законам неупругого удара. Пусть реактивный двигатель ракеты каждую секунду выбрасывает массу $mu $ продуктов горения топлива. Используя закон сохранения импульса и второй закон Ньютона получают, что модуль реактивной силы тяги двигателя ($R$) ракеты равен:
[R=mu u left(2right).]
Формула (2) показывает, что реактивная сила, которая действует на тело переменной массы, пропорциональна массе отделяющихся частиц за единицу времени и скорости движения этих частиц относительно тела.
Примеры задач с решением
Пример 1
Задание. Сила тяги, действующая на тело, находящееся на наклонной плоскости (рис.2) направлена вдоль этой плоскости вверх (рис.2). Какова ее величина, если масса тела равна $m$, угол наклона плоскости $alpha , $ускорение движения тела $a$? Коэффициент трения тела о плоскость равен $mu $. Тело движется с постоянной скоростью в гору.
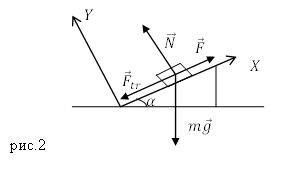
Решение. Запишем второй закон Ньютона для сил, действующих на тело, учтем, что тело движется равномерно:
[moverline{g}+overline{N}+overline{F}+{overline{F}}_{tr}=0left(1.1right).]
Запишем проекции уравнения (1.1) на оси X и Y:
[left{ begin{array}{c}
X: -mg{sin alpha + }F-F_{tr}=0left(1.2right);; \
Y: N-mg{cos alpha =0left(1.3right). } end{array}
right.]
Сила трения связана с силой нормального давления как:
[F_{tr}=mu N left(1.4right).]
Выразим из (1.3) $N$, используем выражение (1.4), получим из (1.2) силу тяги:
[-mg{sin alpha + }F-mu mg{cos alpha }=0to F=mu mg{cos alpha }+mg{sin alpha . }]
Ответ. $F=mg(mu {cos alpha }+{sin alpha ). }$
Пример 2
Задание. Ракету, массой (в начальный момент времени) равной $M,$ запустили вертикально вверх. Относительная скорость выброса продуктов горения равна $u$, расход горючего составляет $mu $. Каким будет ускорение ракеты через время $t$ после старта, если сопротивление воздуха не учитывать, поле силы тяжести считать однородным.
Решение. Сделаем рисунок.
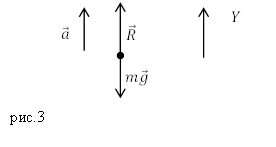
На ракету (из условий задачи) будут действовать две силы: сила тяжести и реактивная сила тяги. Запишем уравнение движения ракеты:
[moverline{g}+overline{R}=moverline{a}left(2.1right).]
В проекции на ось Y уравнение (2.1) запишем как:
[R-mg=ma left(2.2right).]
Реактивная сила тяги может быть найдена как:
[R=mu u left(2.3right).]
Учитывая равенство (2.3) уравнение преобразуем к виду:
[mu u-mg=mato a=frac{mu u-mg}{m}left(2.4right).]
Масса ракеты в момент времени $t$ равна:
[m=M-mu tleft(2.5right).]
Подставим (2.5) в (2.4) имеем:
[a=frac{mu u-left(M-mu tright)g}{M-mu t}=frac{mu u}{M-mu t}-g.]
Ответ. $a=frac{mu u}{M-mu t}-g.$
Читать дальше: скорость.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
При вытягивании объекта с помощью веревки приложенная сила передается через веревку. Тогда мы можем сказать, что веревка находится под действием тягового усилия. Короче говоря, тяга состоит из приложения пары сил к телу в противоположных направлениях.
Индекс содержания:
- Который
- Расчет
- Примеры
- видео
Что такое тяга?
Несмотря на то, что это слово имеет несколько значений, в физике тяга – это тип силы, прикладываемой к телу со смыслом, обращенным к его внешней части. Тяговое усилие заставляет атомы реорганизоваться, так что тело, которое тянут, удлиняется в направлении приложенной силы.
Хотя во многих местах величины напряжения и тяги представлены как синонимы, по строгости определений это не одно и то же. Проще говоря, натяжение в теле – это мера силы, действующей на площадь поперечного сечения веревки, кабеля, цепи или чего-то подобного.
Единица измерения напряжения (в единицах Международной системы) – Н / м² (Ньютон на квадратный метр), что является той же единицей измерения давления. С другой стороны, тяга – это сила, прикладываемая к телу с целью приложения усилий к нему в противоположных направлениях, без учета области, в которой эта сила действует.
расчет тяги
К сожалению, конкретного уравнения для расчета тяги нет. Однако мы должны следовать стратегии, аналогичной той, которая используется в случаях, когда необходимо найти нормальную силу. То есть мы используем уравнение второго закона Ньютона, чтобы найти связь между движением объекта и задействованными силами. Для этого мы можем опираться на следующие процедуры:
- Проанализируйте силы, участвующие в движении, с помощью диаграммы сил;
- Используйте второй закон Ньютона (Fр = ma) и записать его в направлении тянущего усилия;
- Найдите притяжение из второго закона Ньютона.
См. Ниже, как рассчитать тягу в некоторых случаях:
тяга к телу

Рассмотрим любое тело массы m, которое покоится на совершенно гладкой поверхности без трения. Таким образом, следуя описанным выше процедурам, мы получаем, что:
T = среднее
На что,
- Т: тяга (Н);
- м: масса (кг);
- В: ускорение (м / с2).
Это тело тянется за счет силы тяги Т, параллельной поверхности, создаваемой посредством пренебрежимо малого размера и нерастяжимой нити. В этом случае расчет тяги максимально прост. Здесь единственная сила, действующая на систему, – это тянущая сила.
Тяга на наклонной плоскости

Отметим, что PТопор и PАу – соответственно горизонтальная и вертикальная составляющие массы тела А. Также обратите внимание, что для упрощения расчетов мы рассматриваем поверхность наклонной плоскости как горизонтальную ось нашей системы координат.
Теперь предположим, что это же тело массы m расположено на наклонной плоскости, где также нет трения между блоком и поверхностью. Таким образом, тяговое усилие составит:
Т – ПТопор= среднее
На что,
- Т: тяга (Н);
- ДЛЯТопор: горизонтальная составляющая силового веса (Н);
- м: масса (кг);
- В: ускорение (м / с2).
Анализируя рисунок и следуя процедурам, упомянутым выше, можно заметить, что мы можем использовать второй закон Ньютона только в горизонтальном направлении нашей системы координат. Кроме того, существует вычитание между натяжением и горизонтальной составляющей веса блока, потому что две силы имеют противоположные направления.
угол тяги

Рассмотрим тело массы m на поверхности без трения. Объект тянет тянущая сила T, которая не параллельна поверхности. Таким образом, тяговое усилие составит:
Tcosϴ = среднее
На что,
- Tcosϴ: горизонтальная проекция тягового усилия (Н);
- м: масса (кг);
- В: ускорение (м / с2).
Это тело тянется за счет тягового усилия Т, создаваемого посредством нити пренебрежимо малых и нерастяжимых размеров. Этот пример аналогичен случаю приложения силы тяги к телу на поверхности без трения. Однако здесь единственной силой, действующей на систему, является горизонтальная составляющая тянущего усилия. Из-за этого при расчете тяги мы должны учитывать только горизонтальную проекцию тягового усилия.
Тяга на поверхности трения

Рассмотрим любое тело массы m, которое опирается на поверхность с трением. Таким образом, следуя описанным выше процедурам, мы получаем, что:
Т – Ждо = среднее
На что,
- Т: тяга (Н);
- Fдо: сила трения (Н);
- м: масса (кг);
- В: ускорение (м / с2).
Это тело тянется за счет тягового усилия Т, создаваемого посредством нити пренебрежимо малых и нерастяжимых размеров. Кроме того, мы должны учитывать силу трения между блоком и поверхностью, на которой он лежит. Таким образом, стоит отметить, что если система находится в равновесии (то есть, если, несмотря на то, что когда к проволоке прикладывается сила, блок не движется или развивает постоянную скорость), поэтому T – Fдо = 0. Если система находится в движении, то T – Fдо = ма
Тяга между телами одной системы

Обратите внимание, что сила, которую тело a прикладывает к телу b, обозначается Tа, б. Сила, которую тело b прикладывает к телу a, обозначается Tб,.
Теперь предположим, что два (или более) тела соединены кабелями. Они будут двигаться вместе и с одинаковым ускорением. Однако, чтобы определить силу притяжения, которую одно тело оказывает на другое, мы должны рассчитать чистую силу отдельно. Таким образом, следуя описанным выше процедурам, мы получаем, что:
Тб, = мВа (тело а)
Та, б – F = мBа (тело b)
На что,
- Та, б: тяга тела a к телу b (N);
- Тб,: тяга тела b к телу a (N);
- F: сила, приложенная к системе (Н);
- мВ: масса тела а (кг);
- мB: масса тела b (кг);
- В: ускорение (м / с2).
Только один кабель соединяет два тела, поэтому по третьему закону Ньютона сила, которую тело a прикладывает к телу b, имеет ту же силу, что и сила, которую тело b прикладывает к телу a. Однако эти силы имеют противоположное значение.
тянуть маятник

При маятниковом движении траектория, описываемая телами, является круговой. Сила натяжения проволоки действует как компонент центростремительной силы. Таким образом, в самой нижней точке траектории получаем, что:
Т – П = Fcp
На что,
- Т: тяга (Н);
- ДЛЯ: вес (Н);
- Fcp: центростремительная сила (Н).
В самой нижней точке движения маятника сила тяги противостоит весу тела. Таким образом, разница между двумя силами будет равна центростремительной силе, которая эквивалентна произведению массы тела на квадрат его скорости, деленной на радиус траектории.
тянуть проволоку

Если тело подвешено на идеальной проволоке и находится в равновесии, сила тяги будет равна нулю.
Т – Р = 0
На что,
- Т: тяга (Н);
- ДЛЯ: вес (Н).
Это связано с тем, что в соответствии с третьим законом Ньютона натяжение проволоки одинаково на обоих концах. Поскольку тело находится в равновесии, сумма всех действующих на него сил равна нулю.
Примеры тяги в повседневной жизни
Есть простые примеры приложения силы тяги, которые можно наблюдать в нашей повседневной жизни. Смотреть:
Перетягивание каната
Сила тяги прилагается игроками к обеим сторонам веревки. Более того, мы можем связать этот случай с примером тяги между телами одной системы.

Лифт
Трос лифта натягивается на одном конце весом лифта и его людей, а на другом конце – силой, прилагаемой его двигателем. Если лифт остановлен, силы с обеих сторон имеют одинаковую интенсивность. Кроме того, здесь мы можем рассматривать случай, аналогичный примеру с натяжением, прилагаемым к проволоке.

Остаток средств
Игра на качелях очень распространена среди людей всех возрастов. Кроме того, мы можем рассматривать движение этой игрушки как движение маятника и соотносить его со случаем тяги на маятнике.

Как можно было видеть, тяга напрямую связана с нашей повседневной жизнью. Будь то в играх или даже в лифтах.
Видео о тяговых усилиях
Как насчет того, чтобы потратить время на то, чтобы углубиться в предмет, просмотрев предложенные видео?
Простой маятник и конический маятник
Углубите свои знания в области изучения движения маятника!
Эксперимент по силе тяги
Посмотрите на практическое применение тягового усилия.
Решенное упражнение на тягу на телах той же системы
Аналитическое применение концепции тяги к телам той же системы.
Как можно было видеть, концепция тяги очень широко присутствует в нашей повседневной жизни и, хотя ее нет. нет конкретной формулы для его расчета, нет серьезных трудностей при разборе кейсов предложил. Чтобы пройти тест, не опасаясь ошибки, подкрепите свои знания этим содержанием о статический.
использованная литература
m = 4 т = 4000 кг.
g = 10 м/с2.
а = 0,2 м/с2.
∠α = 30°.
μ = 0,04.
Fт – ?
Для движения автомобиля по наклонной плоскости Запишем 2 закон Ньютона в векторной форме: m * a = Fт + m * g + N + Fтр, где Fт – сила тяги двигателя, m * g – сила тяжести, N – сила реакции поверхности наклонной плоскости, Fтр – сила трения.
ОХ: m * a = Fт – Fтр – m * g * sinα.
ОУ: 0 = – m * g * cosα + N.
Fт = m * a + Fтр + m * g * sinα.
N = m * g * cosα.
Силу трения Fтр выразим формулой: Fтр = μ * N = μ * m * g * cosα.
Fт = m * a + μ * m * g * cosα + m * g * sinα = m * (a + μ * g * cosα + g * sinα).
Fт = 4000 кг * (0,2 м/с2 + 0,04 * 10 м/с2 * cos30° + 10 м/с2 * sin30°) = 22185,6 Н.
ответ: сила тяги двигателя автомобиля составляет Fт = 22185,6 Н.
Проецирование сил. Движение по наклонной плоскости

Задачи по динамике.
I и II закон Ньютона.
Ввод и направление осей.
Неколлинеарные силы.
Проецирование сил на оси.
Решение систем уравнений.
Самые типовые задачи по динамике
Начнем с I и II законов Ньютона.
Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых… Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.
I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.
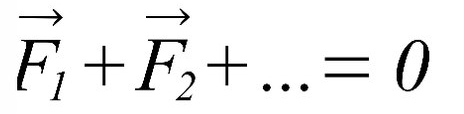
Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.
II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.
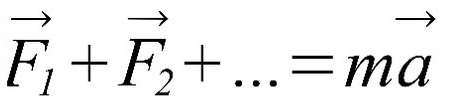
Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.
При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.
Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².
Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:
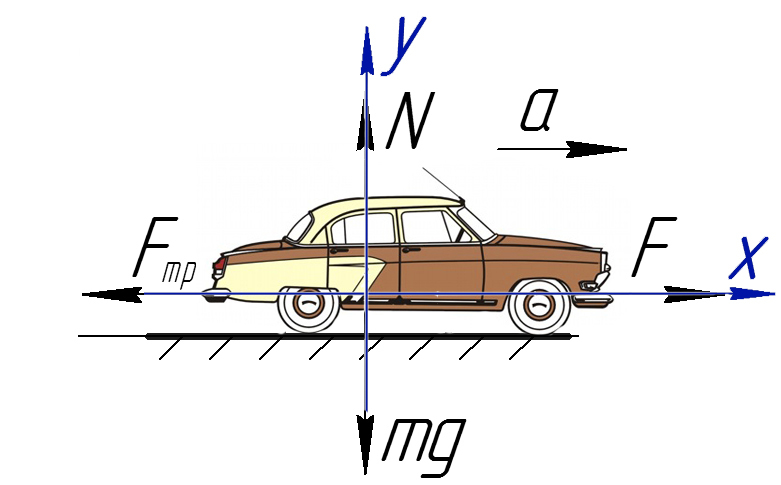
На Ось Х: движение с ускорением
На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)
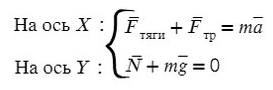
Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.
По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.
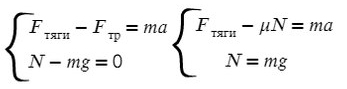
Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.
Получаем, что:
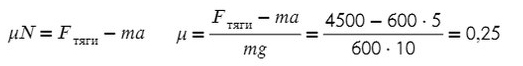
Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.
Ответ: 0,25
Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.
Сделаем рисунок, покажем силы, которые дествуют на груз
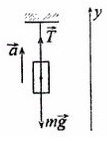
T – сила натяжения нити
На ось X: нет сил
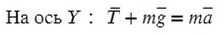
Разберемся с направлением сил на ось Y:
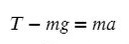
Выразим T (силу натяжения) и подставим числительные значения:
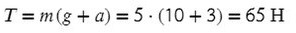
Ответ: 65 Н
Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.
Далеко не всегда все силы, действующие на тело, направлены вдоль осей.
Простой пример: мальчик тянет санки
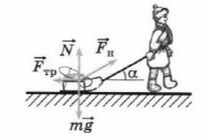
Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.
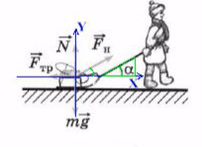 Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.
Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.
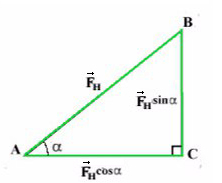
Отношение противолежащего катета к гипотенузе — это синус.
Отношение прилежащего катета к гипотенузе — это косинус.
Сила тяги на ось Y — отрезок (вектор) BC.
Сила тяги на ось X — отрезок (вектор) AC.
Если это непонятно, посмотрите задачу №4.
Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле, ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.
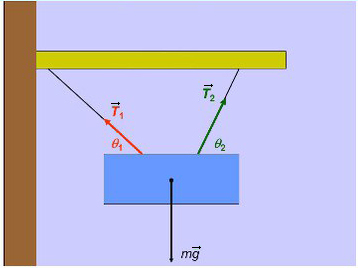
Введем оси и спроецируем силы:
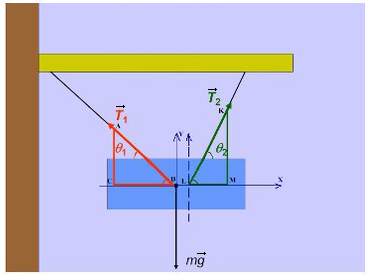
Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.
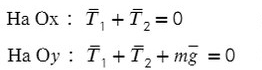
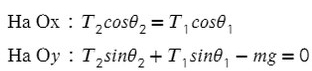
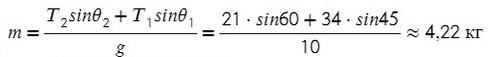
Ответ: 4,22 кг
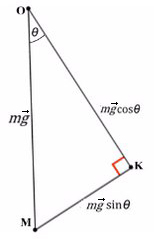
Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?
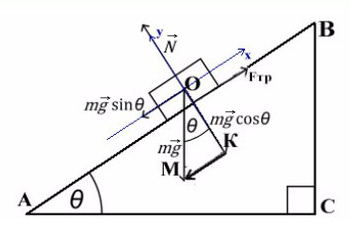
Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).
Рассмотрим поподробнее ΔKOM:
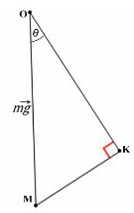
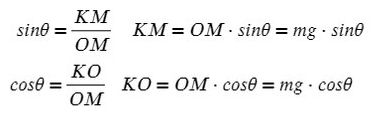 Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).
Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).
Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!
Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:
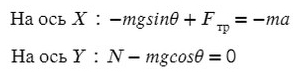
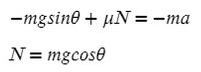
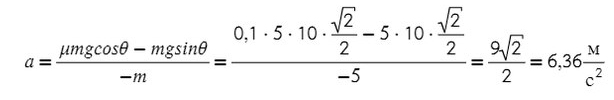
Ответ: 6,36 м/с²
Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.
Сделаем рисунок с силами:
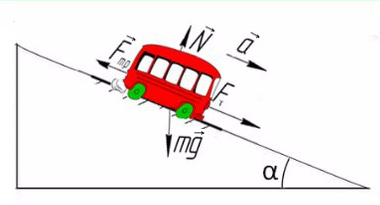
Введем оси X и Y. Спроецируем mg на оси:
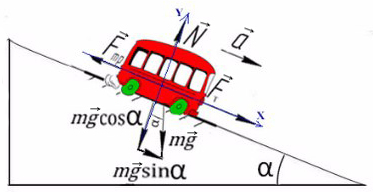
Запишем второй закон Ньютона на X и Y:
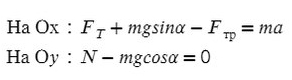
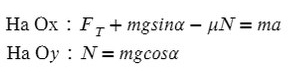

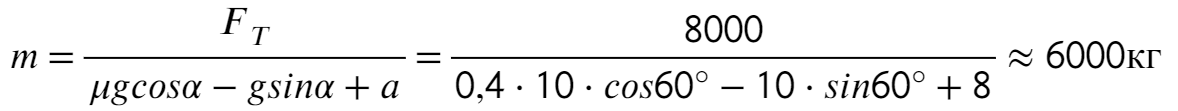
Ответ: 6000 кг
Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.
Самое сложное – понять, какие силы куда действуют, и как угол влияет на них.
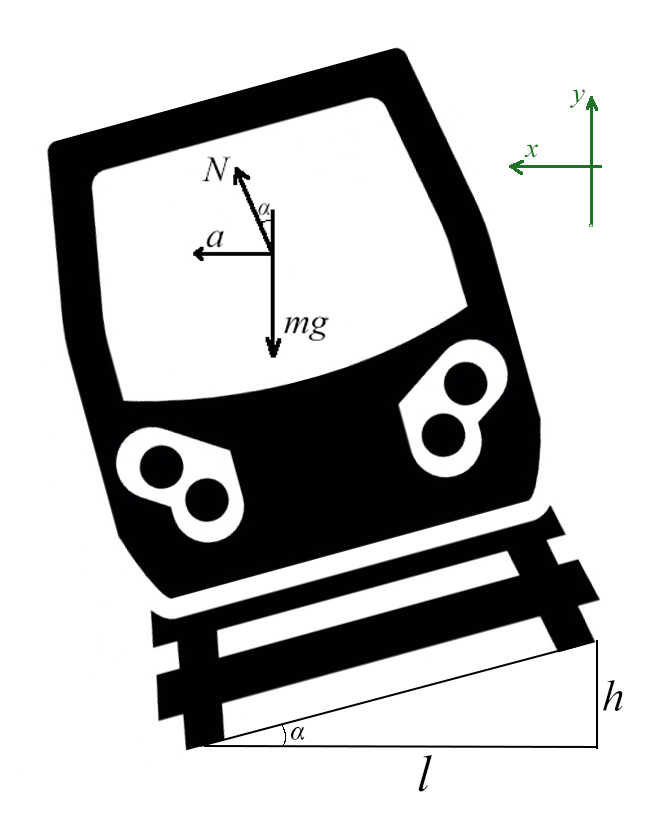
Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!
Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)
Запишем какие силы действуют на оси:
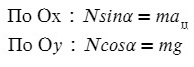
Ускорение в данной задачи центростремительное!
Поделим одно уравнение на другое:
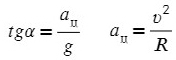
Тангенс – это отношение противолежащего катета к прилежащему:
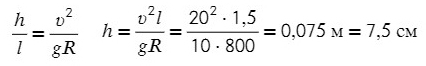
Ответ: 7,5 см
Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.
В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.
Будь в курсе новых статеек, видео и легкого технического юмора.
Как найти силу тяги
Силу тяги, приводящей тело в движение, вы найдете, рассчитав векторную сумму всех сил, действующих на тело. При равномерном движении по горизонтальной поверхности сила тяги компенсирует силы сопротивления движению. В случае если тело движется по наклонной плоскости, ему приходится преодолевать еще и силу тяжести – при расчетах учитывайте это.

Вам понадобится
- динамометр, весы, таблица коэффициентов трения, акселерометр.
Инструкция
Непосредственное измерение силы тяги Положите тело на поверхность, по которой вы будете его перемещать. Прикрепите к нему динамометр и начните двигать с постоянной скоростью, снимите показания динамометра в ньютонах – это и будет значение силы тяги.
Измерение силы тяги, действующей на прямолинейно движущееся телоВ том случае, если тело движется по горизонтальному участку пути, узнайте материалы, из которых сделано тело и поверхность. В таблице коэффициентов трения для разных материалов, подберите нужную комбинацию и соответствующий ей коэффициент. С помощью весов или любым другим способом измерьте массу двигающегося тела. Измерьте ускорение, с которым движется тело акселерометром или рассчитайте его, если известны скорости в начале и конце пути и его длина или время прохождения. Для того чтобы найти силу тяги, умножьте коэффициент трения на 9,81 (ускорение свободного падения), прибавьте к результату значение ускорения, а получившееся число умножьте на массу тела (F=m•(μ•9,81+a)). Если тело движется равномерно, ускорение будет равно нулю.
В том случае, если тело движется по наклонной плоскости, измерьте угол ее наклона. Чтобы найти силу тяги в случае, когда тело поднимается по ней, умножите коэффициент трения на 9,81 и косинус угла наклона плоскости к горизонту, к этому числу прибавьте произведение 9,81 на синус этого угла, к полученному результату прибавьте ускорение. Полученное число умножьте на массу тела, которую нужно измерить заранее F=m•(μ•9,81•Cos(α)+9,81•Sin(α)+a). При свободном падении тела роль силы тяги выполняет сила тяжести. Для того чтобы найти ее, нужно массу тела умножить на ускорение свободного падения (9,81): F=m•9,81.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
