Основы динамики автомобиля
Скоростная характеристика двигателя
Скоростная характеристика двигателя определяется зависимостями эффективной мощности Ne и крутящего момента Mк от частоты вращения n коленчатого вала.
Ведущие колеса автомобиля приводят его в движение в результате возникновения силы тяги, которая возникает при приложении крутящего момента к полуосям ведущих колес со стороны трансмиссии:
Pт = Mт/r, (1)
где Pт – сила тяги, Н;
Mт – крутящий (тяговый) момент на ведущем колесе, Нм;
r – радиус колеса, м.
Крутящий момент на ведущих колесах зависит от величины момента, развиваемого двигателем на коленчатом валу, передаточного числа iтр трансмиссии и ее КПД – ηтр:
Мт = Мкiтрηтр. (2)
Сила тяги Pт на ведущих колесах может быть определена не только по формуле (1), но и с учетом скорости vi движения автомобиля на i-й передаче и развиваемой двигателем эффективной мощности Nе:
Pт = 3600Nеηтр/vi. (3)
Скорость vi движения автомобиля на i-й передаче пропорциональна частоте n вращения коленчатого вала, радиусу r ведущего колеса и обратно пропорциональна передаточному числу iтрi трансмиссии на i-й передаче:
vi = 0,377nr/iтрi. (4)
Таким образом, частота вращения n коленчатого вала является определяющим параметром для показателей эффективной мощности Nе, крутящего момента Mк и силы тяги на ведущих колесах Pт.
На рисунке 1 приведена внешняя скоростная характеристика двигателя при полностью открытой дроссельной заслонке, которая определяет предельные возможности двигателя при значениях частоты вращения коленчатого вала от nmin до nmax.
Анализ графика показывает, что максимальная эффективная мощность и максимальный крутящий момент, развиваемый двигателем, доступен в узком интервале частот вращения коленчатого вала. При небольшой частоте вращения коленчатого вала величина этих динамических показателей недостаточна для появления на ведущих колесах требуемой для движения автомобиля силы тяги, а при превышении частотой вращения коленвала некоторого максимального порога двигатель начинает терять мощность и тяговые показатели, или, как говорят механики, начинает работать «вразнос».
По этой причине эффективная эксплуатация двигателя внутреннего сгорания возможна лишь в некотором узком диапазоне частот вращения коленчатого вала.
Скоростная характеристика двигателя во многом зависит от типа двигателя: чем круче кривая эффективной мощности Nе, тем большей приемистостью обладает двигатель.
***
Тяговая характеристика автомобиля
Тягово-скоростные свойства автомобиля удобно оценивать с помощью тяговой характеристики, т. е. зависимостью силы тяги на ведущих колесах от скорости движения на различных передачах (рис. 2).
Используя скоростную характеристику и задавая частоты вращения коленчатого вала от nmin до nmax при соответствующих значениях эффективной мощности или крутящего момента для каждой передачи по формуле (4) находят значения скорости v, а по формуле (3) находят значение тяговой силы Pт.
Число кривых на тяговой характеристике (рис. 2) соответствует числу ступеней в коробке передач.
Тяговая характеристика позволяет быстро определить максимальное значение силы тяги на ведущих колесах, которая может быть обеспечена при данной скорости движения автомобиля, поскольку она рассчитывается по наибольшей для данной частоты вращения коленчатого вала мощности двигателя. Меньшее значение силы тяги получается при недоиспользовании мощности двигателя, т. е. при неполной подаче топлива. Следовательно, с помощью тяговой характеристики можно оценить предельные тяговые возможности автомобиля в фактическом интервале скоростей его движения.
***
Силы и моменты, действующие на ведущие колеса
На ведущие колеса автомобиля действуют силы со стороны автомобиля (т. е. со стороны двигателя посредством агрегатов трансмиссии), а также силы со стороны дороги. Обозначим силы, действующие со стороны автомобиля, буквой Р, а со стороны дороги – буквой R (рис. 3).
***
Реактивные силы, действующие на колеса
Тяговый момент Мт на ведущих колесах стремится сдвинуть назад верхний слой дорожного покрытия, в результате чего со стороны дороги на ведущее колесо в зоне контакта действует противоположно направленная сила Rx – горизонтально направленная касательная реакция дороги.
Так как на автомобиле используются эластичные пневматические шины, то неизбежна частичная потеря момента Мт, поэтому продольную (горизонтальную) реакцию со стороны дороги, обеспечивающую качение колеса, можно записать как разность между силой тяги и потерями в шине:
Rx = Рт – Рш,
где Рш – сила, учитывающая потери энергии в шинах ведущих колес.
Таким образом, касательная реакция дороги создает силу тяги.
Автомобиль своим весом G действует на каждое колесо, передавая усилие на дорогу, и, соответственно, вызывая нормальную реакцию дороги Rz. Следует учитывать, что при наличии на колесе крутящего момента нормальная реакция Rz прикладывается не к оси симметрии опорной площадки колеса, а на некотором расстоянии αш от нее, поскольку имеет место смещение центра давления из-за эластичности шины.
Эпюра элементарных нормальных реакций дороги, показанная на рисунке 4, объясняет причину смещения точки приложения реакции Rz. Это происходит из-за того, что нормальные реакции на переднем и заднем участках опорной площадки колеса различны по величине, так как силы, возникающие в упругом материале шины при приложении и снятии нагрузки неодинаковы.
Это объясняется действием сил внутреннего трения между взаимно перемещающимися частицами материала шины. При приложении нагрузки эти силы и силы упругости направлены в одну и ту же сторону, а при снятии – в противоположные стороны.
Боковая сила Рy значительно увеличивается при криволинейном движении автомобиля или при движении по косогору. Боковая реакция Ry со стороны дороги удерживает колеса автомобиля от бокового скольжения (заноса) при движении автомобиля поперек косогора или при выполнении маневра.
***
Сила тяги на ведущих колесах
Сила тяги Рт на ведущих колесах может быть определена, как отношение крутящего (тягового) момента Mт, подводимого к колесам, к их радиусу r:
Pт = Mт/r.
При этом не учитываются затраты энергии на деформацию дорожного покрытия, трение внутри шины и силы инерции, обусловленные ускорением вращающихся масс колес и деталей трансмиссии в случае неравномерного движения.
Следует учитывать, что радиус колеса вследствие эластичности шины является переменной величиной.
Различают следующие радиусы автомобильных колес:
- статический радиус колеса rст – расстояние от поверхности дороги до оси неподвижного колеса, воспринимающего вертикальную нагрузку, обусловленную силой тяжести, действующей на автомобиль (т. е. его весом G). Значения статического радиуса приводятся заводом-изготовителем шины в технических характеристиках;
- динамический радиус колеса rд – расстояние от поверхности дороги до оси катящегося колеса. Динамический радиус колеса во время движения может превышать его статический радиус, поскольку в результате нагрева шины давление внутри нее увеличивается.
Кроме того, под действием центробежных сил с возрастанием скорости автомобиля шина растягивается в радиальном направлении, вследствие чего динамический радиус увеличивается. Динамический радиус, также, зависит от величины вертикальной нагрузки Pz. - радиус качения колеса rк – радиус условного недеформирующегося катящегося без скольжения колеса, которое имеет с данным эластичным колесом одинаковую угловую и линейную скорости.
Радиус качения колеса определяется по формуле:
rк = S/(2πnк),
где S – путь, пройденный колесом; nк – число оборотов колеса на пути S.
Если проскальзывание колеса относительно дороги отсутствует, что характерно для ведомого колеса, то радиусы rд и rк почти равны между собой. В случае полного буксования колеса его пройденный путь будет равен нулю, и тогда (согласно приведенной выше формуле) его радиус качения тоже будет равен нулю.
В случае движения колеса юзом (скольжение без вращения) число оборотов будет равно нулю, и, соответственно, радиус качения rк будет стремиться к бесконечности.
Различают еще и свободный радиус колеса rсв, который является половиной диаметра ненагруженного колеса при отсутствии его контакта с опорной поверхностью.
На дорогах с сухим покрытием скольжение ведущих колес и изменение радиуса незначительны. Поэтому радиусы статический rст, динамический rд и качения rк при расчетах считаются одинаковыми и обозначаются буквой r.
***
Силы, действующие на автомобиль
Тяговая
характеристика автомобиля представляет
собой зависимость между силой тяги ()
и скоростью(,
км/ч) движения автомобиля.
Силу
тяги(,
Н) на ведущих колесах автомобиля
рассчитывают по формуле:
(2.4)
где:–
крутящий момент двигателя, Н·м;
–
передаточное число коробки передач;
–
передаточное число главной передачи;
–
радиус качания колеса, м;
–
к.п.д. трансмиссии, которое принимаем
0,8
Входящий
в формулу (2.4) крутящий момент ()
берут из таблицы 2.1. Он зависит от частоты
вращения ()коленчатого
вала двигателя. Скорость движения
автомобиля ()
определяют по формуле:
км/ч.
(2.5)
Радиус
()
качения колеса, входящий в формулы
(2.4), (2.5), приближенно определяется по
формуле:
мм
(2.6)
где:
d
– внутренний диаметр шины (диаметр обода
колеса), м;
Н–
высота профиля шины в свободном состоянии,
м;
λШ
–
коэффициент нормальной деформации
шины.
Для
шин дорожной проходимости коэффициент
(λШ)
принимаем равным 0,11.
rK=+132(1-
0.11)=295,3
мм
Таблица
2.2.
Расчет тяговой
характеристики автомобиля
|
№ |
ne, мин-1 |
MeN Нм |
Передача |
|||||||||
|
I |
I I |
I I I |
IV |
V |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
540 |
102 |
4 |
4,31 |
7 |
2,67 |
10 |
1,78 |
15 |
1,23 |
20 |
0,95 |
|
2 |
1080 |
112 |
9 |
4,75 |
14 |
2,94 |
21 |
1,96 |
30 |
1,36 |
39 |
1,05 |
|
3 |
1620 |
120 |
13 |
5,09 |
21 |
3,16 |
31 |
2,11 |
45 |
1,46 |
59 |
1,13 |
|
4 |
2160 |
126 |
17 |
5,34 |
28 |
3,31 |
42 |
2,21 |
61 |
1,53 |
78 |
1,18 |
|
5 |
2700 |
129 |
22 |
5,48 |
35 |
3,40 |
52 |
2,26 |
76 |
1,57 |
98 |
1,21 |
|
6 |
3240 |
130 |
26 |
5,52 |
42 |
3,42 |
63 |
2,28 |
91 |
1,58 |
117 |
1,22 |
|
7 |
3780 |
129 |
30 |
5,47 |
49 |
3,39 |
73 |
2,26 |
106 |
1,56 |
137 |
1,21 |
|
8 |
4320 |
125 |
35 |
5,31 |
56 |
3,29 |
84 |
2,19 |
121 |
1,52 |
156 |
1,17 |
|
9 |
4860 |
119 |
39 |
5,05 |
63 |
3,13 |
94 |
2,09 |
136 |
1,44 |
176 |
1,12 |
|
10 |
5400 |
111 |
43 |
4,69 |
70 |
2,91 |
105 |
1,94 |
151 |
1,34 |
195 |
1,04 |

()
и сила тяги ()
при движении на любой другойi-и
передаче можно определить по соотношениям
:

:
-скорость
автомобиля на прямой передаче при
заданном
км/ч;
–
сила тяги на прямой передаче, кН;
–
передаточное число коробки передач на
i-й
передаче.
Суммарная
сила сопротивления дороги ()определяется
по формуле:
(2.7)
где:
ψ
–
коэффициент суммарного сопротивления
дороги;
–
полный вес автомобиля, кН.
Коэффициент
суммарного сопротивления дороги
рассчитывается так:
(2.8)
где:
f
–
коэффициент сопротивления качения;
–
угол подъема дороги.
При
расчете тягового баланса принимаем,
что автомобиль движется по горизонтальной
дороге (=0)
с асфальтобетонным покрытием. Тогда
коэффициент (ψ)
суммарного сопротивления дороги (2.8)
равен коэффициенту (f)
сопротивления качению.
При
скоростях движения автомобиля, превышающих
60-80 км/ч коэффициент (f)надо
определять по эмпирической формуле:
(2.9)
где:
– коэффициент сопротивления качению,
относящийся к малым скоростям движения
автомобиля;
–
скорость движения автомобиля, км/ч.
Cила,
суммарного сопротивления дороги в этих
условиях такова:
(2.10)

дорог с асфальтобетонным покрытием,
находящихся в хорошем состоянии,
коэффициент ()
принимаем равным 0.015. Силу сопротивления
воздуха ()
в кН определяют по формуле:
(2.11)
где:
–
коэффициент сопротивления воздуха;
F
–
лобовая площадь автомобиля, м2.
Лобовая
площадь автомобиля рассчитывается
следующим образом, для легковых
автомобилей:
(2.12)
где:
– наибольшая ширина автомобиля, м;
–
наибольшая высота автомобиля, м;
В
–
колея автомобиля.
Коэффициент
()
сопротивления воздуха можно принять
(в Н·с2/м4)
[1], для легковых
автомобилей 0,25.
F==
Все
полученные результаты сводим в таблицу
2.3,
расчет значений сил (и
),
определяемых для скоростей движения
автомобиля от 0 до наибольшей скорости
на высшей передаче. Промежуточные
значения скорости ()
следует взять по табл.3 для высшей
передачи. По результатам расчета строят
зависимости силы ()
и суммарной (+
)
от скорости
автомобиля, приведенные на рис.2.
Таблица
2.3
Расчет
сил сопротивления движению
|
№ |
Va |
Va2 |
(Va2)/20000 |
1+((Va2)/20000) |
Ψ |
PΨ |
Pw |
PΨ+Pw |
Pз |
|
1 |
20 |
382 |
0,02 |
1,02 |
0,015 |
0,218 |
0,014 |
0,23 |
0,72 |
|
2 |
39 |
1528 |
0,08 |
1,08 |
0,015 |
0,218 |
0,054 |
0,27 |
0,78 |
|
3 |
59 |
3439 |
0,17 |
1,17 |
0,015 |
0,218 |
0,122 |
0,34 |
0,79 |
|
4 |
78 |
6113 |
0,31 |
1,31 |
0,015 |
0,218 |
0,217 |
0,43 |
0,75 |
|
5 |
98 |
9552 |
0,48 |
1,48 |
0,022 |
0,321 |
0,339 |
0,66 |
0,55 |
|
6 |
117 |
13755 |
0,69 |
1,69 |
0,025 |
0,367 |
0,488 |
0,86 |
0,37 |
|
7 |
137 |
18722 |
0,94 |
1,94 |
0,029 |
0,421 |
0,664 |
1,09 |
0,12 |
|
8 |
156 |
24454 |
1,22 |
2,22 |
0,033 |
0,484 |
0,868 |
1,35 |
-0,18 |
|
9 |
176 |
30949 |
1,55 |
2,55 |
0,038 |
0,554 |
1,098 |
1,65 |
-0,54 |
|
10 |
195 |
38209 |
1,91 |
2,91 |
0,044 |
0,633 |
1,356 |
1,99 |
-0,95 |
На
рис. 2.2 показан запас ()
силы тяги, равный (при равномерном
движении автомобиля по горизонтальной
дороге)

силы тяги может использоваться для
разгона автомобиля, преодоления подъемов
и буксировки прицепа.
По
данным таблиц 2.2 и 2.3 строим график
тягового баланса автомобиля
рисунок 2.2.
Рисунок.
2.2. График тягового баланса автомобиля
Соседние файлы в папке курсач по АМ
- #
- #
07.08.201366.17 Кб7тряс11.bak
- #
07.08.201391.21 Кб9тряс11.dwg
- #
07.08.201383.46 Кб8тряс11.frw
- #
07.08.2013452.33 Кб7Тряс2.bak
- #
07.08.2013452.33 Кб8Тряс2.dwg
Содержание:
- Определение и формула силы тяги
- Единицы измерения силы тяги
- Примеры решения задач
В том случае, если тело при перемещении имеет ускорение, то на него кроме всех прочих обязательно действует некоторая сила, которая является
силой тяги в рассматриваемый момент времени. В действительности, если тело движется прямолинейно и с постоянной скоростью, то сила тяги также
действует, так как тело должно преодолевать силы сопротивления. Обычно силу тяги находят, рассматривая силы, действующие на тело, находя
равнодействующую и применяя второй закон Ньютона. Жестко определенной формулы для силы тяги не существует.
Не следует считать, что сила тяги, например, транспортного средства действует со стороны двигателя, так как внутренние силы не могут менять
скорость системы как единого целого, что входило бы в противоречие с законом сохранения импульса. Однако следует отметить, что для получения у
силы трения покоя необходимого направления, мотор вращает колеса, колеса «цепляются за дорогу» и порождается сила тяги. Теоретически было бы
возможно не использовать понятие «сила тяги», а говорить о силе трения покоя или силе реакции воздуха. Но удобнее внешние силы, которые действуют
на транспорт делить на две части, при этом одни силы называть силами тяги
$(/bar{F}_T)$, а другие – силами сопротивления
$bar{F}_S$ . Это делается для того,
чтобы уравнения движения не потеряли свой универсальный вид и полезная механическая мощность (P) имела простое выражение:
$$P=bar{F}_{T} bar{v}(1)$$
Определение и формула силы тяги
Определение
Исходя из формулы (1) силу тяги можно определить через полезную мощность, и скорость транспортного средства (v):
$$F_{T}=frac{P}{v}(2)$$
Для автомобиля, поднимающегося в горку, которая имеет уклон
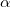
$$F_{T}-F_{s}-m g sin alpha=m a(3)$$
где a – ускорение, с которым движется автомобиль.
Единицы измерения силы тяги
Основной единицей измерения силы в системе СИ является: [FT]=Н
В СГС: [FT]=дин
Примеры решения задач
Пример
Задание. На автомобиль имеющий массу 1 т при его движении по горизонтальной поверхности, действует сила трения,
которая равна $mu$=0,1 от силы тяжести.
Какой будет сила тяги, если автомобиль движется с ускорением 2 м/с?
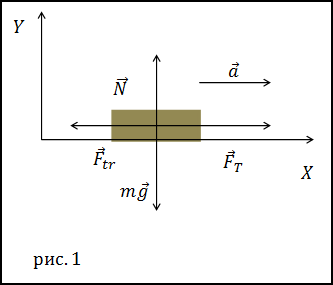
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем второй закон Ньютона:
$$bar{N}+m bar{g}+bar{F}_{t r}+bar{F}_{T}=m bar{a}(1.1)$$
Спроектируем уравнение (1.1) на оси X и Y:
$$
begin{array}{c}
X: F_{T}-F_{t r}=m a(1.2) \
Y: m g=N(1.3)
end{array}
$$
По условию задачи:
$$
F_{t r}=mu cdot m g (1.4)
$$
Подставим правую часть выражения (1.4) вместо силы трения в (1.2), получим:
$$F_{T}=m a+mu cdot m g$$
Переведем массу в систему СИ m=1т=103 кг, проведем вычисления:
$$F_{T}=10^{3}(2+0,1 cdot 9,8)=2,98 cdot 10^{3}(H)$$
Ответ. FT=2,98 кН

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
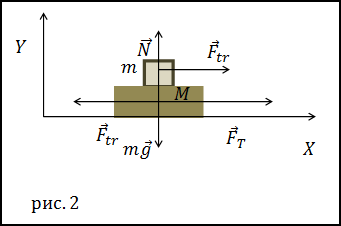
Задание. На гладкой горизонтальной поверхности лежит доска массой M. На доске находится тело массы m.
Коэффициент трения тела о доску равен $mu$ . К доске
приложена сила горизонтальная сила тяги, которая зависит от времени как: F=At (где A=const). В какой момент
времени доска начнет выскальзывать из-под тела?
Решение. Сделаем рисунок.
Для решения задачи нам потребуются проекции сил на осиX и Y, которые отличны от нуля. Для тела массы m:
$$
begin{array}{c}
X: m a_{1}=F_{t r}(2.1) \
Y: m g=N(2.2) \
F_{t r}=mu N=mu m g rightarrow m a_{1}=mu m g rightarrow a_{1}=mu g(2.3)
end{array}
$$
Для тела массы M:
$$M a_{2}=F-F_{t r} rightarrow M a_{2}=A t-F_{t r} rightarrow a_{2}=frac{A t-F_{t r}}{M}(2.2)$$
Обозначим момент времени, в который доска начнет выскальзывать из-под тела t0, тогда
$$mu g=frac{A t_{0}-mu m g}{M} rightarrow t_{0}=frac{m+M}{A} mu g$$
Ответ. $t_{0}=frac{m+M}{A} mu g$
Читать дальше: Формула силы упругости.
Сила тяги
Время чтения: 10 минут
Основное понятие силы тяги в физике
Сила тяги – это показатель силы, которую прикладывают к некоторому телу.
Она служит для обеспечения нахождения данного тела в состоянии равновесия.
Когда сила тяги прекращает свое действие — это может привести к следующим последствиям:
- остановка, которая связана с силой трения;
- состояние вязкости окружающей среды;
- множество других сопутствующих факторов и сил.
Для тела, на которое оказывает свое воздействие сила тяги, характерно постоянное движение. И обозначается следующим значение, а именно: [(v=operatorname t)]
Особым, частным случаем данного движения является состояние покоя.
При котором, скорость равна нулевому значению.
Состояние инерции – характер движения, при котором соблюдается постоянная скорость движения тела.
Чтобы тело поменяло свое состояние, и изменило скорость своего движения, необходимо приложить к нему силу тяги. При данных условиях скорость тела будет изменяться, причиной этого является получаемое ускорение. Также ускорение может быть отрицательным, в таком случае будет наблюдаться замедление скорости.
Показатель величины ускорения по закону физики обратно пропорционален массе тела.
Из состояния инерции труднее всего вывести тело более массивное и тяжелое.
Также величина ускорения прямо пропорциональна значению интенсивности силы, которая оказывает воздействие на тело.
Данное утверждение можно преобразовать и вывести в виде формулы:
[mathrm=mathrm cdot mathrm]
Где: F – сила тяги, m – масса тела, которая оказывает воздействие на тело, a – ускорение.
Данная формула наглядно характеризует второй закон Ньютона.
Основные формулы для расчета силы тяги
Наглядно силу тяги можно рассмотреть на примере спортсмена штангиста.
Именно на данном примере можно подробно понять, как приложенная сила, может вывести тело из состояния равновесия.
Распишем все операции, выполняемые спортсменам поэтапно:
- первоначально штанга находится в состоянии инерции, иными словами имеет состояние покоя;
- при отрыве от поверхности земли штанги, все мышцы спортсмена имеют способность сокращаться, с силой которая не превышает вес самой штанги (иначе это звучит как: величина силы с которой ее к себе притягивает гравитация Земли);
- при отрыве от пола, штанги на определенную высоту, происходит процесс ускорения;
Силой тяги для снаряда, который осуществляет движение будет являться величина силы с которой сокращаются мышцы спортсмена.
Для данного случая, обязательно должно соблюдаться следующее условие:
- [F_] – сила, с которой происходит сокращение мышечной массы (сила тяги для данного случая);
- [F_<т>] сила тяжести или гравитационная;
- m – масса, которая оказывает воздействие на тело;
- g – показатель ускорение свободного падения.
Характер движения тела по инерции всегда нужно уметь отличать от движения, которое совершается равномерно. Следовательно, в случае, когда сила тяги имеет способность уравновешиваться сторонними силами (противодействующими).
Например:
Автомобиль совершает движение и его двигатель находится в состоянии работы. Работающий двигатель придает силу на колеса, через трансмиссию, проделывая следующие операции:
- преодолевает силу трения, которая возникает внутри всего механизма;
- сопротивление воздуха;
- процесс трения колес о любую поверхность.
Для определения силы тяги, необходимо знать следующие данные:
- t – время, за которое происходит разгон транспортного средства;
- [v] – необходимая скорость;
- m – непосредственная масса автомобиля.
Сила определяется по формуле:
Из формулы видно, что ускорение выражено как: деление скорости на время разгона транспортного средства:
Через мощность можно выразить силу.
Мощность – это совершенная работа, любым источником энергии.
Если высокая мощность, то следует что, время за которое источник развивает силу будет уменьшаться. А именно: способность разогнать тело определенной массы равной m до необходимой величины скорости движения.
Значение совершаемой работы прямо пропорционально силе и вычисляется по формуле:
Где: S – расстояние, на которое при помощи силы, перемещается тело;
Расстояние можно определить по формуле, выразив его через скорость тела и время движения:
Затем определяется мощность, которая должна выполнять в единицу времени и выражается следующей формулой:
Что такое сила тяги и по какой формуле её находить ?
Разберёмся в вопросе, что такое сила тяги. Как следует из самого названия – это сила, которую необходимо прикладывать к телу, чтобы оно находилось в состоянии постоянного движения.
Если её убрать, то тело, будь то автомобиль, электровоз, космическая ракета или санки, со временем остановится. Это произойдёт потому, что на тело всегда действуют силы, которые заставляют его стремиться к состоянию покоя:
- силы трения (покоя, качения, скольжения),
- сопротивления воздуха (газа),
- сопротивления воды и др.
Первый и второй законы Ньютона
Обратимся к законам Ньютона, которые хорошо описывают механическое движение тел. Из школьной программы мы знаем, что есть первый закон Ньютона, который описывает закон инерции. Он гласит, что любое тело, если на него не действуют силы, или если их равнодействующая равна нулю, движется прямолинейно и равномерно, или же находится в состоянии покоя. Это означает, что тело, пока на него ничто не действует, будет двигаться с постоянной скоростью v=const или пребывать в состоянии покоя сколько угодно долго, пока какое-то внешнее воздействие не выведет тело из этого состояния. Это и есть движение по инерции.
Надо сказать, что этот закон справедлив лишь в так называемых инерциальных системах отсчёта. В неинерциальных системах отсчёта этот закон не действует и нужно использовать второй закон Ньютона. В таких системах отсчёта тело тоже будет двигаться по инерции, но оно будет двигаться с ускорением, стремясь сохранять своё движение, т.е. на него также не будут действовать никакие внешние силы, кроме силы инерции, стремящейся двигать тело в том направлении, в каком оно двигалось до воздействия. Тут мы приходим к рассмотрению второго закона Ньютона, который также справедлив в инерциальных системах отсчёта, т. е. в таких системах отсчёта, в которых тело движется с постоянной скоростью либо находится в покое.
Этот закон утверждает, что для того, чтобы вывести тело из состояния покоя или равномерного движения, к нему необходимо приложить силу, равную F=m•a, где m — это масса тела, a — ускорение, сообщаемое телу. Зная эти законы, можно рассчитать силу тяги (двигателя автомобиля, ракетного двигателя или, например, лошади, тянущей нагруженную повозку).
Примеры из жизни
Насколько вы сильны?
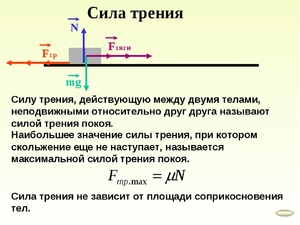
Рассмотрим простейший пример. Ваш ребёнок сел на санки и просит вас его покатать. С какой силой вам нужно тянуть эти санки, чтобы ребёнок остался доволен быстрой ездой ? Пока санки с ребёнком остаются в состоянии покоя, все силы, действующие на них, уравновешены. Состояние покоя — это частный случай инерции. Здесь на санки действуют две силы: тяжести Fт = m•g, направленная вертикально вниз, и нормального давления N, направленная вертикально вверх. Поскольку санки не движутся, то N – m•g = 0. Тогда из этого равенства следует, что N = m•g.
Когда вы решили покатать своего ребёнка, вы прикладываете силу тяги (Fтяги) к санкам с ребёнком. Когда вы начинаете тянуть санки, возникает сопротивление движению, вызванное силой трения (Fтр.), направленной в противоположную сторону. Это так называемая сила трения покоя. Когда тело не движется, она равна нулю. Стоит потянуть за санки — и появляется сила трения покоя, которая меняется от нуля до некоторого максимального значения (Fтр. max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.
Чтобы найти Fтяги, применим второй закон Ньютона: Fтяги – Fтр.max = m•a, где a – ускорение, с которым вы тянете санки, m – масса санок с ребёнком. Допустим, вы разогнали санки до определённой скорости, которая не изменяется. Тогда a = 0 и вышеприведённое уравнение запишется в виде: Fтяги – Fтр. max = 0, или Fтяги = Fтр.max. Есть известный закон из физики, который устанавливает определённую зависимость для Fтр.max и N. Эта зависимость имеет вид: Fтр.max = fmax • N, где fmax – максимальный коэффициент трения покоя.
Если в эту формулу подставить выражение для N, то мы получим Fтр.max = fmax•m•g. Тогда формула искомой силы тяги примет вид: Fтяги = fmax•m•g = fск•m•g, где fск = fmax – коэффициент трения скольжения, g – ускорение свободного падения. Допустим, fск = 0,7, m = 30 кг, g = 9,81 м/с², тогда Fтяги = 0,7 • 30 кг • 9,81 м/с² = 206,01 Н (Ньютона).
Насколько силён ваш автомобиль?
Рассмотрим ещё пример. У вас есть автомобиль, мощность двигателя которого N. вы едете со скоростью v. Как в этом случае узнать силу тяги двигателя вашего автомобиля ? Поскольку скорость автомобиля не меняется, то Fтяги уравновешена силами трения качения, лобового сопротивления, трения в подшипниках и т. д. (первый закон Ньютона). По второму закону Ньютона она будет равна Fтяги = m•a. Чтобы её вычислить, достаточно знать массу автомобиля m и ускорение a.
Допустим, вы разогнали свой автомобиль до скорости v за какое-то время t, проехав расстояние s. Тогда Fтяги будет легко рассчитана по формуле: Fтяги = m•v/t. Как и в примере с санками, справедлива также такая формула: Fтяги = f•m•g, где f – коэффициент трения качения, который зависит от скорости автомобиля (чем больше скорость, тем меньше этот коэффициент).
Но что делать, если масса автомобиля m, коэффициент трения качения f и время разгона t неизвестны ? Тогда можно поступить по-другому. Двигатель вашего автомобиля при разгоне совершил работу A = Fтяги • s. Поскольку формула расстояния имеет вид s = v•t, то выражение для работы будет таким: A = Fтяги • v • t. Разделив обе части этого равенства на t, получим A/t = Fтяги • v. Но A/t = N – это мощность двигателя вашего автомобиля, поэтому N = Fтяги • v. Отсюда уже получим искомую формулу: Fтяги =N/v.
Допустим, вы разогнали свой автомобиль до скорости v = 180 км/ч, а мощность его двигателя N = 200 л. с. (лошадиных сил). Чтобы вычислить Fтяги двигателя, необходимо прежде перевести указанные единицы измерения в единицы СИ, т. е. международной системы измерения. Здесь 1 л. с. = 735,499 Вт, поэтому мощность двигателя составит N = 200 л. с. • 735,499 Вт/л. с. = 147099,8 Вт. Скорость в системе СИ будет равна v = 180 км/ч = 180 • 1000 м/3600 с = 50 м/с. Тогда искомое значение будет равно Fтяги = 147099,8 Вт/50 (м/с) = 2941,996 Н
2,94 кН (килоньютона).
Около 3 килоньютонов. Много это или мало ? Допустим, вы жмёте 100 килограммовую штангу. Чтобы её поднять, вам нужно преодолеть её вес, равный P = m•g = 100 кг • 9,81 м/с² = 981 Н (ньютон)
0,98 кН. Полученное для автомобиля значение Fтяги больше веса штанги в 2,94/0,98 = 3 раза. Это равносильно тому, что вы будете поднимать штангу массой в 300 кг. Такова сила тяги двигателя вашего автомобиля (на скорости 180 км/ч).
Таким образом, зная школьный курс физики, мы можем с лёгкостью вычислить силу тяги:
- человека,
- лошади,
- паровоза,
- автомобиля,
- космической ракеты и всех прочих видов техники.
В нашем видео вы найдете интересные опыты, поясняющие, что такое сила тяги и сила сопростивления.
Формула силы тяги
В том случае, если тело при перемещении имеет ускорение, то на него кроме всех прочих обязательно действует некоторая сила, которая является силой тяги в рассматриваемый момент времени. В действительности, если тело движется прямолинейно и с постоянной скоростью, то сила тяги также действует, так как тело должно преодолевать силы сопротивления. Обычно силу тяги находят, рассматривая силы, действующие на тело, находя равнодействующую и применяя второй закон Ньютона. Жестко определенной формулы для силы тяги не существует.
Не следует считать, что сила тяги, например, транспортного средства действует со стороны двигателя, так как внутренние силы не могут менять скорость системы как единого целого, что входило бы в противоречие с законом сохранения импульса. Однако следует отметить, что для получения у силы трения покоя необходимого направления, мотор вращает колеса, колеса «цепляются за дорогу» и порождается сила тяги. Теоретически было бы возможно не использовать понятие «сила тяги», а говорить о силе трения покоя или силе реакции воздуха. Но удобнее внешние силы, которые действуют на транспорт делить на две части, при этом одни силы называть силами тяги $(/bar_T)$, а другие – силами сопротивления $bar_S$ . Это делается для того, чтобы уравнения движения не потеряли свой универсальный вид и полезная механическая мощность (P) имела простое выражение:
Определение и формула силы тяги
Исходя из формулы (1) силу тяги можно определить через полезную мощность, и скорость транспортного средства (v):
Для автомобиля, поднимающегося в горку, которая имеет уклон 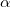
$$F_-F_-m g sin alpha=m a(3)$$
где a – ускорение, с которым движется автомобиль.
Единицы измерения силы тяги
Основной единицей измерения силы в системе СИ является: [FT]=Н
Примеры решения задач
Задание. На автомобиль имеющий массу 1 т при его движении по горизонтальной поверхности, действует сила трения, которая равна $mu$=0,1 от силы тяжести. Какой будет сила тяги, если автомобиль движется с ускорением 2 м/с?
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем второй закон Ньютона:
Спроектируем уравнение (1.1) на оси X и Y:
По условию задачи:
Подставим правую часть выражения (1.4) вместо силы трения в (1.2), получим:
$$F_=m a+mu cdot m g$$
Переведем массу в систему СИ m=1т=10 3 кг, проведем вычисления:
Ответ. FT=2,98 кН
Задание. На гладкой горизонтальной поверхности лежит доска массой M. На доске находится тело массы m. Коэффициент трения тела о доску равен $mu$ . К доске приложена сила горизонтальная сила тяги, которая зависит от времени как: F=At (где A=const). В какой момент времени доска начнет выскальзывать из-под тела?
Решение. Сделаем рисунок.
Для решения задачи нам потребуются проекции сил на осиX и Y, которые отличны от нуля. Для тела массы m:
$$ begin X: m a_<1>=F_(2.1) \ Y: m g=N(2.2) \ F_=mu N=mu m g rightarrow m a_<1>=mu m g rightarrow a_<1>=mu g(2.3) end $$
Для тела массы M:
$$M a_<2>=F-F_ rightarrow M a_<2>=A t-F_ rightarrow a_<2>=frac>(2.2)$$
Обозначим момент времени, в который доска начнет выскальзывать из-под тела t0, тогда
Ответ. $t_<0>=frac mu g$
[spoiler title=”источники:”]
http://liveposts.ru/articles/education-articles/fizika/chto-takoe-sila-tyagi-i-po-kakoj-formule-eyo-nahodit
http://www.webmath.ru/poleznoe/formules_21_31_sila_tjagi.php
[/spoiler]