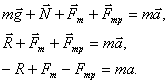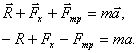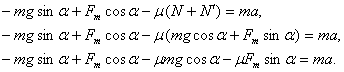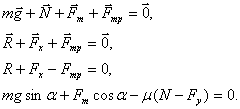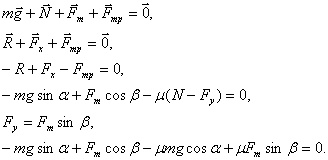Сила тяги, теория и онлайн калькуляторы
Сила тяги
Понятие сила тяги
Определение
Понятие «сила тяги» часто встречается в задачах по физике, когда речь идеи о механической мощности или движении транспорта.
Вообще говоря, это гипотетическая сила, которая вводится для удобства при решении задач.
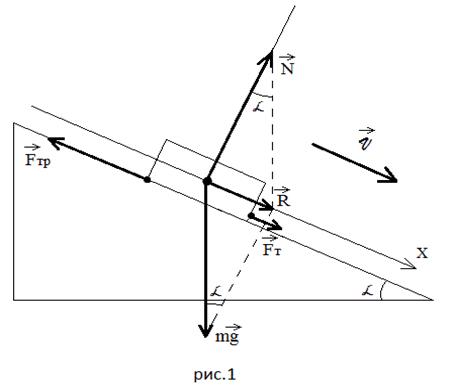
Поясним эту мысль. Рассмотрим движение автобуса. Сила тяги (обозначим ее как ${overline{F}}_t$) в этом случае является силой трения покоя, которая действует на нижние точки колес со стороны поверхности шоссе. Для реализации движения автобуса по дороге колеса транспортного средства вращает двигатель так, чтобы сила трения была направлена в сторону перемещения (рис.1). В этом случае силу тяги определим как силу трения, которая возникает между ведущими колесами и поверхностью, по которой колеса катятся. Если сила трения отсутствует (колесо находится на льду), то автобус не двигается с места, так как колеса проскальзывают. Трение, которое появляется между колесами и поверхностью дороги создает поступательное перемещение.
Так как сила тяги зависит от силы трения, то для увеличения величины $F_t $ следует увеличить трение. Трение увеличивается при росте коэффициента трения и (или) с увеличением силы нормального давления, которое зависит от массы тела.
Возникает вопрос о необходимости введения некоей силы тяги вместо того, чтобы использовать привычную силу трения. При выделении из внешних сил, которые действуют на наш автобус силы тяги и силы сопротивления движению уравнения движения имеют универсальный вид, и, используя силу тяги, просто выражается полезная механическая мощность ($N$):
[N={overline{F}}_tcdot overline{v}left(1right),]
где $overline{v}$ – скорость движения тела (у нас автобуса).
Отметим, что у силы тяги нет четко определенной формулы, как, например, у гравитационной силы или силы Архимеда и других сил. Ее часто вычисляют, используя второй закон Ньютона и рассматривая все силы, которые действуют на тело.
Реактивная сила тяги
Уравнения движения тел переменной массы и формулу для вычисления реактивной силы получил первым И.В. Мещерский в 1897 г. Формула реактивной силы является основой для расчета силы тяги ракетных и турборакетных двигателей всех систем.
Пусть ракета перемещается со скоростью $overline{v}$ относительно Земли. Вместе с ней с такой же скоростью движется часть топлива, которая сгорает в ближайшую секунду. При сгорании продукты горения этой части топлива получают дополнительную скорость $overline{u}$ относительно ракеты. Относительно Земли они имеют скорость $overline{v}-overline{u}$. При этом сама ракета увеличивает скорость. После выброса продукты горения не взаимодействуют с ракетой. Поэтому систему ракета плюс продукты горения топлива рассматривают как систему из двух тел, которые взаимодействуют при горении по законам неупругого удара. Пусть реактивный двигатель ракеты каждую секунду выбрасывает массу $mu $ продуктов горения топлива. Используя закон сохранения импульса и второй закон Ньютона получают, что модуль реактивной силы тяги двигателя ($R$) ракеты равен:
[R=mu u left(2right).]
Формула (2) показывает, что реактивная сила, которая действует на тело переменной массы, пропорциональна массе отделяющихся частиц за единицу времени и скорости движения этих частиц относительно тела.
Примеры задач с решением
Пример 1
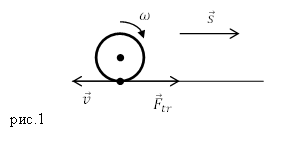
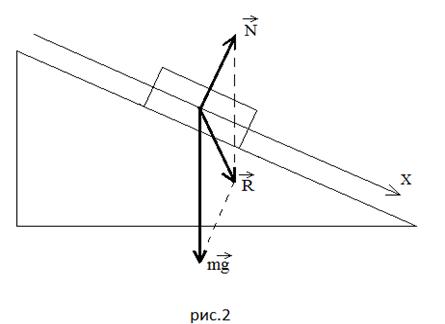
Задание. Сила тяги, действующая на тело, находящееся на наклонной плоскости (рис.2) направлена вдоль этой плоскости вверх (рис.2). Какова ее величина, если масса тела равна $m$, угол наклона плоскости $alpha , $ускорение движения тела $a$? Коэффициент трения тела о плоскость равен $mu $. Тело движется с постоянной скоростью в гору.
Решение. Запишем второй закон Ньютона для сил, действующих на тело, учтем, что тело движется равномерно:
[moverline{g}+overline{N}+overline{F}+{overline{F}}_{tr}=0left(1.1right).]
Запишем проекции уравнения (1.1) на оси X и Y:
[left{ begin{array}{c}
X: -mg{sin alpha + }F-F_{tr}=0left(1.2right);; \
Y: N-mg{cos alpha =0left(1.3right). } end{array}
right.]
Сила трения связана с силой нормального давления как:
[F_{tr}=mu N left(1.4right).]
Выразим из (1.3) $N$, используем выражение (1.4), получим из (1.2) силу тяги:
[-mg{sin alpha + }F-mu mg{cos alpha }=0to F=mu mg{cos alpha }+mg{sin alpha . }]
Ответ. $F=mg(mu {cos alpha }+{sin alpha ). }$
Пример 2
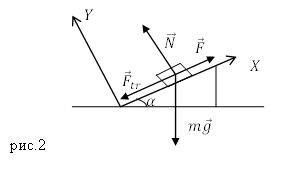
Задание. Ракету, массой (в начальный момент времени) равной $M,$ запустили вертикально вверх. Относительная скорость выброса продуктов горения равна $u$, расход горючего составляет $mu $. Каким будет ускорение ракеты через время $t$ после старта, если сопротивление воздуха не учитывать, поле силы тяжести считать однородным.
Решение. Сделаем рисунок.
На ракету (из условий задачи) будут действовать две силы: сила тяжести и реактивная сила тяги. Запишем уравнение движения ракеты:
[moverline{g}+overline{R}=moverline{a}left(2.1right).]
В проекции на ось Y уравнение (2.1) запишем как:
[R-mg=ma left(2.2right).]
Реактивная сила тяги может быть найдена как:
[R=mu u left(2.3right).]
Учитывая равенство (2.3) уравнение преобразуем к виду:
[mu u-mg=mato a=frac{mu u-mg}{m}left(2.4right).]
Масса ракеты в момент времени $t$ равна:
[m=M-mu tleft(2.5right).]
Подставим (2.5) в (2.4) имеем:
[a=frac{mu u-left(M-mu tright)g}{M-mu t}=frac{mu u}{M-mu t}-g.]
Ответ. $a=frac{mu u}{M-mu t}-g.$
Читать дальше: скорость.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Итак, постараюсь подробно описать ход моих
рассуждений по этому вопросу. На первом уроке
ставлю перед учащимися вопрос: как может тело
двигаться по наклонной плоскости? Вместе
отвечаем: скатываться равномерно, с ускорением;
покоиться на наклонной плоскости; удерживаться
на ней; съезжать под действием силы тяги
равномерно, с ускорением; заезжать под действием
силы тяги равномерно, с ускорением. На рисунках
на двух-трех примерах показываем, какие при этом
на тело действуют силы. Попутно ввожу понятие
скатывающей равнодействующей. Записываем
уравнение движения в векторной форме, затем в нем
заменяем сумму 
скатывающей
равнодействующей 
(обозначайте,
как вам нравится). Это делаем по двум причинам:
во-первых, нет необходимости проецировать
векторы сил на ось 
и решать два уравнения; во-вторых,
правильно будет показано соотношение сил, исходя
из условия задачи.
Покажу на конкретных примерах. Пример 1: тело
под действием силы тяги съезжает равномерно
(Рисунок 1).
Ученики первым делом должны усвоить алгоритм
построения рисунка. Изображаем наклонную
плоскость, посередине нее – тело в виде
прямоугольника, через середину тела параллельно
наклонной плоскости проводим ось 
. Направление оси не
существенно, но в случае равноускоренного
движения лучше показать в сторону вектора 
, чтобы в
алгебраической форме в уравнении движения в
правой части перед 
был знак «плюс». Далее строим силы.
Силу тяжести 
проводим
вертикально вниз произвольной длины (требую
рисунки делать крупными, чтобы всем было все
понятно). Затем из точки приложения силы тяжести
– перпендикуляр к оси , вдоль которого пойдет сила реакции
опоры 
.
Параллельно этому перпендикуляру из конца
вектора проводим
пунктирную линию до пересечения с осью . Из этой точки –
пунктирную линию, параллельную до пересечения с
перпендикуляром – получаем вектор правильной длины.
Таким образом, мы построили параллелограмм на
векторах и , автоматически
указав правильную величину силы реакции опоры и
построив по всем правилам векторной геометрии
равнодействующую этих сил , которую я называю скатывающей
равнодействующей (диагональ, совпадающая с осью ). В этом месте,
воспользовавшись методом из учебника, на
отдельном рисунке показываю силу реакции опоры
произвольной длины: сначала короче, чем нужно, а
потом длиннее, чем нужно. Показываю
равнодействующую силы тяжести и силы реакции
опоры: в первом случае она направлена вниз под
углом к наклонной плоскости (Рисунок 2), во втором
случае – вверх под углом к наклонной плоскости
(Рисунок 3).
Делаем очень важный вывод: соотношение между
силой тяжести и силой реакции опоры должно быть
таким, чтобы тело под их действием (или под
действием скатывающей равнодействующей) в
отсутствие других сил двигалось вниз вдоль
наклонной плоскости. Далее я спрашиваю:
какие еще силы действуют на тело? Ребята
отвечают: сила тяги и сила трения. Я задаю
следующий вопрос: какую силу покажем сначала, а
какую потом? Добиваюсь правильного и
обоснованного ответа: сначала в этом случае надо
показать силу тяги, а затем силу трения, модуль
которой будет равен сумме модулей силы тяги и
скатывающей равнодействующей: 
, т.к. по условию задачи тело
движется равномерно, следовательно,
равнодействующая всех сил, действующих на тело,
должна равняться нулю согласно первому закону
Ньютона. Для контроля задаю провокационный
вопрос: так сколько сил действует на тело? Ребята
должны ответить – четыре (не пять!): сила тяжести,
сила реакции опоры, сила тяги и сила трения.
Теперь записываем уравнение движения в
векторной форме согласно первому закону Ньютона:
.
. Заменяем сумму векторов скатывающей равнодействующей :
.
.Получаем уравнение, в котором все векторы
параллельны оси .
Теперь запишем это уравнение через проекции
векторов на ось :
.
.Эту запись в дальнейшем можно пропускать.
Заменим в уравнении проекции векторов на их
модули с учетом направлений:
.
.Пример 2: тело под действием силы тяги
заезжает на наклонную плоскость с ускорением
(Рисунок 4).
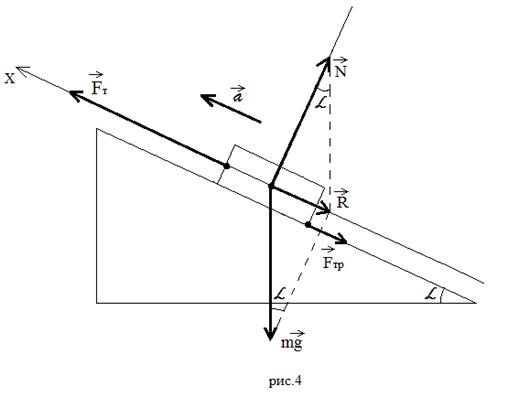
В этом примере ученики должны сказать, что
после построения силы тяжести, силы реакции
опоры и скатывающей равнодействующей следующей
надо показать силу трения, последним – вектор
силы тяги, который должен быть больше суммы
векторов 
, т.к.
равнодействующая всех сил должна быть
направлена так же, как вектор ускорения согласно второму
закону Ньютона. Уравнение движения тела должны
записать согласно второму закону Ньютона:
Если есть возможность на уроке рассмотреть
другие случаи, то не пренебрегаем этой
возможностью. Если нет, то даю это задание домой.
Кто-то может рассмотреть все оставшиеся случаи,
кто-то некоторые – право выбора учеников. На
следующем уроке проверяем, исправляем ошибки и
переходим к решению конкретных задач,
предварительно выразив из векторных
треугольников и
:
,
.
,
.Равенство (2) желательно проанализировать для
различных углов 
.
При 
имеем: 
, как при движении
горизонтально под действием горизонтальной силы
тяги. С ростом угла его косинус уменьшается,
следовательно, уменьшается и сила реакции опоры
и становится все меньше и меньше силы тяжести.
При угле 
она
равна нулю, т.е. тело не действует на опору и
опора, соответственно, «не реагирует».
Предвижу вопрос оппонентов: как применить эту
методику для случаев, когда сила тяги
горизонтальна или направлена под углом к
наклонной плоскости? Отвечу на конкретных
примерах.
а) Тело с ускорением затаскивают на наклонную
плоскость, прикладывая силу тяги горизонтально
(Рисунок 5).
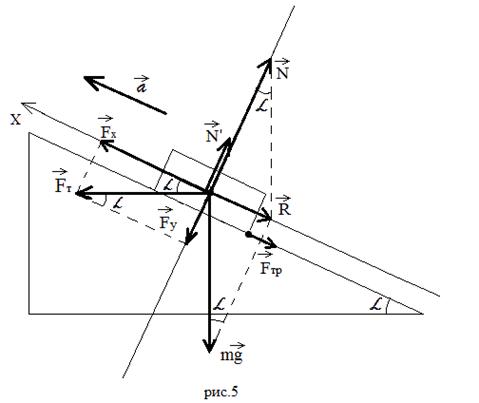
Горизонтальную силу тяги 
раскладываем на две
составляющие: вдоль оси – 
и
перпендикулярную оси – 
(операция,
обратная построению равнодействующей
перпендикулярных сил). Записываем уравнение
движения:
.
.Заменяем скатывающей
равнодействующей, а вместо пишем :
Из векторных треугольников выражаем 
: 
и 
: 
.
Под действием горизонтальной силы тело не только
поднимается вверх по наклонной плоскости, но еще
и дополнительно прижимается к ней. Поэтому
возникает дополнительная сила давления, равная
модулю вектора и,
согласно третьему закону Ньютона,
дополнительная сила реакции опоры 
: 
. Тогда сила трения будет: 
.
Уравнение движения примет вид:
Вот мы полностью расшифровали уравнение
движения. Теперь осталось выразить из него
искомую величину. Попробуйте решить эту задачу
традиционным способом и вы получите такое же
уравнение, только решение будет громоздче.
б) Тело стаскивают равномерно с наклонной
плоскости, прикладывая силу тяги горизонтально
(Рисунок 6).
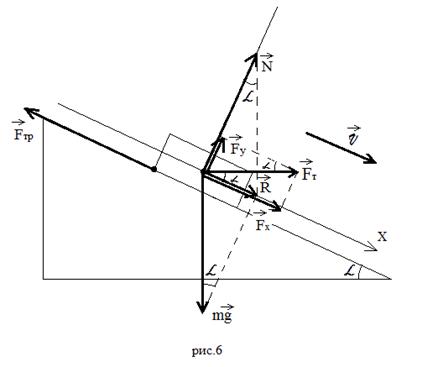
В этом случае сила тяги кроме стаскивания тела
вниз вдоль наклонной плоскости еще и отрывает
его от наклонной плоскости. Итак, окончательное
уравнение имеет вид:
.
.в) Тело затаскивают равномерно на наклонную
плоскость, прикладывая силу тяги под углом 
к наклонной
плоскости (Рисунок 7).
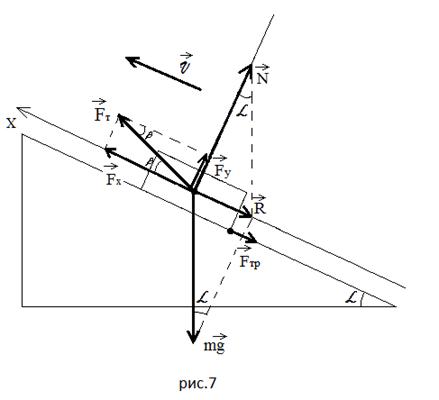
Предлагаю рассмотреть конкретные задачи, дабы
еще убедительнее прорекламировать мой
методический подход к решению таких задач. Но
прежде обращаю внимание на алгоритм решения (я
думаю, все учителя физики на него обращают
внимание учеников, и все мое повествование было
подчинено этому алгоритму):
1) внимательно прочитав задачу, выяснить, как
движется тело;
2) сделать рисунок с правильным, исходя из условия
задачи, изображением сил;
3) записать уравнение движения в векторной форме
согласно первому или второму закону Ньютона;
4) записать это уравнение через проекции векторов
сил на ось x (этот шаг в дальнейшем, когда умение
решать задачи по динамике будет доведено до
автоматизма, можно опустить);
5) выразить проекции векторов через их модули с
учетом направлений и записать уравнение в
алгебраической форме;
6) выразить модули сил по формулам (если есть
необходимость);
7) выразить искомую величину.
Задача 1. За какое время 
тело массой 
соскальзывает с наклонной
плоскости высотой 
и углом наклона , если по наклонной плоскости с
углом наклона оно
движется равномерно?
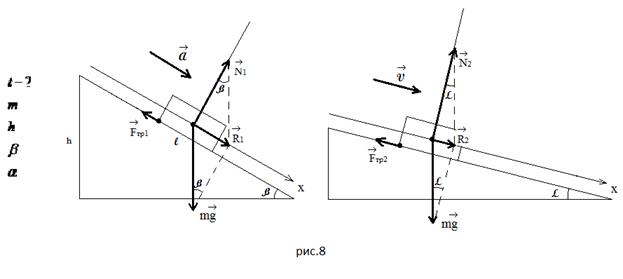
Каково было бы решать эту задачу привычным
способом!
Задача 2. Что легче: удержать тело на
наклонной плоскости или двигать его по ней
равномерно вверх?
Здесь при объяснении без скатывающей
равнодействующей, на мой взгляд, не обойтись.
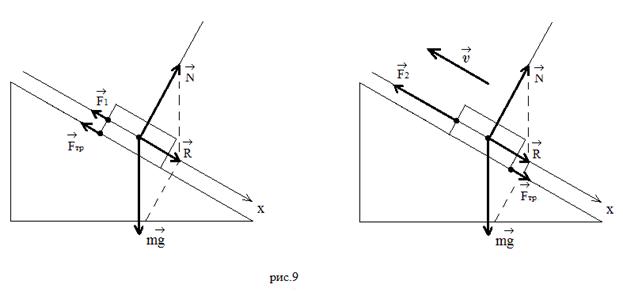
Как видно из рисунков, в первом случае сила
трения помогает удерживать тело (направлена в ту
же сторону, что и удерживающая сила), во втором
случае она вместе со скатывающей
равнодействующей направлена против движения. В
первом случае 
,
во втором случае 
.
Как найти силу тяги
Силу тяги, приводящей тело в движение, вы найдете, рассчитав векторную сумму всех сил, действующих на тело. При равномерном движении по горизонтальной поверхности сила тяги компенсирует силы сопротивления движению. В случае если тело движется по наклонной плоскости, ему приходится преодолевать еще и силу тяжести – при расчетах учитывайте это.
Вам понадобится
- динамометр, весы, таблица коэффициентов трения, акселерометр.
Инструкция
Непосредственное измерение силы тяги Положите тело на поверхность, по которой вы будете его перемещать. Прикрепите к нему динамометр и начните двигать с постоянной скоростью, снимите показания динамометра в ньютонах – это и будет значение силы тяги.
Измерение силы тяги, действующей на прямолинейно движущееся телоВ том случае, если тело движется по горизонтальному участку пути, узнайте материалы, из которых сделано тело и поверхность. В таблице коэффициентов трения для разных материалов, подберите нужную комбинацию и соответствующий ей коэффициент. С помощью весов или любым другим способом измерьте массу двигающегося тела. Измерьте ускорение, с которым движется тело акселерометром или рассчитайте его, если известны скорости в начале и конце пути и его длина или время прохождения. Для того чтобы найти силу тяги, умножьте коэффициент трения на 9,81 (ускорение свободного падения), прибавьте к результату значение ускорения, а получившееся число умножьте на массу тела (F=m•(μ•9,81+a)). Если тело движется равномерно, ускорение будет равно нулю.
В том случае, если тело движется по наклонной плоскости, измерьте угол ее наклона. Чтобы найти силу тяги в случае, когда тело поднимается по ней, умножите коэффициент трения на 9,81 и косинус угла наклона плоскости к горизонту, к этому числу прибавьте произведение 9,81 на синус этого угла, к полученному результату прибавьте ускорение. Полученное число умножьте на массу тела, которую нужно измерить заранее F=m•(μ•9,81•Cos(α)+9,81•Sin(α)+a). При свободном падении тела роль силы тяги выполняет сила тяжести. Для того чтобы найти ее, нужно массу тела умножить на ускорение свободного падения (9,81): F=m•9,81.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Цель работы:
Убедиться на опыте в том, что полезная работа, выполненная с помощью простого механизма (наклонной плоскости), меньше полной.
Приборы и материалы:
Доска, динамометр, измерительная лента или линейка, брусок, штатив с муфтой и лапкой (рис. 206).
Указания к работе:
1. Повторите по учебнику § 65 “Коэффициент полезного действия механизма”.
2. Определите с помощью динамометра вес бруска.
3. Закрепите доску в лапке штатива в наклонном положении.
4. Положите брусок на доску, прикрепив к нему динамометр.
5. Перемещайте брусок с постоянной скоростью вверх по наклонной доске.
6. Измерьте с помощью линейки путь s, который проделал брусок, и высоту наклонной плоскости h.
7. Измерьте силу тяги F.
8. Вычислите полезную работу по формуле
А
п
=
P
h
, а затраченную − по формуле
А
з
=
F
s
.
9. Определите КПД наклонной плоскости:
η
=
А
п
А
з
.
10. Результаты измерений и вычислений занесите в таблицу 15.
Дополнительное задание.
1. Используя “золотое правило” механики, рассчитайте, какой выигрыш в силе даёт наклонная плоскость, если не учитывать трение.
2. Измените высоту наклонной плоскости и для неё определите полезную, полную работу и КПД.
рис. 206.
Таблица 15.
reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. №11 Определение КПД при подъеме тела по наклонной плоскости. Номер №1
Решение
При выполнении данной работы необходимо вспомнить «золотое правило» механики. А именно, работа по равномерному перемещению тела по наклонной плоскости без трения на высоту h равна работе, совершенной при подъеме тела на высоту h по вертикали.
При подъеме по вертикали на высоту h, полезная работа равна:
А
п
=
m
g
h
.
При подъеме по плоскости работа равна:
А
з
=
F
s
, где F− сила, с которой груз поднимается равномерно, l — пройденный телом путь,
А
з
— затраченная работа.
В идеальном случае, когда нет силы трения,
А
п
=
А
з
.
Но поскольку при движении тела по плоскости возникает сила трения, то
А
п
<
А
з
.
Коэффициент полезного действия наклонной плоскости равен:
η
=
А
п
А
з
∗
100
.
Ход работы.
1. Определим с помощью динамометра вес бруска. Вес равен 2,2 Н.
2. Закрепим доску в лапке штатива в наклонном положении.
3. Положим брусок на доску, прикрепив к нему динамометр.
4. Переместим брусок с постоянной скоростью вверх по наклонной доске.
5. Измерим с помощью линейки путь s, который проделал брусок. Он равен 0,4 м. Измерим также высоту наклонной плоскости h, она равна 0,2 м.
6. Измерим силу тяги F. Сила тяги по показаниям динамометра равна 1,8 Н.
7. Вычислим полезную работу по формуле
А
п
=
P
h
, а затраченную − по формуле
А
з
=
F
s
.
А
п
=
2
,
2
∗
0
,
2
=
0
,
44
Дж;
А
з
=
1
,
8
∗
0
,
4
=
0
,
72
Дж.
8. Определим КПД наклонной плоскости:
η
=
А
п
А
з
∗
100
;
η
=
0
,
44
0
,
72
∗
100
%;
9. Результаты измерений и вычислений занесём в таблицу 15.
Таблица 15.
| h, м | Р, Н |
А п , ДжА п = |
s, м | F, Н |
А з , ДжА з = |
η = А п А з * 100% |
|---|---|---|---|---|---|---|
| 0,2 | 2,2 | 0,44 | 0,4 | 1,8 | 0,72 | 61 |
Дополнительное задание.
1. В соответствии с “золотым правилом” механики:
А
п
=
А
з
;
Ph = Fs;
P
F
=
s
h
=
0
,
4
0
,
2
= 2.
Наклонная плоскость при отсутствии силы трения дала бы выигрыш в силе в 2 раза.
2. Изменим высоту наклонной плоскости и для неё определим полезную, полную работу и КПД.
А
п
=
2
,
2
∗
0
,
3
=
0
,
66
Дж;
А
з
=
1
,
9
∗
0
,
4
=
0
,
76
Дж;
η
=
0
,
66
0
,
76
∗
100
=
87
%;
3. Результаты измерений и вычислений занесём в таблицу.
| h, м | Р, Н |
А п , ДжА п = |
s, м | F, Н |
А з , ДжА з = |
η = А п А з * 100% |
|---|---|---|---|---|---|---|
| 0,3 | 2,2 | 0,66 | 0,4 | 1,9 | 0,76 | 87 |
Проецирование сил. Движение по наклонной плоскости
Задачи по динамике.
I и II закон Ньютона.
Ввод и направление осей.
Неколлинеарные силы.
Проецирование сил на оси.
Решение систем уравнений.
Самые типовые задачи по динамике
Начнем с I и II законов Ньютона.
Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых… Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.
I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.
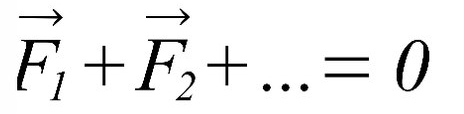
Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.
II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.
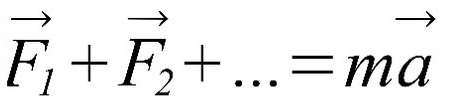
Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.
При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.
Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².
Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:
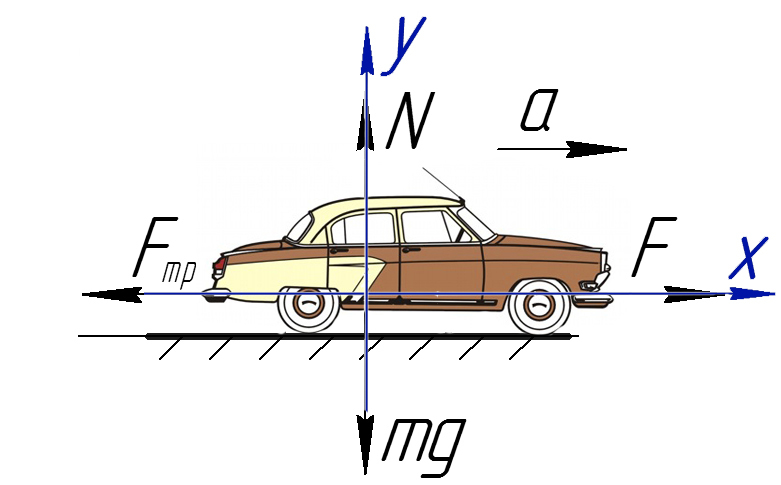
На Ось Х: движение с ускорением
На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)
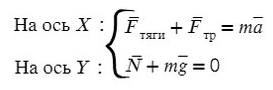
Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.
По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.
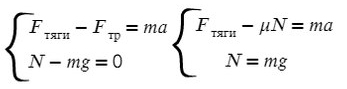
Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.
Получаем, что:
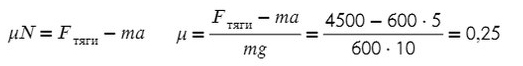
Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.
Ответ: 0,25
Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.
Сделаем рисунок, покажем силы, которые дествуют на груз
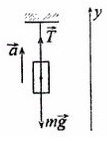
T – сила натяжения нити
На ось X: нет сил
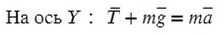
Разберемся с направлением сил на ось Y:
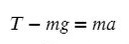
Выразим T (силу натяжения) и подставим числительные значения:
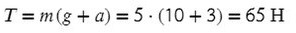
Ответ: 65 Н
Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.
Далеко не всегда все силы, действующие на тело, направлены вдоль осей.
Простой пример: мальчик тянет санки
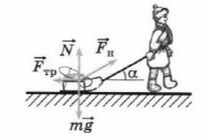
Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.
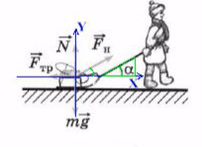Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.
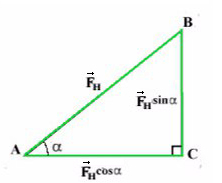
Отношение противолежащего катета к гипотенузе — это синус.
Отношение прилежащего катета к гипотенузе — это косинус.
Сила тяги на ось Y — отрезок (вектор) BC.
Сила тяги на ось X — отрезок (вектор) AC.
Если это непонятно, посмотрите задачу №4.
Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле, ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.
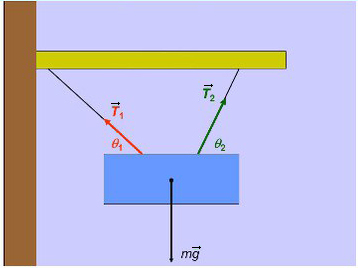
Введем оси и спроецируем силы:
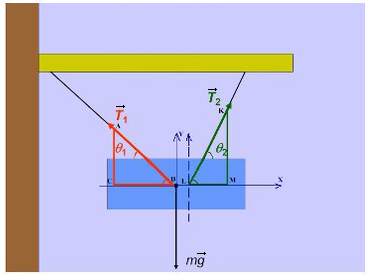
Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.
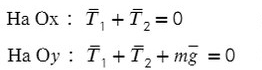
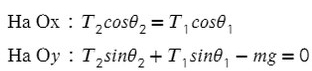
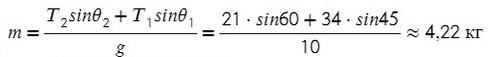
Ответ: 4,22 кг
Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?
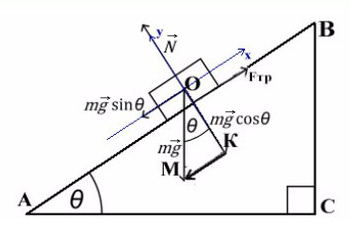
Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).
Рассмотрим поподробнее ΔKOM:
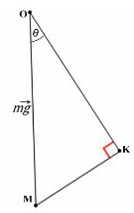
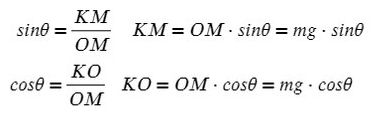Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).
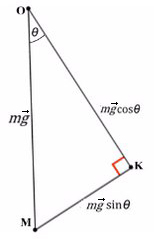
Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!
Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:
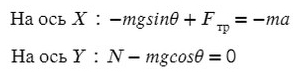
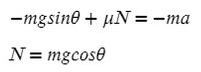
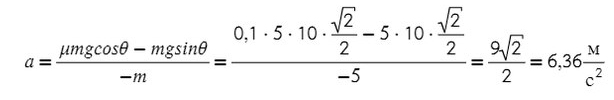
Ответ: 6,36 м/с²
Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.
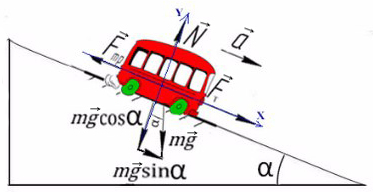
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.
Сделаем рисунок с силами:
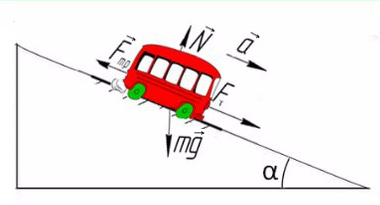
Введем оси X и Y. Спроецируем mg на оси:
Запишем второй закон Ньютона на X и Y:
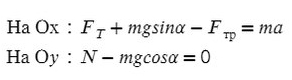
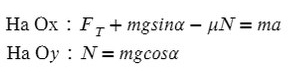
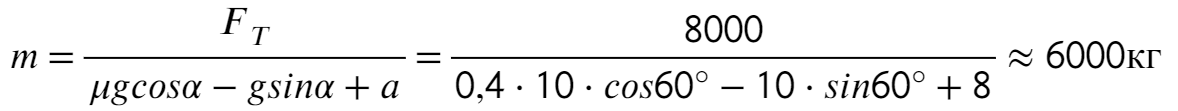
Ответ: 6000 кг
Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.
Самое сложное – понять, какие силы куда действуют, и как угол влияет на них.
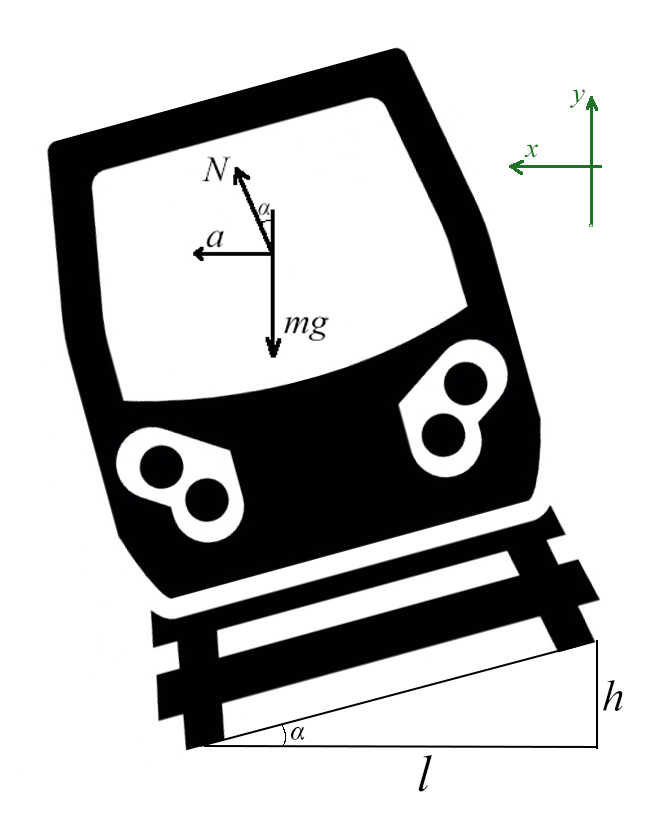
Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!
Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)
Запишем какие силы действуют на оси:
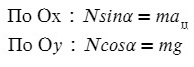
Ускорение в данной задачи центростремительное!
Поделим одно уравнение на другое:
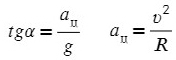
Тангенс – это отношение противолежащего катета к прилежащему:
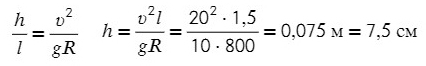
Ответ: 7,5 см
Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.
В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.
Будь в курсе новых статеек, видео и легкого технического юмора.
