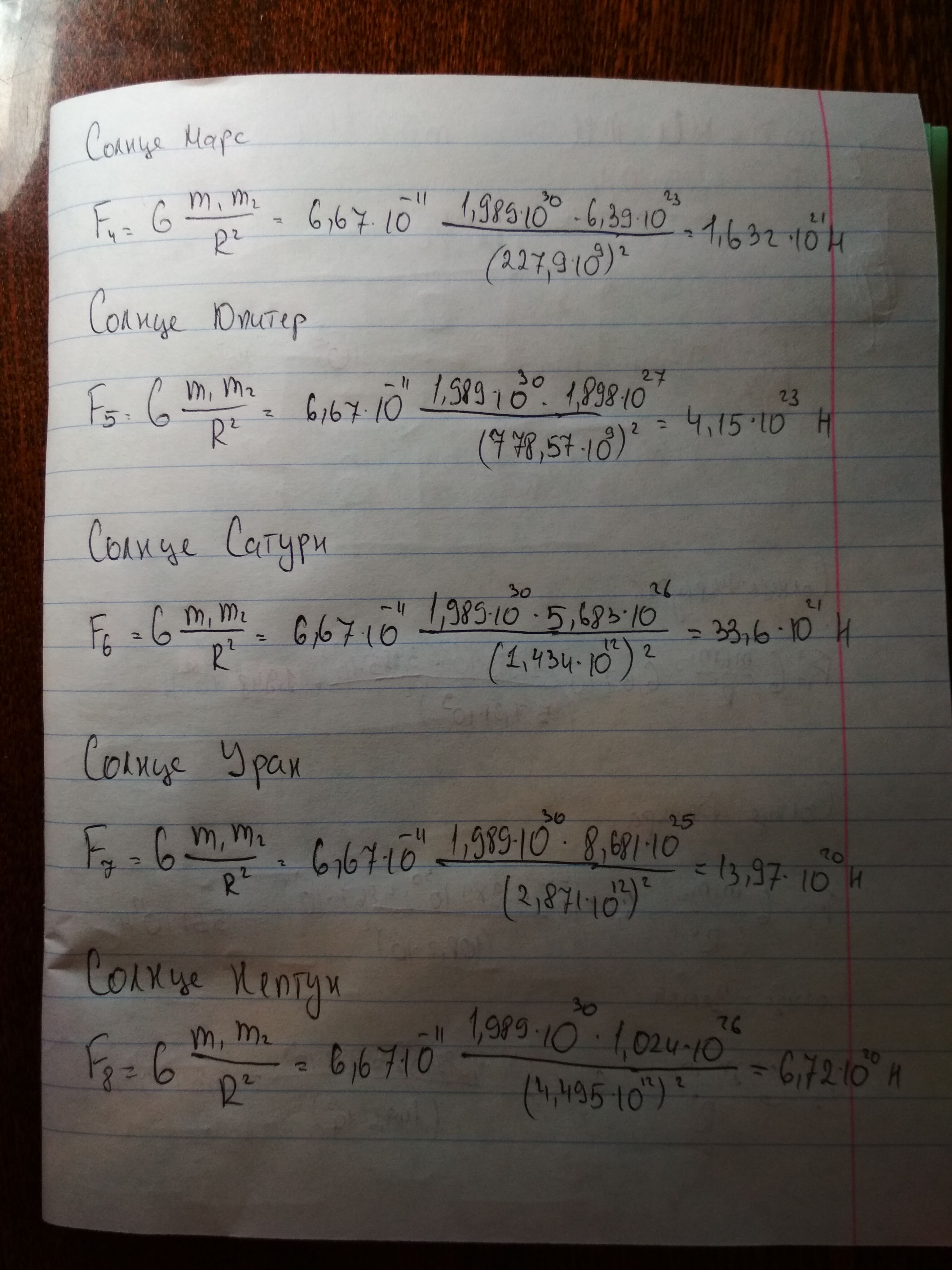Содержание
- Как найти силу тяготения между двумя планетами
- Понимание гравитации и силы тяготения
- Как найти массу планеты
- Как найти расстояние между планетами
- Пример расчета силы тяготения между двумя планетами
- Итог
- Как найти силу тяготения между двумя планетами?
- Физические законы и формулы
- Как определить массу планеты?
- Как определить расстояние между планетами?
- Примеры расчета силы тяготения
- Общий итог
- Как найти силу тяготения между двумя планетами
- Шаг 1: Определите массы планет
- Шаг 2: Определите расстояние между планетами
- Шаг 3: Используйте формулу Ньютона для вычисления силы тяготения
- Шаг 4: Используйте конвертеры единиц, если необходимо
- Итог
Как найти силу тяготения между двумя планетами
Сила тяготения – это сила, которая притягивает объекты друг к другу. Она является одной из важнейших сил во Вселенной и играет ключевую роль в движении планет и галактик.
Когда речь идет об изучении динамики движения планет, необходимо знать силу тяготения между ними. В этой статье мы расскажем, как найти силу тяготения между двумя планетами.
Понимание гравитации и силы тяготения
Силу тяготения можно понять только понимая, что такое гравитация и как она работает. Гравитация – это сила, которая притягивает объекты друг к другу в зависимости от их массы и расстояния между ними.
Сила тяготения – это сила гравитации между двумя объектами с массами M1 и M2, разделенными расстоянием r.
Формула для расчета силы тяготения: F = G * (M1 * M2) / r^2, где G – гравитационная постоянная.
Можно заметить, что сила тяготения уменьшается с увеличением расстояния между планетами, и увеличивается с увеличением массы этих планет.
Как найти массу планеты
Найти массу планеты можно разными способами. Один из них – исследование влияния планеты на другие объекты в космосе. Например, Айзек Ньютон использовал это наблюдение для расчета массы Земли, исследуя ее влияние на спутник Луны.
Современные методы включают измерение периодов вращения планеты и ее орбиты, изучение гравитационного поля и расчет массы на основе этих данных. Большинство масс планет известно по сравнению их размеров и плотности с другими известными объектами.
Как найти расстояние между планетами
Расстояние между планетами можно найти, используя спутники и космические аппараты, а также измеряя время, которое требуется для того, чтобы свет достиг планеты. Для более точных измерений используют лазерные измерения расстояния и другие технологии.
Расстояния между планетами не являются постоянными и меняются в зависимости от их положения на орбите вокруг Солнца.
Пример расчета силы тяготения между двумя планетами
Давайте рассмотрим пример расчета силы тяготения между Землей и Солнцем. Масса Земли – 5,97 x 10^24 кг, а масса Солнца – 1,99 x 10^30 кг. Расстояние между ними – около 149,6 миллионов километров.
Сначала необходимо перевести расстояние в метры: 149,6 миллионов километров * 1000 м / 1 километр = 1,496 x 10^11 м.
Затем нужно перевести массы в килограммы: 5,97 x 10^24 кг и 1,99 x 10^30 кг.
После этого можно применить формулу:
F = G * (M1 * M2) / r^2
Гравитационная постоянная G – 6.67 x 10^-11 м^3 / (кг * с^2)
Таким образом, сила тяготения между Землей и Солнцем равна:
F = 6.67 x 10^-11 м^3 / (кг * с^2) * ((5,97 x 10^24 кг) * (1,99 x 10^30 кг)) / (1,496 x 10^11 м)^2 = 3,52 x 10^22 Н.
Итог
Найти силу тяготения между двумя планетами можно, зная их массы и расстояние между ними. Сила тяготения играет важную роль в движении планет и галактик, и понимание ее поведения помогает нам лучше понять природу вселенной и предсказывать ее движение.
- Сила тяготения – это сила, которая притягивает объекты друг к другу.
- Сила тяготения между двумя объектами с массами M1 и M2, разделенными расстоянием r, рассчитывается по формуле: F = G * (M1 * M2) / r^2.
- Массу планеты можно найти разными способами, включая изучение влияния планеты на другие объекты в космосе и измерение периодов вращения и ее орбиты.
- Расстояние между планетами можно найти, используя различные методы ее измерения, включая лазерные измерения расстояния.
- Для расчета силы тяготения между двумя планетами нужно знать их массы и расстояние между ними.
Как найти силу тяготения между двумя планетами?
Сила тяготения — это взаимодействие между двумя телами, обусловленное их массой и расстоянием между ними. При расчете этой силы многие факторы играют важную роль. Один из них — расстояние между телами. В этой статье мы рассмотрим, как использовать физические законы для определения силы тяготения между двумя планетами.
Физические законы и формулы
Для расчета силы тяготения мы будем использовать законы Ньютона о движении и закон Гравитации. Они формулируются следующим образом:
«Закон Ньютона о движении: каждое тело сохраняет свое состояние покоя или равномерного прямолинейного движения, пока на него не действует внешняя сила соответствующего направления.»
«Закон Гравитации: любые два тела во Вселенной притягивают друг друга силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.»
Эти законы можно использовать для расчета силы тяготения между двумя планетами. Формула для расчета этой силы:
F = G * (m1 * m2) / r^2
- F — сила тяготения, измеряется в ньютонах (Н);
- G — гравитационная постоянная, равная 6.67 * 10^-11 Н * м^2 / кг^2;
- m1 и m2 — массы двух планет, измеряются в килограммах (кг);
- r — расстояние между двумя планетами, измеряется в метрах (м).
Как определить массу планеты?
Определение массы планеты — это ключевой элемент в расчете силы тяготения между двумя планетами. Но как вычислить ее? Существует несколько методов.
Первый метод — использование данных об орбите луны, которая вращается в околопланетном пространстве. Она подвержена силе тяготения планеты и сохраняет постоянную орбиту. Определяя орбиту луны, ученые могут вычислить массу планеты.
Второй метод — это использование измерения гравитационного поля планеты. Особенно это эффективно на планетах, у которых нет атмосферы. Этот метод может быть использован для многих планет, включая Землю.
Третий метод — это изучение вращения планеты и ее реакции на волнения в окружающей среде. Существуют многие другие методы для определения массы планеты, но эти являются наиболее точными и эффективными.
Как определить расстояние между планетами?
Определение расстояния между планетами — это другой ключевой элемент в расчетах силы тяготения. Расстояние между планетами — это расстояние между центрами масс двух планет. Как же мы можем определить это расстояние?
Первый метод — это использование астрономических наблюдений. Это включает использование парадов планет, затмений и переходов по диску Солнца. С этой целью могут быть использованы специальные инструменты, такие как телескопы и инфракрасные приборы.
Второй метод — использование оптических дальномеров. Этот способ включает использование лазерной технологии для точного измерения расстояний между планетами.
Третий метод — это использование радаров. Эти инструменты используются для измерения расстояний между космическими объектами, включая планеты.
Примеры расчета силы тяготения
Давайте посмотрим на несколько примеров расчета силы тяготения между двумя планетами.
Пример 1: расчет силы тяготения между Землей и Луной.
- Масса Земли (m1) = 5,97 x 10^24 кг;
- Масса Луны (m2) = 7,35 x 10^22 кг;
- Расстояние между Землей и Луной (r) = 384 400 км = 3,844 x 10^8 м.
Используя формулу для расчета силы тяготения, мы получим:
F = G * (m1 * m2) / r^2 = 6,67 x 10^-11 x [(5,97 x 10^24) x (7,35 x 10^22)] / (3,844 x 10^8)^2 = 1,99 x 10^20 Н
Пример 2: расчет силы тяготения между Землей и Солнцем.
- Масса Земли (m1) = 5,97 x 10^24 кг;
- Масса Солнца (m2) = 1,99 x 10^30 кг;
- Расстояние между Землей и Солнцем (r) = 149,6 млн км = 1,494 x 10^11 м.
Подставляя значения в формулу, получаем:
F = G * (m1 * m2) / r^2 = 6,67 x 10^-11 x [(5,97 x 10^24) x (1,99 x 10^30)] / (1,494 x 10^11)^2 = 3,52 x 10^22 Н
Общий итог
Конечно, расчет силы тяготения между двумя планетами может быть сложной задачей, требующей использования различных методов и формул. Тем не менее, понимание физических законов и тщательный анализ данных позволяют ученым достичь впечатляющих результатов. Надеемся, что эта статья помогла раскрыть некоторые из тайн нашей Вселенной и способствовала лучшему пониманию этой сложной темы.
Как найти силу тяготения между двумя планетами
Силу тяготения между двумя планетами может быть вычислена, используя закон всемирного тяготения Ньютона. Этот закон представляет собой математическую формулу, которая позволяет определить силу тяготения между двумя телами, основываясь на их массе и расстоянии между ними.
Шаг 1: Определите массы планет
Первый шаг заключается в вычислении масс двух планет. Масса планеты обычно измеряется в килограммах и указывается научным обозначением.
Пример: Масса Земли равна 5,97 × 10 ^ 24 кг
Информацию о массе планеты можно найти в интернете на специализированных сайтах и в научных изданиях.
Шаг 2: Определите расстояние между планетами
Следующий шаг заключается в определении расстояния между двумя планетами. Расстояние обычно измеряется в метрах. Для этого нужно использовать специализированные программы или формулы.
Пример: Расстояние между Землей и Луной составляет 385,000 км
Шаг 3: Используйте формулу Ньютона для вычисления силы тяготения
Зная массы планет и расстояние между ними, можно использовать формулу Ньютона, чтобы вычислить силу тяготения между ними.
Пример: Сила тяготения между Землей и Солнцем равна 3,52 × 10 22 Н (ньютон)
Здесь важно помнить, что единица измерения силы — ньютон.
Шаг 4: Используйте конвертеры единиц, если необходимо
Если сила тяготения была измерена не в ньютоне, необходимо использовать конвертеры единиц для перевода в ньютон.
Итог
В результате, для вычисления силы тяготения между двумя планетами, необходимо определить массы планет, расстояние между ними и использовать математическую формулу Ньютона. Знание силы тяготения между двумя планетами является важным для понимания процессов, которые происходят в космосе.
- Силу тяготения можно вычислить, используя формулу Ньютона
- Расстояние между планетами и их массы являются важными факторами для определения силы тяготения
- Единица измерения силы тяготения — ньютон
Skir Lametan
Профи
(940)
11 лет назад
Сила притяжения выражается через массы планет и расстояние между ними (т. е. их центрами) в следующем виде:
сила = гравитационная постоянная*масса первой планеты*масса второй планеты / квадрат расстояния между центрами планет. Гравитационная постоянная равна 6,673848*(10 в степени -11).
Елена Непийвода
Ученик
(158)
6 лет назад
Задача для формування думки та розвитку школярів старших класів.
Відомо, що сила тяжіння поміж Землею та Місяцем впливає на приливи-відливи, на самопочуття деяких людей. А чи може впливати взаємодія між Землею та найближчою зіркою сузір’я Зодіака, скажімо, Водолея?
Відомо, що сила тяжіння поміж планетами розраховується за формулою:
F= (G х M1 х M2) : R2 =…
Потрібно вирахувати силу тяжіння:
1.Між Землею та Місяцем.
2.Між Землею та найближчою зіркою сузір’я Зодіака, скажімо, Водолея, чи будь-якого іншого знака.
3.Порівняти ці сили і зробити висновок, чи можуть знаки Зодіака впливати на фізиологічний стан людини, якто: здоров’я, характер, відносини між людьми і т. п.
Підказка:
Для цього потрібно знати: масу і відстані між Землею та Місяцем, між Землею та зірками Зодіака та їхні маси.
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Лапчик А.Д.
1
1 ГБПОУ МО “Ногинский колледж”
Эта статья популярно рассматривает принцип работы одной из трех главных сил в механике — силу тяжести (также называемой силой притяжения) и как она меняется в зависимости от планеты, на которой может находится тело. Приведены три гипотетических сценария с падением тела, при которых углубленно объясняется концепция Закона всемирного тяготения Ньютона и представлена формула силы тяжести, с помощью которой можно найти силу тяжести действующую на тело (вес), если даны его масса и ускорение свободного падения. Чтобы рассчитать силу тяжести на других планетах, дана формула, которая учитывает массу и радиус данной планеты. В измерении силы тяжести других небесных тел используется либо показатель свободного падения в м/с², либо значением g (1g = 9,81 м/с²), т. к. сила тяжести и ускорение свободного падения пропорционально связаны друг с другом. Вычислены силы притяжения всех планет солнечной системы и других небесных тел, проведены сравнения и сделаны выводы по поводу схожих показателей силы тяжести у планет со значительной разницей в радиусе и массе.
сила тяжести
сила притяжения
гравитация
формула силы тяжести
закон всемирного тяготения ньютона
ускорение свободного падения
масса
солнечная система
гравитационная постоянная
радиус планеты
1. Маженов Н. А. Уточненный закон всемирного тяготения Ньютона // Наука и техника – электронная библиотека.– 2000 [Электронный ресурс]. URL: http://n-t.ru/tp/iz/uzn.htm (дата обращения: 07.10.2019).
2. Williams M. How Strong is Gravity on Other Planets? // Universe Today.– 2015 [Электронный ресурс]. URL: https://www.universetoday.com/35565/gravity-on-other-planets/ (дата обращения: 07.10.2019).
3. Колпаков Г. Гравитационную постоянную наконец-то измерили с большой точностью // Газета.Ru. 2014.– 19 февр [Электронный ресурс]. URL: https://www.gazeta.ru/science/2014/06/19_a_6076849.shtml (дата обращения: 07.10.2019).
4. Генденштейн Л.Э., Дик. Ю. И. Физика. 10 кл.: Учебник базового уровня для общеобразоват. учебн. заведений.– 2-е изд.– М.: Илекса, 2007.– 82 с.
5. Gerbis N. How Much Would You Weigh on Other Planets? // Live Science.– 2011 [Электронный ресурс]. URL: https://www.livescience.com/33356-weight-on-planets-mars-moon.html (дата обращения: 07.10.2019).
6. Williams M. How strong is gravity on other planets? // Phys.org – News and Articles on Science and Technology.– 2016 [Электронный ресурс]. URL: https://phys.org/news/2016-01-strong-gravity-planets.html (дата обращения: 07.10.2019).
7. Sun Fact Sheet // NASA Space Science Data Coordinated Archive [Электронный ресурс]. URL: https://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html (дата обращения: 07.10.2019).
Почему, когда вы отпускаете любое тело с высоты, если это конечно не частица света или нейтрино, оно падает вниз? Дело в том, что при падении на этот объект в основном действует сила притяжения самой Земли.
Но что такое сила притяжения? Сила притяжения (также называемая силой тяжести) всегда направлена вертикально вниз и подразумевает в себе феномен гравитации. Согласно Закону всемирного тяготения Ньютона, гравитация — это явление, в котором любые два объекта взаимно притягивают друг друга; чем больше масса хотя бы у одного из объектов, тем мощнее сила, а чем больше расстояние (в квадрате) между ними — тем она слабее [1]. Находится Сила всемирного тяготения по следующей формуле (1):
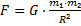
В данной формуле F — это сила тяготения, G — гравитационная постоянная (6,6742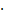
Вернемся к нашему гипотетическому сценарию. А что, если вы скинете ранее упомянутое тело с вершины самого высокого здания в мире — Бурдж-Халифа — с высотой 828 метров? Это тело будет падать и приобретать скорость с ускорением около 9,81 м/с² до тех пор, пока оно не достигнет скорость витания, которая учитывает силу сопротивления воздуха, и продолжит движение уже с постоянной скоростью (но это уже аэродинамика, лезть туда не стоит). Но почему же тело ускоряется, когда падает? Взглянув на формулу (1), можно сделать вывод, что чем больше расстояние (в квадрате) между двумя объектами, тем слабее сила (в этом случае — сила тяжести), а значит, чем меньше расстояние, тем она, разумеется, больше. При падении, тело сокращает дистанцию между собой и центром Земли (а сила исходит именно оттуда), а так как сила тяготения обратно пропорциональна квадрату расстояния между двумя объектами, тело ускоряется [1].
А если вы скинете тот же самый объект уже с высоты 10 километров? В этом случае, объект войдет в состояние свободного падения, то есть на него будет действовать только сила притяжения и, по сравнению с ней, сила сопротивления воздуха пренебрежимо мала. Силу тяжести объекта (и вес, если на него не действует постороннее ускорение) на Земле можно найти используя формулу (2):
Fтяж = mg (2)
Fтяж — это сила тяжести, m — масса объекта и g — ускорение свободного падения, которая на Земле равна около 9,81 м/с². Но, что если расширить диапазон мышления до других планет солнечной системы, и да, даже Плутона. Как будет отличаться сила тяжести на планетах земной группы и газовых гигантов от Земли?
Сначала стоит найти логический способ рассчитать силу тяжести на других планетах. Чтобы найти приблизительное ускорение свободного падения, а затем и силу тяжести планеты, можно использовать формулу (3):
g = G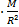
g — это ускорение свободного падения, G — гравитационная постоянная (6,67408
В сравнении силы тяжести планет может использоваться показатель ускорения (в м/с²) или буква g с коэффициентом (1g = ускорение свободного падения Земли), так как сила тяжести и ускорение свободного падения пропорционально связаны друг с другом. То есть, чем больше ускорение свободного падения на планете, тем сильнее сила тяжести. Чтобы найти силу тяжести тела на планете, можно подставить значение g определенной планеты в формулу (1).
Начнем с Плутона, самой маленькой планеты солнечной системы до 2006 года. Скорость свободного падения на этом небесном теле составляет лишь 0,6 м/с² или 0,06 g [5]. Даже у Луны сила тяжести больше чем у Плутона — 1,62 м/с² или около 0,166 g. У Меркурия показатели — 3,7 м/с² или примерно 0,38g [6]. Если масса данного тела 10 килограммов, то на Земле оно будет весить около 98 Ньютонов ( Fтяж = mg = 10кг 
Сестра Земли, Венера, имеет скорость свободного падения 8,87 м/с² или около 0,904 g, но приблизительно такие же цифры показывает Уран, газовый гигант (8,69 м/с²или 0,886 g). Еще одна аномалия — ускорение свободного падения Марса составляет лишь 3,93 м/с², а это 0,38 g, хотя радиус Марса только в 1,88 раза меньше Земли! На самом деле, никакой аномалии здесь нет, так как в формуле ускорения свободного падения (3) учитывается как радиус, так и масса планеты, а у Марса она в 9,35 раза меньше Земли [6]. Так как в формуле масса делится на радиус в квадрате, можно сделать вывод, что в ней принимается во внимание и плотность планеты, что объясняет конфуз с Венерой и Ураном, так как плотность составляющих Урана намного ниже Венеры.
У Сатурна и Нептуна тоже похожие ускорения (10,44 м/с² и 11,15 м/с²; 1,065 g и 1,14 g соответственно). Самая массовая планета солнечной системы, Юпитер, может похвастаться показателями 23,95 м/с² или 2,55 g [6]. Но даже Юпитер не может сравниться с Солнцем — 274,0 м/с² или 28 g [7].
Подведем итоги. Сила тяжести, или сила притяжения, это одна из трех видов сил в механике, которая является последствием силы гравитации. По формуле (2), можно сделать вывод, что сила тяжести зависит от массы тела и ускорения свободного падения. Однако, ускорение свободного падения на Земле отличается от остальных планет из-за разных показателей не только массы, но и радиуса. Для того, чтобы найти ускорение свободного падения небесного тела, а впоследствии и силу тяжести, нужно воспользоваться формулой (3). Затем, чтобы найти саму силу в Ньютонах, можно вновь использовать формулу, подставляя новое значение g (2). Чем больше ускорение свободного падения на планете, тем сильнее на ней сила тяжести. Так что, если вы собираетесь на интерпланетное турне, стоит заодно посмотреть погоду и силу притяжения вашего места назначения.
Библиографическая ссылка
Лапчик А.Д. СИЛА ТЯЖЕСТИ И ЕЕ ЗНАЧЕНИЯ НА ДРУГИХ ПЛАНЕТАХ // Международный студенческий научный вестник. – 2020. – № 2.
;
URL: https://eduherald.ru/ru/article/view?id=19979 (дата обращения: 23.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Сила тяжести на других планетах Солнечной системы
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Семёнова Д.С. 1
1ГБПОУ МО “Ногинский колледж” г.Балашиха
Чумаков С.А. 1
1ГБПОУ МО «НОГИНСКИЙ КОЛЛЕДЖ» г.Балашиха
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
Физические условия на поверхности планет Солнечной системы были и остаются в центре внимания астрономии. Определение силы тяжести с необходимой точностью выполняются для планирования и совершения разнообразных межпланетных миссий и применяются в проектах по освоению соседних с Землёй, планет. Необходимо точно представлять себе, какая именно сила будет воздействовать на людей со стороны планеты, чтобы вычислить вес космонавтов. Это поможет при нахождении технических решений для будущих экспедиций, например, при конструировании скафандров.
Объект исследования: сила тяжести планет Солнечной системы
Цель исследования: найти вес человека на планетах Солнечной системы.
Методы исследования: сбор и анализ информации по теме с использованием различных литературных источников.
3
Основная часть
Планеты нашей Солнечной системы представляли живой интерес для физиков и астрономов с самого момента их обнаружения на обширном космическом пространстве. При их детальном изучении в течение долгого времени было установлено, что все планеты различны по своему весу и размеру, составу поверхности, физическим и химическим свойствам, а в особенности по величине силы тяжести.
Что же такое сила тяжести? Согласно определению Большой Российской энциклопедии, «сила тяжести – это сила, действующая на любое физическое тело, находящиеся вблизи поверхности источника притяжения (астрономического тела)». Она складывается из гравитационного притяжения планеты и центробежной силы, возникающей при вращении. Как уже было сказано выше, сила тяжести на разных планетах отличается. Итак, между любой парой тел во Вселенной действует сила притяжения. Этот вывод сделан на основе расчетов Ньютона, что выявил закон всемирного тяготения, согласно которому все материальные тела притягивают друг друга, однако сила притяжения не зависит от физических и химических свойств тела. Этот закон объясняет механическое устройство Солнечной системы, с ее помощью можно рассчитать космическую скорость. Например, для того, чтобы покинуть Землю, (имеется в виду преодолеть ее гравитационное притяжение), тело должно иметь скорость 11,2 км/с. Рассмотрим показатели силы тяжести на других планетах подробнее, для наглядности сравнив их с показателями на Земле.
Как известно из большинства источников, сила тяжести может быть рассчитана по формуле F=m*g, где масса тела m умножается на величину ускорения свободного падения g. Для примера возьмём вес человека, равный 60 кг и округлим величину g до показателя в 10 м/с., следовательно, на Земле сила тяжести будет равна 600 Н. Аналогично проведём расчёт по формуле силы тяжести для других планет, используя величину свободного ускорения,
4
полученную астрономом О. Н. Коротцевым. Итак, имеем следующие данные:
Плутон – 36 Н (0,6 м/с * 60 кг)
Меркурий – 222 Н (3,7 м/с * 60 кг)
Марс – 234 Н (3,9 м/с * 60 кг)
Сатурн – 624 Н (10,4 * 60 кг)
Уран – 534 Н (8,9 м/с * 60 кг)
Венера – 540 Н (9 м/с * 60 кг)
Земля – 600 Н (10 м/с * 60 кг)
Нептун – 660 Н (11 м/с * 60 кг)
Юпитер – 1440 Н (24 м/с * 60 кг)
Как видно из расчётов, Земля по показателю силы тяжести находится между гигантами, где на Сатурне и Уране она меньше, а на Юпитере и Нептуне выше. Причём стоит отметить, что на Юпитере ключевой фактор величины силы тяжести не только в его огромных размерах, но и в величине центробежного ускорения. На Венере человек весом в 60 кг будет примерно на 10 % легче, в то время как на Меркурии и Марсе легче почти в 2,6 раза. Наиболее лёгким человек будет на Плутоне, где разница составляет 16,6 раза.
5
Заключение
Как итог, сила тяжести на различных планетах действительно различается: на одних разница невелика, а на других может достигать десятки раз. Это зависит не только от размеров планеты, твёрдости или газообразности её поверхности, но и от величины её центробежного ускорения, а также от распределения масс в недрах небесного тела.
Список литературы
Cила тяжести // Энциклопедия физики и техники URL: http://www.femto.com.ua/articles/part_2/3625.html (дата обращения: 20.10.2019).
О. Н. Коротцев Астрономия для всех. – М.: Азбука-классика, 2008.
6
Просмотров работы: 19619
Вопрос.ру
Физика, 9 класс
Готов
Вопрос от Harry Hart
1317 дней назад
Рассчитать силу всемирного тяготения между солнцем и всеми планетами(кроме плутона). Всего 8 ответов)
солнце и меркурий
солнце и …
…
Ответ от Павел
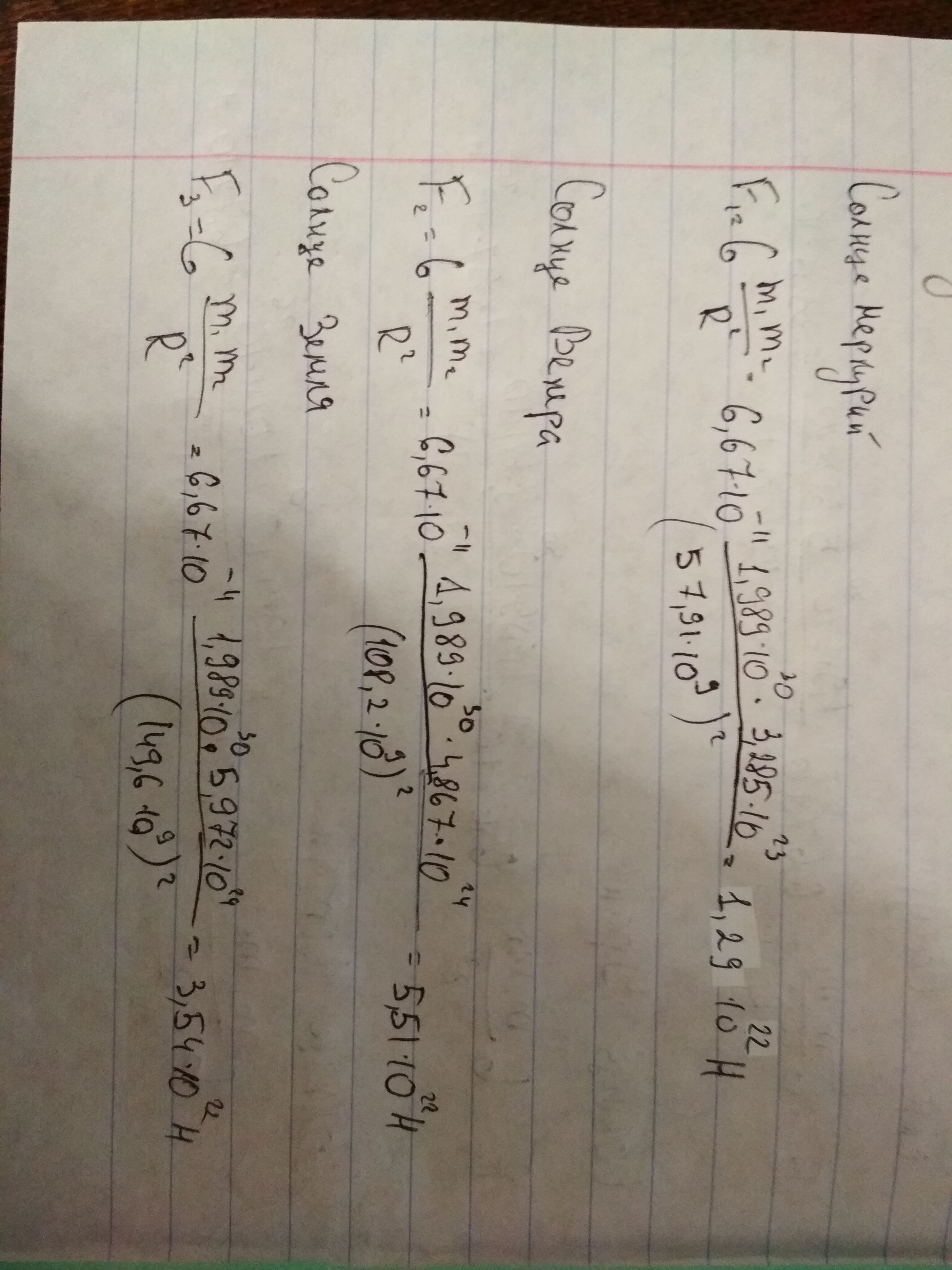
Вернуться к списку вопросов