Запрос «сила притяжения» перенаправляется сюда; см. также другие значения.
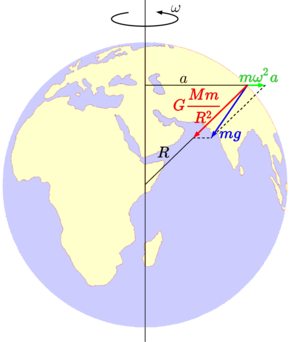
Cила тяжести mg складывается из гравитационного притяжения планеты
GMm/r2 и центробежной силы инерции
mω2a.
Си́ла тя́жести — сила, действующая на любое физическое тело вблизи поверхности астрономического объекта (планеты, звезды) и складывающаяся из силы гравитационного притяжения этого объекта и центробежной силы инерции, вызванной его суточным вращением[1][2].
Прочие приложенные к телу силы — такие как силы Кориолиса[3][4][5] при движении тела по поверхности планеты и Архимеда при наличии атмосферы или жидкости — в силу тяжести не включаются.
В большинстве практических случаев анализируется сила тяжести вблизи Земли. Для неё величина центробежной силы составляет доли процента от величины гравитационной и иногда игнорируется.
Сила тяжести 
, действующая на материальную точку массой 
, вычисляется по формуле[6]
,
где 
— ускорение свободного падения[7]. Сила тяжести является консервативной[8]. Она сообщает любому телу, независимо от его массы, ускорение [6]. Значение 
диктуется параметрами (массой 
, размерами, скоростью вращения 
) планеты или звезды и координатами на её поверхности.
Если в пределах протяжённого тела поле тяжести приблизительно однородно, то равнодействующая сил тяжести, действующих на элементы этого тела, приложена к центру масс тела[9].
В нерусскоязычной литературе термин «сила тяжести» не вводится — вместо этого говорят о фундаментальном гравитационном взаимодействии, при необходимости делая уточнение о центробежной добавке.
История[править | править код]
Личности, внёсшие исторический вклад в развитие представлений о силе тяжести:
Аристотель объяснял силу тяжести движением тяжёлых физических стихий (земля, вода) к своему естественному месту (центру Вселенной внутри Земли), причём скорость тем больше, чем ближе тяжёлое тело к нему[10].
Архимед рассмотрел вопрос о центре тяжести параллелограмма, треугольника, трапеции и параболического сегмента. В сочинении «О плавающих телах» Архимед доказал закон гидростатики, носящий его имя[10].
Иордан Неморарий в сочинении «О тяжестях» при рассмотрении грузов на наклонной плоскости разлагал их силы тяжести на нормальную и параллельную наклонной плоскости составляющие, был близок к определению статического момента[11].
Стевин экспериментально определил, что тела разных масс падают с одинаковым ускорением, установил теоремы о давлении жидкости в сосудах (давление зависит только от глубины и не зависит от величины, формы и объёма сосуда) и о равновесии грузов на наклонной плоскости (на наклонных плоскостях равной высоты силы, действующие со стороны уравновешивающихся грузов вдоль наклонных плоскостей, обратно пропорциональны длинам этих плоскостей). Доказал теорему, согласно которой в случае равновесия центр тяжести однородного плавающего тела должен находиться выше центра тяжести вытесненной жидкости[12].
Галилей экспериментально исследовал законы падения тел (ускорение не зависит от веса тела), колебаний маятников (период колебаний не зависит от веса маятника) и движения по наклонной плоскости[13].
Гюйгенс создал классическую теорию движения маятника, оказавшую значительное влияние на теорию тяготения[13].
Декарт разработал кинетическую теорию тяготения, объяснявшую силу тяжести взаимодействием тел с небесным флюидом, выдвинул гипотезу о зависимости силы тяжести от расстояния между тяжёлым телом и центром Земли[13].
Ньютон из равенства ускорений падающих тел и второго закона Ньютона сделал вывод о пропорциональности силы тяжести массам тел и установил, что сила тяжести является одним из проявлений силы всемирного тяготения[14][15]. Для проверки этой идеи он сравнил ускорение свободного падения тел у поверхности Земли с ускорением Луны на орбите, по которой она движется относительно Земли[16].
Эйнштейн объяснил факт равенства ускорений падающих тел независимо от их массы (эквивалентность инертной и тяжёлой массы)
как следствие принципа эквивалентности равномерно ускоренной системы отсчёта и системы отсчёта, находящейся в гравитационном поле[17].
Сила тяжести в различных ситуациях[править | править код]
Сферически симметричный небесный объект[править | править код]
В соответствии с законом всемирного тяготения, модуль силы гравитационного притяжения 
, действующей на материальную точку на поверхности астрономического объекта со сферически симметричным распределением массы по объёму, определяется соотношением
- ,
где 
— гравитационная постоянная, равная 6,67384(80)·10−11 м3·с−2·кг−1, 
— радиус астрономического тела, — его масса, — масса материальной точки. Сила гравитационного притяжения направлена к центру тела.
Модуль центробежной силы инерции 
, действующей на материальную точку, задаётся формулой
- ,
где 
— расстояние между частицей и осью вращения рассматриваемого астрономического объекта, — угловая скорость его вращения. Центробежная сила инерции перпендикулярна оси и направлена от неё.
Сила тяжести вычисляется по теореме косинусов:
- .
Здесь 
— «широта» места на планете или звезде, для которого производится расчёт.
Планеты Солнечной системы в шаровом приближении[править | править код]
Приближённо, Солнце и планеты Солнечной системы можно рассматривать как сферически симметричные астрономические объекты, а при грубом вычислении 
брать широту = 450 («посредине»). Сравнение силы тяжести, оцененной в таком приближении, на поверхностях[18] ряда планет представлено в таблице. За единицу принята сила тяжести на Земле[19].
| Земля | 1,00 | Солнце | 27,85 |
| Луна | 0,165 | Меркурий | 0,375—0,381 |
| Венера | 0,906 | Марс | 0,394 |
| Юпитер | 2,442 | Сатурн | 1,065 |
| Уран | 0,903 | Нептун | 1,131 |
В условиях Земли и других планет, поправки, вносимые общей теорией относительности в закон всемирного тяготения, крайне малы (модуль гравитационного потенциала на поверхности Земли, равный половине квадрата второй космической скорости 
, крайне мал по сравнению с квадратом скорости света: 
)[20].
Планета Земля с учётом особенностей её формы[править | править код]
Форма Земли (геоид) отличается от строго шарообразной и близка к сплюснутому эллипсоиду.
Соответственно, в более точном, чем шаровое, приближении, сила гравитационного притяжения, действующая на материальную точку массой , определяется выражением
- ,
где 
— элемент массы Земли (
— плотность), 
и 
— радиус-векторы точки измерения и элемента массы Земли соответственно. Интегрирование выполняется по всему объёму Земли.
В векторной форме выражение для центробежной силы инерции можно записать в виде
- ,
где 
— вектор, перпендикулярный оси вращения и проведённый от неё к точке измерения.
Сила тяжести является суммой и :
Сила тяжести вблизи поверхности Земли зависит от широты места и высоты 
над уровнем моря. Широтное изменение связано как с отклонением формы Земли от шарообразной, так и с наличием центробежной силы. Приблизительное выражение для абсолютной величины силы тяжести в системе СИ имеет вид[7]
Угол 
между силой тяжести и силой гравитационного притяжения к Земле равен[21]:
- .
Он изменяется в пределах от нуля (на экваторе, где 
и на полюсах, где 
) до 
рад или 
(на широте 
).
Дополнительно, можно учесть эффект притяжения Луны и Солнца (искусственно введя временные изменения гравитационного поля Земли, то есть добавки к ), несмотря на его малость[22][23][24].
Статика и динамика тела в поле тяжести Земли[править | править код]
Устойчивость тела в поле силы тяжести[править | править код]
Для тела в поле силы тяжести, опирающегося на одну точку (например при подвешивании тела за одну точку или помещении шара на плоскость) для устойчивого равновесия необходимо, чтобы центр тяжести тела занимал наинизшее положение по сравнению со всеми возможными соседними положениями[25].
Для тела в поле силы тяжести, опирающегося на несколько точек (например, стол) или на целую площадку (например, ящик на горизонтальной плоскости) для устойчивого равновесия необходимо, чтобы вертикаль, проведённая через центр тяжести, проходила внутри площади опоры тела. Площадью опоры тела называется контур, соединяющий точки опоры или внутри площадки, на которую опирается тело[25].
Потенциальная энергия поднятого над Землёй тела[править | править код]
Потенциальная энергия поднятого над Землёй тела может быть найдена как взятая с обратным знаком работа силы тяжести при перемещении тела с поверхности Земли в данное положение. Если пренебречь центробежной силой и считать Землю шаром, эта энергия равна:
- ,
где — гравитационная постоянная, — масса Земли, — масса тела, 
— радиус Земли, — расстояние от тела до центра Земли.
При удалении тела от поверхности Земли не небольшие, по сравнению с , расстояния поле тяготения можно считать однородным, а ускорение свободного падения постоянным. В этом случае при подъёме тела массой на высоту 
от поверхности Земли сила тяжести совершает работу 
. Поэтому потенциальная энергия тела составляет 
, если за нуль энергии взята энергия на поверхности планеты. Тело, находящееся на глубине от поверхности Земли, обладает отрицательным значением потенциальной энергии 
[26].
Движение тел под действием силы тяжести Земли[править | править код]
В случае, когда модуль перемещения тела много меньше расстояния до центра Земли, можно считать силу тяжести постоянной, а движение тела равноускоренным. Если начальная скорость тела отлична от нуля и её вектор направлен не по вертикали, то под действием силы тяжести тело движется по параболической траектории.
При бросании тела с некоторой высоты параллельно поверхности Земли дальность полёта увеличивается с ростом начальной скорости. При больших значениях начальной скорости для вычисления траектории тела необходимо учитывать шарообразную форму Земли и изменение направления силы тяжести в разных точках траектории.
При некотором значении скорости, называемом первой космической скоростью, тело, брошенное по касательной к поверхности Земли, под действием силы тяжести при отсутствии сопротивления со стороны атмосферы может двигаться вокруг Земли по окружности, не падая на Землю. При скорости, превышающую вторую космическую скорость, тело уходит от поверхности Земли в бесконечность по гиперболической траектории. При скоростях, промежуточных между первой и второй космическими, тело движется вокруг Земли по эллиптической траектории[27].
Глобальная роль силы тяжести в природе[править | править код]
В эволюции строения планет и звёзд[править | править код]
Сила тяжести играет огромную роль в процессах эволюции звёзд. Для звёзд, находящихся на этапе главной последовательности своей эволюции, сила тяжести является одним из важных факторов, обеспечивающих условия, необходимые для термоядерного синтеза. На заключительных этапах эволюции звёзд, в процессе их коллапса, благодаря силе тяжести, не скомпенсированной силами внутреннего давления, звёзды превращаются в нейтронные звёзды или чёрные дыры.
Сила тяжести важна для формирования внутренней структуры планет, включая Землю, и тектонической эволюции их поверхностей[28]. Чем больше сила тяжести, тем большая масса метеоритного материала выпадает на единицу поверхности планеты[29]. За время существования Земли её масса существенно увеличилась благодаря силе тяжести: ежегодно на Землю оседает 30-40 млн тонн метеоритного вещества, в основном в виде пыли, что значительно превышает рассеяние лёгких компонентов верхней атмосферы Земли в космосе[30].
Потенциальная энергия перемещаемых тектоническими процессами масс горных пород тратится на перемещение продуктов разрушения горных пород с повышенных участков поверхности на нижерасположенные[31].
В создании условий для жизни на Земле[править | править код]
Сила тяжести чрезвычайно значима для жизни на Земле[32]. Только благодаря ей у Земли есть атмосфера. Вследствие силы тяжести, действующей на воздух, существует атмосферное давление[33].
Без потенциальной энергии силы тяжести, непрерывно переходящей в кинетическую, круговорот вещества и энергии на Земле был бы невозможен[34].
При испарении воды с поверхности Земли энергия солнечной радиации трансформируется в потенциальную энергию водяного пара в атмосфере. Затем при выпадении атмосферных осадков на сушу она переходит при стоке в кинетическую энергию и совершает эрозионную работу в процессе переноса денудационного материала всей суши и делает возможным жизнь органического мира на Земле[35].
У всех живых организмов с нервной системой есть рецепторы, определяющие величину и направление силы тяжести и служащие для ориентировки в пространстве. У позвоночных организмов, в том числе человека, величину и направление силы тяжести определяет вестибулярный аппарат[36].
Наличие силы тяжести привело к возникновению у всех многоклеточных наземных организмов прочных скелетов, необходимых для её преодоления. У водных живых организмов силу тяжести уравновешивает гидростатическая сила[37].
Роль силы тяжести в процессах жизнедеятельности организмов изучает гравитационная биология[38].
Применение силы тяжести Земли в технике[править | править код]
Сила тяжести и принцип эквивалентности инертной и гравитационной массы используются для определения масс предметов путём их взвешивания на весах. Сила тяжести используется при отстойной сепарации газовых и жидких смесей, в процессах гравитационного обогащения полезных ископаемых, в некоторых типах часов, в отвесах и противовесах, машине Атвуда, машине Обербека и жидкостных барометрах. Сила тяжести используется на железнодорожном транспорте для скатывания вагонов с уклона на сортировочных горках, на заводах строительных изделий для транспортировки материалов в спускных лотках и спускных трубах.[39]
Точные измерения силы тяжести и её градиента (гравиметрия) используются при исследовании внутреннего строения Земли и при гравиразведке различных полезных ископаемых[40].
Методы измерения силы тяжести[править | править код]
Основной источник: [41]
Силу тяжести измеряют динамическими и статическими методами. Динамические методы используют наблюдение за движением тела под действием силы тяжести и измеряют время перехода тела из одного заранее определённого положения в другое. Они используют: колебания маятника, свободное падение тела, колебания струны с грузом. Статические методы используют наблюдение за изменением положения равновесия тела под действием силы тяжести и некоторой уравновешивающей её силы и измеряют линейное или угловое смещение тела.
Измерения силы тяжести бывают абсолютными и относительными. Абсолютные измерения определяют полное значение силы тяжести в заданной точке. Относительные измерения определяют разность силы тяжести в заданной точке и некоторого другого, заранее известного значения. Приборы, предназначенные для относительных измерений силы тяжести, называются гравиметрами.
Динамические методы определения силы тяжести могут быть как относительными, так и абсолютными, статические — только относительными.
См. также[править | править код]
- Вес
- Ускорение свободного падения
- Гравиметрия (геодезия)
Примечания[править | править код]
- ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 372. — 560 с. — ISBN 5-9221-0225-7.
- ↑ Тарг С. М. Сила тяжести // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 496. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Тарасов, 2012, с. 200, 270.
- ↑ Савельев, 1987, с. 128.
- ↑ Бутенин, 1971, с. 253—259.
- ↑ 1 2 Савельев, 1987, с. 70.
- ↑ 1 2 Ускорение свободного падения // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5. — С. 245—246. — 760 с. — ISBN 5-85270-101-7.
- ↑ Савельев, 1987, с. 82—83.
- ↑ Савельев, 1987, с. 156.
- ↑ 1 2 Зубов В. П. Физические идеи древности // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 38, 54-55;
- ↑ Зубов В. П. Физические идеи средневековья // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 114;
- ↑ Зубов В. П. Физические идеи ренессанса // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 151;
- ↑ 1 2 3 Кузнецов Б. Г. Генезис механического объяснения физических явлений и идеи картезианской физики // отв. ред.
Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 160—161, 169—170, 177; - ↑ Ньютон, 1989, с. 7.
- ↑ Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 189—191;
- ↑ Сивухин Д. В. Общий курс физики. Механика. — М., Наука, 1979. — Тираж 50 000 экз. — с. 323
- ↑ Иваненко Д. Д. Основные идеи общей теории относительности // отв. ред. Григорьян А. Т., Полак Л. С.
Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 300; - ↑ У газовых гигантов «поверхность» понимается как область высот в атмосфере, где давление равно атмосферному давлению на Земле на уровне моря (1,013×105 Па).
- ↑ Данные взяты из статьи Википедии Ускорение свободного падения
- ↑ Грищук Л. П., Зельдович Я. Б. Тяготение // Физика космоса. Маленькая энциклопедия. — М., Советская энциклопедия, 1986. — С. 676
- ↑ Савельев, 1987, с. 122.
- ↑ Миронов, 1980, с. 49.
- ↑ Максимальное изменение силы тяжести, обусловленное притяжением Луны, составляет примерно м/с2, Солнца м/с2
- ↑ Миронов, 1980, с. 71.
- ↑ 1 2 Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика, теплота, молекулярная физика. — М., Наука, 1975. — Тираж 350 000 экз. — С. 189—190
- ↑ Кабардин О. Ф., Орлов В. А., Пономарева А. В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — Тираж 143 500 экз. — С. 151—152
- ↑ Жирнов Н. И. Классическая механика. — М., Просвещение, 1980. — Тираж 28000 экз. — с. 121
- ↑ Криволуцкий, 1985, с. 208.
- ↑ Криволуцкий, 1985, с. 77.
- ↑ Криволуцкий, 1985, с. 48, 237-238.
- ↑ Криволуцкий, 1985, с. 70, 234.
- ↑ Зельманов А. Л. Многообразие материального мира и проблема бесконечности Вселенной // Бесконечность и Вселенная. — М., Мысль, 1969. — Тираж 12000 экз. — С. 283
- ↑ Хромов С. П., Петросянц М. А. Метеорология и климатология. — М., МГУ, 2006. — ISBN 5-211-05207-2. — C. 67
- ↑ Криволуцкий, 1985, с. 289.
- ↑ Криволуцкий, 1985, с. 307.
- ↑ Юрий Фролов. https://www.nkj.ru/archive/articles/21172/ Наш гравитационный компас] // Наука и жизнь. — 2012. — № 10.
- ↑ П. Кемп, К. Армс Введение в биологию. — М.: Мир, 1988. — ISBN 5-03-001286-9. — Тираж 125000 экз. — С. 75
- ↑ Лозовская Е. Жизнь с гравитацией и без нее // Наука и жизнь. — 2004. — № 9. Архивировано 31 января 2018 года.
- ↑ Фиделев А. С. Подъемно-транспортные машины и механизмы. — Киев, Будивельник, 1967. — 187—188
- ↑ Миронов, 1980, с. 1—543.
- ↑ Миронов, 1980, с. 94—262.
Литература[править | править код]
- Ньютон И. Математические начала натуральной философии. — М.: Наука, 1989. — 688 с. — ISBN 5-02-000747-1.
- Савельев И. В. Курс общей физики. Т. 1. Механика. Молекулярная физика. — М.: Наука, 1987. — 688 с.
- Криволуцкий А. Е. Голубая планета. Земля среди планет. Географический аспект. — М.: Мысль, 1985. — 335 с.
- Миронов В. С. Курс гравиразведки. — Л.: Недра, 1980. — 543 с.
- Тарасов В. Н., Бояркина И. В., Коваленко М. В., Федорченко Н. П., Фисенко Н. И. Теоретическая механика. — М.: ТрансЛит, 2012. — 560 с.
- Бутенин Н. В. Введение в аналитическую механику. — М.: Наука, 1971. — 264 с. — 25 000 экз.
Разбираетесь с такой физической категорией, как сила тяжести? Формула, ее составляющие и единицы измерения укажут, что сильнее притянет Земля — яблоко или поезд. Отличается ли сила тяжести от силы тяготения? Объясним, как не перепутать эти две величины.
Что такое сила тяжести
Каждый день наблюдаем, как тела вокруг деформируются (меняют форму или размеры), ускоряются или тормозят, падают. В реальной жизни с различными телами происходят самые разнообразные вещи. Причина всех действий и взаимодействий кроется в некой силе. О чем идет речь?
Понятие силы
Силой называют физическую векторную величину, которая оказывает воздействие на тело, а ее источниками становятся другие тела. Что означает понятие векторной величины? Это говорит о том, что сила наделена направлением. В зависимости от того, куда она направлена, можно получить разные результаты.
Это как если стоять на вершине горы на сноуборде, то от направления толчка будет зависеть дальнейшее движение. Таков результат приложения силы в этом случае. Силы, которые изучают ученые-физики, разнообразны и очень важны для нашей повседневной жизни.
Определение и значение силы тяжести
Одна из них носит название сила тяжести. Физика предлагает следующее определение: сила тяжести — это величина, которая показывает, насколько сильно Земля притягивает тело, которое расположено на ее поверхности или рядом с ней. Таким образом, направление этой силы — центр нашей планеты.
Сила тяжести на Земле крайне важна по следующим причинам:
- Наша планета притягивает все, что попадает в сферу действия этой силы, будь то твердое тело, жидкость или газ.
- Благодаря ее существованию стало возможным создание атмосферы (молекулы газов, которые ее составляют, не улетают в космические просторы), появились и остаются на своих местах моря и океаны.
- Любой предмет, который приподнимаем и роняем, обязательно упадет вниз по направлению к Земле.
Кстати, именно из-за воздействия этой силы люди не могут летать. Самостоятельно развить скорость, на которой полет становится возможным (так называемую первую космическую) человек не способен, а потому в обычной жизни всегда твердо стоит ногами на Земле.
Сила тяжести и сила тяготения: отличия
Сила тяжести, определение которой дали выше, схожа с силой тяготения. Оба варианта связывает сила притяжения.
Однако эти две силы не одно и то же, хоть их и часто путают. Давайте разберемся, в чем тут дело.
Еще в 1682 году Исаак Ньютон открыл закон о всемирном тяготении. Сформулирован он был так: тела притягивают друг друга, а сила этого тяготения — величина, прямо пропорциональная произведению их масс и обратно пропорциональна расстоянию, возведенному в квадрат.
Математически силу тяготения записывают так: F = G×M×m/R², где:
- F — сила тяготения, Н;
- M — масса первого тела (часто планеты), кг;
- m — масса второго тела, кг;
- R — дистанция между ними, м;
- G — постоянная величина (G = 6,67×10⁻¹¹ м³×кг⁻¹×с⁻²).
Продемонстрировать эту силу легко — достаточно встать на весы. Стрелка сразу же отклонится, показывая вес тела. Так происходит из-за очень большой массы Земли, благодаря которой мы придавлены к ней. На Луне, масса которой меньше, вес человека меньше в несколько раз.
Итак, закон о всемирном тяготении и соответствующая сила необходимы для вычисления силы взаимодействий между разнообразными телами. При этом их размеры должны быть меньше, чем расстояние между ними.
Теперь вернемся к нашей теме и рассмотрим подробно, что же такое сила тяжести, обозначение которой дали выше, и как она связана с силой тяготения.
Сила тяжести: формула, единицы измерения
Напомним, что когда говорим о силе тяжести, то имеем в виду силу, с которой осуществляет притяжение наша планета.
Формула силы тяжести такова: F = m×g, где:
- F — сила тяжести, Н;
- m — масса тела, кг;
- g — ускорение свободного падения, м/с².
В этой формуле видим новую величину — ускорение свободного падения. Так называют ускорение, которое приобретает тело рядом с Землей во время свободного и беспрепятственного падения. Рядом с поверхностью Земли значение этой величины примерно равняется 9,81 м/с², а в приблизительных расчетах используют округленное значение 10 м/с².
По этой формуле рассчитывается сила тяжести, единица измерения которой — Ньютоны (в честь Исаака Ньютона).
Чему равна сила тяжести? Глядя на эту формулу, можно сказать, что сила тяжести схожа с весом тела. В покое на Земле эта величина и вес будут идентичны. Но это не одно и то же. Почему? Объяснение не сложное:
- Силой, с которой на тела действует Земля, называют силу тяжести.
- Вес тоже сила, с которой тела действуют на опору.
- То есть у них отличаются точки действия: первая направлена на центр массы тел, а вес направлен на опору.
Кроме того, на величину силы тяжести влияет масса и планета, на которой проводятся измерения. Вес определяется также ускорением, с которым происходит движение тела и опоры.
К примеру, вес тела в лифте определяется тем, в каком направлении и как быстро происходит движение тела. Сила тяжести не учитывает, куда и что движется: эти внешние факторы на нее не влияют.
Итак, с весом разобрались. А что же с силой тяготения, которую упоминали выше? Можем ли две эти силы приравнять? На этот раз ответ будет утвердительным. Но только, когда мы говорим о Земле и теле, которое к ней притягивается. В этом случае обе силы будут равны.
Выразим это математически:
- F = m×g.
- F = G×M×m/R².
- m×g = G×M×m/R².
Если обе части полученного уравнения разделить на массу, то получим такую формулу: g = G×M/R².
Величина g (ускорение свободного падения) уникальна для каждой планеты:
- На нашей Земле свободно падающее тело с каждой секундой ускоряется примерно на 9,81 метр (м/с²).
- Ускорение свободного падения рядом с Луной имеет величину всего 1,62 м/с².
- На Юпитере это значение достигает 26,2 м/с². Человек, который весит 60 кг, на этой планете почувствует себя так, будто бы поправился на 100 кг.
Как изменится величина, если тело будет падать 4 секунды? Попробуем подсчитать:
- Скорость падения в начальной точке составит 0 м/с².
- В течение первой секунды она увеличится до 9,81 м/с².
- За вторую секунду величина вырастет вдвое и составит 19,62 м/с².
- Третья секунда добавить еще одну величину ускорения и получится 29,43 м/с².
- В четвертую секунду скорость движения тела достигнет 39,24 м/с², что равняется приблизительно 141 км/ч.
Отметим, что яблоко и кирпич будут падать с равной скоростью. Только очень легкие предметы во время падения замедляет воздух, оказывая им ощутимое сопротивление. Так, птичье перышко будет совершать падение очень медленно и плавно.
Задумываемся об этом или нет, на каждого из нас оказывает воздействие сила тяжести. Формула ее расчета состоит из массы, умноженной на величину ускорения свободного падения. Эта сила показывает воздействие планет на тела, которые находятся рядом с их поверхностями. Поэтому ее величина отличается на Земле и на Луне.
Оригинал статьи: https://www.nur.kz/family/school/1909020-sila-tyazhesti-formula-edinitsy-izmereniya-osobennosti/
Понятие о силе тяжести в физике
Содержание:
- Что такое сила тяжести
-
Формулы для нахождения
- Единица измерения
- Расчет через массу m и ускорение свободного падения g
- Закон всемирного тяготения Ньютона
- Примеры решения задач
Что такое сила тяжести
Сила тяжести — гравитационная сила, с которой Земля или другой астрономический объект притягивает тело на поверхности, или вблизи себя.
Гравитация — универсальное фундаментальное взаимодействие между всеми материальными телами.
Впервые понятие «силы тяжести» возникло в теориях Аристотеля, который объяснял это явление движением тяжелых физических стихий (земля, вода) к своему естественному местоположению (к центру Вселенной, который, как он полагал, находится внутри Земли). Также Аристотель рассуждал от чего зависит скорость притяжения. По его мнению чем ближе тяжелое тело к центру, тем больше скорость притяжения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В дальнейшем, Архимед рассуждал о центрах тяжести геометрических фигур. Стевин на опытах установил, что тела разных масс падают с одинаковым ускорением. Галилей работал в том же направлении и экспериментально изучал законы падения тел. Гюйгенс разработал классическую теорию движения маятника. Декарт создал кинетическую теорию тяготения. Ньютон, благодаря своему II закону и равенству ускорений падающих тел сделал вывод о связи массы тела и силы тяжести, а так же доказал, что сила тяжести — одно из проявлений силы всемирного тяготения.
Примечание
Ошибочно полагать, что сила гравитационного притяжения и сила тяжести — это одно и то же. Эта сила лишь одна составляющая силы тяжести, вторая — центробежная сила инерции.
Формулы для нахождения
Единица измерения
Эта величина в СИ (системе интернациональной), как и любая другая сила измеряется в Ньютонах: (lbrack F_{тяж}rbrack=Н)
Расчет через массу m и ускорение свободного падения g
(F_{тяж}=mg)
Для решения задач обычно используют (gapprox10frac н{кг})
Закон всемирного тяготения Ньютона
Два любых тела притягиваются друг к другу с силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними.
(F=Gfrac{m_1m_2}R), где F — сила притяжения, G — гравитационная постоянная ((G=6,67cdot10^{-11}frac{Нcdot м^2}{кг^2}), m_1,m_2) — массы тел, R — расстояние между ними.
Применим для:
- материальных точек;
- шаров;
- шара большого радиуса и тела.
Из этого закона выводится вторая формула для силы тяжести:
(F_{тяж}=Gfrac{M_пcdot m}{R_п^2}), где (F_{тяж}) — сила тяжести, G — гравитационная постоянная, (M_п) — масса планеты, m — масса тела, (R_п) — радиус планеты.
Примеры решения задач
Задача №1
Какова масса человека, если Земля притягивает его с силой 600 Н?
Дано: (F_{тяж}=600;Н, gapprox10frac н{кг})
Решение: (F_{тяж}=mg), значит (m=frac{F_{тяж}}g; m=frac{600;H}{10;{displaystylefrac Н{кг}}}=60;кг)
Ответ: 60 кг
Задача №2
Найдите силу тяжести тела, масса которого 7 кг?
Дано: (m=7кг, gapprox10frac н{кг})
Решение: (F_{тяж}=mg, F_{тяж}=7;кгcdot10frac Н{кг}=70;Н)
Ответ: 70 Н
Задача №3
Сравните силы тяжести, действующие на тела с массами 3 кг и 6 кг.
Решение: сила тяжести прямо пропорциональна массе тела, т.е. они отличаются в одинаковое количество раз. Масса второго тела в 2 раза больше массы первого, значит сила тяжести второго тела будет в 2 раза больше силы тяжести первого.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 7)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Чтобы найти силу тяжести надо массу умножить на ускорение свободного падения.
То есть сила тяжести вычисляется по формуле:
{ F=mg }
g- величина постоянная.
Она равна : g= 9.8 м/с в квадрате. Иногда, при подсчёте. Её округляют до 10.
Если бы не было силы тяжести человек бы не ходил, а летал.
Схему сил действующих на тело используют при решении задач по физике. Например, вычислить силу тяжести, если известна его масса
Дано:
m=45 кг
g = 9.8
Найти: F – ?
Решение:
F=mg = 45*8= 360 Н
Ответ: 360 Н
Сила измеряется в Ньютонах.
Бывает запись килоньютон, то есть 1 кН= 1000 Н
При решении любой задачи используется краткая запись. Физические величины переводятся по системе СИ.
Прежде чем решить задачу надо записать условие, повторить формулы и определить точные условия в которых находится тело.
В конце обязательно записать ответ и рядом с числом единицу измерения.
Решим, еще задачи.
Чему равна сила тяжести наполненного водой чайника. Если его общая масса равна 2555 г.
Задача 356
Дано:
m = 2555 г = 2,555 кг;
g = 9.81;
Найти: F тяж – ?
Решение:
F тяж = 2,555*9,81 = 25,06455 = 25,07 (Н).
Ответ: 25,07 Н.
Задача 1232
Собака сидит на будке. Какова её масса, если она действует на крышу с силой тяжести равной 65 Н.
Дано:
F тяж = 65 Н;
g = 9,81.
Найти: m – ?
Решение:
m = 65 Н/9,81 = 6,625891 = 6.626 кг.
Ответ: 6,626 кг.
Сила — это векторная физическая величина, имеющая направление и численное значение. Как же определить ее численное значение?
Что значит измерить какую-либо силу? Как вы уже знаете, для этого нам необходимо определить единицу измерения — некий эталон, принятый за единицу. За такую единицу можно принять любую силу. Например, силу тяжести, которая действует на какое-то определенное тело.
Также можно принять и силу упругости выбранной пружины, растянутой до некоторой длины. На данном уроке вы узнаете, какую силу приняли за единицу, получите формулу для определения силы тяжести и научитесь ею пользоваться для решения задач.
Единицы силы
Если изменяется скорость тела, то мы можем сказать, что на него действует сила. Итак, что принято за единицу силы?
За единицу силы принята сила, которая за время $1 space c$ изменяет скорость тела массой $1 space кг$ на $1 frac{м}{с}$.
Данная единица называется ньютоном ($1 space Н$). Она была названа в честь знаменитого английского физика, механика и астронома Исаака Ньютона (рисунок 1).
Часто используются и другие единицы — килоньютон ($кН$) и миллиньютон ($мН$).
$1 space кН = 1000 space Н$,
$1 space Н = 0,001 space кН$.
$1 space Н = 1000 space мН$,
$1 space мН = 0,001 space Н$.
Связь между силой тяжести и массой тела
Теперь мы знаем единицу измерения силы. Но как ее представить? С чем сравнить? Что это за сила в $1 space Н$?
Рассмотрим силу тяжести, равную $1 space Н$.
Доказано, что с такой силой притягивается к Земле тело массой приблизительно $frac{1}{10} space кг$. Если быть более точными, эта масса составляет $frac{1}{9.8} space кг$ (около $102 space г$). Но чему будет равна сила тяжести, действующая на тело другой массы?
Нам известно, что сила тяжести прямо пропорциональна массе рассматриваемого тела. Если мы возьмем два тела с разными массами, то во сколько раз отличаются друг от друга массы двух тел, во столько же раз будут отличаться силы тяжести, действующие на них.
Теперь используем новую информацию.
На тело массой $frac{1}{9.8} space кг$ действует сила тяжести в $1 space Н$.
Возьмем тело с массой в 2 раза большей — $frac{2}{9.8} space кг$. Тогда сила тяжести тоже будет в 2 раза больше — $2 space Н$.
Очевидно, что на тело с массой $frac{7}{9.8} space кг$ будет действовать сила тяжести, равная $7 space Н$, на тело с массой $frac{7.5}{9.8} space кг$ — $7.5 space Н$ и т.д.
А теперь возьмем тело с массой $frac{9.8}{9.8} space кг$. На него будет действовать сила тяжести, равная $9.8 space Н$. Посмотрите внимательнее на массу данного тела: $frac{9.8}{9.8} space кг = 1 space кг$.
На тело массой $1 space кг$ действует сила тяжести, равная $9.8 space Н$
Значение данной силы, действующей на тело массой $1 space кг$, можно записать как: $9.8 space frac{Н}{кг}$.
Формула для расчета силы тяжести. Ускорение свободного падения
Давайте снова используем свойство прямо пропорциональности массы и силы тяжести:
- если мы возьмем тело с массой $2 space кг$ (а это в 2 раза больше, чем масса $1 space кг$), то сила тяжести будет равна $19.6 space Н$ ($9.8 space Н cdot 2$)
- если мы возьмем тело с массой $3 space кг$ (а это в 3 раза больше, чем масса $1 space кг$), то сила тяжести будет равна $29.4 space Н$ ($9.8 space Н cdot 3$)
Так мы можем продолжать бесконечно, рассматривая тела различных масс. Таким образом,
Чтобы определить силу тяжести, действующую на тело любой массы, нужно $9.8 frac{Н}{кг}$ умножить на массу выбранного тела:
$F_{тяж} = 9.8 frac{Н}{кг} cdot m$.
Величину $9.8 frac{Н}{кг}$ обозначают буквой $g$ и называют ускорением свободного падения.
Так мы получили формулу для силы тяжести. Как рассчитать силу тяжести, действующую на тело любой массы?
$F_{тяж} = gm$
Если тело и опора неподвижны или движутся равномерно и прямолинейно, то мы получим формулу для веса тела.
По какой формуле можно определить вес тела?
$$P = F_{тяж} = gm$$
Примеры задач
Если для решения задачи не требуется особой точности, $g = 9.8 frac{Н}{кг}$ округляют до $g = 10 frac{Н}{кг}$. Если в тексте задачи нет информации о точности или используемой величине ускорения свободного падения, то используется $g = 9.8 frac{Н}{кг}$.
Задача №1
На столе лежит книга массой $700 space г$. Определите силу тяжести и вес книги. Покажите эти силы на рисунке, используя масштаб, где за $1 space Н$ равен $0.5 space си$. При расчетах используйте ускорение свободного падения равное $10 frac{Н}{кг}$.
Дано:
$m = 700 space г$
$g = 10 frac{Н}{кг}$
СИ:
$m = 0.7 space кг$
$F_{тяж} — ?$
$P — ?$
Показать решение и ответ
Скрыть
Решение:
Используем формулы: $F_{тяж} = gm$ и $P = gm$.
$F_{тяж} = P approx 10 frac{Н}{кг} cdot 0.7 space кг = 7 space Н$.
Сила тяжести и вес изображены на рисунке 2. Из условия задачи $1 space Н$ будет равен отрезку $0.5 space см$. Тогда сила в $7 space Н$ будет изображаться отрезком длиной $3.5 space см$. Сила тяжести у нас приложена к телу и направлена вертикально вниз (рисунок 2, а), а вес — к опоре и направлен перпендикулярно ей (в данном случае вертикально вниз — рисунок 2, б).
Ответ: $F_{тяж} = P = 7 space Н$.
Задача №2
Найдите вес воды объемом $4 space дм^3$. Вода находится в неподвижном сосуде.
Для решения этой задачи найдем табличное значение плотности воды — $1000 frac{кг}{м^3}$.
Переведем объем, выраженный в $дм^3$, в $м^3$:
$4 space дм^3 = 4 cdot 1 space дм cdot 1 space дм cdot 1 space дм = 4 cdot 0.1 space м cdot 0.1 space м cdot 0.1 space м = 4 cdot 0.001 space м^3 = 0.004 space м^3$.
Теперь можно записать условия задачи и решить ее.
Дано:
$V = 4 space дм^3$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
СИ:
$V = 0.004 space м^3$
$P — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для определения веса имеет вид:
$P = gm$.
Массу воды мы можем определить, зная ее плотность и объем:
$m = rho V$.
Подставим в формулу для определения веса:
$P = gm = g rho V$.
$P = 9.8 frac{Н}{кг} cdot 1000 frac{кг}{м^3} cdot 0.004 space м^3 = 39.2 space Н$.
Ответ: $P = 39.2 space Н$.
Задача №3
Люстра, подвешенная к потолку, действует на него с силой $63.7 space Н$. Найдите массу люстры.
Для того чтобы верно записать условия задачи, нужно понимать, как люстра действует на потолок. Люстра неподвижна, значит, речь идет о весе.
Дано:
$P = 63.7 space Н$
$g = 9.8 frac{Н}{кг}$
$m — ?$
Показать решение и ответ
Скрыть
Решение:
Итак, люстра действует на потолок своим весом. На люстру же действует сила тяжести, численно равная весу люстры.
Воспользуемся формулой:
$P = gm$.
Выразим массу:
$m = frac {P}{g}$.
$m = frac {63.7 space Н}{9.8 frac{Н}{кг}} = 6.5 space кг$.
Ответ: $m = 6.5 space кг$.
Больше задач на расчет силы тяжести, а также веса тела и силы упругости смотрите в отдельном уроке.
Упражнения
Упражнение №1
Определите силу тяжести, действующую на тело массой $3.5 space кг$; $400 space г$; $1.5 space т$; $60 space г$.
Дано:
$m_1 = 3.5 space кг$
$m_2 = 400 space г$
$m_3 = 1.5 space т$
$m_4 = 60 space г$
$g approx 10 frac{Н}{кг}$
СИ:
$m_2 = 0.4 space кг$
$m_3 = 1500 space кг$
$m_4 = 0.06 space кг$
$F_{тяж1} — ?$
$F_{тяж2} — ?$
$F_{тяж3} — ?$
$F_{тяж4} — ?$
Показать решение и ответ
Скрыть
Решение:
Для расчета силы тяжести будем использовать формулу: $F_{тяж} = gm$.
$F_{тяж1} = gm_1$,
$F_{тяж1} = 10 frac{Н}{кг} cdot 3.5 space кг = 35 space Н$.
$F_{тяж2} = gm_2$,
$F_{тяж2} = 10 frac{Н}{кг} cdot 0.4 space кг = 4 space Н$.
$F_{тяж3} = gm_3$,
$F_{тяж3} = 10 frac{Н}{кг} cdot 1500 space кг = 15000 space Н = 15 space кН$.
$F_{тяж4} = gm_4$,
$F_{тяж4} = 10 frac{Н}{кг} cdot 0.06 space кг = 0.6 space Н$.
Ответ: $F_{тяж1} = 35 space Н$, $F_{тяж2} = 4 space Н$, $F_{тяж3} = 15 space кН$, $F_{тяж4} = 0.6 space Н$.
Упражнение №2
Найдите вес тела, масса которого $5 space кг$, $300 space г$.
Дано:
$m_1 = 5 space кг$
$m_2 = 300 space г$
$g approx 10 frac{Н}{кг}$
$P_1 — ?$
$P_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Для расчета веса тел будем использовать формулу: $P = F_{тяж} = gm$.
$P_1 = gm_1$,
$P_1 = 10 frac{Н}{кг} cdot 5 space кг = 50 space Н$.
$P_2 = gm_2$,
$P_2 = 10 frac{Н}{кг} cdot 0.3 space кг = 3 space Н$.
Ответ: $P_1 = 50 space Н$, $P_2 = 3 space Н$.
Упражнение №3
Вес человека $700 space Н$. Определите его массу. Сделайте рисунок и покажите вес тела.
Дано:
$P = 700 space Н$
$g approx 10 frac{Н}{кг}$
$m — ?$
Показать решение и ответ
Скрыть
Решение:
Мы знаем, что вес тела будет равен силе тяжести, действующей на человека. Запишем формулу, связывающую эти величины, и рассчитаем массу тела человека.
$P = F_{тяж} = gm$,
$m = frac{P}{g}$,
$m = frac{700 space Н}{10 frac{Н}{кг}} = 70 space кг$.
На рисунке 3 изображен вес тела человека.
Масштаб: $200 space Н$ соответствует отрезку длиной $1 space см$. Так, вес изображен отрезком длиной $3.5 space см$.
В отличие от силы тяжести вес тела приложен к опоре, а не к центру тела. Так как человек стоит на полу, то вес приложен к точке между подошвами его обуви и полом.
Ответ: $m = 70 space кг$.
Упражнение №4
Выразите в ньютонах следующие силы: $240 space кН$, $25 space кН$, $5 space кН$, $0.2 space кН$.
Показать решение
Скрыть
Решение:
$F_1 = 240 space кН = 240 space 000 space Н$.
$F_2 = 25 space кН = 25 space 000 space Н$.
$F_3 = 5 space кН = 5000 space Н$.
$F_4 = 0.2 space кН = 200 space Н$.
Упражнение №5
На столе стоит телевизор массой $5 space кг$. Определите силу тяжести и вес телевизора. Изобразите эти силы на рисунке.
Дано:
$m = 5 space кг$
$g approx 10 frac{Н}{кг}$
$F_{тяж} — ?$
$P — ?$
Показать решение и ответ
Скрыть
Решение:
Телевизор неподвижен, поэтому вес тела и сила тяжести будут равны друг другу. Рассчитаем их:
$P = F_{тяж} = gm$,
$P = F_{тяж} = 10 frac{Н}{кг} cdot 5 space кг = 50 space Н$.
Для изображения сил выберем масштаб: $10 space Н$ соответствует отрезок длиной $1 space см$. На рисунке 4, а показана сила тяжести, действующая на телевизор. Она приложена к его центру. На рисунке 4, б показан вес, действующий на телевизор. Он приложен к опоре. Эти силы равны по модулю, поэтому при их изображении обратите внимание на то, чтобы отрезки были одинаковой длины (по $5 space см$ каждый).
Ответ: $P = F_{тяж} = 50 space Н$.
