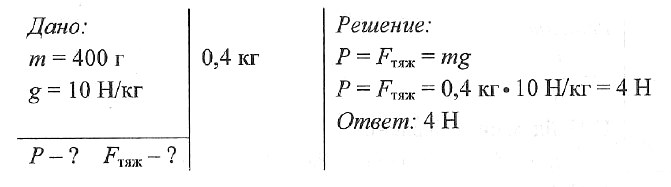Задачи на силу тяжести
и вес тела с решениями
Формулы, используемые на уроке «Задачи на силу тяжести и вес тела»
Название величины |
Обозначение |
Единицы измерения |
Формула |
Масса |
m |
кг |
m = F / g |
Вес тела |
P |
H |
P = m *g |
Сила тяжести |
Fтяж |
H |
Fтяж = mg |
Постоянная (сила тяжести, действующая на тело массой 1 кг) |
g = 10 H/кг |
H/кг |
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Определите силу тяжести, действующую: а) на человека массой m = 100 кг; б) на автомобиль массой М = 1,5 т; в) на монет массой m = 5 г.
Задача № 2.
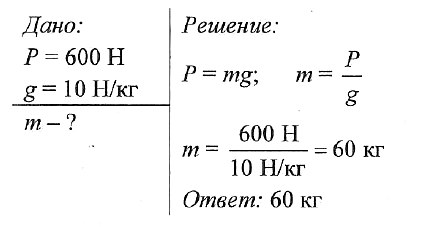
Какова масса свинцового шара, если он весит 600 Н?
Задача № 3.
Масса футбольного мяча 400 г. Вычислите вес мяча и силу тяжести, действующую на него.
Задача № 4.
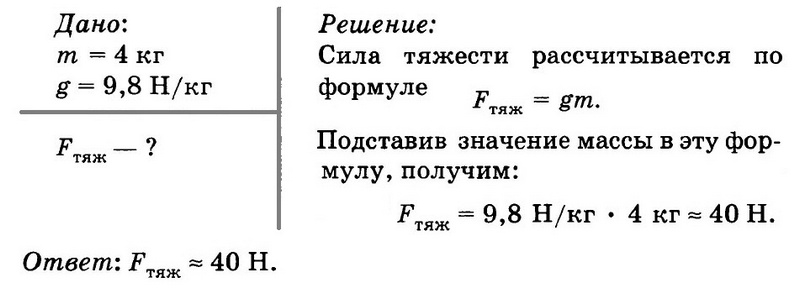
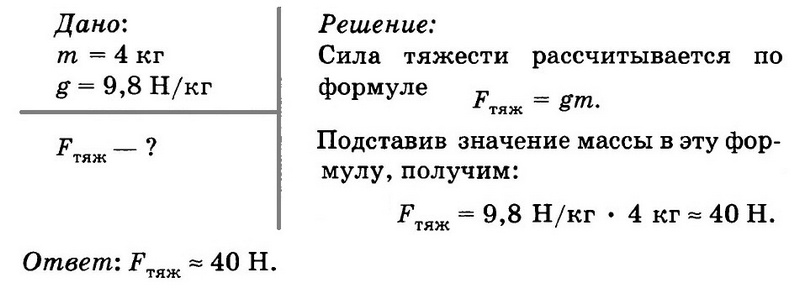
Чему равна сила тяжести тела, масса которого 4 кг?
Задача № 5.
Какой вес имеет вода объемом 3 дм3?
Задача № 6.
Подвешенная к потолку люстра действует на потолок с силой 49 Н. Какова масса люстры?
Задача № 7.
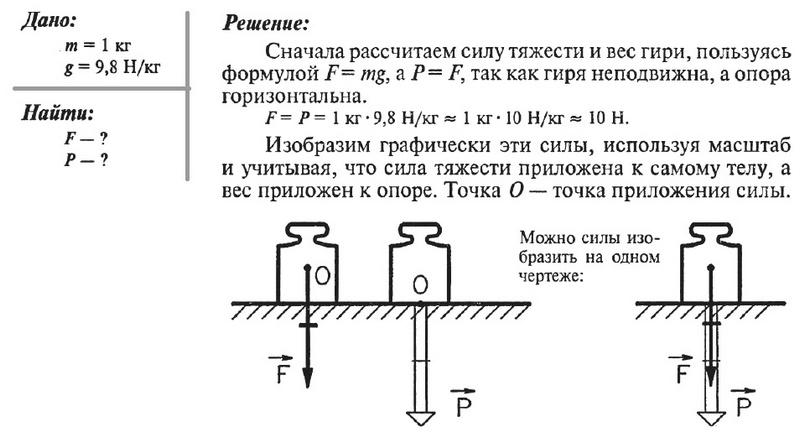
Изобразите графически силу тяжести и вес гири массой 1 кг.
Задача № 8.
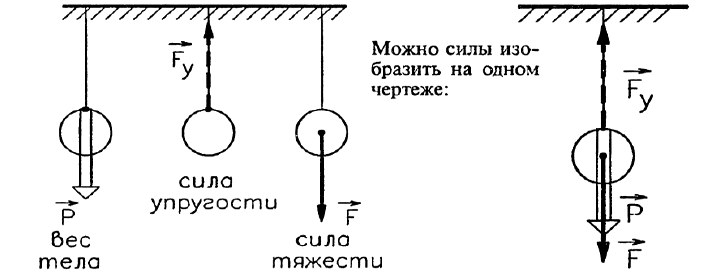
Изобразите графически силы, действующие на шар, висящий на нити.
Решение. На шар, висящий на нити, действуют несколько сил: сила тяжести, приложенная к шару, сила упругости нити, приложенная к нити, и вес тела, приложенный к подвесу. Шар неподвижен, поэтому численно эти силы равны, следовательно, длина стрелок, изображающих силы, будет одинакова.
Задача № 9 (повышенной сложности).
Как изменяются сила тяжести, действующая на космонавта, и его вес, когда он перемещается с Земли на орбитальную станцию?
ОТВЕТ: сила тяжести — незначительно, а вес будет равен нулю.
РЕШЕНИЕ: Сила тяжести уменьшается незначительно (менее чем на 10% при высоте орбиты 300 км), так как она зависит только от массы тела и расстояния до центра Земли, которое при перемещении на орбитальную станцию изменяется всего на несколько процентов. Если бы не сила притяжения к Земле, орбитальная станция покинула бы околоземную орбиту и улетела далеко в космическое пространство. А вот вес космонавта в орбитальной станции равен нулю, поскольку космонавт вместе со станцией находится в состоянии свободного падения на Землю.
Краткая теория к задачам на силу тяжести и вес тела
Конспект урока «Задачи на силу тяжести и вес тела с решениями».
Следующая тема: «Задачи на давление твердых тел».
Задачи на силу тяжести
На тело, массой ( 1 кг ) действует сила тяжести равная ( 9,8 ) Ньютонов
На тело, массой ( 2 кг ) действует сила тяжести равная ( 19,6 ) Ньютонов
то есть в два раза больше.
Число ( 9,8 ) обозначают буквой (g ) и называют ускорением свободного падения.
С тем, что такое ускорение мы познакомимся в девятом классе, а пока запомним, что:
( g=9,8 Н/кг )
Запишем формулу для нахождения силы тяжести:
(F_{тяж}=m cdot g )
То есть для нахождения силы тяжести нужно просто умножить его массу на ( 9,8 )
Репетитор по физике
+7 916 478 10 32
Очень часто (g ) округляют до ( 10 ), то есть (g approx 10 Н/кг )
Задача 1. (Сила тяжести.)
Найти силу тяжести, действующую на предмет массой (m=1 кг .)
(g=9,8 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 2. (Сила тяжести . )
Какая сила тяжести действует на утюг, если его масса 2 кг?
(g=9,8 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 3. (Сила тяжести. )
Вычислить силу тяжести, приложенную к ящику массой 10 кг.
(g=9,8 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 4. (Сила тяжести. )
Масса грузового автомобиля равна 6 тоннам.
Какая сила тяжести действует на этот автомобиль?
(g=9,8 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 5. (Сила тяжести. )
Масса голубого кита равна 120 тоннам.
Какая сила тяжести действует на этого кита?
(g=9,8 Н/кг . )
Дать ответ в килоньютонах.
Показать ответ
Показать решение
Видеорешение
Задача 6. (Сила тяжести. )
Полная масса самолета Боинг 747-800 может достигать 440 тонн.
Найти силу тяжести, действующую на этот самолет.
В этой задаче принять (g=10 Н/кг . )
Дать ответ в меганьютонах. 1 МН=1000000 Н.
Показать ответ
Показать решение
Видеорешение
Задача 7. (Сила тяжести. )
Масса детали равняется 500 граммам.
Вычислите силу тяжести, действующую на эту деталь.
В этой задаче принять (g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 8. (Сила тяжести. )
Масса жука Геркулеса равняется 100 граммам.
Вычислите силу тяжести, действующую на этого жука.
В этой задаче принять (g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 9. (Сила тяжести. )
Масса монеты составляет 15 грамм.
Какая сила тяжести действует на эту монету?
В этой задаче принять (g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 10. (Сила тяжести. )
Масса стрекозы составляет 1 грамм.
Вычислите силу тяжести, действующую на эту стрекозу.
В этой задаче принять (g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 11. (Сила тяжести.)
На человека действует сила тяжести ( F_{тяж}=900 Н . )
Найти массу этого человека.
В этой задаче принять (g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 12. (Сила тяжести.)
На камень
действует сила тяжести ( F_{тяж}=1 Н . )
Какова масса этого камня?
В этой задаче принять (g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 13. (Сила тяжести.)
Какова масса воробья, если на него
действует сила тяжести ( F_{тяж}=0,35 Н ? )
В этой задаче принять (g=10 Н/кг . )
Дать ответ в граммах.
Показать ответ
Показать решение
Видеорешение
В окружающем нас мире на различные тела действуют множество сил. Вы уже познакомились с несколькими из них: весом тела, силой тяжести и силой упругости.
- Сила тяжести действует на все тела находящиеся на Земле и всегда направлена вертикально вниз:
$F_{тяж} = gm$,
где $m$ — масса тела, $g$ — ускорение свободного падения ($g = 9.8 frac{Н}{кг}$) - Вес тела — это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес. Вес тела приложен всегда к опоре или подвесу.
Если тело и опора/подвес неподвижны или движутся прямолинейно и равномерно, то вес будет численно равен силе тяжести, действующей на это тело:
$P = F_{тяж}$ - Сила упругости возникает в теле в результате его деформации и стремится вернуть тело в исходное положение.
Закон Гука определяет зависимость этой силы от деформации тела:
$F_{упр} = k Delta l$,
где $k$ — коэффициент упругости (жесткость тела), $Delta l$ — изменение длины тела
В данном уроке мы рассмотрим задачи и их подробные решения, чтобы вы научились уверенно использовать новые понятия и вычислять изученные силы.
Задача №1
Вычислите силу тяжести, действующую на тело массой: $1.5 space кг$; $500 space г$; $2.5 space т$; $20 space г$.
Дано:
$m_1 = 1.5 space кг$
$m_2 = 500 space г$
$m_3 = 2.5 space т$
$m_4 = 20 space г$
$g = 9.8 frac{Н}{кг}$
СИ:
$m_2 = 0.5 space кг$
$m_3 = 2500 space кг$
$m_4 = 0.02 space кг$
$F_{тяж1}, F_{тяж2}, F_{тяж3}, F_{тяж4} — ?$
Показать решение и ответ
Скрыть
Решение:
Сила тяжести рассчитывается по формуле $F_{тяж} = gm$.
Для того чтобы получить верный ответ при таких простых вычислениях, всегда обращайте внимание на единицы измерения данных величин. Мы уже перевели единицы массы в $кг$. Если бы мы этого не сделали, то получили бы неверные ответы.
Рассчитаем силу тяжести, действующую на каждое тело:
- $F_{тяж1} = gm_1$,
$F_{тяж1} = 9.8 frac{Н}{кг} cdot 1.5 space кг = 14.7 space Н$ - $F_{тяж2} = gm_2$,
$F_{тяж2} = 9.8 frac{Н}{кг} cdot 0.5 space кг = 4.9 space Н$ - $F_{тяж3} = gm_3$,
$F_{тяж3} = 9.8 frac{Н}{кг} cdot 2500 space кг = 24 space 500 space Н = 24.5 space кН$ - $F_{тяж4} = gm_4$,
$F_{тяж4} = 9.8 frac{Н}{кг} cdot 0.02 space кг = 0.196 space Н$
Ответ: $F_{тяж1} = 14.7 space Н$, $F_{тяж2} = 4.9 space Н$, $F_{тяж3} = 24.5 space кН$, $F_{тяж1} = 0.196 space Н$.
Задача №2
Банка объемом $5 space дм^3$ заполнена водой. Какой вес имеет вода?
Дано:
$V = 5 space дм^3$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
СИ:
$V = 5 cdot 10^{-3} space м^3$
Показать решение и ответ
Скрыть
Решение:
У нас в задаче не сказано, что банка каким-либо образом движется, поэтому мы будем считать, что она неподвижна. Если банка неподвижна, то и вода в ней тоже. Тогда вес воды мы можем рассчитать следующим способом:
$P = F_{тяж} = gm$.
Массу воды выразим через ее плотность и объем банки, который она заполняет:
$m = rho V$.
Подставим в нашу формулу и рассчитаем вес воды:
$P = g rho V$,
$P = 9.8 frac{Н}{кг} cdot 1000 frac{кг}{м^3} cdot 5 cdot 10^{-3} space м^3 = 49 space Н$.
Ответ: $P = 49 space Н$.
Задача №3
Два кубика изготовлены из одного материала. Объем первого кубика в 12.2 раза больше, чем второго. На какой кубик действует большая сила тяжести и во сколько раз?
Дано:
$V_1 = 12.2 V_2$
$rho_1 = rho_2 = rho$
$frac{F_{тяж1}}{F_{тяж2}} — ?$
Показать решение и ответ
Скрыть
Решение:
Сила тяжести рассчитывается по формуле:
$F_{тяж} = gm$.
Выразим массу кубиков через их объем и плотность:
$m_1 = rho V_1 = rho 12.2 V_2$,
$m_2 = rho V_2$.
Мы видим, что масса первого кубика в 12.2 раза больше массы второго. Это означает, что и сила тяжести, действующая на него, будет в 12.2 раза больше, чем сила тяжести, действующая на второй кубик:
$frac{F_{тяж1}}{F_{тяж2}} = frac{rho 12.2 V_2}{rho V_2} = 12.2$.
Ответ: на первый, в 12.2 раза.
Задача №4
Какой вес имеет человек, имеющий массу $65 space кг$ и находящийся на Земле?
Дано:
$m = 65 space кг$
$g = 9.8 frac{Н}{кг}$
$P — ?$
Показать решение и ответ
Скрыть
Решение:
Если человек находится на Земле неподвижно или движется равномерно и прямолинейно, то его вес будет равен силе тяжести, действующей на него:
$P = F_{тяж} = gm$,
$P = 9.8 frac{Н}{кг} cdot 65 space кг = 637 space Н$.
Ответ: $P = 637 space Н$.
Задача №5
Стальная проволока удлиняется на $2 space мм$ при действии на нее груза в $320 space Н$. Вычислите коэффициент жесткости проволоки.
Дано:
$Delta l = 2 space мм$
$F_{упр} = 320 space Н$
СИ:
$Delta l = 2 cdot 10^{-3} space м$
$k — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем закон Гука:
$F_{упр} = k Delta l$.
Выразим отсюда коэффициент жесткости проволоки и рассчитаем его:
$k = frac{F_{упр}}{Delta l}$,
$k = frac{320 space Н}{2 cdot 10^{-3} space м} = 160 cdot 10^3 frac{Н}{м} = 160 frac{кН}{м}$.
Ответ: $k = 160 frac{кН}{м}$.
Задача №6
Под действием груза в $200 space Н$ пружина динамометра удлинилась на $0.5 space см$. Каково удлинение пружины под действием груза в $700 space Н$?
Дано:
$Delta l_1 = 0.5 space см$
$F_{упр1} = 200 space Н$
$F_{упр2} = 700 space Н$
$Delta l_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Закон Гука описывает силу упругости, возникающую в пружине при ее удлинении:
$F_{упр1} = k Delta l_1$.
Выразим отсюда жесткость пружины и рассчитаем ее:
$k = frac{F_{упр1}}{Delta l_1}$,
$k = frac{200 space Н}{0.5 space см} = 400 frac{Н}{см}$.
Используя тот же закон Гука рассчитаем удлинение пружины при другой силе упругости, измерений динамометром:
$F_{упр2} = k Delta l_2$,
$Delta l_2 = frac{F_{упр2}}{k}$,
$Delta l_2 = frac{700 space Н}{400 frac{Н}{см}} = 1.75 space см$.
Ответ: $Delta l_2 = 1.75 space см$.
Под действием силы давления вагона $50 space кН$ буферные пружины между вагонами сжимаются на $1 space см$. С какой силой давит вагон, если пружины сжались на $4 space см$?
Дано:
$F_{упр1} = 50 space кН$
$Delta l_1 = 1 space см$
$Delta l_2 = 4 space см$
$F_{упр2} — ?$
Показать решение и ответ
Скрыть
Решение:
Вследствие давления вагона, буферные пружины сжимаются и в них возникает сила упругости, равная $50 space кН$. Найдем жесткость этих пружин:
$F_{упр1} = k Delta l_1$,
$k = frac{F_{упр1}}{Delta l_1}$,
$k = frac{50 space кН}{1 space см} = 50 frac{кН}{см}$.
Рассчитаем силу, с которой давит вагон, (силу упругости, возникающую в пружинах под таким давлением), если изменение длины пружин составило $4 space см$:
$F_{упр2} = k Delta l_2$,
$F_{упр2} = 50 frac{кН}{см} cdot 4 space см = 200 space кН$.
Ответ: $F_{упр2} = 200 space кН$.
Задача №8
Пружина без нагрузки длиной $20 space см$ имеет коэффициент жесткости $20 frac{Н}{м}$. Какой станет длина растянутой пружины под действием силы $2 space Н$?
Дано:
$l = 20 space см$
$k = 20 frac{Н}{м}$
$F_{упр1} = 2 space Н$
СИ:
$l = 0.2 space м$
$F_{упр2} — ?$
Показать решение и ответ
Скрыть
Решение:
Для того чтобы узнать длину растянутой пружины, нам нужно вычислить ее изменение длины — длину, на которую она растянется:
$l_1 = l + Delta l$.
Если бы пружина сжималась под действием силы, то мы бы отнимали удлинение от первоначальной длины.
Рассчитаем удлинение пружины:
$F_{упр} = k Delta l$,
$Delta l = frac{F_{упр}}{k}$,
$Delta l = frac{2 space Н}{20 frac{Н}{м}} = 0.1 space м$.
Теперь рассчитаем длину растянутой пружины:
$l_1 = 0.2 space м + 0.1 space м = 0.3 space м = 30 space см$.
Ответ: $l_1 = 30 space см$.
Задача №9
На рисунке 1 изображен график зависимости модуля силы упругости от удлинения пружины. Найдите жесткость пружины.
Показать решение и ответ
Скрыть
Решение:
Для того чтобы определить коэффициент жесткости нам нужно силу упругости разделить на удлинение пружины:
$k = frac{F_{упр}}{Delta l}$.
Пользуясь графиком, вы можете выбрать любую удобную для вас точку. График демонстрирует линейную зависимость силы упругости от удлинения, коэффициент жесткости при этом — величина постоянная.
Мы выберем точку, в которой сила упругости равна $4 space Н$. Этому значению силы соответствует удлинение пружины, равное $0.4 space м$.
Рассчитаем коэффициент жесткости:
$k = frac{4 space Н}{0.4 space м} = 10 frac{Н}{м}$.
Ответ: $k = 10 frac{Н}{м}$.
Задача №10
Круглый стальной брус диаметром $2 space см$, длиной $16 space м$ растягивается силой, равной $36 space кН$. Найдите удлинение этого бруса.
Дано:
$d = 2 space см$
$l = 16 space м$
$F_{упр} = 36 space кН$
$E = 200 cdot 10^9 space Па$
$Delta l — ?$
Модуль упругости $E$ — это физическая величина, характеризующая способность материала сопротивляться растяжению или сжатию.
Модуль упругости является характеристикой материала, для стали он равен $200 cdot 10^9 space Па$.
Он связан с коэффициентом упругости $k$:
$k = frac{ES}{l}$,
где $S$ — площадь поперечного сечения,
$l$ — длина.
Показать решение и ответ
Скрыть
Решение:
Запишем закон Гука:
$F_{упр} = k Delta l$.
Выразим отсюда удлинение стального бруса:
$Delta l = frac{F_{упр}}{k}$.
Коэффициент упругости $k$ мы можем выразить через модуль упругости $E$:
$k = frac{ES}{l}$.
Площадь поперечного сечения $S$ выразим через диаметр:
$S = frac{pi d^2}{4}$.
Подставим эти формулы в закон Гука:
$Delta l = frac{F_{упр}}{frac{ES}{l}} = frac{F_{упр} l}{E frac{pi d^2}{4}} = frac{4 F_{упр} l}{E pi d^2}$.
Рассчитаем удлинение бруса:
$Delta l = frac{4 cdot 36 cdot 10^3 space Н cdot 16 space м}{200 cdot 10^9 space Па cdot 3.14 cdot 0.02^2 space м^2} = frac{2304 cdot Н cdot м}{251 space 200 space Н} approx 0.009 space м approx 9 space мм$.
Ответ: $Delta l = 9 space мм$.
Задачи на силу тяжести
и вес тела с решениями
Формулы, используемые на уроке «Задачи на силу тяжести и вес тела»
Название величины |
Обозначение |
Единицы измерения |
Формула |
Масса |
m |
кг |
m = F / g |
Вес тела |
P |
H |
P = m *g |
Сила тяжести |
Fтяж |
H |
Fтяж = mg |
Постоянная (сила тяжести, действующая на тело массой 1 кг) |
g = 10 H/кг |
H/кг |
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Определите силу тяжести, действующую: а) на человека массой m = 100 кг; б) на автомобиль массой М = 1,5 т; в) на монет массой m = 5 г.
Задача № 2. Какова масса свинцового шара, если он весит 600 Н?
Задача № 3. Масса футбольного мяча 400 г. Вычислите вес мяча и силу тяжести, действующую на него.
Задача № 4. Чему равна сила тяжести тела, масса которого 4 кг?
Задача № 5. Какой вес имеет вода объемом 3 дм3?
Задача № 6. Подвешенная к потолку люстра действует на потолок с силой 49 Н. Какова масса люстры?
Задача № 7. Изобразите графически силу тяжести и вес гири массой 1 кг.
Задача № 8. Изобразите графически силы, действующие на шар, висящий на нити.
Решение. На шар, висящий на нити, действуют несколько сил: сила тяжести, приложенная к шару, сила упругости нити, приложенная к нити, и вес тела, приложенный к подвесу. Шар неподвижен, поэтому численно эти силы равны, следовательно, длина стрелок, изображающих силы, будет одинакова.
Задача № 9 (повышенной сложности). Как изменяются сила тяжести, действующая на космонавта, и его вес, когда он перемещается с Земли на орбитальную станцию?
ОТВЕТ: сила тяжести — незначительно, а вес будет равен нулю.
[idea]РЕШЕНИЕ: Сила тяжести уменьшается незначительно (менее чем на 10% при высоте орбиты 300 км), так как она зависит только от массы тела и расстояния до центра Земли, которое при перемещении на орбитальную станцию изменяется всего на несколько процентов. Если бы не сила притяжения к Земле, орбитальная станция покинула бы околоземную орбиту и улетела далеко в космическое пространство. А вот вес космонавта в орбитальной станции равен нулю, поскольку космонавт вместе со станцией находится в состоянии свободного падения на Землю.[/idea]
Краткая теория к задачам на силу тяжести и вес тела
Конспект урока «Задачи на силу тяжести и вес тела с решениями».
Следующая тема: «Задачи на давление твердых тел».
Сила тяжести. Вес
- Движение тел вблизи поверхности Земли
- Сила тяжести
- Вес тела
- Невесомость
- Задачи
- Лабораторная работа №7. Градуирование шкалы динамометра и измерение силы тяжести
п.1. Движение тел вблизи поверхности Земли
Вблизи поверхности Земли все тела, предоставленные самим себе, падают вниз, независимо от направления начальной скорости.
Такое движение тел называют свободным падением.
п.2. Сила тяжести
Многочисленные эксперименты показали, что в свободном падении все тела вблизи поверхности Земли падают с одинаковым ускорением (overrightarrow{g}), которое направлено вниз, к центру Земли.
В системе отсчета, связанной с Землей, на любое тело массой (m) действует сила тяжести $$ overrightarrow{F_{text{тяж}}}=m overrightarrow{g} $$
 |
Сила тяжести прямо пропорциональна массе тела. Точка приложения силы тяжести – центр масс тела. Сила тяжести всегда направлена вертикально вниз, к центру Земли. |
 |
Измерения показывают, что на средних географических широтах ускорение свободного падения (gapprox 9,81 text{м/с}^2). Т.е., скорость при падении увеличивается на (9,81 text{м/с}) каждую следующую секунду.
В общем случае, ускорение свободного падения зависит от широты рассматриваемого места, высоты над уровнем моря, времени суток и ещё нескольких более «тонких» факторов. В школьных задачах, если другое не оговорено, для вычислений используют приблизительное значение (gapprox 10 text{м/с}^2). |
п.3. Вес тела
Если подвесить тело или положить его на опору, сила тяжести, действующая на тело, будет уравновешена силой, которую называют силой реакции подвеса или силой реакции опоры.
Т.к. силы уравновешивают друг друга, выполняется соотношение $$ moverrightarrow{g}=-overrightarrow{N} $$ где (moverrightarrow{g}) – сила тяжести, (overrightarrow{N}) – реакция подвеса или опоры.
По третьему закону Ньютона, если подвес или опора действуют на тело с силой (overrightarrow{N}), то и тело действует на подвес или опору с силой (overrightarrow{P}=-overrightarrow{N})
Вес тела – это сила, с которой тело действует на подвес или опору.
Получаем, что (overrightarrow{P}=moverrightarrow{g}), вес и сила тяжести равны по величине и направлению, но приложены к разным точкам: сила тяжести – к центру масс тела, вес – к подвесу или опоре.
По своей природе реакции подвеса или опоры являются силами упругости: под действием веса тела подвес или опора деформируются, и силы упругости стремятся восстановить их форму и размеры.
Равенство (overrightarrow{P}=moverrightarrow{g}) выполняется, если подвес или опора покоятся или движутся относительно Земли прямолинейно и равномерно.
Если движение подвеса или опоры равноускоренное с ускорением (overrightarrow{a}ne 0), то (overrightarrow{P}ne moverrightarrow{g}), вес будет больше (при (overrightarrow{a}) направленном вверх) или меньше (при (overrightarrow{a}) направленном вниз) силы тяжести. Подробней этот случай будет рассмотрен в курсе физики для 9 класса.
п.4. Невесомость
Если опора свободно падает вместе с телом, то под действием силы тяжести каждая частица опоры и тела двигается вниз с одним и тем же ускорением (overrightarrow{g}). Ни в опоре, ни в теле не возникают сжатия или растяжения, нет сил упругости, а значит, вес тела равен нулю.
Состояние, при котором в свободно падающих телах исчезают деформации и взаимные давления частиц тел друг на друга, называют невесомостью.
Состояние невесомости можно испытать, если подпрыгнуть – с момента отрыва от земли до момента приземления. В первые моменты прыжка до раскрытия парашюта, парашютисты также находятся в состоянии невесомости.
Движение космического корабля по орбите вокруг Земли представляет собой непрерывное свободное падение, поэтому космонавты испытывают состояние невесомости в течение всего полета, кроме тех моментов, когда передвигаются по кораблю или включают двигатели для маневрирования.
п.5. Задачи
Задача 1. Какой вес имеет человек массой 65 кг, который стоит на земле?
Дано:
(m=65 text{кг})
(gapprox 10 text{м/с}^2)
__________________
(P-?)
Вес равен силе тяжести (P=mg) $$ Papprox 65cdot 10=650 (text{Н}) $$ Ответ: 650 Н
Задача 2. Парашютист равномерно опускается на землю. Сила сопротивления воздуха 900 Н. Масса парашюта 15 кг. Найдите массу парашютиста.
Дано:
(F_{text{сопр}}=900 text{Н})
(m_1=15 text{кг})
(gapprox 10 text{м/с}^2)
__________________
(m_2-?)
На раскрытый парашют действуют две силы: сила сопротивления воздуха, направленная вверх, и суммарный вес (парашюта и парашютиста), направленный вниз.
Т.к. движение равномерное, ускорение (a=0). Значит, вес равен силе тяжести, и begin{gather*} F_{text{сопр}}=P=F_{text{т}}=(m_1+m_2)g\[6pt] m_1+m_2=frac{F_{text{сопр}}}{g}Rightarrow m_2=frac{F_{text{сопр}}}{g}-m_1 end{gather*} Подставляем $$ m_2=frac{900}{10}-15=75 (text{кг}) $$ Ответ: 75 кг.
Задача 3. На сколько сантиметров растянется пружина жесткостью k=267 Н/м, если подвесить к ней медный брусок размерами 5 см х 6 см х 10 см. Плотность меди 8900 кг/м3.
Дано:
(V=5 text{см}times 6 text{см}times 10 text{см}=300 text{см}^3=3cdot 10^{-4} text{м}^3)
(rho=8900 text{кг/м}^3)
(k=1000 text{Н/м})
(gapprox 10 text{м/с}^2)
__________________
(m_2-?)
Вес бруска равен силе тяжести и уравновешивается силой упругости: begin{gather*} mg=F_{text{упр}}=kDelta lRightarrow Delta l=frac{mg}{k}, m=rho V\[6pt] Delta l=frac{rho Vg}{k} end{gather*} Получаем: $$ Delta l=frac{8900cdot 3cdot 10^{-4}cdot 10}{267}=0,1 (text{м}=10 (text{см}) $$ Ответ: 10 см.
Задача 4*. При подвешивании гирьки массой 450 г пружина динамометра растягивается до 8 см. А при подвешивании гирьки массой 300 г – до 6 см. Найдите длину пружины динамометра без груза (ответ запишите в см).
Дано:
(m_1=450 text{г}=0,45 text{кг})
(l_1=8 text{см}=0,8 text{м})
(m_2=300 text{г}=0,3 text{кг})
(l_2=6 text{см}=0,6 text{м})
__________________
(l_0-?)
Вес гирьки равен силе тяжести и уравновешивается силой упругости: begin{gather*} mg=F_{text{упр}}=kDelta lRightarrow k=frac{mg}{Delta l} end{gather*} где (Delta l=l-l_0) – растяжение пружины.
Жесткость пружины begin{gather*} k=frac{m_1g}{Delta l_1}=frac{m_1g}{l_1-l_0}, k=frac{m_2g}{Delta l_2}=frac{m_2g}{l_2-l_0}\[6pt] frac{m_1g}{l_1-l_0}=frac{m_2g}{l_2-l_0} Rightarrow frac{m_1}{l_1-l_0}=frac{m_2}{l_2-l_0} Rightarrow m_2(l_2-l_0)=m_2(l_1-l_0)\[6pt] m_1l_2-m_1l_0=m_2l_1-m_2l_0 Rightarrow m_1l_2-m_2l_1=(m_1-m_2)l_0\[6pt] l_0=frac{m_1l_2-m_2l_1}{m_1-m_2} end{gather*} Получаем $$ l_0=frac{0,45cdot 0,06-0,3cdot 0,08}{0,45-0,3}=frac{0,027-0,024}{0,15}=0,02 (text{м}=2 (text{см}) $$ Ответ: 2 см.
п.6. Лабораторная работа №7. Градуирование шкалы динамометра и измерение силы тяжести
Цель работы
Исследовать зависимость силы упругости от величины деформации. Изготовить шкалу динамометра. Измерить силу тяжести для двух тел неизвестной массы; рассчитать их массу.
Теоретические сведения
 |
При подвешивании груза на пружину, его вес уравновешивается силой упругости. Для неподвижной пружины вес равен силе тяжести. Получаем $$ P=F_{text{т}}=mg=F_{text{упр}} =kDelta l $$ Удлинение пружины $$ Delta l=frac gk m $$ При постоянном ускорении свободного падения (g) и постоянной жесткости (k), удлинение прямо пропорционально массе подвешенного груза. |
В данной работе считаем, что грузу массой 100 г соответствует показание динамометра (F=1 text{Н}), т.е. (overline{g}=frac{1 text{Н}}{100 text{г}}=10frac{text{Н}}{ text{кг}}=10frac{ text{м}}{ text{с}^2}). Более точное стандартное значение (g_0=9,80665frac{ text{м}}{ text{с}^2})
Ошибка метода, связанная с величиной (g) $$ delta_g=frac{|overline{g}-g_0|}{g_0}approx 0,02=2text{%} $$ Тогда грузу массой 200 г соответствует показание 2 Н, 300 г – 3 Н и т.д.
После градуирования в целых значениях Н на динамометре наносятся промежуточные деления с ценой деления (d=0,1 text{Н}).
Ошибка градуирования определяется как степень отклонения от равномерности шкалы, (delta_{text{шк}}).
Теперь с помощью полученного прибора можно непосредственно измерять силу тяжести, действующую на тела. Ошибка метода при определении сил равна сумме (delta=delta_g+delta_{text{шк}}).
Т.к. шкала изготовлена для (overline{g}=10frac{ text{м}}{ text{с}^2}), массу тел находим по формуле (m=frac{F}{overline{g}}), где (F) – показание динамометра. При этом ошибка метода равна (delta=delta_{text{шк}}), т.к. ошибка (delta_g) нивелируется за счет пропорциональности массы и растяжения пружины.
Таким образом, за счет сокращения (overline{g}), полученный прибор позволяет точнее измерять массы по сравнению с измерениями сил.
Приборы и материалы
Лабораторный динамометр на 5Н со шкалой, закрытой чистой бумагой; набор грузиков по 100 г; линейка; карандаш; 2 тела неизвестной массы.
Ход работы
1. Закрепите динамометр в штативе.
2. Подвесьте грузик массой 100 г, сделайте отметку 1Н на шкале.
3. Сделайте отметки 2Н, 3Н, 4Н и 5Н для грузов 200 г, 300 г, 400 г и 500 г соответственно.
4. Снимите динамометр со штатива и проверьте с помощью линейки, насколько равномерной получилась шкала. Оцените относительную ошибку (delta_{text{шк}})
5. С помощью линейки нанесите по 10 промежуточных делений между основными делениями шкалы.
6. Снова закрепите динамометр в штативе и проведите измерения силы тяжести для двух тел неизвестной массы. Найдите абсолютную и относительную погрешность измерений.
7. Рассчитайте массы для обоих тел. Найдите абсолютную и относительную погрешность расчетов. 8. Сделайте выводы.
Результаты измерений и вычислений
Расчетная таблица для оценки равномерности шкалы
| Отрезок шкалы | Длина отрезка, мм | (|x-x_{text{ср}}|) |
| 0-1 Н | 25 | 0 |
| 1-2 Н | 25 | 0 |
| 2-3 Н | 26 | 1 |
| 3-4 Н | 24 | 1 |
| 4-5 Н | 25 | 0 |
| Всего | 125 | 2 |
Средняя длина отрезка $$ x_{text{ср}}=frac{125}{5}=25 (text{мм}) $$ Среднее линейное отклонение $$ Delta =frac 25=0,4 (text{мм}) $$ Цена деления линейки (d_{text{л}}=1 text{мм}), абсолютная погрешность измерений (Delta_{text{л}}=0,5 text{мм})
Т.к. (Delta_{text{л}}gt Delta), принимаем погрешность равномерности шкалы (Delta=Delta_{text{л}}=0,5 text{мм})
Относительная погрешность равномерности шкалы $$ delta_{text{шк}}=frac{0,5}{25}=0,02=2text{%} $$
Относительная погрешность равномерности шкалы
| Показание динамометра (F, text{Н}) |
Ошибка метода (delta=delta_g+delta_{text{шк}}, text{%}) |
Абсолютная погрешность (Delta F=deltacdot F, text{Н}) |
|
| 1-е тело | 2,7 | 4% | 0,11 ≈ 0,1 |
| 2-е тело | 1,9 | 4% | 0,08 ≈ 0,1 |
Цена деления динамометра (d=0,1 text{Н}); погрешность прямых измерений (Delta_0=frac d2=0,05 text{Н})
Полученные абсолютные погрешности больше (Delta_0).
Сила тяжести для первого тела (F_1=(2,7pm 0,1) text{Н}, delta=4text_%)
Сила тяжести для второго тела (F_2=(1,9pm 0,1) text{Н}, delta=4text_%)
Расчет массы $$ m=frac{F}{10} (text{кг})=100F (text{г}) $$
| Масса (m=100F, text{г}) |
Ошибка метода (delta=delta_{text{шк}}, text{%}) |
Абсолютная погрешность (Delta m=deltacdot m, text{г}) |
|
| 1-е тело | 270 | 2% | 5 |
| 2-е тело | 190 | 2% | 4 |
Масса первого тела (m_1=(270pm 5) text{г}, delta=2text{%})
Масса второго тела (m_2=(190pm 4) text{г}, delta=2text{%})
Выводы
На основании проделанной работы можно сделать следующие выводы.
Для градуирования динамометра в ньютонах использовалось значение $$ overline{g}=10 frac{text{м}}{text{с}^2} $$
По сравнению со стандартным значением (g_0=9,80665 text{м/с}^2) это приводит к вкладу в ошибку метода (delta_gapprox 2text{%}).
При градуировании равномерность шкалы дала составляющую ошибки метода (delta_{text{шк}}=2text{%}).
При определении силы тяжести с помощью полученного динамометра ошибка метода равна сумме (delta+delta_g+delta_{text{шк}}=4text{%}).
Для двух тел неизвестной массы были получены следующие значения сил тяжести: $$ F_1=(2,7pm 0,1) text{Н}, F_2=(1,9pm 0,1) text{Н}, delta=4text{%} $$
При расчете массы по формуле (m=frac Fg), ошибка (delta_g) нивелируется за счет пропорциональности растяжения пружины. Ошибка метода уменьшается (delta=delta_{text{шк}}=2text{%}).
Получаем следующие значения масс: $$ m_1=(270pm 5) text{г}, m_2=(190pm 4) text{г}, delta=2text{%} $$ Таким образом, полученный в ходе работы динамометр позволяет измерять силы тяжести в интервале от 0 до 5 Н с погрешностью 4% и рассчитывать массы тел в интервале от 0 до 500 г с погрешностью 2%.