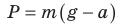Сила упругости. Закон Гука
- Виды деформаций
- Закон Гука
- Измерение силы с помощью динамометра
- Задачи
п.1. Виды деформаций
Под действием силы все тело или отдельные его части приходят в движение.
При движении одних частей тела относительно других происходит изменение формы и размеров.
Деформация – это изменение взаимного положения частиц тела, связанное с их перемещением друг относительно друга под действием приложенной силы, при котором тело изменяет свою форму и размеры.
 |
К простейшим видам деформации относятся:
|
Различают упругие (обратимые) и неупругие (необратимые) деформации.
Деформация является упругой, если, после прекращения действия вызвавших её сил, тело полностью восстанавливает свою форму и размеры.
Например, если немного согнуть школьную линейку, растянуть пружину или надавить на воздушный шарик, после прекращения действия силы линейка выпрямится, пружина сожмется, и шарик опять станет круглым. Эти деформации – упругие, они обратимы.
Если же приложенная сила окажется слишком большой, линейка сломается, пружина так и останется растянутой, а шарик лопнет. Эти деформации – неупругие, они необратимы.
Все здания и сооружения вокруг нас рассчитываются так, чтобы их «нагруженные» части испытывали только упругие деформации; это обеспечивает надёжность и долговечность конструкций.
Восстановление формы и размера тела при упругой деформации происходит под действием силы упругости, которая возникает благодаря межатомным и межмолекулярным взаимодействиям.
Сила упругости уравновешивает действие внешней силы и направлена в сторону, противоположную смещению частиц.
Например (см. рисунок):
- при растяжении сила упругости стремится сжать тело;
- при сжатии сила упругости стремится распрямить тело.
п.2. Закон Гука
 |
Проведем серию опытов с пружиной. Пусть при действии на пружину силой (F) мы получаем деформацию (удлинение) (Delta l). При этом в пружине возникают силы упругости, стремящиеся вернуть её в исходное положение, (overrightarrow{F_{text{упр}}}=-overrightarrow{F}). Если приложенную силу увеличить в 2 раза, то деформация также увеличится в 2 раза. Увеличение силы в 3 раза приводит к росту деформации в 3 раза и т.д. Опыты показывают, что во всех случаях деформация будет прямо пропорциональна приложенной силе. |
Следовательно, сила упругости также будет прямо пропорциональна деформации: $$ F_{text{упр}}simDelta l $$
Для каждого тела отношение силы упругости к величине деформации при малых упругих деформациях является постоянной величиной $$ k=frac{F_{text{упр}}}{Delta l}=const $$ которая называется коэффициентом упругости или жесткостью.
Жесткость тела зависит от формы, размеров и материала, из которого оно изготовлено.
В системе СИ жесткость измеряется в ньютонах на метр, (frac{text{Н}}{text{м}}).
Закон Гука
Сила упругости, возникающая во время упругой деформации тела, прямо пропорциональна удлинению (величине деформации): $$ F_{text{упр}}=kDelta l $$ Сила упругости всегда направлена противоположно деформации.
п.3. Измерение силы с помощью динамометра
 |
Динамометр– это прибор для измерения силы.
Простейший пружинный динамометр состоит из пружины с крючком и дощечки со шкалой (проградуированной в ньютонах). |
В технике используются динамометры более сложных конструкций.
Но принцип действия – использование закона Гука – во многих из них сохраняется.
п.4. Задачи
Задача 1. Резиновая лента удлинилась на 10 см под действием силы 50 Н. Какова жесткость ленты?
Дано:
(Delta l=10 text{см}=0,1 text{м})
(F=50 text{Н})
__________________
(k-?)
Жесткость ленты $$ k=frac{F}{Delta l} $$ $$ k=frac{50}{0,1}=500 left(frac{text{Н}}{text{м}}right) $$ Ответ: 500 Н/м
Задача 2. Под действием силы 300 Н пружина динамометра удлинилась на 0,6 см. Каким будет удлинение пружины под действием силы 700 Н? Ответ запишите в миллиметрах.
Дано:
(F_1=300 text{Н})
(Delta l_1=0,6 text{см}=6cdot 10^{-3} text{м})
(F_2=700 text{Н})
__________________
(Delta l_2-?)
Жесткость пружины begin{gather*} k=frac{F_1}{Delta l_1}=frac{F_2}{Delta l_2}Rightarrow Delta l_2=frac{F_2}{F_1}Delta l_1\[6pt] Delta l_2=frac{700}{300}cdot 6cdot 10^{-3}=14cdot 10^{-3} (text{м})=14 (text{мм}) end{gather*} Ответ: 14 мм
Задача 3. Пружина без груза имеет длину 30 см и коэффициент жесткости 20 Н/м. Найдите длину растянутой пружины, если на нее действует сила 5 Н. Ответ запишите в сантиметрах.
Дано:
(l_0=30 text{cм}=0,3 text{м})
(k=20 text{Н/м})
(F=5 text{Н})
__________________
(l-?)
Удлинение пружины под действием силы: $$ Delta l=frac Fk $$ Длина растянутой пружины begin{gather*} l=l_0+Delta l=l_0+frac Fk\[6pt] l=0,3+frac{5}{20}=0,3+0,25=0,55 (text{м})=55 (text{cм}) end{gather*} Ответ: 55 cм
Задача 4*. Грузовик взял на буксир легковой автомобиль массой 1,5 т с помощью троса. Двигаясь равноускоренно, они проехали путь 600 м за 50 с. На сколько миллиметров удлинился во время движения трос, если его жесткость равна (3cdot 10^5 text{Н/м})?
Дано:
(m=1,5 text{т}=1500 text{кг})
(s=600 text{м})
(t=50 text{c})
(v_0=0)
(k=3cdot 10^5 text{Н/м})
__________________
(Delta l-?)
Сила упругости, возникающая в тросе, уравновешивает силу тяги, передвигающую автомобиль с постоянным ускорением: $$ F_{text{упр}}=kDelta l=F_{text{т}}=ma $$ Перемещение из состояния покоя $$ s=frac{at^2}{2}Rightarrow a=frac{2s}{t^2} $$ Получаем: begin{gather*} kDelta l=mcdotfrac{2s}{t^2}Rightarrow Delta l=frac mkcdot frac{2s}{t^2}\[6pt] Delta l=frac{1500}{3cdot 10^5}cdot frac{2cdot 600}{50^2}=2,4cdot 10^{-3} (text{м})=2,4 (text{мм}) end{gather*} Ответ: 2,4 мм
Сила
упругости. Закон Гука
«Без
сомнения, всё наше
знание
начинается с опыта»
Иммануил
Кант
В
данной теме будет рассмотрен еще один вид силы – сила упругости.
Ранее
говорилось о том, что сила, действующая на тело, является причиной изменения
скорости этого тела. На любое тело, находящееся на Земле, действует сила
тяжести. Остановимся на этом поподробнее. Например, если человек сидит на
лавочке, то на него действует сила тяжести, хотя его скорость не изменяется. Таким
образом, хотя на тело действует сила, но при этом, скорость этого тела не
меняется (то есть, остаётся нулевой в данном случае). Как же это можно
объяснить? Объяснение может быть только одно: на тело действует какая-то
другая сила, которая уравновешивает силу тяжести. Эта сила называется
силой упругости. Сила упругости – это сила, возникающая при деформации и
стремящаяся вернуть тело в исходное положение, придать ему исходную форму.
То есть, из-за силы тяжести, действующей на лавочку, возникает сила упругости,
которая препятствует тому, чтобы лавочка прогибалась, и стремится вернуть
лавочку в исходное положение. То же самое можно сказать и о книге, лежащей на
столе. На неё действует сила тяжести со стороны Земли и сила упругости со
стороны стола.
Проведем
следующий опыт: подвесим тело на пружине. Чем больше пружина будет
растягиваться, тем больше будет сила упругости. В какой-то момент, сила
упругости станет равной силе тяжести, и тогда растяжение прекратится.
Зависимость силы упругости от степени деформации тела была исследована Робертом
Гуком.
Он
установил, что изменение длины тела при растяжении (или сжатии) прямо
пропорционально модулю силы упругости. В этом и заключается закон
Гука.
Fупр = kDl
где Dl –
изменение длины тела;
k
– жёсткость
тела.
Жесткость
зависит от размеров и формы тела и, конечно, от вещества, из которого тело
состоит. Жесткость тела определяется экспериментальным путем. Если выразить
жесткость из формулы, описывающей закон Гука, то можно убедиться, что она равна
отношению силы упругости к удлинению тела.
k = Fупр / Dl
Поскольку
в системе СИ сила измеряется в Н (ньютонах), а длина в м (метрах), следуя
формуле, жесткость измеряется в ньютонах на метр.
[k] = [Н/м]
Необходимо
отметить, что существуют упругие и неупругие деформации. Под упругой
деформацией подразумевается деформация, после которой тело
восстанавливает исходную форму, как только перестают действовать силы,
вызвавшие деформацию. Неупругая деформация – это деформация,
после которой тело не восстанавливает форму, даже после окончания действия сил,
вызвавших деформацию. Например, если растянуть пружину, а потом отпустить
её, то пружина восстановит свою форму. Это будет называться упругой
деформацией. А вот если расплющить монету ударом молотка, то монета не
восстановит свою форму. Это пример неупругой деформации. Так вот, закон Гука
применим только к упругим деформациям.
Действие
сил упругости используется для создания такого прибора, как динамометр. Динамометр
– это прибор для измерения силы.
У
каждого динамометра есть крючок, на который укрепляется груз, а также пружина,
степень деформации которой позволяет судить о приложенной силе. Также на
динамометр нанесена шкала, чтобы можно было считывать его показания. Например,
если подвесить грузик на пружину динамометра, то прибор покажет нам силу
тяжести, действующую на этот грузик. Допустим по шкале прибора видно, что эта
сила составляет 1 Н. Если подвесить еще один такой же грузик, то
динамометр покажет силу, вдвое большую, то есть, 2 Н. Добавив еще один
грузик, можно убедится, что сила уже равна 3 Н. Таким образом, сила
упругости, возникающая при деформации пружины, уравновешивает суммарную силу
тяжести грузиков. На динамометре есть и другая шкала – шкала, с
помощью которой можно измерить удлинение пружины. Если повторить тот же опыт,
то можно убедиться, что удлинение увеличивается пропорционально увеличению силы
упругости. То есть, подтверждается закон Гука.
Таким
образом, когда тело висит на каком-то подвесе, или стоит на опоре, на него
действует сила тяжести, которая уравновешивается силой упругости. Сила,
действующая на опору или подвес, вследствие притяжения тела к Земле, называется
весом тела. Вес тела обозначается большой латинской буквой и
является векторной величиной (как и любая другая сила). Вес направлен
перпендикулярно опоре или вдоль подвеса. В том случае, если тело и опора
находятся в состоянии покоя или движутся равномерно и прямолинейно, вес тела
равен силе тяжести. В чем же тогда разница между весом тела и силой
тяжести? Разница довольно существенная: сила тяжести действует на тело
(то есть, сила тяжести приложена к телу). Вес – это сила, с которой
тело действует на опору (то есть, вес приложен к опоре). Сила
тяжести – это сила, возникающая в результате взаимодействия тела с
Землёй. Вес – это сила, возникающая в результате взаимодействия
тела с опорой или подвесом.
Рассмотрим
пример: тело находится в свободном падении. Почему оно падает? Потому
что на него действует сила тяжести. Но вес тела в этот момент равен нулю,
потому что тело не действует, ни на опору, ни на подвес.
Необходимо
обратить внимание на распространенную ошибку: часто люди спрашивают «сколько
ты весишь?» и получают ответ, например, 50 кг. В килограммах измеряется масса, и именно о ней следует спрашивать. А вес – это
сила, и она измеряется в ньютонах. Опять же, при падении тела, его вес
равен нулю. Но вот масса тела не зависит от того, падает тело или
покоится.
Упражнения.
Задача
1.
Ученик прицепил динамометр к пружине. Когда он растянул пружину на 10 см, он посмотрел на динамометр. Оказалось, что для такого растяжения потребовалось приложить силу,
равную 4 Н. Найдите жесткость данной пружины.
Задача
2.
Шнур длиной 2 м имеет жесткость, 120 Н/м. Какую силу нужно приложить к шнуру,
чтобы его длина составила 205 см?
Задача
3.
На опоре стоит куб, сторона которого равна 15 см. На подвесе висит шар, сделанный из того же материала, что и куб. Найдите объём этого шара,
если его вес вдвое больше, чем вес куба.
Основные
выводы:
–
Сила упругости – это сила, возникающая в теле в результате его
деформации и стремящаяся вернуть тело в исходное положение.
–
Деформации бывают упругими и неупругими.
–
Упругая деформация – это деформация, после которой тело восстанавливает
исходную форму, как только перестают действовать силы, вызвавшие деформацию.
–
Неупругая деформация – это деформация, после которой тело не
восстанавливает форму, даже после окончания действия сил, вызвавших деформацию.
–
Закон Гука (для упругих деформаций)
Fупр = kDl
–
Коэффициентом пропорциональности в этом законе является такая величина,
как жёсткость тела. Эта величина определяется экспериментально.
–
Вес – это сила, действующая на опору или подвес вследствие действия на
тело силы тяжести. Вес направлен перпендикулярно опоре или вдоль подвеса. В случае если и тело, и опора (или подвес) покоятся или
двигаются равномерно и прямолинейно, вес тела равен силе тяжести.
P = Fтяж
Оборудование:
штатив с лапкой и муфтой
набор грузов
динамометр
направляющая прибора для изучения
прямолинейного движения.
Цель работы состоит
в том, чтобы определить коэффициент
жесткости пружины динамометра.
Способ измерения
жесткости пружины, которым пользуются
в работе, основан на использовании
графика зависимости силы упругости,
возникающей в пружине при ее растяжении
от величины удлинения.
Удлиняться пружина
динамометра будет под действием веса
подвешенных к нему грузов. Удлинение
происходит до тех пор, пока вес груза
не уравновесится силой упругости
пружины.
Удлинение пружины
измеряется непосредственно по шкале
направляющей.
Величину силы
упругости определяют по показаниям
динамометра.
1. Подготовьте таблицу
для записи результатов измерений:
|
№ опыта |
Модуль |
Модуль |
2. Закрепите муфту
с лапкой на стержне штатива на высоте
около 30 см от поверхности стола. В лапке
зажмите динамометр, как показано на
рисунке. Направляющую рейку установите
вертикально. Ее шкала должна располагаться
вблизи указателя динамометра.
3. Заметьте положение
стрелки динамометра относительно шкалы.
4. Подвесьте к
динамометру один груз и по шкале с
миллиметровыми делениями определите
удлинение его пружины в миллиметрах.
Удлинение находят как разницу двух
положений указателя динамометра на
шкале при нагруженном и ненагруженном
динамометре.
5. По шкале динамометра
измерьте величину силы упругости. 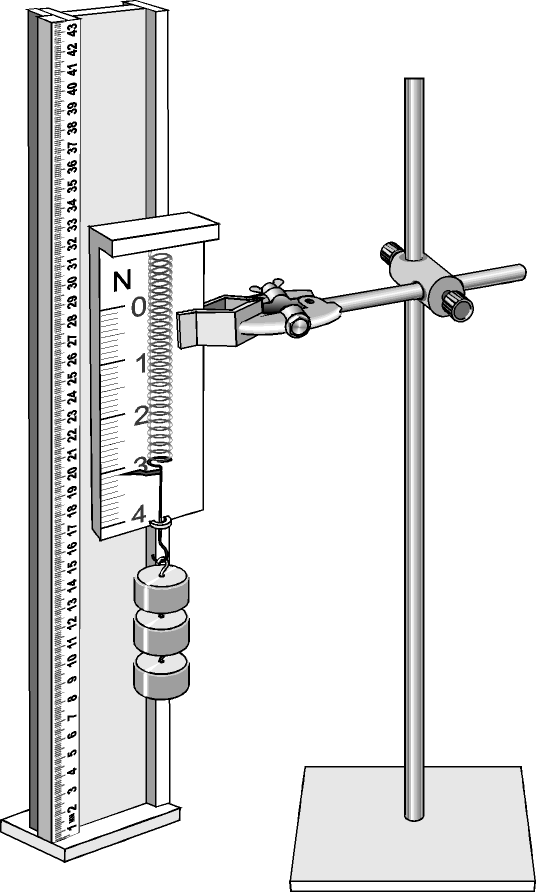
6. Результаты измерений
занесите в таблицу.
7.Подвесьте
к динамометру два груза и вновь определите
удлинение пружины и величину силы
упругости.
8. Повторите опыт с
тремя и четырьмя грузами.
9. Начертите
координатные оси для построения графика
зависимости силы упругости от величины
удлинения.
10. нанесите
на координатной плоскости соответствующие
результатам каждого опыта точки.
11. Постройте график
зависимости силы упругости от величины
удлинения пружины. Если точки не ложатся
на одну прямую, то провести линию графика
надо так, чтобы половина точек расположилась
по одну сторону от нее, а другая половина
– по другую.
12. По графику
определите коэффициент жесткости
пружины. Для этого в средней части
графика возьмите произвольную точку,
опустите от нее перпендикуляры на
координатные оси и определите
соответствующие этой точке величины
удлинения и силы упругости. По полученным
значениям этих величин на основании
закона Гука вычислите коэффициент
жесткости (или, короче, жесткость)
пружины: k =
.
15. Измерение коэффициента трения скольжения
Оборудование:
прибор для изучения прямолинейного
движения динамометр
набор грузов.
Цель работы состоит
в определении коэффициента трения между
пластиковыми
поверхностями направляющей
рейки и каретки.
Измеряют эту величину
по графику зависимости силы трения от
силы нормального давления.
Силу трения можно
определить, если к каретке, лежащей на
горизонтальной поверхности, присоединить
динамометр и потянуть за него вдоль
поверхности так, чтобы каретка стала
бы двигаться равномерно. При равномерном
скольжении сила трения, действующая на
каретку, будет равна силе упругости
растянутой пружины динамометра.
Следовательно, динамометр будет при
этом показывать величину силы трения.
Сила нормального
давления тела на горизонтальную
поверхность, на которой тело покоится
или движется, равна весу этого тела.
Таким образом эту силу можно измерить,
определив с помощью того же динамометра
вес каретки.
Порядок выполнения
работы:
1. Подготовьте таблицу
для записи результатов измерений.
|
№ опыта |
Вес
Рк, |
Вес
Рг, |
Вес
с |
Сила
Fтр, |
2. Направляющую рейки
прибора для изучения прямолинейного
движения положите на стол горизонтально
(см. рисунок в эксперименте 2 “Измерение
силы трения скольжения
и сравнение
ее с весом тела”)
3. Подвесьте каретку
к динамометру и определите ее вес.
4. Разместите каретку
на одном из концов направляющей рейки
крючком по ходу движения. К крючку
прицепите динамометр. Плавно потяните
за динамометр вдоль направляющей рейки
так, чтобы каретка стала перемещаться
с постоянной скоростью.
5. По показанию
динамометра при равномерном движении
каретки определите действующую на нее
силу трения.
6. Данные измерений
первого опыта занесите в первую строчку
таблицы. Вес груза в этом опыте был равен
нулю (Рг = 0).
7. Отсоедините
динамометр от каретки, подвесьте к нему
один груз и определите его вес.
8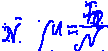
Укрепите груз на каретке, подцепите к
ней динамометр и повторите опыт для
измерения силы трения, действующую на
каретку нагруженную одним грузом. Данные
всех измерений этого опыта занесите во
вторую строчку таблицы.
9. Проведите третий,
а затем и четвертый опыт, нагружая
каретку соответственно двумя и тремя
грузами.
10. По данным таблицы
постройте график зависимости силы
трения от веса каретки. При проведении
линии графика следует стремиться к
тому, чтобы она прошла симметрично
относительно точек, нанесенных на
координатную плоскость. (Точки поровну
должны распределиться по обе стороны
линии.)
11.Возьмите произвольную
точку А на линии графика, опустите из
нее перпендикуляры на оси координат и
определите значение силы трения FтрА
при данном весе каретки РА.
12. Вычислите по этим
данным коэффициент трения
=
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
26.04.2019907.26 Кб3МП.doc
Содержание:
Сила упругости:
Мы уже знаем, что на все тела, которые находятся на Земле или вблизи неё, действует сила тяжести. Эта сила является причиной того, что тела, лишённые опор или подвесов, например капли дождя, брошенный вверх камень, листва, оторвавшаяся от ветви дерева, падают на Землю.
Опыт 1. Положим на две опоры стальную пластину. Она будет находиться в горизонтальном положении (рис. 72, а). Когда на середину ее поставим гирю, то под действием силы тяжести гиря вместе со стальной пластиной будет двигаться вниз до тех пор, пока не остановится (рис. 72, б).
Прекращение движения можно объяснить тем, что кроме силы тяжести, действующей на гирю и направленной вертикально вниз, на неё начала действовать сила, направленная вверх, которая уравновесила силу тяжести. Откуда возникла эта вторая сила ?
Изменение формы или размеров тела называют деформацией. Вследствие движения тела вниз стальная пластина прогибается — деформируется. В результате деформации в пластине возникает сила, с которой она действует на гирю, стоящую на ней. Эту силу назвали силой упругости, она направлена вверх, т. е. в сторону, противоположную силе тяжести. Когда сила упругости по значению сравняется с силой тяжести, опора и тело остановятся.
Сила упругости – это сила, возникающая вследствие деформации тела, и направленная противоположно направлению перемещения частиц тела при деформации.
Одним из видов деформации является прогиб. Чем больше прогибается опора, тем большей становится сила упругости, действующая со стороны опоры на тело. До того как тело поставили на пластину, деформация в ней отсутствовала, как и сила упругости. По мере перемещения гири прогиб пластины возрастал и увеличивалась сила упругости. Свойства упругих тел (пружин) всесторонне изучил более 300 лет назад английский естествоиспытатель Роберт Гук. Проделанные им опыты позволили установить закон, названный его именем — закон Гука, а именно:
Сила упругости прямо пропорциональна деформации (удлинению) тела (пружины) и направлена противоположно направлению перемещения частиц тела при деформации.
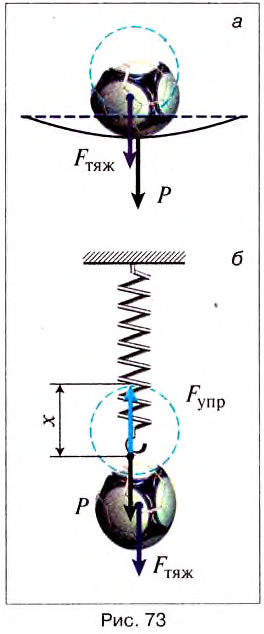
Если удлинение тела, т. е. изменение его длины, обозначить через х (рис. 73, б), а силу упругости — через
где 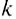
Чем больше жёсткость тела (пружины, провода, стержня и т. п.), тем меньше оно изменяет собственную длину под действием данной силы. Единицей жёсткости в СИ является один ньютон на метр 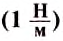
Опыт 2. Установим тело на опору (рис. 73, а). Вследствие взаимодействия деформируется не только опора, но и само тело, которое притягивается Землёй. Деформированное тело давит на опору с силой, которую называют весом тела Р. Если тело подвесить к пружине, то оно деформируется и при этом растягивает пружину, в результате чего возникает сила упругости (рис. 73, б).
Тело действует на подвес с силой, которую называют весом тела Р.
Вес тела – это сила, с которой тело вследствие притяжения к Земле действует на горизонтальную опору или подвес.
Не следует путать силу тяжести с весом тела. Сила тяжести действует на само тело со стороны Земли, а вес этого тела — это сила упругости, которая действует на опору или подвес.
Если горизонтальная опора или подвес с телом находится в состоянии покоя или движется прямолинейно и равномерно, то вес тела равен силе тяжести и определяется по формуле:
где Р— вес тела; 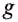
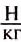
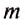
Иногда путают вес тела с его массой — это ошибка. Во-первых, это разные физические величины, из которых вес — направленная величина, вектор, а масса определяется только числовым значением. Они характеризуют разные свойства тел и имеют разные единицы: для веса — ньютон, для массы – килограмм. Во-вторых, каждое тело всегда имеет определённую неизменную массу, а вес тела может изменяться, если опора или подвес движется неравномерно. В этом случае вес тела может увеличиваться или уменьшаться по сравнению с весом тела на неподвижной опоре и даже исчезать, т. е. равняться нулю (состояние невесомости). Например, поднимая грузы с помощью подъёмного крана, нужно учитывать, что во время резких рывков вес груза возрастает, и трос может разорваться. Стоя на платформе медицинских весов, мы замечаем, что их показания изменяются, если мы приседаем или двигаем руками.
Вес тела действует на любую опору: пол, по которому мы ходим, стул, на котором сидим, канат, за который ухватились. Назначение опоры – ограничивать движение тела под действием силы тяжести, отсюда и её название.
Начиная с 4 октября 1957 г., когда космическая ракета вывела на орбиту первый искусственный спутник Земли, началась эра освоения человеком космического пространства. Человек побывал на Луне, готовится экспедиция на Марс. Мы часто слышим по радио и телевидению, читаем в газетах и журналах, что космонавты во время полёта в космическом корабле по орбите вокруг Земли находятся в особом состоянии, называемом невесомостью.
Что это за состояние и можно ли его наблюдать на Зеше?
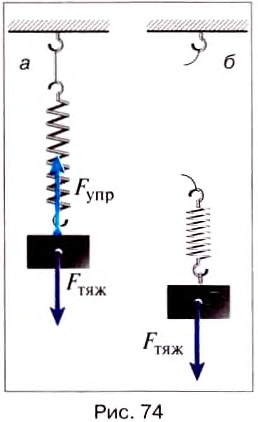
Опыт 3. Верхний конец пружины с помощью нити прикрепим к неподвижной опоре, а к нижнему подвесим грузик (рис. 74, а). Под действием силы тяжести он начинает двигаться вниз. Пружина будет растягиваться до тех пор, пока возникшая в ней сила упругости не уравновесит силу тяжести. Перережем или пережжём нить, которая удерживает тело с пружиной. Пружина и тело начинают свободно падать, при этом растяжение у пружины исчезает, а это и означает, что тело потеряло вес и не действует на подвес (рис. 74, б).
Сила тяжести при этом никуда не исчезает и заставляет тело падать на Землю.
Так же если скорости падения тела и опоры (подвеса) одинаковы, то тело не действует на них, и его вес равен нулю. Если искусственный спутник или космическая станция обращается вокруг Земли, то космонавты и все предметы внутри них двигаются с одинаковой скоростью относительно Земли. Вследствие этого тела, размещённые на подставках, не действуют на них, подвешенные к пружинам тела не растягивают их, разлитая из сосуда вода плавает в виде большой капли, маятниковые часы перестают работать, космонавты без особых усилий передвигаются, «летая» или «плавая» в корабле.
Если бы сила тяжести внезапно исчезла, то космический корабль вследствие инерции удалялся бы от Земли в космическое пространство по прямой линии. В состоянии невесомости находится любое тело во время свободного, т. е. безопорного падения. Если при обычных условиях не учитывать сопротивление воздуха, то в невесомости находится спортсмен, прыгающий с вышки в бассейн или выполняющий упражнения на батуте; любой из нас кратковременно находится в состоянии невесомости во время бега, когда обе ноги отрываются от Земли.
Кстати:
В давние времена благодаря упругим свойствам некоторых материалов (в частности, такого дерева, как тисс) наши пращуры изобрели лук – ручное оружие, предназначенное для метания стрел с помощью силы упругости натянутой тетивы.
Изобретённый приблизительно 12 тыс. лет тому назад, лук на протяжении многих столетий был основным оружием почти всех племён и народов мира. До изобретения огнестрельного оружия лук был наиболее эффективным боевым средством. Английские лучники могли выпускать до 14 стрел в минуту, что при массовом использовании луков в бою образовывало целую тучу стрел. Например, количество стрел, выпущенных в битве при Азенкуре (во время Столетней войны), составляло приблизительно 6 миллионов!
Широкое применение этого грозного оружия в средние века вызвало обоснований протест со стороны определённых слоёв общества. В 1139 г. Латеранский (церковный) собор, собравшийся в Риме, запретил применение этого оружия против христиан. Однако борьба за «лучное разоружение» не имела успеха, и лук как боевое оружие люди продолжали использовать ещё на протяжении 500 лет.
Пример №1
Назовите силы, которые действуют на груз, подвешенный к концу спиральной пружины.
Ответ: на груз действуют сила тяжести, направленная вертикально вниз, и сила упругости, направленная противоположно удлинению пружины.
Пример №2
Каков вес космического аппарата массой 383 кг на поверхности планеты Марс? На Марсе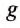
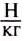
Дано:
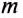
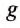
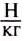
Р – ?
Решение:
Чтобы определить вес космического аппарата, используем формулу:
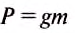

Ответ: Р= 1493,7 Н.
Пример №3
Космонавту в условиях невесомости необходимо заниматься физическими упражнениями. Понадобятся ли ему гантели?
Ответ: обычные упражнения на подъём веса в состоянии невесомости теряют смысл, но упражнения на преодоление инертности гантелей (махи, повороты, разведения рук и т. п.) выполнять вполне возможно. Тем не менее гантели как лишний груз скорее заменят на эспандер.
Измерение силы
Устройство динамометра (от греческих слов динамис — сила; метрео — измеряю) основано на том, что сила упругости пружины по закону Гука прямо пропорциональная удлинению (деформации) пружины.
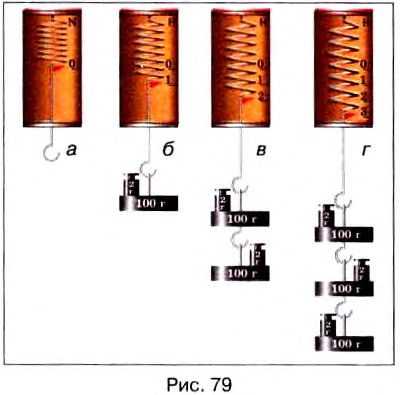
Простейший пружинный динамометр изготовляют так. На дощечке закрепляют пружину, которая заканчивается внизу стержнем с крючком (рис. 79, а). К верхней части стержня прикрепляют указатель. На дощечке отмечают положение указателя — это нулевой штрих. Потом к крючку подвешивают разновесы массой 102 г. На этот грузик действует сила тяжести 1 Н. Под действием силы 1 Н пружина растянется, указатель опустится вниз. Отмечают его новое положение и напротив метки ставят цифру 1 (рис. 79, б). Потом подвешивают разновесы массой 204 г и ставят метку 2, которая означает, что в этом положении сила упругости пружины равна 2 Н (рис. 79, в). С помощью разновесов массой 306 г наносят метку 3
(рис. 79, г) и т. д.
Можно нанести деления, соответствующие десятым долям ньютона: 0,2; 0,4; 0,6 и т. д. Для этого промежутки между соседними штрихами нужно поделить на пять одинаковых частей.
Проградуировать прибор – это значит нанести на него шкалу с делениями.
Проградуированная таким образом пружина и будет простейшим динамометром. Для измерения силы используют такие динамометры (рис. 80): а — школьный лабораторный динамометр; б — школьный демонстрационный динамометр: в – пружинные весы: г — медицинский динамометр-силомер, предназначенный для измерения силы мышц руки человека; д — динамометр-тягомер. Основной частью такого динамометра являются упругие стальные рессоры. Этот прибор используют для измерения силы тяги автомобилей, тракторов и т. п.
Деформация тел
Одним из признаков твердых тел является их свойство сохранять свою форму длительное время. Однако такое свойство наблюдается только тогда, когда на тело не действуют другие тела. Взаимодействуя с другими телами, оно изменяет свою форму. Это изменение не всегда заметно, однако оно всегда существует.
Что такое деформация
Изменение форм или размеров тела называют деформацией.
Явление деформации подчиняется действию определенных законов. Один из таких законов можно проиллюстрировать опытом. Повесим на штативе резиновую нить и измерим ее длину. Подвесим к нити груз определенной массы и увидим, что он начнет опускаться вниз, растягивая нить. Скорость его будет уменьшаться, и он в конце концов остановится, а длина нити будет больше начальной. По результатам опыта можно сделать вывод, что при деформации нити возникла сила, направленная в сторону, противоположную деформации.
Эту силу назвали силой упругости.
Силу, возникающую при деформации называют силой упругости.
Как рассчитать силу упругости
Силу упругости можно рассчитать, если известна деформация тела. Если начальную длину нити обозначить буквой 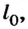
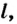
В предыдущем опыте добавим еще одну гирьку. Нить растянется больше. Если измерим изменение длины нити для этого случая, то увидим, что она стала в два раза большей, чем до этого. Такая закономерность характерна для всех случаев незначительной деформации тел и отображает действие закона Гука.
В чем суть закона Гука
Математически эта зависимость записывается так:
Здесь 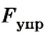
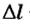
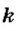
Сила упругости пропорциональна деформации тела и направлена всегда в противоположном деформации направлении.
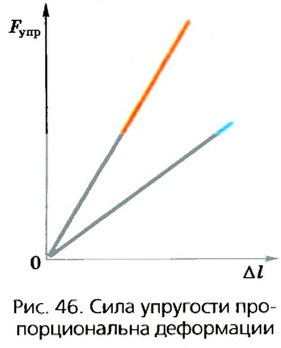
Закон Гука можно проиллюстрировать с помощью графика (рис. 46). На нем зависимость силы упругости от деформации изображена прямой линией, поскольку сила пропорциональна деформации. На рисунке показана зависимость силы упругости от деформации для двух различных тел. Графики являются прямыми линиями, но имеют различный наклон, что свидетельствует о различном значении коэффициента упругости для различных тел.
Закон Гука выполняется для таких деформаций, после снятия которых тело приобретает предыдущие размеры и форму. Такие деформации называют упругими.
- Заказать решение задач по физике
В чем природа сил упругости
Возникновение силы упругости связано с силами взаимодействия между молекулами. При деформации изменяется расстояние между молекулами, а поэтому преобладают или силы притяжения (при растяжении тела), или силы отталкивания (при сжатии тела).
Силы упругости учитывают и используют в различных приспособлениях и машинах. Автомобили, железнодорожные вагоны и другие транспортные средства имеют рессоры. Их использование делает движение более мягким, так как наезд колеса на камень или другое препятствие вызывает только деформацию рессоры и ощутимо не изменяет положения самого транспортного средства.
В странах, где часто бывают землетрясения, дома ставят на специальные пружины, которые во время толчка деформируются, а здание остается практически неподвижным.
Что такое сила упругости
Как известно, взаимодействие тел является не только причиной изменения их скоростей, но и деформации. Сила, вызывающая это явление, называется силой упругости.
Английский естествоиспытатель, ученый и экспериментатор Роберт Гук установил закон, названный его именем. Исследуя упругие деформации различных тел, Гук установил, что при деформации упругих тел их растяжение или сжатие прямо пропорционально силе, которая их растягивает или сжимает (рис. 2.16):
где k – коэффициент пропорциональности, который называется жесткостью, характеризующий способность тела противостоять деформации; х – абсолютная деформация (линейное растяжение или сжатие тела).
Знак «-» показывает, что направление силы упругости противоположно направлению изменения края деформированного тела.
На рисунке 2.17 отображены результаты опыта по определению зависимости растяжения пружины от действующих на 69 нее сил, если к ней подвешен груз массой 100 г, 200 г … в гравитационном поле Земли.
Во время решения задач по расчету силы упругости необходимо четко представлять ее направление и к какому именно телу она приложена. Следует помнить, что деформация тела под действием любой внешней силы вызывает силу упругости, которую определяют по закону Гука.
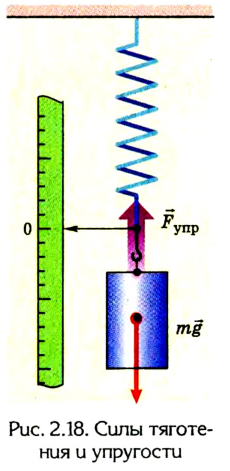
Если в поле силы тяготения к пружине подвесить тело (рис. 2.18), то под действием этой силы оно будет опускаться.
В пружине возникнет сила упругости, которая будет постепенно возрастать.
Когда сила упругости сравняется с силой тяготения (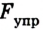
Силу упругости, действующую на тело со стороны подвеса или опоры, называют силой реакции опоры.
Природа сил упругости — электромагнитная. Она обусловлена взаимодействием молекул и атомов, из которых и состоят тела (положительно заряженные протоны, которые входят в состав ядер атомов, и электроны, движущиеся вокруг ядер).
Силы взаимодействия между молекулами и атомами имеют такую особенность: при увеличении расстояния между ними они являются силами притяжения, а при уменьшении — силами отталкивания. Этим и объясняется возникновение сил упругости и направление их действия.
Сила упругости направлена перпендикулярно (нормально) к поверхности столкновения тел, а в случае с деформированными телами (стержнями, пружинами, нитками, тросами и т. п.) – вдоль их осей.
Пример №4
К проволоке подвесили груз массой 10 кг (рис. 2.19). Длина проволоки увеличилась на 0,5 мм. Какова ее жесткость, если ускорение силы тяжести 10
Дано:
m = 10 кг,
х = 0,5мм,
g =10
Груз, подвешенный на пружине, -находится в состоянии покоя. Сила упругости 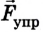
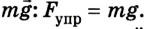
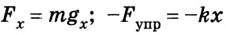
Таким образом, mg = kx, отсюда
Ответ:
Работа силы упругости
Как известно, сила упругости — это сила, возникающая при деформации тела внешними воздействиями. Наиболее удобно изучать действие этой силы на примере пружин или резинового шнура, поскольку достаточно малые внешние силы вызывают значительное изменение их длины, которое легко можно измерить.
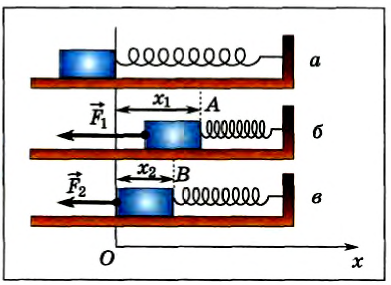
Рассмотрим систему, состоящую из пружины и тела некоторой массы, лежащего на достаточно гладкой горизонтальной поверхности (рис. 137, а). Правый конец пружины прикреплен к стене, а левый — к телу. Направим ось Ох, как показано на рисунке 137. Если тело сместить на расстояние х1 от положения равновесия, то пружина будет действовать на него с силой упругости (рис. 137, б), направленной влево. Модуль проекции этой силы на ось Ox равен kx1, где k — жесткость пружины.
Теперь отпустим тело. Тогда под действием силы упругости пружины тело будет смещаться влево. При этом движении сила упругости совершает работу.
Предположим, что тело переместилось из положения А в положение В (рис. 137, в) так, что расстояние от положения равновесия стало х2. Модуль перемещения тела равен x1-x2. Направления действия силы и перемещения тела совпадают.
Рис. 137
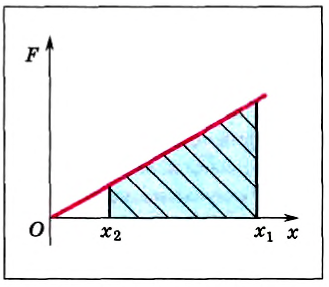
Для нахождения работы, совершенной пружиной по перемещению тела, необходимо учесть, что сила упругости меняется, так как ее величина зависит от удлинения пружины. Воспользуемся графиком зависимости модуля силы от удлинения пружины (рис. 138). Как нам уже известно, работа силы численно равна площади под графиком силы. В нашем случае площади трапеции. Нетрудно сообразить, что
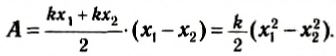
Рис. 138
Из полученной формулы следует, что работа силы упругости пружины зависит только от координат x1 и х2 начального и конечного положений. Из рисунка 137 видно, что x1 и х2 — это и удлинение пружины, и координаты ее конца в выбранной системе координат. Следовательно, работа силы упругости не зависит от формы траектории. А если траектория замкнута, то работа равна нулю. Итак, сила упругости является потенциальной силой. Удлинение пружины или резинового шнура часто обозначают через Δl, поэтому
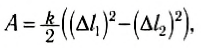
где ∆l1 и Δl2 — удлинения пружины в начальном и конечном положениях.
Формулу (1) для работы силы упругости можно записать и в таком виде:
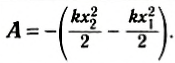
В правой части полученного равенства стоит изменение величины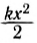
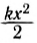
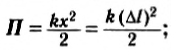
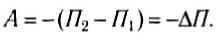
Таким образом, работа силы упругости равна изменению потенциальной энергии упруго деформированного тела (пружины), взятому с противоположным знаком.
Если в конечном состоянии удлинение пружины равно нулю, то формула (5) с учетом (1) принимает вид:
Отсюда следует, что потенциальная энергия упруго деформированной пружины равна работе сил упругости при переходе тела (пружины) в состояние, в котором его деформация равна нулю. Например, растянутая пружина закрывает дверь подъезда (рис. 139).
Рис. 139
О потенциальной энергии тела, на которое действует сила тяжести, мы говорили, что это энергия взаимодействия тела с Землей. Потенциальная энергия упруго деформированного тела — это тоже энергия взаимодействия. Однако в этом случае речь идет о взаимодействии частиц, из которых состоит тело.
Главные выводы:
- Работа силы упругости не зависит от формы траектории тела, а определяется положением тела в начальном и конечном состояниях.
- Сила упругости является потенциальной силой.
- Потенциальная энергия упруго деформированного тела равна работе сил упругости при переходе в недеформированное состояние.
Силы электромагнитной природы
Известно, что наэлектризованные электрическим зарядом тела притягиваются или отталкиваются силами электрического характера. Если же электрические заряды в телах будут двигаться друг относительно друга, то дополнительно к электрическим силам между телами возникают магнитные силы. Эти силы, прочно связанные между собой, невозможно отделить друг от друга, потому что они действуют одновременно. Поэтому говорят, что взаимодействие между наэлектризованными телами происходит в результате действия сил электромагнитной природы. Силы упругости и трения, являющиеся причиной изменения скорости механического движения тела, также являются силами электромагнитной природы.
Сила упругости – это сила электромагнитной природы.
Как вы знаете, любое твердое тело под действием внешней силы испытывает деформацию.
Деформацией называется изменение формы и размеров тела под действием внешней силы. В результате деформации происходит смещение атомов и молекул относительно друг друга: расстояние между атомами или увеличивается, или уменьшается. Такое смещение вызывает соответствующее увеличение или уменьшение действия сил электростатического взаимодействия зарядов внутри атомов (положительных ядер и отрицательных электронов). В результате, в деформированной части тела возникает сила электромагнитной природы, “старающаяся” вернуть тело в первоначальное состояние — силой упругости.
Сила упругости – это сила, возникающая при деформациях твердого тела и действующая в направлении восстановления тела в первоначальном состоянии.
Если после прекращения действия на тело внешней силы оно под действием силы упругости полностью восстанавливает свою форму и размеры, то такая деформация называется упругой деформацией, если же это не происходит, пластической деформацией.
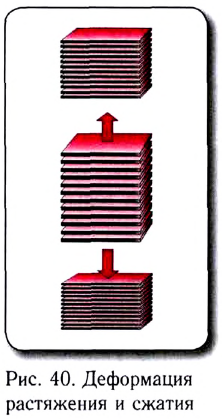
Различают следующие виды деформации: растяжение-сжатие, изгиб, кручение и сдвиг. При деформации растяжение-сжатие изменяется расстояние между частями тела, а при деформации сдвига части тела сдвигаются параллельно друг другу. Деформация изгиб состоит из комбинации деформации сжатия и растяжения частей твердого тела, а деформация кручения из комбинации деформации сдвига (b).
Закон Гука
Деформация растяжение-сжатие твердого тела характеризуется величинами, называемыми абсолютным удлинением и относительным удлинением.
Здесь 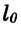
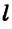
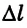
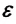
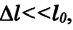

Твердое тело, находящееся в деформированном состоянии, характеризуется механическим напряжением.
Механическое напряжение — это физическая величина, равная отношению модуля силы упругости 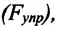
Единица измерения механического напряжения в СИ – паскаль (Па):
Закон Гука: При малых деформациях механическое напряжение прямо пропорционально относительному удлинению:
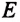
Модуль Юнга – это физическая величина, численно равная механическому напряжению, необходимому для увеличения длины тонкого стержня в два раза. Модуль Юнга зависит от материала, из которого изготовлено тело, единица его измерения в СИ — паскаль:
Приняв во внимание уравнения (2.24) и (2.25) в законе Гука (2.26), получим:
Здесь
называется коэффициентом упругости или жесткостью стержня.
Жесткость, являясь коэффициентом пропорциональности между силой упругости и абсолютным удлинением, зависит от материала, из которого изготовлено тело, и его геометрических размеров.
Приняв во внимание формулу (2.28) в формуле (2.27), закон Гука можно записать следующим образом:
Обычно закон Гука имеет вид:
Где 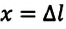
Единица измерения жесткости в СИ:
Диаграмма растяжения
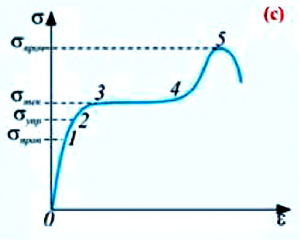
Диаграмма растяжения – это график зависимости механического напряжения от относительного удлинения твердого тела. На диаграмме (с):
a) участок 0-1 – это участок, на котором при малых деформациях механическое напряжение прямо пропорционально относительному удлинению, то есть выполняется закон Гука.
Максимальное значение механического спряжения, при котором еще выполняется закон Гука, называется пределом пропорциональности
На участке графика выше цифры 1 закон Гука нарушается, наблюдается нелинейная деформация;
b) участок 1-2 — соответствует участку, на котором упругая деформация сохраняется, то есть после прекращения внешнего воздействия образец возвращается к своим первоначальным размерам.
Максимальное напряжение, при котором еще возникает упругая деформация, называется пределом упругости 
c) участок 2-3 – механическое напряжение, соответствующее пластической деформации;
d) участок 3-4 — это участок “текучести” образца. Механическое напряжение 
e) участок 4—5 — это участок с резким увеличением механического напряжения, соответствует разрушению тела.
Максимальное механическое напряжение, приводящее к разрушению тела, называется пределом прочности
Силы упругости и упругие деформации
Сила упругости (реакции) возникает в ответ на действие деформирующей силы. Она противоположна по направлению и равна по модулю деформирующей силе. Сила упругости приложена к телу, находящемуся на опоре или подвесе.
Силы упругости обусловлены взаимодействиями между атомами и, как и силы трения, являются по своей природе электромагнитными силами. Они возникают при смещении атомов вещества из положений равновесия. В результате деформации силы электрических взаимодействий стремятся возвратить атомы в первоначальные положения.
Деформация — изменение формы или размеров тела, обусловленное изменением взаимного расположения атомов тела под действием внешних сил или при изменении температуры тела.
Если после прекращения действия сил размер и форма тела полностью восстанавливаются, то деформация называется упругой, а если нет — пластической.
Деформации бывают нескольких видов: растяжение или сжатие (рис. 40); сдвиг (рис. 41); кручение (рис. 42); изгиб (рис. 43).
Упругое тело — одна из механических моделей физических тел, используемая для описания в тех случаях, когда деформацией тела пренебречь нельзя.
Силы упругости возникают между телами только в том случае, если тела деформированы. Движение упругого тела или его взаимодействие с другими телами сопровождается такими изменениями формы, что при прекращении взаимодействия или возврате к исходному механическому состоянию его первоначальная форма восстанавливается. Это означает, что в упругом теле можно пренебречь остаточной деформацией, т. е. изменениями формы и размеров тел после прекращения их взаимодействия.
Особенности сил упругости:
- возникают вследствие деформации одновременно у двух взаимодействующих тел;
- перпендикулярны поверхностям взаимодействующих тел;
- по направлению противоположны смещению частиц деформируемого тела;
- при упругих деформациях выполняется закон Гука:
модуль силы упругости 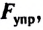
где k — жесткость тела, 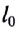
Из соотношения (1) определим жесткость тела:
Единицей жесткости в СИ является ньютон на метр
Жесткость k не зависит от приложенных сил и величины деформации и определяется только размером деформируемого тела и веществом, из которого оно состоит.
Впервые свой закон Роберт Гук опубликовал в 1676 г. в виде анаграммы ut tension sic vis — как напряжение, так сила.
Деформации характеризуют двумя величинами: абсолютное удлинение (сжатие) 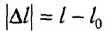
Пружина является моделью деформируемого тела, деформации которого подчиняются закону Гука. Она обладает пренебрежимо малой массой и описывается двумя параметрами — длиной в недеформированном состоянии 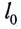
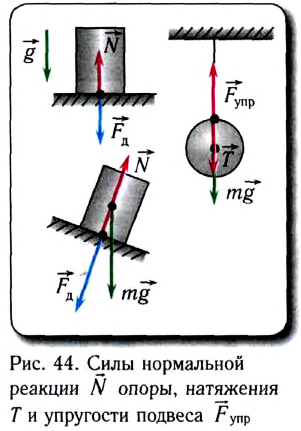
Со стороны опоры на тело действует сила нормальной реакции опоры 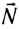
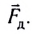
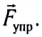
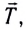
Для тонкого однородного упругого стержня, деформированного некоторой силой 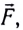
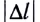
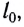
Для выяснения физического смысла модуля Юнга и определения единицы его измерения выразим Е из приведенной формулы:
Если предположить, что в этом соотношении 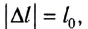
Единицей модуля упругости Е в СИ является ньютон на метр квадратный
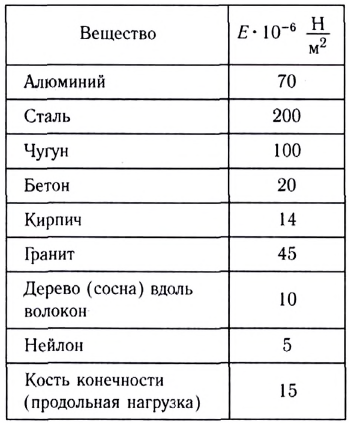
Модули Юнга некоторых веществ приведены в таблице 1.
Таблица 1
Модули Юнга Е некоторых веществ
Еще одной из основных величин, характеризующих механические свойства тел, является механическое напряжение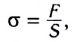
Гука с использованием модуля Юнга и относительного удлинения. Из формулы для модуля упругости следует, что
Откуда, с учетом определения относительного удлинения и напряжения, находим
Жесткость стержня k определяется через модуль упругости (модуль Юнга) Е, его длину 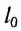
Сила упругости и вес тела
Первый в мире космонавт Ю. А. Гагарин вспоминал: «я почувствовал, что какая-то непреодолимая сила все больше вжимает меня в кресло. И хотя оно было расположено так, чтобы минимизировать влияние гигантского веса, который навалился на мое тело, было трудно пошевелить рукой и ногой».
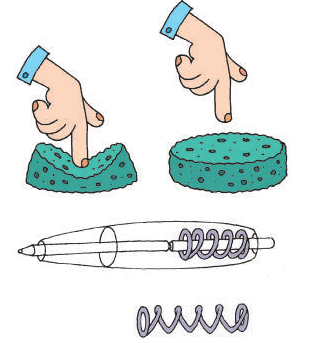
Нажмем на кнопку авторучки — пружина в корпусе сожмется, и ее длина уменьшится; помнем в руке кусочек пластилина — изменится его форма; надавим пальцем на губку — одновременно изменятся и форма, и размеры губки.
Изменение формы и (или) размеров тела называют деформацией.
Если прекратить сжимать пружину, давить на губку, то есть устранить действие внешних сил, и пружина, и губка полностью восстановят свои форму и размеры, то есть перестанут быть деформированными (рис. 12.1). А вот форма кусочка пластилина не восстановится — пластилин ее «не помнит» и останется деформированным.
Рис. 12.1. После прекращения действия силы упругие тела восстанавливают свои форму и размеры
Деформации, которые полностью исчезают после прекращения действия на тело внешних сил, называют упругими; деформации, которые сохраняются, называют пластическими.
Причина возникновения и упругой, и пластической деформаций в том, что под действием сил, приложенных к телу, его различные части смещаются относительно друг друга. По характеру смещения частей различают деформации сжатия, растяжения, сдвига, изгиба, кручения. Остановимся на упругой деформации сжатия и растяжения. Для этого воспользуемся механической моделью твердого тела (рис. 12.2).
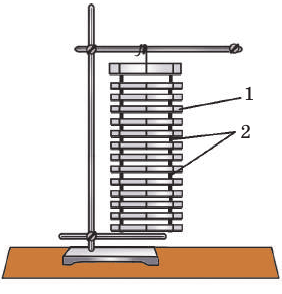
Рис. 12.2. Механическая модель твердого тела: параллельные пластины (1), имитирующие слои молекул, соединены пружинами (2), имитирующими взаимодействия между молекулами
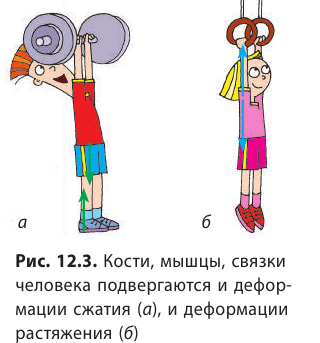
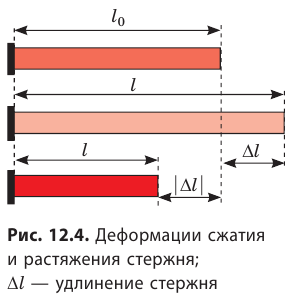
Нажмем на модель твердого тела сверху рукой: верхние пластины начнут смещаться вниз, нижние же останутся почти неподвижными, и в результате модель изменит размеры — деформируется. Примерно так же при сдавливании твердого тела смещаются в направлении действия силы слои его молекул, в результате чего размеры тела уменьшаются. Такую деформацию называют деформацией сжатия — ее испытывают ножки столов и стульев, фундаменты домов и т. п. (см. рис. 12.3, а).
Если же тело растягивать, слои молекул раздвинутся и тело также изменит свои размеры. Такую деформацию называют деформацией растяжения — ее испытывают тросы, цепи в подъемных устройствах, стяжки между вагонами и т. д. (см. рис. 12.3, б).
Физическую величину, равную изменению длины тела при деформации растяжения или сжатия, называют удлинением ∆l (или x):
где l — длина деформированного тела; 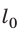
Когда возникает сила упругости
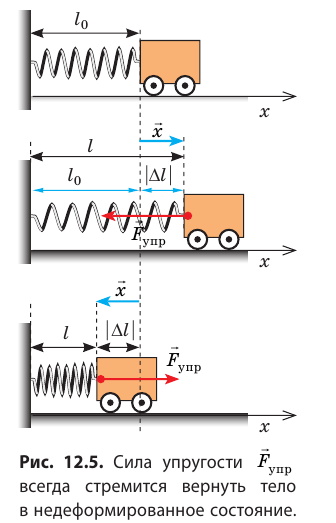
Если вы сгибаете ветку дерева, сжимаете эспандер, натягиваете тетиву лука, то есть деформируете эти тела, вы чувствуете их сопротивление: со стороны тел начинает действовать сила, стремящаяся восстановить то состояние тела, в котором тело находилось до деформации. Эту силу называют силой упругости (рис. 12.5).
Сила упругости 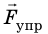
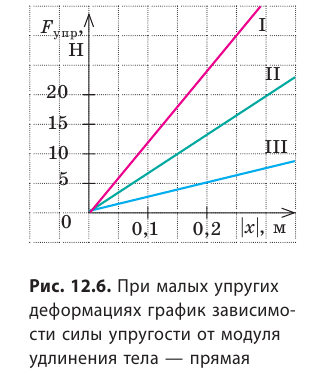
При малых упругих деформациях растяжения или сжатия сила упругости прямо пропорциональна удлинению тела:
Знак «–» показывает, что сила упругости направлена в сторону, противоположную удлинению.
Закон Гука можно записать и для модулей: 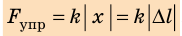
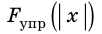
Коэффициент пропорциональности k называют жесткостью тела (стержня, балки, шнура, пружины). Жесткость тела можно определить, воспользовавшись законом Гука:
Единица жесткости в СИ — ньютон на метр: 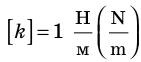
- Жесткость — это характеристика тела, поэтому она не зависит ни от силы упругости, ни от удлинения тела.
- Жесткость зависит от упругих свойств материала, из которого изготовлено тело; от формы тела и его размеров.
Какова природа силы упругости
Известно, что все тела состоят из атомов (молекул, ионов), а те, в свою очередь, — из ядра, имеющего положительный заряд, и электронного облака, заряд которого отрицательный. Между заряженными составляющими частиц вещества существуют силы электромагнитного притяжения и отталкивания.
Если тело не деформировано, силы притяжения равны силам отталкивания. При деформации взаимное расположение частиц в теле изменяется. Если расстояние между частицами увеличивается, то электромагнитные силы притяжения становятся больше, чем силы отталкивания, и частицы начинают притягиваться друг к другу. Если расстояние между частицами уменьшается, то больше становятся силы отталкивания. Другими словами, частицы вещества «стремятся» вернуться к состоянию равновесия. Таким образом, сила упругости — результат электромагнитного взаимодействия частиц вещества.
Некоторые виды сил упругости
Обычно силу упругости обозначают символом 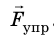
Деформация опоры вызывает появление силы упругости, действующей на тело перпендикулярно поверхности опоры. Эту силу называют силой нормальной реакции опоры и обозначают символом 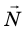
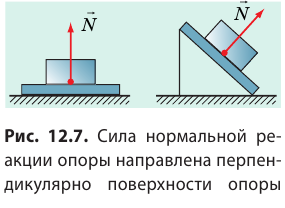
Если тело закрепить на подвесе (нити, жгуте, шнуре), то подвес деформируется (растягивается) и будет действовать на тело с определенной силой упругости, направленной вдоль подвеса, — силой натяжения подвеса 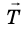
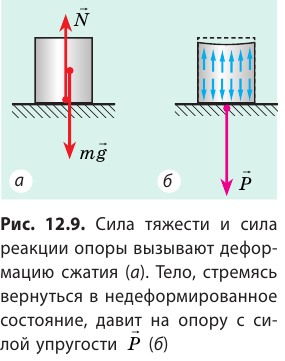
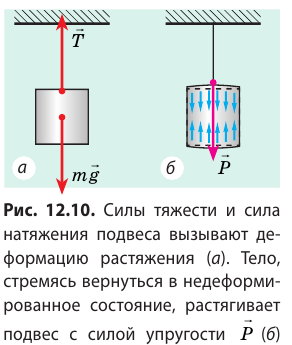
Все тела вследствие гравитационного притяжения сдавливают или прогибают опору либо растягивают подвес. Силу, характеризующую такое действие тел, называют весом и обозначают символом 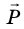
На рис. 12.9, 12.10 показано, как возникает эта сила, если тело находится вблизи поверхности Земли и действует на горизонтальную опору или вертикальный подвес. В таких случаях согласно третьему закону Ньютона вес тела по модулю равен силе нормальной реакции опоры или силе натяжения подвеса и направлен противоположно им: 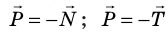
Именно такие случаи возникновения веса тела мы будем рассматривать далее. Обратите внимание! Если тело находится в состоянии покоя или равномерного прямолинейного движения, то вес тела по модулю равен силе тяжести ( 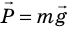
Действительно, в таком случае сила тяжести и сила нормальной реакции опоры (или сила натяжения подвеса) скомпенсированы, поэтому они равны по модулю и противоположны по направлению: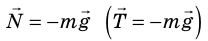
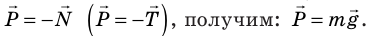
Вес тела и сила тяжести различаются и по своей природе: сила тяжести — это гравитационная сила, а природа веса тела — электромагнитная.
При каких условиях вес тела изменяется
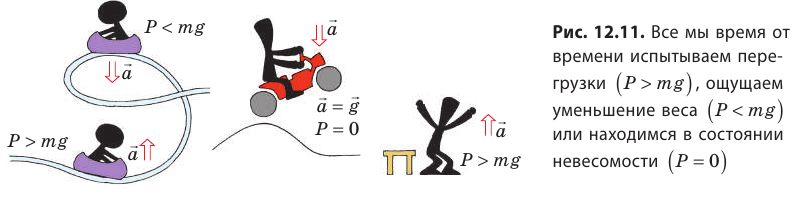
Нам кажется, что в невесомости находятся только космонавты на орбите, а перегрузки испытывают только летчики при выполнении фигур высшего пилотажа и космонавты. Но это не так.
| Увеличение веса (перегрузка) | Увеличение веса (перегрузка) Уменьшение веса |
|---|---|
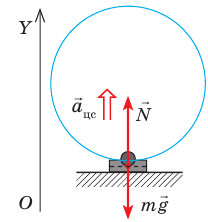
Рассмотрим тело, которое находится на опоре и вместе с ней движется в гравитационном поле Земли с ускорением 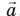 . На тело действуют две силы: сила тяжести . На тело действуют две силы: сила тяжести 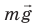 и сила нормальной реакции опоры и сила нормальной реакции опоры 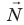 . Свяжем систему координат с Землей и направим ось ОY вертикально вверх. Согласно второму закону Ньютона: . Свяжем систему координат с Землей и направим ось ОY вертикально вверх. Согласно второму закону Ньютона: 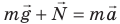 . Запишем это уравнение в проекциях на ось ОY для двух случаев. . Запишем это уравнение в проекциях на ось ОY для двух случаев. |
|
 |
 |
| Вес тела, которое движется с ускорением, направленным вертикально вверх, больше, чем вес этого же тела в состоянии покоя. Когда есть перегрузки, не только тело сильнее давит на опору, но и части тела сильнее давят друг на друга. | Вес тела, которое движется с ускорением, направленным вертикально вниз, меньше, чем вес этого же тела в состоянии покоя. Если в этом случае ускорение движения тела равно ускорению свободного падения 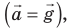 вес тела равен нулю. вес тела равен нулю. |
Как испытать состояние невесомости
Состояние тела, при котором вес тела равен нулю, называют состоянием невесомости. В состоянии невесомости на тело действует только сила тяжести (тело свободно падает), и наоборот: если тело движется только под действием силы тяжести, оно находится в состоянии невесомости. В состоянии невесомости тело не давит на опору и части тела не давят друг на друга; космонавт на орбите (вспомните: на орбите космический корабль движется только под действием силы тяжести) не чувствует своего веса, предмет, выпущенный из его рук, не падает. Дело в том, что сила тяжести сообщает каждому телу и любой части тела одинаковое ускорение.
Чтобы испытать состояние невесомости, достаточно подпрыгнуть. А вот для тренировки космонавтов используют тот факт, что из-за действия силы тяжести траектория тела, брошенного под углом к горизонту, — параболическая. Если в верхних слоях атмосферы самолет направить по восходящей траектории («бросить» под углом к горизонту) и существенно уменьшить тягу двигателей, то некоторое время все тела в самолете будут находиться в состоянии невесомости.
Пример №5
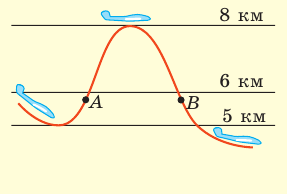
Самолет делает «мертвую петлю», описывая в вертикальной плоскости окружность радиусом 250 м. Во сколько раз вес летчика в нижний части траектории больше силы тяжести, если скорость движения самолета 100 м/с?
Анализ физической проблемы. Самолет движется по окружности, а значит, летчик имеет центростремительное ускорение. На пояснительном рисунке изобразим силы, действующие на летчика, и направление его ускорения. Выберем одномерную систему координат, которую свяжем с точкой на поверхности Земли, ось ОY направим вертикально вверх.
Решение:
По второму закону Ньютона: 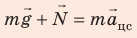
В проекциях на ось ОY:
По третьему закону Ньютона P N= , поэтому
Окончательно:
Найдем значения искомых величин:
Анализ результата. Вес летчика в 5 раз больше силы тяжести — это реальный результат.
Ответ: 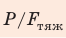
Алгоритм решения задач на движение тела под действием нескольких сил
- Прочитайте условие задачи. Выясните, какие силы действуют на тело, движется тело с ускорением или равномерно прямолинейно.
- Запишите краткое условие задачи. При необходимости переведите значения физических величин в единицы СИ.
- Выполните рисунок, на котором укажите силы, действующие на тело, и направление ускорения движения тела.
- Выберите инерциальную СО. Количество осей координат и их направление выберите, исходя из условия задачи.
- Проверьте единицу, найдите числовое значение искомой величины
- Проанализируйте результат. Запишите ответ.
- Запишите уравнение второго закона Ньютона в векторном виде и в проекциях на оси координат. Запишите формулы для вычисления сил. Получив систему уравнений, решите ее. Если в задаче есть дополнительные условия, используйте их.
Выводы:
- Деформацией называют изменение формы или (и) размеров тела. Если после прекращения действия на тело внешних сил деформация полностью исчезает, это упругая деформация; если деформация сохраняется, это пластическая деформация.
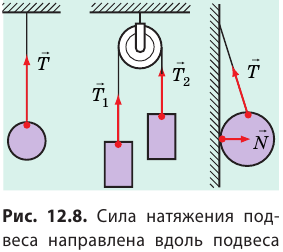
- Силу, которая возникает в теле при его деформации и стремится вернуть тело в недеформированное состояние, называют силой упругости. Сила упругости имеет электромагнитную природу, ее можно рассчитать по закону Гука:
, где k — жесткость тела. Закон Гука выполняется только при малых упругих деформациях.
- Вес тела
— это сила, с которой вследствие гравитационного притяжения тело давит на опору или растягивает подвес. Если опора горизонтальная или подвес вертикальный, согласно третьему закону Ньютона вес тела равен по модулю и противоположен по направлению силе нормальной реакции опоры (силе натяжения подвеса):
.
- Если тело находится в состоянии покоя или движется равномерно прямолинейно, вес тела по модулю равен силе тяжести:
.
- Если тело движется с ускорением, направленным вертикально вверх, это тело испытывает перегрузки (вес тела больше, чем его вес в состоянии покоя):
.
- Если тело движется с ускорением, направленным вертикально вниз, вес тела меньше, чем его вес в состоянии покоя:
Физика в цифрах:
- P= 0 — отсутствие нагрузки (состояние невесомости).
- P=mg — «нормальная» нагрузка (на поверхности Земли).
- P= 3 mg — максимальная нагрузка, которая ощущается на «американских горках».
- P= 4,3 mg — максимальная нагрузка, на которую рассчитаны пассажирские самолеты.
- P= 5 mg — нагрузка, при которой большинство людей теряют сознание.
- P= 9 mg — нагрузка, которую может испытывать человек за штурвалом истребителя при крутых виражах.
- Деформация в физике
- Плотность вещества в физике
- Сила трения в физике
- Вес тела в физике
- Масса тела в физике
- Сила в физике
- Силы в механике
- Сила тяжести в физике
На данном уроке мы познакомимся с новым прибором, с помощью которого можно измерить силу, действующую на тело. Как называют прибор для измерения силы?
Динамометр — это прибор для измерения силы.
Слово «динамометр» образовано от двух греческих слов: «динамис» — «сила» и «метрео» — «измеряю».
Рассмотрим самый простой вид динамометра — пружинный. Это поможет нам разобраться с принципом действия прибора. Основной его частью является стальная пружина.
Не сложно догадаться, что если подвесить к пружине груз, то она растянется. Другими словами, наблюдатель видит, что на подвешенное тело действует сила, и может определить ее величину.
Устройство пружинного динамометра
Как изготовить простейший динамометр?
Простой пружинный динамометр можно изготовить самостоятельно (рисунок 1). Он состоит из нескольких частей:
- стальная пружина с крючком и указателем на конце;
- корпус для крепления пружины;
- шкала.
Сначала закрепляем пружину на корпусе таким образом, чтобы ее нижний конец оставался свободным. Затем к нему прикрепляем указатель. Если разогнуть последний виток пружины, то его можно использовать в качестве указателя.
Градуировка шкалы динамометра
Шкалу можно изготовить из полоски обычной бумаги, нанеся на нее штрихи и числа. Поэтому приклеим бумагу на корпус и сделаем на ней первую отметку (рисунок 2, а). Это будет нулевая отметка, которая показывает, где заканчивается нерастянутая пружина.
Из прошлого урока нам известно, что на груз массой $frac{1}{9.8} space кг$ ($102 space г$) будет действовать сила тяжести, равная $1 space Н$. Поэтому подвесим на крючок груз указанной массы и посмотрим, насколько растянется пружина.
Если пружина прекратила растяжение и груз остановился, это означает, что сила тяжести, действующая на тело, и сила упругости пружины уравнялись. Новое положение указателя отметим на бумаге, поставив цифру 1 (рисунок 1, б).
Так мы уже получили начало шкалы и необходимо ее продолжить. И сделать это можно по-разному:
- Поочередно подвешивать грузы массой $204 space г$, $306 space г$, $408 space г$ и т. д., проставляя соответствующие отметки: 2, 3, 4 и т. д.
- Воспользоваться двумя имеющимися отметками (0 и 1) и с помощью линейки отложить отрезки такой же длины, отметив их числами 2, 3, 4 и т. д.
Теперь у нас есть шкала, которая позволяет измерять силу с точностью до целых. Но точность нашей шкалы можно улучшить до десятых, нанеся на нее дополнительные деления — 0.1; 0.2; 0.3; 0.4 и т. д.
Как нанести на шкалу динамометра деления, соответствующие $0.1 space Н$?
Для этого разделим расстояние между отметками 0 и 1 на 10 одинаковых частей, поставив соответствующие штрихи. Аналогично поделим на части и другие отрезки ( между отметками 2 и 3, 3 и 4, и т. д.).
Описанным способом мы осуществили градуировку шкалы, цена деления которой равна $0.1 space Н$.
Принцип действия динамометра
Итак, мы видим, что для измерения силы, действующей на груз, необходимо уравнять ее с силой растяжения пружины динамометра. Указатель, закрепленный на пружине, покажет величину этой силы согласно шкале. Таким образом, можно сделать вывод, что:
Устройство динамометра основывается на сравнении измеряемой силы с силой упругости пружины.
Например, если подвесить груз какой-то массы, то мы будем сравнивать силу тяжести, действующую на этот груз, и величину силы упругости растянутой пружины.
Если мы возьмем крючок на конце пружины и потянем за него, то мы будем сравнивать силу, приложенную нами, с силой упругости пружины (рисунок 3). Так, с помощью динамометра можно измерять различные силы.
Вспомним закон Гука — он гласит, что сила упругости тела при растяжении прямо пропорциональна изменению длины тела. Принцип работы динамометра подтверждает этот закон — пружина удлиняется во столько же раз, во сколько увеличивается сила ее упругости.
Виды динамометров
Какие типы динамометров вам известны?
Можно выделить несколько видов динамометров на основе принципа их действия:
- Механические динамометры (рычажные или пружинные)
В основе работы механических динамометров лежит деформация. Принцип действия пружинного динамометра подробно описан выше. В рычажном динамометре под действием измеряемой силы происходит деформация рычага, которая и показывает величину силы.
- Гидравлические динамометры
Принцип действия таких динамометров основан на определении количества жидкости, вытесняемой из цилиндра под действием измеряемой силы.
- Электрические динамометры
У таких динамометров имеется датчик, который преобразует деформацию в электрический сигнал. Это вид динамометров стал широко применяться в последнее время.
Современные модели динамометров могу соединять и использовать в себе несколько принципов действия.
Применение динамометров
Динамометры имеют очень широкое применение. Например, в медицине используются специальные медицинские динамометры. Они предназначены для измерения силы различных мышечных групп человека.
Одним из таких приборов является ручной динамометр, который называется силомером (рисунок 4). С его помощью измеряется мускульная сила руки при сжатии кисти в кулак.
Для того чтобы измерить тяговые усилия локомотивов, тракторов, морских буксиров и другой техники, используют специальные тяговые динамометры (рисунок 5).
Такие динамометры способны измерять силы до нескольких десятков тысяч ньютонов. Современные модели имеют пульт дистанционного управления с дисплеем (рисунок 6).
При монтаже проводов и кабелей используют динамометры для определения силы натяжения провода (рисунок 7). Существуют специальные монтажные таблицы с необходимыми значениями.
Динамометры используют не только в специальной технике, но и в обычных для нас местах: в метро, в автобусах и даже в лифте. Здесь эти приборы используют для измерения силы сжатия створок различных автоматических дверей.
Упражнения
Упражнение №1
Определите цену деления каждого прибора и силу тяжести, действующую на каждый груз (рисунок 8).
Показать ответ
Скрыть
Определим цену деления динамометра, изображенного на рисунке 8, а. Возьмем два крайних подписанных деления: $1 space Н$ и $0 space Н$. Вычтем меньшее значение из большего и разделим на количество делений между ними:
$frac{1 space Н space − space 0 space Н}{10} = 0.1 space Н$.
Цена деления этого динамометра равна $0.1 space Н$.
На подвешенный груз действует сила тяжести, равная $1 space Н$.
Определим цену деления динамометра, изображенного на рисунке 8, б. Возьмем два крайних подписанных деления: $1 space Н$ и $0 space Н$. Вычтем меньшее значение из большего и разделим на количество делений между ними:
$frac{1 space Н space − space 0 space Н}{2} = 0.5 space Н$.
Цена деления этого динамометра равна $0.5 space Н$.
На подвешенный груз действует сила тяжести, равная $6 space Н$.
Упражнение №2
Чему равен вес каждого груза на рисунке 8? Укажите точку его приложения.
Показать ответ
Скрыть
Груза и динамометры у нас неподвижны, поэтому вес каждого груза будет равен силе тяжести, действующей на него. Значение же силы тяжести мы видим по показаниям динамометров.
Для груза на рисунке 8, а:
$P = F_{тяж} = 1 space Н$.
Для груза на рисунке 8, б:
$P = F_{тяж} = 6 space Н$.
На рисунке 9 изображен вес этих тел. Вес приложен к подвесу в обоих случаях.
Упражнение №3
По рисунку 10 определите, с какой силой растягивается каждая пружина под действием подвешенного к ней груза (масса одного груза $102 space г$).
Дано:
$m = 102 space г$
$g = 10 frac{Н}{кг}$
СИ:
$m = 0.102 space кг$
$F_1 — ?$
$F_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Под действием какой силы будет растягиваться пружина? Она растягивается под влиянием силы тяжести, действующей на подвешенный к ней груз.
Рассчитаем силу, растягивающую причину на рисунке 10, а:
$F_1 = F_{тяж1} = gm$,
$F_1 = 10 frac{Н}{кг} cdot 0.102 space кг = 1.02 space Н$.
Рассчитаем силу, растягивающую причину на рисунке 10, б:
$F_2 = F_{тяж2} = g cdot 2m$,
$F_2 = 10 frac{Н}{кг} cdot 2 cdot 0.102 space кг = 2.04 space Н$.
Ответ: $F_1 = 1.02 space Н$, $F_2 = 2.04 space Н$.


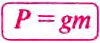


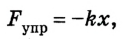
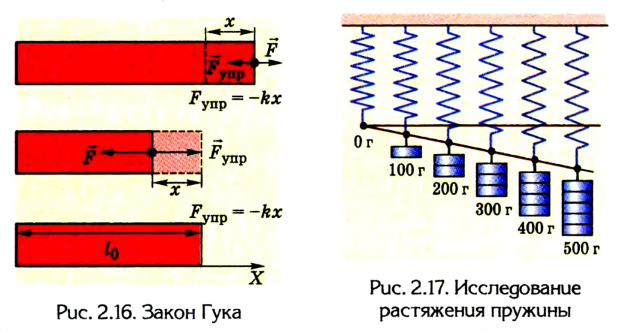
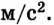
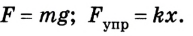
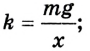
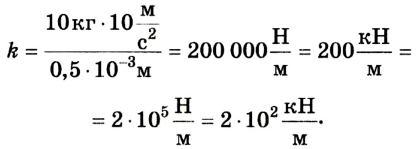
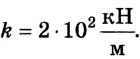
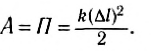



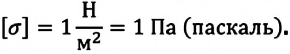
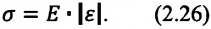
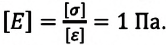
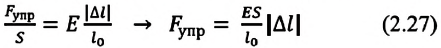

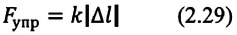
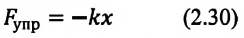
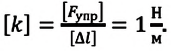



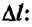


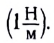
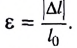


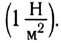
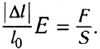


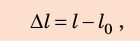
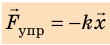
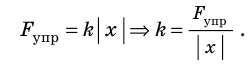
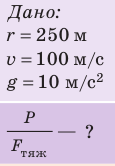
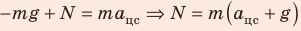
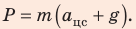
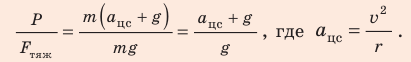
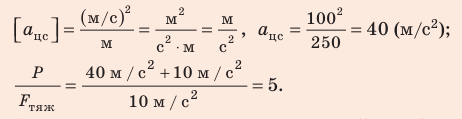
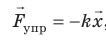 , где k — жесткость тела. Закон Гука выполняется только при малых упругих деформациях.
, где k — жесткость тела. Закон Гука выполняется только при малых упругих деформациях.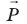 — это сила, с которой вследствие гравитационного притяжения тело давит на опору или растягивает подвес. Если опора горизонтальная или подвес вертикальный, согласно третьему закону Ньютона вес тела равен по модулю и противоположен по направлению силе нормальной реакции опоры (силе натяжения подвеса):
— это сила, с которой вследствие гравитационного притяжения тело давит на опору или растягивает подвес. Если опора горизонтальная или подвес вертикальный, согласно третьему закону Ньютона вес тела равен по модулю и противоположен по направлению силе нормальной реакции опоры (силе натяжения подвеса): 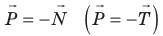 .
.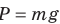 .
.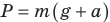 .
.