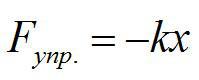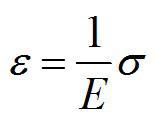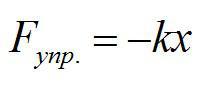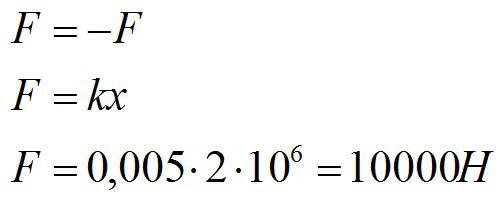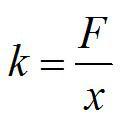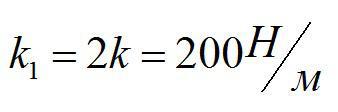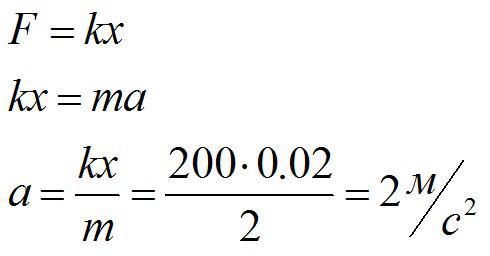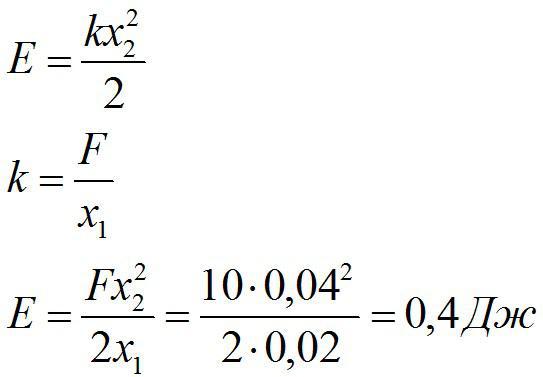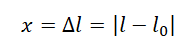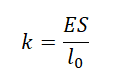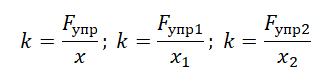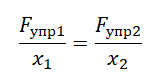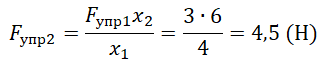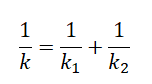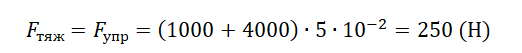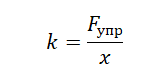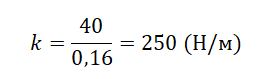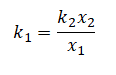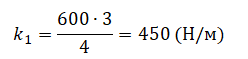Способность к упругим и пластическим деформациям зависит от природы вещества, из которого состоит тело, условий, в которых оно находится; способов его изготовления. Например, если взять разные сорта железа или стали, то у них можно обнаружить совершенно разные упругие и пластичные свойства. При обычных комнатных температурах железо является очень мягким, пластичным материалом; закаленная сталь, наоборот, — твердый, упругий материал.
Пластичность многих материалов представляет собой условие для их обработки, для изготовления из них нужных деталей. Поэтому она считается одним из важнейших технических свойств твердого вещества.
При деформации твердого тела происходит смещение частиц (атомов, молекул или ионов) из первоначальных положений равновесия в новые положения. При этом изменяются силовые взаимодействия между отдельными частицами тела. В результате в деформированном теле возникают внутренние силы, препятствующие его деформации.
Различают деформации растяжения (сжатия), сдвига, изгиба, кручения.
Силы упругости
Силы упругости имеют электромагнитную природу. Они препятствуют деформациям и направлены перпендикулярно поверхности соприкосновения взаимодействующих тел, а если взаимодействуют такие тела, как пружины, нити, то силы упругости направлены вдоль их оси.
Силу упругости, действующую на тело со стороны опоры, часто называют силой реакции опоры. Абсолютное удлинение:
где и длина тела в деформированном и недеформированном состоянии соответственно.
Относительное удлинение:
[custom_ads_shortcode1]
Закон Гука
Небольшие и кратковременные деформации с достаточной степенью точности могут рассматриваться как упругие. Для таких деформаций справедлив закон Гука:
- Сила упругости, возникающая при деформации тела прямо пропорциональна абсолютному удлинению тела и направлена в сторону, противоположную смещению частиц тела:
где проекция силы на ось жесткость тела, зависящая от размеров тела и материала, из которого оно изготовлено, единица жесткости в системе СИ Н/м.
[custom_ads_shortcode2]
Примеры решения задач
| Понравился сайт? Расскажи друзьям! |
Закон Гука был открыт в XVII веке англичанином Робертом Гуком. Это открытие о растяжении пружины является одним из законов теории упругости и выполняет важную роль в науке и технике. Формулировка этого закона выглядит следующим образом: сила упругости, которая появляется в момент деформации тела, пропорциональна удлинению тела и направлена противоположно движению частиц этого тела относительно других частиц при деформации.
Математическая запись закона выглядит так:
Рис. 1. Формула закона Гукагде Fупр – соответственно сила упругости, x – удлинение тела (расстояние, на которое изменяется исходная длина тела), а k – коэффициент пропорциональности, называемый жесткостью тела. Сила измеряется в Ньютонах, а удлинение тела – в метрах.
Для раскрытия физического смысла жесткости, нужно в формулу для закона Гука подставить единицу, в которой измеряется удлинение – 1 м, заранее получив выражение для k.
Рис. 2. Формула жесткости телаЭта формула показывает, что жесткость тела численно равна силе упругости, которая возникает в теле (пружине), когда оно деформируется на 1 м. Известно, что жесткость пружины зависит от ее формы, размера и материала, из которого произведено данное тело.
Теперь, когда известно, какая формула выражает закон Гука, необходимо разобраться в его основной величине. Основной величиной является сила упругости. Она появляется в определенный момент, когда тело начинает деформироваться, например, когда пружина сжимается или растягивается.
Она направлена в обратную сторону от силы тяжести. Когда сила упругости и сила тяжести, действующие на тело, становятся равными, опора и тело останавливаются.
Деформация – это необратимые изменения, происходящие с размерами тела и его формой. Они связанны с перемещением частиц относительно друг друга. Если человек сядет в мягкое кресло, то с креслом произойдет деформация, то есть изменятся его характеристики. Она бывает разных типов: изгиб, растяжение, сжатие, сдвиг, кручение.
Так как сила упругости относится по своему происхождению к электромагнитным силам, следует знать, что возникает она из-за того, что молекулы и атомы – наименьшие частицы, из которых состоят все тела, притягиваются друг другу и отталкиваются друг от друга. Если расстояние между частицами очень мало, значит, на них влияет сила отталкивания. Если же это расстояние увеличить, то на них будет действовать сила притяжения. Таким образом, разность сил притяжения и сил отталкивания проявляется в силах упругости.
Сила упругости включает в себя силу реакции опоры и вес тела. Сила реакции представляет особый интерес. Это такая сила, которая действует на тело, когда его кладут на какую-либо поверхность. Если же тело подвешено, то силу, действующую на него, называют, силой натяжения нити. Как мы уже выяснили, сила упругости возникает при деформации, и направлена она на восстановление первоначальных форм и размеров строго перпендикулярно к деформируемой поверхности. У сил упругости также есть ряд особенностей.
- они возникают во время деформации;
- они появляются у двух деформируемых тел одновременно;
- они находятся перпендикулярно поверхности, по отношению к которой тело деформируется.
- они противоположны по направлению смещению частиц тела.
Закон Гука применяется как в технических и высокотехнологичных устройствах, так и в самой природе. Например, силы упругости встречаются в часовых механизмах, в амортизаторах на транспорте, в канатах, резинках и даже в человеческих костях. Принцип закона Гука лежит в основе динамометра – прибора, с помощью которого измеряют силу.
Рис. 3. ДинамометрСтатья подробно знакомит учащихся с материалом о том, как формулируется обобщенный закон Гука, который изучают в 7 классе, и его основной величине – силе упругости. Средняя оценка: 4.3. Всего получено оценок: 375.
Page 2
ОбразовакаФизика
- МанометрТест
- Закон ГукаТест
- Закон ПаскаляТест
- Сообщающиеся сосудыТест
ОГЭ 2018 по физике ›
Твёрдые тела под действием силы способны изменять свои форму и (или) объём. Взяв за концы металлическую линейку, можно её согнуть. Если перестать прикладывать силу, то линейка восстановит свою форму. Если сжать пружину (рис. 35), то она сократится, т.е. деформируется. При прекращении действия силы пружина вернётся в первоначальное состояние.
Изменение формы или объёма тела при действии на него силы называется деформацией.
Если длина пружины в недеформированном состоянии ( l_0 ), а после растяжения ( l ), то изменение её длины ( l=l-l_0=x ), где ( l ) или ( x ) – удлинение или деформация.
При деформации в теле возникает сила упругости, которая стремится вернуть его в первоначальное состояние. Сила упругости ( (vec{F}_{упр}) ) — сила, возникающая в теле в результате деформации, стремящаяся вернуть тело в первоначальное состояние и направленная в сторону, противоположную деформации (удлинению).
Так, при растяжении пружины эта сила направлена влево к положению равновесия, при
сжатии пружины сила упругости направлена вправо (рис. 36).
Если тело после прекращения действия силы принимает первоначальную форму, то деформация является упругой. Если тело после прекращения действия силы не принимает первоначальную форму, то деформация является неупругой или пластической.
При малых деформациях сила упругости прямо пропорциональна удлинению. Поскольку сила упругости и деформация направлены в противоположные стороны, то: ( F_{упр}=-kDelta l ), где ( k ) — коэффициент пропорциональности, называемый жёсткостью тела. Жёсткость зависит от размеров тела, его формы, материала, из которого сделано тело.
None Формула ( F_{упр}=-kDelta l ) выражает закон Гука: сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению (деформации) тела и направлена в сторону, противоположную деформации.
Важно понимать, что закон Гука справедлив при малых деформациях.
На рисунке 37 приведён график зависимости модуля силы упругости от деформации. Поскольку эта зависимость линейная, то графиком зависимости является прямая, проходящая через начало координат и составляющая угол ( alpha ) с осью абсцисс. По графику можно определить жёсткость тела. Например, значению деформации 2 см соответствует сила упругости 4 Н. Разделив 4 Н на 0,02 м, получим ( k ) = 200 Н/м. В треугольнике АОВ жёсткость ( k ) равна тангенсу угла ( alpha ): ( k=mathrm{tg}alpha ).
Существуют разные виды деформации: растяжения, сжатия, сдвига, изгиба и кручения. В рассмотренных примерах линейка подвергалась деформации изгиба, пружина — деформации растяжения и сжатия, винты, гайки, болты при закручивании испытывают деформацию кручения, тяжёлые предметы при перемещении по полу — деформацию сдвига.
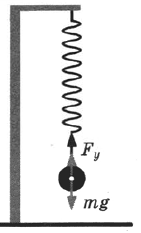
Предположим, что на полу стоит ящик (рис. 38). На него действует сила тяжести ( vec{F}_т ), направленная вертикально вниз. Ящик, взаимодействуя с полом, деформирует его и деформируется сам. И на ящик, и на пол действует сила упругости, характеризующая их взаимодействие. Сила упругости ( vec{N} ), действующая на ящик со стороны пола, приложена к ящику и направлена вертикально вверх; сила упругости ( vec{P} ), действующая со стороны ящика на пол, приложена к полу и направлена вертикально вниз. Эта сила называется весом тела.
Весом тела называют силу, с которой тело, вследствие его притяжения к Земле, действует на опору или подвес. В отличие от силы тяжести, вес тела приложен не к телу, а к опоре или к подвесу. Вес — это сила упругости.
Если тело покоится или движется равномерно и прямолинейно, вес тела численно равен силе тяжести, действующей на него: ( vec{P}=mvec{g} ).
На тело, движущееся вместе с платформой или подвесом вертикально вниз с ускорением ( vec{a} ), направленным в сторону движения, действуют сила тяжести ( vec{F}_{т} ) и сила упругости ( N ) со стороны опоры или подвеса (рис. 39, 40).
Второй закон Ньютона для этой ситуации: ( mvec{g}+vec{N}=mvec{a} ). В проекциях на координатную ось: ( mg-N=ma ) или ( N=mg-ma ). Поскольку ( N=P ), ( P = m(g — a) ).
Если тело движется вниз вместе с опорой или подвесом с ускорением, направленным так же, как и ускорение свободного падения, то его вес меньше силы тяжести, т.е. меньше веса покоящегося тела. Если ускорение тела равно ускорению свободного падения ( vec{a}=vec{g} ), то тело находится в состоянии невесомости.
В таком состоянии находится космонавт в космическом корабле, прыгун с трамплина во время полёта вниз.
На тело, движущееся вместе с платформой или подвесом вертикально вверх с ускорением ( vec{a} ), направленным в сторону движения, действуют сила тяжести ( vec{F}_т ) и сила упругости ( vec{N} ) со стороны опоры или подвеса (рис. 40).
Второй закон Ньютона для этой ситуации: ( mvec{g}+vec{N}=mvec{a} ). В проекциях на координатную ось: ( mg-N=-ma ) или ( N=mg+ma ). Поскольку ( N=P ), ( P=m(g+a) ).
Таким образом, если тело движется вверх вместе с опорой или подвесом с ускорением, направленным противоположно ускорению свободного падения, то его вес больше силы тяжести, т.е. больше веса покоящегося тела. Увеличение веса тела при движении с ускорением называют перегрузкой. Перегрузки испытывают космонавт в космическом корабле, пилот реактивного самолёта при взлёте и посадке.
Содержание.
- ПРИМЕРЫ ЗАДАНИЙ
- Ответы
[custom_ads_shortcode3]
ПРИМЕРЫ ЗАДАНИЙ
[custom_ads_shortcode1]
Часть 1
Имеются две абсолютно упругие пружины. Под действием одной и той же силы первая пружина удлинилась на 8 см, а вторая — на 4 см. Сравните жёсткость ( k_2 ) второй пружины с жёсткостью ( k_1 ) первой пружины.
1) ( k_1=k_2 )
2) ( 4k_1=k_2 )
3) ( 2k_1=k_2 )
4) ( k_1=2k_2 )2. Имеются две абсолютно упругие пружины: одна жёсткостью 200 Н/м, другая жёсткостью 400 Н/м. Сравните силу упругости ( F_2 ), возникающую во второй пружине, с силой упругости ( F_1 ), возникающей в первой пружине, при одинаковом их удлинении.
1) ( F_2=F_1 )
2) ( F_2=4F_1 )
3) ( 2F_2=F_1 )
4) ( 0.5F_2=F_1 )3. Ученик, растягивая пружину динамометра последовательно на 1Н, 2Н, ЗН и 4Н, каждый раз измерял её удлинение и результаты измерений вносил в таблицу. Определите по данным таблицы жёсткость пружины динамометра.
1) 0,02 Н/м 2) 0,5 Н/м 3) 2 Н/м 4) 50 Н/м4. На рисунке приведены графики зависимости силы упругости от удлинения. Сравните жёсткость пружин.
1) ( k_2=k_1 ) 2) ( k_2>k_1 ) 3) ( k_2<k_1 ) 4) ( k_2geq k_1 )5. Учащийся выполнял эксперимент по измерению удлинения ( x ) пружин при подвешивании к ним грузов. Полученные учащимся результаты представлены на рисунке в виде диаграммы. Какой вывод о жёсткости пружин ( k_1 ) и ( k_2 ) можно сделать из анализа диаграммы, если к концам пружин были подвешены грузы одинаковой массы?
1) ( k_2=4k_1 ) 2) ( k_1=2k_2 ) 3) ( k_2=2k_1 ) 4) ( k_1=k_2 )6. Под действием силы 3 Н пружина удлинилась на 4 см. Чему равна сила, под действием которой удлинение этой пружины составит 6 см?
1) 3,5 Н 2) 4 Н 3) 4,5 Н 4) 5 Н7. Две пружины растягиваются одинаковыми силами. Жёсткость первой пружины ( k_1 ) в 2 раза больше жесткости второй пружины ( k_2 ). Удлинение первой пружины ( Delta l_1 ), удлинение второй пружины ( Delta l_2 ) равно1) ( 0.5Delta l_1 ) 2) ( 0.67Delta l_1 ) 3) ( 1.5Delta l_1 ) 4) ( 2.5Delta l_1 )8. В лифте, движущемся вниз равноускоренно из состояния покоя, стоит ящик. Модуль веса ящика1) равен модулю силы тяжести 2) больше модуля силы тяжести 3) меньше модуля силы тяжести 4) увеличивается с увеличением скорости лифта9. Человек испытывает перегрузки при1) равномерном движении вниз 2) равномерном движении вверх 3) равноускоренном движении вверх из состояния покоя 4) равноускоренном движении вниз с ускорением свободного падения10. Различие веса тела на экваторе и на полюсе можно обнаружитьА. Взвешивая тело на рычажных весах Б. Взвешивая тело на пружинных весахПравильный ответ1)только А 2)только Б 3) и А, и Б 4) ни А, ни Б11. Установите соответствие между физической величиной (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответовФИЗИЧЕСКАЯ ВЕЛИЧИНА A. Модуль силы упругости пружины Б. Жёсткость пружины B. Модуль удлинения пружиныХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ 1) уменьшается 2) увеличивается 3) не изменяется12. Из приведённых ниже высказываний выберите два верных и запишите их номера в таблицу.
1) Закон Гука справедлив при любых деформациях. 2) Сила упругости направлена в сторону, противоположную деформации. 3) Жёсткость зависит только от материала, из которого изготовлено тело.
4) Вес тела всегда равен действующей на него силе тяжести. 5) Вес приложен к опоре или к подвесу.
[custom_ads_shortcode2]
Часть 2
Груз массой 5 кг начинают поднимать вертикально вверх с ускорением 2 м/с. Чему равен вес груза?
[custom_ads_shortcode3]
Ответы
Обзор материала
Мы живем в мире физических тел, которые действуют друг на друга, т. е взаимодействуют. В результате взаимодействия тела могут изменить скорость, форму, размеры. Мерой взаимодействия тел является сила. При объяснении механических явлений необходимы знания о силе тяжести, силе упругости и силе трения. Известно, что на любое тело действует сила тяжести, но многие тела не падают, а находятся в покое. Неподвижны стол, книги на столе, люстра, телевизор, человек в кресле. Кроме силы тяжести на эти тела действует и сила упругости. Актуальность темы заключается в том, сила упругости противодействует внешней нагрузке и восстанавливает форму тела, что имеет огромное значение в природе, технике, науке и в жизни каждого человека. В 7 классе силе упругости посвящен только один параграф, нет ни одной лабораторной работы, что недостаточно для полного представления об этой силе. Дополнительные знания необходимы и для успешного изучения механики в 9 классе. Объект учебно-исследовательской работы – сила упругости. Предмет – три пружины различной жесткости. Гипотеза – экспериментально наблюдаемая закономерность является общей ( законом Гука). Цель работы – определение зависимости силы упругости от величины деформации. Поставленную цель можно реализовать, решив следующие задачи: 1) изучить теоретический материал по теме работы; 2) провести эксперимент по определению значений силы упругости и удлинений пружин; 3) построить график зависимости силы упругости от удлинения; 4) по графику определить жёсткость пружин; 5) провести анализ полученных результатов. Методы исследования – поиск информации, анализ материалов, эксперимент. Сила упругости. Закон Гука Упругие силы возникают в твердых телах, жидкостях и газах. Изменение объёма или формы тела называется деформацией. Сила упругости – это сила, возникающая при деформации тела и зависящая от величины деформации. Твердые тела сохраняют свой объём и форму. При усилии изменить их возникают силы упругости. Жидкости не сохраняют форму, поэтому при их переливании из одного сосуда в другой силы упругости не появляются. Если же попробовать сжать жидкость, то сразу же возникают огромные силы упругости. Силы упругости действуют при сжатии газа. Чтобы удержать газ в определённом объёме, нужны внешние силы. Силы упругости появляются при деформации, но не всегда деформация приводит к появлению сил упругости. Например, при деформации тел из глины, пластилина тоже возникает сила, но это не сила упругости, так как её значение зависит не от величины деформации, а от скорости изменения деформации. Чем больше эта скорость, тем больше сила. Силы упругости являются электромагнитными силами, так как они появляются в результате взаимодействия зарядов. Молекулы состоят из атомов, атомы – из заряженных частиц (электронов и протонов). В недеформированном теле атомы находятся на таком расстоянии, при котором силы притяжения и отталкивания уравновешиваются. При деформации расстояния между молекулами или атомами изменяются, поэтому начинают преобладать либо силы притяжения, либо силы отталкивания. Электрические силы стремятся вернуть частицы в первоначальное положение. В результате возникает сила упругости. Эта сила всегда направлена так, чтобы уменьшить величину деформации тела. Деформации бывают упругими и пластическими. Упругая деформация – это деформация, при которой после прекращения внешнего воздействия тело принимает первоначальные форму и размеры. Металлы, стекло, камни можно упруго растянуть, но всего лишь на несколько процентов. Хорошими упругими свойствами обладает резина. Её можно растянуть на несколько сот процентов. Пластическая деформация – это деформация, которая сохраняется после прекращения внешнего воздействия. Такие деформации характерны для пластилина, свинца. Металлы стали незаменимыми конструкционными материалами, так как они обладают твердостью при комнатных температурах и пластичностью при высоких. К упругим деформациям относятся деформации растяжения, сжатия, кручения, изгиба, сдвига и среза. Для упругих деформаций выполняется закон Гука. Роберт Гук, английский ученый, родился в 1635 г. В детстве увлекался рисованием и изобретением механических игрушек. В школе изучал несколько языков, любил математику. Поступил в колледж Оксфордского университета. Не имея достаточных средств, вынужден был подрабатывать певчим в церкви, ассистентом по химии. Закончив колледж, получил степень магистра искусств. Р. Гук был членом и секретарем Лондонского Королевского общества, профессором Лондонского университета. Это был разносторонний ученый: построил воздушный насос, усовершенствовал барометр, зеркальный телескоп, микроскоп, предсказал закон всемирного тяготения И. Ньютона. Р. Гук был и архитектором: по его проектам было построено несколько зданий в Лондоне. Большое значение имеет закон, открытый в 1660 г., названный законом Гука: изменение длины тела при растяжении (или сжатии) прямо пропорционально модулю силы упругости. Формула закона Гука: Fупр.= k ∆l, где Fупр. – модуль силы упругости; k – жесткость тела, зависит от формы и размеров, материала; ∆l – величина деформации. Закон Гука справедлив при малых, т. е упругих деформациях. По удлинению пружины можно судить о силе, действующей на неё. Это используется в динамометре, приборе для измерения сил. Закон Гука имеет большое практическое значение в природе, технике, нашей повседневной жизни. Растения и животные могут выдерживать большие нагрузки. В результате действия силы упругости деревья выдерживают порывы ветра, налипший слой снега Все тела, находящиеся на Земле, выдерживают силу атмосферного давления. Еще больше нагрузку выдерживают животные и растения, обитающие на дне глубоких водоемов. Чтобы ловить добычу, пауки плетут паутину разных типов. Паутинная нить пауков-кругопрядов самое прочное натуральное волокно в мире. Прежде чем порваться, она растягивается на треть длины. Участок кости, испытывающий постоянную нагрузку, может разрушиться. Периодические же нагрузки стимулируют откладку костной ткани. Если нагрузка будет отсутствовать, то кость станет хрупкой и даже атрофируется. Эти явления наблюдаются при длительном пребывании человека в космосе в условиях невесомости. Мышцы способны сокращаться и расслабляться, но благодаря своей эластичности они способны возвращаться к исходным размерам и форме. Все тела, подвешенные на одной или нескольких опорах, испытывают деформацию изгиба, при которой нарушается прямолинейность главной оси тела. Балки и стержни, расположенные горизонтально, под действием силы тяжести или нагрузок прогибаются. Деформируются батуты, гимнастические снаряды, водные трамплины, теннисные ракетки. Деформация растяжения — вид деформации, при которой нагрузка прикладывается продольно от тела. Такую деформацию испытывают тросы, канаты, цепи в подъемных устройствах, стяжки между вагонами. Это находит большое применение в строительстве. Кручение испытывают валы всех машин, винты, отвертки. При этом к телу приложен крутящий момент, вызванный парой сил, действующих в перпендикулярной плоскости оси тела. Движение машины, вертолетов было бы не возможно без деформации кручения. Любой инструмент (молоток, гаечный ключ, ножницы, отвертка) испытывает при работе различные виды деформации и при изготовлении рассчитываются на упругие деформации. Инструменты сохраняют рабочее состояние в течение долгого времени, потому что остаточные деформации у них малы и накапливаются за большой срок их использования. В производственных процессах фрезы, сверла, резцы станков также подвергаются разным деформациям, но служат человеку долго вследствие того, что эти деформации являются упругими. В современном производстве широко используется и остаточные деформации. Например, в штамповке, ковке, чеканке, лепке, прокатке, формовке. Свойство тел восстанавливать свое первоначальное положение после удаления нагрузки называют упругостью. Охотничий или спортивный лук, длинные пролеты мостов, автомобильные шины, различные пружины, надувные матрасы, подошвы для обуви обладают большой упругостью. Вводя в металл примеси, изменяют его упругие свойства. Из железа делают сталь, из меди – латунь и бронзу. Композиты — твердые тела, в которых атомы располагаются упорядоченно в определенной области пространства, но этот порядок не повторяется с регулярной периодичностью. Композиты, такие, как дерево, бетон, кость, кровеносные сосуды и др., состоят из различных, связанных друг с другом материалов. Композитные материалы лишь недавно стали использоваться. Их механические свойства часто превосходят естественные материалы. К композиционным материалам относят железобетон (сочетание бетона и стальной арматуры), железографит (железо и графит), стеклопластик (смесь стеклянных волокон и отвердевшей смолы). В современном строительстве часто древесину смешивают с полимерами, получая композит. Комбинируя объем содержания компонентов, ученые получают материал с требуемой прочностью, жаростойкостью, абразивной стойкостью и другими свойствами. Применение композитов позволяет снизить массу конструкции на 25 – 50%, трудоемкость ее изготовления — в 1,5 – 3 раза. Эти материалы начали использоваться в авто-, судо-, самолетостроении, спортинвентаре, обувной промышленности. Из композитов делают целые строения, аттракционы, офисную и торговую мебель, корпуса медицинских и прочих установок, буровой инструмент. А еще — сверхстойкие сальники и уплотнительные шнуры, электрообогреваемые изделия из углеродных волокон (например, одежду). Из углепластиков делают насосы, трубопроводы, цистерны для агрессивных веществ, подшипники скольжения, работающие без смазки. За счет повышения прочности и упругости деталей конструкций, механизмов возможно увеличение нагрузки, продление срока их службы. На их изготовление тратится меньше материалов и энергии. Знание физики позволяет изменять свойства материалов, меняя их упругость и прочность. 2.1. Установление зависимости силы упругости пружины от её деформации выяснить зависимость силы упругости пружины от её деформации. три пружины различной жёсткости, набор грузов по 100 г, штатив, линейка, миллиметровая бумага. к пружине подвешивается груз и измеряется вызванное им удлинение; к первому грузу поочередно добавляются второй, третий и четвертый, при этом каждый раз измеряется удлинение пружины; опыты повторяются для второй и третьей пружин; по результатам измерений на миллиметровой бумаге строится график зависимости силы упругости от удлинения пружин. Результаты измерений и вычислений:
экспериментальные точки находятся на прямой, проходящей через начало координат, следовательно, модуль силы упругости при растяжении пружины прямо пропорционален её удлинению (величине деформации); экспериментально наблюдаемая закономерность в частном опыте является общей, что подтверждает выдвинутую гипотезу: при упругой деформации любого твердого тела модуль силы упругости прямо пропорционален деформации; мы экспериментально убедились в справедливости закона Гука. 2.2. Расчет жесткости пружины рассчитать жесткость трёх пружин, определить от каких параметров и как зависит жесткость пружины. результаты измерений и вычислений выполненных опытов по формуле k = Fупр. / x, где х = х – х, вычисляется жесткость пружины; по формуле kср = k+ k + k+ k / 4 вычисляется среднее значение жесткости.
Среднее значение жесткости нет необходимости определять, так как вычисленные значения в проведенных опытах совпали. для одной и той же пружины жесткость остается величиной постоянной; для разных пружин жесткость имеет разные значения, следовательно, коэффициент пропорциональности зависит от формы, размеров и материала; чем больше угол наклона графика к оси абсцисс, тем больше жесткость пружины; жесткость характеризует упругие свойства пружины. В курсе школьной физики большое место занимает изучение трёх видов сил: сил всемирного тяготения, сил упругости, сил трения. В работе рассматривается сила упругости, которая возникает при деформации тела. Причиной возникновения этой силы является взаимодействие молекул. На малых расстояниях молекулы отталкиваются, на больших – притягиваются. При деформации расстояния между молекулами увеличиваются или уменьшаются, поэтому начинают преобладать либо силы притяжения, либо силы отталкивания, что приводит к возникновению силы упругости. Сила упругости – это сила электромагнитной природы. Она направлена так, чтобы уменьшить величину деформации. При малых (упругих) деформациях справедлив закон Гука. По удлинению пружины можно определить силу, действующую на неё. Это используется для измерения сил с помощью динамометра. Закон Гука имеет большое значение в природе, технике, в жизни человека. Растения и животные могут выдерживать большие нагрузки. Периодические нагрузки на кости человека стимулируют откладку костной ткани. Если нагрузка будет отсутствовать, то кость станет хрупкой и даже атрофируется. Мышцы способны сокращаться и расслабляться, но благодаря своей эластичности они способны возвращаться к исходным размерам и форме. Любой инструмент испытывает при работе различные виды деформации и при изготовлении рассчитываются на упругие деформации. За счет повышения прочности и упругости деталей конструкций, механизмов возможно увеличение нагрузки, продление срока их службы. На их изготовление тратится меньше материалов и энергии. В практической части работы было доказано, что модуль силы упругости при растяжении пружины прямо пропорционален её удлинению. Экспериментально наблюдаемая закономерность в частном опыте является общей, что подтверждает справедливость закона Гука. Была вычислена жёсткость трёх пружин и определено, от каких параметров зависит этот коэффициент пропорциональности. В ходе выполнения работы были расширены теоретические знания, приобретены экспериментальные и вычислительные навыки по теме «Сила упругости». Эту работу можно использовать в качестве дополнительного материала к урокам физики в 7 классе и для подготовки к итоговой аттестации в 9 классе.
Источники:
- ru.solverbook.com
- obrazovaka.ru
- fizi4ka.ru
- pedtehno.ru
Физика, 10 класс
Урок 9. Закон Гука
Перечень вопросов, рассматриваемых на этом уроке
1.Закона Гука.
2.Модели видов деформаций.
3. Вычисление и измерение силы упругости, жёсткости и удлинение пружины.
Глоссарий по теме
Сила упругости – это сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение.
Деформация – изменение формы или размеров тела, происходящее из-за неодинакового смещения различных частей одного и того же тела в результате воздействия другого тела. Виды деформаций: сжатие, растяжение, изгиб, сдвиг, кручение.
Закон Гука – сила упругости, возникающая при деформации тела (растяжение или сжатие пружины), пропорциональна удлинению тела (пружины), и направлена в сторону противоположную направлению перемещений частиц тела
Основная и дополнительная литература по теме:
Г.Я. Мякишев., Б.Б.Буховцев., Н.Н.Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017стр. 107-112
Рымкевич А.П. Сборник задач по физике. 10-11класс.- М.:Дрофа,2009. Стр 28-29
ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.
Основное содержание урока
В окружающем нас мире мы наблюдаем, как различные силы заставляют тела двигаться, делать прыжки, перемещаться, взаимодействовать.
Однако можно также наблюдать как происходят разрушения, так называемые деформации, различных сооружений: мостов, домов, разнообразных машин.
Что необходимо знать инженеру конструктору, строителю, чтобы строить надёжные сооружения: дома, мосты, машины?
Почему деформации различны, какие виды деформации могут быть у конкретных тел? Почему одни тела после деформации могут восстановиться, а другие нет? От чего зависит и можно ли рассчитать величину этих деформаций?
Деформация – это изменение формы или размеров тела, в результате воздействия на него другого тела.
Почему деформации не одинаковы у различных тел, если мы их, к примеру, сжимаем? Давайте вспомним что мы знаем о строении вещества.
Все вещества состоят из частиц. Между этими частицами существуют силы взаимодействия- эти силы электромагнитной природы. Эти силы в зависимости от расстояний между частицами проявляются, то как силы притяжения, то как силы отталкивания.
Сила упругости – сила, возникающая при деформации любых тел, а также при сжатии жидкостей и газов. Она противодействует изменению формы тел.
Мы можем наблюдать несколько видов деформаций: сжатие, растяжение, изгиб, сдвиг, кручение.
При деформации растяжения межмолекулярные расстояния увеличиваются. Такую деформацию испытывают струны в музыкальных инструментах, различные нити, тросы, буксирные тросы.
При деформации сжатия межмолекулярные расстояния уменьшаются. Под такой деформацией находятся стены, фундаменты сооружений и зданий.
При деформации изгиба происходят неординарные изменения, одни межмолекулярные слои увеличиваются, а другие уменьшаются. Такие деформации испытывают перекрытия в зданиях и мостах.
При кручении – происходят повороты одних молекулярных слоёв относительно других. Эту деформацию испытывают: валы, витки цилиндрических пружин, столярный бур, свёрла по металлу, валы при бурении нефтяных скважин. Деформация среза тоже является разновидностью деформации сдвига.
Первое научное исследование упругого растяжения и сжатия вещества провёл английский учёный Роберт Гук.
Роберт Гук установил, что при малых деформациях растяжения или сжатия тела абсолютное удлинение тела прямо пропорционально деформирующей силе.

F упр = k ·Δℓ = k · Iℓ−ℓ0I закон Гука.
k− коэффициент пропорциональности, жёсткость тела.
ℓ0 – начальная длина.
ℓ – конечная длина после деформации.
Δℓ = I ℓ−ℓ₀ I- абсолютное удлинение пружины.

При больших деформациях изменение длины перестаёт быть прямо пропорциональным приложенной силе, а слишком большие деформации разрушают тело.
Для расчёта движения тел под действием силы упругости, нужно учитывать направление этой силы. Если принять за начало отсчёта крайнюю точку недеформированного тела, то абсолютное удлинение тела можно характеризовать конечной координатой деформированного тела. При растяжении и сжатии сила упругости направлена противоположно смещению его конца.
Закон Гука можно записать для проекции силы упругости на выбранную координатную ось в виде:
F упр x = − kx – закона Гука.
k – коэффициент пропорциональности, жёсткость тела.
x = Δℓ = ℓ−ℓ0 удлинение тела (пружины, резины, шнура, нити….)
Fупр x = − kx
Закон Гука:
Fупр = k·Δℓ = k · Iℓ−ℓ0I
Графиком зависимости модуля силы упругости от абсолютного удлинения тела является прямая, угол наклона которой к оси абсцисс зависит от коэффициента жёсткости k. Если прямая идёт круче к оси силы упругости, то коэффициент жёсткости этого тела больше, если же уклон прямой идёт ближе к оси абсолютного удлинения, следует понимать, что жёсткость тела меньше.
График, зависимости проекции силы упругости на ось ОХ, того же тела от значения х.
Необходимо помнить, что закон Гука хорошо выполняется при только при малых деформациях. При больших деформациях изменение длины перестаёт быть прямо пропорциональным приложенной силе.
Разбор тренировочных заданий
1. По результатам исследования построен график зависимости модуля силы упругости пружины от её деформации. Чему равна жёсткость пружины? Каким будет удлинение этой пружины при подвешивании груза массой 2кг?
Решение: По графику идёт линейная зависимость модуля силы упругости и удлинение пружины. Зависимость физических величин по Закону Гука:
F упр x = − kx (1)
Fупр = k·Δℓ = k · Iℓ−ℓ0I (2)
Из формулы (1) выражаем:

Зная что Fт = mg = 20 Н, Fт = Fупр= k·Δℓ следовательно

Ответ: жёсткость пружины равна 200 Н/м, удлинение пружины равно 0,1м.
2. К системе из кубика массой 1 кг и двух пружин приложена постоянная горизонтальная сила. Система покоится. Между кубиком и опорой трения нет. Левый край первой пружины прикреплён к стенке. Удлинение первой пружины 0,05 м. Жёсткость первой пружины равна 200 Н/м. Удлинение второй пружины 0,25 м.
- Чему равна приложенная к системе сила?
- Чему равна жёсткость второй пружины?
- Во сколько раз жёсткость второй пружины меньше чем первой?
Решение:
1. По условию задачи система находится в покое. Зная жёсткость и удлинение пружины найдём силу, которая уравновешивает приложенную постоянную горизонтальную силу.
F = F упр = k1·Δℓ1 = 200 Н/м·0,05 м = 10 Н
2. Жёсткость второй пружины:

3. k1/ k2 = 200/40 = 5
Ответ: F=10 Н; k2 = 40 Н/м; k1/k2 = 5.
Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.
Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
- пружины сжимаются и разжимаются в матрасе;
- мокрое белье колышется на натянутой веревке;
- лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
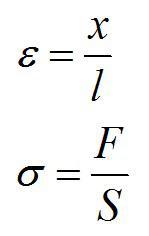
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
Здесь Е – модуль Юнга, зависящий от свойств материала.
Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.
Вопросы на силу упругости и закон Гука
Вопрос 1. Какие бывают деформации?
Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.
Вопрос 3. Как направлена сила упругости?
Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.
Вопрос 4. Какую природу имеет сила упругости?
Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?
Ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.
Задачи на силу упругости и закон Гука с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Расчет силы упругости
Условие
Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение
Запишем закон Гука:
По третьему закону Ньютона:
Ответ: 10 кН.
Задача №2. Нахождение жесткости пружины
Условие
Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?
Решение
По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.
Ответ: 200 Н/м
При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.
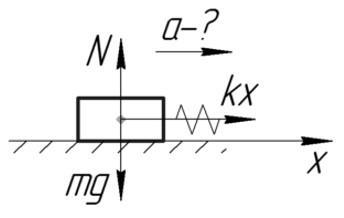
Задача №3. Нахождение ускорения тела
Условие
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.
Решение
За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:
Ответ: 2 м/с^2.
Задача №4. Нахождение жесткости пружины по графику
Условие
На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.
Решение
Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.
Ответ: k=10 Н/м.
Задача №5. Определение энергии деформации
Условие
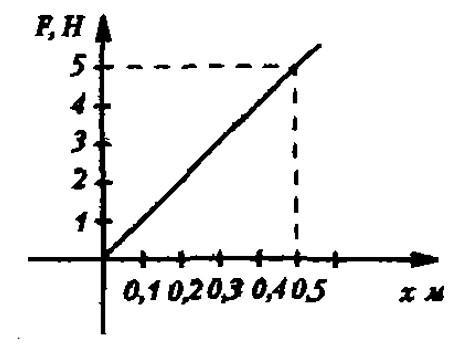
Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.
Решение
Энергия сжатой пружины равна:
Ответ: 0,4 Дж.
Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.
Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.
Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.
Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение
Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
[ large L_{0} + Delta L = L ]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).
[ large boxed{ Delta L = L — L_{0} }]
( L_{0} left(text{м} right) ) – начальная длина пружины;
( L left(text{м} right) ) – конечная длина растянутой пружины;
( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;
Величину ( Delta L ) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]
( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.
Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.
[ large boxed{ F_{text{упр}} = k cdot Delta L }]
Эту формулу назвали законом упругости Гука.
( F_{text{упр}} left( H right) ) – сила упругости;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.
Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
[ large F_{text{упр}} — m cdot g = 0 ]
Подставим в это уравнение выражение для силы упругости
[ large k cdot Delta L — m cdot g = 0 ]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:
[ large boxed{ k = frac{ m cdot g }{Delta L} }]
(g) – ускорение свободного падения, оно связано с силой тяжести.
Соединяем две одинаковые пружины
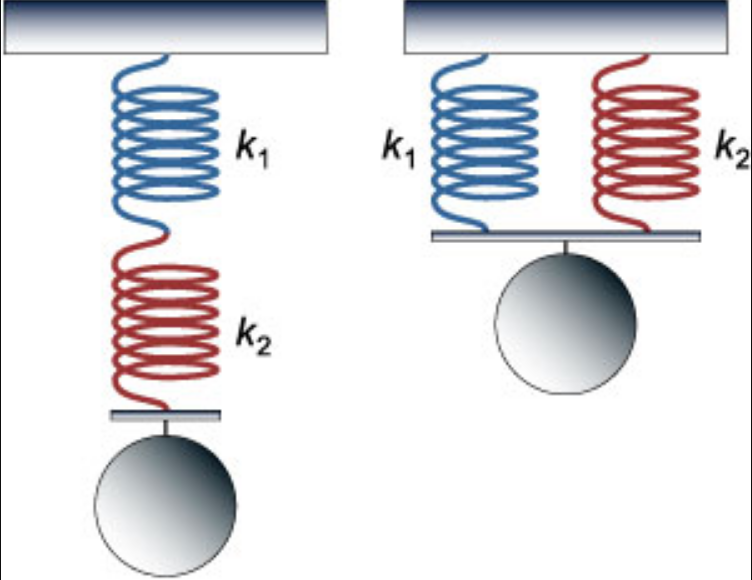
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.
Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две параллельные пружины:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]
Умножим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{параллел}} = 2k_{1} } ]
Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений
Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две последовательные пружины:
[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{послед}} cdot 2 = k_{1} ]
Разделим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]
Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.
Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]
( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.
Сила упругости — сила, которая возникает при деформациях тел в качестве ответной реакции на внешнее воздействие. Сила упругости имеет электромагнитную природу.
Деформация — изменение формы или объема тела.
Виды деформаций
- сжатие;
- растяжение;
- изгиб (сжатие и растяжение в комбинации);
- сдвиг;
- кручение (частный случай сдвига).
Сила упругости обозначается как Fупр. Единица измерения — Ньютон (Н). Сила упругости направлена противоположно перемещению частиц при деформации.
Если после окончания действия внешних сил тело возвращает прежние форму и объем, то деформацию и само тело называю упругими. Если после окончания действия внешних сил тело остается деформированным, то деформацию и само тело называют пластическими, или неупругими.
Примеры упругой деформации:
- Сжатый воздушный шарик распрямляется после того, как его отпустят.
- Если согнуть ластик, а затем отпустить, он распрямится.
- Мостик из доски, перекинутой через ручей, прогибается под пешеходом. Но когда пешеход ступает на землю, доска распрямляется.
Примеры пластической деформации:
- Скомканная бумага остается скомканной и после того, как ее отпустили.
- Пластилин сохраняет форму вылепленной из него фигуры.
- Согнутая металлическая пластина остается согнутой.
Закон Гука
При упругой деформации есть взаимосвязь между силой упругости, возникающей в результате деформации, и удлинением деформируемого тела. Эту взаимосвязь первым обнаружил английский ученый Роберт Гук.
Закон Гука
Модуль силы упругости, возникающей при деформации тела, пропорционален его удлинению.
x — абсолютное удлинение (деформация), k — коэффициент жесткости тела.
Абсолютное удлинение определяется формулой:
l0 — начальная длина тела, l — длина деформированного тела, ∆l — изменение длины тела.
Коэффициент жесткости тела определяется формулой:
E — модуль упругости (модуль Юнга). Каждое вещество обладает своим модулем упругости. S — площадь сечения тела.
Важно! Закон Гука не работает в случае, если деформация была пластической.
Пример №1. Под действием силы 3Н пружина удлинилась на 4 см. Найти модуль силы, под действием которой удлинение пружины составит 6 см.
Согласно третьему закону Ньютона модуль силы упругости будет равен модулю приложенной к пружине силе. В обоих случаях постоянной величиной окажется только жесткость пружины. Выразим ее из закона Гука и применим к каждому из случаев:
Приравняем правые части формул:
Выразим и вычислим силу упругости, возникающую, когда удлинение пружины составит 6 см:
Полезные факты
Если пружину растягивают две противоположные силы, то модули силы упругости и модули этих сил равны между собой:
F1 = F2 = Fупр
Если груз подвешен к пружине, сила упругости будет равна силе тяжести, действующей на это тело:
Fупр = Fтяж = mg.
Если пружины соединены параллельно, их суммарный коэффициент жесткости будет равен сумме коэффициентов жесткости каждой из этих пружин:
Если пружины соединены последовательно, их обратное значение суммарного коэффициента жесткости будет равен сумме обратных коэффициентов жесткости для каждой из пружин:
Пример №2. Две пружины соединены параллельно. Жесткость одной из пружин равна 1000 Нм, второй — 4000 Нм. Когда к пружинам подвесили груз, они удлинились на 5 см. Найти силу тяжести груза.
Переведем сантиметры в метры: 5 см = 5∙10–2 м.
Запишем закон Гука с учетом параллельного соединения пружин:
Модуль силы тяжести согласно третьему закону Ньютона равен модулю силы упругости. Отсюда:
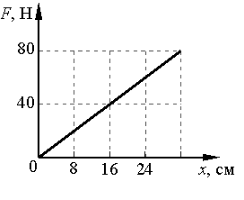
Задание E17590
а) 250 Н/м
б) 160 Н/м
в) 2,5 Н/м
г) 1,6 Н/м
Алгоритм решения
2.Выразить из закона Гука формулу для вычисления коэффициента упругости.
3.Выбрать любую точку графика и извлечь из нее исходные данные.
4.Перевести единицы измерения в СИ.
5.Вычислить коэффициент упругости, используя извлеченные из графика данные.
Решение
Запишем закон Гука:
Fупр = kx
Отсюда коэффициент упругости пружины равен:
Возьмем на графике точку, соответствующую удлинению пружины 16 см. Ей соответствует модуль силы упругости, равный 40 Н. Переведем сантиметры в метры: 16 см = 0,16 м.
Вычислим жесткость пружины:
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18489
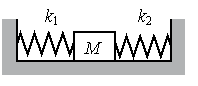
Алгоритм решения
- Записать исходные данные.
- Записать закон Гука.
- Применить закон Гука к обеим пружинам.
- Применить третий закон Ньютона.
- Выразить жесткость первой пружины.
- Вычислить искомую величину.
Решение
Запишем исходные данные:
- Сжатие первой пружины x1 — 4 см.
- Сжатие второй пружины x2 — 3 см.
- Жесткость второй пружины k2 — 600 Н/м.
Запишем закон Гука:
Fупр = kx
Применим этот закон к обеим пружинам:
Fупр1 = k1x1
Fупр2 = k2x2
Силы упругости обеих пружин уравновешены, так как тело между ними покоится. Согласно третьему закону Ньютона:
Fупр1 = Fупр2
Отсюда:
k1x1 = k2x2
Выразим отсюда жесткость первой пружины:
Подставим известные данные и вычислим:
Внимание! В данном случае переводить единицы измерения в СИ не нужно. Отношение длин постоянно независимо от выбранной единицы измерения.
Ответ: 450
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17520
Две упругие пружины растягиваются силами одной и той же величины F. Удлинение второй пружины Δl2 в 2 раза меньше, чем удлинение первой пружины Δl1. Жёсткость первой пружины равна k1, а жёсткость второй k2 равна…
а) 0,25k1
б) 2k1
в) 0,5k1
г) 4k1
Алгоритм решения
- Записать исходные данные.
- Записать закон Гука.
- Применить закон Гука к обеим пружинам.
- Выразить величину жесткости второй пружины.
Решение
Записываем исходные данные:
- Первая и вторая пружины растягиваются под действием одной и той же силы. Поэтому: F1 = F2 = F.
- Удлинение первой пружины равно: Δl1 = 2l.
- Удлинение второй пружины вдвое меньше удлинения первой. Поэтому: Δl2 = l.
Закон Гука выглядит следующим образом:
F = k Δl
Применим закон Гука для обеих пружин:
F1 = k1 Δl1
F2 = k2 Δl2
Так как первая и вторая силы равны, можем приравнять правые части выражений. Получим:
k1 Δl1 = k2 Δl2
Перепишем выражение с учетом значения удлинений первой и второй пружин:
k1 2l = k2 l
«l» в левой и правой частях выражения взаимоуничтожаются, отсюда жесткость второй пружины равна:
k2 = 2k1
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.9k