Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.

Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение
Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
[ large L_{0} + Delta L = L ]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).
[ large boxed{ Delta L = L — L_{0} }]
( L_{0} left(text{м} right) ) – начальная длина пружины;
( L left(text{м} right) ) – конечная длина растянутой пружины;
( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;
Величину ( Delta L ) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]
( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.
[ large boxed{ F_{text{упр}} = k cdot Delta L }]
Эту формулу назвали законом упругости Гука.
( F_{text{упр}} left( H right) ) – сила упругости;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
[ large F_{text{упр}} — m cdot g = 0 ]
Подставим в это уравнение выражение для силы упругости
[ large k cdot Delta L — m cdot g = 0 ]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:
[ large boxed{ k = frac{ m cdot g }{Delta L} }]
(g) – ускорение свободного падения, оно связано с силой тяжести.
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две параллельные пружины:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]
Умножим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{параллел}} = 2k_{1} } ]
Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две последовательные пружины:
[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{послед}} cdot 2 = k_{1} ]
Разделим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]
Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]
( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.
Лучший ответ
Koko
Мастер
(1080)
11 лет назад
по закону Гука
где f – сила упругости; х – удлинение (деформация) тела; k – коэффициент пропорциональности, зависящий от размеров и материала тела, называемый жесткостью. Единица жесткости в СИ – ньютон на метр (Н/м) .
f=-kx
Остальные ответы
Вадим Наумов
Ученик
(38)
11 лет назад
сила=коэффициент жесткость пружины*удлинение пружины
НиКиТа НоВоДрАнОв
Ученик
(141)
7 лет назад
Веруська, в учебнике не написано как находить силы!
Nastusha
Профи
(505)
7 лет назад
Fупр=k*l
RostanDreeks
Профи
(773)
6 лет назад
F упр = k (коэффициент упругости) * дельта X (растяжение пружины, верёвки и т. д.)
Сергей Сластин
Знаток
(348)
6 лет назад
F упр = k (коэффициент упругости) * дельта X (растяжение пружины, верёвки и т. д.)
Сафия Салимова
Ученик
(138)
6 лет назад
найдите пажалуйста силу упругости с помощью которой пуржина жесткостью 200н. м на метр удленяется на 10см.
Oleg Vince
Знаток
(428)
5 лет назад
лол
Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины. Что же это за величина, и как она связана с деформацией тел и законом Гука?
Содержание:
- Сила упругости и закон Гука
- Определение коэффициента жесткости
- Расчет жесткости системы
- Последовательное соединение системы пружин
- Параллельное соединение системы пружин
- Вычисление коэффициента жесткости опытным методом
- Примеры задач на нахождение жесткости
- Видео
Сила упругости и закон Гука
Для начала определим основные термины, которые будут использоваться в данной статье. Известно, если воздействовать на тело извне, оно либо приобретет ускорение, либо деформируется. Деформация — это изменение размеров или формы тела под влиянием внешних сил. Если объект полностью восстанавливается после прекращения нагрузки, то такая деформация считается упругой; если же тело остается в измененном состоянии (например, согнутом, растянутом, сжатым и т. д. ), то деформация пластическая.
Примерами пластических деформаций являются:
- лепка из глины;
- погнутая алюминиевая ложка.
В свою очередь, упругими деформациями будут считаться:
- резинка (можно растянуть ее, после чего она вернется в исходное состояние);
- пружина (после сжатия снова распрямляется).
В результате упругой деформации тела (в частности, пружины) в нем возникает сила упругости, равная по модулю приложенной силе, но направленная в противоположную сторону. Сила упругости для пружины будет пропорциональна ее удлинению. Математически это можно записать таким образом:
F = – k·x;
где F — сила упругости, x — расстояние, на которое изменилась длина тела в результате растяжения, k — необходимый для нас коэффициент жесткости. Указанная выше формула также является частным случаем закона Гука для тонкого растяжимого стержня. В общей форме этот закон формулируется так: «Деформация, возникшая в упругом теле, будет пропорциональна силе, которая приложена к данному телу». Он справедлив только в тех случаях, когда речь идет о малых деформациях (растяжение или сжатие намного меньше длины исходного тела).

Определение коэффициента жесткости
Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:
k = F/x.
Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.
Единица измерения жесткости в СИ — Н/м.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.

Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
k = k1 + k2 + … + ki.
Измерение жесткости пружины опытным путем – в этом видео.
Вычисление коэффициента жесткости опытным методом
С помощью несложного опыта можно самостоятельно рассчитать, чему будет равен коэффициент Гука. Для проведения эксперимента понадобятся:
- линейка;
- пружина;
- груз с известной массой.
Последовательность действий для опыта такова:
- Необходимо закрепить пружину вертикально, подвесив ее к любой удобной опоре. Нижний край должен остаться свободным.
- При помощи линейки измеряется ее длина и записывается как величина x1.
- На свободный конец нужно подвесить груз с известной массой m.
- Длина пружины измеряется в нагруженном состоянии. Обозначается величиной x2.
- Подсчитывается абсолютное удлинение: x = x2-x1. Для того чтобы получить результат в международной системе единиц, лучше сразу перевести его из сантиметров или миллиметров в метры.
- Сила, которая вызвала деформацию, — это сила тяжести тела. Формула для ее расчета — F = mg, где m — это масса используемого в эксперименте груза (переводится в кг), а g — величина свободного ускорения, равная приблизительно 9,8.
- После проведенных расчетов остается найти только сам коэффициент жесткости, формула которого была указана выше: k = F/x.
Примеры задач на нахождение жесткости
Задача 1
На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.
- Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
- По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.
Ответ: жесткость пружины составит 2500 Н/м.
Задача 2
Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.
- Найдем силу тяжести, деформирующей пружину: F = mg = 10 · 9.8 = 98 Н.
- Определим коэффициент упругости: k = F/x = 98 / 0.04 = 2450 Н/м.
- Рассчитаем, с какой силой действует второй груз: F = mg = 25 · 9.8 = 245 Н.
- По закону Гука запишем формулу для абсолютного удлинения: x = F/k.
- Для второго случая подсчитаем длину растяжения: x = 245 / 2450 = 0,1 м.
Ответ: во втором случае пружина растянется на 10 см.
Видео
Из этого видео вы узнаете, как определить жесткость пружины.
Примеры задач с решением
Задание. Пружина в отсутствии нагрузки имеет длину $l=0,01$ м и жесткость равную 10 $frac. $Чему будет равна жесткость пружины и ее длина, если на пружину действовать силой $F$= 2 Н? Считайте деформацию пружины малой и упругой.

Решение. Жесткость пружины при упругих деформациях является постоянной величиной, значит, в нашей задаче:
При упругих деформациях выполняется закон Гука:
[F=kDelta l left(1.2right).]
Из (1.2) найдем удлинение пружины:
Длина растянутой пружины равна:
Вычислим новую длину пружины:
Ответ. 1) $k’=10 frac$; 2) $l’=0,21$ м
Задание. Две пружины, имеющие жесткости $k_1$ и $k_2$ соединили последовательно. Какой будет удлинение первой пружины (рис.3), если длина второй пружины увеличилась на величину $Delta l_2$?
Решение. Если пружины соединены последовательно, то деформирующая сила ($overline$), действующая на каждую из пружин одинакова, то есть можно записать для первой пружины:
Для второй пружины запишем:
Если равны левые части выражений (2.1) и (2.2), то можно приравнять и правые части:
[k_1Delta l_1=k_2Delta l_2left(2.3right).]
Из равенства (2.3) получим удлинение первой пружины:
Ответ. $Delta l_1=frac$
Как появился первый вариант формулы
Формула для расчета жесткости пружины, которая получила название закона Гука, была установлена экспериментально. В процессе опытов с подвешенными на упругом элементе грузами разной массы замерялась величина его растяжения. Так и выяснилось, что одна и та же испытуемая деталь под разными нагрузками претерпевает различные деформации. Причем подвешивание определенного количества гирек, одинаковых по массе, показало, что каждая добавленная/снятая гирька увеличивает/уменьшает длину упругого элемента на одинаковую величину.
В итоге этих экспериментов появилась такая формула: kx=mg, где k – некий постоянный для данной пружины коэффициент, x – изменение длины пружины, m – ее масса, а g – ускорение свободного падения (примерное значение – 9,8 м/с²).
Так было открыто свойство жесткости, которое, как и формула для определения коэффициента упругости, находит самое широкое применение в любой отрасли промышленности.
Сила упругости.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: силы в механике, сила упругости, закон Гука.
Как мы знаем, в правой части второго закона Ньютона стоит равнодействующая (то есть векторная сумма) всех сил, приложенных к телу. Теперь нам предстоит изучить силы взаимодействия тел в механике. Их три вида: сила упругости, гравитационная сила и сила трения. Начинаем с силы упругости.
Особенности расчета жесткости соединений пружин
Важный моментом является расчет нескольких упругих элементов, соединенных последовательно или параллельно.
При параллельном расположении нескольких деталей общая жесткость этой системы определяется простой суммой коэффициентов отдельных комплектующих. Как нетрудно заметить, жесткость системы больше, чем отдельной детали.
При последовательном расположении формула более сложная: величина, обратная суммарной жесткости, равна сумме величин, обратных к жесткости каждой комплектующей. В этом варианте сумма меньше слагаемых.
Используя эти зависимости, легко определиться с правильным выбором упругих комплектующих для конкретного случая.
Определение коэффициента жесткости
Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:
Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.
Единица измерения жесткости в СИ — Н/м.
Как найти удлинение пружины?
Эта формула, а точнее закон Гука, выглядит так: F=|kx|, где k – это коэффициент упругости пружины, x – это удлинение пружины или же, как её ещё называют, величина деформации пружины.
Интересные материалы:
Что происходит с внутренней энергией воды при нагревании? Что происходит с водой при нагревании и при охлаждении? Что происходит с водой в ночь на 19 января? Что стало причиной уменьшения стока воды в Аральское море? Что такое мутить воду? Что такое нерастворимые в воде вещества? Что такое пудровая туалетная вода? Что такое тестер туалетная вода? Что такое вода для 2 класса? Что такое вода для инъекций?
Деформация.
Силы упругости возникают при деформациях тел. Деформация — это изменение формы и размеров тела. К деформациям относятся растяжение, сжатие, кручение, сдвиг и изгиб. Деформации бывают упругими и пластическими. Упругая деформация полностью исчезает после прекращения действия вызывающих её внешних сил, так что тело полностью восстанавливает форму и размеры. Пластическая деформация сохраняется (быть может, частично) после снятия внешней нагрузки, и тело уже не возвращается к прежним размерам и форме.
Частицы тела (молекулы или атомы) взаимодействуют друг с другом силами притяжения и отталкивания, имеющими электромагнитное происхождение (это силы, действующие между ядрами и электронами соседних атомов). Силы взаимодействия зависят о расстояний между частицами. Если деформации нет, то силы притяжения компенсируются силами отталкивания. При деформации изменяются расстояния между частицами, и баланс сил взаимодействия нарушается.
Например, при растяжении стержня расстояния между его частицами увеличиваются, и начинают преобладать силы притяжения. Наоборот, при сжатии стержня расстояния между частицами уменьшаются, и начинают преобладать силы отталкивания. В любом случае возникает сила, которая направлена в сторону, противоположную деформации, и стремится восстановить первоначальную конфигурацию тела.
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Сила упругости:
1. действует между соседними слоями деформированного тела и приложена к каждому слою; 2. действует со стороны деформированного тела на соприкасающееся с ним тело, вызывающее деформацию, и приложена в месте контакта данных тел перпендикулярно их поверхностям (типичный пример — сила реакции опоры).
Силы, возникающие при пластических деформациях, не относятся к силам упругости. Эти силы зависят не от величины деформации, а от скорости её возникновения. Изучение таких сил выходит далеко за рамки школьной программы.
В школьной физике рассматриваются растяжения нитей и тросов, а также растяжения и сжатия пружин и стержней. Во всех этих случаях силы упругости направлены вдоль осей данных тел.
Закон Гука.
Деформация называется малой, если изменение размеров тела много меньше его первоначальных размеров. При малых деформациях зависимость силы упругости от величины деформации оказывается линейной.
Закон Гука. Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину , сила упругости даётся формулой:
где — коэффициент жёсткости пружины.
Коэффициент жёсткости зависит не только от материала пружины, но также от её формы и размеров.
Из формулы (1) следует, что график зависимости силы упругости от (малой) деформации является прямой линией (рис. 1 ):
Коэффициент жёсткости — о угловой коэффициент в уравнении прямой . Поэтому справедливо равенство:
где — угол наклона данной прямой к оси абсцисс. Это равенство удобно использовать при экспериментальном нахождении величины .
Подчеркнём ещё раз, что закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела. Когда деформации перестают быть малыми, эта зависимость перестаёт быть линейной и приобретает более сложный вид. Соответственно, прямая линия на рис. 1 — это лишь небольшой начальный участок криволинейного графика, описывающего зависимость от при всех значениях деформации .
Понятие жесткости
Жесткость как физическая величина характеризует силу, которую нужно приложить к пружине для достижения определенной степени растяжения или сжатия.
Коэффициент жесткости рассчитывается по формуле Гука:
где $F$ — сила, развиваемая пружиной, $k$ — коэффициент жесткости, зависящий от ее характеристик (см. выше) и измеряемый в ньютонах на метр, $x$ — абсолютное приращение расстояния, на которое изменилась длина пружины после приложения внешней силы. Знак минус в правой части формулы свидетельствует о том, что сила, порождаемая пружиной, действует в противоположном по отношению к нагрузке направлении.
Коэффициент жесткости можно вычислить экспериментально, подвешивая на расположенную вертикально и закрепленную за верхний конец пружину грузы с известной массой. В этом случае имеет место зависимость
$m cdot g — k cdot x = 0$,
где $m$ — масса, $g$ — ускорение свободного падения. Отсюда
Содержание:
- Определение и формула силы упругости
- Характеристики упругих свойств твердых тел
- Продольное растяжение (сжатие)
- Деформация сдвига
- Единицы измерения силы упругости
- Примеры решения задач
При действии на тело внешней силы онодеформируется (происходит изменение размеров, объема и часто формы тела). В ходе деформации
твердого тела возникают смещения частиц, находящихся в узлах кристаллической решетки из начальных положений равновесия в новые положения.
Такому сдвигу препятствуют силы, с которыми частицы взаимодействуют. В результате появляются внутренние силы упругости, уравновешивающие
внешние силы. Эти силы приложены к деформированному телу. Величина сил упругости пропорциональна деформации тела.
Определение и формула силы упругости
Определение
Силой упругости называют силу, имеющую электромагнитную природу, которая возникает в результате деформации тела, как ответ на внешнее воздействие.
Упругой называют деформацию, при которой после прекращения действия внешней силы тело восстанавливает свои прежние форму и размеры,
деформация исчезает. Деформация носит упругий характер только в том случае, если внешняя сила не превышает некоторого определенного значения,
называемого пределом упругости. Сила упругости при упругих деформациях является потенциальной. Направление вектора силы упругости противоположно
направлению вектора перемещения при деформации. Или по-другому можно сказать, что сила упругости направлена против перемещения частиц при деформации.
Характеристики упругих свойств твердых тел
Упругие свойства твердых тел характеризуют при помощи напряжения, которое часто обозначают буквой
$sigma$ .
Напряжение – это физическая величина, равная упругой силе, которая приходится на единичное сечение тела:
$$sigma=frac{d F_{u p r}}{d S}(1)$$
где dFupr – элемент силы упругости тела; dS – элемент площади сечения тела. Напряжение называется нормальным,
если вектор $d bar{F}_{u p r}$ перпендикулярен к dS.
Формулой для расчета силы упругости служит выражение:
$$d F_{u p r}=sigma d S=K frac{Delta x}{x} d S(2)$$
где $frac{Delta x}{x}$ – относительная деформация,
$Delta x$ – абсолютная деформация, x–первоначальное значение величины, которая характеризовала
форму или размеры тела; K – модуль упругости (
$k = sigma$ при
( $frac{Delta x}{x} = 1$ ). Величину обратную модулю упругости называют коэффициентом упругости.
Проще говоря, сила упругости по величине пропорциональная величине деформации.
Продольное растяжение (сжатие)
Продольное (одностороннее) растяжение состоит в том, что под действием растягивающей (сжимающей) силы происходит увеличение
(уменьшение) длины тела. Условием прекращения такого рода деформации является выполнение равенства:
$F = F_{upr} (3)$
где F – внешняя сила, приложенная к телу, Fupr – сила упругости тела. Мерой деформации в рассматриваемом процессе является
относительное удлинение (сжатие) $left(frac{Delta l}{l}right)$ .
Тогда модуль силы упругости можно определить как:
$$F_{u p r}=E frac{Delta l}{l} S(4)$$
где E – модуль Юнга, который в рассматриваемом случае равен модулю упругости (E=K) и характеризующий упругие свойства тела;
l – первоначальная длина тела; $Delta l$ – изменение длины при нагрузке
F=F_upr. При $Delta l=l E=frac{F}{S}=sigma$ – площадь поперечного сечения образца.
Выражение (4) называют законом Гука.
В простейшем случае рассматривают силу упругости, которая возникает при растяжении (сжатии) пружины. Тогда закон Гука записывают как:
$$F_{x}=k x(5)$$
где Fx – модуль проекции силы упругости; k – коэффициент жесткости пружины, x – удлинение пружины.
Деформация сдвига
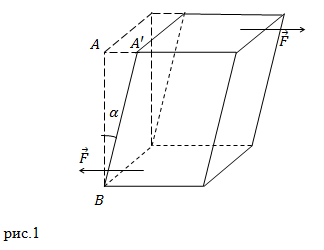
Сдвигом называют деформацию, при которой все слои тела, являющиеся параллельными некоторой плоскости, смещаются друг относительно друга.
При сдвиге объем тела, которое было деформировано, не изменяется. Отрезок, на который смещается одна плоскость относительно другой,
называют абсолютным сдвигом (рис.1 отрезок AA’). Если угол сдвига ($alpha$) мал, то
$alpha approx t g alpha=frac{A A^{prime}}{A B}$ . Этим углом ? (относительный сдвиг)
характеризуют относительную деформацию. При этом напряжение $sigma$ равно:
$$sigma=G alpha(6)$$
где G – модуль сдвига.
Единицы измерения силы упругости
Основной единицей измерения сил упругости (как и любой другой силы) в системе СИ является: [Fupr]=H
В СГС: [Fupr]=дин
Примеры решения задач
Пример
Задание. Какова работа силы упругости при деформации пружины жёсткость, которой равна k? Если первоначальное удлинение
пружины составляло x1, последующее удлинение составило x2.
Решение. В соответствии с законом Гука модуль силы упругости найдем как:
$$F = kx (1.1)$$
При этом сила упругости при первой деформации будет равна:
$$F_1 = kx_1 (1.2)$$
В случае второй деформации имеем:
$$F_2 = kx_2 (1.3)$$
Работу (A) сил упругости можно найти как:
$$A=langle Frangle S cos alpha(1.4)$$
где $langle Frangle$ – средняя величина силы упругости, равная:
$$langle Frangle=frac{F_{1}+F_{2}}{2}(1.5)$$
S- модуль перемещения, равный:
$S = x_2 – x_1 (1.6)$
$alpha=180^{circ}$ – угол между векторами перемещения и вектором сил упругости (эти векторы направлены в противоположные стороны).
Подставим выражения (1.2), (1.3), (1.5) и (1.6) в формулу для работы (1.4), получим:
$$A=frac{k x_{1}+k x_{2}}{2}left(x_{2}-x_{1}right) cos left(180^{circ}right)=-frac{k x_{1}+k x_{2}}{2}left(x_{2}-x_{1}right)$$
Ответ. $A=-frac{k}{2}left(x_{1}+x_{2}right)left(x_{2}-x_{1}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Тело массой m (которое можно считать материальной точкой) привязано к резиновому шнуру.
Это тело описывает в горизонтальной плоскости окружность с частотой вращения n. Угол отклонения шнура от вертикали равен
$alpha$.
Жёсткость шнура равна k. Какова длина нерастянутого шнура (l0)?
Решение. Сделаем рисунок.
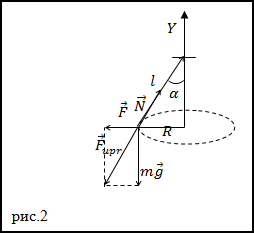
Сила натяжения (N) шнура вызывает его растяжениена величину ($Delta l$). При этом возникающая
сила упругости равна по модулю и противоположна по направлению силе натяжения:
$$bar{F}_{u p r}=-bar{N}(2.1)$$
Сила натяжения шнура равна (из рис.2 и второго закона Ньютона):
$$N=frac{m g}{cos alpha}(2.2)$$
Но так как сила натяжения равна по модулю силе упругости, то можно записать, что:
$$N=k Delta l rightarrow Delta l=frac{N}{k}(2.3)$$
Рассмотрение рис.2 дает:
$$frac{l}{R}=frac{N}{F} rightarrow l=frac{N R}{F}(2.4)$$
где l – длина растянутой нити, R – радиус окружности по которой движется точка. Применяя второй закон Ньютона, получим:
$$F=N sin alpha=m frac{v^{2}}{R}=4 pi^{2} n^{2} m R(2.5)$$
Подставим в (2.4) выражение для F, получаем:
$$l=frac{N}{4 pi^{2} n^{2} m}(2.6)$$
В таком случае длина нерастянутого шнура:
$$l_{0}=l-Delta l=frac{N}{4 pi^{2} n^{2} m}-frac{N}{k}=left(frac{1}{4 pi^{2} n^{2} m}-frac{1}{k}right) frac{m g}{cos alpha}$$
Ответ. $l_{0}=left(frac{1}{4 pi^{2} n^{2} m}-frac{1}{k}right) frac{m g}{cos alpha}$
Читать дальше: Формула скорости.
