Отдельные частицы любого тела — твердого, жидкого или газообразного — взаимодействуют друг с другом. Поэтому если какая-то частица начинает колебаться, то благодаря взаимодействию между частицами это движение с некоторой скоростью начинает распространяться во все стороны.
Определение
Волна — колебания, распространяющиеся в пространстве с течение времени.
В воздухе, твердых телах и внутри жидкостей механические волны возникают благодаря силам упругости. Эти силы осуществляют связь между отдельными частями тела. В образовании волн на поверхности воды играют роль сила тяжести и сила поверхностного натяжения. Такие волны позволяют наиболее наглядно рассмотреть главные особенности волнового движения.

Волна на поверхности воды представляет собой бегущие вперед валы округлой формы. Расстояние между валами, которые также называют гребнями, примерно одинаковы. Волны распространяются в среде с определенной скоростью. Так, если чайка летит вперед, а по ней в любой момент времени оказывается один и тот же гребень, то скорость распространения волны можно принять равной скорости полета чайки. Волны на воде наблюдать удобно потому, что скорость их распространения невелика.
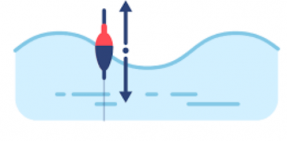
Если бросить в воду легкий предмет, он не будет увлекаться волной, а начнет совершать колебания вверх и вниз, оставаясь примерно на одном месте, как поплавок. Это говорит о том, что частицы воды остаются на месте в то время, как волна распространяется на большие расстояния.
Если же резко толкнуть горизонтальную пружину, можно будет наблюдать, как в одних местах она разрежается, в других — уплотняется. Это тоже волна. Видно, что энергия, полученная от толчка руки, переносится через пружину, хотя ее частицы остаются на месте.

Примеры с поплавком на воде и горизонтальной пружиной позволяют сделать вывод, что волна переносит энергию, но не переносит вещество среды.
Виды механических волн
По характеру колебаний частиц среды относительно положения равновесия различают два вида волн:
Определения
- Поперечная волна — волна, при которой частицы среды колеблются перпендикулярно направлению распространения этой волны.
- Продольная волна — волна, при которой частицы среды колеблются параллельно направлению распространения этой волны.
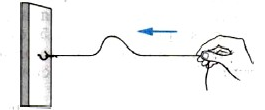
Волны, распространяющиеся вдоль резинового шнура, являются поперечными (см. рисунок ниже). Чтобы появилась волна, нужно взять конец шнура, прикрепленного к вертикальной опоре, и дернуть его. При этом волна побежит к вертикальной опоре, а сам шнур будет менять свою форму. Каждая частица шнура станет совершать колебания относительно своего неизмененного положения равновесия сверху вниз (перпендикулярно направлению распространения волны).
Рассмотрим поперечные волны подробнее. Каждый участок шнура обладает массой и упругостью. При деформации шнура в любом его сечении появляются силы упругости. Эти силы стремятся возвратить шнур в исходное положение. Благодаря инертности участок колеблющегося шнура не останавливается в положении равновесия, а проходит его, продолжая двигаться до тех пор, пока силы упругости не остановят этот участок в момент максимального отклонения от положения равновесия.
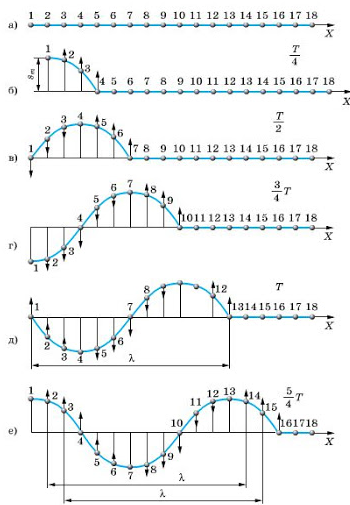
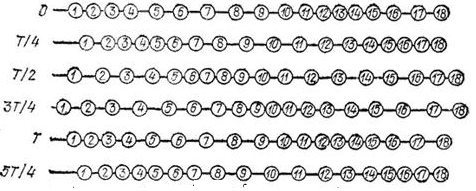
На рисунках а, б, в, г, д и е изображен процесс распространения поперечной волны. На них показаны положения частиц среды в последовательные моменты времени.
Теперь рассмотрим распространение в среде продольной волны. Такую волну можно наблюдать, собрав установку из цепочки массивных шариков, связанных пружинками. Шары подвешены так, чтобы они могли колебаться только вдоль цепочки (см. рисунок ниже).
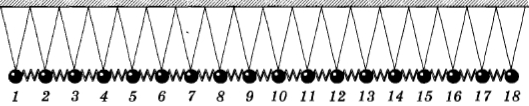
Если первый шар привести в колебательное движение, то вдоль цепочки побежит продольная волна, состоящая из чередующихся уплотнений и разрежений шаров. Уплотнения и разрежения (см. рисунок ниже) появляются вследствие горизонтальных колебаний шаров у положения равновесия. Волна также распространяется горизонтально.
Физические характеристики волны
Обратимся к рисункам д, е еще раз. Видно, что когда частица 1 находится в положении равновесия и движется вверх, частица 13 тоже находится в положении равновесия и движется вверх. Спустя четверть период частица 1 будет максимально отклонена от положения равновесия, ровно, как и частица 13. Так как частицы 1 и 13 движутся одинаково, говорят, что колебания этих частиц происходят в одинаковых фазах. Расстояние между этими частицами называют длиной волны.
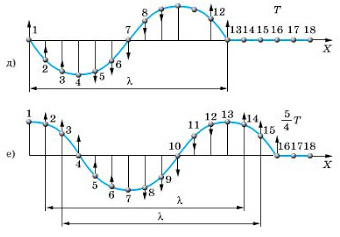
Внимание! В действительности частица 13 отстает по фазе от частицы 1 на 2π. Но поскольку такая разница фаз не приводит к различию в состояниях колеблющихся частиц, можно считать, что частицы колеблются в одинаковых фазах.
Определение
Длина волны — расстояние между двумя ближайшими точками волны, колеблющимися в одинаковых фазах.
Длина волны обозначается как λ (лямбда). Единица измерения длины волны — метр (м).
Согласно рисунку е, в одинаковых фазах колеблются частицы 1 и 13, 2 и 14, 3 и 15, 4 и 16. Поэтому расстояния между этими частицами равно длине волны. Но частицы 1 и 7, находящиеся на расстоянии λ2, колеблются в противоположных фазах. Посмотрите на рисунок д: когда 1 частица находится в положении равновесия и движется вверх, частица 7 находится в положении равновесия и движется низ. На рисунке е обе частицы максимально отклонены от положения равновесия, но в противоположных направлениях.
Волна распространяется на расстояние λ за время, равное периоду колебаний частиц вещества. Зная расстояние, на которое распространилась волна, и время, в течение которого это распространение происходило, можно найти скорость волны:
v=λT
Но мы знаем, что период равен величине, обратной частоте колебаний:
T=1ν
Тогда скорость распространения волны равна:
v=λν
Скорость волны равна произведению длины волны на частоту колебаний.
При распространении волны мы имеем дело с периодичностью двоякого рода:
- Во-первых, каждая частица среды совершает периодические колебания во времени. В случае гармонических колебаний (эти колебания происходят по синусоидальному или косинусоидальному закону) частота постоянна и амплитуда одинакова во всех точках. Колебания отличаются только фазами.
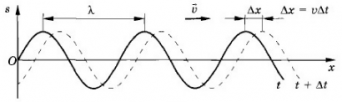
- Во-вторых, в данный момент времени форма волны повторяется в пространстве через отрезки длиной λ вдоль линии распространения волны. На рисунке ниже показан профиль волны в определенный момент времени (сплошная линия). С течением времени вся эта картина перемещается со скоростью v направо. Спустя промежуток времени ∆t волна будет иметь вид, изображенный на том же рисунке прерывистой линией.
Пример №1. Определите скорость распространение волны на поверхности воды, если расстояние между ее гребнями равно 1 метру. Учитывайте, что мимо наблюдателя за 5 секунд прошло 10 волн.
Обычно под волной на воде люди понимают гребни — частицы воды, максимально отклоненные от положения равновесия. Расстояние между гребнями равно длине волны. Чтобы найти скорость распространения волны, нужно знать частоту колебания молекул воды. Ее можно вычислить по следующей формуле:
ν=nt
где n — количество «волн», прошедших мимо наблюдателя.
Тогда скорость волны равна:
v=λν=λnt=1·105=2 (мс)
Уравнение бегущей волны
Определение
Бегущая волна — волна, распространяющаяся в пространстве.
Колебания гармонической волны в любой точке происходят по гармоническому закону с одной и той же амплитудой. Найдем уравнение, описывающее колебательный процесс в любой точке пространства при распространении гармонической волны.
Будем рассматривать волну, бегущую по длинному тонкому резиновому шнуру. Ось Ox направим вдоль шнура, а начало отсчета свяжем с левым концом шнура. Смещение любой колеблющейся точки шнура от положения равновесия обозначим буквой s. Для описания волнового процесса необходимо знать значение s в любой точке шнура в любой момент времени. Следовательно, нужно знать вид функции:
s = s(x, t)
Заставим конец шнура (точка х = 0) совершать гармонические колебания с частотой ω. Если начальную фазу колебаний считать равной 0, то колебания этой точки будут происходить по закону:
s = smaxsin ωt
smax — амплитуда колебаний (рис. а).
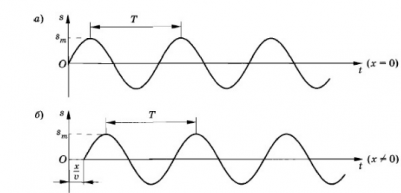
Колебания распространяются вдоль шнура (оси Ox) со скоростью v и в произвольную точку шнура с координатой х придут спустя время, которое можно определить следующим выражением:
τ=xv
Эта точка также начнет совершать гармонические колебания с частотой ω, но с запаздыванием на время τ (рис. б). Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой smax, но с другой фазой:
Уравнение бегущей волны
s=smaxsin [ω(t−τ)]=smaxsin [ω(t−xv)]
Это уравнение называется уравнением бегущей волны, распространяющейся в положительном направлении оси Ox.
Пример №2. Уравнение бегущей волны имеет вид s(x, t)=0,1sin(2πt−xπ2). Найдите частоту волны, скорость её распространения и длину.
Запишем уравнение бегущей волны:
s=smaxsin [ω(t−τ)]=smaxsin [ω(t−xv)]
Сопоставляя эти два уравнения можно определить, что циклическая частота и скорость распространения соответственно равны:
ω=2π (радс)
v=4 (мс)
Циклическую частоту также можно рассчитать по формуле:
ω=2πν
Тогда частота волны равна:
ν=ω2π=2π2π=1 (Гц)
Тогда длина волны равна:
λ=vν=41=4 (м)
Задание EF18242
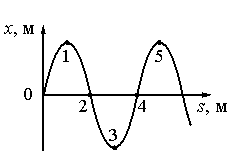 На рисунке показан профиль бегущей волны в некоторый момент времени. Разность фаз колебаний точек 1 и 5 равна
На рисунке показан профиль бегущей волны в некоторый момент времени. Разность фаз колебаний точек 1 и 5 равна
Ответ:
а) π/3
б) π/2
в) π
г) 2π
Алгоритм решения
- Определить характер движения указанных точек.
- По характеру движения точек определить их разность фаз.
Решение
Точки 1 и 5 соответствуют максимальной амплитуде колебаний. В этот момент они меняют направление движения (до этого двигались вверх, теперь меняют направление в противоположную сторону). Поскольку точки 1 и 5 движутся одинаково, можно считать, что они колеблются в одинаковых фазах. Это возможно, если разность фаз кратна 2π.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22628
Какова скорость звуковых волн в среде, если при частоте 400 Гц длина волны λ = 4 м?
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу, которая связывает скорость волны с ее частотой и длиной.
3.Выполнить решение задачи в общем виде.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Частота звуковой волны: ν = 400 Гц.
Скорость звука — это отношение длины волны к ее периоду. Но период — это обратная величина частоте. Следовательно, скорость звука — есть произведение длины волны на частоту:
v=λν=4·400=1600 (мс)
Ответ: 1600
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18803
На расстоянии 510 м от наблюдателя рабочие вбивают сваи с помощью копра. Какое время пройдёт от момента, когда наблюдатель увидит удар копра, до момента, когда он услышит звук удара? Скорость звука в воздухе равна 340 м/с.
Алгоритм решения
1.Записать исходные данные.
2.Выполнить решение задачи в общем виде.
3.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Скорость распространения звука в воздухе: v = 340 м/с.
• Расстояние наблюдателя до источника звука: s = 510 м.
Звук от удара проделает путь, равный одинарному расстоянию от наблюдателя до источника звука. Следовательно, для нахождения времени, через которое наблюдатель услышит звук, нужно разделить этот путь на скорость звука в воздухе:
t=sv=510340=1,5 (с)
Ответ: 1,5
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 3.1k
Механические колебания и волны

Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Отличительными признаками колебательного движения являются:
- повторяемость движения;
- возвратность движения.
Для существования механических колебаний необходимо:
- наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
- наличие малого трения в системе.
Механические волны – это процесс распространения колебаний в упругой среде.
Содержание
- Виды волн
- Гармонические колебания
- Амплитуда и фаза колебаний
- Период колебаний
- Частота колебаний
- Свободные колебания (математический и пружинный маятники)
- Вынужденные колебания
- Резонанс
- Длина волны
- Звук
- Основные формулы по теме «Механические колебания и волны»
Виды волн
- Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.

Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.
- Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.

Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.
Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.
Гармонические колебания
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:
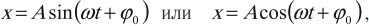
где ( x ) – координата тела – смещение тела от положения равновесия в данный момент времени; ( A ) – амплитуда колебаний; ( omega t+varphi_0 ) – фаза колебаний; ( omega ) – циклическая частота; ( varphi_0 ) – начальная фаза.
Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
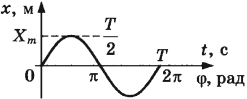
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.
Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:
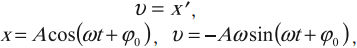
где ( v ) – мгновенное значение скорости, т. е. скорость в данный момент времени.
Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:
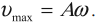
Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:
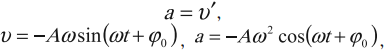
где ( a ) – мгновенное значение ускорения, т. е. ускорение в данный момент времени.
Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:
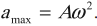
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:
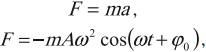
где ( F ) – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.
Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
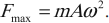
Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:
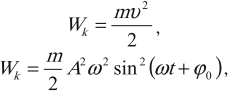
где ( W_k ) – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.
Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
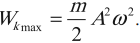
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:
- потенциальная энергия равна нулю;
- кинетическая энергия максимальна.
При максимальном отклонении от положения равновесия:
- кинетическая энергия равна нулю;
- потенциальная энергия максимальна.
Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:
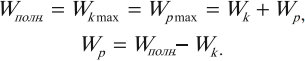
Важно!
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.
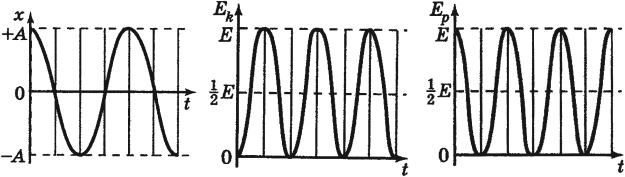
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.
Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).
Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ( A, (X_{max}) ), единицы измерения – м.
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ( varphi ), единицы измерения – рад (радиан).
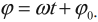
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
( varphi_0 ) – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Период колебаний
Период колебаний – это время одного полного колебания.
Обозначение – ( T ), единицы измерения – с.

Период гармонических колебаний – постоянная величина.
Частота колебаний
Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ( nu ), единицы времени – с-1 или Гц (Герц).
1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:

Период и частота колебаний – взаимно обратные величины:

Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ( omega ), единицы измерения – рад/с.

Свободные колебания (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
- при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
- силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
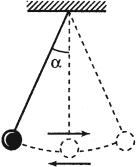
Период колебаний математического маятника:
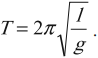
Частота колебаний математического маятника:
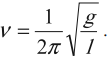
Циклическая частота колебаний математического маятника:
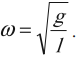
Максимальное значение скорости колебаний математического маятника:
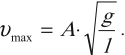
Максимальное значение ускорения колебаний математического маятника:
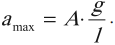
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
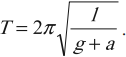
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
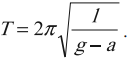
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
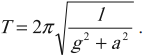
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ( h ), определяется по формуле:
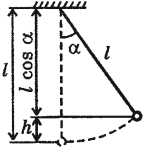
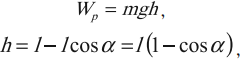
где ( l ) – длина нити, ( alpha ) – угол отклонения от вертикали.
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
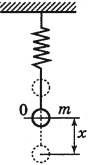
Период колебаний пружинного маятника:
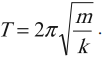
Частота колебаний пружинного маятника:
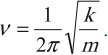
Циклическая частота колебаний пружинного маятника:
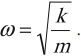
Максимальное значение скорости колебаний пружинного маятника:
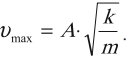
Максимальное значение ускорения колебаний пружинного маятника:
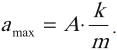
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
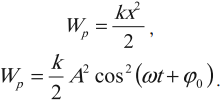
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
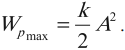
Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.
Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
Резонанс
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
Условие резонанса:
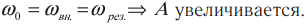
( v_0 ) – собственная частота колебаний маятника.
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.
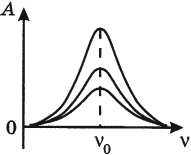
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.
Длина волны
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ( lambda ), единицы измерения – м.
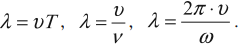
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
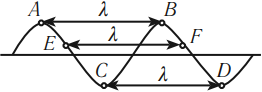
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук (( nu ) < 16 Гц);
- звуковой диапазон (16 Гц < ( nu ) < 20 000 Гц);
- ультразвук (( nu ) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
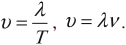
Скорость звука зависит
- от упругих свойств среды:
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
- от температуры среды:
в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.
Основные формулы по теме «Механические колебания и волны»



Механические колебания и волны
3 (59.31%) 144 votes
Длина волны


4.1
Средняя оценка: 4.1
Всего получено оценок: 226.
4.1
Средняя оценка: 4.1
Всего получено оценок: 226.
Для описания волновых процессов в Природе используется ряд специальных величин, специфичных для распространения волн. Важнейшим среди них является длина волны. Рассмотрим это понятие, а также его связь с другими понятиями волновых процессов.
Волна и ее распространение
Движение – форма существования материи. Одним из широко распространенных в природе движений является колебательное движение, при котором измеряемая величина изменяется не монотонно, а циклически увеличивая и уменьшая свое значение.

В протяженных объектах любые изменения (и в том числе колебательные процессы), как правило, происходят не сразу во всем объекте, а сперва начинаются в одной его части, а потом распространяются на остальной объект.
Для наблюдения распространения колебательных движений удобно использовать поверхность воды. В первый момент колеблются только частицы воды непосредственно в месте возникновения волны. Далее происходит распространение колебательного движения. При этом сами частицы воды в горизонтальном направлении не движутся, движется лишь само колебание водной глади.

Волна – это колебания среды, распространяющиеся в ней с течением времени.
Параметры волны
Фаза, период и частота
Для распространяющейся волны можно ввести параметр, который называется фазой. Фаза – это одинаковое состояние среды распространения. Для поверхности воды фаза – это величина отклонения от спокойного состояния (от нулевого уровня). Точки волны, находящиеся в одинаковом состоянии, будут находиться в одинаковых фазах. Если записывать в таблицу время, проходящее между одинаковыми фазами какой-то точки, то можно заметить, что это время будет кратно некоторому минимальному значению. Это значение, минимальное время, за которое волна оказывается в одной и той же фазе, называется периодом колебаний $T$ волны. Число периодов за одну секунду называется частотой волны $nu$ (для обозначения используется греческая буква «ню»):
$$nu={1over T}$$
Фазу можно сопоставить с углом на координатной плоскости. Полная волна соответствует углу $2pi$, все фазы повторяются с этим периодом точно так же, как повторяется значение круговых функций (синуса, косинуса и других).
Одному значению отклонения от нулевого значения соответствуют две фазы – одна в момент возрастания, другая – в момент спадания волны (исключение – самый «пик» или самое «дно» волны). Это разные фазы, путать их не следует.
Скорость распространения и длина волны
Поскольку волна распространяется не мгновенно, то, отметив одинаковую фазу волны (движущийся гребень), можно определить скорость этого распространения $v$ относительно неподвижных предметов (например, относительно берега, в случае, когда волна распространяется вдоль него). Для вычисления используется обычная формула скорости – отношение пройденного расстояния к прошедшему времени. Кроме того, можно ввести понятие «длина волны».
Расстояние, которое проходит волна за один период колебания, называется длиной волны, для обозначения используется греческая буква $lambda$ (лямбда). Формула длины волны:
$$lambda=vT$$
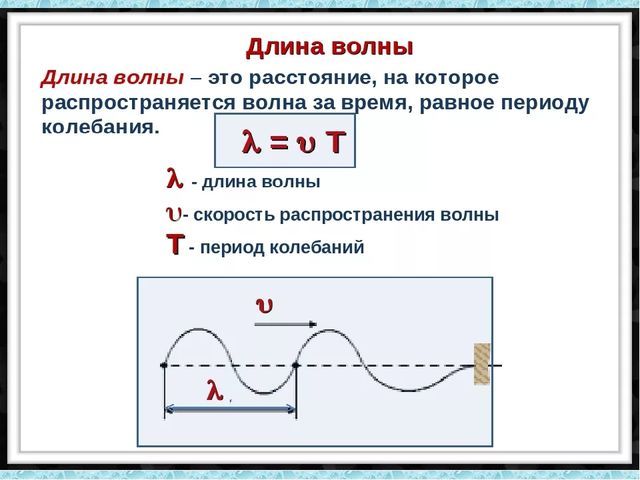
Если известна частота колебаний, для расчета удобнее пользоваться другой формулой (она вытекает из определения частоты):
$$lambda={vover nu}$$
Слышимый звук представляет из себя колебания плотности воздуха. Распространяется он в нормальных условиях со скоростью, имеющей значения порядка 300-350м/с, и имеет длину волны от ~15мм (самые высокие частоты) до ~15м (самые низкие частоты)

Что мы узнали?
Волна – это колебания среды, распространяющиеся в ней с течением времени. Волна характеризуется рядом параметров, среди которых фаза, период, скорость распространения, длина.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Егор Князев
7/10
Оценка доклада
4.1
Средняя оценка: 4.1
Всего получено оценок: 226.
А какая ваша оценка?
Содержание:
Волны:
Стоя на берегу озера или пруда, вы могли наблюдать, как кольцами разбегаются волны от места, куда был брошен камень, как волны раскачивают лодку или катер. Ветер нарушает равновесие морской поверхности, кажется, что море надвигается на берег, но это не так. Не перемещаются по полю колосья, когда «волнуется» нива, они только наклоняются и опять выпрямляются. Вслед за кораблем или лодкой всегда возникает типичная картина волн.
Волновые процессы широко распространены в природе. Физические основы волновых движений различны, но все они объясняются одинаковыми законами.
Что же такое волна и каковы причины возникновения волн
Вам известно, что твердые, жидкие и газообразные тела состоят из частей, взаимодействующих между собой. Если частица тела начинает совершать колебания, то в результате взаимодействия ее с другими частицами тела это движение распространяется с определенной скоростью во всех направлениях.
Волна — процесс распространения колебаний в любой среде. Волна — это изменение состояния среды, распространяющееся в пространстве и переносящее энергию.
Наблюдения. Рассмотрим особенности распространения волн. Если рассматривать волны на поверхности воды (рис. 204), то они кажутся валами, движущимися в определенном направлении, причем расстояния между валами, или гребнями, одинаковы.

Если бросить в воду поплавок, его не будет относить волной, а он начнет совершать колебания вверх-вниз, оставаясь почти на одном месте.
При распространении волны изменяется состояние колеблющейся среды, но не перенос вещества. От брошенного камня начинает колебаться определенный участок воды, эти колебания передаются соседним участкам и постепенно распространяются во все стороны. Течение воды не возникает, перемещается только форма ее поверхности.
Опыт 1. Закрепим один конец длинного резинового шнура и легонько заставим шнур колебаться. По шнуру побежит волна (рис. 205). Чем сильнее колеблется шнур, тем больше скорость распространения волны. Волна добежит до точки крепежа, отразится и побежит в обратном направлении.

При распространении волны изменяется только форма шнура, а каждый его участок колеблется относительно своего положения равновесия, причем колебания происходят в направлении, перпендикулярном направлению распространения волны (рис. 206). Такие волны называют поперечными волнами.
Поперечные волны
Поперечные волны — это волны, в которых частицы совершают колебания в направлении, перпендикулярном направлению распространения волны.
Опыт 2. Если ударить по одному из концов длинной мягкой пружины большого диаметра, то по пружине «побежит» сжатие. Повторяя удары, можно возбудить в пружине волну, представляющую собой последовательные сжатия и растяжения пружины, «бегущие» друг за другом (рис. 207). Любой виток пружины совершает колебания вдоль направления распространения волны. Такую волну называют продольной волной.
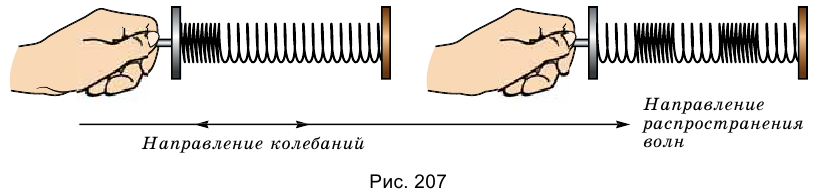
Продольные волны
Продольные волны — это волны, в которых частицы совершают колебания вдоль направления распространения волны.
При распространении волны движение передается от одного участка тела к другому. С передачей движения связана передача энергии. Передача энергии без передачи вещества – основное свойство всех волн.
Любые волны характеризуются длиной и скоростью их распространения.
Длина волны — это расстояние между ближайшими друг к другу точками волны, колеблющимися в одинаковых фазах (рис. 208).
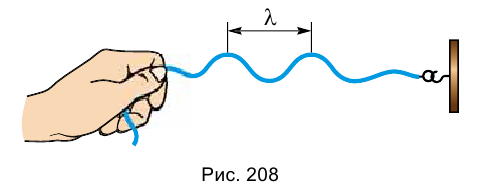
Длину волны обозначают греческой буквой А. (лямбда). Ее единицей является один метр (1 м).
Волны любого происхождения распространяются в пространстве не мгновенно, а с определенной скоростью. Например, можно увидеть, как чайка летит над морем будто все время над одним гребнем волны. В этом случае скорость полета чайки равна скорости распространения волны.
А как можно определить скорость распространения волны?
Вы уже знаете, что любое колебание характеризуется периодом колебаний, то есть временем, после которого колебания повторяются. Тогда можно сказать, что за один период волна распространяется на расстояние 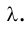 . Поэтому скорость ее распространения можно найти по формуле:
. Поэтому скорость ее распространения можно найти по формуле:
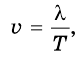
где v – скорость распространения волны (м/с); 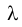 – длина волны (м); Т – период колебаний (с).
– длина волны (м); Т – период колебаний (с).
Так как период и частота связаны соотношением 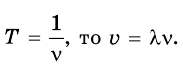
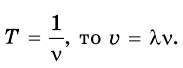
Пример №1
Определите скорость распространения волны на воде, если ее длина равна 180 м, а период колебаний – 15 с.
Дано:
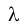 = 180 м
= 180 м
Т = 15 с
v – ?
Решение
По формуле 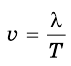 определяем скорость распространения волны на воде.
определяем скорость распространения волны на воде.
v = 180 м : 15 с = 12 м/с.
Ответ: 12 м/с.
Пример №2
Каково основное свойство механической волны?
Ответ: переносить энергию.
Интерференция волн
Для волн не очень больших амплитуд справедлив принцип суперпозиции: если в точку пространства приходят волны от нескольких источников, то эти волны накладываются друг на друга. В результате такого наложения в некоторых точках пространства может наблюдаться постоянное усиление колебаний, а в некоторых — ослабление. Выясним, почему и когда это происходит. Пусть в некоторую точку M поступают две когерентные волны — волны от двух источников 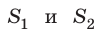 , колеблющихся синхронно, то есть в одинаковых фазах и с одинаковой частотой (рис. 22.6, а).
, колеблющихся синхронно, то есть в одинаковых фазах и с одинаковой частотой (рис. 22.6, а).
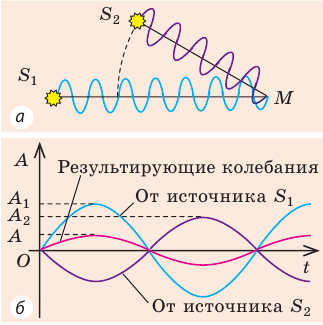
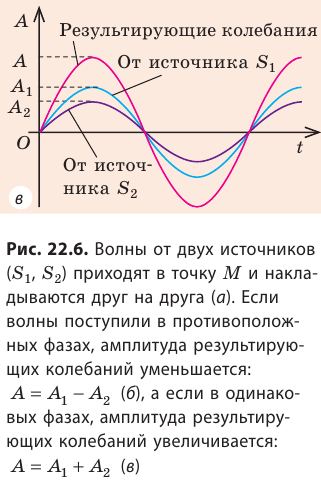
Если волны приходят в точку М в противоположных фазах (в один и тот же момент времени одна волна «толкает» точку М вверх, а вторая «толкает» ее вниз), то волны будут постоянно гасить друг друга (рис. 22.6, б). Если же волны приходят в точку М в одинаковых фазах, то в точке M будут все время наблюдаться колебания с увеличенной амплитудой (рис. 22.6, в). явление наложения волн, вследствие которого в некоторых точках пространства наблюдается устойчивое во времени усиление или ослабление результирующих колебаний, называют интерференцией.
Дифракция волн
Судно, плывущее по морю, образует на поверхности воды волну. Если на своем пути волна встретит скалу или торчащую из воды ветку, то за скалой образуется тень (то есть непосредственно за скалу волна не проникает), а за веткой тень не образуется (волна ветку огибает).
Явление огибания волнами препятствий называют дифракцией (от лат. difractus — разломанный) (рис. 22.8).
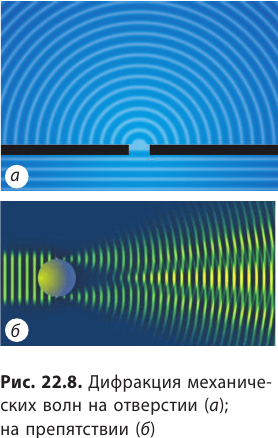
В приведенном примере дифракция волны происходит на ветке, но не происходит на скале. Но это не всегда так. Если скала достаточно удалена от берега, то на некотором расстоянии от скалы тень исчезнет — волна обогнет и скалу. Дело в том, что дифракция наблюдается в двух случаях: 1) когда линейные размеры препятствий, на которые находит волна (или размеры отверстий, сквозь которые проходит волна), сопоставимы с длиной волны; 2) когда расстояние от препятствия до места наблюдения намного больше размера препятствия.
Выводы:
- Распространение в пространстве колебаний вещества или поля называют волной. Механической волной называют распространение колебаний в упругой среде.
- Волна распространяется в пространстве не мгновенно, а с конечной скоростью. При распространении волны происходит перенос энергии без переноса вещества. В некоторых точках пространства вследствие наложения волн друг на друга может наблюдаться устойчивое во времени усиление или ослабление результирующих колебаний — это явление называют интерференцией. Волны могут огибать препятствия — это явление называют дифракцией.
- Волну, в которой частицы среды колеблются перпендикулярно направлению распространения волны, называют поперечной. Волну, в которой частицы среды колеблются вдоль направления распространения волны, называют продольной.
- Волна периодична во времени и пространстве. Периодичность волны во времени характеризуется периодом колебаний каждой отдельной точки волны. Периодичность волны в пространстве характеризуется длиной волны. Длина волны — это расстояние, на которое распространяется волна за время, равное периоду колебаний. Длина λ, частота ν и скорость v распространения волны связаны формулой волны: v = λν .
Звуковые волны
Звучание флейты, шум мегаполиса, шорох травы, грохот водопада, человеческая речь, музыкальный звук, шум, акустический резонанс… Все это связано с распространением в пространстве определенных механических волн, которые называют звуковыми волнами. Их изучает акустика — наука о звуке. С элементами акустики вы начали знакомиться в курсе физики 9 класса. Итак, вспоминаем и узнаем новое.
Звуковые (акустические) волны — это механические волны с частотами от 20 Гц до 20 кГц. Звуковые волны обычно доходят до уха через воздух — в виде последовательных сгущений и разрежений (то есть в воздухе звуковые волны являются продольными). В зонах сгущений (разрежений) давление воздуха незначительно больше (меньше) атмосферного (рис. 23.1).
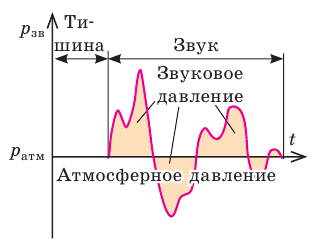
Рис. 23.1. Человеческое ухо воспринимает звуковые волны с избыточным (звуковым) давлением примерно от 20 мкПа (0 децибелов — порог слышимости) до 20 Па (120 децибелов — болевой порог). Для сравнения 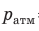 =100 000 Па
=100 000 Па
Звук — механическая волна, потому все свойства волнового движения касаются и звука.
- Звук распространяется в среде с конечной скоростью, зависящей от температуры, плотности, состава и других характеристик среды. Так, в жидкостях звук распространяется быстрее, чем в газах, и медленнее, чем в твердых телах. Скорость распространения звука обычно увеличивается с увеличением температуры среды (в воздухе при температуре 0 °С скорость распространения звука составляет около 330 м/с, а при 20 °С — 340 м/с). Кроме того, чем меньше масса молекул среды, тем быстрее распространяется звук.
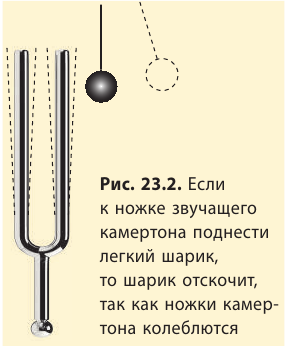
- Источником звука является колеблющееся тело (рис. 23.2). Такие колебания могут быть вынужденными (диффузор громкоговорителя), свободными (струна гитары), автоколебаниями (струны смычковых инструментов).
- Звук не распространяется в вакууме.
- При распространении звука не происходит переноса вещества, но происходит перенос энергии.
- Звуковые волны могут накладываться друг на друга (явление интерференции); могут огибать препятствия (явление дифракции).
Как связаны субъективные и объективные характеристики звука
Все физические величины, характеризующие механические волны (амплитуда, частота, длина, энергия), являются и характеристиками звука. Эти величины не зависят от особенностей восприятия звука человеком, поэтому их называют объективными, или физическими, характеристиками звука. Субъективные характеристики звука (громкость, высота, тембр) обусловлены особенностями слуха человека, поэтому их называют физиологическими. Понятно, что физические и физиологические характеристики звука связаны (см. таблицу).
- Заказать решение задач по физике
| Субъективные (физиологические) характеристики звука | |
|---|---|
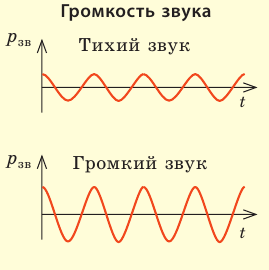 |
Громкость звука определяется прежде всего амплитудой звуковой волны (звуковым давлением), однако зависит и от частоты звуковой волны. Человеческое ухо плохо воспринимает звуки низких (около 20 Гц) и высоких (около 20 кГц) частот, лучше всего — средних частот (1–3 кГц). Громкость звука измеряют в децибелах (дБ). Так, при частоте звука 1 кГц и звуковом давлении 20 Па громкость звука составляет 120 дБ — это болевой порог звука — наиболее громкий звук, который может воспринимать человек, не чувствуя боли (звук такой громкости издает двигатель реактивного самолета). |
| Обратите внимание! Громкий звук может привести к ухудшению слуха и даже к глухоте, особенно это касается прослушивания громкой музыки в наушниках. Слушать музыку в наушниках следует при минимальной громкости! | |
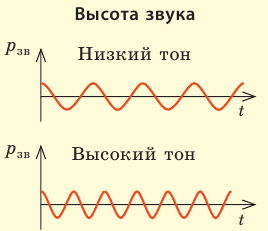 |
Высота звука определяется в основном частотой звуковой волны: чем больше ее частота, тем выше тон звука. Например, ноте «ля» первой октавы соответствует частота 440 Гц; ноте «ля» второй октавы — частота 880 Гц. Свойство человеческого уха различать звуки по их частоте также зависит от интенсивности звуков. При увеличении интенсивности звука его высота кажется более низкой. |
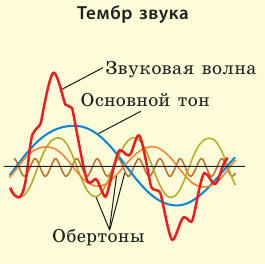 |
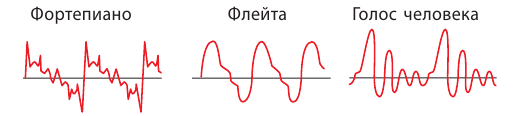
Тембр звука определяется составом звуковой волны: кроме основной частоты (по которой мы и оцениваем высоту звука) любой звук содержит несколько более слабых и более высоких дополнительных частот — обертонов. Именно благодаря тембру мы узнаем человека по голосу, отличаем звуки фортепиано от звуков флейты и т. д. Каждый музыкальный инструмент, каждый человек или животное имеют свой тембр.
|
Что такое акустический резонанс
На любое тело, расположенное в пределах распространения звуковой волны, действует периодическая сила, частота которой равна частоте волны. Под действием этой силы тело начинает совершать вынужденные колебания. Если частота собственных колебаний тела сов падает с частотой звуковой волны, то амплитуда колебаний тела увеличивается и оно начинает издавать звук — наблюдается акустический резонанс.
Акустический резонанс — это явление резкого возрастания амплитуды звукового сигнала при приближении частоты сигнала-возбудителя к частоте собственных колебаний системы.
Наблюдать акустический резонанс можно с помощью опыта с двумя камертонами, имеющими одинаковую частоту (рис. 23.3).
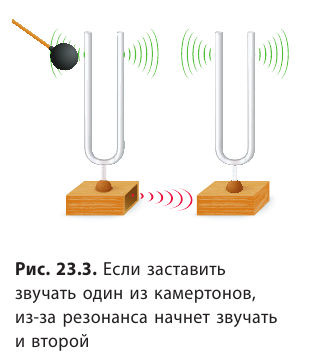
Акустический резонанс используют для увеличения интенсивности звука, созданного некоторым источником (струной, ножками камертона, голосовыми связками и т. д.). Например, для увеличения громкости камертона его присоединяют к деревянному ящику (резонатору), собственная частота колебаний воздуха в котором равна частоте колебаний камертона. Камертон, присоединенный к резонатору, звучит гораздо громче, чем тот, который держат в руке.
Акустический резонанс используют во многих музыкальных инструментах. Воздух в трубах органа, корпусах арф, бандур, гитар и т. д. резонирует с тонами и обертонами звуков, издаваемых колеблющимися телами, и усиливает их. Полость рта — резонатор для звуковых волн, которые создаются благодаря колебаниям голосовых связок. Рис. 23.3. Если заставить звучать один из камертонов, из-за резонанса начнет звучать и второй
Звуковая волна, достигнув уха, испытывает ряд преобразований. Сначала она действует на барабанную перепонку, заставляя ее вибрировать. Чем громче звук, тем сильнее вибрирует перепонка, передавая звуковые колебания в среднее ухо, где они усиливаются.
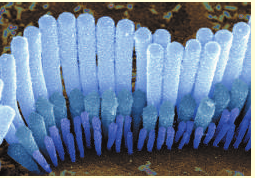
Усиленный звук попадает во внутреннее ухо с заполненной жидкостью улиткой. Поверхность улитки покрыта волосковыми клетками, количество которых достигает 15 000. Каждая клетка резонирует с определенным диапазоном частот. Обнаружив «собственную» частоту, клетка начинает колебаться, возбуждая нервные окончания, и в мозг идет нервный импульс — человек слышит звук.
С возрастом количество волосковых клеток уменьшается (от 15 000 у ребенка до 4 тысяч у пожилого человека). Первыми погибают клетки, «отвечающие» за высокую частоту, поэтому взрослый человек не слышит высоких звуков (подросток слышит звуки до 22 кГц, пожилой человек — до 12 кГц).
Вспоминаем инфра- и ультразвук
Инфразвук (от лат. infra — ниже, под) — это механические волны, частота которых меньше 20 Гц. Инфразвуковые волны возникают во время штормов, землетрясений, цунами, извержений вулканов, вследствие ударов о берег морских волн. Некоторые существа способны воспринимать инфразвуковые волны (рис. 23.4). Источником инфразвука могут быть и объекты, созданные человеком: турбины, двигатели внутреннего сгорания и т. д. В городах наибольший уровень инфразвука около автомагистралей.

Инфразвук очень опасен для животных и человека: он может вызывать симптомы морской болезни, головокружение, потерю зрения, стать причиной повышенной агрессивности. При длительном воздействии интенсивное инфразвуковое излучение может привести к остановке сердца. При этом человек даже не понимает, что происходит, ведь он не слышит инфразвука. Механические волны, частота которых превышает 20 кГц, называют ультразвуковыми волнами (от лат. ultra — сверх, за пределами).
Ультразвук есть в шуме ветра и водопада, в звуках, которые издают некоторые живые существа. Установлено, что ультразвук до 100 кГц воспринимают многие насекомые и грызуны; улавливают его и собаки.
Слабый ультразвук — основа ультразвуковой локации — определения расположения и характера движения объекта с помощью ультразвука. Так, летучие мыши и дельфины, излучая ультразвук и воспринимая его эхо, могут даже в полной темноте найти дорогу или поймать добычу. Ультразвуковое исследование позволяет «увидеть» еще не родившегося младенца, исследовать состояние внутренних органов, выявить инородные тела в тканях. Ультразвуковую локацию применяют также на морских судах — для выявления объектов в воде (сонары) и исследования рельефа морского дна (эхолоты); в металлургии — для выявления и установления размеров дефектов в изделиях (дефектоскопы).
Мощный ультразвук применяют в технике (обработка прочных материалов, сварка, очистка поверхностей от загрязнений); медицине (измельчение камней в организме, что позволяет избежать хирургических операций); пищевой промышленности (изготовление сыров, соусов); косметологии (изготовление кремов, зубной пасты).
Выводы:
- Механические волны с частотами 20 Гц — 20 кГц называют звуковыми волнами (звуком). Субъективные характеристики звука: высота звука (определяется частотой звуковой волны); громкость звука (определяется амплитудой и частотой звуковой волны); тембр звука (определяется спектром звуковой волны).
- Явление резкого возрастания амплитуды звукового сигнала в случае приближения частоты сигнала-возбудителя к частоте собственных колебаний системы называют акустическим резонансом. Акустические резонаторы имеют почти все музыкальные инструменты.
- Механические волны, частота которых меньше 20 Гц, называют инфразвуковыми волнами (инфразвук). Механические волны, частота которых превышает 20 кГц, называют ультразвуковыми волнами (ультразвук).
- Волновое движение в физике
- Продольные и поперечные волны в физике
- Звуковые волны в физике
- Электрическое поле в физике
- Электромагнитные явления в физике
- Электромагнитные волны и их свойства
- Магнитные явления в физике
- Магнитный поток
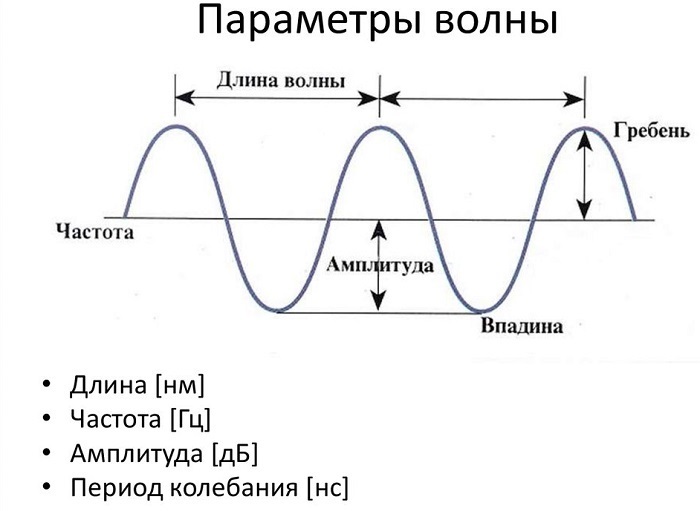
Длина волны – это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.
Цикл – это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.
На рисунке показаны основные параметры волны, используемые в физике:
Определение и формула длины волн
Волна – это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.
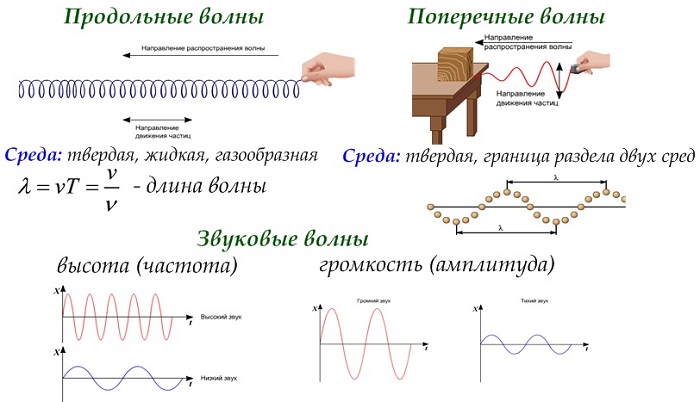
Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.
Греческая буква “λ” (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

Период Т — время завершения полного колебания, единица измерения секунды (с).
Длинная волна соответствует низкой частоте, а короткая – высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.
Пространственный период волны – это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.
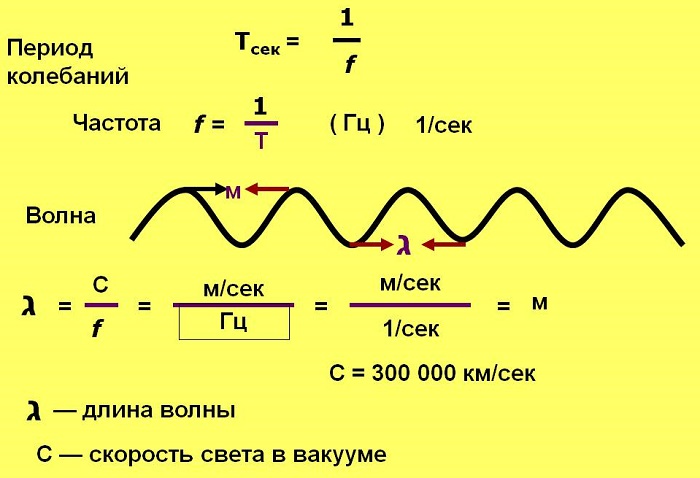
Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).
При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).
Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 108 м/с поделить на длину в метрах.
Единицы измерения длины волны λ – нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).
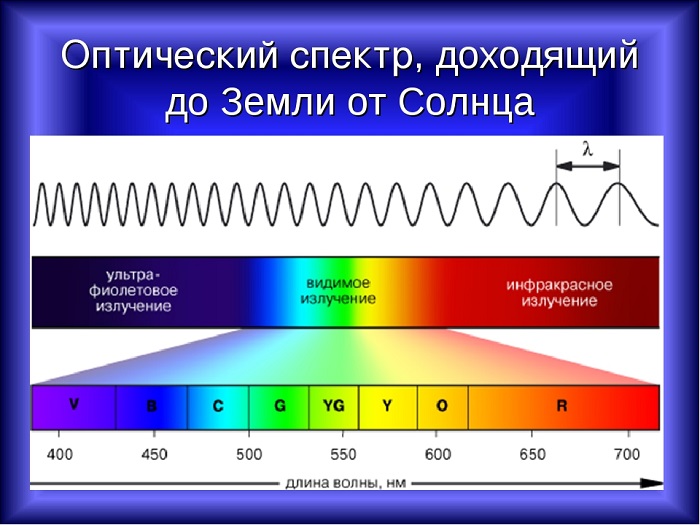
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной – красный, который составляет около 700 нм.
Таблица показывает длину волны в зависимости от цвета:
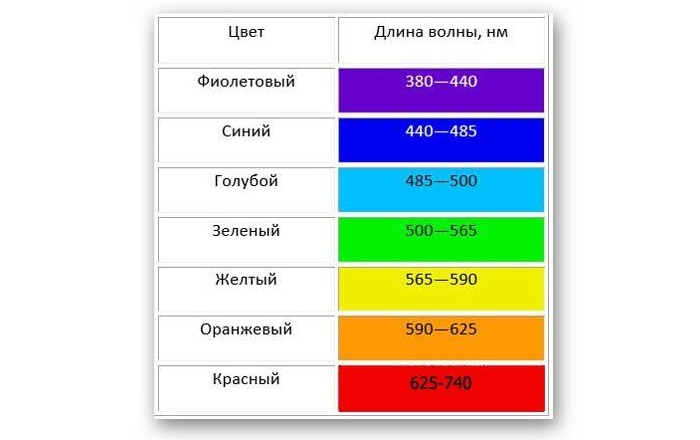
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.
Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.
Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:
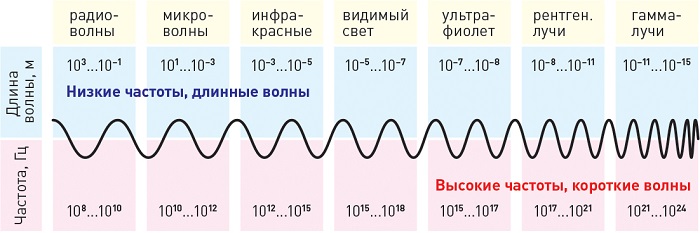
Примеры расчета длины волны для звуковых, электромагнитных и радиоволн
Задача №1
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.