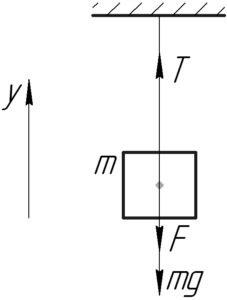
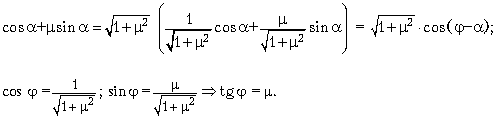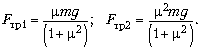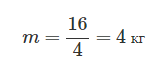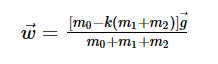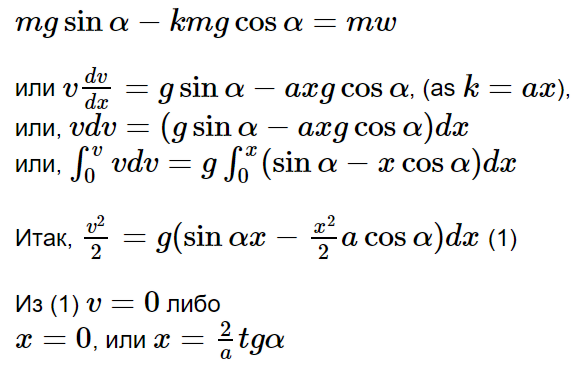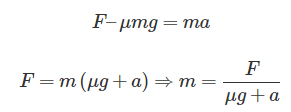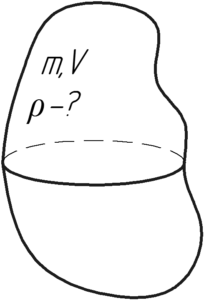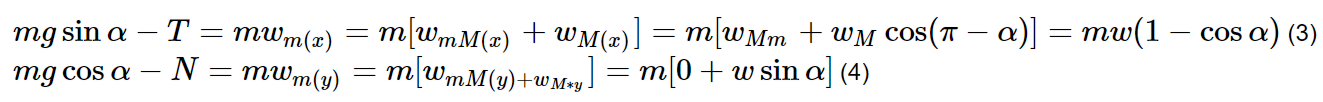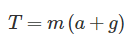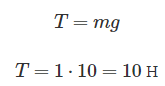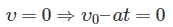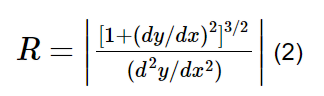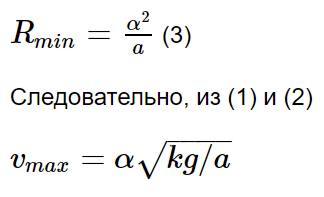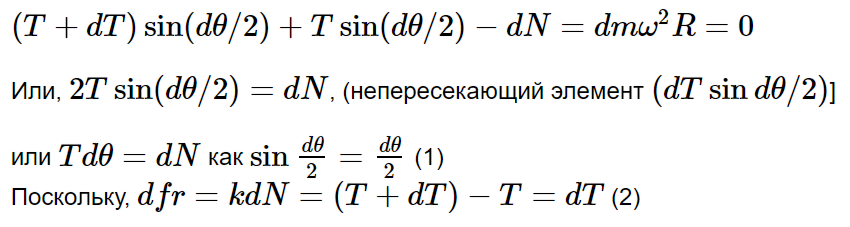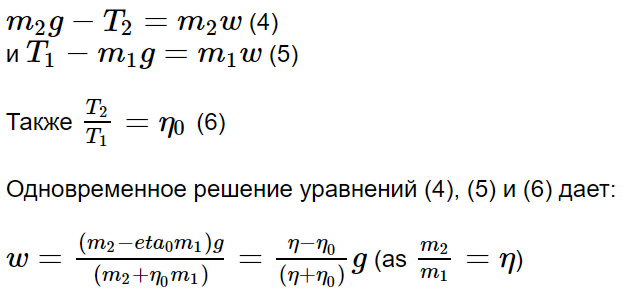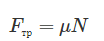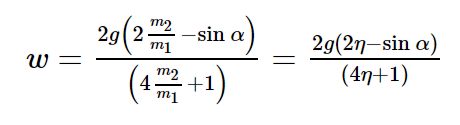Условие задачи:
Два бруска одинаковой массы 0,2 кг поставили на наклонную плоскость с углом наклона 45°. Коэффициент трения нижнего бруска о плоскость 1, а верхнего 0,01. Найти силу взаимодействия брусков при их совместном соскальзывании.
Задача №2.3.18 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=0,2) кг, (alpha=45^circ), (mu_1=1), (mu_2=0,01), (F-?)
Решение задачи:
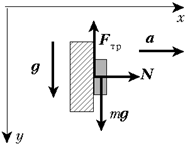
[left{ begin{gathered}
mg cdot sin alpha – {F_{тр1}} + F = ma hfill \
mg cdot sin alpha – {F_{тр2}} – F = ma hfill \
end{gathered} right.]
Вычтем из первого равенства системы второе:
[2F – {F_{тр1}} + {F_{тр2}} = 0]
[F = frac{{{F_{тр1}} – {F_{тр2}}}}{2};;;;(1)]
Получается, чтобы дорешать задачу, нужно определить силы трения, действующие на каждый брусок. Покажем это для первого бруска, для второго определение силы трения аналогично. Применим первый закон Ньютона в проекции на ось (y):
[N_1 = mg cdot cos alpha ]
Сила трения скольжения определяется по следующей формуле:
[{F_{тр1}} = mu_1 N_1]
Тогда:
[{F_{тр1}} = {mu _1}mg cdot cos alpha ]
Если вы выполните аналогичные действия и для второго бруска, то получите:
[{F_{тр2}} = {mu _2}mg cdot cos alpha ]
C учетом последних полученных выражений формула (1) примет вид:
[F = frac{{left( {{mu _1} – {mu _2}} right)mg cdot cos alpha }}{2}]
Теперь посчитаем численный ответ к задаче:
[F = frac{{left( {1 – 0,01} right) cdot 0,2 cdot 10 cdot cos 45^circ }}{2} = 0,7; Н = 700; мН]
Ответ: 700 мН.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.3.17 Чему должен быть равен минимальный коэффициент трения между шинами
2.3.19 На тележке, скатывающейся без трения с наклонной плоскости, установлен стержень
2.3.20 По наклонной плоскости с углом наклона 60 градусов соскальзывает без трения клин
2017-05-07
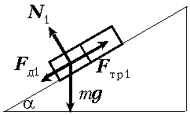
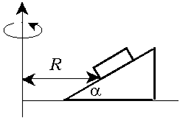
На наклонную плоскость, составляющую угол $alpha$ с горизонтом, поместили два соприкасающихся бруска 1 и 2 (рис.). Массы брусков равны $m_{1}$ и $m_{2}$, коэффициенты трения между наклонной плоскостью и этими брусками — соответственно $k_{1}$ и $k_{2}$, причем $k_{1} > k_{2}$. Найти:
а) силу взаимодействия между брусками в процессе движения;
б) минимальное значение угла $alpha$, при котором начнется скольжение.
Решение:
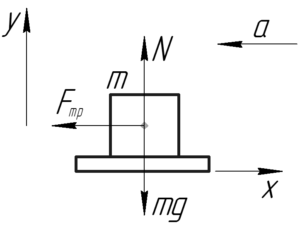
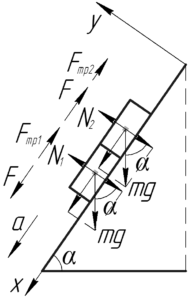
Направим положительное направление оси х вдоль уклона (рис.). На рисунках показана диаграмма сил для брусков.
Пусть $R$ – сила взаимодействия между брусками, и они, очевидно, скользят вниз с тем же постоянным ускорением $w$.
Второй закон Ньютона движения в проекции вдоль оси x для брусков дает:
$m_{1} g sin alpha – k_{1}m_{1} g cos alpha + R = m_{1}w$ (1)
$m_{2} g sin alpha – R – k_{2}m_{2}g cos alpha = m_{2} w$ (2)
Решая уравнения (1) и (2) одновременно, получим
$w = g sin alpha – g cos alpha frac{k_{1}m_{1} + k_{2}m_{2}}{m_{1} + m_{2}}$ и $R = frac{m_{1}m_{2}(k_{1} – k_{2})g cos alpha}{m_{1} + m_{2}}$ (3)
(б) когда бруски просто скользят вниз по плоскости, $w = 0$, то из уравнения (3)
$g sin alpha – g cos alpha frac{k_{1}m_{1} + k_{2}m_{2}}{m_{1} + m_{2}} = 0$
Или, $(m_{1} + m_{2}) sin alpha = ( k_{1}m_{1} + k_{2} m_{2}) cos alpha$
Следовательно, $tg alpha = frac{(k_{1}m_{1} + k_{2}m_{2})}{m_{1} + m_{2}}$
Окончание. См. № 23/06
Ш.Г.ЗИЯТДИНОВ,
лицей при БирГПИ, г. Бирск, Республика
Башкортостан
Капризная сила – сила трения
Задача № 21. С каким
горизонтальным ускорением надо двигать кирпич
вправо, чтобы шайба, прислонённая к его
вертикальной поверхности, не падала? Коэффициент
трения скольжения между шайбой и поверхностью
кирпича равен .
Решение. По второму закону
Ньютона, для шайбы можно записать:
ma = mg + Fтр
+ N.
Проецируя это уравнение на оси
координат, получим:
ma = N; Fтр = N = mg
a = g/
.
Задача № 22. Сила
взаимодействия двух брусков одинаковых масс m
при их совместном соскальзывании с наклонной
плоскости с углом наклона при коэффициентах трения
соответственно 1
(для нижнего бруска) и 2 (
1
> 2), равна:
А)
Б)

В)
Г)
Д)
Решение.
Второй закон Ньютона для первого
бруска в проекции на направление движения
запишется в виде:
ma = mgsin + Fд1 – Fтр1 = mgsin
+ Fд1 –
1mg cos
.
Аналогично для второго бруска:
ma = mgsin – Fд2 – Fтр2 = mgsin
– Fд2 –
2mgcos
,
при этом Fд1 = Fд2 = Fвз
(третий закон Ньютона). Из приведённых уравнений
находим, что
Fвз =
Задача № 23. Сила, равномерно
перемещающая вверх по наклонной плоскости груз
(коэффициент трения = 0,58), минимальна при её угле наклона к
плоскости:
А) 15°; Б) 30°; В) 45°; Г) 60°; Д) 75°.
Решение.
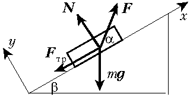
Введём угол – между наклонной плоскостью и
горизонтом – и угол – между наклонной плоскостью и
направлением вектора силы F.
Запишем основное уравнение динамики в векторной
форме:
ma = mg + N
+ F + Fтр.
По условию, тело скользит равномерно,
поэтому Fтр = N и а = 0. Тогда условие
равномерного движения тела по наклонной
плоскости вверх можно выразить в проекциях на
оси Х и Y так:
Fcos
= mgsin + Fтр
= mgsin +
N,
где N = mgcos – Fsin
.
Из двух последних равенств находим:
(*)
Как видно, числовое значение силы F
определяется лишь углом (числитель – величина постоянная).
Минимальное значение F может иметь при
максимуме знаменателя (cos +
sin
). Из курса
тригонометрии известно преобразование:
Полученное выражение имеет
максимальное значение при cos( –
)
= 1. Отсюда: –
= 0
=
=
= arc tg = arc
tg0,58 = 30° .
Отметим, что минимальный угол можно
было найти, используя понятие производной и
исследуя выражение (*) на максимум.
Задача № 24. Найдите
минимальное время t, за которое груз массой m
можно переместить по горизонтальной поверхности
на расстояние L, приложив к нему постоянную
силу F, такую, что F < mg, где
– коэффициент трения скольжения.
Величины L, m, g, F считать
известными.
Указания. Время перемещения t
будет минимальным, когда ускорение движения
максимально, а это зависит от значения выражения
т.е. от значения (сos +
sin
). Таким образом,
физическая задача сводится к исследованию
функции
f() = сos
+
sin
на экстремум. Исследование показывает, что
функция f()
максимальна при tg
= .
Задача № 25.
Если угол между верхней гранью клина и
горизонтальной нижней гранью = 30°, коэффициент трения
= 0,2, а расстояние между
небольшим бруском, помещённым на верхнюю грань
клина, и вертикальной осью, вокруг которой
вращается клин, R = 0,5 м, то максимальная
угловая скорость вращения клина, при которой
брусок не проскальзывает по грани клина, равна:
А) 2,6 рад/с; Б) 3,0 рад/с; В) 3,4 рад/с;
Г) 3,8 рад/с; Д) 4,2 рад/с.
Решение. Роль
центростремительной силы в этом случае играет
горизонтальная составляющая результирующей
силы нормальной реакции опоры (клина) и
максимальной силы трения покоя:
Fц = m2R = (N + Fтр.
пок.max)x =
откуда = 4,2
рад/с.
Задача № 26. Небольшое тело
массой m движется с коэффициентом трения k
по горизонтальной плоскости ХY. Закон
движения х = аsint, у = –аcos
t, где а и
—константы. Мощность,
развиваемая силой трения, равна:
А) –а
kmg; Б) a
kmg; В) –ma2
3;
Г) –а
kmg(sin
t
+ cost); Д) 0.
Решение. Отметим, что такого рода
задачи в школьной программе совсем не
рассматриваются, а в вузе их относят к теме
«Сложение взаимно перпендикулярных
гармонических колебаний». Если внимательно
проанализировать зависимости от t координат
х и у тела, то можно заметить, что
сложное двухмерное движение тела представляет
собой равномерное вращательное движение тела по
окружности радиусом а против часовой
стрелки с угловой скоростью вращения . Представить учащимся такое
движение довольно сложно. В данном случае
Подставив выражение для силы трения,
получим N = kmgcos180° = –kmg • a
. Здесь использована формула
для линейной скорости движения шарика по
окружности = а
.
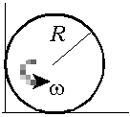
Задача № 27. Тонкий обруч
радиусом R = 0,50 м раскрутили до угловой
скорости = 30,2 с–1
и затем поместили в угол (коэффициент трения
между стенкой, полом и обручем = 0,50).
Сколько оборотов сделает обруч до
остановки?
Решение.
Поскольку между обручем, стенкой и
полом есть трение, угловая скорость вращения
обруча со временем уменьшится до нуля, причём
изменение кинетической энергии обруча равно
работе сил трения, действующих на обруч:
Екин
= 0 – Екин 0 = –m2/2 = Aтр1 + Aтр2
= – (Fтр1 + Fтр2)s.
При этом очевидны равенства: =
R; s = 2
Rn, где n – число оборотов обруча
до его остановки.
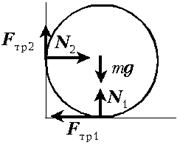
Найдём силы трения. Тело поступательно
не перемещается. Это означает, что
равнодействующая всех сил, указанных на чертеже,
равна нулю, т.е. в проекциях на вертикальную и
горизонтальную оси имеют место два равенства:
mg – N1 – Fтр2 = mg
– N1 – N2
= 0; N2 – Fтр1 = N2 – N1 = 0.
Из них находим:
Объединяя все полученные выражения,
получим:
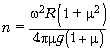
оборотов.

Два бруска с одинаковой массой m 0.2 кг поставили на наклонную плоскость с углом наклона 45(градусов). Коэффициент трения верхнего бруска о плоскость
0,01, нижнего 1. Найти силу взаимодействия брусков при их совместном соскальзывании
Светило науки – 22 ответа – 0 раз оказано помощи
Сила нормального давления mgcosa, где а – угол наплона плоскости.
сила трения на нижний брусок F1=mgcosa, сила трения ни верхний брусок F2=0,1mgcosa.
пусть Т -сила взаимодействия между брусками.
Поскольку оба бруска движутся с одним ускорением, тогда
a1=a2;
ma1=mgsina-mgcosa+T;
ma2=mgsina-0,1mgcosa-T.
Далее получаем 2T=0,9mgcosa.
Пример 1:
Аэростат массы m начал опускаться с постоянным ускорением ww. Определить массу балласта, который следует сбросить за борт, чтобы аэростат получил такое же ускорение, но направленное вверх. Сопротивлением воздуха пренебречь.
Решение от преподавателя:
Решение:
Пусть R – сила действующая на аэростат массы m, опускающегося с постоянным ускорением w. Применяя второй закон движения Ньютона для аэростата в проекционной форме
Пример 2:
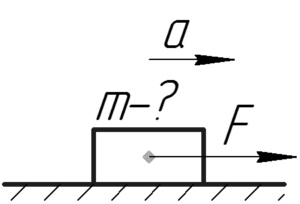
Тело движется прямолинейно под действием силы 16 Н. Зависимость пути от времени имеет вид S=10−5t+2t2 м. Найти массу тела.
Решение от преподавателя:
В общем случае зависимость пути от времени для прямолинейного равноускоренного движения выглядит следующим образом:
Сопоставим эту общую зависимость с той, которая дана нам в условии задачи.
Получается, что модули (то есть их численные значения) начальной скорости и ускорения тела равны:
Вообще, если вам в условии дано уравнение движения тела, то коэффициент перед членом t2 равен половине ускорения. Но будьте внимательны, так как если имеются члены более высокого порядка (t3,t4), то движение уже не равноускоренное, а коэффициент перед членом t2 равен уже половине начального ускорения. Согласно второму закону Ньютона (краткое обозначение – 2ЗН), ускорение тела, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе тела.
Выразим из этой формулы массу тела:
Посчитаем ответ:
Ответ: 4 кг.
Пример 3:
Пуля, пробив доску толщиной h, изменила свою скорость от v0 до v. Найти время движения пули в доске, считая силу сопротивления пропорциональной квадрату скорости.
Решение от преподавателя:
Решение:
В соответствии с уловием задачи
Интегрирование, с учетом пределов,
Получим значение k, перепишем
Проинтегрируем
Подставляя значение k из (2) в (1), получим
Пример 4:
Тело массой 3 кг движется горизонтально с ускорением 4 м/с2. Определить действующую на него силу.
Решение от преподавателя:
Второй закон Ньютона гласит, что ускорение тела прямо пропорционально действующей на него силе и обратно пропорционально массе тела. Аналитически этот закон выглядит так:
Выразим из формулы действующую на тело силу F.
Посчитаем численный ответ к задаче.
Ответ: 12 Н.
Пример 5:
В установке (рис.) массы тел равны m0,m1, и m2, массы блока и нитей пренебрежимо малы и трения в блоке нет. Найти ускорение w , с которым опускается тело m0, и натяжение нити, связывающей тела m1 и m2, если коэффициент трения между этими телами и горизонтальной поверхностью равен k.
Решение от преподавателя:
Решение:
Запишем основное уравнение динамики для всех трех блоков в терминах проекций, взяв положительное направление осей x и y, как показано на рис.
И используя тот факт, что блоки движутся с одинаковым ускорением w
Одновременное решение уравнений (1), (2) и (3) дает:
Поскольку блок m0 движется вниз с ускорением w, поэтому в векторной форме
Пример 6:
На тело массой 5 кг подействовали горизонтальной силой 4 Н. Какую скорость приобретет тело за 10 с при отсутствии трения?
Решение от преподавателя:
Так как на тело не будет действовать сила трения, т.е. действует только одна сила F, то согласно второму закону Ньютона (2ЗН) ускорение тела можно найти из такого соотношения:
Так как тело в момент приложения силы покоилось, значит у него отсутствовала начальная скорость, поэтому скорость тела через время tt можно найти по такой формуле:
Подставим формулу (1) в (2), тогда получим решение задачи в общем виде.
Подставляем в эту формулу численные значения входящих в неё величин и считаем ответ.
Ответ: 28,8 км/ч.
Пример 7:
На наклонную плоскость, составляющую угол αα с горизонтом, поместили два соприкасающихся бруска 1 и 2 (рис.). Массы брусков равны m1 и m2, коэффициенты трения между наклонной плоскостью и этими брусками — соответственно k1 и k2, причем k1>k2. Найти:
а) силу взаимодействия между брусками в процессе движения;
б) минимальное значение угла αα, при котором начнется скольжение.
Решение от преподавателя:
Решение:
Направим положительное направление оси х вдоль уклона (рис.).
На рисунках показана диаграмма сил для брусков.
Пусть R – сила взаимодействия между брусками, и они, очевидно, скользят вниз с тем же постоянным ускорением ww. Второй закон Ньютона движения в проекции вдоль оси x для брусков дает:
Решая уравнения (1) и (2) одновременно, получим
(б) когда бруски просто скользят вниз по плоскости, w=0, то из уравнения (3)
Или
Следовательно
Пример 8:
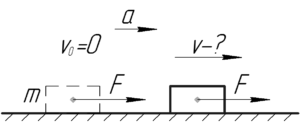
Небольшой брусок начинает скользить по наклонной плоскости, составляющей угол α с горизонтом. Коэффициент трения зависит от пройденного пути x по закону k=ax, где a — постоянная. Найти путь, пройденный бруском до остановки, и максимальную скорость его на этом пути.
Решение от преподавателя:
Решение:
Из второго закона Ньютона для бруска в проекции х: Fx=mwx, получаем
Поскольку движение бруска является однонаправленным, оно останавливается после прохождения расстояния
Из (1), при vmax,
Следовательно, максимальная скорость будет на расстоянии,
Подставляя это значение xx в (1) получаем максимальную скорость,
Пример 9:
В установке (рис.) известны угол αα наклонной плоскости с горизонтом и коэффициент трения k между телом m1 и наклонной плоскостью. Массы блока и нити пренебрежимо малы, трения в блоке нет. Считая, что в начальный момент оба тела неподвижны, найти отношение масс m2/m1, при котором тело m2:
а) начнет опускаться;
б) начнет подниматься;
в) будет оставаться в покое.
Решение от преподавателя:
Решение:
В начальный момент, очевидно, натяжение нити, соединяющей m1 и m2 равно весу m2
(a) Для того, чтобы блок m2 опустился или блок m1 поднялся, условия составляют
Где T – натяжение, а fr – трение, которое в предельном случае равно
Тогда или
или
(б) Аналогичным образом в случае
(в) Для этого случая ни один вид движения невозможен, и fr не должен быть неограничена. Следовательно,
Пример 10:
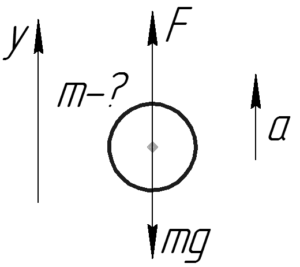
Под действием какой силы прямолинейное движение частицы массой 100 г описывается уравнением x=1+3t−t2.
Решение от преподавателя:
Из второго закона Ньютона следует, что сила, действующая на тело, равна произведению массы тела на её ускорение.
Уравнение прямолинейного ускоренного движения в общем случае записывается так:
Сравнивая его с уравнением движения, данным в условии задачи, можно прийти к выводу, что начальная координата, модуль начальной скорости и модуль ускорения тела равны:
Поскольку мы теперь знаем ускорение, с которым движется тело, то по формуле (1) сможем найти ответ к задаче. Переведем массу тела в единицы системы СИ, то есть из граммов в килограммы.
Ответ: 200 мН.
Пример 11:
В установке (рис.) шарик 1 имеет массу в η=1,8 раза больше массы стержня 2. Длина последнего l=100см. Массы блоков и нитей, а также трение пренебрежимо малы. Шарик установили на одном уровне с нижним концом стержня и отпустили. Через сколько времени он поравняется с верхним концом стержня?
Решение от преподавателя:
Решение:
Предположим, шар поднимается с ускорением w1 а стержень спускается с ускорением w2.
Поскольку длина нити постоянна, 2w1=w2(1)
Из второго закона Ньютона в проекционной форме вдоль оси, направленной вверх, для шара, и вертикально вниз для стержня соответственно получаем,
Но T=2T (поскольку блок безмассовый)
Из уравнений (1), (2), (3) и (4)
Из кинематического уравнения в проекционной форме получаем:
Так как, w1 и w2 противоположно направленны.
Подставляя значения w1 и w2, получаем искомое время
Пример 12:
На горизонтальной плоскости с коэффициентом трения kk лежит тело массы mm. В момент t=0 к нему приложили горизонтальную силу, меняющуюся со временем по закону F=at, где a — постоянный вектор. Найти путь, пройденный телом за первые t секунд после начала действия этой силы.
Решение от преподавателя:
Решение:
Поскольку приложенная сила пропорциональна времени, а к телу приложена сила трения, движение не начинается сразу после приложения силы. Тело начинает свое движение, когда F равно предельному трению.
Пусть движение начинается после времени t0, тогда
Итак, при t≤t0, тело остается в покое и при t>t0 очевидно
Интегрируя и замечая, что v=0 при t=t0, получаем, при t>t0
таким образом
Пример 13:
В системе (рис.) масса тела 1 в η=4,0 раза больше массы тела 2. Высота h=20см. Массы блоков и нитей, а также трение пренебрежимо малы. В некоторый момент тело 2 отпустили, и система пришла в движение. На какую максимальную высоту от пола поднимется тело 2?
Решение от преподавателя:
Решение:
Используя второй закон Ньютона в проекционной форме вдоль оси x для тела 1 и вдоль отрицательной оси x для тела 2 соответственно, получим
При опускании блока вниз по закону Ньютона вдоль оси х,
Так как длина нити постоянна,
Одновременное решение вышеприведенных уравнений дает,
Очевидно, что в течение временного интервала, в котором тело 1, пройдет расстояние h и достигает поверхности, тело 2 переместиться вверх на расстояние 2h. В тот момент, когда тело 2 находится на высоте 2h от пола, его скорость определяется выражением:
После того, как тело m1 коснется пола, натяжение нити станет равным нулю, в результате чего тело 2 будет находится только под действием силы тяжести для его последующего движения.
Скорость тела 2 будет равна v2 на высоте 2h, далее оно будет поднимается под действием силы тяжести на расстояние,
Таким образом, искомая максимальная высота, достигнутая телом 2:
Пример 14:
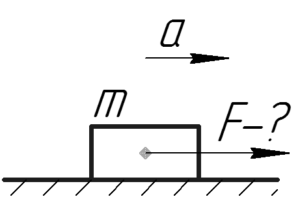
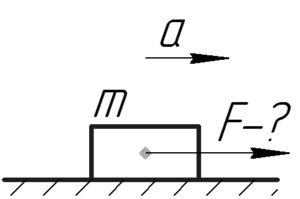
Под действием горизонтальной силы, равной 12 Н, тело движется по горизонтальной поверхности по закону x=x0+1,2t2. Найти массу тела, если коэффициент трения равен 0,1.
Решение от преподавателя:
Сначала разберемся с каким ускорением движется тела. Сравним уравнение (1), данное в условии, и уравнение (2) прямолинейного ускоренного движения тела в общем виде.
Можно прийти к выводу, что начальная скорость тела равна нулю, а ускорение равно 2,4 м/с2.
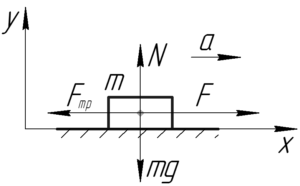
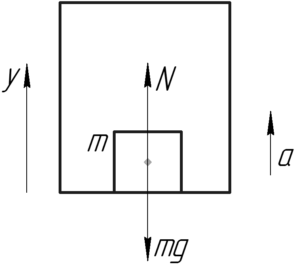
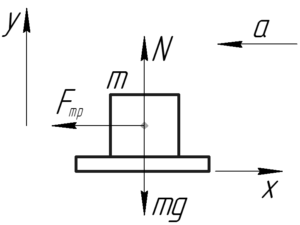
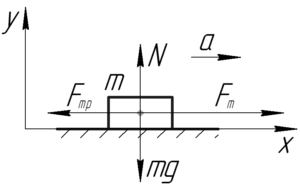
Силы, действующие на тело, изображены на рисунке. Одно замечание – на самом деле сила трения приложена к линии контакта тела с поверхностью, а у нас на рисунке – к центру тела, но в этой задаче это допущение не играет никакой роли. Запишем следствия из второго закона Ньютона в проекция на оси x и y.
Сила трения скольжения Fтр равна произведению коэффициента трения μ на силу нормальной реакции опоры N. Используя равенство (4), запишем:
Подставим полученное в выражение (3), откуда и выразим искомую массу тела m.
Численно масса тела равна:
Ответ: 3,53 кг.
Пример 15:
Найти ускорения стержня А и клина В в установке (рис.), если отношение массы клина к массе стержня равно ηη и трение между всеми соприкасающимися поверхностями пренебрежимо мало.
Решение от преподавателя:
Решение:
Запишем все силы действующие на тела, а также проведем кинематическую диаграмму ускорений, проанализировав направления движения А и В. Кинематическая связь ускорений такова:
Напишем второй закон Ньютона для обоих тел в проекциях, взяв положительные направления осей у и х, как показано на рисунке.
Одновременное решение (1), (2) и (3) дает:
Пример 16:
Тело массы m бросили вертикально вверх со скоростью v0. Найти скорость v′, с которой тело упадет обратно, если сила сопротивления воздуха равна kv2, где k — постоянная, v — скорость тела.
Решение от преподавателя:
Решение:
При движении вверх, из второго закона Ньютона в вертикальном направлении
На максимальной высоте h скорость v=0, поэтому
Интегрируя и решая, получаем,
Когда тело падает вниз, конечная сила, действующая на тело в направлении вниз, равна (mg−kv2), Следовательно, конечное ускорение при движении вниз, согласно второму закону движения
Таким образом,
Интегрируя и подставляя значение h из (1), получаем:
Пример 17:
В системе (рис.) известны массы клина M и тела m. Трение имеется только между клином и телом m. Соответствующий коэффициент трения равен k. Массы блока и нити пренебрежимо малы. Найти ускорение тела mm относительно горизонтальной поверхности, по которой скользит клин.
Решение от преподавателя:
Решение:
Оценим все силы действующие на тела и зафиксируем систему координат, как показано на рисунке. Проанализировав движение MM и mm по рисункам, проведем кинематическую диаграмму ускорений (рис.). Так как длина нитей постоянна, то
То из закона сложения векторов
Одновременное решение уравнений (2), (3) и (4) дает:
Следовательно, используя уравнение (1)
Пример 18:
Определить плотность тела массой 100 г и объемом 500 см3.
Решение от преподавателя:
Плотность ρ – это физическая величина, равная отношению массы тела mm на его объем V.
Единицей измерения плотности в системе СИ является кг/м3, хотя существуют и другие внесистемные единицы измерения, например, г/см3, в которых мы и посчитаем ответ к этой задаче. Численно плотность тела будет равна:
Чтобы измерить плотность тела, нужно знать его массу и объем. Если первая определяется очень просто с помощью весов, то нахождение второй, особенно для тел со сложной геометрией, было затруднительным. Но Архимед нашел выход, заметив, что тела при погружении в воду вытесняют объем воды, равный их собственному объему.
Ответ: 0,2 г/см3.
Пример 19:
С каким минимальным ускорением следует перемещать в горизонтальном направлении брусок А (рис.), чтобы тела 1 и 2 не двигались относительно него? Массы тел одинаковы, коэффициент трения между бруском и обоими телами равен k. Массы блока и нитей пренебрежимо малы, трения в блоке нет.
Решение от преподавателя:
Решение:
Тела 1 и 2 останутся в покое относительно A при
wmin ≤ w ≤ wmax,
где wmin – искомое минимальное ускорение бруска.
Вне этих пределов будет относительное движение между бруском и телами.
При
0 ≤ w ≤ wmin,
движение тела 1 относительно бруска A должно быть направлено вправо и противоположно при
w ≥ wmax.
Основываясь на приведенном выше рассуждении, трение покоя тела 2 по А направлено вверх, а 1 по А – для вычисления wmin.
Напишем второй закон Ньютона для тел 1 и 2 в проекции на положительную ось х (рис.).
Поскольку тело 2 не имеет ускорения в вертикальном направлении, то
Из (1) и (3) следует,
Из (4) и (5) следует,
Следовательно,
Пример 20:
Частица массы m движется в некоторой плоскости P под действием постоянной по модулю силы F, вектор которой поворачивается в этой плоскости с постоянной угловой скоростью ω. Считая, что в момент t=0 частица покоилась, найти:
а) ее скорость в зависимости от времени;
б) путь, проходимый частицей между двумя последовательными остановками, и среднюю скорость за это время.
Решение от преподавателя:
Решение:
Зафиксируем координатную систему x – y на плоскости, взяв ось x в направлении, вдоль которого вектор силы был ориентирован в момент t=0, тогда основное уравнение динамики, выраженное через проекцию на x и y-оси дают,
(a) Используя условие v(0)=0, получаем
Следовательно,
(б) Видим, что скорость v превращается в нуль после интервала времени Δt, который можно найти из соотношения,
Следовательно, искомое расстояние,
Средняя скорость,
Таким образом,
Пример 21:
На горизонтальной поверхности находится призма 1 массы m1 с углом α (см. рис.) и на ней брусок 2 массы m2. Пренебрегая трением, найти ускорение призмы.
Решение от преподавателя:
Решение:
Запишем второй закон Ньютона для обоих тел в проекции вдоль положительных осей y2 и x1, как показано на рис.
Решая (1) и (2), получаем
Пример 22:
Определить вес человека массой 70 кг в лифте, опускающемся равнозамедленно с ускорением 1 м/с2.
Решение от преподавателя:
Вес тела P – это сила взаимодействия тела с опорой, в данном случае с лифтом. По третьему закону Ньютона вес равен силе нормальной реакции опоры. Оно и понятно, ведь с какой силой тело взаимодействует с опорой, с такой же силой и опора взаимодействует с телом. Заметим, что они противоположны по направлению.
Изобразим на рисунке все силы, действующие на человека. Обязательно обратите внимание на направление ускорения: так как тело опускалось равнозамедленно, то ускорение направленно вверх. Из второго закона Ньютона в проекции на ось yy следует:
Учитывая равенство (1), следует:
Считаем ответ, подставив данные задачи в формулу.
Ответ: 770 Н.
Пример 23:
В системе (рис.) известны массы кубика mm и клина M, а также угол клина α. Массы блока и нити пренебрежимо малы. Трения нет. Найти ускорение клина M.
Решение от преподавателя:
Решение:
Чтобы проанализировать кинематические отношения между телами, рассмотрим все силы действующие на каждое тело, как показано на рисунке.
На основе диаграммы силы очевидно, что клин M будет двигаться вправо, а блок будет двигаться вниз вдоль клина. Так как длина нити постоянна, расстояние, пройденное кубиком на клине, должно быть равно расстоянию, пройденному клином на поверхности.
Для кубика mm зафиксируем (x-y) систему координат в системе отсчета земли и по второму законоу ньютона в проекционной форме вдоль осей x и y (рис.) получаем
Решая приведенные выше уравнения одновременно, получаем
Пример 24:
Небольшую шайбу А положили на наклонную плоскость, составляющую угол α с горизонтом, и сообщили начальную скорость v0 (рис.). Найти зависимость скорости шайбы от угла ϕ, если коэффициент трения k=tgα и в начальный момент ϕ0=π/2.
Решение от преподавателя:
Решение:
Ускорение шайбы по плоскости определяется проекцией силы тяжести на эту плоскость Fx=mgsinα и силой трения fr=kmgcosα. В нашем случае k=tgα и, следовательно,
Найдем проекцию ускорения на направление касательной к траектории и по оси x:
Видим, что wy=wx, что означает, что скорость v и ее проекция vxvx отличаются только постоянным значением C, которое не меняется со временем, Т.е.
Пример 25:
Частица массы m движется по окружности радиуса R. Найти модуль среднего вектора силы, действующей на частицу на пути, равном четверти окружности, если частица движется:
а) равномерно со скоростью v;
б) с постоянным тангенциальным ускорением wτ без начальной скорости.
Решение от преподавателя:
Решение:
Рассмотрим движения частицы с массой mm по окружности радиуса R и обозначим оси x и y, как показано на рисунке:
(a) Для частицы изменение импульса
Так как
И время, затраченное на описание четверти круга,
Следовательно,
(б) В этом случае
Так как
Следовательно,
Пример 26:
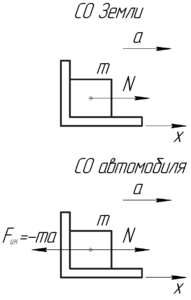
С какой силой давит человек массой 70 кг на вертикальную спинку сиденья автомобиля, который движется по горизонтальному участку с ускорением 3 м/с2?
Решение от преподавателя:
На рисунке покажем силы, действующие на тело. Получается, что на тело действует только одна реакция опоры NN, которая численно равна искомой силе давления P согласно третьему закону Ньютона (3ЗН).
Из второго закона Ньютона следует:
Тогда понятно, что:
Посчитаем численно силу давления P.
Хотелось бы сделать замечания к этой задаче. Непонятно откуда взялась реакция опоры N (особенно если рассматривать систему отсчета (СО), связанную с автомобилем), если вдоль этого направления не действует больше других сил. Но все станет на свои места, если заметить, что автомобиль не является инерциальной системой отсчета, так как он движется с ускорением. В этой СО человек покоится, а влияние ускорения автомобиля компенсируется силой инерции
где знак “минус” показывает направление, которое противоположно направлению ускорения. Тогда понятно, что реакция N вызвана этой силой инерции Fин.
Ответ: 210 Н.
Пример 27:
Самолет делает «мертвую петлю» радиуса R=500м с постоянной скоростью v=360км/ч. Найти вес летчика массы m=70кг в нижней, верхней и средней точках петли.
Решение от преподавателя:
Решение:
При движении в петле сила реакции, оказываемая на летчика в разных точках нескомпенсирована весом летчика. (a) Когда самолет находится в самой нижней точке, второй закон движения Ньютона в проекционной форме
Fn=mwn
дает
(б) Когда он находится в самой верхней точке, опять из
Fn=mwn получаем
(в) Когда самолет находится в средней точке петли, опять от Fn=mwn
Нескомпенсированный вес mg. Таким образом, эффективный вес равен действует под углом.
Пример 28:
Цепочку длины l поместили на гладкую сферическую поверхность радиуса R так, что один ее конец закреплен на вершине сферы. С каким ускорением но начнет двигаться каждый элемент цепочки, если ее верхний конец освободить? Предполагается, что длина цепочки l<1/2πR.
Решение от преподавателя:
Решение:
Рассмотрим элемент длины ds под углом ϕ от вертикального диаметра. Поскольку скорость этого элемента равна нулю в начальный момент времени, его центростремительное ускорение равно нулю, и, следовательно,
где λ – линейная плотность массы цепи. Пусть T и T+dT напряжение на верхнем и нижнем концах ds, из Ft=mwt имеем,
Если просуммировать приведенное выше уравнение для всех элементов, то член
поскольку на свободных концах нет натяжения, поэтому
Следовательно,
Поскольку wn=a в начальный момент
Пример 29:
Шарик, подвешенный на нити, качается в вертикальной плоскости так, что его ускорения в крайнем и нижнем положениях равны по модулю друг другу. Найти угол отклонения нити в крайнем положении.
Решение от преподавателя:
Решение:
Мяч имеет только нормальное ускорение в самом низком положении и только касательное ускорение в любом крайнем положении. Пусть v – скорость шара в его самом низком положении и l – длина нити, тогда согласно задаче
Где α – максимальный угол отклонения закон Ньютона в проекционной форме:
Интегрированием обеих сторон в их пределах.
Примечание. Уравнение (2) легко получить, рассматривая механическую энергию шара в однородном поле тяжести. Из уравнений (1) и (2) с θ=α
Пример 30:
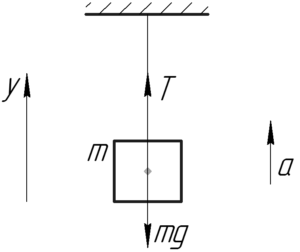
К нити подвешен груз массой 1 кг. Определить силу натяжения нити, если нить с грузом поднимать с ускорением 5 м/с2.
Решение от преподавателя:
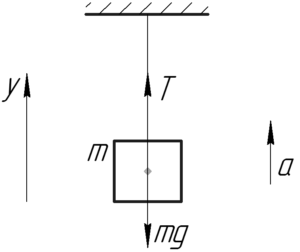
На рисунке покажем силы, действующие на груз: это сила тяжести mgmg, сила натяжения нити T. Ускорение груза a направлено вверх. Такой опыт можно повторить, привязав нить с грузом к штативу и двигая штатив вверх с ускорением. Из второго закона Ньютона (2ЗН) в проекции на ось y следует, что:
В итоге сила натяжения равна:
Видно, что сила натяжения в таком случае больше, чем если бы груз покоился, так как в состоянии покоя сила натяжения равна:
Ответ: 15 Н.
Пример 31:
Небольшое тело А начинает скользить с вершины гладкой сферы радиуса R. Найти угол θ (рис.), соответствующий точке отрыва тела от сферы, и скорость тела в момент отрыва.
Решение от преподавателя:
Решение:
Из Ft=mwt
Интегрируя обе стороны для получения v(θ)
В тот момент, когда тело теряет контакт с поверхностью, N=0N=0 и, следовательно, уравнение (2) становится
Где v и θ соответствуют моменту, когда тело теряет контакт с поверхностью. Решение уравнений (1) и (3), получим
Пример 32:
Частица массы m равномерно движется по окружности с заданной, скоростью v под действием силы F=a/rn, где a и n — постоянные, r — расстояние от центра окружности. При каких значениях nn движение по окружности будет устойчивым? Каков радиус такой окружности?
Решение от преподавателя:
Решение:
Это не задача центральной силы, путь частицы является кругом вокруг указанной точки. Здесь Ft (тангенциальная сила) обращается в нуль по условию задачи. Таким образом, уравнение движения становится,
Последнее уравнение можно рассматривать как равновесие при двух силах. Когда движение нарушается, мы записываем r=r0+x, и конечная сила, действующая на частицу,
Пример 33:
Велосипедист едет по круглой горизонтальной площадке, радиус которой R, а коэффициент трения зависит только от расстояния rr до центра О площадки по закону k=k0(1−r/R), где k0 — постоянная. Найти радиус окружности с центром в точке О, по которой велосипедист может ехать с максимальной скоростью. Какова эта скорость?
Решение от преподавателя:
Решение:
Согласно задаче, велосипедист движется по круговой траектории и центростремительный сила обеспечивается силой трения. Таким образом, из уравнения
Fn=mwn
Пример 34:
Поезд, подъезжая к станции со скоростью 72 км/ч, начинает тормозить. Каково наименьшее время торможения поезда до полной остановки, безопасное для спящих пассажиров (пассажиры не падают с полок)? Коэффициент трения о полки 0,2.
Решение от преподавателя:
Формула скорости для прямолинейного равнозамедленного движения поможет нам определить время торможения.
Конечная скорость поезда, очевидно, равна нулю, то есть
υ=0,
поэтому:
Рассмотрим силы, действующие на спящего пассажира. На него действует сила тяжести, сила реакции опоры и сила трения покоя (так как пассажиры не соскальзывают с полок). Запишем законы Ньютона в проекции на оси:
Согласно закону Кулона-Амантона сила трения покоя равна действующей на тело внешней силе и не может превышать по величине силу трения скольжения.
Возьмем случай равенства, когда сила трения покоя уже равна силе трения скольжения, но движение тела еще не началось.
Используя равенства (2) и (3), получим:
Подставим полученное выражение в формулу (1) и сосчитаем ответ:
Переведем начальную скорость поезда из км/ч в м/с, то есть в систему СИ.
Ответ: 10 с.
Пример 35:
Автомашина движется с постоянным тангенциальным ускорением wτ=0,62м/с2 по горизонтальной поверхности, описывая окружность радиуса R=40м. Коэффициент трения скольжения между колесами машины и поверхностью k=0,20. Какой путь пройдет машина без скольжения, если в начальный момент ее скорость равна нулю?
Решение от преподавателя:
Решение:
Так как начальная скорость равна нулю
При wt>0 скорость автомобиля увеличивается со временем или расстоянием. До момента начала скольжения трение покоя обеспечивает требуемое центростремительное ускорение автомобиля.
Пример 36:
Муфточка А может свободно скользить вдоль гладкого стержня, изогнутого в форме полукольца радиуса R (рис.). Систему привели во вращение с постоянной угловой скоростью ωω вокруг вертикальной оси OO′. Найти угол θ, соответствующий устойчивому положению муфточки.
Решение от преподавателя:
Решение:
На муфту действуют две силы, вес F1 и центробежная сила F2. Мы находим тангенциальную и нормальную составляющую обоих сил, тогда конечная тангенциальная направленная вниз сила, действующая на муфту:
Оно исчезает при θ=0 и при
Всегда положительна при малых значениях θ и следовательно, конечная тангенциальная сила в окрестностях θ=0выступает против любого смещения от положения равновесия. θ=0 – стабильное состояние.
отрицательно для малых θ вблизи θ=0 и θ=0 тогда неустойчиво. Однако θ=θ0 устойчив, потому что сила, как правило, заставляет муфту находиться вблизи положения равновесия θ=θ0.
Если ω2R=g, то обе позиции совпадают и становятся устойчивой точкой равновесия.
Пример 37:
Автомашина движется равномерно по горизонтальному пути, имеющему форму синусоиды y=asin(x/a), где a и α — некоторые постоянные. Коэффициент трения между колесами и дорогой равен k. При какой скорости движение автомашины будет происходить без скольжения?
Решение от преподавателя:
Решение:
Поскольку автомобиль следует по кривой, поэтому максимальная скорость, с которой он может двигаться без скольжения в точке минимального радиуса кривизны, является искомой скоростью, и, очевидно, в этом случае трение покоя между автомобилем и дорогой является предельным. Следовательно, из уравнения
Fn=mw
Мы знаем, что радиус кривизны кривой в любой точке (x, y) задается как,
Для данной кривой,
Подставляя это значение в (2), получим,
и, следовательно, соответствующий радиус кривизны
Пример 38:
Поезд, подъезжая к станции со скоростью 60 км/ч, тормозит. За какое минимальное время он может остановиться, чтобы лежащие на полках чемоданы при коэффициенте трения 0,2 не сдвинулись с места? Торможение происходит с постоянным ускорением.
Решение от преподавателя:
На чемоданы действует сила трения покоя, которая равна действующей внешней силе (в данном случае это сила инерции). Максимальное значение силы трения покоя определяется законом Кулона-Амантона:
На рисунке, изображенном справа, показаны все силы, действующие на чемодан. Спроецируем все силы на оси координат и запишем законы Ньютона:
Подставим (3) в (1), и полученное выражение в (2), тогда:
Время замедления легко найти по формуле определению ускорения (в ней уже учтено, что движение равнозамедленное):
Так как конечная скорость
υ=0
у поезда отсутствует, то:
В итоге конечная формула:
Переведем скорость поезда в систему СИ.
Численно время до остановки равно:
Ответ: 8,33 с.
Пример 39:
Цепочка массы mm, образующая окружность радиуса R, надета на гладкий круговой конус с углом полураствора θ. Найти натяжение цепочки, если она вращается с постоянной угловой скоростью со вокруг вертикальной оси, совпадающей с осью симметрии конуса.
Решение от преподавателя:
Решение:
Искомое растягивающее напряжение действует на каждый элемент цепи. Поэтому разделим цепочку на маленькие элементы, чтобы каждый элемент можно было считать частицей. Рассмотрим один такой элемент массы dm, который образует угол dαdα с центром. Цепь движется по окружности известного радиуса R с известной угловой скоростью ω и на нее действуют определенные силы. Мы должны найти одну из этих сил.
Из второго закона Ньютона в проекционной форме
Fx=mwx получаем
Пример 40:
Винтовку навели на вертикальную черту мишени, находящейся точно в северном направлении, и выстрелили. Пренебрегая сопротивлением воздуха, найти, на сколько сантиметров и в какую сторону пуля, попав в мишень, отклонится от черты. Выстрел произведен в горизонтальном направлении на широте ϕ=60∘, скорость пули v=900м/с и расстояние до мишени s=1,0км.
Решение от преподавателя:
Решение:
Определим оси, как показано на рисунке z направленым вдоль локальной вертикали, x на восток и y на север. (Мы предполагаем, что находимся в северном полушарии). Тогда сила Кориолиса
Поскольку vx мало, когда направление, в котором стреляет пушка, находится на севере. То, уравнение движения (пренебрегая центробежными силами) имеет вид
Интегрируя, получим
Наконец,
Так как v≫gt в данном случае, так что,
Пример 41:
Через закрепленный блок перекинута невесомая нить, к концам которой прикреплены грузы с массами m1 и m2. Между нитью и блоком имеется трение. Оно таково, что нить начинает скользить по блоку, когда отношение m2/m1=η0. Найти:
а) коэффициент трения;
б) ускорение грузов, если m2/m1=η>η0.
Решение от преподавателя:
Решение:
Рассмотрим малый элемент нити и и силы действующие на этот элемент, (а)
Применяя второй закон Ньютона в проекционной форме,
Fn=mwn для этого элемента,
Из уравнений (1) и (2),
(б) Когда m2/m1=η, которая больше, чем η0, блоки будут двигаться с одинаковым значением ускорения, w и, очевидно, m2 движется вниз. Из второго закона Ньютона в проекционной форме (вниз для m2 и вверх для m1) получаем:
Пример 42:
При каком ускорении разорвется трос, прочность которого на разрыв равна 15 кН, при подъеме груза массой 500 кг?
Решение от преподавателя:
Прочность троса на разрыв – это максимальная сила натяжения, которую трос может выдержать. Поэтому в этой задаче нарисуем схему, на котором изобразим все действующие на груз силы, чтобы определить силу натяжения. Из второго закона Ньютона в проекции на ось y следует, что:
Выразим из этой формулы ускорение a:
Когда трос начнет рваться, то его сила натяжения T станет равной прочности троса на разрыв Tmax.
Считаем ответ:
Ответ: 20 м/с2.
Пример 43:
Частица массы m движется по внутренней гладкой поверхности вертикального цилиндра радиуса R. Найти силу давления частицы на стенку цилиндра, если в начальный момент ее скорость равна v0 и составляет угол αα с горизонтом.
Решение от преподавателя:
Решение:
Сила, с которой стенка цилиндра воздействует на частицу, создает центростремительную силу, необходимую для движения частицы, и поскольку в горизонтальном направлении нет ускорения, горизонтальная составляющая скорости будет оставаться постоянной во время движения.
Пример 44:
Горизонтальный диск вращают с постоянной угловой скоростью ω=6,0рад/с вокруг вертикальной оси, проходящей через его центр. По одному из диаметров диска движется небольшое тело массы m=0,50кг с постоянной относительно диска скоростью v′=50см/с. Найти силу, с которой диск действует на это тело в момент, когда оно находится на расстоянии r=30см от оси вращения.
Решение от преподавателя:
Решение:
На диск действуют три силы, которые взаимно перпендикулярны. Это сила реакции, mg, направленная вертикально вверх, сила Кориолиса 2mv′ω, перпендикулярная плоскости вертикали и по диаметру, и mω2r наружу по диаметру. Результирующая сила,
Пример 45:
Найти модуль и направление вектора силы, действующей на частицу массы m при ее движении в плоскости xy по закону x=asinωt,y=bcosωt, где a,b,ω — постоянные.
Решение от преподавателя:
Решение:
Очевидно, радиус-вектор, описывающий положение частицы относительно начала координат,
Дифференцируя дважды по времени:
Таким образом,
Пример 46:
Груз массой 2 кг подвешен на динамометре. Снизу груз тянут с силой 10 Н. Что показывает динамометр?
Решение от преподавателя:
Динамометр покажет силу натяжения нити, на которой подвешен груз. Внутри него есть пружина и проградуированная шкала. Когда груз потянут, пружина динамометра растянется, в конце концов сила упругости пружины уравновесится с силой натяжения нити. По тому, куда указывает стрелка динамометра можно узнать силу натяжения нити. Запишем первый закон Ньютона (1ЗН) в проекции на ось y.
Сила натяжения нити равна:
Численно же динамометр покажет усилие:
Ответ: 30 Н.
Пример 47:
Тело массы m бросили под углом к горизонту с начальной скоростью v0. Пренебрегая сопротивлением воздуха, найти:
а) приращение импульса Δp тела за первые t секунд движения.
Решение от преподавателя:
Решение:
Пример 48:
Горизонтально расположенный гладкий стержень АВ вращают с постоянной угловой скоростью ω=2,00рад/с вокруг вертикальной оси, проходящей через его конец А. По стержню свободно скользит муфточка массы m=0,50кг, движущаяся из точки А с начальной скоростью v0=1,00м/с. Найти действующую на муфточку силу Кориолиса (в системе отсчета, связанной с вращающимся стержнем) в момент, когда муфточка оказалась на расстоянии r=50см от оси вращения.
Решение от преподавателя:
Решение:
Муфта свободно скользит вдоль стержня АВ. Таким образом, на него воздействует только центробежная сила. Уравнение,
Таким образом,
v0 – начальная скорость, когда r=0. Тогда сила Кориолиса,
Пример 49:
Частица массы mm в момент t=0 начинает двигаться под действием силы F=F0sinωt, где F0 и ω — постоянные. Найти путь, пройденный частицей, в зависимости от времени t. Изобразить примерный график этой зависимости.
Решение от преподавателя:
Решение:
Имеем F=F0sinωt
Интегрируем,
Пример 50:
Автомобиль массой 1,2 т движется с места с ускорением 0,8 м/с2. Какую силу тяги развивает двигатель, если коэффициент трения 0,02?
Решение от преподавателя:
Изобразим на схеме автомобиля все силы, действующие на него. Запишем законы Ньютона в проекции на введенные оси.
Сила трения скольжения Fтр определяется по формуле:
Так как сила нормальной реакции опоры согласно выражению (2) равна силе тяжести, то:
Подставим это выражение в (1), получим:
В итоге ответ к задаче в общем виде выглядит так:
Подставим данные задачи в формулу, не забывая перевести массу из тонн в килограммы (в 1 тонне – 1000 килограмм).
Ответ: 1200 Н.
Пример 51:
Небольшое тело пустили снизу вверх по наклонной плоскости, составляющей угол α=15∘ с горизонтом. Найти коэффициент трения, если время подъема тела оказалось в η=2,0 раза меньше времени спуска.
Решение от преподавателя:
Решение:
Случай 1.
Когда тело запустили вверх:
Пусть k – коэффициент трения, u – скорость проекции и l – пройденное вдоль наклонной плоскости.
Сила замедления тела = mgsinα+kmgcosα = mgsinα + kmgcosα
и, следовательно,
запаздывание =gsinα+kgcosα=gsinα+kgcosα.
Используя уравнение кинематики частиц вдоль наклонного участка,
Или
Случай (2).
Когда тело запускают вниз, сумма сил на теле =mgsinα−kmgcosα=mgsinα−kmgcosα и, следовательно, его ускорение =gsinα−kgcosα=gsinα−kgcosα.
Пусть t – требуемое время,
Из уравнений (3) и (4)
Пример 52:
Горизонтальный диск радиуса R вращают с постоянной угловой скоростью ω вокруг неподвижной вертикальной оси, проходящей через его край. По периферии диска равномерно относительно него движется частица массы m. В момент, когда она оказывается на максимальном расстоянии от оси вращения, результирующая сил инерции Fин, действующих на частицу в системе отсчета «диск», обращается в нуль. Найти:
а) ускорение ω′ частицы относительно диска; б) зависимость Fин от расстояния до оси вращения.
Решение от преподавателя:
Решение:
Диск OBAC вращается с угловой скоростью ω вокруг оси OO′, проходящей через O. Уравнение движения во вращающейся системе координат,
Где Fин– результирующая инерциальная сила (псевдосила), которая является векторной суммой центробежных сил и силы Кориолиса.
(a) В точке A, Fin обращается в нуль. Таким образом,
(б) В точке B
Его величина равна
Пример 53:
В установке (рис.) известны угол αα наклонной плоскости с горизонтом и коэффициент трения k между телом m1 и наклонной плоскостью. Массы блока и нити пренебрежимо малы, трения в блоке нет. Считая, что в начальный момент оба тела неподвижны, найти отношение масс m2/m1, при котором тело m2:
а) начнет опускаться;
б) начнет подниматься;
в) будет оставаться в покое.
Решение от преподавателя:
Решение:
В начальный момент, очевидно, натяжение нити, соединяющей m1 и m2 равно весу m2
(a) Для того, чтобы блок m2 опустился или блок m1 поднялся, условия составляют
и
(б) Аналогичным образом в случае
(в) Для этого случая ни один вид движения невозможен, и fr не должен быть неограничена. Следовательно,
Пример 54:
Под действием силы 30 Н тело поднимается вверх с ускорением 10 м/с2. Определить массу тела.
Решение от преподавателя:
Перед нами простая задача по динамике на применение второго закона Ньютона. На схеме изображены все силы, действующие на тело: сила тяжести mg и сила F. Ускорение тела направленно вверх. Из второго закона Ньютона следует:
Выразим из полученного равенства искомую массу тела m.
Мы получили решение задачи в общем виде. Теперь посчитаем численный ответ.
Ответ: 1,5 кг.
Пример 55:
На гладкой горизонтальной плоскости лежит доска массы m1 и на ней брусок массы m2. К бруску приложили горизонтальную силу, увеличивающуюся со временем t по закону F=at где a – постоянная. Найти зависимости от t ускорений доски w1 и бруска w2, если коэффициент трения между доской и бруском равен k. Изобразить примерные графики этих зависимостей.
Решение от преподавателя:
Решение:
Запишем второй закон Ньютона в проекциях вдоль положительной оси x для доски и бруска
В начальный момент, fr представляет собой трение покоя, а по мере увеличения силы F сила трения fr, возрастает предельного значения то есть
Если это значение не достигнуто, оба тела движутся как одно тело с равным ускорением. Но как только сила fr достигает предела, стержень начинает скользить по доске, т.е. w2≥w1.
Подставляя сюда значения w1 и w2, взятые из (1) и принимая во внимание, что fr=km2g, получаем
знак “=” соответствует моменту t=t0
На этом основании графики w1(t) и w2(t) показаны на рисунке.
Пример 56:
Локомотив массы начинает двигаться со станции так, что его скорость меняется по закону v=a√s, где aa — постоянная, s — пройденный путь. Найти суммарную работу всех сил, действующих на локомотив, за первые t секунд после начала движения.
Решение от преподавателя:
Решение:
Дифференцируя v(s) по времени
(Поскольку локомотив находится в однонаправленном движении) Следовательно, сила, действующая на локомотив
Пусть при v=0 при t=0 расстояние, пройденное за первые t секунд
Следовательно, искомая работа,
Пример 57:
Небольшое тело А начинает скользить с вершины клина, основание которого l=2,10м(рис.). Коэффициенты трения между телом и поверхностью клина k=0,140. При каком значении угла а время соскальзывания будет наименьшим? Чему оно равно?
Решение от преподавателя:
Решение:
Теперь из кинематического уравнения:
Пример 58:
Брусок массы m втаскивают за нить с постоянной скоростью вверх по наклонной плоскости, составляющей угол α с горизонтом (рис.). Коэффициент трения равен k. Найти угол β, который должна составлять нить с наклонной плоскостью, чтобы натяжение нити было наименьшим. Чему оно равно?
Решение от преподавателя:
Решение:
Выберем систему отсчета х – у относительно клина, взяв ось х вверх по наклонной плоскости и перпендикулярной к ней ось у (рис.).
Теперь нарисуем все силы действующие на тело.
Применим второй закон Ньютона в проекционном виде вдоль оси х и у для стержня:
Поодставлля значение β в уравнении (3) получаем:
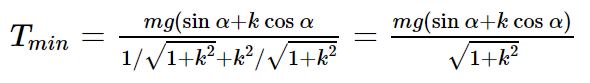
Пример 59:
На небольшое тело массы m, лежащее на гладкой горизонтальной плоскости, в момент t=0 начала действовать сила, зависящая от времени по закону F=at, где a — постоянная. Направление этой силы все время составляет угол α с горизонтом (рис.). Найти:
а) скорость тела в момент отрыва от плоскости;
б) путь, пройденный телом к этому моменту.
Решение от преподавателя:
Решение:
Прежде всего рассмотрим все силы действующие на тело массы mm и обозначим ось x вдоль горизонтальной плоскости и ось y, перпендикулярно к ней, как показано на рисунке.
Пусть тело отрывается от плоскости при t=t0, т.е. N=0.
Интегрируя, уравнение (2) для s(t)
Используя значение t=t0 из уравнения (1), в уравнениях (2) и (3)
Пример 60:
К бруску массы m, лежащему на гладкой горизонтальной плоскости, приложили постоянную по модулю силу F=mg/3. В процессе его прямолинейного движения угол αα между направолением этой силы и горизонтом меняют по закону α=as, где a — постоянная, s – пройденный бруском путь (из начального положения). Найти скорость бруска как функцию угла α.
Решение от преподавателя:
Решение:
Второй закон Ньютона в проекции на ось х, Fx=mwx, дает.
Интегрируя по пределам для v(s)
Это и является искомой зависимостью.
Пример 61:
На горизонтальной плоскости с коэффициентом трения k находятся два тела: брусок и электромотор с батарейкой на подставке. На ось электромотора намотана нить, свободный конец которой соединен с бруском. Расстояние между обоими телами равно l. После включения мотора брусок, масса которого в два раза больше массы другого тела, начал двигаться с постоянным ускорением w. Через сколько времени оба тела столкнутся?
Решение от преподавателя:
Решение:
Второй закон Ньютона в проекциях на плоскость:
Теперь, из уравнения кинематики в системе отсчета бруска или двигателя:
Из (1), (2) и (3) получаем время столкновения
Пример 62:
ерез блок, прикрепленный к потолку кабины лифта, перекинута нить, к концам которой привязаны грузы с массами m1 и m2. Кабина начинает подниматься с ускорением w0. Пренебрегая массами блока и нити, а также трением, найти:
а) ускорения груза m1 относительно шахты лифта и относительно кабины;
б) силу, с которой блок действует на потолок кабины.
Решение от преподавателя:
Решение:
Запишем второй закон Ньютона в векторной форме
для обоих блоков (в системе отсчета Земли).
Эти два уравнения содержат три неизвестных Величин w1,w2 и T. Третье уравнение указывает кинематическую связь между ускорениями:
Где w′ – это ускорение массы m1 относительно блока или кабины лифта. Суммируя по левую или правые части этих кинематических уравнений, получим
Совместное решение уравнений (1), (2) и (4) дает
Используя этот результат в уравнении. (3), получим,
Используя результаты в уравнении (3) получаем
(б) очевидно, сила, действующая на блок, сцепленный с потолком
Примечание: эту проблему можно решить и в системе отсчета лифта.
Пример 63:
Найти ускорение w тела 2 в системе (рис.), если его масса в ηη раз больше массы бруска 1 и угол между наклонной плоскостью и горизонтом равен α. Массы блоков и нитей, а также трение пренебрежимо малы. Исследовать возможные случаи.
Решение от преподавателя:
Решение:
Запишем второй закон Ньютона как для бруска 1, так и для тела 2 в проекции, взяв положительное направление x1 и x2, как показано на рисунке, и предположим, что тело 2 начинает скользить, вверх по наклонной плоскости
Для блока, движущегося в вертикальном направлении из уравнения
так как масса блока mp=0
Поскольку длина нитей постоянна, кинематическая связь ускорений равна
Одновременное решение всех этих уравнений дает:
Пример 64:
В системе рис. массы тел равны m0,m1,m2 трения нет, массы блоков и нитей пренебрежимо малы. Найти ускорение тела m1. Исследовать возможные случаи.
Решение от преподавателя:
Решение:
Запишем второй закон Ньютона для масс m1 и m2 и движущегося блока в вертикальном направлении вдоль положительной оси x (рис.):
Опять используя второй закон Ньютона в проекционной форме для массы m0 вдоль положительного направления x1 (Рис.), Получим
Кинематическая связь между ускорениями масс дает в терминах проекции на ось x
Одновременное решение полученных пяти уравнений дает:
В векторной форме
Пример 65:
В установке (рис.) известны массы стержня M и шарика m, причем M>m. Шарик имеет отверстие и может скользить по нити с некоторым трением. Масса блока и трение в его оси пренебрежимо малы. В начальный момент шарик находился напротив нижнего конца стержня. После того как систему предоставили самой себе, оба тела стали двигаться с постоянными ускорениями. Найти силу трения между шариком и нитью, если через t секунд после начала движения шарик оказался напротив верхнего конца стержня. Длина стержня равна l.
Решение от преподавателя:
Решение:
Поскольку нить не связана с m, поэтому, если бы не было трения между нитью и шаром m, натяжение нити было бы равно нулю, и в результате оба тела находятся в свободном падении.
Очевидно, что в данной задаче сила трения, создаваемая шаром на нити, является натяжением нити.
Из условия задачи wM>wm и так как оба ускорения направлены вниз, относительное ускорение
M=wM−wm
направлено вниз. Кинематическое уравнение для шара в системе отсчета стержня в проекционной форме вдоль направления вверх дает:
Второй закон Ньютона в проекции вертикально вниз стержня и шара дает,
Умножая уравнение (2) на mm и формулу. (3) на M и затем вычитая уравнение (3) из (2) и после использования уравнения (1) получим