Как найти силу зная потенциал

Между
потенциальной энергией системы
взаимодействующих тел и консервативной
силой, обусловливающей наличие этой
энергии, существует вполне определенная
связь. Установим эту связь.

1.
Если в каждой точке пространства на
тело действует консервативная сила, то
говорят, что оно находится в потенциальном
поле.

2.
При изменении положения тела в этом
поле потенциальная энергия тела
изменяется, при этом консервативная
сила совершает вполне определенную
работу. Выразим эту работу обычным
образом.

Будем
полагать, что тело переместилось в
произвольном направлении
на бесконечно малое расстояние(рис.25). Тогда

, (19.1)

где
– проекция вектора силы на направление.
Но(19.2)

Приравнивая
правые части выражений (19.1) и (19.2),
получим:,
откуда.
(19.3)

есть
производная потенциальной энергии по
направлению
;
эта величина показывает,насколько
быстро изменяется потенциальная энергия
вдоль этого направления.

Таким
образом, проекция
силы на
произвольное направление равна по
величине и противоположна по знаку
производной
от потенциальной энергии по этому
направлению.

Выясним
смысл знака «минус». Если в направлении
потенциальная энергия возрастает (>
0), то согласно (19.3)<
0. Это значит, что направление силыобразует с направлениемтупой угол,
следовательно, составляющая этой силы,
действующая вдоль
,
противоположна направлению.
И наоборот, если< 0, то проекция> 0, угол между силойи направлениемострый,
со-

ставляющая
этой силы, действующая вдоль
,
совпадает с направлением.

3.
В общем случае потенциальная энергия
может изменяться не только в направлении
,
но и в любом другом направлении. Можно
рассматривать, например, изменениявдоль осей,декартовой системы координат.

Тогда (19.4)

(значок
означает, что беретсячастная
производная).

Зная
проекции силы
легко найти вектор силы:

. (19.5)

Учитывая
(19.4) будем иметь:

. (19.6)

Вектор,
стоящий в правой части соотношения
(19.6), называется градиентом
величины
и обозначается.

Следовательно,

=
–. (19.7)

Консервативная
сила, действующая на тело, равна по
величине и противоположна по направлению
градиенту потенциальной энергии этого
тела. Градиент потенциальной энергии
– это вектор, указывающий направление
быстрейшего возрастания потенциальной
энергии и численно равный изменению
энергии, приходящемуся на единицу длины
этого направления.

При
перемещении тела в направлении
действия
консервативной силы
совершаетсямаксимальная
работа (так как
=1).
Но.
Следовательно, направление силыуказывает направление быстрейшегоуменьшения
потенциальной энергии.

20 Графическое представление потенциальной

ЭНЕРГИИ

1.
Потенциальная энергия является функцией
координат.
В некоторых простейших случаях она
зависит только от одной координаты
(например, в случае поднятого над Землей
тела
зависит только от высоты).
Зависимость потенциальной энергии
системы от той или иной координаты может
быть представленаграфически.

График,
изображающий зависимость потенциальной
энергии от соответствующей координаты,
называют потенциальной
кривой.

Проанализируем
одну из возможных потенциальных кривых
(рис.26). Кривая
(),
изображенная на рисунке, показывает,
как изменяется потенциальная энергия
системы частиц, если одна из частиц
перемещается вдоль оси,
а все остальные остаются на своих местах.
Каждая точка графика дает возможность
определитьсистемы, соответствующую координате
частицы.

2.
По наклону потенциальной кривой можно
судить о величине и направлении силы,
действующей на частицу вдоль
соответствующего направления.
Величина и знак проекции этой силы на
рассматриваемое направление определяется
величиной и знаком тангенса угла наклона
касательной к кривойв соответствующих точках; в нашем
случае,
(20.1)

так
как .

Таким
образом, чем
круче идет
потенциальная кривая, тем больше
сила,
действующая на частицу вдоль
соответствующего направления. На
восходящих участках потенциальной
кривой тангенсы углов наклона касательных
положительны, следовательно, проекция
силы отрицательна.
Это значит, что направление силы,
действующей вдоль
данной оси, противоположно
направлению этой оси, сила препятствует
удалению частицы из системы (рис.26, точка
).

В
точках же, соответствующих нисходящим
участкам потенциальной кривой, проекции
силы
положительны,
сила способствует дви-жению частицы
вдоль данного направления (точка
).
В точках, в которых=0,
сила на частицу не действует (точка).

3.
Если же при удалении одной из частиц (в
любом направлении) потенциальная энергия
системы резко возрастает
(потенциальная кривая «взмывает» вверх),
то говорят о существовании потенциального
барьера.
Говорят о высоте
барьера и
его ширине в соответствую-

щих
местах. Так, если частица находится в
точке с координатой(рис.26), то ее потенциальная энергия
равна,
высота потенциального барьера для нее,
ширина барьера.
Если потенциальный барьер встречается
на пути частицы при ее движении, как в
положительном, так и в отрицательном
направлении выбранной оси, то говорят,
что частица находится впотенциальной
яме. Форма
и глубина потенциальной ямы зависит от
природы сил взаимодействия и конфигурации
системы.

4.
Приведем некоторые примеры. На рис.27
изображена потенци-

альная
кривая тела, поднятого над Землей. Как
известно, потенциальная энергия такого
тела зависит только от одной координаты
– высоты
:
=P.

Проекция
силы тяжести на ось
равна.

Знак
«минус» означает, что направление силы
тяжести противоположно направлению
оси.
На рис.28 изображена потенциальная кривая
тела, скрепленного с пружиной и
совершающего колебания. Как видно из
рисунка, такое тело находится в
потенциальной яме с симметричными
стенками. Потенциальная энергия этого
тела и проекция силы, действующей на
него, равны соответственно:

,.

Кривая,
изображенная на рис.29, характерна для
взаимодействия атомов и молекул в
твердом теле. Особенностью этой кривой
является то, что она асимметрична; один
край ее крутой, другой – пологий.

Наконец,
кривая на рис.30 характеризует, в первом
приближении, потенциальную энергию
свободных электронов в металле. Стенки
этой ямы почти вертикальны. Это значит,
что сила, действующая на электроны на
границе металла, весьма велика.

Гладкое
горизонтальное дно ямы означает, что
на электроны внутри металла сила не
действует.

ПРИМЕРЫ
РЕШЕНИЯ ЗАДАЧ

Пример
1.
Определить
работу по сжатию пружины железнодорожного
вагона на 5 см,
если под
действием
силы
пружина сжимается на

Решение.
Пренебрегая
массой пружины, можно считать, что при
ее сжатии действует только переменная
сила давления, равная по величине упругой
силе, определяемой по закону Гука
.
Работу этой силы при сжатии пружины на
5см
надо определить. Считая на малом
перемещении
силу
постоянной, определим элементарную
работу как

.

Здесь
коэффициент жесткости пружины равен
.

Всю
работу найдем взяв интеграл от
в пределах отх₁
= 0 до

х₂
= 5
см.

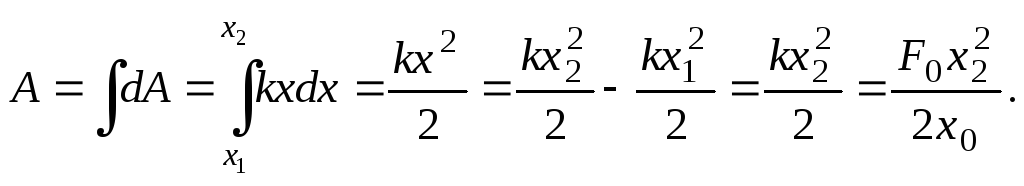
После вычислений
будем иметь

.

Пример
2. Самолет
массы m=3
т
для взлета должен иметь скорость
=360км/ч и
длину разбега S=600
м.
Какова должна быть минимальная мощность
мотора, необходимая для взлета самолета?
Коэффициент трения k
колес о землю равен 0,2. Движение при
разгоне самолета считать равноускоренным.

Решение.
В задаче
требуется определить мгновенную
мощность мотора в
момент взлета
самолета. Она и будет являться той
минимальной мощностью, при которой
самолет может еще набрать скорость,
необходимую для взлета.

.

Силу
тяги
определим из уравнения (второй закон
динамики)

Ускорение
найдем из уравнения равнопеременного
движения
;

С учетом сделанных
замечаний минимальная мощность равна

.

Пример
3. Скорость
реактивного самолета на некотором
участке меняется с расстоянием по закону
.
Найти работу за промежуток времени (,
если масса самолетаm.
В момент времени
скорость равна

Решение.
Примем, что
работа равна разности кинетических
энергий в моменты времени
и,
т.е..
Необходимо определить закон изменения
скорости со временем. Ускорение самолетаОткуда.
После интегрирования и потенцирования
последнего выражения получим, что
скорость в момент времениравна

Таким образом
работа, за заданный промежуток времени,
равна

Пример
4. Тело массой
m
под действием
постоянной силы ветра движется
прямолинейно, причем зависимость
пройденного пути от времени меняется
по закону
.
Найти работу силы ветра за промежуток
времени от 0 доt.

Решение.
Работа силы
ветра при малом перемещении тела равна

,
где перемещение найдем как производную
от пути по времени, т.е.
Сила по второму закону динамики равна

Полная
работа за промежуток времени от 0 до t
равна
интегралу от

Пример
5. Шар массой
движется со скоростьюнавстречу
шару массой,
движущемуся со скоростью
.
Найти величину и объяснить причину
изменения кинетической энергии системы
шаров после неупругого центрального
удара.

Решение.
Энергия
системы шаров до удара

После
неупругого удара шары будут двигаться
с одинаковой скоростью u,
которую найдем, применяя закон сохранения
импульса

.

Откуда

Энергия системы
шаров после удара

.

Убыль кинетической
энергии после удара

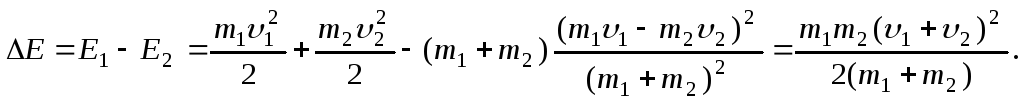
Изменение
кинетической энергии расходуется на
деформацию и в конечном счете на
нагревание шаров:

Пример
6. Автомобиль
массой
,
движущийся по горизонтальному участку
пути со скоростью,
развивает мощность, равную.
Какую мощность должен развивать
автомобиль при движении его в гору с
уклономс той же скоростью?

Определить
крутизну спуска (угол наклона), по
которому автомобиль будет идти со
скоростью 30 км/час,
при выключенном моторе.

Решение.
1) Мощность
автомобиля при движении в гору будет
определяться силой тяги и скоростью
движения

.

Сила
трения определяется как
,
где сила нормального давления на
наклонной плоскости.
Если считать коэффициент трения
одинаковым на всем пути движения, то на
горизонтальном участке он равен.
Сила трения может быть найдена из
соотношения (при равномерном горизонтальном
движении),
т.е.и.
Тогда сила трения на наклонной плоскости

Скатывающая
сила равна
.
С учетом сделанных замечаний мощность
автомобиля, движущегося в гору будет
равна

Подставим данные
задачи

2)
При движении
под гору при выключенном двигателе сила
тяги равна нулю. Действуют только
скатывающая сила
и сила тренияС учетом их направления

–,

откуда
.

Таким
образом, крутизна спуска равна
.

Пример
7. Тяжелый
шарик соскальзывает без трения по
наклонному желобу, образующему ”мертвую
петлю” радиуса R.
С какой высоты шарик должен начать
движение, чтобы не оторваться от желоба
в верхней точке траектории?

Решение.
Дана задача
о неравномерно переменном движении
материальной точки по окружности. Причем
в процессе движения изменяется положение
тела по высоте. Такие задачи решаются
с применением закона сохранения энергии
и составлением уравнения по второму
закону динамики для направления нормали.
Так как для замкнутой системы энергия
остается неизменной, то запишем это в
виде
.

Примем
за начальное положение шарика начало
движения, за конечное – положение в
верхней точке траектории. Уровень
отсчета высоты установим от поверхности
стола.

Энергия
шарика в первом положении
,
во втором положении.
Следовательно,
откуда

. (1)

Для
определения h
необходимо знать скорость шарика в
верхней точке. При этом учтем, что в
верхней точке петли на шарик в общем
случае действуют вниз две силы – сила
тяжести Р и
сила реакции со стороны опоры N.
Под действием этих сил шарик движется
по окружности, т.е.

При
спуске с достаточно большой высоты
шарик приобретает такую скорость, что
в каждой точке петли давит на желоб с
некоторой силой
.
По третьему закону Ньютона желоб
действует на шарик с такой же по величине
силойN
в противоположную сторону и отжимает
его на дугу окружности радиуса R.

По
мере уменьшения начальной высоты
скорость шарика уменьшается и при
некотором значении h
становится такой, что он пролетает
верхнюю точку петли, лишь касаясь желоба.
Для такого предельного случая N
= 0 и уравнение
второго закона динамики примет вид

или

откуда
(2)

Подставив
(2) в (1) и решая последнее уравнение
относительно h,
получим

ВОПРОСЫ
ДЛЯ САМОПРОВЕРКИ.

1.
Что называется энергией? Что называется
кинетической энергией? Что называется
потенциальной энергией?

2.
Что такое работа? Как вычисляется работа
постоянной и переменной силы?

3. Что такое
мощность?

4.
Какова связь между механической работой
и кинетической энергией?

5.
Докажите, что сила тяжести является
консервативной силой.

6.
Какова связь между работой консервативных
сил и потенциальной энергией?

7.Что
такое нулевой уровень потенциальной
энергии? Как он выбирается?

8.
Какова связь между потенциальной
энергией тела и консервативной силой,
действующей на него?

9. Что такое
потенциальная яма и потенциальный
барьер?

ИСПОЛЬЗУЕМАЯ
ЛИТЕРАТУРА

Савельев
И. В. Курс общей физики: в 3 т.; учебное
пособие для вузов. т.1: Механика.
Молекулярная физика. /И.В. Савельев.-4-е
изд. стер.-СПб.: Лань, 2005.

Зисман
Г. А. Курс общей физики. Т.1 /Г.А. Зисман,
О.М.Тодес.– М.:Наука,1972.

Детлаф
А. А. Курс физики: учебное пособие для
втузов. /А.А. Детлаф, Б.М. Яворский.-4-е
изд., испр.- М.: Высш.шк.,2002.- 718 с.

Трофимова
Т.И. Курс физики: учебное пособие для
вузов. /Т.И.Трофимова.- 7-е изд., стер.- М.:
Высш. шк., 2001.- 541 с.

Чертов
А.Г. Задачник по физике: учебное пособие
для втузов./А.Г.Чертов, А.А.Воробьев.- 8-е
изд., перераб. и доп.- М.: Физматлит, 2006.-
640 с.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

III. Основы электродинамики

Тестирование онлайн

Работа электростатического поля

Рассмотрим ситуацию: заряд q₀ попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q₀ со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.

Потенциал

Система “заряд – электростатическое поле” или “заряд – заряд” обладает потенциальной энергией, подобно тому, как система “гравитационное поле – тело” обладает потенциальной энергией.

Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал – это характеристика электростатического поля.

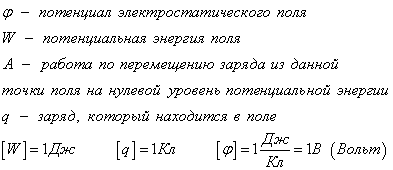
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.

Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.

В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело – наоборот.

Потенциальная энергия поля – это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.

Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.

Разность потенциалов

Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов

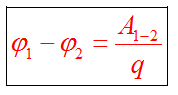
Эту формулу можно представить в ином виде

Эквипотенциальная поверхность (линия) – поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.

Напряжение

Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.

Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.

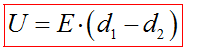
От величины напряжения зависит ток в цепи и энергия заряженной частицы.

Принцип суперпозиции

Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности

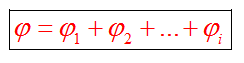
Как определить знак потенциала

Зависимость напряженности и потенциала от расстояния

Напряжение в природе

Энергия взаимодействия зарядов*

Потенциал. Разность потенциалов.

Разность потенциалов (напряжение) между 2-мя точками поля равняется отношению работы поля по перемещению заряда из начальной точки в конечную к этому заряду:

,

Так как работа по перемещению заряда в потенциальном поле не зависит от формы траектории, то, зная напряжение между двумя точками, мы определим работу, которая совершается полем по перемещению единичного заряда.

Если есть несколько точечных зарядов, значит, потенциал поля в некоторой точке пространс­тва определяется как алгебраическая сумма потенциалов электрических полей каждого заряда в данной точке:

.

Эквипотенциальной поверхностью, или поверхностью равного потенциала, является поверхность, для любых точек которой разность потенциалов равна нулю. Это означяет, что работа по перемещению заряда по такой поверхности равна нулю, следовательно, линии напряженности электрического поля перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности однородного поля представляют собой плоскости, а точечного заряда — концентрические сферы.

Вектор напряженности (как и сила ) перпендикулярен эквипотенциальным поверхнос­тям. Эквипотенциальной является поверхность любого проводника в электростатическом поле, так как силовые линии перпендикулярны поверхности проводника. Внутри проводника разность потенциалов между любыми его точками равна нулю.

Напряжение и напряженность однородного поля .

В однородном электрическом поле напряженность E в каждой точке одинакова, и работа A по перемещению заряда q параллельно на расстояние d между двумя точками с потенциалами φ₁, и φ₂ равна:

,

.

Т.о., напряженность поля пропорциональна разности потенциалов и направлена в сторону уменьшения потенциала. Поэтому положительный заряд будет двигаться в сторону уменьшения потенциала, а отрицательный — в сторону его увеличения.

Единицей напряжения (разности потенциалов) является вольт. Исходя из формулы , , разность потенциалов между двумя точками равна одному вольту, если при перемещении заряда в 1 Кл между этими точками поле совершает работу в 1 Дж.

Электрический потенциал простыми словами: формулы, единица измерения

Электрический потенциал – это скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.

Если вы хотите расширить свои знания об электрическом потенциале или сначала узнать, что такое электрический потенциал, то вы пришли по адресу.

Простое объяснение

В классической механике рассмотрение проблемы с точки зрения энергии может значительно упростить ситуацию по сравнению с рассмотрением ее с точки зрения сил, действующих на систему. В частности, в этом контексте существенную роль играет тот факт, что энергия является сохраняющейся переменной.

Также в классической электродинамике рассмотрение на энергетическом уровне оказывается очень полезным. Поэтому электрический потенциал φ (также называемый электростатическим потенциалом) определяется как отношение потенциальной энергии E_пот пробного электрического заряда и его величины электрического заряда q: φ = E_пот / q .

Возможность определения такого электрического потенциала обусловлена тем, что электрическое поле E распределения заряда и результирующая электростатическая сила F_c на пробном электрическом заряде является консервативной силой, подобной гравитационной силе.

Электрический потенциал имеет единицу измерения вольт В или также джоуль на кулон Дж / Кл .

Формулы

В этом разделе мы познакомим вас с двумя важными формулами для электрического потенциала определенных распределений электрических зарядов. Мы также кратко обсудим аналогию между электрическим потенциалом и гравитацией.

Пластинчатый конденсатор

Мы рассматриваем ситуацию, когда две плоские пластины расположены параллельно на расстоянии d друг от друга. Кроме того, пусть одна из двух пластин заряжена положительно, а другая – отрицательно. Такая комбинация также называется пластинчатым конденсатором. Обозначим точку на положительной пластине через A, а точку на отрицательной пластине через B. Тогда для разности потенциалов между этими двумя точками получим:

Здесь E – величина электрического поля между двумя пластинами, которое предполагается однородным. Такая разность потенциалов также называется электрическим напряжением, которое существует между этими двумя точками.

Из этого уравнения видно, что электрический потенциал на положительно заряженной пластине (пластина A) выше, чем потенциал на отрицательно заряженной пластине (пластина B). Поэтому положительный заряд в пластинчатом конденсаторе перемещается к отрицательной пластине. В общем случае электрическое поле – а значит, и направление движения положительного заряда – направлено в ту сторону, в которой электрический потенциал убывает быстрее всего.

Рис. 1. Пластинчатый конденсатор

Аналогия с гравитационным полем

Если умножить уравнение (приведенное выше в статье) на величину электрического заряда q пробного электрического заряда и предположить, что отрицательно заряженная пластина имеет электрический потенциал, равный нулю, то электрическая потенциальная энергия на расстоянии h от пластины равна:

E_{пот. эл} = q * φ = q * E * h

Здесь φ обозначает электрический потенциал в точке пробного электрического заряда.

Сравним это уравнение с потенциальной энергией в однородном гравитационном поле:

E_{пот. гр} = m * g * h .

Мы определяем, что количество заряда электрического q играет роль массы m, а величина электрического поля E играет роль гравитационного ускорения g. Масса, находящаяся на высоте h над землей, ускоряется по направлению к земле под действием земного притяжения.

Таким образом, масса движется в том направлении, в котором уменьшается ее потенциальная энергия. Аналогично, положительный электрический заряд движется в направлении, в котором его электрическая потенциальная энергия будет уменьшаться. Поскольку электрическая потенциальная энергия и электрический потенциал линейно связаны, это наблюдение аналогично тому, что положительно заряженная частица движется в направлении уменьшения электрического потенциала.

Рис. 2. Аналогия с гравитационным полем

Подобно потенциальной энергии, только разность потенциалов имеет физический смысл, поскольку при определении электрического потенциала необходимо произвольно определить точку отсчета, от которой затем можно обозначить другие точки в пространстве. В этом смысле электрический потенциал сам по себе не имеет реального физического смысла, поскольку для данной точки в пространстве его значение можно изменить, выбрав другую точку отсчета. Таким образом, электрический потенциал ведет себя подобно высоте, потому что вы не можете говорить о высоте, пока у вас нет точки отсчета.

На топографической карте – пути, вдоль которых высота не меняется, называются изолиниями. Аналогично, пути, вдоль которых электрический потенциал постоянен, называются эквипотенциальными линиями.

Заряженные частицы

Предположим, что частица с зарядом q находится в начале выбранной нами системы координат. Пусть положение другой точки равно r и пусть r – расстояние между двумя точками. Для электрического потенциала в точке r действует следующее соотношение:

φ (r) = q / 4 * π * ε₀ * r ,

здесь ε₀ – электрическая постоянная.

В этом уравнении предполагается, что под действием электрического поля положительный пробный электрический заряд переносится из бесконечности в положение r.

Примеры задач

Наконец, давайте вместе рассчитаем небольшой пример. Предположим, что электрон ускоряется от отрицательно заряженной пластины к положительно заряженной через разность потенциалов 2000 В. Как изменяется потенциальная энергия электрона?

Для разности электрических потенциалов между двумя пластинами: φ_B – φ_A = ΔE_пот / q , преобразованной в искомое изменение потенциальной энергии, получаем:

Величина электрического заряда электрона равна q_e = e = – 1,6 * 10 -19 Кл и поэтому получаем:

ΔE_пот = e * ( φ_B – φ_A ) = – 1,6 * 10 -19 Кл * 2000 В = -3,2 * 10 -19 Дж.

Обратите внимание, что [ В ] = Дж / Кл. Кроме того, мы предположили, что пластина с точкой B заряжена положительно, поэтому перед 2000 В нет знака минус. Расчет показывает, что потенциальная энергия электрона уменьшается.

Найти потенциал электрического поля в точке, лежащей посредине между двумя

Найти потенциал электрического поля в точке, лежащей посредине между двумя зарядами по 50 нКл, расположенными на расстоянии 1 м в вакууме.

Задача №6.3.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Решение задачи:

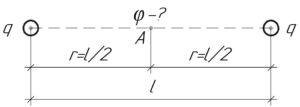
Так как заряды одинаковы, и они находятся на одинаковом расстоянии (r) от точки A, в которой нужно определить потенциал, значит потенциалы электрических полей в точке A, создаваемых каждым зарядом, также одинаковы. Это видно из формулы:

Здесь (k) – коэффициент пропорциональности, равный 9·10 9 Н·м 2 /Кл 2 .

Учитывая, что точка A находится посредине между двумя зарядами ((r=frac)), то:

Искомый потенциал (varphi) равен сумме потенциалов электрических полей в точке A, создаваемых каждым зарядом, поскольку потенциал – величина скалярная. Учитывая вышесказанное, имеем:

В итоге решение задачи в общем виде выглядит так:

Ответ: 1,8 кВ.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.