Как найти силу зная разность потенциалов

Закон Ома

Чтобы посчитать Закон Ома воспользуйтесь нашим очень удобным онлайн калькулятором:

Закон Ома для участка цепи

Закон Ома для участка цепи гласит, что сила тока (I) на участке электрической цепи прямо пропорциональна напряжению (U) на концах участка цепи и обратно пропорциональна его сопротивлению (R).

Онлайн калькулятор

Найти силу тока

Найти напряжение

Найти сопротивление

Закон Ома для полной цепи

Закон Ома для полной цепи гласит, что сила тока в цепи пропорциональна действующей в цепи электродвижущей силе (ЭДС) и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.

Онлайн калькулятор

Найти силу тока

Найти ЭДС

Найти внутреннее сопротивление источника напряжения

Найти сопротивление всех внешних элементов цепи

См. также

Закон Ома назван в честь своего открывателя это ученый Георг Симон Ом. Свои эксперименты в области электричества он начал вдохновляясь опытами Фурье. Ом проводил свои опыты с различными материалами и изучение их электропроводности. Так была разработана знаменитая формула, которая стала краеугольной в современной физике, которая вошла в школьные учебники: I=U/R. Сила тока пропорциональна величине напряжения и имеет обратную пропорциональность сопротивлению.

В статье подробно разобраны области теории и практического применения принципов закона Ома в современной электротехнике. В качестве дополнения, в материале содержатся два обучающих видеоролика и один научный материал на тему статьи.

Закон Ома

Закон Ома показывает отношения между напряжением (U), током (I) и сопротивлением (R). Записано это может быть тремя разными способами:

U = I × R

или

I = V/R

или

R = V/I

Где:

• V – напряжение в вольтах (В);
• I – сила тока в амперах (А);
• R – сопротивление в омах (Ом);

Для большинства схем амперы – слишком большие величины, а омы – слишком маленькие. Поэтому в формулу можно подставлять миллиамперы и килоомы. Если силу тока подставлять в миллиамперах (мА), то сопротивление обязательно должно быть в килоомах (кОм) и наоборот. Напряжение – всегда в вольтах.

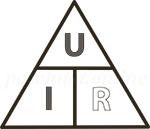
Чтобы проще запомнить три разные версии определения Закона Ома, можно воспользоваться «VIR-треугольником».

• Если надо вычислить напряжение, закрываем пальцем V. У нас остаются I и R. Они на одном уровне, значит между ними ставим знак умножения. Получается: V = I × R .
• Если вычисляем ток, закрываем пальцем I. У нас остаётся V над R. Значит напряжение делится на сопротивление:  I = V/R .
• Аналогичным образом поступаем при вычислении сопротивления. Закрываем R. Остаётся V над I. Значит: R = V/I .

Закон Ома, определение: Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Есть также частный случай – Закон Ома для участка цепи – сила тока в участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка.

Закон Ома для цепи

Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).

Итак, закон Ома для рассматриваемого участка цепи имеет вид:

φ1-φ2=I*R, где

• I – ток, протекающий по участку цепи.
• R – сопротивление этого участка.
• φ1-φ2 – разность потенциалов между точками 1-2.

Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).

В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:

• U1=I*R1
• U2=I*R2
• Un=I*Rn
• U=I*(R1+R2+…+Rn

Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:

U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn

Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.

Для ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:

Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.

Для полной цепи

Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.

Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.

Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:

I = U / (R + r)

Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.

Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.

Для переменного тока

Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).

Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.

Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.

Для замкнутой цепи

На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.

Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.

Формула для расчета падения напряжения на индуктивном сопротивлении:

U = I ⋅ ωL

Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).

Формула для расчета падения напряжения на емкостном сопротивлении:

U = I / ω ⋅ С

С – емкость реактивного сопротивления.

Эти две формулы – частные случаи закона Ома для переменных цепей.

Полный же будет выглядеть следующем образом:

I = U / Z

Здесь Z – полное сопротивление переменной цепи известное как импеданс.

Сфера применения

Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:

• Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
• В сверхпроводниках;
• Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
• В вакуумных и газовых радиолампах;
• В диодах и транзисторах.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

• I = I1= I2 ;
• U = U1+ U2 ;
• R = R1+ R2

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

• I = I1+ I2 … ;
• U = U1= U2 … ;
• 1 / R = 1 / R1+ 1 / R2 + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.

Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

Друзья, не забывайте подписываться на обновления блога, ведь чем больше читателей подписано на обновления, тем больше я понимаю что  делаю что-то важное и полезное и это чертовски мотивирует на новые статьи и материалы.

При выборе какого-либо электрического оборудования одним из важных параметров, на который обращается внимание, является мощность изделия. Этот параметр неразрывно связан с силой тока и напряжением. Чтобы рассчитать силу тока, напряжение или мощность в электрической цепи, используются несложные формулы. Но чтобы осмысленно проводить такие вычисления, желательно понимать физическую природу возникновения этих величин.

Физическое понятие величин

Любая электрическая цепь характеризуется рядом параметров. Наиболее важными из них являются сила тока, напряжение, мощность и сопротивление. Эти характеристики связаны между собой и зависят друг от друга. Явление, объединяющее их, называется электричеством.

Это понятие было введено ещё в 1600 году английским физиком Уильямом Гилбертом, изучающим магнитные и электрические явления. Исследуя магнетизм в природе, учёный установил, что некоторые тела при трении начинают обладать силой притяжения по отношению к другим предметам, в частности, к янтарю. Поэтому он и назвал открытое явление ēlectricus, что в переводе с латинского обозначает «янтарный».

Продолжая его исследования, немецкий физик Отто фон Герике в 1663 году изобрёл электрическую машину, которая представляла собой металлический стержень с одетым на него серным шаром. В результате он выяснил, что материалы могут не только притягивать вещества, но и отталкивать. Но только через восемьдесят лет американец Бенджамин Франклин создал теорию электричества, введя такие термины, как отрицательный и положительный заряд.

Дальнейшее развитие электричество получило после опытов Шарля Кулона и открытия им закона взаимодействия зарядов. Заключался он в следующем: сила влияния двух точечных зарядов друг на друга в вакууме прямо пропорциональна их произведению и обратно пропорциональна расстоянию между ними в квадрате. После этого благодаря экспериментам таких учёных, как Джоуль, Ленц, Ом, Ампер, Фарадей, Максвелл были введены понятия ток, напряжение и электромагнетизм.

Так, в 1897 году англичанин Джозеф Томсон установил, что носителями зарядов являются электроны. Ранее, в 1880 году, электротехник из России Дмитрий Лачинов сформулировал необходимые условия для передачи электричества на расстояния.

После этих открытий были выработаны фундаментальные определения электричества. Сегодня под ним понимаются свойства материалов образовывать вокруг себя электрическое поле, оказывающее воздействие на располагающиеся рядом другие заряженные частицы. Заряды условно принято разделять на положительные и отрицательные. При их перемещении возникает магнитное поле, при этом одинакового знака заряды притягиваются, а разного — отталкиваются.

Сила тока

Ток — это упорядоченное движение носителей заряда, происходящее под влиянием электрического поля. В качестве положительно заряженных частиц выступают электроны, а отрицательных — дырки. Математически это явление описывается с помощью формулы I = Q*T, где I — ток проводимости (А), Q — заряд частицы (Кл), T — время ©.

То есть электрическим током называется количество зарядов, прошедших через поперечное сечение вещества. Но эта формулировка верна только для тока постоянной величины, в то время как для изменяемого во времени она будет выглядеть I (T) = dQ/dT.

Плотность движения носителей заряда в материале, то есть количество электричества, проходящего за условно принятое время, называется силой тока. Согласно Международной системе (СИ) его единицей измерения является ампер. Один ампер равен перемещению электрического заряда, равного одному кулону, через поперечное сечение за одну секунду.

Носители заряда могут двигаться как упорядоченно, так и хаотично. При их движении возникает электрическое поле, обозначаемое латинской буквой E. Значение, определяющееся отношением тока к поперечному сечению проводника, называется плотностью тока. За единицу её измерения принимается А/мм².

По своему виду ток различают на следующие типы:

1. Переноса. Характеризуется движением зарядов, осуществляемым в свободном пространстве. Этот тип характерен для газоразрядных приборов.
2. Смещения. Возникает в диэлектриках и определяется упорядоченным перемещением связанных заряженных частиц.
3. Полный. Определяется суммарным значением тока: проводимости, переноса и смещения.
4. Постоянный. Это такой вид, который может изменять величину, но не изменяет направление движения, то есть свой знак.
5. Переменный. Такого вида ток может изменяться как по величине, так и по направлению (знаку).

Переменный вид разделяется по форме и может быть синусоидальным и несинусоидальным. Для расчёта силы тока синусоидальной формы используется формула Is = Ia*sin ωt, где Ia — максимальное значение тока (A), ω — угловая скорость, равная 2πf (Гц).

Физические тела, в которых возможно протекание тока, называют проводниками, а в тех, где возникают препятствия его прохождению — диэлектриками. Промежуточное состояние между ними занимают полупроводники.

Разность потенциалов

Напряжением принято называть физическую величину, характеризующую электрическое поле. Она показывает, какую работу понадобится совершить полю для того, чтобы переместить единичный заряд из одной точки в другую. При этом принимается, что этот перенос не влияет на распределение зарядов в источнике поля. Согласно Международной системе единиц напряжение измеряется в вольтах.

Работа по переносу складывается из двух величин — электрических и сторонних. Если сторонние силы не действуют, то напряжение на участке цепи равно разности потенциалов и вычисляется по формуле U = φ1-φ2. При этом потенциал определяется отношением напряжённости электрического поля к заряду. Для его расчёта используют формулу φ = W/q.

Другими словами, это характеристика поля в определённой точке, не зависящей от величины заряда, находящегося в нём. То есть напряжение в общем случае определяется работой электростатического поля, возникающего при движении заряда вдоль его силовых линий. Математически его можно рассчитать по формуле U = A/q, где А — совершаемая работа по перемещению (Дж), q — энергия заряда (Кл).

Применительно к сети переменного тока для напряжения используются следующие понятия:

1. Мгновенное. Это значение физической величины, измеренное в конкретный момент времени: U = U (t). Для синусоидального сигнала мгновенное напряжение находится с помощью выражения U (t) = Ua sin (ὤt + φ).
2. Амплитудное. Характеризуется наибольшей величиной мгновенного значения без учёта знака: Ua = max (U (t)).
3. Среднее. Определяется за полный период сигнала по формуле Us = 1/T ʃ U (t)*dt. Для синусоидальной формы это значение равно нулю.

Проводя расчёт напряжения, редко используется понятие электрического потенциала. Связано это с тем, что условно принято за одну из точек потенциала принимать землю.

Это значение берётся равным нулю, а все остальные потенциалы считаются относительно неё. Говоря, что напряжение в определённой точке составляет 300 вольт, имеется в виду разность потенциалов между этой точкой и землёй, равная этому значению.

Электрическая мощность

Электрическая мощность характеризует скорость передачи электрической энергии или её преобразование. Единицей её измерения является ватт. Для того чтобы посчитать мощность на определённом участке цепи, необходимо перемножить значение напряжения и силы тока на этом участке. Исходя из определения электрического напряжения, можно сказать, что заряд при движении совершает работу, численно равную ей на участке цепи. Если же умножить работу на количество зарядов, то можно найти общее значение работы, которую совершили заряды на этом участке.

Исходя из физического определения, что мощность — это работа за единицу времени, получается выражение P = A/Δt, где A — работа, совершаемая зарядом при перемещении от начальной точки к конечной (Дж), Δt — время, затраченное на полное перемещение заряда ©.

Для всех зарядов в цепи мощность можно найти благодаря формуле P = (U/ Δt) * Q, где Q — общее число зарядов.

Так как ток представляет собой заряд, протекающий в единицу времени (I = Q/ Δt), то получается, что мощность равна произведению тока на напряжение, то есть P = U*I (Вт).

В цепи с постоянным током его сила и напряжение всегда имеют постоянное значение в определённой точке, поэтому для любого момента времени мощность можно вычислить по формуле P = I*U = I2*R = U2/R, где R — сопротивление прохождению тока в электрической цепи (Ом). Если же в этой сети находится источник электродвижущей силы, то мощность находится как P = I*E+ I2*r, где Е — электродвижущая сила или ЭДС (В), r — внутреннее сопротивление источника ЭДС (Ом).

Для цепи, в которой её параметры изменяются по какому-то циклу, мощность в определённой точке интегрируется по времени. При этом существуют следующие виды мощности:

1. Активная. Для её нахождения используется расчёт, учитывающий угол сдвига фаз φ. Находится согласно формуле P = U*I*cos φ.
2. Реактивная. Характеризуется нагрузками, создаваемыми электрическими устройствами в виде колебаний энергии электромагнитного поля. Её вычисление осуществляется по формуле P = U*I*sin φ.
3. Полная. Определяется произведением действующих значений тока и напряжения, связана с другими видами мощности выражением S= √(P ² +Q ²).

Закон Ома для цепи

Проводя расчёты мощности по напряжению и току на практике, часто используют закон Ома. Он устанавливает связь между током, сопротивлением и напряжением. Этот закон был открыт путём проведения Симоном Омом ряда экспериментов и сформулирован им в 1826 году. Он выяснил, что величина тока на участке цепи прямо пропорциональна разности потенциалов и обратно пропорциональна сопротивлению этого участка.

Закон Ома можно записать в следующем виде: I = U/R, где I — значение силы тока (А), U — разность потенциалов (В), R — сопротивление цепи прохождению тока (Ом).

Для полной же цепи эту формулу можно записать так: I = E/(R+ r0), где E — ЭДС источника питания (В), r0 — внутреннее сопротивление источника напряжения (Ом).

Таким образом, для участка цепи будет справедливо выражение P = U2/R = I2R, а для полной цепи — P = (E/(R+ R0))²*R. Именно эти две формулы и используются чаще всего для расчётов электрических сетей или мощности необходимого оборудования.

Различные компоненты электрической сети в определённый момент времени потребляют разную величину тока. Поэтому очень важно правильно рассчитать, какое количество энергии подводится в тот или иной момент в определённое место цепи, чтобы не допустить перегрузок на линии и возникновения аварийных ситуаций.

Этим и занимаются разработчики схем, упрощая их до состояния, когда можно рассчитать необходимую мощность, используя закон Ома.

Практический расчёт

Например, пусть понадобится узнать, на какой ток необходимо приобрести устанавливаемый на участок цепи автоматический выключатель. При этом известно, что в линию, на которой он будет установлен, одновременно будут включаться холодильник с максимальной мощностью потребления энергии один киловатт, бойлер (два киловатта) и люстра, потребляющая 90 ватт. В месте установки используется однофазная сеть, рассчитанная на рабочее напряжение 220 вольт.

На первом этапе расчёта понадобится суммировать всю мощность подключаемых к линии электроприборов. Так, P общ. = 1000 + 2000 + 90 +220 = 3310 Вт. Используя формулу P = I*U, находится необходимое значение тока: I = P/U = 3310/220 = 15,04 А.

Из стандартного ряда выключателей наиболее близкое значение имеет автомат на 16 А. Поскольку необходимо покупать устройство защиты с небольшим запасом, то для рассматриваемого примера подойдёт выключатель, рассчитанный на 20 ампер.

Благодаря таким вычислениям можно рассчитать любой параметр электрической цепи, но это при учёте достаточного количества вводных данных.

ЭДС. Закон Ома для полной цепи

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд :

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная против движения заряда (т.е. против направления тока).

к оглавлению ▴

Сторонняя сила

Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :

(1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

к оглавлению ▴

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь

Наша задача — найти силу тока в цепи и напряжение на резисторе .

За время по цепи проходит заряд . Согласно формуле (1) источник тока совершает при этом работу:

(2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:

(3)

Итак, , и мы приравниваем правые части формул (2) и (3):

После сокращения на получаем:

Вот мы и нашли ток в цепи:

(4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:

(5)

Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина неотличима от , и формула (5) снова даёт нам .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

к оглавлению ▴

КПД электрической цепи

Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим .

Если сила тока в цепи равна , то

Некоторое количество теплоты выделяется также на источнике тока:

Полное количество теплоты, которое выделяется в цепи, равно:

КПД электрической цепи — это отношение полезного тепла к полному:

КПД цепи равен единице лишь в том случае, если источник тока идеальный .

к оглавлению ▴

Закон Ома для неоднородного участка

Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3  показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно , можно просто заменить резистор на резистор ).

Рис. 3. ЭДС «помогает» току:

Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: . За время через участок проходит заряд , при этом стационарное электрическое поле совершает работу:

Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):

Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло: .

Подставляем сюда выражения для , и закон Джоуля–Ленца:

Сокращая на , получаем закон Ома для неоднородного участка цепи:

(6)

или, что то же самое:

(7)

Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то . Тогда из формулы (6) получаем — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на :

Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

Тогда закон Ома для неоднородного участка примет вид:

(8)

или:

где по-прежнему — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Повторим основные понятия и определения по теме «Закон Ома».

Напомним, что напряжение измеряется в вольтах.

Сила тока измеряется в амперах.

Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.

Основные определения, которые мы используем в решении задач:

Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.

Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.

Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.

Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.

По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).

Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.

Сопротивление измеряют в омах (Ом).

Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника  r (Ом).

Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:

1. Сопротивление проводника тем больше, чем больше его длина.
2. Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.

Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением:  (Ом*мм²/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:

Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.

Задача 1. На ри­сун­ке приведён гра­фик за­ви­си­мо­сти на­пря­же­ния на кон­цах же­лез­но­го про­во­да пло­ща­дью по­пе­реч­но­го се­че­ния 0,05 мм² от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм²/м.

Решение:

Из закона Ома для проводника или участка цепи без источника следует:

По графику: при 

Из формулы сопротивления выражаем и находим длину проводника:

Ответ: 10.

Задача 2. Через по­пе­реч­ное се­че­ние про­вод­ни­ков за 8 с про­шло 10²⁰ элек­тро­нов. Ка­ко­ва сила тока в про­вод­ни­ке? Ответ дайте в амперах.

Решение:

По определению силы тока:

Заряд всех электронов:  где е — модуль заряда электрона,  Кл.

Тогда 

Ответ: 2.

Задача 3. Иде­аль­ный ам­пер­метр и три ре­зи­сто­ра общим со­про­тив­ле­ни­ем 66 Ом вклю­че­ны по­сле­до­ва­тель­но в элек­три­че­скую цепь, со­дер­жа­щую ис­точ­ник с ЭДС рав­ной 5 В, и внут­рен­ним со­про­тив­ле­ни­ем r=4 Ом. Ка­ко­вы по­ка­за­ния ам­пер­мет­ра? (Ответ дайте в ам­пе­рах, округ­лив до сотых.)

Решение:

По закону Ома для полной цепи:

Тогда

Ответ: 0,07.

Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.

Решение:

Сила тока короткого замыкания определяется следующим образом:

Отсюда выражаем и находим внутреннее сопротивление источника:

При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:

Отсюда выражаем сопротивление резистора и находим его:

Ответ: 1,9.

Задача 5. На ри­сун­ке изоб­ра­же­на схема элек­три­че­ской цепи, со­сто­я­щей из ис­точ­ни­ка по­сто­ян­но­го на­пря­же­ния с ЭДС 5 В и пре­не­бре­жи­мо малым внут­рен­ним со­про­тив­ле­ни­ем, ключа, ре­зи­сто­ра с со­про­тив­ле­ни­ем 2 Ом и со­еди­ни­тель­ных про­во­дов. Ключ за­мы­ка­ют. Какой заряд про­те­чет через ре­зи­стор за 10 минут? Ответ дайте в ку­ло­нах.

Решение:

Выражаем время в секундах: t = 10 минут = 600 с.

Определяем силу тока по закону Ома для полной цепи:

Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.

По определению силы тока:

Отсюда  Кл.

Ответ: 1500.

Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн