У этого термина существуют и другие значения, см. Звук (значения).
Звук — физическое явление, представляющее собой распространение упругих волн в газообразной, жидкой или твёрдой среде. В узком смысле под звуком имеют в виду эти волны, рассматриваемые в связи с тем, как они воспринимаются органами чувств.[1]
Источником звука может выступать тело, совершающее механические колебания по определённому закону.
В общем случае звук является совокупностью волн различных частот. Распределения интенсивности по частотам 

Обычный человек способен слышать звуковые колебания в диапазоне частот от 16—20 Гц до 15—20 кГц[2]. Звук ниже диапазона слышимости человека называют инфразвуком; выше: до 1 ГГц, — ультразвуком, от 1 ГГц — гиперзвуком.
В первом приближении громкость звука диктуется амплитудой волны, а тон, высота звука — частотой. Более точно, громкость сложным образом зависит от эффективного звукового давления, частоты и формы колебаний, а высота звука — не только от частоты, но и от величины звукового давления.
Среди слышимых звуков выделяются фонетические, речевые звуки и фонемы (из которых состоит устная речь) и музыкальные звуки (из которых состоит музыка). Музыкальные звуки содержат не один, а несколько тонов (волн фиксированных частот 
Понятие о звуке[править | править код]
Звуковые волны в воздухе — чередующиеся области сжатия и разрежения
Звуковые волны могут служить примером колебательного процесса. Всякое колебание связано с нарушением равновесного состояния системы и выражается в отклонении её характеристик от равновесных значений с последующим возвращением к исходному значению. Для звуковых колебаний такой характеристикой является давление в точке среды, а её отклонение — звуковым давлением.
Если произвести резкое смещение частиц упругой среды в одном месте (например, с помощью поршня), то в этом месте увеличится давление. Благодаря упругим связям частиц давление передаётся на соседние частицы, которые, в свою очередь, воздействуют на следующие, и область повышенного давления как бы перемещается в упругой среде. За областью повышенного давления следует область пониженного давления, и, таким образом, образуется ряд чередующихся областей сжатия и разрежения, распространяющихся в среде в виде волны. Каждая частица упругой среды в этом случае будет совершать колебательные движения.
более детальная информация
Скорость колебательного движения частиц упругой среды — колебательная скорость — измеряется в м/с или см/с. В энергетическом отношении реальные колебательные системы характеризуются изменением энергии вследствие частичной её затраты на работу против сил трения и излучение в окружающее пространство. В упругой среде колебания постепенно затухают. Для характеристики затухающих колебаний используются коэффициент затухания (S), логарифмический декремент (D) и добротность (Q).
Коэффициент затухания отражает быстроту убывания амплитуды с течением времени. Если обозначить время, в течение которого амплитуда уменьшается в е = 2,718 раз, через 
.
Уменьшение амплитуды за один цикл характеризуется логарифмическим декрементом. Логарифмический декремент равен отношению периода колебаний ко времени затухания 
Если на колебательную систему с потерями действовать периодической силой, то возникают вынужденные колебания, характер которых в той или иной мере повторяет изменения внешней силы. Частота вынужденных колебаний не зависит от параметров колебательной системы. Напротив, амплитуда зависит от массы, механического сопротивления и гибкости системы. Такое явление, когда амплитуда колебательной скорости достигает максимального значения, называется механическим резонансом. При этом частота вынужденных колебаний совпадает с частотой собственных незатухающих колебаний механической системы.
При частотах воздействия, значительно меньших резонансной, внешняя гармоническая сила уравновешивается практически только силой упругости. При частотах возбуждения, близких к резонансной, главную роль играют силы трения. При условии, когда частота внешнего воздействия значительно больше резонансной, поведение колебательной системы зависит от силы инерции или массы.
Свойство среды проводить акустическую энергию, в том числе и ультразвуковую, характеризуется акустическим сопротивлением. Акустическое сопротивление среды выражается отношением звуковой плотности к объёмной скорости ультразвуковых волн. Удельное акустическое сопротивление среды устанавливается соотношением амплитуды звукового давления в среде к амплитуде колебательной скорости её частиц. Чем больше акустическое сопротивление, тем выше степень сжатия и разрежения среды при данной амплитуде колебания частиц среды. Численно, удельное акустическое сопротивление среды (Z) находится как произведение плотности среды (
Удельное акустическое сопротивление измеряется в паскаль-секундах на метр (Па·с/м) или дин•с/см³ (СГС); 1 Па·с/м = 10−1 дин • с/см³.
Значение удельного акустического сопротивления среды часто выражается в г/с·см², причём 1 г/с·см² = 1 дин•с/см³. Акустическое сопротивление среды определяется поглощением, преломлением и отражением ультразвуковых волн.
Звуковое, или акустическое, давление в среде представляет собой разность между мгновенным значением давления в данной точке среды при наличии звуковых колебаний и статическим давлением в той же точке при их отсутствии. Иными словами, звуковое давление есть переменное давление в среде, обусловленное акустическими колебаниями. Максимальное значение переменного акустического давления (амплитуда давления) может быть рассчитано через амплитуду колебания частиц:
где Р — максимальное акустическое давление (амплитуда давления);
- f — частота;
- с — скорость распространения ультразвука;
— плотность среды;
- А — амплитуда колебания частиц среды.
На расстоянии в половину длины волны (λ/2) значение звукового давления из положительного становится отрицательным. Разница давлений в двух точках с максимальным и минимальным его значением (отстоящих друг от друга на λ/2 вдоль направления распространения волны) равна 2Р.
Для выражения звукового давления в единицах СИ используется паскаль (Па), равный давлению в один ньютон на квадратный метр (Н/м²). Звуковое давление в системе СГС измеряется в дин/см²; 1 дин/см² = 10−1 Па = 10−1 Н/м². Наряду с указанными единицами часто пользуются внесистемными единицами давления — атмосфера (атм) и техническая атмосфера (ат), при этом 1 ат = 0,98⋅106 дин/см² = 0,98⋅105 Н/м². Иногда применяется единица, называемая баром или микробаром (акустическим баром); 1 бар = 106 дин/см².
Давление, оказываемое на частицы среды при распространении волны, является результатом действия упругих и инерционных сил. Последние вызываются ускорениями, величина которых также растёт в течение периода от нуля до максимума (амплитудное значение ускорения). Кроме того, в течение периода ускорение меняет свой знак.
Максимальные значения величин ускорения и давления, возникающие в среде при прохождении в ней ультразвуковых волн, для данной частицы не совпадают во времени. В момент, когда перепад ускорения достигает своего максимума, перепад давления становится равным нулю. Амплитудное значение ускорения (а) определяется выражением:
Если бегущие ультразвуковые волны наталкиваются на препятствие, оно испытывает не только переменное давление, но и постоянное. Возникающие при прохождении ультразвуковых волн участки сгущения и разрежения среды создают добавочные изменения давления в среде по отношению к окружающему её внешнему давлению. Такое добавочное внешнее давление носит название давления излучения (радиационного давления). Оно служит причиной того, что при переходе ультразвуковых волн через границу жидкости с воздухом образуются фонтанчики жидкости и происходит отрыв отдельных капелек от поверхности.
Этот механизм нашёл применение в образовании аэрозолей лекарственных веществ. Радиационное давление часто используется при измерении мощности ультразвуковых колебаний в специальных измерителях — ультразвуковых весах.
В жидких и газообразных средах, где отсутствуют значительные колебания плотности, акустические волны имеют продольный характер, то есть направление колебания частиц совпадает с направлением перемещения волны. В твёрдых телах, помимо продольных деформаций, возникают также упругие деформации сдвига, обусловливающие возбуждение поперечных (сдвиговых) волн; в этом случае частицы совершают колебания перпендикулярно направлению распространения волны (поперечная волна). Скорость распространения продольных волн значительно больше скорости распространения сдвиговых волн.
В философии, психологии и экологии средств коммуникации звук исследуется в связи с его воздействием на восприятие и мышление (речь идёт, например, об акустическом пространстве как пространстве, создаваемом воздействием электронных средств коммуникации).
Физические параметры звука[править | править код]
Спектр звука[править | править код]
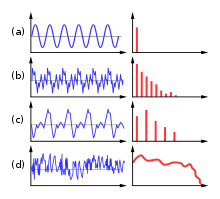
Примеры форм звуковых сигналов (слева) и соответствующих спектров: a-c — дискретные; d — непрерывный
Под спектром понимается распределение звуковой энергии по частоте 



Применительно к музыкальным звукам вместо слова «спектр» используется понятие «тембр» в том же значении.
Интенсивность звука[править | править код]
Интенсивность (сила) звука — скалярная физическая величина, характеризующая мощность, переносимую в направлении распространения звука. Учитывает весь частотный диапазон, а именно 


Длительность звука[править | править код]
Длительность звука — общая продолжительность колебаний источника упругих волн в секундах или, в музыке, в единицах музыкального ритма (см. длительность (музыка)).
Скорость звука[править | править код]
Скорость звука — скорость распространения звуковых волн в среде.
Как правило, в газах скорость звука меньше, чем в жидкостях.
Скорость звука в воздухе зависит от температуры и в нормальных условиях составляет примерно 340 м/с.
Скорость звука в любой среде вычисляется по формуле:
,
где 

Громкость звука[править | править код]
Громкость звука — субъективное восприятие силы звука (абсолютная величина слухового ощущения). Громкость главным образом зависит от звукового давления, амплитуды и частоты звуковых колебаний. Также на громкость звука влияют его спектральный состав, локализация в пространстве, тембр, длительность воздействия звуковых колебаний, индивидуальная чувствительность слухового анализатора человека и другие факторы[3][4].
Генерация звука[править | править код]
Обычно для генерации звука применяются колеблющиеся тела различной природы, вызывающие колебания окружающего воздуха. Примером такой генерации может служить использование голосовых связок, динамиков или камертона. Большинство музыкальных инструментов основано на том же принципе. Исключением являются духовые инструменты, в которых звук генерируется за счёт взаимодействия потока воздуха с неоднородностями в инструменте. Для создания когерентного звука применяются так называемые звуковые или фононные лазеры[5].
В технике применяются генераторы звука.
Ультразвук[править | править код]
Ультразвук — упругие звуковые колебания высокой частоты. Человеческое ухо воспринимает распространяющиеся в среде упругие волны частотой приблизительно до 16 Гц-20 кГц; колебания с более высокой частотой представляют собой ультразвук (за пределом слышимости). На явлении отражения основана ультразвуковая диагностика.
- Поглощение ультразвуковых волн
Поскольку среда, в которой распространяется ультразвук, обладает вязкостью, теплопроводностью и имеет другие причины внутреннего трения, то при распространении волны происходит поглощение, то есть по мере удаления от источника амплитуда и энергия ультразвуковых колебаний становятся меньше. Среда, в которой распространяется ультразвук, вступает во взаимодействие с проходящей через него энергией и часть её поглощает. Преобладающая часть поглощённой энергии преобразуется в тепло, меньшая часть вызывает в передающем веществе необратимые структурные изменения.
Под глубиной проникновения ультразвука понимают глубину, при которой интенсивность уменьшается вдвое. Эта величина обратно пропорциональна поглощению: чем сильнее среда поглощает ультразвук, тем меньше расстояние, на котором интенсивность ультразвука ослабляется наполовину.
Если в среде имеются неоднородности, то происходит рассеяние звука, которое может существенно изменить простую картину распространения ультразвука и, в конечном счёте, также вызвать затухание волны в первоначальном направлении распространения.
На границе раздела сред (напр., эпидермис — дерма — фасция — мышца) будет наблюдаться преломление ультразвуковых волн.
- Бегущие и стоячие ультразвуковые волны
Если при распространении ультразвуковых волн в среде не происходит их отражения, образуются бегущие волны. В результате потерь энергии колебательные движения частиц среды постепенно затухают, и чем дальше расположены частицы от излучающей поверхности, тем меньше амплитуда их колебаний.
Если же на пути распространения ультразвуковых волн имеются ткани с разными удельными акустическими сопротивлениями, то в той или иной степени происходит отражение ультразвуковых волн от пограничного раздела. Наложение падающих и отражающихся ультразвуковых волн может приводить к возникновению стоячих волн. Для возникновения стоячих волн расстояние от поверхности излучателя до отражающей поверхности должно быть кратным половине длины волны.
Инфразвук[править | править код]
Инфразву́к (от лат. infra — ниже, под) — звуковые колебания, имеющие частоты ниже воспринимаемых человеческим ухом. За верхнюю границу частотного диапазона инфразвука обычно принимают 16—25 Гц. Нижняя же граница инфразвукового диапазона условно определена как 0,001 Гц. Практический интерес могут представлять колебания от десятых и даже сотых долей герц, то есть с периодами в десяток секунд.
Поскольку природа возникновения инфразвуковых колебаний такая же, как и у слышимого звука, инфразвук подчиняется тем же закономерностям, и для его описания используется такой же математический аппарат, как и для обычного слышимого звука (кроме понятий, связанных с уровнем звука). Инфразвук слабо поглощается средой, поэтому может распространяться на значительные расстояния от источника. Из-за очень большой длины волны ярко выражена дифракция.
Инфразвук, образующийся в море, называют одной из возможных причин нахождения судов, покинутых экипажем[6].
Опыты и демонстрации[править | править код]
Видеоурок: возникновение звука
Для демонстрации стоячих волн звука служит труба Рубенса.
Различие в скоростях распространения звука наглядно, когда вдыхают вместо воздуха гелий, и говорят что-либо, выдыхая им, — голос становится выше. Если же газ — гексафторид серы SF6, то голос звучит ниже[7]. Связано это с тем, что газы примерно одинаково хорошо сжимаемы, поэтому в обладающем очень низкой плотностью гелии по сравнению с воздухом происходит увеличение скорости звука, и понижение — в гексафториде серы с очень высокой для газов плотностью, размеры же ротового резонатора человека остаются неизменными, в итоге меняется резонансная частота, так как чем выше скорость звука, тем выше резонансная частота при остальных неизменных условиях.
О скорости звука в воде можно визуально получить представление в опыте дифракции света на ультразвуке в воде. В воде по сравнению с воздухом, скорость звука выше, так как даже при существенно более высокой плотности воды (что должно было бы привести к падению скорости звука), вода настолько плохо сжимаема, что в итоге в ней скорость звука оказывается всё равно в несколько раз выше.
В 2014 году была представлена установка, которая звуковыми волнами поднимает сантиметровые предметы[8].
См. также[править | править код]
- Акустика / Музыкальная акустика
- Гранулярный синтез
- Эффект Доплера
- Второй звук в жидком гелии
- АЧХ / Логарифмический масштаб
Примечания[править | править код]
- ↑ И. П. Голямина. Звук // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия (т. 1—2); Большая Российская энциклопедия (т. 3—5), 1988—1999. — ISBN 5-85270-034-7.
- ↑ Слух — общая информация. Дата обращения: 25 августа 2010. Архивировано из оригинала 12 января 2013 года.
- ↑ Архив журнала «Звукорежиссёр», 2000, #8 Архивная копия от 27 февраля 2007 на Wayback Machine
- ↑ Архив журнала «Звукорежиссёр», 2000, #9 Архивировано 27 февраля 2007 года.
- ↑ Jacob B. Khurgin. Phonon lasers gain a sound foundation (англ.) // Physics. — 2010. — Vol. 3. — P. 16.
- ↑ Мезенцев В. А. В тупиках мистики. М.: Московский рабочий, 1987.
- ↑ Демонстрация изменения голоса с гексафторидом серы на YouTube
- ↑ Акустический «силовой луч» притягивает предметы на расстоянии Архивная копия от 17 мая 2014 на Wayback Machine // Популярная механика
Литература[править | править код]
- Звук // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Радзишевский А. Ю. Основы аналогового и цифрового звука. — М.: Вильямс, 2006. — С. 288. — ISBN 5-8459-1002-1.
Ссылки[править | править код]
- Sounds Amazing; a KS3/4 learning resource for sound and waves Архивная копия от 13 марта 2012 на Wayback Machine (uses Flash)
- HyperPhysics: Sound and Hearing Архивная копия от 2 февраля 2009 на Wayback Machine
- Introduction to the Physics of Sound Архивная копия от 23 декабря 2008 на Wayback Machine
- Hearing curves and on-line hearing test Архивная копия от 21 января 2009 на Wayback Machine
- Audio for the 21st Century
- Conversion of sound units and levels Архивная копия от 18 января 2009 на Wayback Machine
- Sound calculations Архивная копия от 18 января 2009 на Wayback Machine
- Audio Check: a free collection of audio tests and test tones playable on-line Архивная копия от 3 октября 2019 на Wayback Machine
- More Sounds Amazing; a sixth-form learning resource about sound waves Архивная копия от 10 февраля 2019 на Wayback Machine
-
Субъективные характеристики звука
Субъективные
характеристики звука определяются
способностью органов
слуха человека
воспринимать
звуковые колебания. Восприятие
индивидуально.
Уровень силы
звука и разность уровней силы звука
Замечено, что ухо
человека регистрирует изменение силы
звука по логарифмическому закону. Это
означает, что важно не абсолютное
значение силы (интенсивности) звука, а
её логарифмическое значение. Величину
lg(I),
равную
десятичному логарифму силы (или
интенсивности)
звука, называют
логарифмическим
уровнем
силы звука.
Единицей измерения уровня звука служит
бел:
.
Ухо улавливает
изменение этой величины, т. е.
.
Величину
L,
равную
разности логарифмических уровней,
называют
разностью
уровней
силы звука.
Её можно записать в виде:
.
(53)
Единица измерения
разности уровней силы звука – бел:
.
Один
бел
– это разность уровней силы звука по
шкале десятичных логарифмов, если
отношение силы звука равно 10:
.
Иначе
говоря, десятикратное
увеличение силы звука соответствует 1
белу
,
стократное
увеличение силы звука соответствует
двум белам
,
тысячекратное
– трём белам
.
На практике
оказывается, что бел
является слишком большой величиной для
изменения уровня. Минимальная разница
уровней интенсивности звука, которую
способно воспринять наше ухо, равна
одному децибелу:
.
В децибелах формула
(53) примет вид:
.
(54)
Замечание:
Если уровень звука определять не
десятичным, а натуральным логарифмом
,
то единицей
измерения служит непер:
.
Один
непер
– это разность уровней силы звука по
шкале натуральных логарифмов, если
отношение силы звука равно 10
:
.
Связь между белом
и непером:
Для того, чтобы мы
смогли услышать тот или иной звук, его
сила должна быть больше определенного
значения I0
, называемого порогом
слышимости
.
Порог
слышимости
— это минимальная интенсивность
воспринимаемого звука определённой
частоты. Если
звуковая волна данной частоты имеет
интенсивность ниже этого порога
,
то человек не
воспринимает её. Относительно порога
слышимости разность уровней силы звука
определяют по формулам:
(53*)
(54*)
Если сила звука
равна порогу слышимости, то
Это
величина L0
принята
за нулевой
(или пороговый)
уровень
громкости.
Пример:
Выражение “уровень
звука в колонках равен ста децибелам”
означает, что относительно порога
слышимости разность уровней силы звука
равна
или

Учитывая
формулу (53*), получим
.
Поскольку, с другой
стороны,
то можно найти
кратность увеличения силы звука
относительно порога слышимости,
приравнивая выражения для разности
уровней (LI):

Следовательно,
можно определить и абсолютное значение
силы звука:
.
Восприятие
звука имеет не только нижний предел, но
и верхний. Человек слышит
звук только до определенного максимального
значения интенсивности, который
называется
болевым
порогом:
.
Если
интенсивность выше этого максимума
,
то
возникает боль в ушах и нормальное
восприятие звука невозможно.
Разница между
уровнями болевого порога и порога
слышимости называется динамическим
диапазоном слуха
и составляет
.
(55)
Если звук издаётся
двумя и более источниками звука с
уровнями силы звука L1
, L2
, … , Li
,
…, L
N
, то
их суммарный уровень звука определяется
по формуле:
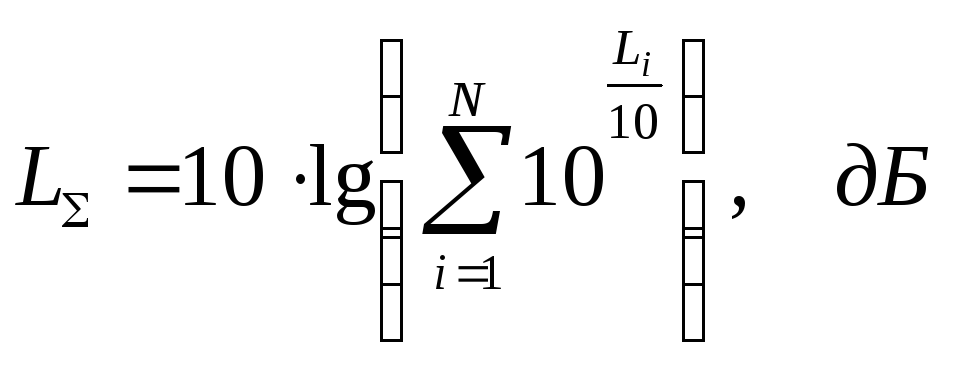
Уровень громкости
и разность уровней громкости
Согласно соотношению
(51) или (51*) сила звука пропорциональна
квадрату амплитуды звукового давления:

Величину
Lp
, равную
разности
, (57)
называют
разностью
уровней
звукового
давления (или
разностью уровней громкости).
Разность уровней звукового давления
определяют в белах
и децибелах
по формулам, аналогичным (53), (54) для
разности уровней интенсивности, но с
коэффициентом “2” вследствие
квадратичной зависимости между
интенсивностью звука и звуковым
давлением:
а) в общем случае

(58)
а) относительно
порогового минимального давления на
стандартной частоте 1000
Гц
(59)
(60)
Соседние файлы в папке арх_физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Звук в физике, теория и онлайн калькуляторы
Звук
Определение и основные понятия звуковых волн (звука)
Определение
Звуковыми (акустическими) волнами называют упругие волны, распространяющиеся в среде,
имеющие частоты в диапазоне $16le nu le 20~000 $Гц.
Оказывая воздействие на слуховой аппарат человека, такие волны вызывают ощущение звука. Волны, частоты которых меньше 16 Гц, называют инфразвуковыми. Волны, имеющие частоту больше, чем 20~000 Гц называют ультразвуковыми. Инфразвук и ультразвук человек не слышит.
Волны звука в газах и жидкостях могут быть только продольными, потому что эти вещества имеют упругость только по отношению к сжатию (растяжению). В твердых телах волны звука могут быть и продольными и поперечными, так как твердые тела могут быть упругими по отношению к деформациям сжатия (растяжения) и сдвига.
Характеристики звуковых волн
Определение
Интенсивностью звука (силой звука) ($I$) называют величину, которую определяют средней по времени энергией ($leftlangle Erightrangle $), переносимой волной звука за единицу времени, через единичную площадку, нормальную к направлению распространению волны:
[I=frac{leftlangle Erightrangle }{St}left(1right).]
Единицей измерения силы звука служит в Международной системе единиц (СИ) ватт деленный на квадратный метр:
[left[Iright]=frac{Вт}{м^2}.]
Для того чтобы человек слышал звук, волна звука должна иметь некую минимальную интенсивность, но если сила звука превысила некоторый предел, то человек звук не слышит, но ощущает боль. Для каждой частоты колебаний существует наименьшая (пороговая слышимость) и наибольшая (порог болевых ощущений) сила звука, которую человек способен воспринимать.
Громкость звука – это субъективная характеристика звука, которая связана с его силой. Громкость звука зависит от частоты. По закону из физиологии, при увеличении интенсивности звука его громкость растет по закону логарифма. На этом основании вводится объективная оценка громкости звука:
[L={lg left(frac{I}{I_0}right) }left(2right),]
где $I_0$ – интенсивность звука на пороге слышимости, для всех звуков ${10}^{-12}frac{Вт}{м^2}$; $L$ – уровень интенсивности звука. Единицей измерения $L$ является бел (Б). Чаще используют такую единицы уровня интенсивности звука как децибел (дБ), он в 10 раз меньше, чем бел.
Уровень громкости – физиологическая характеристика звука, единицей измерения которой, является фон. Громкость для звука 1000 Гц (частота стандартного тона) составляет 1 фон, если его уровень интенсивности 1 дБ. Так, шепот на расстоянии один метр имеет уровень громкости примерно 20 фон.
Звук в действительности представляет собой наложение гармонических колебаний большим набором частот. При этом говорят, что звук имеет акустический спектр. Этот спектр может быть сплошным или линейчатым. В линейчатом спектре имеются отделенные друг от друга частоты.
Высота звука – это качество звука, которое человек определяет субъективно на слух. Высота звука зависит от его частоты. С увеличением частоты высота звука увеличивается.
Тембром звука называют звуковое ощущение, которое определяет характер акустического спектра и распределения энергии между определенными частотами.
Любое тело, совершающее колебания в упругой среде с частотой звука может стать источником звуковых волн. Колеблющееся тело вызывает колебания частичек среды, в котором оно находится с частотой колебаний тела. В веществе распространяется волна, имеющая частоту источника колебаний. Скорость ($v$) распространения волны зависит от плотности и упругих свойств вещества. Для газа она равна:
[v=sqrt{frac{gamma RT}{mu }}left(3right),]
где $gamma =frac{c_{mu p}}{c_{mu V}}$; $c_{mu p}$ -молярная теплоемкость газа при постоянном давлении; $c_{mu V}$ – молярная теплоемкость газа при постоянном объеме; $R$ – универсальная газовая постоянная; $T$ – температура; $mu $ – молярная масса. Формула (3) является идеализированной. Так, при распространении звука в атмосфере следует учесть скорость и направление ветра, влажность воздуха, преломление и отражение волн на границе сред, вязкость.
Если источник и приёмник звука находятся в состоянии покоя относительно среды, то длина волны звука равна:
[lambda =vT=frac{v}{nu }left(4right),]
где $v$ – скорость распространения волны в веществ; $nu $ – частота звука.
Примеры задач с решением
Пример 1
Задание. Какова интенсивность звука, если уровень его интенсивности равен $L=67$дБ? Интенсивность звука, на пороге слышимости составляет ${I_0=10}^{-12}frac{Вт}{м^2}$.
Решение. Основой для решения задачи нам будет служить формула для уровня интенсивности звука:
[L={lg left(frac{I}{I_0}right) }left(1.1right).]
Выразим из нее интенсивность звука:
[frac{I}{I_0}={10}^Lto I={10}^Lcdot I_0.]
Переведем $L=67$дБ=6,7 Б, вычислим искомую величину:
[I={10}^{6,7}cdot {10}^{-12}approx 5cdot {10}^{-6}left(frac{Вт}{м^2}right).]
Ответ. $I=5cdot {10}^{-6}frac{Вт}{м^2}$
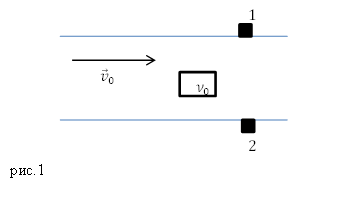
Пример 2
Задание. На рис.1 изображена река. Скорость движения воды в реке равна $v_0$. В воде установлен источник звуковых колебаний с частотой ${nu }_0$. На двух берегах реки на равных расстояниях установлены неподвижные приемники колебаний (1 и 2). Какую частоту звука зарегистрируют приемники?
Решение. Пусть скорость распространения звуковой волны в воде равна $v$, то длина волны:
[lambda =vT=frac{v}{{nu }_0}left(2.1right).]
Рассмотрим первый приемник. При распространении в воде, волна достигнет приемника и вызовет колебания его звукочувствительного элемента с частотой, равной:
[{nu }_1=frac{v}{lambda }=frac{v}{vT}={nu }_0.]
Частота звука, регистрируемого приемником равна частоте, которою испускает источник.
Ответ. ${nu }_1={nu }_2={nu }_0$
Читать дальше: импульс тела.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Энергия
звуковой волны. Интенсивность звука
Распространение
звуковой волны сопровождается переносом энергии, которая зависит от звукового
давления p
и колебательной скорости v
в каждой точке среды.
Средний
поток звуковой энергии, проходящий в единицу времени через единицу поверхности,
нормальной к направлению распространения волны, называется интенсивностью звука или силой звука
(Вт/м2):
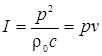
Векторная
величина, характеризующая также направление переноса энергии в волне, называется
вектором Умова:
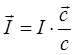
Наряду
с интенсивностью звука используют величину плотность звуковой
энергии 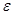
равную энергии колебаний в единице объема звукового поля.
Можно
показать, что в бегущей волне
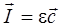
Таким
образом: 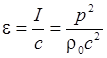
Передача
энергии звуковой волны в область, ранее не затронутую волнами, требует
непрерывного расходования энергии со стороны источника, возбуждающего звук. В
тех зонах, где волна уже возникла, энергия непрерывно передается дальше со
скоростью звука. Возникающие в среде переменные давления непрерывно совершают
работу, ввиду чего и возникает волновое сопротивление (импеданс) 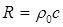
среды.
Формулы
для силы звука:
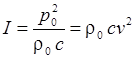
подобны формулам закона Джоуля–Ленца для
мощности электрического тока, только мощность, затрачиваемая при действии сил
давления, расходуется не на выделение тепла, а на передачу энергии новым частям
среды. Поэтому величину 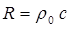
излучения среды.
Логарифмическая
шкала силы звука. Децибелы
Отношение
максимальной и минимальной интенсивности слышимого человеческим ухом звука очень
велико и составляет 1014 раз (для звукового давления 107
раз). Поэтому для характеристики силы звука удобнее пользоваться
логарифмическими величинами:
уровнем
интенсивности звука,
выраженным в децибелах (дБ):
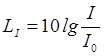
и
уровнем звукового давления
(дБ):
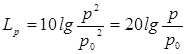
где
I0
и p0
– значения, соответствующие порогу слышимости на частоте 1000 Гц (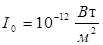
p0
= 2∙10-5 Па).
Значение
p0 выбрано таким образом, чтобы при нормальных атмосферных
условиях LI
= Lp.
Поэтому в дальнейшем будем использовать величину L
=
LI
= Lp,
которую называют уровнем звука в
децибелах.
Уровень
звука, соответствующий порогу слышимости на частоте 1000 Гц, равен 0 дБ.
Болевой порог восприятия звука соответствует Iб
=
102 Вт/м2 и рб = 2∙102 Па, что
дает значение Lб
= 140 дБ.
Введению
логарифмических единиц измерения способствовало также то обстоятельство, что ухо
человека реагирует не на абсолютное изменение интенсивности звука, а на
относительное. Разница уровней в 1 дБ соответствует минимальной величине,
различимой слухом, при этом интенсивность звука изменяется в 1,26 раза или на
26%. Если же разница уровней составляет 3 дБ, то сила звука изменяется уже в 2
раза.
Рассмотрим,
как рассчитать суммарный уровень звука для звукового поля, создаваемого
несколькими источниками. Возьмем для простоты два
источника.
В
любой точке пространства звуковое давление равно:
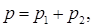
где
р1 и р2 – мгновенные значения звуковых
давлений, создаваемых в этой точке соответственно первым и вторым
источником.
Результирующая
интенсивность звука равна:
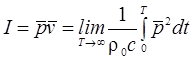
Если
источники звука некогерентные, то есть создаваемые ими давления не связаны по
фазе, то средний квадрат звукового давления 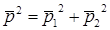
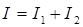
равна сумме интенсивностей источников.
Таким
образом, если поле создается N
некогерентными источниками, то
I
=
I1+I2+…+IN
, а 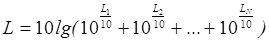
где
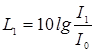
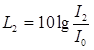
каждым
источником
в расчетной точке.
При
N
одинаковых источниках шума, равноудаленных от расчетной точки, с уровнями
звукового давления L0,
суммарный уровень равен:
L
= L0+10lgN.
Презентация к разделу 2
< Предыдущая Оглавление Следующая >
Перед тем, как приступить к рассмотрению темы, дадим определение такому явлению, как звук.
Звук или звуковые волны – это волны, которые способно воспринять человеческое ухо.
При этом звуковые частоты имеют диапазон: примерно от 20 Гц до 20 кГц.
Инфразвук – звуковые волны, имеющие частоту менее 20 Гц.
Ультразвук – волны звука, имеющие частоту более 20 кГц.
Волнам звукового диапазона свойственно распространяться как в газе, так и в жидкости (продольные волны), и в твердом теле (продольные и поперечные волны). Особенно интересно для науки заниматься изучением распространения звуковых волн в газообразной среде, что по сути есть среда нашего обитания.
Акустика – это направление физики, занимающееся изучением звуковых явлений.
Когда звук получает распространение в газе, атомы и молекулы испытывают колебания вдоль направления распространения волны, следствием чего становится изменение локальной плотности ρ и давления p.
Звуковые волны в газе зачастую называют волнами плотности или волнами давления.
В случае простых гармонических звуковых волн, получающих распространение вдоль оси OX, изменение давления p(x, t) имеет зависимость от координаты x и времени t, которая записывается так:
p(x,t)=p0cosωt±kx.
В аргументе косинуса мы видим два противоположных знака, что имеет отношение к двум направлениям распространения волны. Запишем выражение, которое покажет соотношение таких величин, как круговая частота ω, волновое число k, длина волны λ, скорость звука υ (соотношение будет таким же, как применимо для поперечных волн в струне или резиновом жгуте):
υ=λT=ωk; k=2πλ; ω=2πf=2πT.
Одной из ключевых характеристик звука является скорость распространения.
Скорость распространения – величина, описывающая звуковую волну, задаваемая инертными и упругими свойствами среды и определяемая для продольных волн в любой однородной среде при помощи формулы:
υ=Bρ.
В указанной формуле B является модулем всестороннего сжатия, ρ – средней плотностью среды.
Формула Лапласа
Первые попытки рассчитать значение скорости звука предпринял Ньютон, предположив равенство упругости воздуха атмосферному давлению pатм. В таком случае значение скорости звука в воздушной среде – менее 300 м/с, в то время как истинная скорость звука при нормальных условиях (температура 0 °С и давление 1 атм) равна 331,5 м/с, а скорость звука при температуре 20 °С и давлении 1 атм составит 343 м/с. Лишь по прошествии более ста лет было показано, почему предположение Ньютона не выполняется. Французский физик П. Лаплас указал, что ньютоновское видение равносильно предположению о быстром выравнивании температуры между областями разрежения и сжатия, и невыполнение его связано с плохой теплопроводностью воздуха и малым периодом колебаний в звуковой волне. В действительности между областями разрежения и сжатия газа появляется разность температур, существенным образом влияющая на упругие свойства. Лаплас, в свою очередь, выдвинул предположение, что сжатие и разрежение газа в звуковой волне происходят в соответствии с адиабатическим законом: в отсутствии влияния теплопроводности. В 1816 году физик вывел формулу, предназначенную для расчета скорости звуковой волны в воздухе и получившей название формулы Лапласа.
Формула Лапласа для определения скорости звука имеет запись:
υ=γpρ.
Где p является значением среднего давления в газе, ρ – средней плотности, а γ есть некоторая константа, находящаяся в зависимости от свойств газа.
В нормальных условиях скорость звука, рассчитанная по формуле Лапласа, равна υ=332 м/с.
В термодинамике имеется доказательство, что константа γ представляет собой отношение теплоемкостей при постоянном давлении Cp и постоянном объеме CV .
Формула Лапласа может быть записана несколько иначе, если использовать уравнение состояния идеального газа. Таким образом, окончательный вид формулы для определения скорости звука будет такой:
υ=γRTM.
В данной формуле T – абсолютная температура, M – молярная масса,
R=8,314 Дж/моль·К – универсальная газовая постоянная. Скорость звука находится в сильной зависимости от свойств газа: скорость звука тем больше, чем легче газ, в котором звуковая волна получает распространение.
Для наглядности приведем некоторые примеры.
Когда звук распространяется в воздушной среде (M=29·10–3 кг/моль) при нормальных условиях: υ=331,5 м/с;
Когда звук распространяется в гелии (M=4·10–3 кг/моль): υ=970 м/с;
Когда звук распространяется в водороде (M=2·10–3 кг/моль): υ=1270 м/с.
В жидкостях и твердых телах скорость звуковых волн еще больше. В воде, например, υ=1480 м/с (при 20 °С), в стали υ=5–6 км/с.
Характеристики звуковых волн
Помимо скорости распространения звук имеет и другие характеристики, связанные с восприятием его человеческими органами слуха.
Громкость звука
Рассуждая о том, как человеческое ухо воспринимает звук, в первую очередь мы говорим об уровне громкости, который зависит от потока энергии или интенсивности звуковой волны. А то, как воздействует звуковая волна на барабанную перепонку, зависит от звукового давления.
Звуковое давление – это амплитуда p0 колебаний давления в волне
Природа отлично потрудилась, создавая такое совершенное устройство, как человеческое ухо: оно способно воспринимать звуки в обширнейшем диапазоне интенсивностей. Мы имеем возможность слышать как слабый писк комара, так и грохот вулкана.
Порог слышимости – минимальное значение величины звукового давления, при котором звук этой частоты еще воспринимается человеческим ухом.
Болевой порог – это верхняя граница диапазона слышимости человека; та величина звукового давления, при котором звук вызывает в человеческом ухе ощущение боли.
Порог слышимости представляет собой значение p0 около 10–10 атм, т. е. 10–5 Па: такой слабый звук характеризуется колебанием молекул воздуха в волне звука с амплитудой всего лишь 10–7 см! Болевой же порог соответствует значению p0 порядка 10–4 атм или 10 Па. Т.е., человеческое ухо способно к восприятию волн, в которых звуковое давление изменяется в миллион раз. Поскольку интенсивность звука пропорциональна квадрату звукового давления, диапазон интенсивностей оказывается порядка 1012!
Человеческое ухо, восприимчивое к звукам такого огромного диапазона интенсивности, допустимо сравнить с прибором, которым возможно измерить как диаметр атома, так и размеры футбольного поля.
Для общей информированности заметим, что обычным разговорам людей в комнате соответствует интенсивность звука, примерно в 106 раз превышающая порог слышимости, а интенсивность звука на рок-концерте находится очень близко к болевому порогу.
Высота звука
Высота звуковой волны – еще одна характеристика звука, влияющая на слуховое восприятие. Человеческие ухо воспринимает колебания в гармонической звуковой волне как музыкальный тон.
Высокий тон – это звуки с колебаниями высокой частоты.
Низкий тон – это звуки с колебаниями низкой частоты.
Звуки, которые издают музыкальные инструменты, а также звуки голоса человека значимо отличаются друг от друга по высоте тона и по диапазону частот.
К примеру, диапазон наиболее низкого мужского голоса – баса – находится в пределах примерно от
80 до 400 Гц, а диапазон высокого женского голоса – сопрано – от 250 до 1050 Гц.
Октава – это диапазон колебаний звука, который соответствует изменению частоты колебаний в 2 раза.
Скрипка, к примеру, звучит в диапазоне примерно трех с половиной октав (196–2340 Гц),
а пианино – семи с лишним октав (27,5–4186 Гц).
Говоря о частоте звука, который извлекается при помощи струн любого струнного музыкального инструмента, будем иметь в виду частоту f1 основного тона. Однако колебания струн содержат также гармоники, частоты fn которых отвечают соотношению:
fn=nf1, (n=1, 2, 3,…).
Таким образом, звучащая струна способна излучать целый спектр волн с кратными частотами. Амплитуды An этих волн имеют зависимость от способа возбуждения струны, будь то смычок или молоточек. Эти амплитуды необходимы для придания музыкальной окраски звуку (тембру).
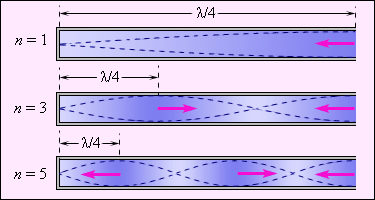
Аналогичный процесс мы наблюдаем, когда звучат духовые музыкальные инструменте. Трубы духовых инструментов служат акустическими резонаторами – акустическими колебательными системами, имеющими способность возбуждаться (резонировать) от звуковых волн определенных частот. Определенные же условия способствуют возникновению внутри трубы стоячей звуковой волны. Рисунок 2.7.1 демонстрирует несколько видов стоячих волн (мод) в органной трубе, закрытой с одного конца и открытой с другого. Звучание духовых инструментов, так же, как и струнных, состоит из целого спектра волн с кратными частотами.
Рисунок 2.7.1. Стоячие волны в трубе органа (закрыта лишь с одной стороны). Стрелки указывают направления движения частиц воздуха за один полупериод колебаний.
Музыкальные инструменты необходимо периодически настраивать.
Камертон – устройство для настройки музыкальных инструментов, состоящее из настроенных в резонанс деревянного акустического резонатора и соединенной с ним металлической вилки.
Удар молоточка по вилке вызывает возбуждение всей системы камертона с последующим звучанием чистого музыкального тона.
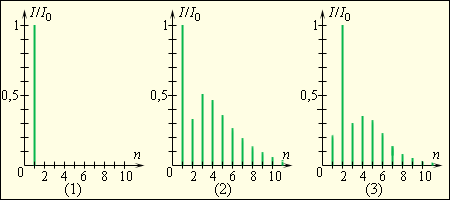
Гортань певца – по сути тоже акустический резонатор. Рисунок 2.7.2 демонстрирует спектры звуковых волн, издаваемых камертоном, струной пианино и низким женским голосом (альтом), звучащими на одной и той же ноте.
Рисунок 2.7.2. Относительные интенсивности гармоник в спектре волну звука при звучании камертона (1), пианино (2) и низкого женского голоса (альт) (3) на ноте «ля» контроктавы (f1=220 Гц). По оси ординат отложены относительные интенсивности II0 .
Звуковые волны, чьи частотные спектры показаны на рисунке 2.7.2, имеют одну и ту же высоту, но различные тембры.
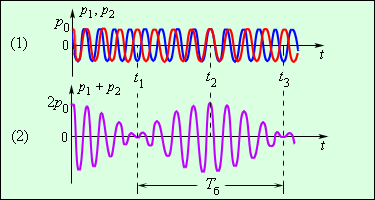
Биения
Разберем также такое явление, как биения.
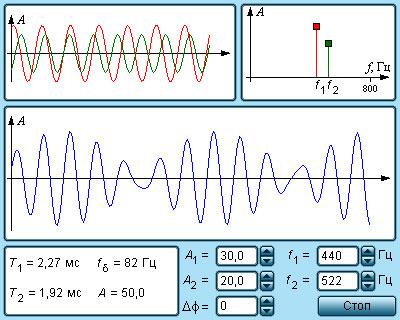
Биение – это явление, возникающее, когда две гармонические волны с близкими, но все же имеющими отличия частотами, накладываются друг на друга.
Биения сопровождают, к примеру, одновременное звучание двух струн, имеющих настройки практически одинаковой частоты. Человеческий орган слуха воспринимает биения как гармонический тон с громкостью, периодически изменяющейся во времени. Запишем выражения, показывающие закономерность изменения звуковых давлений p1 и p2, которые осуществляют воздействие на ухо:
p1=A0cos ω1t и p2=A0cos ω2t.
Для удобства примем, что амплитуды колебаний звуковых давлений являются одинаковыми и равны p0=A00.
Согласно принципу суперпозиции полное давление, которое вызывается обеими волнами в каждый момент времени, есть совокупность звуковых давлений, задаваемых каждой волной в тот же момент времени. Запишем выражение, показывающее суммарное воздействие волн, используя тригонометрические преобразования:
p=p1+p2=2A0cosω1-ω22tcosω1+ω22t=2A0cos12∆ωtcosωсрt,
где ∆ω=ω1-ω2, аωср=ω1+ω22.
Рисунок 2.7.3(1) отображает, каким образом давления p1 и p2 зависимы от времени t. В момент времени t=0 оба колебания находятся в фазе, и их амплитуды суммируются. Поскольку частоты колебаний имеют хоть и небольшие, но отличия, через некоторое время t1 колебания войдут в противофазу. В этот момент суммарная амплитуда станет равна нулю: колебания взаимно «погасятся». К моменту времени t2=2t1 колебания вновь окажутся в фазе и т. д. (рисунок 2.7.3(2)).
Период биений Тб – это минимальное значение интервала между двумя моментами времени, которым соответствуют максимальная и минимальная амплитуда колебаний.
Формула, которая определяет медленно изменяющуюся амплитуду A результирующего колебания, имеет запись:
A=2A0cos12∆ωt.
Период Тб изменения амплитуды равен 2πΔω. Мы можем это продемонстрировать, приняв следующее предположение: периоды колебаний давлений в звуковых волнах T1 и T2 являются такими, что T1<T2 (т. е. ω1>ω2). За период биений Тб наблюдается некоторое число n полных циклов колебаний первой волны и (n–1) циклов колебаний второй волны:
Tб=nT1=(n-1)T2.
Отсюда следует:
Tб=T1T2T2-T1=2πω1-ω2=2π∆ω или fб=1Tб=1T1-1T2=f1-f2=∆f.
fб есть частота биений, определяемая как разность частот Δf двух звуковых волн, которые воспринимаются ухом одновременно.
Органы слуха человека способны к восприятию звуковых биений до частот 5–10 Гц. Прослушивание биений – это важный элемент техники настройки музыкальных инструментов.
Рисунок 2.7.3. Биения, возникающие, когда накладываются две звуковые волны с близкими частотами.
Рисунок 2.7.4. Модель явления биений.