Как найти силы действующие на стержни

Вопрос от пользователя

Найти силы F1 и F2, действующие на стержни АВ и ВС если α = 60о, а масса фонаря m = 3 кг.

Ответ от эксперта

ответ к заданию по физике
 

Легче всего решать задачу, если все приложенные к телу силы параллельны – тогда можно получить ответ, используя лишь правило моментов. Если же силы непараллельные, то иногда для получения ответа требуется дополнительно применять второй закон Ньютона.

Параллельные силы

Алгоритм решения задач на правило моментов (параллельные силы)

• Выполнить чертеж. Указать на нем все силы с точкой их приложения и направлением действия. В этом вам поможет таблица.

Сила	Точка приложения	Направление
Сила тяжести, действующая на груз	Центр груза	Вертикально вниз
Сила тяжести, действующая на однородный стержень	Центр тяжести	Вертикально вниз
Сила тяжести, действующая на неоднородный стержень	Центр масс, положение которого указывают в условии задачи	Вертикально вниз
Вес	Точка опоры или подвеса	Вес тела направлен противоположно вектору силы нормальной реакции опоры или вектору силы натяжения подвеса
Сила реакции опоры	Точка соприкосновения стержня и опоры	Перпендикулярно вверх
Сила натяжения нити	Точка соединения с подвесом	Вдоль оси подвеса

• Выбрать положение оси вращения. Обычно ось выбирают в месте, где находится неизвестная сила или сила, искать которую не нужно.
• Указать значение плеч. Если в задаче нужно указать некоторое расстояние (к примеру, от центра стержня или от места приложения некоторой силы), то это расстояние следует обозначать за x. Размер плеч сил нужно определять с учетом размеров стержня и расстояния x.
• Записать правило моментов и решить задачу.

Типовы задачи на правило моментов при параллельных силах

Прямая неоднородная балка длиной l и массой m подвешена за концы на вертикально натянутых тросах. Балка занимает горизонтальное положение. Найдите силу натяжения первого троса T2, если центр тяжести балки находится на расстоянии a от левого конца балки.	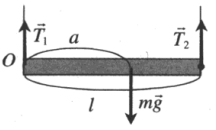Для решения задачи в качестве положения оси вращения удобно выбрать точку приложения силы натяжения первого троса (потому что ее искать не нужно). Тогда плечом силы тяжести будет расстояние a, а плечом силы натяжения второго троса — l. Поэтому правило моментов можно записать так: T2l = mga T2 = mga/l
Рельс длиной l и массой m поднимают равномерно в горизонтальном положении на двух вертикальных тросах, первый из которых укреплен на конце рельса, а второй — на расстоянии x от другого конца. Определите натяжение второго троса.	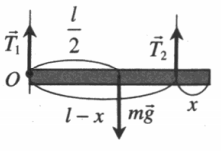В этой задаче положение оси вращения также удобно выбрать в точке О, соответствующей точке приложения силы натяжения нити первого троса (так как ее искать не нужно). Тогда плечом силы натяжения второго троса будет служить разность длины рельса и расстояния x, а плечом силы тяжести — половина длины рельса. Поэтому правило моментов примет вид: mgl/2 = T2(l – x) T2 = mgl2(l−x)

Пример №1. К левому концу невесомого стержня прикреплен груз массой 3 кг (см. рисунок). Стержень расположили на опоре, отстоящей от груза на 0,2 длины. Груз какой массы надо подвесить к правому концу, чтобы стержень находился в равновесии?

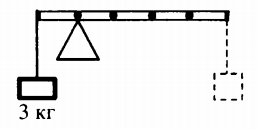
Условие равновесие будет выполняться, если произведение силы тяжести первого груза на ее плечо будет равно произведению силы тяжести второго груза на ее плечо:

F_тяж1d₁ = F_тяж2d₂

Согласно рисунку, второй груз будет подвешен на расстоянии 0,8 от опоры. Следовательно:

Fтяж2=Fтяж2d1d2=m1gd1d2

m2g=m1gd1d2

m2=m1d1d2=3·0,20,8=0,75 (кг)

Непараллельные силы

Алгоритм решения задач на правило моментов (непараллельные силы)

• Выполнить чертеж и указать все силы. Правильно определить точку приложения и направление сил поможет таблица:

Сила	Точка приложения	Направление
Сила реакции опоры	Точка соприкосновения с опорой	Перпендикулярно плоскости опоры
Сила трения покоя	Точка соприкосновения с опорой	В сторону возможного движения
Сила тяжести	Центр масс (у однородных тел центр масс совпадает с центром тела)	Вертикально вниз
Архимедова сила	Центр масс погруженной части тела	Вертикально вверх

• Определить плечи сил как кратчайшее расстояние между осью вращения и направлением действия силы.
• Записать правило моментов и решить задачу.

Внимание! Иногда для решения задачи может потребоваться использование второго закона Ньютона в проекциях на оси Ox и Oy.

Типовы задачи на правило моментов при непараллельных силах

Рабочий удерживает за один конец доску массой m так, что она образует угол α с горизонтом, опираясь о землю другим концом. С какой силой рабочий удерживает доску, если эта сила перпендикулярна доске?	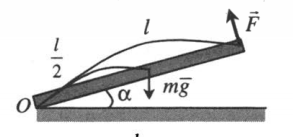За точку равновесия примем точку касания доски с землей. Плечо силы тяжести будет равно нижнему катету треугольника, образованного при опускании перпендикуляра к земле из точки приложения этой силы: d1 = l cosα/2 Плечо силы, с которой рабочий поднимает доску, равно длине доски: d2 = l Отсюда: mglcosα2=Fl F=2lmglcosα=2mgcosα
В гладкий высокий цилиндрический стакан с внутренним радиусом R помещают карандаш длиной l и массой m. С какой силой действует на стакан верхний конец карандаша?	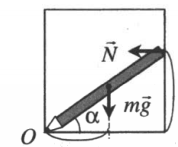За точку равновесия примем нижнюю точку карандаша. Сила давления верхнего конца карандаша на стакан по модулю будет равна силе нормальной реакции опоры в этой точке. Поэтому плечо ее силы будет равно произведению длины карандаша на синус угла между ним и дном стакана: d1 = l sinα Минимальным расстоянием между линией действия силы тяжести и точкой равновесия будет половина произведения длины карандаша на косинус угла между ним и дном стакана: d2 = l сosα/2 Отсюда: Nl sinα = mgl сosα/2 N=mglcosα2lsinα Плечо силы тяжести также равно радиусу стакана, а плечо силы реакции опоры можно найти из теоремы Пифагора. Отсюда: N=mgR√l2−4R2
Колесо радиусом R и массой m стоит перед ступенькой высотой h. Какую наименьшую горизонтальную силу надо приложить, чтобы оно могло подняться на ступеньку? Сила трения равна нулю.	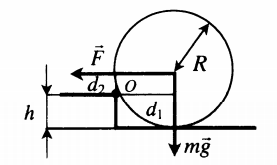За точку равновесия примем точку касания колеса со ступенькой. Плечо силы тяжести является катетом треугольника, образованного с радиусом колеса и плечом прикладываемой силы. Плечо этой силы равно разности радиуса и высоты ступеньки. d1=√R2−d22 d2 = R – h Отсюда: mg√R2−d22=F(R−h) F=mg√R2−d22R−h=mg√h(2R−h)R−h
Лестница массой m приставлена к гладкой вертикальной стене пол углом α. Найдите силу давления лестницы на стену. Центр тяжести лестницы находится в ее середине.	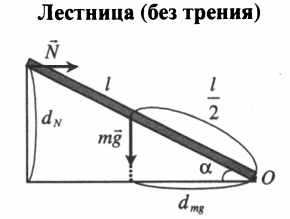Плечо силы тяжести равно половине произведения длины лестницы на косинус угла α. Плечо силы реакции опоры равно произведению этой длины на синус α. Поэтому правило моментов записывается так: Nlsinα=mglcosα2 Отсюда: N=mglcosα2lsinα=mg2tanα
Лестница длиной l приставлена к идеально гладкой стене под углом α к горизонту. Коэффициент трения между лестницей и полом μ. На какое расстояние x вдоль лестницы может поднять человек, прежде чем лестница начнет скользить? Массой лестницы пренебречь.	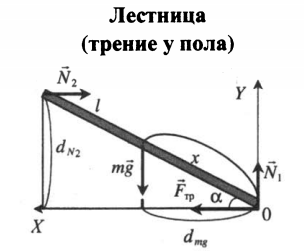Правило моментов: mgxcosα=N2lsinα Второй закон Ньютона в проекциях на оси Ox и Oy соответственно: Fтр – N2 = 0 N1 – mg = 0 Сила трения: Fтр = μmg = N2 Следовательно: mgxcosα=μmglsinα x=μmglsinαmgxcosα=μltanα
Однородная лестница приставлена к стене. При каком наименьшем угле α между лестницей и горизонтальным полом лестница сохранит равновесие, если коэффициент трения между лестницей и полом μ1, а между лестницей и стеной — μ2?	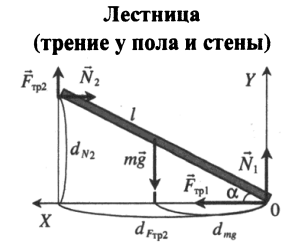Правило моментов: mgl2cosα=Fтр2lcosα+N2lsinα Второй закон Ньютона в проекциях на ось Ox: Fтр1 – N2 = 0 μ1N1 – N2 = 0 На ось Oy: Fтр2 + N1 – mg = 0 μ2N2 +N2μ1 = mg N2(μ2+1μ1)=mg N2=mgμ2+1μ1=mgμ1μ1μ2+1 Fтр2=mg−N1=mg−N2μ1=mg−mgμ1μ2+1=mg(1−1μ1μ2+1) mgl2cosα=mg(1−1μ1μ2+1)lcosα+mgμ1μ1μ2+1lcosα Преобразуем выражение и получим: tanα=1−μ1μ21μ1
Какую минимальную горизонтальную силу нужно приложить к верхнему ребру куба массой m, находящегося на горизонтальной плоскости, чтобы перекинуть его через нижнее ребро?	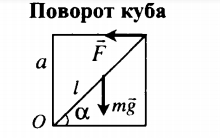Правило моментов примет вид: mgl2cosα=Flsinα У куба угол α равен 45 градусам, а синус и косинус этого угла равны. Длины диагонали взаимоуничтожаются. Остается: F=mg2

Пример №2. Невесомый стержень длиной 1 м, находящийся в ящике с гладким дном и стенками, составляет угол α = 45^о с вертикалью (см. рисунок). К стержню на расстоянии 25 см от его левого конца подвешен на нити шар массой 2 кг. Каков модуль силы N, действующий на стержень со стороны левой стенки ящика?

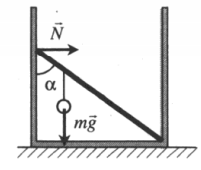
25 см = 0,25 м

Пусть точкой равновесия будет точка касания нижнего конца стержня с дном ящика. Тогда плечом силы тяжести будет:

d₁ = (l – 0,25)sinα

Плечом силы реакции опоры будет:

d₂ = l cosα

Запишем правило моментов:

mg(l−0,25)sinα=Nlcosα

Отсюда:

N=mg(l−0,25)sinαlcosα

Так как косинус и синус угла 45^о равны, получим:

N=mg(l−0,25)l=2·10(1−0,25)1=15 (Н)

Задание EF17982

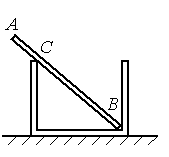Однородный стержень АВ массой 100 г покоится, упираясь в стык дна и стенки банки концом В и опираясь на край банки в точке С (см. рисунок). Модуль силы, с которой стержень давит на стенку сосуда в точке С, равен 0,5 Н. Чему равен модуль горизонтальной составляющей силы, с которой стержень давит на сосуд в точке В, если модуль вертикальной составляющей этой силы равен 0,6 Н? Трением пренебречь.

Ответ:

а) 0,3 Н

б) 0,25 Н

в) 0,6 Н

г) 0,13 Н

---

Алгоритм решения

1. Записать исходные данные и перевести единицы измерения величин в СИ.
2. Выполнить чертеж. Выбрать ось вращения. Указать силы и их плечи.
3. Использовать второй и третий законы Ньютона, чтобы выполнить общее решение.
4. Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса стержня: m = 100 г.
• Модуль силы, с которой стержень давит на стенку сосуда в точке С: F_C = 0,5 Н.
• Модуль вертикальной составляющей силы, с которой стержень давит на сосуду в точке В: F_By = 0,6 Н.

Переведем единицы измерения в СИ:

100 г = 0,1 кг

Выполним чертеж:

Поскольку стержень покоится, согласно второму закону Ньютона, равнодействующая всех сил, действующих на него, должна быть равна нулю. На стержень действует три силы:

• сила тяжести (mg);
• сила реакции опоры в точке С (F_C);
• сила реакции опоры в точке В (F_В).

Поэтому:

m→g+→FC+→FB=0

Запишем проекции на оси Ox и Oy соответственно:

FCx=FBx

FCy+FBy=mg

Модуль горизонтальной составляющей силы в точке В можно выразить через теорему Пифагора:

FCx=√F2C−F2Cy

Но вертикальная составляющая силы в точке C равна разности силы тяжести и горизонтальной составляющей силы в точке В:

FCy=mg−FBy

Отсюда:

FBx=FCx=√F2C−F2Cy=√F2C−(mg−FBy)2

Подставим известные данные и вычислим:

FBx=√0,52−(0,1·10−0,6)2=√0,25−0,16=0,3 (Н)

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18697

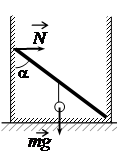Невесомый стержень, находящийся в ящике с гладкими дном и стенками, составляет угол 45° с вертикалью (см. рисунок). К середине стержня подвешен на нити шарик массой 1 кг. Каков модуль силы упругости N, действующей на стержень со стороны левой стенки ящика?

---

Алгоритм решения

1.Записать исходные данные.

2.Записать правило моментов.

3.Выполнить решение в общем виде.

4.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Угол между стержнем и стенкой ящика: α = 45^o.

• Масса шарика: m = 1 кг.

Чтобы записать правило моментов, нужно определить плечи силы тяжести и силы упругости. В качестве точки равновесия выберем точку опоры нижнего конца стержня. Тогда плечо силы тяжести будет равно произведению половины длины стержня на косинус угла между дном ящика и стержнем. Он тоже будет равен 45 градусам, так как он равен разности 180 градусов и угла α = 45^o. Отсюда:

dmg=l2cosα

Плечо силы упругости будет равно расстоянию от дна ящика до верхней точки стержня. Оно определяется как произведение длины стержня на синус угла α:

dN=lsinα

Запишем правило моментов:

mgl2cosα=Nlsinα

Отсюда:

N=mgl2lsinαcosα

Длина стержня в числителе и знаменателе сократится, косинус и синус угла тоже, так как при 45 градусах они одинаковые. Следовательно:

N=mg2=1·102=5 (Н)

Ответ: 5

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 7.8k

Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.

Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!

Что же давай приступим к изучению!

Построение эпюры продольных сил

В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.

Что такое эпюра?

Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.

Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.

Что такое продольная сила?

Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.

Расчёт эпюры продольных сил

Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.

То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.

Правило знаков для продольных сил

Правило знаков для продольных сил следующее:

• если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
• если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках

На первом участке сила F₁ растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:

Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F₁, также действует сила F₂, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:

Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке

Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.

Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.

Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:

То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.

Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:

А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.

Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.

Построение эпюры нормальных напряжений

В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.

Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.

Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A₁=2 см², а на втором и третьем A₂ = A₃ = 4 см².

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.

Построение эпюры осевых перемещений поперечных сечений

Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.

Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:

Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.

Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:

А также удлинения (или укорочения) участка между расчетными сечениями:

В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).

Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.

Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.

Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину W_D (т. к. значение W_D — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.

Учёт распределённой нагрузки

А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил

На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:

Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:

Рассчитываем продольную силу на третьем участке:

Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений

Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений

Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче: 

Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):

Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.

Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.

То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.

Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:

Отмечаем найденное значение на эпюре перемещений:

Пусть для двух концевых сечений стержня 5 = 0 и 8 = 1, причем I положительно. Тогда А а В можно определить как суммы компонент по осям хну внешних сил давления, действующих на конец стержня 5 = 0. Вместо Л и Б введем суммы соответственных компонент внешних давлений, действующих на другой конец стержня. Обозначим их через X и У, тогда получим  [c.355]

Пример. К узлам фермы (фиг. 23, а) приложены шесть внешних сил три сверху по I т каждая и три снизу по 2 т каждая, требуется определить реакции опор и силы, действующие на стержни фермы.  [c.42]

Во многих деталях стержневой формы основная нагрузка действует вдоль оси стержня (штоки прессов, шатуны, рабочие лопатки паровых турбин и пр.), которые в этих условиях растягиваются или сжимаются. Используя метод сечений, можно установить, что в любом сечении растянутого (сжатого) стержня равнодействующая внутренних спл Р равна внешней силе Q, действующей на оставшуюся часть стержня (рис. 2).  [c.7]

Внешняя сила О, действующая на клин при его забивании, определяется из условия равновесия сил, действующих на клин и расположенных поперек стержня.  [c.132]

Рассматривая растяжение и сжатие стержней, мы учитывали действие на стержни только внешних сил. Но, кроме внешних сил, на напряжения и деформации стержня влияет его собственный вес.  [c.19]

Второе уравнение получается из условия равенства нулю полного момента сил, приложенных к данному элементу. Пусть М есть момент сил внутренних напряжений, действующих на площадь сечения стержня. Этот момент берётся относительно точки (начала координат), лежащей в самой плоскости этого сечения его компоненты определяются формулами (18,6). Будем вычислять суммарный момент, приложенный к данному элементу стержня, относительно точки (назовём её точкой О), лежащей в плоскости его верхнего основания. Тогда внутренние напряжения на этом основании дают момент M + dM. Момент же (относительно О) сил внутренних напряжений в нижнем основании элемента складывается из момента — М этих сил относительно начала координат в плоскости нижнего основания (точка О ) и момента (относительно О) суммарной силы — F, действующей на этом основании. Этот второй момент равен [(—dl)(—F)], где d — вектор элемента длины стержня от О к О. Момент же, обусловленный внешними силами К, является малой величиной высшего порядка. Таким образом, полный действующий на элемент стержня момент сил есть dM-j-[dIF]. В равновесии он должен быть равным нулю  [c.728]

Кручение возникает при действии на стержень внешних сил, образующих момент относительно оси стержня (рис. 5). Деформация кручения сопровождается поворотом поперечных сечений стержня относительно друг друга вокруг его оси. Угол поворота одного сечения стержня относительно другого, находящегося на расстоянии  [c.10]

Для практического вычисления усилий и моментов в сечении следует иметь в виду следующее N численно равно алгебраической сумме проекций на ось стержня (на нормаль к сечению) всех внешних сил, действующих на одну из частей (левую или правую) рассеченного стержня Qy — то же, но на ось у — то же, но на ось 2 Мкр численно равен алгебраической сумме моментов относительно оси стержня всех внешних сил, действующих на одну из частей (левую или правую) рассеченного стержня Му — то же относительно оси у, — то же, но относительно оси г. К этому выводу легко прийти, если рассмотреть равновесие каждой из частей рассеченного стержня. При этом сумма проекций (или моментов) сил, расположенных слева от сечения, должна быть приложена к правой стороне сечения и наоборот.  [c.38]

Брус прямоугольного сечения. На практике часто встречаются стержни некруглого сечения, подверженные действию крутящих и изгибающих моментов. В качестве примера рассмотрим брус прямоугольного сечения (рнс. 341, а), нагруженный силами Pi и Pj, вызывающими в поперечных сечениях изгибающие моменты и а также поперечные силы Qy и Расчет выполняем в такой последовательности. Раскладываем заданные нагрузки (силы Pi и Pj) на составляющие вдоль координатных осей и приводим их к оси вала при этом получаем в поперечных сечениях, в плоскостях которых находятся точки приложения сил, внешние скручивающие моменты и Mwi = Mix- Полученная таким образом расчетная схема представлена на рис. 341, б.  [c.349]

Итак, для нахождения внутренних усилий необходимо 1) разрезать стержень или систему стержней 2) отбросить одну часть 3) приложить в сечении усилия, способные уравновесить внешние силы, действующие на отсеченную часть 4) найти  [c.16]

Пример 9. Применить леммы о пулевых стержнях к определению незагруженных стержней ферм, изображенных вместе с действующими на них внешними силами и реакциями опор (рис. 46—50).  [c.33]

Усилия, возникающие во всех стержнях под действием внешних нагрузок, определены. Теперь рассмотрим узел К. Вырезав этот узел и составив для сил У5, Уб, и N4, действующих на него,  [c.147]

Метод Риттера. Диаграмма Максвелла — Кремоны дает усилия во всех стержнях фермы путем последовательного построения связанных между собой силовых многоугольников методом Риттера можно определить усилие для любого стержня фермы непосредственно, независимо от остальных. Этот метод состоит в том, что ферма рассекается на две части таким образом, чтобы в сечении было не более трех стержней с неизвестными усилиями отбрасывая отсеченную часть фермы и рассматривая оставшуюся часть фермы в равновесии под действием приложенных к ней внешних сил и усилий, заменяющих действие рассеченных стержней, получим для этой части фермы три уравнения равновесия, в которые войдут три неизвестных усилия. Эти уравнения удобно брать в виде равенства нулю суммы моментов всех сил. действующих на оставшуюся часть фермы, относительно трех различных центров (см. 24, п. 2), принимая за центры моментов те точки, в которых попарно пересекаются рассеченные стержни (или их продолжения) тогда уравнение моментов для каждого центра будет содержать только одно неизвестное, а именно усилие в том стержне, направление которого через этот центр не проходит.  [c.270]

Пример. Рассмотрим ферму, изображенную на рис. 284, вместе с действующими на нее внешними активными силами и реакциями опор и определим усилие S47 в стержне 47. Проведем сечение хх, пересекающее  [c.270]

Определить модуль главного вектора внешних сил, действующих на шатун АВ кри-вошипно-ползунного механизма в момент If/////)/ времени, когда угол ф = 180, а точки А. и В имеют ускорения = 10 м/с , Дд = = 14 м/с . Шатун массой m = 5 кг считать однородным стержнем. (60)  [c.223]

По заданному уравнению вращения = = 2(г + 1) наклонного стержня с осевым моментом инерции = 0,05 кг определить главный момент внешних сил, действующих на тело. (0,2)  [c.263]

По заданному уравнению вращения = = 3/ – 1 стержня с осевым моментом инерции = V кг м определить главный момент внешних сил, действующих на стержень. (1)  [c.263]

Для определения граничных условий на поверхности стержня замечаем, что благодаря малой толщине стержня действующие на его боковую поверхность внешние силы малы по сравнению  [c.88]

Аналогично тому, что мы имели в случае изгиба пластинок и кручения стержней, и при изгибе тонких стержней внешние силы, действующие на боковую поверхность стержня, малы по сравнению с возникающими внутри стержня напряжениями, и при определении граничных условий на этой поверхности их  [c.93]

Если рассматривать два бесконечно близких сечения как поверхности оснований вырезаемого ими элемента стержня, то на верхнее основание действует сила F + dF, а на нижнее—сила—F их сумма есть дифференциал dF. Пусть далее К есть действующая на стержень внешняя сила, отнесенная к единице его длины. Тогда на элемент длины dl действует внешняя сила К dl. Равнодействующая всех сил, действующих на этот элемент, есть, следовательно, dF + К dl. В равновесии эта сила должна обращаться в нуль. Таким образом, получаем  [c.102]

Если действующие на стержень внешние силы являются, как говорят, сосредоточенными, т. е. приложены только к отдельным изолированным его точкам, то на участках стержня между точками приложения сил уравнения равновесия заметно упрощаются. Из (19,2) имеем при К = О  [c.103]

Решение. Механической системой здесь будет стержень ОА. Пусть положение О А есть промежуточное положение этого стержня. Внешними силами, действующими на стержень, будут сила веса Р и реакция М со стороны шарнира в точке О.  [c.650]

На рис. 1.1 показаны два положения стержня положение 1 соответствует ненагруженному состоянию (естественному), положение 2 —нагруженному состоянию. Под действием медленно нарастающих сил Р и моментов Т (рассматривается статика) стерл<ень, деформируясь, переходит из состояния 1 в состояние 2. Из рис. 1.1 следует, что упругие перемещения могут быть настолько большими, что форма осевой линии нагруженного стержня может как угодно сильно отличаться от первоначальной. Внешние силы в процессе деформации стержня могут также сильно изменяться по направлению (на рис. 1.1 направления векторов Рг и Тг в момент приложения к стержню показаны пунктиром).  [c.15]

В прикладных задачах возможны и более сложные случаи поведения внешних нагрузок, когда часть нагрузок, приложенных к стержню, являются следящими, а часть — мертвыми , или когда только отдельные проекции нагрузок являются следящими или мертвыми . На рис. 1.14 показан консольный стержень, на конце которого установлен реактивный двигатель. В результате стержень нагружается двумя силами силой тяжести Pi — мертвой силой и силой тяги Рг —следящей силой. Возможны и случаи (рис. 1.15), когда линия действия внешней силы в процессе нагружения стержня должна проходить через фиксированную точку (точка А). В этом случае проекции силы как  [c.28]

Приведенные выше соображения относятся к тому простому случаю, когда внешнюю силу, действующую на конец стержня, можно считать заданной, т. е. считать, что она не зависит от характера движения конца стержня. Но это предположение справедливо только при определенных условиях. Чтобы выяснить, каковы должны быть эти условия, рассмотрим механизм, который на конец стержня может действо-  [c.688]

Рассмотренные случаи, когда жесткость связи, через которую действует внешняя сила, либо гораздо меньше, либо гораздо больше жесткости стержня, позволяют считать заданными соответственно либо внешнюю силу, либо движение конца стержня. Если же жесткость связи и жесткость стержня сравнимы между собой и задачу нельзя отнести ни к тому, ни к другому из рассмотренных предельных случаев, то не могут быть заданы ни сила, действующая на стержень, ни движение конца стержня. В этом случае приходится рассматривать взаимодействие стержня и приводящего его в колебание механизма, вследствие чего задача очень усложняется. Для того чтобы осуществить случай заданного движения конца жесткого сплошного стержня, потребовался бы очень жесткий механизм, приводящий в движение конец стержня. Но о помощью камертона на струне случай заданного движения легко может быть реализован (рис. 442).  [c.689]

Учтя все сказанное, мы можем констатировать, что частоты нормальных колебаний стержня и частоты действующей на стержень внешней силы, при которых амплитуды стоячих волн в пучностях достигают максимума, при аналогичных краевых условиях совпадают при одинаковых краевых условиях на обоих концах стержня на длине стержня должно укладываться целое число полуволн, а при разных краевых условиях на обоих концах стержня — нечетное число четвертей волн.  [c.692]

Тепловой эффект при деформации упругих твердых тел. Предположим для определенности, что упругий твердый стержень, находящийся в среде с постоянными давлением и температурой, подвергается растяжению внешней силой. Работа упругих сил стержня при удлинении на у равняется — Рду (здесь Р — внешняя сила, действующая на стержень Р/И — напряжение,  [c.160]

Анализируем систему сил, которые действуют на стержни. Во-первых, для стержневой системы в целом внешними будут силы Р, приложенные в узлах С, В и , а также реакция со стороны опоры в шарнире А. В шарнире А отсоединяем опору и ее действие заменяем реактивной силой. Конструкция находится под действием плоской симметричной системы параллельных сил. Для такой системы можно записать только одно независимое уравнение равновесия. Это может быть или равенство нулю суммы проекций сил на ось, параллельную силам, или равенство нулю суммы моментов относительно любой точки, не лежащей на оси симметрии. Запишем С5шму проекций сил на вертикальную ось у и найдем реакцию  [c.40]

Решение, Применим к внешним силам и силам инерции, действующим на стержень АВ, следствия из принципа Даламбера в форме шести условий равновесия. Неизвестные реакции Рд н векторный момент в заделке Мд разложим по осям координат. Если разбить весь стержень на элементарные участки одинаковой длины, то ускорения средни этих участков распределятся вдоль стержня по линепно.му закону (рнс. 261, б), так как ускорение каждой точки стержня  [c.348]

Р е ш е и и е. П е р в ы й шаг. Внешними св.Шямп для стержня АВ служат угол и выступ. Отбросив их и заменив соответствующими реакциями, рассмотрим стержень как свободное тело, находящееся под действием произвольной плоской системы сил. Реакцию, действующую на стержень в точке А, представим в виде двух неизвестных составляющих (см. 1.4). Реакция выступа в точке С направлена перпендикулярно стержню, так как стержень по условию задачи гладкий (рис. 1.54, б).  [c.59]

Эпюра Су на этом участке отложена влево от оси стержня (проекция на ось1/ внешней силы Ив, действующей на отсеченную часть, направлена вправо).  [c.108]

Векториое определение усилий. Начнем с рассмотрения какой угодно неизменяемой системы без лишних стержней (неособой), п узлов которой пусть будут Pi, Р ,…, и, как в 2, обозначим через F , F , , F соответствующие внешние, прямо приложенные силы, предполагая, что все они лежат в плоскости системы. Конфигурация системы здесь задана, а в конкретных задачах следует считать известными таклсе и положения отдельных узлов, так что речь будет идти об определении усилий, которым под действием указанной системы внешних сил подвергается каждый отдельно взятый стержень. После того как будут найдены усилия, действующие на стержни, на основании принципа равенства действия и противодействия можно также определить и силы, действующие на узлы.  [c.171]

В прикладных задачах статики стержней часто внешние силы, действующие на стержни, зависят от перемещений стержня (или от их первых двух производных). Классическим примером являются стержни на упругом основании (рис. 2.1). При нагружении стержня возникают со стороны основания распределенные силы, зависящие от перемещений (прогибов) стержня. Стержни (вернее конструкции или элементы конструкций, которые сводятся к модели стержня) из разных областей техники показаны на рис. 2.2 — 2.6. Упругий металлический элемент прибора, находящийся в магнитном поле, изображен на рис. 2.2. Сила притяжения (распределенная) зависит от прогибов стержня аналогично случаю балки на упругом основании. Стержень, находящийся на вращаю.щейся платформе (см. рис. 2.3), нагружается силами, зависящими от прогибов, причем в этом случае наряду с нормальной распределенной нагрузкой qy (у) появляется и осевая распределенная нагрузка у). При продольно-поперечном изгибе (см. рис. 2.4) в произвольном сечении стержня возникает момент от осевой силы, пропорциональный прогибу. К этому классу относятся задачи статики трубопроводов, зашолненных движущейся жидкостью. При поперечном изгибе трубопровода (см. рис. 2.5) из-за появляющейся кривизны осевой линии стержня возникают распределенные силы, обратно пропорциональные радиусу кривизны. К этому классу можно причислить задачи, относяшд1еся к плавающим объектам и сводящиеся к схеме стержней (см. рис. 2.6), например понтон.  [c.33]

Решение. Пользуясь принципо> Даламбера, присоединяем к действующим на стержень внешним силам f, Т, Х , силы инерции. Для каждого элемента стержня с массой Ат центробежная сила инерции равна Атагах, где х — расстояние элемента от оси вращения Оу. Равнодействующая этих-распределенных по линейному закону параллельных сил (см. 21) проходит через центр тяжести треугольника АВЕ, т. е. на расстоянии h=(2l/3) os а от оси Ах. Так как эта равнодействующая равна главному вектору сил инерции , то по формуле (89)  [c.352]

Для графического определения усилий в стержнях фермы удобно пользоваться методом вырезаьия узлов , который состоит в том, что каждый узел вырезывается из фермы и рассматривается отдельно, как находящийся в равновесии под действием приложенных к нему внешних сил и реакций разрезанных стержней, которые направлены по стержням в сторону узла, если усилие сжимающее, и в противоположную, — если усилие растягивающее. Система сил, действующих на узел, есть плоская система сходящихся сил, находящаяся в равновесии поэтому силовой многоугольник, построенный из этих сил, должен быть замкнутым. Построение многоугольников следует начинать с узла, в котором сходятся два стержня. Так как действующие на узел внешние силы (активные и реакции опор) известны, то построением замкнутого многоу ольника (треугольника) найдутся усилия в этих двух стержнях. После этого можно переходить к следующему узлу и т. д. при этом каждый следующий узел выбирается так, чтобы в нем сходилось не более двух стержней, для которых усилия еще не найдены. Построив силовые многоугольники для всех узлов фермы, графически определим усилия в стер>йнях.  [c.267]

Переходим к определению внутренних усилий в стержнях фермы. Как уже было сказано (см. задачу № 8), усилием в стержне называют силу, действующую вдоль стержня, растягивающую или сжимающую его если стержень растянут, то на шарнир действует сила, направленная к стержню, а если сжат, то от него. В уравнения равновесия, выводимые в статике твердого тела, входят только внешние силы, потому что внутренние силы согласно принципу равенства действия и противодействия jjonapno равны и противоположны.  [c.90]

Внешние силы, действующие на систему силы тяжести стержня, шаров и реакция закрепления на оси вращения. Моменты этих сил относительно оси Z будут равны нулю. Следовательно, используя уравнение вращения тела вокруг оси, найдем что 2УгЫ при обоих положениях щаров будет неизменна. Обозначим момент инерции стержня относительно оси Z через /г. Принимая щары за материальные точки массы m = G/g, найдем  [c.319]

Учет сил взаимодействия стержня с внешним потоком приводит к более сложным задачам по сравнению с задачами, рассмотренными в предыдущих главах. На рис. 6.1 показан элемент стержня,, находящийся в потоке воздуха произвольного направления (скорость потока Vo) с действующими на него аэрогидродинамически-ми силами qa, q и qi. Стержни, находящиеся в потоке, могут очень сильно отклоняться от первоначальной (без потока) равновесной формы, а От формы осевой линии стержня (угла фа между касательной к осевой линии стержня — вектором ei на рис. 6.1 и вектором местной скорости Vo потока) зависят аэродинамические силы. Получить общие аналитические выражения для возникающих аэродинамических сил, учитывающих непрерывное изменение этого угла в процессе нагружения стержня потоком, можно только экспериментально-теоретическим методом путем обобщения экспериментальных данных частных случаев обтекания стержня потоком.  [c.229]

Многие преподаватели не решают задачи на определение допускаемой нагрузки, так как, вероятно, опыт подсказывает им, что для учащихся задачи этого типа труднее других. Конечно, идти по ЛИНИН наименьшего сопротивления в ущерб знаниям и навыкам учащихся непозволительно. Определение допускаемой нагрузки целесообразно отрабатывать на стержневых системах, при их решении надо составить условие прочности для каждого из. двух—четырех стержней, входящих в систему. Продольные силы, возникающие в поперечных сечениях стержней, должны быть на основе метода сечений выражены через внешнюю силу, действующую на систему. Из условий прочности будут определены два (три или четыре) допускаемых значения силы. Далее очень важно, чтобы учащиеся сами правильно решили вопрос о том, какое из этих значений искомо (наименьшее). Необходимо проверить, что правильный ответ не случаен, учащиеся доллгны ясно и логично его обосновать.  [c.84]

При построении эпюр на III участке (рис. 6-8, г) целесообразно предварительно заменить силы, действующие на остазленную часть, силой и парой, приложенными в сечении С (привести силы к точке С по правилам статики твердого тела). Отсеченная часть стержня с приложенными к ней внешними и внутренними силами показана отдельно на рис. 6-8, д. Внешняя сила, приложенная справа от сечения, направлена вниз, поэтому эпюра Qy на этом участке отложена вверх. Изгибающий момент меняется по линейному закону, причем в начале участка сжаты верхние волокна, в конце участка — нижние. На IV участке (рис. 6-8, ё)  [c.104]

---

Содержание:

1. Расчет усилий в стержнях фермы
2. Простые фермы
3. Определение усилий в стержнях фермы
4. Определения усилий в стержнях фермы
5. Порядок решения задач на тему: Расчет усилий в стержнях фермы
6. Способ вырезания узлов
7. Способ сечений (метод Риттера)
8. Примеры решения задач на тему: Расчет усилий в стержнях фермы

Расчет ферм состоит в определении продольных усилий в стержнях, а также перемещений отдельных узлов. Настоящий параграф посвящен определению усилий в стержнях ферм. Для нахождения внутренних усилий мысленно разрезают ферму на две части и рассматривают условия равновесия одной из частей, к которой прикладывают внешние силы и пока неизвестные усилия в разрезанных стержнях.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Расчет усилий в стержнях фермы

Фермой называется конструкция, состоящая из стержней, соединённых между собой шарнирами, которые называются узлами фермы. Внешняя нагрузка на ферму передаётся через эти узлы. Каждый стержень в ферме находится в условиях простого осевого растяжения – сжатия, но общая деформация фермы – изгибная, то есть ферма работает на изгиб.

Простые фермы

Фермой называется геометрически неизменная конструкция, состоящая из стержней, соединенных между собой на концах шарнирами (рис.6.1).

Шарниры, соединяющие стержни между собой, называются узлами фермы. Стержни, расположенные внутри контура фермы, образуют ее решетку. Если все стержни, образующие ферму, расположены в одной плоскости, то такая ферма называется плоской.

При расчете ферм принимается, что весом стержней можно пренебречь и шарниры расположены на концах стержней. Поскольку нагрузки, действующие на ферму, передаются в шарнирах, то каждый стержень будет воспринимать усилие, которое направлено вдоль оси стержня, то есть будет либо растянут или сжат.

Среди разнообразных типов ферм различают два основных вида:

1. фермы без лишних стержней.

2. фермы, в которых есть лишние стержни.

В дальнейшем будем рассматривать простые плоские фермы, которые строятся следующим образом: к основному стержневому треугольнику двумя стержнями присоединяется новый шарнир (узел), к него второй и т.д.

По своему назначению фермы подразделяются в основном на мостовые, стропильные и крановые (рис.6.1 а, б, в).

Зависимость между числом стержней и числом узлов    для фермы без лишних стержней имеет вид:

Если , то число стержней является недостаточным для обеспечения геометрической неизменности фермы. Если же , то ферма имеет лишние стержни.

При расчете ферм предполагается, что выполняются следующие условия:

1. все стержни фермы – прямолинейные.

2. трение в шарнирах отсутствует.

3. силы, действующие на ферму, лежат в плоскости этой фермы и приложены только к ее узлам.

4. собственный вес каждого стержня фермы настолько мал по сравнению с силами приложенными к узлам фермы, что им можно пренебречь.

Основной задачей расчета простых ферм является определение усилий в стержнях фермы, которые представляют собой внутренние силы, возникающие в стержнях под действием внешних сил.

Определение усилий в стержнях фермы

Ограничимся двумя аналитическими способами определения усилий в стержнях простых ферм:

1. способ вырезания узлов.

2. способ сечений (метод Риттера).

Способ вырезания узлов состоит в том, что каждый узел вырезают из фермы и рассматривают отдельно в равновесии под действием приложенных к нему внешних сил и усилий разрезанных стержней.

Метод Риттера позволяет определить усилия в любом стержне фермы независимо от усилий в других стержнях и заключается в том, что ферма рассекается на две части таким образом, чтобы в сечении было не более трех стержней с неизвестными усилиями.

Определения усилий в стержнях фермы

Определение усилий в стержнях ферм упрощается, если при рассмотрении равновесия узла встречаются следующие случаи.

1. Узел фермы с двумя стержнями без нагрузка (рис.6.2).

В этом случае усилия в каждом из стержней равны нулю, поскольку иначе равновесие узла было бы невозможно.

2. Узел фермы с двумя стержнями, по оси одного из которых приложена сила  (рис.6.3).

Реакция стержня, с осью которого совпадает направление силы, по модулю равна, а по направлению противоположна силе . Усилие же во втором стержне равно нулю.

3. Узел фермы с тремя стержнями, оси двух стержней которого направлены вдоль прямой (рис.6.4).

В этом случае усилие в третьем стержне равно нулю, а в каждом из первых двух или тоже равны нулю, либо равны между собой по величине и направлены в противоположные стороны, то есть эти стержни либо не подвергаются нагрузкам, либо оба сжаты (растянуты) с одинаковыми силами.

4. Узел фермы с тремя стержнями, у которого оси двух стержней направлены вдоль одной прямой, а по направлению оси третьего стержня приложена сила (рис.6.5).

В этом случае реакция третьего стержня по величине равна, а по направлению противоположна силе . Усилия в первых двух стержнях либо равны нулю, либо равны между собой по величине и направлены в противоположные стороны.

5. К узлу фермы с тремя стержнями с осью одного из стержней приложена сила , а усилие в одном из двух других стержней равно нулю (рис.6.6).

В этом случае реакция стержня, ось которого совпадает с линией действия силы , по величине равна, а по направлению противоположна силе .Усилия во втором и третьем стержнях равны нулю.

6. Узел фермы с четырьмя стержнями, в которой оси стержней попарно расположены по одной прямой (рис.6.7).

В этом случае усилия или:

а) равны нулю в каждом стержне;
б) равны нулю только в двух стержнях, что расположены по одной прямой, а в двух других равны по модулю и противоположны по направлению;
в) для каждой пары стержней, что расположены по одной прямой, равны между собой по модулю и противоположны по направлению.

Порядок решения задач на тему: Расчет усилий в стержнях фермы

Существует два способа:

Способ вырезания узлов

1. Выделить ферму, равновесие которой надо рассмотреть для нахождения неизвестных величин.

2. Приложить активные силы, действующие на объект равновесия.

3. Отбросить связи и заменить их действие реакциями.

4. Рассмотреть равновесие фермы, как твердого тела, под действием активных сил и реакций связей.

5. Определить реакции опор.

6. Вырезать узел, к которому сходятся два стержня и рассмотреть его равновесие под действием активных сил и реакций разрезанных стержней. (При выборе направления реакции стержня, лучше принимать что он растянут, то есть направлять реакцию от узла стержня).

7. Пользуясь условиями равновесия плоской системы сходящихся сил, определить реакции разрезанных стержней.

8. Двигаясь по ферме от узла к узлу, аналогично рассматривается равновесие каждого узла. При этом, в каждом последующем вырезанном узле должно быть только два стержня, реакции в которых неизвестны.

Способ сечений (метод Риттера)

1. Определить опорные реакции, рассматривая равновесие фермы как твердого тела, находящегося под действием плоской системы сил.

2. Мысленно разрезать ферму, к которой приложены все внешние силы, на две части таким образом, чтобы число разрезанных стержней не было больше трех.

3. Отбросить одну из частей фермы и заменить ее действие реакциями разрезанных стержней. (Рекомендуется принимать, что все стержни растянуты).

4. Рассмотреть равновесие выбранной части фермы под действием активных сил и реакций разрезанных стержней. (При составлении условий равновесия лучше руководствоваться тем, чтобы в каждое уравнение входила одна неизвестная реакция. Для этого, за центр моментов выбирают точку, где пересекаются линии действия двух неизвестных реакций, а в случае, когда два разрезанных стержня параллельны, составляют уравнение проекций на ось, которая перпендикулярна этим стержням).

5. Решить составленную систему уравнений, определить неизвестные усилия в стержнях.

Примеры решения задач на тему: Расчет усилий в стержнях фермы

Ферма (рис.6.8) нагружена вертикальными силами , ,  и .

Определить опорные реакции и усилия в стержнях, если 

Решим задачу первым способом – методом вырезания узлов.

Для определения опорных реакций рассмотрим равновесие фермы в целом.

На ферму действуют активные силы , ,  и  и реакции опор  и .

Свяжем с фермой систему координат : ось направим горизонтально через опоры  и ; ось – вертикально вверх.

Реакция шарнирно-подвижной опоры направлена перпендикулярно опорной поверхности, то есть вертикально. Поскольку все активные силы и реакция перпендикулярны оси , то и реакция шарнирно-неподвижной опоры тоже будет перпендикулярна оси .

Составим уравнения равновесия для системы сил, действующей на ферму:

где 

Из второго уравнения получим :

Из первого уравнения найдем :

После определения реакций опор перейдем к определению усилий в стержнях. Для этого надо рассмотреть равновесие каждого узла фермы в отдельности, мнимо отбросив все сходящиеся к нему стержни и заменив их действие на узел реакциями.

Первыми надо рассматривать узлы, к которым приложены только две неведомые силы. В данной задаче таким требованиям соответствуют два узла  и . Расчет можно начинать с любого из этих узлов.

Начнем с узла . Узел находится в равновесии под действием реакции , активной силы и неизвестных реакций и стержней 1 и 5 (рис.6.9). 

Реакции стержней направим от узла, предполагая, что стержни растянуты.

Через точку проводим оси  и  и составляем уравнения равновесия плоской системы сходящихся сил:

Решив последовательно уравнения (4) и (3), получим:

Отрицательное значение реакции указывает на то, что действительное ее направление в противоположную показанному на рис.6.9. Стержень 5 не растянут, а сжат. Стержень 1 – растянут.

Следующим рассмотрим узел , поскольку к узлу надо будет приложить три неизвестных реакции и , а к узлу – только две – и , усилие в стержне 5 этого узла уже определено.

Узел находится в равновесии под действием: активной силы ; известной реакции , которая по величине равна реакции , приложенной к узлу , но направлена в противоположную сторону; неизвестных реакций и стержней 4 и 6 (рис.6.10).

Проведем через точку оси координат и составим уравнения равновесия узла:

Из уравнения (5) выразим :

Подставим выражение для в (6) и найдем :

Тогда:

Таким образом, стержень 6 растянут, как и предполагалось, а стержень 4 – сжат.

Следующим вырезаем узел .

К узлу приложены две неизвестные реакции и стержней 7 и 2; две известные реакции , и , стержней 6 и 1, которые за величинами равны реакциям и , приложенным соответственно к узлам и , но направлены в противоположные стороны (рис.6.11).

Проводим через точку координатные оси и составляем уравнения равновесия узла :

Из уравнения (8) найдем

Из уравнения (7) находим :

Таким образом, стержень 2 растянут, а стержень 7 – сжат.

Рассмотрим равновесие узла  (рис.6.12).

На узел действуют неизвестна реакция стержня 3; активная сила ; известна реакция  стержня 4, которая по модулю равна реакции , приложенной к узлу , но противоположно направлена; известна реакция  стержня 7, которая по модулю равна реакции , что приложена к узлу , но противоположно направлена.

Через точку проводим оси координат  и . Поскольку на узел действует только одна неизвестная сила , то достаточно составить только одно уравнение равновесия:

Отсюда:

Стержень 3 – сжатый.

Таким образом определены усилия во всех стержнях фермы. Выяснено, что стержни 1, 2, 6 – растянуты, а стержни 3, 4, 5 и 7 – сжаты.

Рассмотрение равновесия узла (рис.6.13), позволяет проверить правильность расчета фермы.

Уравнения равновесия для узла :

Подставив в эти уравнения числовые данные, получим:

Уравнения (10) и (11) преобразуются в тождества, что указывает на правильность выполненного расчета.

Проверим, насколько верно определены усилия в отдельных стержнях фермы методом сечений (методом Риттера).

Для определения усилий в стержнях 1, 6, 4 рассечем ферму сечением на две части таким образом, чтобы в сечение попало не более трех стержней, усилия в которых неизвестны (рис.6.14). Отбросим правую часть фермы, заменив ее действие реакциями стержней  и . Реакции стержней направим от узлов и , представив, что все стержни растянуты (рис.6.15).

Таким образом, левая часть фермы будет находиться в равновесии под действием реакции опоры , активных сил  ,  и реакций стержней , .

Составим уравнения равновесия для левой части фермы.

Воспользуемся формой условий равновесия в виде 3-х уравнений моментов для произвольной плоской системы сил.

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех сил относительно трех произвольных центров, которые не лежат на одной прямой, были равны нулю:

Выберем за центры моментов точки:

, где пересекаются линии действия неизвестных реакций и ;

, где пересекаются линии действия неизвестных реакций   и ;

, где пересекаются линии действия неизвестных реакций и .

Из уравнения (12) определим реакцию :

где  – плечо сил и относительно центра ;

 – плечо реакции  относительно центра ,

Из уравнения (13) определим:

где  – плечо сил  и  относительно центра ;

 – плечо силы  относительно центра ,

 – плечо реакции  относительно центра ,

Из уравнения (14) найдем:

где  – плечо сил  и  относительно центра ,

 – плечо реакции  относительно центра ,

Таким образом, при определении усилий в стержнях фермы методом сечений, имеем что полностью совпадает с результатами, которые найдены методом вырезания узлов.

Ответ:      

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Момент силы
4. Пара сил
5. Произвольная система сил
6. Плоская произвольная система сил
7. Трение
8. Расчет ферм
9. Пространственная система сил
10. Произвольная пространственная система сил
11. Плоская система сходящихся сил
12. Пространственная система сходящихся сил
13. Равновесие тела под действием пространственной системы сил
14. Естественный способ задания движения точки
15. Центр параллельных сил
16. Параллельные силы
17. Система произвольно расположенных сил
18. Сосредоточенные силы и распределенные нагрузки
19. Кинематика
20. Кинематика твердого тела
21. Движения твердого тела
22. Динамика материальной точки
23. Динамика механической системы
24. Динамика плоского движения твердого тела
25. Динамика относительного движения материальной точки
26. Динамика твердого тела
27. Кинематика простейших движений твердого тела
28. Общее уравнение динамики
29. Работа и мощность силы
30. Обратная задача динамики
31. Поступательное и вращательное движение твердого тела
32. Плоскопараллельное (плоское) движение твёрдого тела
33. Сферическое движение твёрдого тела
34. Движение свободного твердого тела
35. Сложное движение твердого тела
36. Сложное движение точки
37. Плоское движение тела
38. Статика твердого тела
39. Равновесие составной конструкции
40. Равновесие с учетом сил трения
41. Центр масс
42. Колебания материальной точки
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки