Как найти силы сопротивления воздуха автомобиля

На расход топлива, в особенности при больших скоростях движения, значительное влияние оказывает сопротивление воздуха (аэродинамическое сопротивление), сила аэродинамического сопротивления пропорциональна квадрату скорости и рассчитывается по формуле
Pv = cx·S·v2·ρ/2,
где S – площадь фронтальной проекции автомобиля, м2; v – скорость движения автомобиля относительно воздуха, м/с; ρ – плотность воздуха, кг/м3; cх – коэффициент аэродинамического сопротивления.
Аэродинамическое сопротивление не зависит от массы автомобиля [2]. Площадь фронтальной проекции автомобиля определяется формой кузова и требованиям по обеспечению комфортного расположения водителя и пассажиров на сиденьях. Например, автомобиль большого класса может быть ниже, чем малого, так как сиденья у него зачастую располагаются ниже. У автомобиля малого класса из-за его небольшой массы и длины сиденья расположены выше над полом, и поэтому расстояние между передними и задними сиденьями меньше. Более прямое расположение водителя и пассажиров в автомобиле малого класса требует его большей высоты, но меньшей длины. Площади фронтальных проекций обоих автомобилей при этом почти одинаковы, но низкий и длинный кузов автомобиля большого класса аэродинамически более выгоден.
Мощность двигателя, необходимая для преодоления аэродинамического сопротивления, пропорциональна, следовательно, кубу скорости:
Nv = Pv·v/3600 (кВт),
где v — относительная скорость движения автомобиля, км/ч.
Коэффициент аэродинамического сопротивления, как видно из таблицы, представленной ниже, изменяется в широком диапазоне в зависимости от формы кузова автомобиля.
Аэродинамическое сопротивление различных автомобилей Кузов автомобиля
Мощность, необходимая для преодоления
аэродинамического сопротивления (кВт),
40 км/ч 80 км/ч 120 км/ч
Открытый четырёхместный 1,18 – 1,47 9,6 – 11 .8 31,0 – 40,5
Закрытый, с наличием углов и граней 0,96 – 1,18 8,0 – 9,6 26,4 – 30,8
Закрытый, с закруглением углов и граней 0,80 – 0,96 6,6 – 8,0 22,0 – 26,4
Закрытый понтонообразный 0,66 – 0,80 5,2 – 6,6 17,6 – 22,0
Закрытый, хорошо обтекаемый 0,52 – 0,66 3,7 – 5,2 13,2 – 17,6
Закрытый, аэродинамически совершенный 0,33 – 0,44 2,6 – 3,3 9,8 – 11,0
Коэффициент аэродинамического сопротивления устанавливается продувкой автомобиля или его макета в аэродинамической трубе или приближенно в ходе эксплуатационных испытаний. При испытаниях в аэродинамической трубе на макетах получаются менее точные значения, чем при тех же испытаниях на реальных автомобилях. Это вызвано тем, что на изменение сопротивления воздуха оказывают влияние неточности изготовления некоторых узлов и деталей автомобиля: ручек дверей, днища кузова, бамперов, зеркал заднего вида и т. д. Кроме того, значительное влияние на величину сх оказывает воздух, проходящий в кузов для охлаждения и вентиляции.

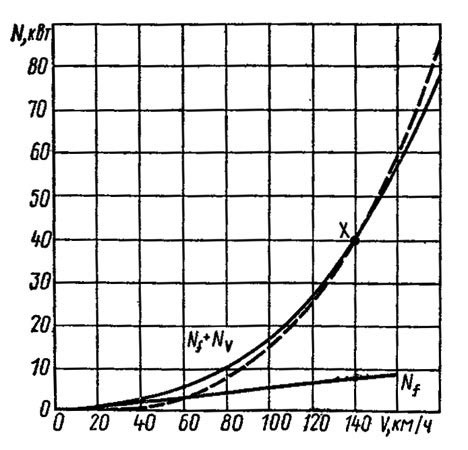
При больших скоростях движения автомобиля аэродинамическое сопротивление является преобладающим.

На рисунке ниже показано изменение мощностей, необходимых для преодоления сопротивления качению Nf и аэродинамического сопротивления Nv в зависимости от скорости v для автомобиля среднего класса. При скорости 60 км/ч мощности, необходимые для преодоления сопротивления качению и сопротивления воздуха, равны, что характерно для данного вида автомобилей. По сумме потребляемых мощностей можно убедиться в важности сопротивления воздуха. При скорости 80 км/ч мощность, затрачиваемая на его преодоление, в 4 раза больше, чем при скорости 40 км/ч, а при скорости выше, чем 120 км/ч, общая мощность, необходимая для движения, растет почти пропорционально кубу скорости автомобиля.

При определении мощности двигателя, необходимой для достижения максимальной скорости, большей той, которую обеспечивает номинальная мощность установленного на автомобиле двигателя, можно использовать без значительной ошибки следующее соотношение:

N2 = N1·(v2/v1)3,

где N2 – требуемая мощность, кВт; N1 – достигнутая максимальная мощность, кВт; v2 – требуемая скорость, км/ч; v1 – достигнутая максимальная скорость, км/ч.

Через точку X – максимальная мощность N1 при максимальной скорости v1 – проведена кривая зависимости мощности от куба скорости. Разница между этой кривой и линией мощности, требуемой для движения при максимальной скорости, незначительна.

Показанная сумма мощностей сопротивления качению Nf и аэродинамического сопротивления Nv представляет собой мощность сопротивления равномерному движению автомобиля по горизонтальному участку дороги при безветрии.

Сила сопротивления подъему

Вес
автомобиля, который движется на подъеме,
можно разло­жить на две составляющие
(см. рис. 3.12): параллельную и перпен­дикулярную
поверхности дороги. Составляющая силы
тяжести, параллельная поверхности
дороги, представляет собой силу
со­противления подъему, Н:

где
G
— вес
автомобиля
, Н; α-угол подъёма,ْ
.

В
качестве характеристики крутизны
подъема наряду с углом α
используют величину i,
называе­мую уклоном и равную
,
где
Н_п
— высота
подъема; В_п
—
длина
его проекции на горизон­тальную
плоскость.

Сила
сопротивления подъему может быть
направлена как в сто­рону движения,
так и против него. В процессе подъема
она дей­ствует в направлении,
противоположном движению, и является
силой сопротивления движению. При спуске
эта сила, направлен­ная в сторону
движения, становится движущей.

Зная
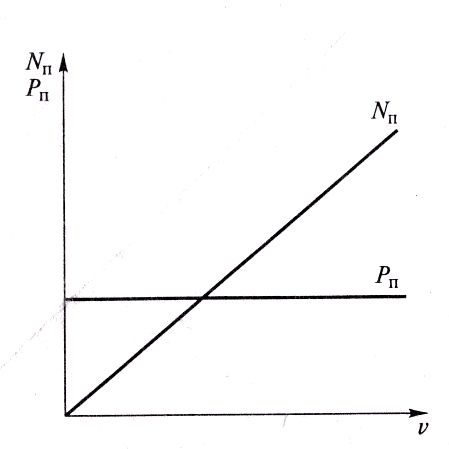
силу сопротивления подъему, можно
определить мощ­ность, кВт, необходимую
для преодоления этого сопротивления:

Рис.
3.16. Зависимости силы сопро­тивления
подъему Р_п
и
мощности N_п
,необходимой
для его преодоле­ния,
от скорости автомобиля

где

—
скорость автомобиля, м/с.

Зависимости
силы сопротивления подъему Р_п
и мощности N_П,
необходимой для преодоления этого
сопротивления, от скорости автомобиля
v
приведены
на рис. 3.16.

Сила сопротивления дороги

Сила
сопротивления дороги представляет
собой сумму сил со­противления качению
и сопротивления подъему:

или

Выражение
в скобках, характеризующее дорогу в
общем слу­чае, называется коэффициентом
сопротивления дороги:

При
малых углах подъема (не превышающих
5°), характерных для большинства
автомобильных дорог с твердым покрытием,
ко­эффициент сопротивления дороги

Сила
сопротивления дороги в этом случае

Зная
силу сопротивления доро­ги, можно
определить мощность, кВт, необходимую
для его преодо­ления:

Рис.
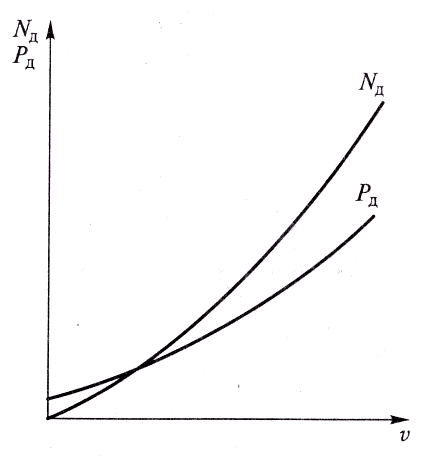
3.17. Зависимости силы сопро­тивления
дороги Р_д
и мощности N_д,
затрачиваемой
на его преодоление, от
скорости автомобиля

где
скорость автомобиля

выражена
в м/с, вес G
— в
Н, мощ­ность Nд
— в кВт.

Зависимости
силы сопротивления дороги Р_Д
и мощности
N_д,
затрачиваемой на его преодоление, от
скорости автомобиля

представлены
на рис. 3.17.

Сила сопротивления воздуха

При
движении действие силы сопротивления
воздуха обуслов­лено перемещением
частиц воздуха и их трением о поверхность
автомобиля. Если он движется при
отсутствии ветра, то сила со­противления
воздуха, Н:

тогда
как при наличии ветра

где
k_в
— коэффициент
сопротивления воздуха (коэффициент
об­текаемости), Н-с²/м⁴;
F_а
— лобовая
площадь автомобиля, м²;

—
скорость
автомобиля, м/с;
_в
— скорость
ветра, м/с (знак «+» со­ответствует
встречному ветру, знак «-» — попутному).

Коэффициент
сопротивления воздуха, зависящий от
формы и качества поверхности автомобиля,

Рис.
3.18. Площади лобового сопротивления
легкового (а)
и
грузового(б)
автомобилей

Рис.
3.20. Зависимости силы сопротивления
разгону Р_н
и
мощности
N_И,
необходимой для
преодоления этого сопро­тивления,
от скорости автомобиля

определяется
эксперимен­тально при продувке в
аэродинамической трубе.

Коэффициент
сопротивления воздуха, Н-с²/м⁴,
составляет 0, 2. ..0,35 для легковых
автомобилей, 0, 35. ..0, 4 — для автобусов и
0, 6. ..0, 7 — для грузовых автомобилей. При
наличии прицепов со­противление
воздуха увеличивается, так как возрастает
наружная поверхность трения и возникают
завихрения воздуха между
тягачомиприцепами.Приэтом45

каждый
прицеп вызывает увеличение коэффициента
k_в
в среднем на 15…25 %.

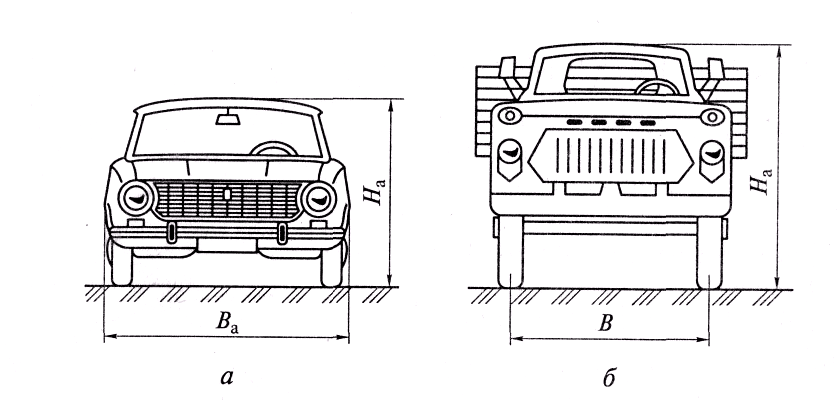
Лобовая
площадь автомобиля зависит от его типа
(рис. 3.18). Ее приближенное значение, м²,
можно вычислить по следующим фор­мулам:

— для
грузовых автомобилей и автобусов;

— для
легковых автомобилей,

где
B
— колея
колес автомобиля, м; Н_а
— наибольшая
высота автомобиля, м; В_а
— наибольшая
ширина автомобиля, м.

Мощность, кВт,
затрачиваемая на преодоление сопротивле­ния
воздуха:

—
отсутствии
ветра;

— при
наличии ветра.

Зависимости
силы сопротивления воздуха Р_B
и
мощности N_В,
необхо­димой для преодоления этого
сопро­тивления, от скорости автомобиля
v
приведены
на рис. 3.19.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Коэффицие́нт аэродинами́ческого сопротивле́ния — безразмерная величина, равная отношению силы лобового сопротивления автомобиля к произведению скоростного напора на площадь миделевого сечения автомобиля . Обычно обозначается как :

Скоростной, или аэродинамический напор, имеет размерность давления (в СИ измеряется в паскалях) и определяется как:

где  — скорость, м/с;

 — плотность воздуха, кг/м³.

Лобовое аэродинамическое сопротивление:

зависит только от формы автомобиля и числа Рейнольдса, при равенстве всех критериев подобия, в данном случае существенно число Рейнольдса, одинаков для всех геометрически подобных тел, независимо от их конкретных размеров. в широком диапазоне чисел Рейнольдса (Re), от ~1000 до ~10⁵ приблизительно постоянно. При малых Re увеличивается из-за перехода обтекающего потока в ламинарное течение, для автомобиля такое Re соответствует скорости нескольким десяткам сантиметрам в секунду. При Re>10⁵ наступает полное развитие турбулентности как на лобовой, так и на тыльной сторонах обтекаемого тела и снижается.

Чем меньше , тем меньше лобовое сопротивление движению автомобиля и меньше расход топлива при прочих равных условиях. современных легковых серийно выпускаемых автомобилей лежит в пределах от 0,2 до 0,35. У грузовых автомобилей и внедорожников, из-за плохо обтекаемого воздухом массивного кузова — до 0,5 и более.

Некоторые производители указывают в спецификациях эффективную площадь сопротивления автомобиля :

Эта величина равна площади тонкой плоской пластины, ориентированной перпендикулярно набегающему потоку и испытывающей равную силу сопротивления с автомобилем, движущемся с той же скоростью, так как тонкой пластины близок к 1. Эффективная площадь зависит не только от формы, но и от размеров автомобиля, точнее, от площади его миделева сечения. Эффективная площадь современных серийных автомобилей составляет от 0,5 м² для легковых до 2 и более квадратных метров у внедорожников и грузовиков.

Коэффициент сопротивления определяется экспериментальным путём продувкой макетов автомобилей в аэродинамической трубе, либо расчётным путём с помощью компьютерного моделирования.

Мощность двигателя, затрачиваемая на преодоление сопротивления воздуха[править | править код]

Мощность, затрачиваемая на перемещение тела с силой равна произведению этой силы на скорость

Так как сила аэродинамического сопротивления пропорциональна квадрату скорости, то часть мощности двигателя, идущей на преодоление сопротивления воздуху пропорциональна кубу скорости, т. е увеличение скорости в два раза требует увеличения мощности на преодоление сопротивления в восемь раз:

Пример

У автомобиля в летний день (плотность воздуха ~1,2 кг/м³), с эффективной площадью 1 м², движущегося со скоростью 10 м/с (36 км/час) двигатель затрачивает на преодоление сопротивления воздуха около 600 Вт, а при движении со скоростью 30 м/с (108 км/час) уже ~16 кВт (~22 л. с.).

Примеры[править | править код]

Некоторые примеры коэффициентов аэродинамического сопротивления современных автомобилей:

Серийно выпускаемые автомобили[править | править код]

• 

• 

• 

Несерийные и уникальные автомобили[править | править код]

• 

• 

• 

См. также[править | править код]

• Лобовое сопротивление
• Турбулентное течение
• Каммбэк
• Спойлер
• Аэродинамика автомобиля

Ссылки[править | править код]

• Унесенные ветром: Аэродинамика автомобилей, autotechnic.su, 30.10.2009
• Кадр дня: Сверхлегкий и сверхэкономичный автомобиль, Иван Карташев, 21 июня 2007 (Loremo AG: LS / GT)

При движении электромобиля (автомобиля) на скоростях, превышающих скорость пешехода, заметное влияние оказывает сила сопротивления воздуха. Для расчета силы сопротивления воздуха используют следующую эмпирическую формулу:

Fвозд. = Cx*S*ρ*ν2/2

Где:

Fвозд. – сила сопротивления воздуха, Н
Cx – коэффициент сопротивления воздуха (коэффициент обтекаемости) , Н*с2/(м*кг) . Cx определяется эксперементально для каждого кузова.
ρ – плотность воздуха (1,29кг/м3 при нормальных условиях)
S – лобовая площадь электромобиля (автомобиля) , м2. S является площадью проекции кузова на плоскость, перпендикулярную продольной оси.
ν – скорость электромобиля (автомобиля) , км/ч

Для расчета разгонных характеристик электромобиля (автомобиля) следует учитывать силу сопротивления разгону (силу инерции) . Причем, нужно учитывать не только инерцию самого электромобиля, но и влияние момента инерции вращающихся масс внутри электромобиля (ротор, коробка передач, кардан, колеса) . Далее приведена формула расчета силы сопротивления разгону:

Fин. = m*a*σвр

Где:

Fин. – сила сопротивления разгону, Н
m – масса электромобиля, кг
a – ускорение электромобиля, м/с2
σвр – коэффициент учета вращающихся масс

Приблизительно коэффициент учета вращающихся масс σвр можно рассчитать по формуле:

σвр=1,05 + 0,05*u2кп

Где uкп – передаточное число коробки передач

Осталось описать силу сцепления колес с дорогой. Однако, данная сила в дальнейших расчетах малоприменима, поэтому пока оставим ее на-потом.

И вот, мы уже имеем представление об основных силах, действующих на электромобиль (автомобиль) . Знание этого теоретического вопроса вскоре сподвигнет нас на изучение следующего вопроса – вопроса расчета характеристик электромобиля, необходимых для обоснованного выбора двигателя, аккумуляторной батареи и контроллера.

Читайте также: Электромобиль (автомобиль) – расчет параметров двигателя

Copyright © Дмитрий Спицын, 2007.

Данная страница создана с помощью Smart HTML Editor

Силовой баланс автомобиля



Силы, действующие на автомобиль при прямолинейном движении

Прямолинейным движением автомобиля будем считать его равномерное или ускоренное движение по горизонтальной или наклонной прямой дороге (без виражей и поворотов). В этом случае на автомобиль действуют следующие силы:

• сила тяжести автомобиля G, приложенная к центру тяжести, находящемся на расстоянии h_ц от поверхности дороги;
• сила сопротивления атмосферного воздуха P_ω, приложенная к центру парусности, расположенному на расстоянии h_ω от поверхности дороги;
• суммарная касательная реакция R_x2 или сила тяги Р_т, направленная по ходу движения автомобиля;
• нормальные реакции дороги на колеса R_z1 и R_z2, направленные перпендикулярно поверхности дороги;
• сила сопротивления качению колес P_f, направленная в сторону, противоположную движению автомобиля (совпадает с касательной реакцией R_x1);;
• силы инерции поступательного движения P_j (проявляются при ускоренном движении), приложенная к центру тяжести автомобиля и направленная в сторону, противоположную ускорению;
• сила сопротивления подъему P_α, приложенная к центру тяжести и направленная в сторону, противоположную движению (возникает при движении по дороге с уклоном);
• сила Р_пр на буксирном крюке в случае буксировки прицепа.

На рисунке 1 представлены все эти силы с учетом их направления по отношению к направлению движения автомобиля.

Для дальнейших теоретических выкладок примем следующие условия (допущения):

• Два одноименных колеса (правые и левые) будем рассматривать, как одно.
• Участок дороги на всем протяжении однородный с постоянным углом наклона α к горизонту и не имеет неровностей.
• Нормальные реакции дороги прикладываются к осям колес.
• Деформация шин и грунта (погружение колес в грунт) учитываются при определении силы сопротивления качению, но на схеме не показываются.

Сила тяги Р_т подробно рассмотрена в предыдущей статье. При принятых выше условиях не имеет значения, сколько колес автомобиля являются ведущими и сколько ведомыми.

***

Сила сопротивления качению

Силой сопротивления качению автомобиля P_j называется сумма сил сопротивления качению всех его колес. В реальных условиях сопротивление качению отдельных колес автомобиля не бывает одинаковым даже при движении автомобиля по дороге с твердым покрытием.
На деформируемых грунтах любое сопротивление качению задних колес, движущихся по уже уплотненному грунту, значительно меньше, чем для передних. Для решения теоретических задач сопротивление качению определяется для автомобиля в целом.
На сопротивление качению влияют:

• нормальная нагрузка на колеса;
• характер и состояние дорожного покрытия;
• удельное давление на грунт;
• скорость движения автомобиля;
• конструкция и состояние пневматических шин.

Нормальная нагрузка обусловлена полным весом автомобиля и влияет на сопротивление качению непосредственно, поскольку реакции дорожного покрытия или грунта можно считать пропорциональными нормальной нагрузке.
Потери, связанные с деформацией резины в шине (гистерезисные потери) зависят от радиальной деформации шины. Эти потери возрастают при увеличении нагрузки.
Кроме того, рост нормальной нагрузки приводит к увеличению удельного давления, а следовательно, и сопротивлению качения.

Дорожное покрытие оказывает существенное влияние на силу сопротивления качению колес P_f в случае, если оно не является твердым. Величина этой силы определяется работой прессования и выдавливанием в стороны грунта при погружении в него колес.

Удельное давление на грунт – это нормальная нагрузка на единицу площади опорного участка шины и может быть определено по формуле:

q = c_qp₀,

где c_q – коэффициент, определяемый жесткостью каркаса шины, c_q = 1 + p₀;
p₀ – давление воздуха в шинах.

Понижение удельного давления влияет на силу сопротивления качению колес P_f неоднозначно. При понижении давления возрастает деформация шин, вследствие чего растут гистерезисные потери.
В то же время понижение давления значительно уменьшает погружение шин в грунт (при отсутствии твердого покрытия) и тем самым снижает P_f.

Увеличение скорости движения приводит к увеличению потерь в шинах, в частности из-за того, что их упругие свойства не могут быть полностью использованы (часть шины не успевает полностью распрямиться). Кроме того, при повышении скорости деформации возрастает внутреннее трение в покрышке, что также ведет к увеличению P_f.

Большое значение имеют конструкция и состояние шин, их число и диаметр, а также рисунок протектора, форма и расположение грунтозацепов.

Увеличение числа колес приводит к возрастанию суммарных потерь. Чем больше диаметр колеса, чем оно меньше погружается в грунт, а значит, меньше сопротивление качению.
Чем крупнее грунтозацепы и рельефнее протектор шины, тем сильнее колесо деформирует грунт, что также приводит к увеличению силы сопротивления качению колес P_f.
На дорогах с твердым покрытием увеличенные грунтозацепы и рельефный рисунок протектора также приводят к увеличению P_f, поскольку в этом случае растут гистерезисные потери в шине.

При изношенном протекторе уменьшается сопротивление качению, но при этом резко ухудшаются сцепные качества шины с дорогой.

Для эксплуатационных расчетов принимаются два допущения:

• сопротивление качению прямо пропорционально нормальной нагрузке на колеса автомобиля;
• для автомобилей с шинами низкого давления (0,15…0,45 МПа) на одном и том же грунте и при одинаковой нагрузке сопротивление качению одинаково независимо от их конструктивных особенностей.

Тогда сила сопротивления качению может быть выражена через нормальную нагрузку (или равную ей реакцию грунта R_z) и коэффициент пропорциональности, называемый коэффициентом сопротивления качению f:

P_f = fR_z.

Коэффициент сопротивления качению f зависит от характера и состояния дорожного покрытия. Так, для асфальта, бетона или асфальтобетона он равен 0,1…0,3, для укатанной сухой грунтовой дороги – 0,02…0,03, для разбитой мокрой грунтовой дороги – 0,1…0,25, для обледенелой дороги – 0,01…0,03 и т. д.

Влияние скорости движения на коэффициент f сопротивления качению учитывает эмпирическая формула:

f = f₀(1 + v²/1500),

где f₀ – коэффициент сопротивления качению при движении автомобиля со скоростью менее 15 м/с;
v – скорость автомобиля.

***

Сила тяжести и сопротивление движению

Сила тяжести G обусловлена массой m автомобиля, указываемой в его технической характеристике и может быть определена по известной формуле: G = mg, где g – ускорение свободного падения.

Масса снаряженного автомобиля – масса автомобиля без груза, полностью заправленного топливом, смазочными материалами и охлаждающей жидкостью, с запасным колесом, инструментом и оборудованием.
Полная масса автомобиля включает в себя еще массу водителя и груза по номинальной грузоподъемности (для грузового автомобиля) или по номинальной пассажировместимости (для автобусов и легковых автомобилей).
В расчетах обычно принимается полная масса.

Положение центра масс определяется у двухосного автомобиля расстояниями l₁ и l₂ до геометрических осей вращения колес соответственно переднего и заднего мостов. У трехосного автомобиля l₂ – расстояние от центра масс до оси балансира задней тележки.
Расстояние L = l₁ + l₂ называют базой автомобиля.

При движении автомобиля по наклонному участку дороги с углом подъема α сила тяжести раскладывается на две составляющие:

• G cosα – нормальная нагрузка автомобиля на дорогу, перпендикулярная дороге;
• G sinα – сила сопротивления подъему (при спуске – скатывающая сила), обозначается P_α и направлена параллельно поверхности дороги: P_α = G sinα.

На крутых подъемах сопротивление подъему значительно превышает сопротивление качению. Так, при α = 20˚ P_α будет равна примерно 0,36G, при α = 30˚ Р_α = 0,5G, тогда как P_f редко превышает 0,05…0,08G.

При небольших значениях угла α синус может быть заменен тангенсом. В дорожном строительстве тангенс угла наклона дороги к горизонту называют продольным уклоном i, выражаемым в процентах. В этом случае сила сопротивления подъему равна:

P_α = G_i.

Сила сопротивления качению и сила сопротивления подъему зависят от дорожных условий, так как коэффициент сопротивления качению f и угол подъема дороги α в совокупности определяют качество дороги, поэтому можно ввести такое понятие, как сила сопротивления дороги:

P_ψ = P_f + P_α.

При движении автомобиля по наклонной дороге сила сопротивления качению определится из соотношения:

P_f = Gf cosα.

Получим следующую формулу для вычисления силы сопротивления дороги:

P_ψ = G(f cosα + sinα) ≈ G(f + i).

Выражение в скобках называется коэффициентом сопротивления дороги и обозначается ψ:

ψ = f cosα + sinα.

Тогда сила сопротивления дороги:

P_ψ = G_ψ.

***

Сила инерции

Сила инерции (или сила сопротивления разгону) при поступательном движении автомобиля может быть определена из соотношения:

P_j = mj,           (1)

где j – ускорение автомобиля, m – масса автомобиля.

Так как в автомобиле имеются вращающиеся детали значительной массы, то они также влияют на сопротивление разгону автомобиля, создавая инерционные моменты.
Максимальный инерционный момент сопротивления изменению угловой скорости создают маховик двигателя и колеса, а также массивные детали агрегатов и узлов трансмиссии.
Чтобы учесть влияние вращающихся масс вводят коэффициент учета вращающихся масс δ_вр, который показывает, во сколько раз сила, необходимая для разгона с заданным ускорением поступательно движущихся и вращающихся масс автомобиля, больше силы, необходимой для разгона только его поступательно движущихся масс.

С учетом коэффициента δ_вр уравнение (1) будет иметь вид:

P_j = m j δ_вр.          (2)

Значение коэффициента δ_вр определяется по формуле:

δ_вр = 1 + (j_мη_трi²_тр + j_к)/(mr²),

где j_м – момент инерции маховика; η_тр – КПД трансмиссии; i_тр – передаточное число трансмиссии; j_к – суммарный момент инерции всех колес автомобиля; m – масса автомобиля; r – радиус колеса.

Энергия, затрачиваемая на разгон деталей двигателя на прямой передаче, в два-три раза, а на низших передачах в восемь-десять раз больше энергии, расходуемой на разгон колес.

В случае, если точное значение моментов инерции маховика и колес неизвестно, то коэффициент учета вращающихся масс δ_вр определяют по эмпирической формуле:

δ_вр = 1 + (δ₁ + δ₂i²_тр)m_a/m,

где δ₁ ≈ δ₂ от 0,03 до 0,05; m_а – масса автомобиля с полной нагрузкой; m – фактическая масса автомобиля.

При движении автомобиля с отключенной от двигателя трансмиссией коэффициент учета вращающихся масс может быть приближенно определен по формуле:

δ_вр ≈ 1 + 0,5m_а/m.

***



Сила сопротивления воздуха

Как и всякое тело, перемещающееся в воздушной среде, автомобиль со стороны атмосферного воздуха испытывает сопротивление движению, которое обуславливается двумя факторами: трением, возникающим в пограничных с поверхностью автомобиля слоях воздуха, и вихреобразованием в окружающих его потоках.

Движущийся автомобиль увлекает за собой непосредственно прилегающий к нему слой воздуха, который взаимодействует на соседний с ним слой и т. д., увлекая его за собой. Скорость каждого последующего слоя воздуха меньше, чем предыдущего, что и вызывает силы трения между слоями. Чем выше скорость движения автомобиля, тем большие массы воздуха будут увлекаться в движение, и тем больше суммарная сила трения, возникающая между слоями и поверхностью автомобиля.
Однако при скоростях, с которыми передвигаются автомобили, сопротивление, вызываемое трением в пограничных с автомобилем слоях очень мало, и им можно пренебречь в большинстве расчетов.

Образование вихревых потоков можно представить, предположив, что на неподвижный автомобиль направлен с достаточной скоростью поток воздуха. Ударяясь о лобовую поверхность кабины и кузова автомобиля, струи воздуха изменяют направление своего движения (рис. 1). При этом чем менее обтекаемую форму имеет автомобиль, тем интенсивнее и объемнее будут вызываемые им завихрения воздушных струй.
В результате вихреобразования возникает разрежение воздуха сзади автомобиля, тогда как перед ним воздух уплотняется, вследствие чего создается разность давлений воздуха впереди и сзади автомобиля.

Сопротивление воздуха при вихреобразовании зависит от площади поперечного сечения автомобиля (лобовой проекции), и особенно от его формы.
Усилению вихреобразования способствует наличие выступающих частей, прямых углов и резких переходов в профильной проекции автомобиля. Обтекаемые формы современных легковых, и особенно – гоночных автомобилей, существенно снижают сопротивление воздуха, вызываемое вихреобразованием.

Сопротивление воздуха при проектировании кузовов автомобилей определяют чаще всего опытным путем с помощью аэродинамической трубы, которая позволяет получить равномерный прямолинейный установившийся воздушный поток заданной скорости и даже температуры. В аэродинамической трубе можно не только исследовать обтекаемость автомобиля, но и определить эффективность очистки ветрового стекла и ряд других параметров, связанных с воздействием воздушного потока на автомобиль.

Для расчета силы сопротивления воздуха P_ω аналитическими методами можно использовать формулу, полученную опытным путем (эмпирическая зависимость), которая справедлива для всех скоростей автомобиля, кроме самых малых:

P_ω = ρcFv²,           (3)

где ρ – плотность воздуха;
c – коэффициент сопротивления воздуха, зависящий от формы автомобиля;
F – площадь лобового сопротивления, т. е. площадь проекции автомобиля на плоскость, перпендикулярную направлению движения;
v – скорость автомобиля.

Считая, что плотность ρ воздуха в реальных условиях движения автомобиля величина относительно постоянная, вводят понятие коэффициента k_ω обтекаемости автомобиля, который тоже можно считать постоянной величиной:

k_ω = ρc.

Тогда формула (3) примет вид:

P_ω = k_ω Fv².

Значения коэффициента обтекаемости зависят от формы кузова. Так, например, для автобусов капотной компоновки он равен 0,45…0,55, для автобусов вагонной компоновки – 0,35…0,45, для легковых автомобилей – 0,2…0,35, для гоночных автомобилей – 0,15…0,2 и т. д.

Площадь лобового сопротивления с достаточной степенью точности (погрешность не более 10%) можно определить по следующим зависимостям:

• для грузового автомобиля F = BH, где H – высота автомобиля; B – колея автомобиля;
• для легковых автомобилей F = 0,78B_aH, где B_a – наибольшая ширина автомобиля.

При расчетах силы сопротивления воздуха P_ω важно определить место приложения данной силы, так называемый центр парусности.

Точное положение центра парусности автомобиля определяется опытным путем в аэродинамической трубе. Для приблизительных расчетов принимают высоту положения центра парусности равной половине высоты автомобиля, а его расположение по горизонтали – на оси симметрии лобовой проекции автомобиля.

При скоростях выше 100…120 км/ч со стороны воздушных потоков на автомобиль начинает действовать так называемая подъемная сила, имеющая аэродинамическую природу, направленная вертикально вверх и стремящаяся оторвать автомобиль от поверхности дороги.
Это негативное явление приводит к потере устойчивости и управляемости автомобиля, и связано с тем, что под днищем автомобиля, благодаря его плоской форме, скорость потока воздуха ниже, а давление в воздушном потоке выше, чем над автомобилем, где, благодаря ускорению воздушных масс из-за криволинейной формы кузова автомобиля, давление снижается. В результате на автомобиль начинает действовать подъемная сила, аналогичная подъемной силе, действующей на крыло самолета.
У спортивных автомобилей благодаря специальной форме кузова и использованию аэроэлементов (антикрыло) эту силу направляют вниз, увеличивая сцепление колес с дорогой.

***

Силы, возникающие при буксировке прицепов

В случае буксировки прицепа с помощью буксирного устройства на крюке возникает сила Р_пр, которая тоже направлена в сторону, противоположную силе тяги.
Разложив силу Р_пр на составляющие можно записать:

Р_пр = G’ sinα + P’_j + P’_f,

***

Нормальная реакция дороги

Нормальная реакция дороги R_z не совершает ни полезной работы, ни работы сопротивления движению, поскольку направлена перпендикулярно направлению движения автомобиля. Однако при изучении тягово-скоростных свойств автомобиля их необходимо учитывать, поскольку R_z определяет силы сопротивления качению и сцепление колес с опорной поверхностью (дорогой).
Нормальные реакции необходимы при оценке таких эксплуатационных свойств автомобиля, как торможение, управляемость, устойчивость и проходимость, а также при расчетах мостов.

Сила тяжести G автомобиля распределяется по всем его колесам, и со стороны дороги действуют соответствующие нормальные реакции на каждое колесо. При этом равномерное распределение массы автомобиля на его колеса хотя и могут иметь место, но в порядке исключения. Поэтому на разные колеса автомобиля действуют разные по величине нормальные реакции, в соответствии с распределением нагрузки на оси и мости, а также на каждое колесо.

Рассмотрим силы, действующие на автомобиль, стоящий на горизонтальной поверхности (рис. 2, а).
Из центра тяжести автомобиля действует вектор силы тяжести G, расположенный на расстоянии l₁ от передней оси, и на расстоянии l₂ от оси заднего моста. В соответствии с законами статики нормальные реакции R_z1 и R_z2 на колеса передней и задней оси обратно пропорциональны расстоянию от центра тяжести до этих осей:

R_z1 = Gl₂/L;
   R_z2 = Gl₁/L,

где L – расстояние между осями автомобиля.

Во время движения нормальные реакции дороги изменяются под действием различных сил и моментов. На рис. 2,б показана схема сил, действующих на автомобиль при его разгоне и на подъеме. Расчетным путем можно доказать, что нормальнее реакции дороги на передние колеса уменьшаются, а на задние увеличиваются с ростом крутизны подъема, интенсивности разгона, а также с увеличением силы сопротивления воздуха движению автомобиля.

Изменение динамических нормальных реакций относительно статических учитывает коэффициент изменения нормальных реакций m_p, который представляет собой отношение нормальных реакций, действующих на мост автомобиля при его движении, к реакциям, действующим на этот же мост неподвижного автомобиля:

• для передних колес: m_p1 = R_z1/R_z1ст;
• для задних колес: m_p2 = R_z2/R_z2ст.

Во время разгона автомобиля предельные значения коэффициентов составляют:
m_p1 от 0,55 до 0,7; m_p2 от 1,2 до 1,35, т. е. во время разгона нагрузка на передний мост уменьшается, а на задний увеличивается по сравнению с нагрузками в статическом положении.
При торможении автомобиля наблюдается обратное явление. Это объясняется тем, что при разгоне автомобиль как бы «приседает» на задние колеса, а при торможении испытывает «кивок» вперед.

***

Уравнение движения автомобиля