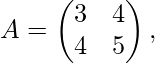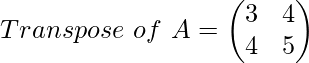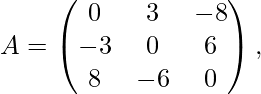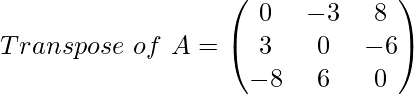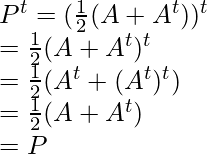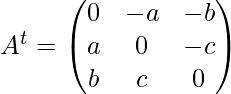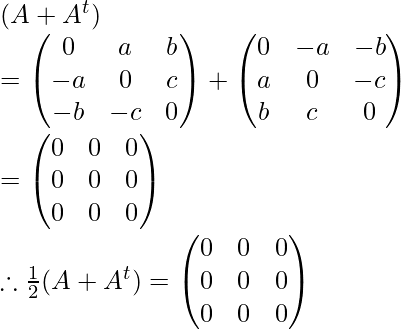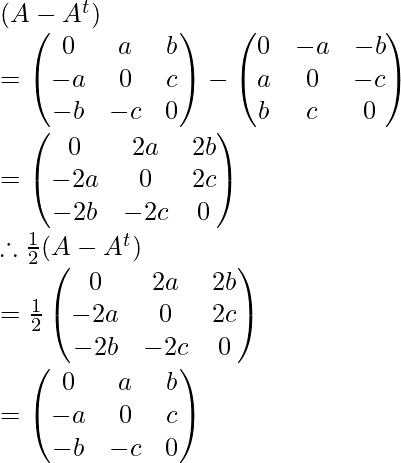Содержание
Симметричная матрица
В настоящем разделе симметричная матрица предполагается вещественной; ее порядок обозначен $ n $.
Матрица имеет вид
$$
A=left( begin{array}{ccccc}
a_{11} & color{Red}a_{12} & color{Blue}a_{13} & dots & color{Green}a_{1n} \
color{Red}a_{12} & a_{22} & color{Grey}a_{23} & dots & color{Cyan}a_{2n} \
color{Blue}a_{13} & color{Grey}a_{23} & a_{33} & dots & a_{3n} \
vdots & & & ddots & vdots \
color{Green}a_{1n} & color{Cyan}a_{2n} & a_{3n} & dots & a_{nn}
end{array}
right) ;
$$
характеризуется свойством
$$ A^{top}=A . $$
Для задания симметричной матрицы порядка $ n_{} $ необходимо, в общем случае, задать $ C_n^2=n(n-1)/2 $ ее элементов — стоящих на главной диагонали и выше ее (или ниже).
Т
Теорема. Для любой матрицы $ A_{} $ матрицы $ A_{}A^{top} $ и $ A^{top} A $ — симметричны.
Для любой квадратной матрицы $ A_{} $ матрица $ A_{}+A^{top} $ — симметрична.
Определитель
Распишем полное разложение определителя симметричной матрицы с символьными (буквенными) элементами:
$$
det A_{3times 3} = a_{11}a_{22}a_{33}-a_{11}a_{23}^2-a_{12}^2a_{33}+2,a_{12}a_{13}a_{23}-a_{13}^2a_{22} ;
$$
$$
det A_{4times 4} = a_{11}a_{22}a_{33}a_{44}-a_{11}a_{22}a_{34}^2-a_{11}a_{23}^2a_{44}+2,a_{11}a_{23}a_{24}a_{34}-
$$
$$
-a_{11}a_{24}^2a_{33}-a_{12}^2a_{33}a_{44}+a_{12}^2a_{34}^2+2,a_{12}a_{13}a_{23}a_{44}-2,a_{12}a_{23}a_{14}a_{34}-
$$
$$
-2,a_{12}a_{24}a_{13}a_{34}+2,a_{12}a_{24}a_{14}a_{33}-a_{22}a_{13}^2a_{44}+2,a_{13}a_{22}a_{14}a_{34}+
$$
$$
+a_{13}^2a_{24}^2-2,a_{13}a_{24}a_{14}a_{23}-a_{22}a_{14}^2a_{33}+a_{14}^2a_{23}^2 .
$$
Т
Теорема [Кэли]. В полном разложении определителя симметричной матрицы порядка $ n $ обозначим $ mathfrak s_n $ число слагаемых, $ mathfrak s_n^{(+)} $ — число слагаемых
с положительным знаком, $ mathfrak s_n^{(-)} $ — число слагаемых с отрицательным знаком, а $ mathfrak d_n =mathfrak s_n^{(+)} – mathfrak s_n^{(-)} $. Имеют место соотношения:
$$ mathfrak s_{n+1}=(n+1)mathfrak s_n- C_n^2 mathfrak s_{n-2} ; $$
$$ mathfrak d_{n+1}=-(n-1)mathfrak d_n- C_n^2 mathfrak d_{n-2} . $$
=>
Имеют место пределы:
$$ lim_{nto infty} frac{sqrt{n} mathfrak s_n }{n!} = frac{e^{4/3}}{sqrt{pi}} ; lim_{nto infty} frac{(-1)^{n-1}sqrt{n^3} mathfrak d_n }{n!} = frac{e^{-4/3}}{2,sqrt{pi}} . $$
Миноры: тождества Кронекера
Т
Теорема [Кронекер]. Для симметричной матрицы $ A_{} $ порядка $ n ge k+1 $ имеет место тождество
$$
Aleft(begin{array}{ccccc}
1 & 2 & dots & k-2 & k \
2 & 3 & dots & k-1 & k+1
end{array}
right)-
Aleft(begin{array}{ccccc}
2 & 3 & dots & k-1 & k \
1 & 2 & dots & k-2 & k+1
end{array}
right)=
$$
$$
= Aleft(begin{array}{cccccc}
1 & 2 & dots & k-3 & k-2 & k-1 \
2 & 3 & dots & k-2 & k & k+1
end{array}
right) ,
$$
связывающее три ее минора порядка $ k-1 $.
П
Пример. Для $ k=4 $:
$$ Aleft(begin{array}{ccc}
1 & 2 & 4 \
2 & 3 & 5
end{array}
right)-
Aleft(begin{array}{ccc}
2 & 3 & 4 \
1 & 2 & 5
end{array}
right)=
Aleft(begin{array}{ccc}
1 & 2 & 3 \
2 & 4 & 5
end{array}
right)
$$
$$
iff
left| begin{array}{lll}
a_{12} & a_{13} & a_{15} \
a_{22} & a_{23} & a_{25} \
a_{24} & a_{34} & a_{45}
end{array}
right|-
left| begin{array}{lll}
a_{12} & a_{22} & a_{25} \
a_{13} & a_{23} & a_{35} \
a_{14} & a_{24} & a_{45}
end{array}
right|=
left| begin{array}{lll}
a_{12} & a_{14} & a_{15} \
a_{22} & a_{24} & a_{25} \
a_{23} & a_{34} & a_{35}
end{array}
right| .
$$
Ранг
В настоящем разделе минор матрицы $ A $
$$
Aleft(
begin{array}{lll}
j_1 & dots & j_k \
j_1 & dots & j_k
end{array}
right) =
left|begin{array}{cccc}
a_{j_1j_1} & a_{j_1j_2} & dots & a_{j_1j_k} \
a_{j_2j_1} & a_{j_2j_2} & dots & a_{j_2j_k} \
vdots & & ddots & vdots \
a_{j_kj_1} & a_{j_kj_2} & dots & a_{j_kj_k}
end{array}
right|
, quad 1le j_1<j_2< dots < j_k le n
$$
составленный из элементов матрицы, стоящих в строках и столбцах с одинаковыми номерами, будет называться ведущим минором $ k $-го порядка матрицы $ A $. В частном случае $ j_1=1, j_2=2,dots,j_k=k $ этот минор будет называться главным минором $ k $-го порядка матрицы $ A $.
См. замечание о терминологии
☞
ЗДЕСЬ.
Т
Теорема. Если $ mathfrak r = operatorname{rank} (A)ge 1 $, то в матрице $ A $ существует ненулевой ведущий минор порядка $ mathfrak r $.
Произведение
Произведение симметричных матриц — не обязательно симметричная матрица!
T
Теорема. Для того, чтобы произведение симметричных матриц $ A $ и $ B $ было симметричной матрицей необходимо и достаточно, чтобы матрицы
$ A $ и $ B $ коммутировали: $ AB = BA $.
Обратная матрица
Т
Теорема. Обратная к симметричной матрице (если существует) будет симметричной матрицей.
Характеристический полином, собственные числа, собственные векторы
Т
Теорема 1. Все собственные числа симметричной матрицы вещественны.
Доказательство
☞
ЗДЕСЬ.
=>
Если $ lambda=0 $ корень кратности $ mathfrak m $ характеристического полинома симметричной матрицы $ A $, т.е.
$$ det (A-lambda E)equiv(-1)^n lambda^n+a_1lambda^{n-1}+dots+a_{n-mathfrak m} lambda^{mathfrak m} quad npu a_{n-mathfrak m}ne 0 $$
то $ operatorname{rank} (A)=n-mathfrak m $.
=>
Если в характеристическом полиноме некоторый коэффициент $ a_j $ при $ j notin {0,n} $ обращается в нуль, то соседние с ним в нуль не обращаются и имеют различные знаки:
$ a_{j-1} a_{j+1} < 0 $.
Т
Теорема 2. Собственные векторы, принадлежащие различным собственным числам симметричной матрицы $ A_{} $, ортогональны, т.е. если $ mathfrak X_1 $ принадлежит собственному числу $ lambda_{1} $, а $ mathfrak X_2 $ принадлежит собственному числу $ lambda_{2} $ и $ lambda_1 ne lambda_2 $, то
$$ {mathfrak X}_2^{^{top}} {mathfrak X}_1 =0 . $$
Доказательство. Если $ {mathbf A}{mathfrak X}_1=lambda_1 {mathfrak X}_1,
{mathbf A}{mathfrak X}_2=lambda_2 {mathfrak X}_2 $
и $ lambda_1 ne lambda_2 $, то
$$
a= {mathfrak X}_2^{^{top}} {mathbf A}{mathfrak X}_1 =left{begin{array}{ll} {mathfrak X}_2^{^{top}} lambda_1 {mathfrak X}_1
& =lambda_1{mathfrak X}_2^{^{top}} {mathfrak X}_1 ;\
{mathfrak X}_2^{^{top}} {mathbf A}^{^{top}}{mathfrak X}_1
=({mathbf A}{mathfrak X}_2)^{^{top}} {mathfrak X}_1 &
=lambda_2{mathfrak X}_2^{^{top}} {mathfrak X}_1. end{array} right.
$$
Тогда
$$ 0=a-a=(lambda_1 – lambda_2){mathfrak X}_2^{^{top}} {mathfrak X}_1 Rightarrow
{mathfrak X}_2^{^{top}} {mathfrak X}_1=0 , $$
т.е. $ {mathfrak X}_1 bot {mathfrak X}_2 $.
♦
Локализация собственных чисел
Т
Теорема 3 [Коши].
Для симметричной матрицы $ A_{} $ число ее собственных чисел, лежащих на интервале $ ]a,b_{}[ $, определяется по формуле:
$$operatorname{nrr} { det (A-lambda E) =0 | a< lambda<b }= $$
$$= {mathcal P}(1, H_1(a), H_2(a),dots, H_n(a))-
{mathcal P}(1, H_1(b), H_2(b),dots, H_n(b)) . $$
Здесь $ H_1(lambda), H_2(lambda),dots, H_n(lambda) $ —
главные миноры матрицы $ A-lambda, E $, а $ {mathcal P}_{} $ — число знакопостоянств.
Доказательство и примеры
☞
ЗДЕСЬ.
Согласно этой теореме, главные миноры матрицы $ A-lambda, E $ играют роль системы полиномов Штурма для характеристического полинома симметричной матрицы $ A_{} $.
=>
Если все главные миноры
$$ A_1,A_2,dots,A_{n} $$
симметричной матрицы $ A_{} $ отличны от нуля, то
число положительных собственных чисел матрицы $ A_{} $ равно числу знакопостоянств, а число отрицательных собственных чисел — числу знакоперемен в ряду $ 1,A_1,dots,A_n $:
$$ operatorname{nrr} { det (A-lambda E) =0 | lambda>0 } = {mathcal P}(1,A_1,dots,A_n),
$$
$$
operatorname{nrr} { det (A-lambda E) =0 | lambda<0 }={mathcal V}(1,A_1,dots,A_n) .
$$
Численные методы нахождения собственных чисел
§
QR-алгоритм поиска всех собственных чисел
☞
ЗДЕСЬ.
Часто в приложениях требуется вычислить значения не всех собственных чисел симметричной матрицы, а только небольшого (по сравнению с порядком матрицы) количества максимальных по модулю. Численный метод решения этой задачи изложен
☞
ЗДЕСЬ.
Диагонализуемость
Т
Теорема 4. Существует ортогональная матрица $ P_{} $, приводящая симметричную матрицу $ A_{} $ к диагональному виду:
$$
P^{-1}AP=P^{^{top}}AP=
left( begin{array}{cccc}
lambda_1 & & & mathbb O \
& lambda_2 & & \
&& ddots & \
mathbb O&& & lambda_n
end{array}
right).
$$
Доказательство особенно просто в случае когда все собственные числа $ lambda_1,dots, lambda_n $ различны. На основании теоремы 1 матрица
$ A_{} $ диагонализуема над множеством вещественных чисел и на основании теоремы 2
матрица $ P $, приводящая к диагональному виду, может быть выбрана ортогональной.
Для общего случая доказательство производится индукцией по порядку $ n $ матрицы $ A $. Окончание доказательства
☞
ЗДЕСЬ.
♦
Теорема утверждает что даже при наличии кратных корней у характеристического полинома
$$ f(lambda)=(-1)^n(lambda – lambda_1)^{{mathfrak m}_1} times
dots times (lambda – lambda_{mathfrak r})^{{mathfrak m}_{mathfrak r}}, quad
{mathfrak m}_1+dots+{mathfrak m}_{{mathfrak r}}=n, lambda_k ne
lambda_{ell} npu k ne ell $$
алгебраическая кратность собственного числа $ lambda_j $ совпадает с его геометрической кратностью:
$$operatorname{dfc} , (A-lambda_j, E)= {mathfrak m}_j, npu quad forall jin {1,dots,mathfrak r} .$$
Или, что то же: размерность собственного подпространства
$$ left{Xin mathbb R^n , big| , (A-lambda_j, E)X=mathbb O_{ntimes 1} right} $$
равна $ {mathfrak m}_j $. При нахождении фундаментальной системы решений (ФСР) указанной системы уравнений
мы получим $ {mathfrak m}_j $ линейно независимых собственных векторов
$ {{mathfrak X}_{j1},dots, {mathfrak X}_{j{mathfrak m}_j} } $ , принадлежащих $ lambda_j $. Однако
при традиционных способах построения ФСР вовсе не гарантирована ортогональность этих векторов. Как построить
ФСР так, чтобы она удовлетворяла условию теоремы,
т.е. была ортонормированной? Воспользуемся для этого процессом ортогонализации Грама-Шмидта, применив его к системе $ {{mathfrak X}_{j1},dots, {mathfrak X}_{j{mathfrak m}_j} } $.
Результатом процесса будет новая система векторов $ {{mathfrak Y}_{j1},dots, {mathfrak Y}_{j {mathfrak m}_j} } $
такая что ее линейная оболочка совпадает с линейной оболочкой исходной системы:
$$ {mathcal L} left({mathfrak Y}_{j1},dots, {mathfrak Y}_{j {mathfrak m}_j} right)=
{mathcal L} left({mathfrak X}_{j1},dots, {mathfrak X}_{j{mathfrak m}_j} right) quad
mbox{ и } quad langle {mathfrak Y}_{jk},{mathfrak Y}_{jell} rangle =0 mbox{ при } k ne ell
, ,
$$
т.е. векторы $ {mathfrak Y}_{j1},dots, {mathfrak Y}_{j {mathfrak m}_j} $ остаются собственными векторами, принадлежащими $ lambda_j $. Но теперь эти новые векторы попарно ортогональны. Нормировав их, мы получим требуемую теоремой систему из
$ {mathfrak m}_j $ ортогонормированных столбцов матрицы $ P $, соответствующих кратному
собственному числу $ lambda_j $.
П
Пример. Диагонализовать матрицу
$$
A=left(
begin{array}{rrrrrrrr}
0&1&0&1&0&0&0&-1 \
1&0&1&0&0&0&-1&0 \
0&1&0&1&0&-1&0&0 \
1&0&1&0&-1&0&0&0 \
0&0&0&-1&0&1&0&1 \
0&0&-1&0&1&0&1&0 \
0&-1&0&0&0&1&0&1 \
-1&0&0&0&1&0&1&0
end{array}
right)
$$
с помощью ортогональной матрицы.
Решение. Имеем:
$$ det (A-lambda E) equiv (lambda-3)(lambda+3)(lambda-1)^3(lambda+1)^3 , . $$
Ищем собственные векторы. Для простых собственных чисел:
$$ lambda_1=-3 Rightarrow mathfrak X_1=left[1,-1,1,,-1,-1,1,-1,1right]^{top} ; $$
$$ lambda_2=3 Rightarrow mathfrak X_2=left[-1,-1,-1,-1,1,1,1,1right]^{top} . $$
Эти столбцы войдут в состав матрицы $ P $, только их надо нормировать: $ mathfrak X_{j} /|mathfrak X_{j}| $.
Для кратных собственных чисел $ lambda_j in {-1,1} $ сначала находим произвольные ФСР
$$
lambda_3=1 Rightarrow
left{begin{array}{rrrrrrrrr}
x_1&-x_2 & &-x_4 & & & &+x_8 & =0 \
& x_2 &-x_3 & +x_4 & & -x_6 & & & =0 \
& & x_3 & +x_4 & & & -x_7 &-x_8& =0 \
& & & 3,x_4 &+x_5 & -x_6 & -2,x_7 & -x_8 & =0 \
& & & & x_5 & -x_6 & +x_7 & -x_8 & =0
end{array}
right.
$$
$$
Rightarrow
mathfrak X_{3,1} =left[1,1,0,0,1,1,0,0 right]^{top} ;mathfrak X_{3,2} =left[ 0,-1,0,1,-1,0,1,0 right]^{top};
mathfrak X_{3,3} =left[0,1,1,0,1,0,0,1 right]^{top} .
$$
$$
lambda_4=-1 Rightarrow quad left{ begin{array}{l}
mathfrak X_{4,1} =left[-1,1,0,0,-1,1,0,0 right]^{top}\
mathfrak X_{4,2} =left[ 0,1,-1,0,-1,0,0,1 right]^{top} \
mathfrak X_{4,3} =left[0,1,0,-1,-1,0,1,0 right]^{top}
end{array}
right}, .
$$
Применяем к каждой из них алгоритм ортогонализации Грама-Шмидта:
$$mathfrak Y_{3,1}=mathfrak X_{3,1}=left[1,1,0,0,1,1,0,0 right]^{top}; $$
$$ mathfrak Y_{3,2}=mathfrak X_{3,2}+{color{RubineRed} alpha } mathfrak Y_{3,1}, quad langle mathfrak Y_{3,2},mathfrak Y_{3,1} rangle =0 quad
Rightarrow {color{RubineRed} alpha }=-frac{langle mathfrak X_{3,2},mathfrak Y_{3,1} rangle}{langle mathfrak Y_{3,1},mathfrak Y_{3,1} rangle }=frac{1}{2} quad
Rightarrow
$$
$$
Rightarrow mathfrak Y_{3,2}=left[frac{1}{2},-frac{1}{2},0,1,-frac{1}{2},frac{1}{2},1,0 right]^{top} ;
$$
$$
mathfrak Y_{3,3}=mathfrak X_{3,3}+{color{RubineRed} beta } mathfrak Y_{3,1}+{color{RubineRed} gamma } mathfrak Y_{3,2}, quad
langle mathfrak Y_{3,3},mathfrak Y_{3,1} rangle =0, langle mathfrak Y_{3,3},mathfrak Y_{3,2} rangle =0
quad
Rightarrow
$$
$$
{color{RubineRed} beta } =-frac{langle mathfrak X_{3,3},mathfrak Y_{3,1} rangle}{langle mathfrak Y_{3,1},mathfrak Y_{3,1} rangle}=-frac{1}{2},
{color{RubineRed} gamma } =-frac{langle mathfrak X_{3,3},mathfrak Y_{3,2} rangle }{langle mathfrak Y_{3,2},mathfrak Y_{3,2} rangle }=frac{1}{3} quad
Rightarrow
$$
$$
Rightarrow mathfrak Y_{3,3}=left[-frac{1}{3},frac{1}{3},1,frac{1}{3},frac{1}{3},-frac{1}{3},frac{1}{3},1 right]^{top} , .
$$
$$
mathfrak Y_{4,1}=mathfrak X_{4,1}=left[-1,1,0,0,-1,1,0,0 right]^{top}, mathfrak Y_{4,2}=left[frac{1}{2},frac{1}{2},-1,0,-frac{1}{2},-frac{1}{2},0,1 right]^{top},
$$
$$
mathfrak Y_{4,3}=left[frac{1}{3},frac{1}{3},frac{1}{3},-1,-frac{1}{3},-frac{1}{3},1,-frac{1}{3} right]^{top} , .
$$
После нормирования, составляем из этих векторов ортогональную матрицу:
$$
P=
left(begin{array}{rrrrrrrr}
-sqrt{2}/4 & sqrt{2}/4 & 1/2 & sqrt{3}/6 & -sqrt{6}/12 & -1/2 & sqrt{3}/6 & sqrt{6}/12 \
-sqrt{2}/4 & -sqrt{2}/4 & 1/2 & -sqrt{3}/6 & sqrt{6}/12 & 1/2 & sqrt{3}/6 & sqrt{6}/12 \
-sqrt{2}/4 & sqrt{2}/4 & 0 & 0 & sqrt{6}/4 & 0 & -sqrt{3}/3 & sqrt{6}/12 \
-sqrt{2}/4 & -sqrt{2}/4 & 0 & sqrt{3}/3 & sqrt{6}/12 & 0 & 0 & -sqrt{6}/4 \
sqrt{2}/4 & -sqrt{2}/4 & 1/2 & -sqrt{3}/6 & sqrt{6}/12 & -1/2 & -sqrt{3}/6 & -sqrt{6}/12 \
sqrt{2}/4 & sqrt{2}/4 & 1/2 & sqrt{3}/6 & -sqrt{6}/12 & 1/2 & -sqrt{3}/6 & -sqrt{6}/12 \
sqrt{2}/4 & -sqrt{2}/4 & 0 & sqrt{3}/3 & sqrt{6}/12 & 0 & 0 & sqrt{6}/4 \
sqrt{2}/4 & sqrt{2}/4 & 0 & 0 & sqrt{6}/4 & 0 & sqrt{3}/3 & -sqrt{6}/12
end{array}
right) , .
$$
$$
P^{top}AP=
left(
begin{array}{rrrrrrrr}
3&&&&&&& \
&-3&&&&&& \
&&1&&&&& \
&&&1&&&& \
&&&&1&&& \
&&&&&-1&& \
&&&&&&-1& \
&&&&&&&-1
end{array}
right) , .
$$
♦
Квадратичная форма
Экстремальное свойство собственных чисел
?
Пусть уравнение $ X^{^{top}}A X=1 $ задает эллипсоид в $ mathbb R^3 $, т.е. квадратичная форма положительно определена. Построить посылочный ящик минимального объема (минимальный параллелепипед), содержащий данный эллипсоид.
Решение. Если уравнение эллипсоида приведено к каноническому виду
$$
frac{x_1^2}{a^2}+frac{x_2^2}{b^2}+frac{x_3^2}{c^2}=1,
$$
то ответ геометрически очевиден: эллипсоид «шире всего» в направлении оси, соответствующей максимальному из трех чисел $ a,b,c $, и «уже всего» в направлении оси, соответствующей минимальному из этих чисел. То есть размер оптимального посылочного ящика — $ (2,a, 2,b, 2,c) $. В случае, если уравнение $ X^{^{top}}A X=1 $ не приведено к каноническому виду, его можно привести к нему с помощью ортогональной замены переменных. Такая замена оставляет инвариантными размеры эллипсоида, а результатом ее становится уравнение эллипсоида в каноническом виде
$$ lambda_1 y_1^2+lambda_2 y_2^2+lambda_3 y_3^2=1 , . $$
Здесь $ lambda_1,lambda_2,lambda_3 $ — собственные числа матрицы $ A $, они являются положительными ввиду предположения о положительной определенности этой матрицы. Соответствующие собственные векторы матрицы определяют главные оси эллипсоида1). Сравнивая два канонических вида уравнения эллипсоида, можем размеры посылочного ящика сформулировать в терминах собственных чисел матрицы: максимальный размер эллипсоид имеет равным $ 2/sqrt{min {lambda_1,lambda_2,lambda_3}} $, а минимальный — равным $ 2/sqrt{max {lambda_1,lambda_2,lambda_3}} $. Если эллипсоид нельзя поворачивать вокруг начала координат, то для того, чтобы поместить его в ящик размеров $ 2/sqrt{lambda_1}, 2/sqrt{lambda_2}, 2/sqrt{lambda_3} $ последний надо ориентировать в пространстве: рёбра должны быть параллельны собственным векторам матрицы $ A $.
♦
Замеченное свойство собственных чисел симметричной матрицы распространяется и в многомерное пространство. Традиционно его формулируют в несколько ином виде — хотя и менее наглядном, но более ориентированном на приложения в задачах механики и статистики.
Задача. Найти условные экстремумы квадратичной формы $ F(X)=X^{^{top}}A X $ на единичной
сфере
$$ mathbb S= { Xin mathbb R^n mid x_1^2+dots+ x_n^2=1 }, . $$
В курсе математического анализа показывается, что, во-первых, указанные
экстремумы существуют2), и, во-вторых,
могут быть найдены применением метода множителей Лагранжа.
Т
Теорема. Если $ lambda_{max} $ — максимальное, а $ lambda_{min} $ — минимальное
собственные числа матрицы $ A $, то
$$ max_{X in mathbb S} X^{^{top}}A X =lambda_{max}, qquad
min_{X in mathbb S} X^{^{top}}A X =lambda_{min} , . $$
Указанные экстремумы квадратичная форма достигает
на соответствующих собственных векторах матрицы $ A $ единичной длины.
Доказательство. Применяем метод множителей Лагранжа, т.е. составляем функцию
$$L(X,lambda) = F(X)- lambda (X^{top}X-1)$$
и ищем ее абсолютные экстремумы (как функции $ (n+1) $-го аргумента).
На основании теоремы о стационарных точках полинома эти экстремумы должны достигаться
на вещественных решениях системы уравнений
$$
left{
begin{array}{lll}
{partial L }big/{partial x_1 }=&2left(a_{11}x_1+a_{12}x_2+dots+a_{1n}x_n
right)-2 lambda x_1 &=0, \
dots & & dots \
{partial L }big/{partial x_n}=&2left(a_{n1}x_1+a_{n2}x_2+dots+a_{nn}x_n
right)-2 lambda x_n &=0, \
{partial L }big/{partial lambda }=&x_1^2+dots +x_n^2-1 &= 0 , .
end{array}
right.
$$
Решаем эту систему. Первые $ n $ уравнений перепишем в матричном виде
$$AX-lambda X=mathbb O iff (A-lambda , E) X=mathbb O ,
. $$
Из последнего уравнения системы следует, что $ X ne mathbb O $.
Следовательно, решениями системы будут
исключительно только собственные векторы $ {mathfrak X}_j $ матрицы $ A $, при
$ lambda $ равном соответствующему собственному числу $ lambda_j $ этой матрицы.
При $ X={mathfrak X}_j $ и $ lambda=lambda_j $ получаем экстремальные значения
функции $ F(X) $:
$$F({mathfrak X}_j)={mathfrak X}_j^{^{top}}A {mathfrak X}_j
= lambda_j {mathfrak X}_j^{^{top}}{mathfrak X}_j=lambda_j , . $$
Откуда и следует утверждение теоремы.
♦
§
Еще один вариант экстремального свойства симметричной матрицы излагается
☞
ЗДЕСЬ.
Кососимметричная матрица
рассматривается
☞
ЗДЕСЬ.
Эрмитова матрица
Обобщение понятия симметричной матрицы на матрицы с комплексными элементами можно было бы формально произвести по той же определяющей формуле $ A=A^{top} $. Однако такое обобщение практически не используется ввиду потери ряда полезных свойств вещественных симметричных матриц. Вместо этого используют матрицы вида
$$ A=P+ mathbf i Q quad mbox{при} {P,Q} in mathbb R^{ntimes n}, P=P^{top}, Q=-Q^{top} , $$
т.е. матрица $ P $ — симметричная, а $ Q $ — кососимметричная. Такие матрицы удовлетворяют равенству
$$ overline{A}^{top}= A , $$
где $ overline{A} $ означает комплексное сопряжение всех элементов матрицы $ A $. Матрицы такого вида называются эрмитовыми.
Они рассматривается
☞
ЗДЕСЬ.
Обратно симметричная матрица
определяется
☞
ЗДЕСЬ.
Задачи
Источники
[1]. Полиа Г., Сегё Г. Задачи и теоремы из анализа. Т.2. М.Наука. 1978, с.122
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 ноября 2021 года; проверки требует 1 правка.
Симметричной (Симметрической) называют квадратную матрицу, элементы которой симметричны относительно главной диагонали. Более формально, симметричной называют такую матрицу 

Это означает, что она равна её транспонированной матрице:
Примеры[править | править код]
Свойства[править | править код]
Симметричная матрица всегда квадратная.
Для любой симметричной матрицы A с вещественными элементами справедливо следующее:
- она имеет вещественные собственные значения
- её собственные векторы, соответствующие разным собственным значениям, ортогональны друг другу:

Положительно (отрицательно) определённые матрицы[править | править код]
Симметричная матрица 


Условие отрицательно, неположительно и неотрицательно определённой матрицы формулируется аналогично с соответствующим изменением знака неравенства.
Для выяснения характера определённости матрицы может использоваться критерий Сильвестра.
См. также[править | править код]
- Персимметричная матрица
- Транспозиционная матрица
- Матрица Лемера
Литература[править | править код]
- Беллман Р. Введение в теорию матриц. — М.: Мир, 1969 (djvu).
- Гантмахер Ф. Р. Теория матриц. — 5-е изд. — М.: Физматлит, 2004. — 560 с. — ISBN 5-9221-0524-8.; (2-е изд.). — М.: Наука, 1966 (djvu).
- Голуб Дж. (Gene H. Golub), Ван Лоун Ч. (Charles F. Van Loan) Матричные вычисления. — М.: Мир, 1999. — 548 с. — ISBN 5-03-002406-9
- Курош А. Г. Курс высшей алгебры. — 9-е изд. — М.: Наука, 1968. — 432 с.
The knowledge of matrices is necessary for various branches of mathematics. Matrices are one of the most powerful tools in mathematics. Now see one of the features of the matrix in this article. Here we discuss Symmetric and Skew Symmetric Matrices. According to matrices, only the square matrices can be symmetric or skew-symmetric form. Later in this article, we will discuss all things.
Symmetric Matrix
If for a matrix, the transposed form of that matrix is the same as the original matrix, then that matrix is said to be a Symmetric Matrix. Let, a square matrix A of size n x n is said to be symmetric if
At = A
Where, [aij] = [aji], for 1 ≤ i ≤ n, and 1 ≤ j ≤ n. In this case [aij] is an element at position (i, j) which is ith row and jth column in matrix A, and [aji] is an element at position (j, i) which is jth row and ith column in matrix A. So it is the transposed form of matrix A.
Example
So, this matrix is a Symmetric Matrix, because the transposed form of this matrix is itself the original matrix.
Skew-Symmetric Matrices
If for a matrix, the transposed form of that matrix is the same as the negative of the original matrix, then that matrix is said to be a Skew-Symmetric Matrix. Let, a square matrix A of size n x n is said to be skew-symmetric if
At = -A
Where, [aij] = [aji], for 1 ≤ i ≤ n, and 1 ≤ j ≤ n. In this case [aij] is an element at position (i, j) which is ith row and jth column in matrix A, and [aji] is an element at position (j, i) which is jth row and ith column in matrix A.
Example
Here, in the transposed form the matrix looks like the negative of the original matrix.
Properties of Symmetric and Skew-Symmetric Matrices
There are some rules that come from the concept of Symmetric and Skew-Symmetric Matrices,
1. If matrix A is a square matrix then (A + At) is always symmetric.
Prove:
To find if a matrix symmetric or not, first, we have to find the transposed form of the given matrix
So, let’s find the transpose of (A + At)
= (A + At)t
= At + (At)t
= At + A [here, (At)t = A]
= (A + At)
So, this is the same as the given matrix, so it is symmetric.
2. If matrix A is a square matrix then (A – At) is always skew-symmetric.
Prove:
To find if a matrix skew-symmetric or not, first, we have to find the transposed form of the given matrix
So, let’s find the transpose of (A – At)
= (A − At)t
= At − (At)t
= At − A [here, (At)t = A]
= − (A − At)
So, this form is the negative of the given matrix, so it is skew-symmetric.
Expressing Matrix in the form of Symmetric and Skew-Symmetric Matrices
Every square matrix can be expressed uniquely as the sum of symmetric and skew-symmetric matrices.
Prove:
Let A be a square matrix,
We can write, A = A/2 + A/2
Let, A = P + Q
Now, find Pt and Qt
and,
So, here P is symmetric and Q is skew-symmetric matrices and A is the sum of P and Q.
Example
Express matrix A as the sum of a symmetric and skew-symmetric matrix, Where
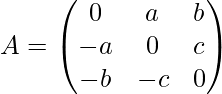
Answer:
First, find the transpose of A
Now find (A + At) and (A – At)
Similarly:
Now, check the sum of (1/2)(A + At) and (1/2)(A – At) is the same as A or not,
So here A is expressed as the sum of the symmetric and skew-symmetric matrix.
Last Updated :
26 Nov, 2020
Like Article
Save Article
Симметрическая матрица
Квадратная Матрица S = llsikll, в которой любые два элемента, симметрично расположенные относительно главной диагонали, равны между собой: sik = ski (i, k = 1,2. n). С. м. часто рассматривается как матрица коэффициентов некоторой квадратичной формы (См. Квадратичная форма); между теорией С. м. и теорией квадратичных форм существует тесная связь.
Спектральные свойства С. м. с действительными элементами: 1) все корни λ1, λ2. λn характеристического уравнения (См. Характеристическое уравнение) С. м. действительны; 2) этим корням соответствуют n попарно ортогональных собственных векторов (См. Собственные векторы) С. м. (n — порядок С. м.). С. м. с действительными элементами всегда представима в виде: S’= ODO -1
VMath
Страница — в разработке. Начало работ — 08.03.2014, окончание — .
Симметричная матрица
Матрица имеет вид $$ A=left( begina_ & colora_ & colora_ & dots & colora_ \ colora_ & a_ & colora_ & dots & colora_ \ colora_ & colora_ & a_ & dots & a_ \ vdots & & & ddots & vdots \ colora_ & colora_ & a_ & dots & a_ end right) ; $$ характеризуется свойством $$ A^=A . $$ Для задания симметричной матрицы порядка $ n_ $ необходимо, в общем случае, задать $ C_n^2=n(n-1)/2 $ ее элементов — стоящих на главной диагонали и выше ее (или ниже).
Теорема. Для любой матрицы $ A_ $ матрицы $ A_A^ $ и $ A^ A $ — симметричны. Для любой квадратной матрицы $ A_ $ матрица $ A_+A^ $ — симметрична.
Определитель
Теорема [Кэли]. В полном разложении определителя симметричной матрицы порядка $ n $ обозначим $ mathfrak s_n $ число слагаемых, $ mathfrak s_n^ $ — число слагаемых с положительным знаком, $ mathfrak s_n^ $ — число слагаемых с отрицательным знаком, а $ mathfrak d_n =mathfrak s_n^ — mathfrak s_n^ $. Имеют место соотношения:
$$ mathfrak s_=(n+1)mathfrak s_n- C_n^2 mathfrak s_ ; $$ $$ mathfrak d_=-(n-1)mathfrak d_n- C_n^2 mathfrak d_ . $$
Имеют место пределы:
Миноры: тождества Кронекера
Теорема [Кронекер]. Для симметричной матрицы $ A_ $ порядка $ n ge k+1 $ имеет место тождество
$$ Aleft(begin1 & 2 & dots & k-2 & k \ 2 & 3 & dots & k-1 & k+1 end right)- Aleft(begin2 & 3 & dots & k-1 & k \ 1 & 2 & dots & k-2 & k+1 end right)= $$ $$ = Aleft(begin1 & 2 & dots & k-3 & k-2 & k-1 \ 2 & 3 & dots & k-2 & k & k+1 end right) , $$ связывающее три ее минора порядка $ k-1 $.
Пример. Для $ k=4 $:
В настоящем разделе минор матрицы $ A $ $$ Aleft( beginj_1 & dots & j_k \ j_1 & dots & j_k end right) = left|begina_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ vdots & & ddots & vdots \ a_ & a_ & dots & a_ end right| , quad 1le j_1<j_2< dots < j_k le n $$ составленный из элементов матрицы, стоящих в строках и столбцах с одинаковыми номерами, будет называться ведущим минором $ k $-го порядка матрицы $ A $. В частном случае $ j_1=1, j_2=2,dots,j_k=k $ этот минор будет называться главным минором $ k $-го порядка матрицы $ A $.
Теорема. Если $ mathfrak r = operatorname (A)ge 1 $, то в матрице $ A $ существует ненулевой ведущий минор порядка $ mathfrak r $.
Произведение
Теорема. Для того, чтобы произведение симметричных матриц $ A $ и $ B $ было симметричной матрицей необходимо и достаточно, чтобы матрицы $ A $ и $ B $ коммутировали: $ AB = BA $.
Обратная матрица
Теорема. Обратная к симметричной матрице (если существует) будет симметричной матрицей.
Характеристический полином, собственные числа, собственные векторы
Теорема 1. Все собственные числа симметричной матрицы вещественны.
Доказательство ☞ ЗДЕСЬ.
Если $ lambda=0 $ корень кратности $ mathfrak m $ характеристического полинома симметричной матрицы $ A $, т.е.
$$ det (A-lambda E)equiv(-1)^n lambda^n+a_1lambda^+dots+a_ lambda^ quad npu a_ne 0 $$ то $ operatorname (A)=n-mathfrak m $.
Если в характеристическом полиноме некоторый коэффициент $ a_j $ при $ j notin $ обращается в нуль, то соседние с ним в нуль не обращаются и имеют различные знаки: $ a_ a_ < 0 $.
Теорема 2. Собственные векторы, принадлежащие различным собственным числам симметричной матрицы $ A_ $, ортогональны, т.е. если $ mathfrak X_1 $ принадлежит собственному числу $ lambda_ $, а $ mathfrak X_2 $ принадлежит собственному числу $ lambda_ $ и $ lambda_1 ne lambda_2 $, то
Локализация собственных чисел
Теорема [Коши]. Для симметричной матрицы $ A_ $ число ее собственных чисел, лежащих на интервале $ ]a,b_[ $, определяется по формуле:
Доказательство и примеры ☞ ЗДЕСЬ.
Согласно этой теореме, главные миноры матрицы $ A-lambda, E $ играют роль системы полиномов Штурма для характеристического полинома симметричной матрицы $ A_ $.
$$ A_1,A_2,dots,A_ $$ симметричной матрицы $ A_ $ отличны от нуля, то число положительных собственных чисел матрицы $ A_ $ равно числу знакопостоянств, а число отрицательных собственных чисел — числу знакоперемен в ряду $ 1,A_1,dots,A_n $:
Численные методы нахождения собственных чисел
QR-алгоритм поиска всех собственных чисел ☞ ЗДЕСЬ.
Часто в приложениях требуется вычислить значения не всех собственных чисел симметричной матрицы, а только небольшого (по сравнению с порядком матрицы) количества максимальных по модулю. Численный метод решения этой задачи изложен ☞ ЗДЕСЬ.
Диагонализуемость
Теорема. Существует ортогональная матрица $ P_ $, приводящая симметричную матрицу $ A_ $ к диагональному виду:
Доказательство особенно просто в случае когда все собственные числа $ lambda_1,dots, lambda_n $ различны. На основании теоремы 1 матрица $ A_ $ диагонализуема над множеством вещественных чисел и на основании теоремы 2 матрица $ P $, приводящая к диагональному виду, может быть выбрана ортогональной.
Для общего случая доказательство производится индукцией по порядку $ n $ матрицы $ A $. Окончание доказательства ☞ ЗДЕСЬ. ♦
Теорема утверждает что даже при наличии кратных корней у характеристического полинома $$ f(lambda)=(-1)^n(lambda — lambda_1)^_1> times dots times (lambda — lambda_)^_>, quad _1+dots+_>=n, lambda_k ne lambda_ npu k ne ell $$ алгебраическая кратность собственного числа $ lambda_j $ совпадает с его геометрической кратностью: $$operatorname , (A-lambda_j, E)= _j, npu quad forall jin .$$ Или, что то же: размерность собственного подпространства $$ left right> $$ равна $ _j $. При нахождении фундаментальной системы решений (ФСР) указанной системы уравнений мы получим $ _j $ линейно независимых собственных векторов $ _,dots, __j> > $ , принадлежащих $ lambda_j $. Однако при традиционных способах построения ФСР вовсе не гарантирована ортогональность этих векторов. Как построить ФСР так, чтобы она удовлетворяла условию теоремы, т.е. была ортонормированной? Воспользуемся для этого процессом ортогонализации Грама-Шмидта, применив его к системе $ _,dots, __j> > $. Результатом процесса будет новая система векторов $ _,dots, __j> > $ такая что ее линейная оболочка совпадает с линейной оболочкой исходной системы: $$ left(_,dots, __j> right)= left(_,dots, __j> right) quad mbox quad langle _,_ rangle =0 mbox k ne ell , , $$ т.е. векторы $ _,dots, __j> $ остаются собственными векторами, принадлежащими $ lambda_j $. Но теперь эти новые векторы попарно ортогональны. Нормировав их, мы получим требуемую теоремой систему из $ _j $ ортогонормированных столбцов матрицы $ P $, соответствующих кратному собственному числу $ lambda_j $.
Пример. Диагонализовать матрицу
Решение. Имеем: $$ det (A-lambda E) equiv (lambda-3)(lambda+3)(lambda-1)^3(lambda+1)^3 , . $$ Ищем собственные векторы. Для простых собственных чисел: $$ lambda_1=-3 Rightarrow mathfrak X_1=left[1,-1,1,,-1,-1,1,-1,1right]^ ; $$ $$ lambda_2=3 Rightarrow mathfrak X_2=left[-1,-1,-1,-1,1,1,1,1right]^ . $$ Эти столбцы войдут в состав матрицы $ P $, только их надо нормировать: $ mathfrak X_ /|mathfrak X_| $. Для кратных собственных чисел $ lambda_j in $ сначала находим произвольные ФСР $$ lambda_3=1 Rightarrow left x_1&-x_2 & &-x_4 & & & &+x_8 & =0 \ & x_2 &-x_3 & +x_4 & & -x_6 & & & =0 \ & & x_3 & +x_4 & & & -x_7 &-x_8& =0 \ & & & 3,x_4 &+x_5 & -x_6 & -2,x_7 & -x_8 & =0 \ & & & & x_5 & -x_6 & +x_7 & -x_8 & =0 end right. $$ $$ Rightarrow mathfrak X_ =left[1,1,0,0,1,1,0,0 right]^ ;mathfrak X_ =left[ 0,-1,0,1,-1,0,1,0 right]^; mathfrak X_ =left[0,1,1,0,1,0,0,1 right]^ . $$ $$ lambda_4=-1 Rightarrow quad left mathfrak X_ =left[-1,1,0,0,-1,1,0,0 right]^\ mathfrak X_ =left[ 0,1,-1,0,-1,0,0,1 right]^ \ mathfrak X_ =left[0,1,0,-1,-1,0,1,0 right]^ end right>, . $$ Применяем к каждой из них алгоритм ортогонализации Грама-Шмидта: $$mathfrak Y_=mathfrak X_=left[1,1,0,0,1,1,0,0 right]^; $$ $$ mathfrak Y_=mathfrak X_+ alpha > mathfrak Y_, quad langle mathfrak Y_,mathfrak Y_ rangle =0 quad Rightarrow alpha >=-frac,mathfrak Y_ rangle>,mathfrak Y_ rangle >=frac quad Rightarrow $$ $$ Rightarrow mathfrak Y_=left[frac,-frac,0,1,-frac,frac,1,0 right]^ ; $$ $$ mathfrak Y_=mathfrak X_+ beta > mathfrak Y_+ gamma > mathfrak Y_, quad langle mathfrak Y_,mathfrak Y_ rangle =0, langle mathfrak Y_,mathfrak Y_ rangle =0 quad Rightarrow $$ $$ beta > =-frac,mathfrak Y_ rangle>,mathfrak Y_ rangle>=-frac, gamma > =-frac,mathfrak Y_ rangle >,mathfrak Y_ rangle >=frac quad Rightarrow $$ $$ Rightarrow mathfrak Y_=left[-frac,frac,1,frac,frac,-frac,frac,1 right]^ , . $$ $$ mathfrak Y_=mathfrak X_=left[-1,1,0,0,-1,1,0,0 right]^, mathfrak Y_=left[frac,frac,-1,0,-frac,-frac,0,1 right]^, $$ $$ mathfrak Y_=left[frac,frac,frac,-1,-frac,-frac,1,-frac right]^ , . $$ После нормирования, составляем из этих векторов ортогональную матрицу: $$ P= left(begin-sqrt/4 & sqrt/4 & 1/2 & sqrt/6 & -sqrt/12 & -1/2 & sqrt/6 & sqrt/12 \ -sqrt/4 & -sqrt/4 & 1/2 & -sqrt/6 & sqrt/12 & 1/2 & sqrt/6 & sqrt/12 \ -sqrt/4 & sqrt/4 & 0 & 0 & sqrt/4 & 0 & -sqrt/3 & sqrt/12 \ -sqrt/4 & -sqrt/4 & 0 & sqrt/3 & sqrt/12 & 0 & 0 & -sqrt/4 \ sqrt/4 & -sqrt/4 & 1/2 & -sqrt/6 & sqrt/12 & -1/2 & -sqrt/6 & -sqrt/12 \ sqrt/4 & sqrt/4 & 1/2 & sqrt/6 & -sqrt/12 & 1/2 & -sqrt/6 & -sqrt/12 \ sqrt/4 & -sqrt/4 & 0 & sqrt/3 & sqrt/12 & 0 & 0 & sqrt/4 \ sqrt/4 & sqrt/4 & 0 & 0 & sqrt/4 & 0 & sqrt/3 & -sqrt/12 end right) , . $$ $$ P^AP= left( begin3&&&&&&& \ &-3&&&&&& \ &&1&&&&& \ &&&1&&&& \ &&&&1&&& \ &&&&&-1&& \ &&&&&&-1& \ &&&&&&&-1 end right) , . $$ ♦
Квадратичная форма
Экстремальное свойство собственных чисел
Пусть уравнение $ X^>A X=1 $ задает эллипсоид в $ mathbb R^3 $, т.е. квадратичная форма положительно определена. Построить посылочный ящик минимального объема (минимальный параллелепипед), содержащий данный эллипсоид.
Решение. Если уравнение эллипсоида приведено к каноническому виду $$ frac+frac+frac=1, $$ то ответ геометрически очевиден: эллипсоид «шире всего» в направлении оси, соответствующей максимальному из трех чисел $ a,b,c $, и «уже всего» в направлении оси, соответствующей минимальному из этих чисел. То есть размер оптимального посылочного ящика — $ (2,a, 2,b, 2,c) $. В случае, если уравнение $ X^>A X=1 $ не приведено к каноническому виду, его можно привести к нему с помощью ортогональной замены переменных. Такая замена оставляет инвариантными размеры эллипсоида, а результатом ее становится уравнение эллипсоида в каноническом виде $$ lambda_1 y_1^2+lambda_2 y_2^2+lambda_3 y_3^2=1 , . $$ Здесь $ lambda_1,lambda_2,lambda_3 $ — собственные числа матрицы $ A $, они являются положительными ввиду предположения о положительной определенности этой матрицы. Соответствующие собственные векторы матрицы определяют главные оси эллипсоида 1) . Сравнивая два канонических вида уравнения эллипсоида, можем размеры посылочного ящика сформулировать в терминах собственных чисел матрицы: максимальный размер эллипсоид имеет равным $ 2/sqrt> $, а минимальный — равным $ 2/sqrt> $. Если эллипсоид нельзя поворачивать вокруг начала координат, то для того, чтобы поместить его в ящик размеров $ 2/sqrt, 2/sqrt, 2/sqrt $ последний надо ориентировать в пространстве: рёбра должны быть параллельны собственным векторам матрицы $ A $. ♦
Замеченное свойство собственных чисел симметричной матрицы распространяется и в многомерное пространство. Традиционно его формулируют в несколько ином виде — хотя и менее наглядном, но более ориентированном на приложения в задачах механики и статистики.
Задача. Найти условные экстремумы квадратичной формы $ F(X)=X^>A X $ на единичной сфере $$ mathbb S= \, . $$
В курсе математического анализа показывается, что, во-первых, указанные экстремумы существуют 2) , и, во-вторых, могут быть найдены применением метода множителей Лагранжа.
Теорема. Если $ lambda_ $ — максимальное, а $ lambda_ $ — минимальное собственные числа матрицы $ A $, то
$$ max_ X^>A X =lambda_, qquad min_ X^>A X =lambda_ , . $$ Указанные экстремумы квадратичная форма достигает на соответствующих собственных векторах матрицы $ A $ единичной длины.
Доказательство. Применяем метод множителей Лагранжа, т.е. составляем функцию $$L(X,lambda) = F(X)- lambda (X^X-1)$$ и ищем ее абсолютные экстремумы (как функции $ (n+1) $-го аргумента). На основании теоремы о стационарных точках полинома эти экстремумы должны достигаться на вещественных решениях системы уравнений $$ left big/=&2left(a_x_1+a_x_2+dots+a_x_n right)-2 lambda x_1 &=0, \ dots & & dots \ big/=&2left(a_x_1+a_x_2+dots+a_x_n right)-2 lambda x_n &=0, \ big/=&x_1^2+dots +x_n^2-1 &= 0 , . end right. $$ Решаем эту систему. Первые $ n $ уравнений перепишем в матричном виде $$AX-lambda X=mathbb O iff (A-lambda , E) X=mathbb O , . $$ Из последнего уравнения системы следует, что $ X ne mathbb O $. Следовательно, решениями системы будут исключительно только собственные векторы $ _j $ матрицы $ A $, при $ lambda $ равном соответствующему собственному числу $ lambda_j $ этой матрицы. При $ X=_j $ и $ lambda=lambda_j $ получаем экстремальные значения функции $ F(X) $: $$F(_j)=_j^>A _j = lambda_j _j^>_j=lambda_j , . $$ Откуда и следует утверждение теоремы. ♦
Еще один вариант экстремального свойства симметричной матрицы излагается ☞ ЗДЕСЬ.
Симметричная матрица

Другими словами, симметричная матрица является квадратной матрицей и идентична матрице после замены строк на столбцы и столбцов на строки.
Требования
Чтобы любая матрица была симметричной, она должна удовлетворять следующим ограничениям:
Учитывая симметричную матрицу п порядка n,
- Быть квадратная матрица.
Количество строк (n) должно быть таким же, как количество столбцов (m). То есть порядок матрицы должен быть n при n = m.
- Исходная матрица должна быть равна ее транспонированная матрица.

Характеристики
- Сопряженная матрица симметричной матрицы также является симметричной матрицей.
- Сложение или вычитание двух симметричных матриц приводит к другой симметричной матрице.
Для двух симметричных матриц п Y Т порядка 3, получаем другую симметричную матрицу S от суммы.

Почему это называется симметричной матрицей?
Свойство симметрии придают элементы вокруг главной диагонали. Поскольку квадратная матрица является симметричной матрицей, она всегда будет иметь одинаковое количество элементов выше и ниже главной диагонали. Эти элементы одинаковы симметрично. То есть главная диагональ действует как зеркало.
Доказательство симметрии и асимметрии матрицы
Симметричная матрица

Письмо d представляет собой элементы главной диагонали. Остальные буквы обозначают любое действительное число. Мы видим, что главная диагональ действует как зеркало: она отражает элементы с обеих сторон. Другими словами, когда элементы по обе стороны от диагонали симметрично равны, мы говорим, что матрица п является симметричной матрицей.
Несимметричная матрица

Матрица Икс Это несимметричная матрица, поскольку это не квадратная матрица, и ее транспонированная матрица отличается от исходной матрицы. К тому же у него нет и главной диагонали.
Симметричные и антисимметричные матрицы
:
Квадратная матрица A называется
симметричной, если AT=A
В частности, симметричной является
любая диагональная матрица. Если забыли,
что такое диагональная матрица, гляньте
на рис. 2 . Попробуйте эту матрицу с
рисунка 2 мысленно транспонировать.
Диагональные элементы при этом,
оказывается, остаются на месте.
А
теперь посмотрите на симметричную
матрицу на рисунке 9. Вы видите симметрию?
Попробуйте и эту матрицу мысленно
транспонировать.
Определение:
Квадратная матрица A называется
антисимметричной , если AT
= -A .
Теперь посмотрите на антисимметричную
матрицу. Чем она отличается от симметричной?
Обратите внимание, что все её диагональные
элементы равны нулю. У антисимметричных
матриц все диагональные элементы равны
нулю. Подумайте, почему?
Отметим
некоторые свойства операций над
симметричными и антисимметричными
матрицами. 1. Если A и B — симметричные
(антисимметричные) матрицы, то и A + B —
симметричная (антисимметричная) матрица.
2.Если A — симметричная (антисимметричная)
матрица, то xA также является симметричной
(антисимметричной) матрицей. (в самом
деле, если умножить матрицы из рисунка
9 на какое – нибудь число, симметрия то
всё равно сохранится)
3. Произведение
AB двух симметричных или двух антисимметричных
матриц A и B есть матрица симметричная
при AB = BA и антисимметричная при AB = -BA.
4. Если A — симметричная матрица, то и
Am
(m = 1, 2, 3, . . .) — симметричная матрица.
Если A — антисимметричная матрица, то
Am
(m = 1, 2, 3, . . .) яв ляется симметричной
матрицей при четном m и антисимметричной
— при нечетном.
5. Произвольную
квадратную матрицу A можно представить
в виде суммы двух матриц. (назовём
эти
матрицы,
например
A(s)
и
A(a)
)
A=A(s)+A(a)
A(s)=(A+AT)/2
A(a))=(A-AT)/2
-
Обратная
матрица. Матричный метод решения СЛАУ.
Обра́тная
ма́трица —
такая матрица
A−1,
при умножении на которую исходная
матрица A
даёт в результате единичную
матрицу
E:
![]()
Квадратная
матрица
обратима тогда и только тогда, когда
она невырожденная, то есть её определитель
не равен нулю. Для неквадратных матриц
и вырожденных
матриц
обратных матриц не существует. Однако
возможно обобщить это понятие и ввести
псевдообратные
матрицы,
похожие на обратные по многим свойствам.
Ма́тричный
метод
решения (метод решения через обратную
матрицу)
систем
линейных алгебраических уравнений
с ненулевым определителем
состоит в следующем.
Пусть
дана система линейных уравнений с
![]() неизвестными
неизвестными
(над произвольным полем):
![]()
Тогда
её можно переписать в матричной форме:
![]() ,
,
где
![]() —
—
основная матрица системы,![]() и
и![]() —
—
столбцы свободных членов и решений
системы соответственно:
![]()
Умножим
это матричное уравнение слева на
![]() —
—
матрицу, обратную к матрице![]() :
:![]()
Так
как
![]() ,
,
получаем![]() .
.
Правая часть этого уравнения даст
столбец решений исходной системы.
Условием применимости данного метода
(как и вообще существования решения
неоднородной системы линейных уравнений
с числом уравнений, равным числу
неизвестных) являетсяневырожденность
матрицы A. Необходимым и достаточным
условием этого является неравенство
нулю определителя
матрицы
A:
![]() .
.
Для
однородной системы линейных уравнений,
то есть когда вектор
![]() ,
,
действительно обратное правило: система![]() имеет
имеет
нетривиальное (то есть ненулевое) решение
только если![]() .
.
Такая связь между решениями однородных
и неоднородных систем линейных уравнений
носит названиеальтернативы
Фредгольма.
решение
системы линейных алгебраических
уравнений матричным методом определяется
по формуле
![]() .
.
Другими словами, решение СЛАУ находится
с помощью обратной матрицы![]() .
.
Мы
знаем, что квадратная матрица А
порядка n
на n
имеет обратную матрицу
![]() только
только
тогда, когда ее определитель не равен
нулю. Следовательно, СИСТЕМУn
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n
НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ
МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ
ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ
НУЛЯ
С
помощью обратной матрицы найдите решение
системы линейных уравнений
![]() .
.
Решение.В
матричной форме исходная система
запишется как
![]() ,
,
где![]() .
.
Вычислим определитель основной матрицы
и убедимся, что он отличен от нуля. В
противном случае мы не сможем решить
систему матричным методом. Имеем![]() ,
,
следовательно, для матрицыА
может быть найдена обратная матрица
![]() .
.
Таким образом, если мы отыщем обратную
матрицу, то искомое решение СЛАУ определим
как![]() .
.
Итак, задача свелась к построению
обратной матрицы![]() .
.
Найдем ее.
Мы
знаем, что для матрицы
![]() обратная
обратная
матрица может быть найдена как![]() ,
,
где![]() –
–
алгебраические дополнения элементов![]() .
.
В
нашем случае

Тогда
 Выполним
Выполним
проверку полученного решения ,
,
подставив его в матричную форму исходной
системы уравнений![]() .
.
Это равенство должно обратиться в
тождество, в противном случае где-то
была допущена ошибка.
Следовательно,
решение найдено верно.
Ответ:
![]() или
или
в другой записи
![]() .
.
-
Ранг
матрицы. Элементарные операции с
матрицей.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #