Как построить симметричную точку
Строить симметричные точки учат на уроках геометрии в средней школе. Это умение может в дальнейшем пригодиться на уроках черчения, а также на занятиях в высших учебных заведениях.

Инструкция
Прочитайте условие задачи и определите, относительно чего должна быть симметрична точка. Например, может потребоваться построение точки, симметричной относительно другой точки, оси симметрии, начала координат, оси Ох или Оу и т.п.
Если вам нужно построить точку А1, симметричную А относительно начала координат, сначала определите координаты точки А. А1 будет иметь те же координаты, но с противоположным знаком. Например, А1 (3; -5) будет симметрична А (-3; 5). Найдите и постройте на графике точку А1 с полученными координатами.
Чтобы построить точку А1, симметричную А относительно оси Ох, нужно найти точку с такой же абсциссой, но при этом с ординатой, противоположной по знаку. Это значит, что точке А (х; у) будет симметрична А1 (х; -у). Например, если А имеет координаты 6 по оси Ох и 2 по оси Оу, то вам нужно будет найти и построить точку А1 (6; -2).
Если требуется построить А1, симметричную А относительно оси Оу, найдите А1, ордината которой будет равна А, а абсцисса противоположна абсциссе А по знаку. Это означает, что А1 (-х; у) будет симметрична А (х; у). Например, если дана А (4; 8), то нужно найти и построить А1 (-4; 8).
Если необходимо построить точку А1, симметричную А относительно точки В, то нужно сначала начертить луч из А, проходящий через В. Измерьте расстояние от А до В и постройте точку А1 на таком же расстоянии от В, но в противоположной стороне луча. В результате у вас получится отрезок АА1, центром которого является точка В.
Чтобы построить точку А1, симметричную А относительно прямой, постройте луч с начальной точкой А, пересекающийся с прямой и перпендикулярный ей. Измерьте расстояние от А до точки пересечения прямой и луча, а затем постройте точку А1 на том же расстоянии от прямой, но в противоположной стороне. У вас должен получиться отрезок АА1, который разделен прямой ровно пополам.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
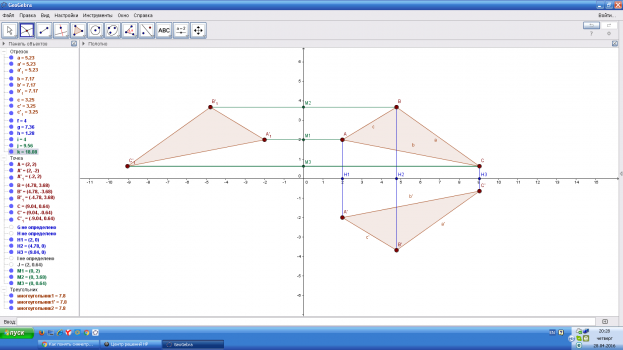
Чтобы построить точку симметрично оси Ох нужно:
1) провести из данной точки (например, точки А) перпендикуляр к оси Ох (на рис. это АН1)
2) на этом перпендикуляре в другой полуплоскости от оси Ох отложить отрезок равный построенному (на рис. это А’Н1=АН1)
Точка А’ будет симметрична точке А относительно оси Ох (и наоборот)
Чтобы построить фигуру симметрично оси Ох нужно симметрично отобразить все точки этой фигуры. Например, треугольник однозначно определяется тремя вершинами, поэтому чтобы построить треугольник симметричный данному относительно оси Ох, мы строим точки симметричные вершинам (на рис. это точки А’, B’, C’) Треугольник A’B’C’ симметричен треугольнику АВС относительно Ох
Симметрия относительно Оу определяется аналогично, только перпендикуляры теперь проводим именно к оси Оу. Точка А’1 симметрична точке А относительно Оу, а треугольник A’1B’1C’1 симметричен данному треугольнику АВС относительно прямой Оу.
Warning: include_once(): Failed opening ‘/home/zarab1/matemonline.com/www/wp-content/plugins/yet-another-related-posts-plugin/includes/template_functions.php’ for inclusion (include_path=’.:/usr/local/pear/php56′) in /home/zarab1/matemonline.com/www/wp-content/plugins/yet-another-related-posts-plugin/yarpp.php on line 52
Симметрии графиков функций
Прямая х=а является осью симметрии графика функции у=f(x) тогда и только тогда, когда для любого $xin D(f)$ выполняется равенство f(x)=f(2a-x).
Прямая х=а является осью симметрии графика функции f в том и только в том случае, когда для любого х из ее области определения выполняется равенство f(a+х)=f(a-х).
Точка (а, b) является центром симметрии графика функции у=f(x) тогда и только тогда, когда для любого $xin D(f)$ выполняется равенство f(x)+f(2а-х)=b.
Точка (а, b) является центром симметрии графика функции f в том и только в том случае, когда для любого х из ее области определения выполняется равенство f(a+х)+f(a-х)=b.
Пример 1: Сколько вертикальных осей симметрии может иметь график периодической функции?
Ответ: Если график функции f с периодом Т имеет ось симметрии х=а, то скорее всего — из геометрических соображений — осью симметрии будет и прямая х=а+Т. Но так как прямая х=с является осью симметрии графика функции у=f(x) тогда и только тогда, когда для любого $xin D(f)$ выполняется равенство f(x)=f(2с-х), то для прямой х=а+Т надо проверить выполнение равенства f(а+Т)=f(2а-а-Т), или f(a+Т)=f(aТ), a это равенство верно.
Так как периодов у периодической функции бесконечно много, то и осей симметрии бесконечно много, если, конечно, есть хотя бы одна.
Пример 2: График функции у=f(x) имеет вертикальную ось и центр симметрии. Что можно сказать о графике функции у=2f(x)-1?
Ответ: Так как график функции у=f(x) имеет вертикальную ось симметрии, например х=а, то для всякого х имеет место равенство f(a+х)=f(а-х), а тогда очевидно 2f(a+х)-1=2f(а-x)-1, так что функция у=2f(x)-1 имеет ту же ось симметрии. Если же график функции у=f(x) имеет центр симметрии, например, Q=(а, b), то для всякого х имеет место равенство f(а+х)+f(а-х)=2b, и в этом случае (2f(а+х)-1)+(2f(а-х)-1)=2b<-2, так что функция у=2f(x)-1 имеет центр симметрии в точке (а, 2b-2).
Комментарий. При рассуждении можно употреблять термины «растяжение-сжатие» и «сдвиг». Можно также пользоваться утверждением «Прямая х=а является осью симметрии графика функции у=f(x) тогда и только тогда, когда для любого $xin D(f)$ выполняется равенство f(x)=f(2а-x)».
Материалы по теме:
- Пример нахождения площади криволинейной трапеции через определённый интеграл.
- Функции четные и нечетные
- Находим асимптоты до графика функции.
- Периодические функции
![]() Загрузка…
Загрузка…

|
Рис. 4.26. Координатные отрезки точки F |
Рис. 4.27. Построение проекций точки F |
4.Завершите оформление чертежа: нанесите точки в виде окружностей, скорректируйте положение текстовых надписей, заполните основную надпись. Сохраните файл.
Симметрией называют преобразование положения точек плоскости или пространства, при котором каждая точка по некоторой закономерности переходит в другую точку этой плоскости или пространства. Преобразование положения точек может осуществляться относительно некоторого неподвижного геометрического объекта, называемого элементом симметрии.
В зависимости от вида элемента симметрии и направления преобразования различают следующие основные разновидности симметрии:
центральная симметрия — прямолинейное преобразование относительно точки;
осевая симметрия — ортогональное преобразование относительно прямой линии;
зеркальная симметрия — ортогональное преобразование относительно плоскости;
симметрия вращения — преобразование при повороте на некоторый угол;
симметрия переноса — преобразование при параллельном переносе.

Считается, что для построения фигур, симметричных заданной, достаточно научиться строить симметричную точку, поскольку любую фигуру можно представить как совокупность точек.
Координаты точки, симметричной некоторой исходной точке, по абсолютной величине равны координатам исходной точки, но отличаются знаком:
если элементом симметрии является начало координат, то меняется знак координат по всем трем осям;
если элементом симметрии является ось проекций, то меняется знак координат по двум другим осям;
если элементом симметрии является плоскость проекций, то меняется знак координаты по оси, перпендикулярной этой плоскости проекций.
Пример 7. Построить точку K, симметричную точке G (см. рис. 4.17) относительно плоскости проекций 1.
1. В нашем примере элемент симметрии — плоскость проекций 1, следовательно, меняется знак координат только по оси z:
xK = xG, yК = yG, zК = –zG;
ОKx = ОGx , ОKy
= ОGx , ОKy = ОGy , ОKz
= ОGy , ОKz = – ОGz .
= – ОGz .
2.Откладываем на осях координаты точки K. Отмечаем точки Kx, Ky (Ky 1
и Ky 3) и Kz (рис. 4.28).
Рис. 4.28. Построение координат точки K

3.Строим ортогональные проекции точки K (K , K и K
и K ), аналогично рассмотренным выше примерам (рис. 4.29).
), аналогично рассмотренным выше примерам (рис. 4.29).
4.Строим аксонометрическую проекцию точки K (рис. 4.30) подобно построению аксонометрической проекции точки G. Сопоставляя положение точек G и K с принятой нумерацией октантов, приходим к выводу, что точка G находится во II-м октанте, а точка K — в III.
Рис. 4.29. Построение проекций точки K
Рис. 4.30. Построение аксонометрической проекции точки K
Соседние файлы в предмете Геополитика
- #
- #
- #
- #
27.03.201875.81 Mб12Пестриков В.М., Морозов Е.М. – Механика разрушения на базе компьютерных технологий. Практикум – 2007.pdf
- #
- #
- #
- #
- #
Срочно!!! Нужны правила построения зеркально симметричных точек!! ! Как построить зеркально симметричную точку ???
Знаток
(315),
закрыт
8 лет назад
Лизьен
Знаток
(322)
10 лет назад
1
Прочитайте условие задачи и определите, относительно чего должна быть симметрична точка. Например, может потребоваться построение точки, симметричной относительно другой точки, оси симметрии, начала координат, оси Ох или Оу и т. п.
2
Если вам нужно построить точку А1, симметричную А относительно начала координат, сначала определите координаты точки А. А1 будет иметь те же координаты, но с противоположным знаком. Например, А1 (3; -5) будет симметрична А (-3; 5). Найдите и постройте на графике точку А1 с полученными координатами.
3
Чтобы построить точку А1, симметричную А относительно оси Ох, нужно найти точку с такой же абсциссой, но при этом с ординатой, противоположной по знаку. Это значит, что точке А (х; у) будет симметрична А1 (х; -у) . Например, если А имеет координаты 6 по оси Ох и 2 по оси Оу, то вам нужно будет найти и построить точку А1 (6; -2).
4
Если требуется построить А1, симметричную А относительно оси Оу, найдите А1, ордината которой будет равна А, а абсцисса противоположна абсциссе А по знаку. Это означает, что А1 (-х; у) будет симметрична А (х; у) . Например, если дана А (4; 8), то нужно найти и построить А1 (-4; 8).
5
Если необходимо построить точку А1, симметричную А относительно точки В, то нужно сначала начертить луч из А, проходящий через В. Измерьте расстояние от А до В и постройте точку А1 на таком же расстоянии от В, но в противоположной стороне луча. В результате у вас получится отрезок АА1, центром которого является точка В.
6
Чтобы построить точку А1, симметричную А относительно прямой, постройте луч с начальной точкой А, пересекающийся с прямой и перпендикулярный ей. Измерьте расстояние от А до точки пересечения прямой и луча, а затем постройте точку А1 на том же расстоянии от прямой, но в противоположной стороне. У вас должен получиться отрезок АА1, который разделен прямой ровно пополам.
