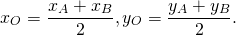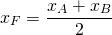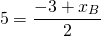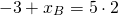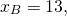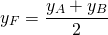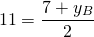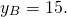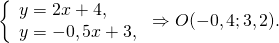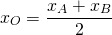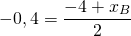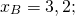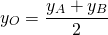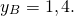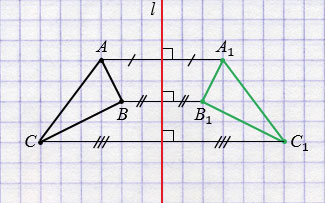Как найти симметричную точку относительно координатных осей

Как найти симметричную точку относительно координатных осей

Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.

I. Две точки A(xA;yA) и B(xB;yB) симметричны относительно точки O(xO;yO), если точка O является серединой отрезка AB.

По формулам координаты середины отрезка получаем связь координат этих точек:

    [ x_O = frac{{x_A + x_B }}{2},y_O = frac{{y_A + y_B }}{2}. ]

Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.

То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от  координат точки A только знаками:

A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.

Примеры.

1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).

Решение:

Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда

    [ x_F = frac{{x_A + x_B }}{2} ]

    [ 5 = frac{{ - 3 + x_B }}{2} ]

    [ - 3 + x_B = 5 cdot 2 ]

    [ x_B = 13, ]

    [ y_F = frac{{y_A + y_B }}{2} ]

    [ 11 = frac{{7 + y_B }}{2} ]

    [ y_B = 15. ]

Ответ: (13;15).

2) Найти точку, симметричную точке C (9;-4) относительно начала координат.

Решение:

Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).

Ответ: (-9;4).

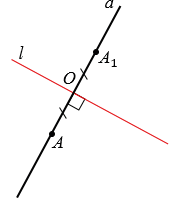
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.

Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:

  • Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
  • Найти точку O пересечения прямых f и g.
  • Зная конец отрезка A и его середину O найти другой конец B.

Пример

Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.

Решение:

Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:

5=-0,5·(-4)+b, откуда b=3.

Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.

Найдём координаты точки пересечения прямых:

    [ left{ begin{array}{l} y = 2x + 4, \ y = - 0,5x + 3, \ end{array} right. Rightarrow O( - 0,4;3,2). ]

    [ x_O = frac{{x_A + x_B }}{2} ]

    [ - 0,4 = frac{{ - 4 + x_B }}{2} ]

    [ x_B = 3,2; ]

    [ y_O = frac{{y_A + y_B }}{2} ]

    [ y_B = 1,4. ]

Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.

Ответ: (3,2;1,4).

Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:

 для точки A(x;y)
симметрия относительно:
оси Ox A1(x;-y)
оси Oy A2(-x;y)

биссектрисы I и II координатных

четвертей (прямой y=x)

 A3(y;x)

биссектрисы I b II координатных

четвертей (прямой y= -x)

 A4(-y;-x)
Источник

Как построить симметричную точку

Строить симметричные точки учат на уроках геометрии в средней школе. Это умение может в дальнейшем пригодиться на уроках черчения, а также на занятиях в высших учебных заведениях.

Как построить симметричную точку

Инструкция

Прочитайте условие задачи и определите, относительно чего должна быть симметрична точка. Например, может потребоваться построение точки, симметричной относительно другой точки, оси симметрии, начала координат, оси Ох или Оу и т.п.

Если вам нужно построить точку А1, симметричную А относительно начала координат, сначала определите координаты точки А. А1 будет иметь те же координаты, но с противоположным знаком. Например, А1 (3; -5) будет симметрична А (-3; 5). Найдите и постройте на графике точку А1 с полученными координатами.

Чтобы построить точку А1, симметричную А относительно оси Ох, нужно найти точку с такой же абсциссой, но при этом с ординатой, противоположной по знаку. Это значит, что точке А (х; у) будет симметрична А1 (х; -у). Например, если А имеет координаты 6 по оси Ох и 2 по оси Оу, то вам нужно будет найти и построить точку А1 (6; -2).

Если требуется построить А1, симметричную А относительно оси Оу, найдите А1, ордината которой будет равна А, а абсцисса противоположна абсциссе А по знаку. Это означает, что А1 (-х; у) будет симметрична А (х; у). Например, если дана А (4; 8), то нужно найти и построить А1 (-4; 8).

Если необходимо построить точку А1, симметричную А относительно точки В, то нужно сначала начертить луч из А, проходящий через В. Измерьте расстояние от А до В и постройте точку А1 на таком же расстоянии от В, но в противоположной стороне луча. В результате у вас получится отрезок АА1, центром которого является точка В.

Чтобы построить точку А1, симметричную А относительно прямой, постройте луч с начальной точкой А, пересекающийся с прямой и перпендикулярный ей. Измерьте расстояние от А до точки пересечения прямой и луча, а затем постройте точку А1 на том же расстоянии от прямой, но в противоположной стороне. У вас должен получиться отрезок АА1, который разделен прямой ровно пополам.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Рис. 4.26. Координатные отрезки точки F

Рис. 4.27. Построение проекций точки F

4.Завершите оформление чертежа: нанесите точки в виде окружностей, скорректируйте положение текстовых надписей, заполните основную надпись. Сохраните файл.

Симметрией называют преобразование положения точек плоскости или пространства, при котором каждая точка по некоторой закономерности переходит в другую точку этой плоскости или пространства. Преобразование положения точек может осуществляться относительно некоторого неподвижного геометрического объекта, называемого элементом симметрии.

В зависимости от вида элемента симметрии и направления преобразования различают следующие основные разновидности симметрии:

центральная симметрия — прямолинейное преобразование относительно точки;

осевая симметрия — ортогональное преобразование относительно прямой линии;

зеркальная симметрия — ортогональное преобразование относительно плоскости;

симметрия вращения — преобразование при повороте на некоторый угол;

симметрия переноса — преобразование при параллельном переносе.

Считается, что для построения фигур, симметричных заданной, достаточно научиться строить симметричную точку, поскольку любую фигуру можно представить как совокупность точек.

Координаты точки, симметричной некоторой исходной точке, по абсолютной величине равны координатам исходной точки, но отличаются знаком:

если элементом симметрии является начало координат, то меняется знак координат по всем трем осям;

если элементом симметрии является ось проекций, то меняется знак координат по двум другим осям;

если элементом симметрии является плоскость проекций, то меняется знак координаты по оси, перпендикулярной этой плоскости проекций.

Пример 7. Построить точку K, симметричную точке G (см. рис. 4.17) относительно плоскости проекций 1.

1. В нашем примере элемент симметрии — плоскость проекций 1, следовательно, меняется знак координат только по оси z:

xK = xG, yК = yG, zК = –zG;

ОKx= ОGx , ОKy = ОGy , ОKz= – ОGz .

2.Откладываем на осях координаты точки K. Отмечаем точки Kx, Ky (Ky 1

и Ky 3) и Kz (рис. 4.28).

Рис. 4.28. Построение координат точки K

3.Строим ортогональные проекции точки K (K , Kи K), аналогично рассмотренным выше примерам (рис. 4.29).

4.Строим аксонометрическую проекцию точки K (рис. 4.30) подобно построению аксонометрической проекции точки G. Сопоставляя положение точек G и K с принятой нумерацией октантов, приходим к выводу, что точка G находится во II-м октанте, а точка K — в III.

Рис. 4.29. Построение проекций точки K

Рис. 4.30. Построение аксонометрической проекции точки K

Соседние файлы в предмете Геополитика

  • #
  • #
  • #
  • #

    27.03.201875.81 Mб13Пестриков В.М., Морозов Е.М. – Механика разрушения на базе компьютерных технологий. Практикум – 2007.pdf

  • #
  • #
  • #
  • #
  • #
Источник

Содержание

  1. Что значит симметричная точка относительно начала координат
  2. Урок по теме «Симметрия на координатной плоскости»
  3. Ход урока
  4. Осевая и центральная симметрия
  5. Что такое симметрия
  6. Осевая симметрия
  7. Центральная симметрия
  8. Задачи на самопроверку
  9. Координаты симметричных точек

Что значит симметричная точка относительно начала координат

Построить точку, симметричную точке A(x, y) относительно:
а) оси Ox,
б) оси Oy,
в) начала координат.

Две точки M1 и M2 называются симметричными относительно прямой, если отрезок M1M2 перпендикулярен этой прямой, причем его середина лежит на этой прямой.

Две точки M1 и M2 называются симметричными относительно точки O, если точка O является серединой отрезка M1M2.

а) Точка B, симметричная с точкой A(x, y) относительно оси Ox, имеет абсциссу такую же, как и точка A, а ординату, равную по абсолютной величине ординате точки A, но противоположную ей по знаку. Значит, точка B имеет координаты x и —y: B(x, —y) (см. рисунок).

б) Точка C, симметричная с точкой A(x, y) относительно оси Oy, будет иметь ординату такую же, как и точка A, а абсцисса точки C будет по абсолютной величине равна абсциссе точки A, но противоположна ей по знаку. Значит, точка C имеет координаты —x и y: C(-x, y) (см. рисунок)

в) Точка D, симметричная точке A(x, y) относительно начала координат, будет иметь абсциссу и ординату, равные по абсолютной величине абсциссе и ординате точки A, но противоположные им по знаку, т. е. координаты точки D будут равны —x и —y: D(-x, —y) (см. рисунок).

Источник

Урок по теме «Симметрия на координатной плоскости»

Разделы: Математика

  • SMART-BOARD.
  • ПК “КМ-школа”.
  • Мультимедийный проектор.
  • Индивидуальные планшетки, маркер, ватный диск (для удаления и исправления записей).
  • Два листа А4 на каждой парте для работы в группах и в парах.
  • Изображение парусника на миллиметровой бумаге для самостоятельной работы в двух вариантах.

    • Основные цели урока: тренировать способность к определению координат точек и построению точек по их координатам; выявить взаимосвязь между координатами точек симметричных относительно начала координат и повторить взаимосвязь между координатами точек симметричных относительно координатных осей.

    Перед началом урока учитель собирает творческое домашнее задание: на альбомных листах учащиеся оформляли свои рисунки по координатам.

    Ход урока

    1. Самоопределение к деятельности.

    – Я вижу у вас хорошее настроение и боевой настрой. Они нам очень пригодятся. Сегодня у нас пройдёт необычный урок – Морское путешествие. Дело в том, что вчера на сайте нашей школы появился сигнал бедствия от Робинзона Крузо. Он просит помочь ему построить парусник, на котором он смог бы вернуться домой. Чтобы спасти его, нам надо преодолеть большое расстояние. Давайте посмотрим на карту нашего путешествия.

    Маршрут: Бухта знаний – Залив Исторический – Остров сокровищ – Школа Робинзона Крузо – Мыс Настроения – Бухта знаний.

    – Итак, мы отправляемся в путь, но чтобы не сбиться с маршрута, преодолеть все рифы и подводные течения, нам необходимо внимательно следить за координатами нашего корабля. Давайте вспомним, какую тему мы недавно начали изучать? (Координатная плоскость).

    – Чтобы преодолеть залив Исторический и не разбиться о его скалистые берега, давайте вспомним как давно появилось понятие координатной плоскости, и кто впервые ввёл его? ( Рене Декарт.)

    – Что вам о нём известно? Тогда давайте обратимся к нашей энциклопедии.

    – Из чего же состоит координатная плоскость?

    Вызвать ученика. (Весь класс помогает: две пересекающиеся под прямым углом прямые – оси абсцисс и ординат, точка их пересечения – начало отсчёта, стрелочки – указывают положительное направление осей, единичный отрезок.) Ученик заполняет маркером пустые места на координатной плоскости. Оценка.

    – Сколько углов образовалось при построении координатной плоскости? (четыре) Как они называются? (координатные углы или координатные четверти). Покажите, как они расположены.

    Ученик нумерует маркером углы и указывает координаты точек в этих углах схематично с помощью знаков “+” и “-”.

    – Как с помощью неравенств записать знаки координат точек в каждом из углов? Ученики обсуждают в парах и предлагают свои варианты, из которых выбирается верный.

    I. x>0, y>0
    II. x 0
    III. x 0, y 27.01.2012

    Источник

    Осевая и центральная симметрия

    О чем эта статья:

    Что такое симметрия

    Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

    Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

    Центр симметрии — это точка, в которой пересекаются все оси симметрии.

    Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

    Рассмотрите фигуры с осевой и центральной симметрией.

    • Ось симметрии угла — биссектриса.
    • Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
    • Оси симметрии прямоугольника проходят через середины его сторон.
    • У ромба две оси симметрии — прямые, содержащие его диагонали.
    • У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
    • Ось симметрии окружности — любая прямая, проведенная через ее центр.

    Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

    Осевая симметрия

    Вот как звучит определение осевой симметрии:

    Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

    При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

    Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

    В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

    Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

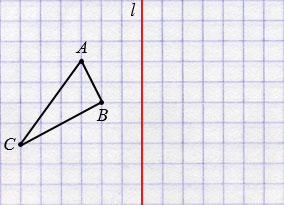
    Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.

    1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
    2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
    3. С другой стороны прямой отложим такие же расстояния.
    4. Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
    5. Получаем два треугольника, симметричных относительно оси симметрии.

    Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

    1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
    2. Измеряем расстояние от вершин до точек на прямой.
    3. Откладываем такие же расстояния на другой стороне оси симметрии.
    4. Соединяем точки и строим треугольник A1B1C1.

    Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.

    1. Проводим через точку А прямую, перпендикулярную прямой l.
    2. Проводим через точку В прямую, перпендикулярную прямой l.
    3. Измеряем расстояния от точек А и В до прямой l.
    4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A1 и B1.
    5. Соединяем точки A1 и B1.

    Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

    Центральная симметрия

    Теперь поговорим о центральной симметрии — вот ее определение:

    Центральной симметрией называется симметрия относительно точки.

    Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

    Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

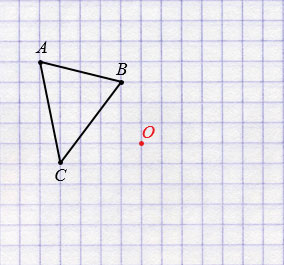
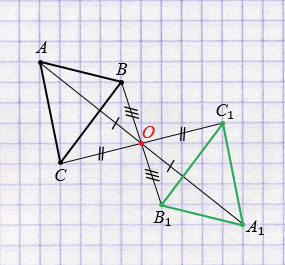
    Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).

    1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
    2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
    3. Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
    4. Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.

    Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).

    1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
    2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
    3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
    4. Чертим на противоположной стороне отрезки А1О и B1О, равные отрезкам АО и АB.
    5. Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.

    Задачи на самопроверку

    В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

    Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

    Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

    Симметрия относительно прямой — осевая
    Симметрия относительно точки — центральная

    Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
    симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.

    Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.

    Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

    Источник

    Координаты симметричных точек

    Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.

    По формулам координаты середины отрезка получаем связь координат этих точек:

    Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.

    То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:

    A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.

    1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).

    Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда

    2) Найти точку, симметричную точке C (9;-4) относительно начала координат.

    Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).

    II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.

    Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:

    • Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
    • Найти точку O пересечения прямых f и g.
    • Зная конец отрезка A и его середину O найти другой конец B.

    Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.

    Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:

    Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.

    Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.

    Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:

    Источник

    Источник
    1. Главная
    2. Справочники
    3. Справочник по математике 5-9 класс
    4. Координаты на плоскости
    5. Осевая и центральная симметрии

    Осевая симметрия

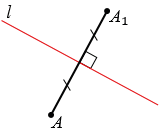
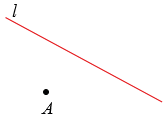
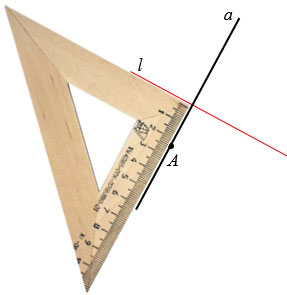
    Рассмотрим построение точки, симметричной данной точке А относительно данной прямой .

    Пусть дана точка А и прямая .

    Точку симметричную точке А относительно прямой , можно построить так. Проведем через точку А прямую , перпендикулярную прямой . Для этого используем чертежный угольник. Прикладываем чертежный угольник так, как показано на рисунке ниже и проводим прямую через точку А.

    Пусть прямые и пересекаются в точке О. Отложим при помощи линейки на прямой отрезок ОА1, равный отрезку ОА.

    Получаем точки А и А1, которые симметричны относительно прямой .

    Также можно построить фигуры, симметричные относительно прямой.

    Построим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой .

    Пусть дан треугольник АВС и прямая .

    Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно прямой (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой .

    Обратите внимание, любые две фигуры, симметричные относительно прямой, равны.

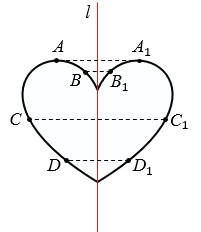
    Если фигура имеет ось симметрии (прямая  ) то, все точки этой фигуры, не принадлежащие этой оси, можно разделить на пары симметричных точек.

    Центральная симметрия

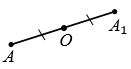
    Точки М и М1 называют симметричными относительно точки О, если точка О является серединой отрезка ММ1 (смотри рисунок ниже).

    Рассмотрим построение точки, симметричной данной точке М относительно данной точки О.

    Пусть даны точки М и О. Точку, симметричную точке М относительно точки О, можно построит так. Проведем луч МО.

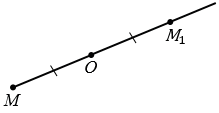
    На луче МО отложим отрезок ОN , равный отрезку ОМ.

    Точки М и М1, которые симметричны относительно точки О.

    Также можно построить фигуры, симметричные относительно точки.

    Построим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.

    Пусть дан треугольник АВС и точки О.

    Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно точки О (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.

    Обратите внимание, любые две фигуры, симметричные относительно точки, равны.

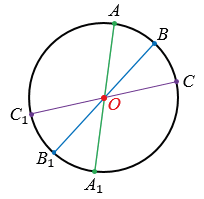
    Рассмотрим окружность с центром в точке О. Все точки окружности можно разбить на пары точек, симметричных относительно точки О.

    В таком случае говорят, что окружность имеет центр симметрии – точку О.

    Также центр симметрии имеют такие фигуры, как отрезок, прямоугольник, эллипс.

    Советуем посмотреть:

    Перпендикулярные прямые

    Параллельные прямые

    Координатная плоскость

    Координаты на плоскости


    Правило встречается в следующих упражнениях:

    6 класс

    Номер 1244,
    Мерзляк, Полонский, Якир, Учебник

    Номер 1246,
    Мерзляк, Полонский, Якир, Учебник

    Номер 1248,
    Мерзляк, Полонский, Якир, Учебник

    Номер 1250,
    Мерзляк, Полонский, Якир, Учебник

    Номер 1258,
    Мерзляк, Полонский, Якир, Учебник

    Номер 1261,
    Мерзляк, Полонский, Якир, Учебник

    Номер 1271,
    Мерзляк, Полонский, Якир, Учебник

    Номер 1273,
    Мерзляк, Полонский, Якир, Учебник

    Номер 1316,
    Мерзляк, Полонский, Якир, Учебник

    Номер 8,
    Мерзляк, Полонский, Якир, Учебник

    Источник

    Добавить комментарий