Как найти симметричную точку относительно оси ординат

Как найти симметричную точку относительно оси ординат

На чтение 2 мин. Просмотров 15k.

  • Две точки А и А1 называются симметричными друг другу относительно прямой m, если прямая m перпендикулярна отрезку АА1 и проходит через его середину. Прямую m называют осью симметрии.
  • При сгибании плоскости чертежа по прямой m – оси симметрии симметричные фигуры совместятся.
  • Прямоугольник имеет две оси симметрии.
  • Квадрат имеет четыре оси симметрии.
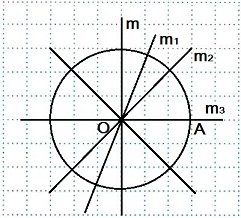
  • Любая прямая, проходящая через центр окружности, является ее осью симметрии. Окружность имеет бесконечное множество осей симметрии.

6.7.3. Осевая симметрия.Точки А и А1 симметричны относительно прямой m, так как прямая m перпендикулярна отрезку АА1 и проходит через его середину.

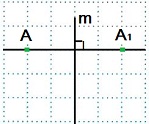
m – ось симметрии.

6.7.3. Осевая симметрия.Прямоугольник ABCD имеет две оси симметрии: прямые m и l.

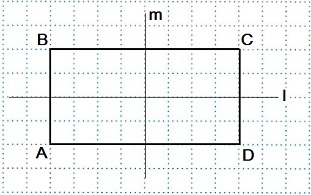
Если чертеж перегнуть по прямой m или по прямой l, то обе части чертежа совпадут.

6.7.3. Осевая симметрия.Квадрат ABCD имеет четыре оси симметрии: прямые m, l,  k и  s.

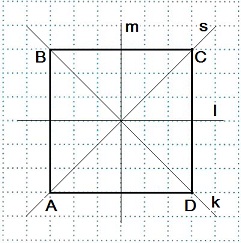
Если квадрат перегнуть по какой-либо из прямых: m, l, k или s, то обе части квадрата совпадут.

6.7.3. Осевая симметрия.Окружность с центром в точке О и радиусом ОА имеет бесчисленное количество осей симметрии. Это прямые:  m, m1, m2, m3 … 

Задание. Построить точку А1, симметричную точке А(-4; 2) относительно оси Ох.

Построить точку А2, симметричную точке А(-4; 2) относительно оси Оy.

6.7.3. Осевая симметрия.Точка А1(-4; -2) симметрична точке А(-4; 2) относительно оси Ох, так как ось Ох перпендикулярна отрезку АА1 и проходит через его середину.

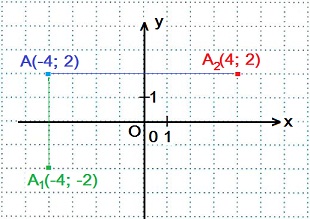
У точек, симметричных относительно оси Ох абсциссы совпадают, а ординаты являются противоположными числами.

Точка А2(4; -2) симметрична точке А(-4; 2) относительно оси Оy, так как ось Оу перпендикулярна отрезку АА2 и проходит через его середину.

У точек, симметричных относительно оси Оу ординаты совпадают, а абсциссы являются противоположными числами.

( 4 оценки, среднее 3.5 из 5 )

Источник

Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.

I. Две точки A(xA;yA) и B(xB;yB) симметричны относительно точки O(xO;yO), если точка O является серединой отрезка AB.

По формулам координаты середины отрезка получаем связь координат этих точек:

    [ x_O = frac{{x_A + x_B }}{2},y_O = frac{{y_A + y_B }}{2}. ]

Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.

То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от  координат точки A только знаками:

A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.

Примеры.

1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).

Решение:

Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда

    [ x_F = frac{{x_A + x_B }}{2} ]

    [ 5 = frac{{ - 3 + x_B }}{2} ]

    [ - 3 + x_B = 5 cdot 2 ]

    [ x_B = 13, ]

    [ y_F = frac{{y_A + y_B }}{2} ]

    [ 11 = frac{{7 + y_B }}{2} ]

    [ y_B = 15. ]

Ответ: (13;15).

2) Найти точку, симметричную точке C (9;-4) относительно начала координат.

Решение:

Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).

Ответ: (-9;4).

II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.

Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:

  • Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
  • Найти точку O пересечения прямых f и g.
  • Зная конец отрезка A и его середину O найти другой конец B.

Пример

Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.

Решение:

Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:

5=-0,5·(-4)+b, откуда b=3.

Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.

Найдём координаты точки пересечения прямых:

    [ left{ begin{array}{l} y = 2x + 4, \ y = - 0,5x + 3, \ end{array} right. Rightarrow O( - 0,4;3,2). ]

    [ x_O = frac{{x_A + x_B }}{2} ]

    [ - 0,4 = frac{{ - 4 + x_B }}{2} ]

    [ x_B = 3,2; ]

    [ y_O = frac{{y_A + y_B }}{2} ]

    [ y_B = 1,4. ]

Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.

Ответ: (3,2;1,4).

Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:

 для точки A(x;y)
симметрия относительно:
оси Ox A1(x;-y)
оси Oy A2(-x;y)

биссектрисы I и II координатных

четвертей (прямой y=x)

 A3(y;x)

биссектрисы I b II координатных

четвертей (прямой y= -x)

 A4(-y;-x)
Источник
  1. Главная
  2. Справочники
  3. Справочник по математике 5-9 класс
  4. Координаты на плоскости
  5. Координатная плоскость

Указать положение точки на плоскости можно с помощью координат. Для этого проведем на плоскости две перпендикулярные координатные прямые так, чтобы их начала отсчета совпадали.

Эти прямые называют осями координат, точку их пересечения О – начало отсчета.

Горизонтальная ось – ось абсцисс, обозначают буквой , поэтому еще называют ось  , пишут: .

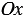
Вертикальная ось – ось ординат, обозначают буквой , поэтому еще называют ось , пишут: .

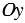
Оси и вместе образуют прямоугольную систему координат на плоскости. Плоскость, на которой выбрана система координат, называют координатной плоскостью.

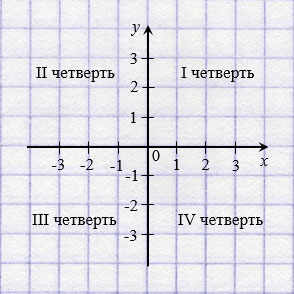
Координатные оси разбивают плоскость на четыре части, которые называют координатными четвертями и нумеруют так, как показано на рисунке ниже.

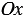
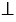
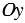
Отметим на координатной плоскости точку А. Проведем через нее прямую АВ, перпендикулярную оси абсцисс (АВ ), и прямую АС, перпендикулярную оси ординат (АС ).

Точка В на оси имеет координату 5, а точка С на оси – координату 3 . Число 5 называют абсциссой точки А, число  3 – ординатой точки А. Числа 5 и 3 однозначно определяют положение точки А на координатной плоскости, поэтому их называют координатами точки А и записывают: А(5; 3).

Обратите внимание, записывая координаты точки, абсциссу всегда ставят на первое место, а ординату – на второе. Если числа 5 и 3 поменять местами, то получим координаты другой точки – точки К(3; 5) (смотри рисунок выше).

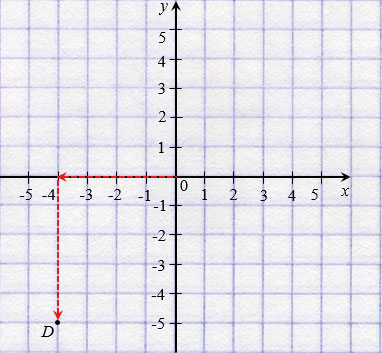
У начала координат абсцисса и ордината равны нулю, записывают так: О(0; 0). Если точка лежит на оси абсцисс, то ее ордината равна нулю, а если на оси ординат, то нулю равна ее абсцисса. На рисунке ниже: Р(2; 0); Е(0; 4).

Чтобы попасть в точку D с координатами (4; 5), нужно сначала пройти по оси от начала отсчета влево на 4 единицы, а потом – на 5 единиц вниз.

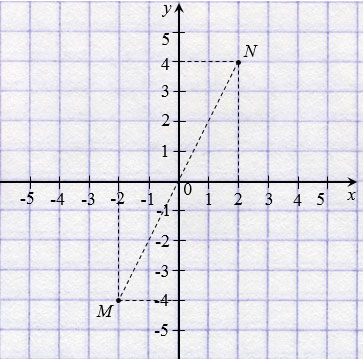
Две точки с противоположными абсциссами и ординатами симметричны относительно начала координат.

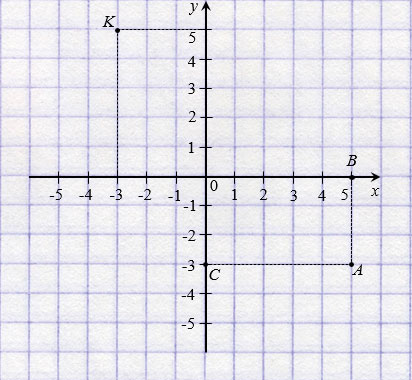
На рисунке ниже точки N(2; 4) и М(2; 4) симметричны относительно начала координат.

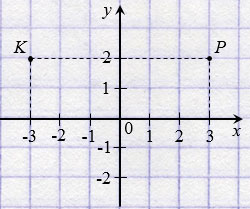
Две точки, имеющие равные ординаты и противоположные абсциссы, симметричны относительно оси ординат.

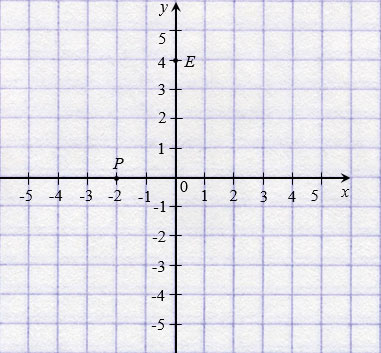
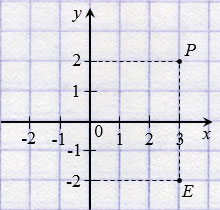
На рисунке ниже точки Р(3; 2) и К(3; 2) симметричны относительно оси ординат.

Две точки, имеющие равные абсциссы и противоположные ординаты, симметричны относительно оси абсцисс.

На рисунке ниже точки Р(3; 2) и Е(3; 2) симметричны относительно оси абсцисс.

Советуем посмотреть:

Перпендикулярные прямые

Осевая и центральная симметрии

Параллельные прямые

Координаты на плоскости


Правило встречается в следующих упражнениях:

6 класс

Номер 1306,
Мерзляк, Полонский, Якир, Учебник

Номер 1310,
Мерзляк, Полонский, Якир, Учебник

Номер 4,
Мерзляк, Полонский, Якир, Учебник

Задание 1391,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1397,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1398,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1467,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1535,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1537,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1542,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 868,
Мерзляк, Полонский, Якир, Учебник

Номер 876,
Мерзляк, Полонский, Якир, Учебник

Номер 882,
Мерзляк, Полонский, Якир, Учебник

Номер 920,
Мерзляк, Полонский, Якир, Учебник

Номер 925,
Мерзляк, Полонский, Якир, Учебник

Номер 987,
Мерзляк, Полонский, Якир, Учебник

Номер 997,
Мерзляк, Полонский, Якир, Учебник

Номер 1026,
Мерзляк, Полонский, Якир, Учебник

Номер 1212,
Мерзляк, Полонский, Якир, Учебник

Номер 7,
Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 309,
Мерзляк, Полонский, Якир, Учебник

Номер 6,
Мерзляк, Полонский, Якир, Учебник

Номер 327,
Мерзляк, Полонский, Якир, Учебник

Номер 330,
Мерзляк, Полонский, Якир, Учебник

Номер 331,
Мерзляк, Полонский, Якир, Учебник

Номер 337,
Мерзляк, Полонский, Якир, Учебник

Номер 341,
Мерзляк, Полонский, Якир, Учебник

Номер 355,
Мерзляк, Полонский, Якир, Учебник

Номер 356,
Мерзляк, Полонский, Якир, Учебник

Номер 362,
Мерзляк, Полонский, Якир, Учебник

Источник

Как построить симметричную точку

Строить симметричные точки учат на уроках геометрии в средней школе. Это умение может в дальнейшем пригодиться на уроках черчения, а также на занятиях в высших учебных заведениях.

Как построить симметричную точку

Инструкция

Прочитайте условие задачи и определите, относительно чего должна быть симметрична точка. Например, может потребоваться построение точки, симметричной относительно другой точки, оси симметрии, начала координат, оси Ох или Оу и т.п.

Если вам нужно построить точку А1, симметричную А относительно начала координат, сначала определите координаты точки А. А1 будет иметь те же координаты, но с противоположным знаком. Например, А1 (3; -5) будет симметрична А (-3; 5). Найдите и постройте на графике точку А1 с полученными координатами.

Чтобы построить точку А1, симметричную А относительно оси Ох, нужно найти точку с такой же абсциссой, но при этом с ординатой, противоположной по знаку. Это значит, что точке А (х; у) будет симметрична А1 (х; -у). Например, если А имеет координаты 6 по оси Ох и 2 по оси Оу, то вам нужно будет найти и построить точку А1 (6; -2).

Если требуется построить А1, симметричную А относительно оси Оу, найдите А1, ордината которой будет равна А, а абсцисса противоположна абсциссе А по знаку. Это означает, что А1 (-х; у) будет симметрична А (х; у). Например, если дана А (4; 8), то нужно найти и построить А1 (-4; 8).

Если необходимо построить точку А1, симметричную А относительно точки В, то нужно сначала начертить луч из А, проходящий через В. Измерьте расстояние от А до В и постройте точку А1 на таком же расстоянии от В, но в противоположной стороне луча. В результате у вас получится отрезок АА1, центром которого является точка В.

Чтобы построить точку А1, симметричную А относительно прямой, постройте луч с начальной точкой А, пересекающийся с прямой и перпендикулярный ей. Измерьте расстояние от А до точки пересечения прямой и луча, а затем постройте точку А1 на том же расстоянии от прямой, но в противоположной стороне. У вас должен получиться отрезок АА1, который разделен прямой ровно пополам.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Сегодня на уроке мы вспомним такое понятие как
осевая симметрия на плоскости, введём понятие осевой симметрии в пространстве,
проверим, будет ли осевая симметрия движением пространства.

Давайте вспомним, что фигура называется симметричной
относительно прямой , если для
каждой точки фигуры симметричная ей точка относительно прямой  также
принадлежит этой фигуре. Прямая  называется осью
симметрии фигуры. Про такую фигуру говорят, что она обладает осевой
симметрией.

Давайте приведём примеры таких фигур
из жизни и геометрии.

Ещё мы давали такое определение:

Точки  и  называются симметричными
относительно прямой , если прямая  проходит через
середину отрезка  и
перпендикулярна к этому отрезку.

Прямая  называется осью
симметрии.

Каждая точка прямой  считается
симметричной самой себе.

В курсе планиметрии мы доказывали, что осевая
симметрия является движением.

Напомним это доказательство.

Пусть точки М и N
– какие-нибудь точки плоскости, а точки М1, и N1
– симметричные им точки относительно прямой А. Здесь может быть несколько
вариантов расположения точек на плоскости.

Рассмотрим один из таких вариантов.

По построению симметричных точек относительно прямой
А, прямая А перпендикулярна прямым ММ1 и NN1
и делит эти отрезки пополам, значит, в треугольниках МОМ1 и NОN1
отрезки ОК и ОЕ будут являться медианами и высотами, проведёнными к
основанию, то есть это равнобедренные треугольники.

.

.

Заменив отрезок  равным ему
отрезком , а отрезок  – равным ему
отрезком , получим, что .

Вывод: таким образом, мы
доказали, что расстояние между точками М и N
равно расстоянию между симметричными им точками М один и N1.

Получаем, что осевая симметрия – пример движения
плоскости.

В пространстве осевой симметрией с осью  мы назовем
такое отображение пространства на себя, при котором любая точка  переходит в
симметричную ей точку  относительно
оси .

Теперь давайте проверим, будет ли осевая симметрия в
пространстве движением пространства.

Для этого введём прямоугольную систему координат Оxyz
так, чтобы ось Оz совпала с осью
симметрии. Теперь давайте попробуем найти связь между координатами точки М с
координатами x, y,
z и точки М1 с
координатами x1,
y1,z1,
симметричных относительно оси Оz.

Если точка М не лежит на оси Оz,
то по определению оси симметрии, ось Оz
проходит через середину отрезка ММ1 и перпендикулярна к этому
отрезку. Поскольку Оz – середина
отрезка ММ1, и абсциссы и ординаты точек оси Оz
равны нулю, то можно записать, что  и .

То есть , .

Условие того, что ось Оz
перпендикулярно прямой ММ1 даёт нам, то что аппликаты точек М и М1
равны .

Если же точка М лежит на оси Оz,
то она отображается сама на себя, по определению оси симметрии, значит, и в
этом случае будут выполнятся полученные равенства.

Вывод: для симметричный точек
относительно оси Оz абсциссы и
ординаты противоположны, а аппликаты равны.

Возникает вопрос, а если ось симметрии совпадает не
с осью Оz, а, например, Оx
или Оy. Тогда связь между
координатами симметричных точек М и М1 будет такая: если ось
симметрии проходит через ось Оx,
то точки М и М1 имеют такие координаты , .

Если осью симметрии будет ось Оy,
то точки М и М1 имеют такие координаты , .

Теперь давайте рассмотрим любые две точки  и . По только что
доказанным формулам для координат симметричных точек получим, что точка . Точка .

Теперь давайте найдём расстояние .

Получим, что .

Теперь давайте найдём расстояние между точками  и .

Очевидно, что оба эти выражения равны, то есть
получим, что . То есть
расстояние между точками при осевой симметрии в пространстве сохраняется,
значит, осевая симметрия в пространстве также является движением,
но уже не плоскости, а пространства.

Задача:
найти координаты точек, в которые переходят точки , ,  при осевой
симметрии относительно координатных осей.

Решение:
сначала найдём координаты точек в которые переходит точки , ,  при осевой
симметрии относительно оси Ох.

Если точка  симметрична
точке  относительно
оси  то справедливы
формулы: .

Точка  отобразится в
точку .

Точка  отобразится в
точку .

Точка  отобразится в
точку .

Если точка  симметрична
точке  относительно
оси  то справедливы
формулы: .

Точка  отобразится в
точку .

Точка  отобразится в
точку .

Точка  отобразится в
точку .

Если точка  симметрична
точке  относительно
оси  то справедливы
формулы: .

Точка  отобразится в
точку .

Точка  отобразится в
точку .

Точка  отобразится в
точку .

Итоги:

Сегодня на уроке мы ввели понятия осевой симметрии в
пространстве. Показали, что и в пространстве осевая симметрия будет примером
движения. Решили несколько задач.

Источник

Добавить комментарий