Аналитическая геометрия для «чайников»
Настоящая книга позволит вам в сжатые сроки (2-3 недели) освоить основы аналитической геометрии и научиться решать наиболее распространённые задачи по теме. Материал предназначен для студентов-заочников и других читателей, которые хотят быстро освоить минимум теории и максимум практики
Сначала немного о предмете…. Наверняка вам сейчас вспомнился курс школьной геометрии с многочисленными теоремами, их доказательствами, чертежами и т.д. Что скрывать, нелюбимый и часто малопонятный предмет для значительной доли учеников. Аналитическая геометрия, как ни странно, может показаться более интересной и доступной. Что означает «аналитическая»? На ум сразу приходят два «штампованных» математических оборота: графический метод решения и аналитический метод решения.
Графический метод связан с построением графиков, чертежей. Аналитический же метод предполагает решение задач преимущественно посредством алгебраических действий. В этой связи алгоритм решения многих задач аналитической геометрии прост и прозрачен, зачастую достаточно аккуратно применить нужные формулы – и ответ готов! Нет, конечно, совсем без чертежей тут не обойдется, к тому же для лучшего понимания материала я постараюсь приводить их сверх необходимости.
Координаты симметричных точек
Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2
Вступление
Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.
Начнем с взаимного расположения точки относительно прямой, луча и отрезка.
Задача №1
Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.
Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P1(x1, y1), P2(x2, y2). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P1P2 и P1M и по его знаку сделать вывод.
Задача №2
Определить принадлежит ли точка лучу.
Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P1(x1, y1) — начало луча, а P2(x2, y2) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P1(x1, y1), где P2(x2, y2) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (P1P2, P1M) ≥ 0 – скалярное произведение (точка лежит на луче)
Задача №3
Определить принадлежит ли точка отрезку.
Решение
Пусть точки P1(x1, y1), P2(x2, y2) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P1, P2. Далее нам нужно определить лежит ли точка между точками P1 и P2, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP1, MP2). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (MP1,MP2) ≤ 0 – скалярное произведение (точка лежит между P1 и P2)
Задача №4
Взаимное расположение двух точек относительно прямой.
Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.
Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P1P2, P1M1] * [P1P2, P1M2] 0 – точки лежат по одну сторону.
3. [P1P2, P1M1] * [P1P2, P1M2] = 0 – одна (или две) из точек лежит на прямой.
Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P1P2, P1M1] * [P1P2, P1M2] ≤ 0.
Задача №5
Определить пересекаются ли две прямые.
Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0. Тогда условие параллельности прямых заключается в том, что a1b2 — a2b1 = 0.
Если же прямые заданы точками P1(x1, y1), P2(x2, y2), M1(x3, y3), M2(x4, y4), то условие их параллельности заключается в проверки косого произведения векторов P1P2 и M1M2: если оно равно нулю, то прямые параллельны.
В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b1, a1), (-b2, a2) которые называются направляющими векторами.
Задача №6
Определить пересекаются ли два отрезка.
Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:
Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P1P2, P1M2] > 0, [P1P2, P1M1] [P1P2, P1M2] * [P1P2, P1M1] 2 + b 2 ).
Задача №8
Расстояние от точки до луча.
Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.
В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.
Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP1P2 – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P1M, P1P2) 2 .
Теперь рассмотрим случай, когда центр второго круга O2 находится между точками O1 и C. В этом случае получим отрицательное значение величины d2. Использование отрицательного значения d2 приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.
Заключение
Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.
[spoiler title=”источники:”]
http://habr.com/ru/post/148325/
[/spoiler]
Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
I. Две точки A(xA;yA) и B(xB;yB) симметричны относительно точки O(xO;yO), если точка O является серединой отрезка AB.
По формулам координаты середины отрезка получаем связь координат этих точек:
![]()
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
Примеры.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Решение:
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: (13;15).
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Решение:
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
Ответ: (-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Пример
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Решение:
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
5=-0,5·(-4)+b, откуда b=3.
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Найдём координаты точки пересечения прямых:
![]()
![]()
![]()
![]()
![]()
![]()
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Ответ: (3,2;1,4).
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
| для точки A(x;y) | |
| симметрия относительно: | |
| оси Ox | A1(x;-y) |
| оси Oy | A2(-x;y) |
|
биссектрисы I и II координатных четвертей (прямой y=x) |
A3(y;x) |
|
биссектрисы I b II координатных четвертей (прямой y= -x) |
A4(-y;-x) |
Прямую в пространстве
всегда можно определить как линию
пересечения двух непараллельных
плоскостей. Если уравнение одной
плоскости
![]() ,
,
уравнение второй плоскости![]() ,
,
тогда уравнение прямой задаётся виде

здесь
![]() неколлинеарен
неколлинеарен![]() .
.
Эти уравнения называютсяобщими
уравнениями
прямой в пространстве.
Канонические
уравнения прямой
Любой ненулевой
вектор, лежащий на данной прямой или
параллельный ей, называется направляющим
вектором этой прямой.
Если известна
точка
![]() прямой и её направляющий вектор
прямой и её направляющий вектор![]() ,
,
то канонические уравнения прямой имеют
вид:
![]() .
.
(9)
Параметрические
уравнения прямой
Пусть заданы
канонические уравнения прямой
![]() .
.
Отсюда, получаем
параметрические уравнения прямой:
 (10)
(10)
Эти уравнения
удобны при нахождении точки пересечения
прямой и плоскости.
Уравнение прямой,
проходящей через две точки
Уравнение прямой,
проходящей через две точки
![]() и
и![]() имеет
имеет
вид:
![]() .
.
Угол между прямыми
Угол между прямыми
![]() и
и
![]()
равен углу между
их направляющими векторами. Следовательно,
его можно вычислить по формуле (4):
 .
.
Условие параллельности
прямых:
![]() .
.
Условие
перпендикулярности плоскостей:
![]() .
.
Расстояние точки
от прямой
П усть
усть
дана точка![]() и прямая
и прямая
![]() .
.
Из канонических
уравнений прямой известны
точка
![]() ,
,
принадлежащая прямой,и
её направляющий
вектор
![]() .
.
Тогда расстояние точки![]() от прямой равно высоте параллелограмма,
от прямой равно высоте параллелограмма,
построенного на векторах![]() и
и![]() .
.
Следовательно,
![]() .
.
Условие пересечения
прямых
Две непараллельные
прямые
![]() ,
,
![]()
пересекаются тогда
и только тогда, когда
 .
.
Взаимное
расположение прямой и плоскости.
Пусть заданы прямая
![]() и плоскость
и плоскость![]() .
.
Угол![]() между ними можно найти по формуле
между ними можно найти по формуле
![]() .
.
Задача 73.
Написать канонические уравнения прямой
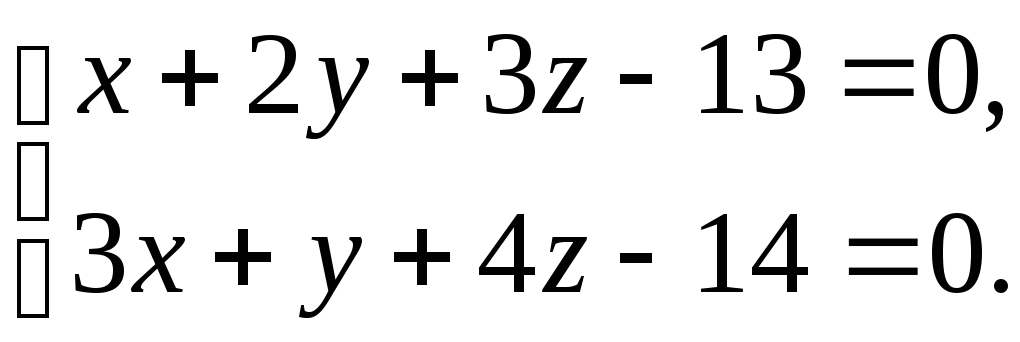
(11)
Решение.
Для того чтобы записать канонические
уравнения прямой (9), необходимо знать
любую точку, принадлежащую прямой, и
направляющий вектор прямой.
Найдём вектор
![]() ,
,
параллельный данной прямой. Так как он
должен быть перпендикулярен к нормальным
векторам данных плоскостей, т. е.
![]() ,
,
![]() ,
,
то
![]() .
.
Из общих уравнений
прямой имеем, что
![]() ,
,![]() .
.
Тогда
 .
.
Так как точка
![]() любая точка прямой, то её координаты
любая точка прямой, то её координаты
должны удовлетворять уравнениям прямой
и одну из них можно задать, например,![]() ,
,
две другие координаты найдём из системы
(11):
 .
.
Отсюда,
![]() .
.
Таким образом,
канонические уравнения искомой прямой
имеют вид:
![]() или
или
![]() .
.
Задача 74.
Вычислить расстояние между параллельными
прямыми:
![]() и
и
![]() .
.
Решение.
Из канонических уравнений первой прямой
известны координаты точки
![]() ,
,
принадлежащей прямой, и координаты
направляющего вектора![]() .
.
Из канонических уравнений второй прямой
также известны координаты точки![]() и координаты направляющего вектора
и координаты направляющего вектора![]() .
.
Расстояние между
параллельными прямыми равно расстоянию
точки
![]() от второй прямой. Это расстояние
от второй прямой. Это расстояние
вычисляется по формуле
![]() .
.
Найдём координаты
вектора
![]() .
.
Вычислим векторное
произведение
![]() :
:
 .
.
Тогда
![]()
Задача 75.
Найти точку
![]() симметричную точке
симметричную точке![]() относительно прямой
относительно прямой
![]() .
.
Решение.
Запишем уравнение плоскости перпендикулярной
к данной прямой и проходящей через точку
![]() .
.
В качестве её вектора нормали![]() можно взять направляющий вектор прямой.
можно взять направляющий вектор прямой.
Тогда![]() .
.
Следовательно,
![]() .
.
Найдём точку
![]() точку
точку
пересечения данной прямой и плоскости
П. Для этого запишем параметрические
уравнения прямой, используя уравнения
(10), получим

Далее, решим
систему, в которую входит уравнение
плоскости и параметрические уравнения
прямой:

Следовательно,
![]() .
.
Пусть
![]() точка
точка
симметричная точке![]() относительно данной прямой. Тогда точка
относительно данной прямой. Тогда точка![]() середина
середина
отрезка![]() .
.
Для нахождения координат точки![]() используем формулы координат середины
используем формулы координат середины
отрезка:
![]() ,
,
![]() ,
,![]() .
.
Получим
![]() ,
,
![]() ,
,
![]() .
.
Итак,
![]() .
.
Задача 76.
Написать уравнение плоскости, проходящей
через прямую
![]() и
и
а) через точку
![]() ;
;
б) перпендикулярно
плоскости
![]() .
.
Решение.
Запишем общие уравнения данной прямой.
Для этого рассмотрим два равенства:

Это означает, что
искомая плоскость принадлежит пучку
плоскостей с образующими
![]() и её уравнение может быть записано в
и её уравнение может быть записано в
виде (8):
![]()
(12)
а) Найдём
![]() и
и![]() из условия, что плоскость проходит через
из условия, что плоскость проходит через
точку![]() ,
,
следовательно, её координаты должны
удовлетворять уравнению плоскости.
Подставим координаты точки![]() в уравнение пучка плоскостей:
в уравнение пучка плоскостей:
![]() .
.
Найденное значение
![]() подставим в уравнение (12). получим
подставим в уравнение (12). получим
уравнение искомой плоскости:
![]()
б) Найдём
![]() и
и![]() из условия, что искомая плоскость
из условия, что искомая плоскость
перпендикулярна плоскости![]() .
.
Вектор нормали данной плоскости![]() ,
,
вектор нормали искомой плоскости![]() (см. уравнение пучка плоскостей (12).
(см. уравнение пучка плоскостей (12).
Два вектора
перпендикулярны тогда и только тогда,
когда их скалярное произведение равно
нулю. Следовательно,
![]() .
.
Отсюда,
![]()
Подставим найденное
значение
![]() в уравнение пучка плоскостей (12). Получим
в уравнение пучка плоскостей (12). Получим
уравнение искомой плоскости:
![]()
Задачи для
самостоятельного решения
Задача 77.
Привести к каноническому виду уравнения
прямых:
1)
 2)
2)
Задача 78.
Написать параметрические уравнения
прямой
![]() ,
,
если:
1)
![]() ,
,![]() ;
;
2)![]() ,
,![]() .
.
Задача 79.
Написать уравнение плоскости, проходящей
через точку
![]() перпендикулярно прямой
перпендикулярно прямой![]()
Задача 80.
Написать уравнения прямой, проходящей
точку
![]() перпендикулярно плоскости
перпендикулярно плоскости![]() .
.
Задача 81.
Найти угол между прямыми:
1)
![]() и
и![]() ;
;
2)
![]() и
и
Задача 82.
Доказать параллельность прямых:
![]() и
и
 .
.
Задача 83.
Доказать перпендикулярность прямых:
![]() и
и
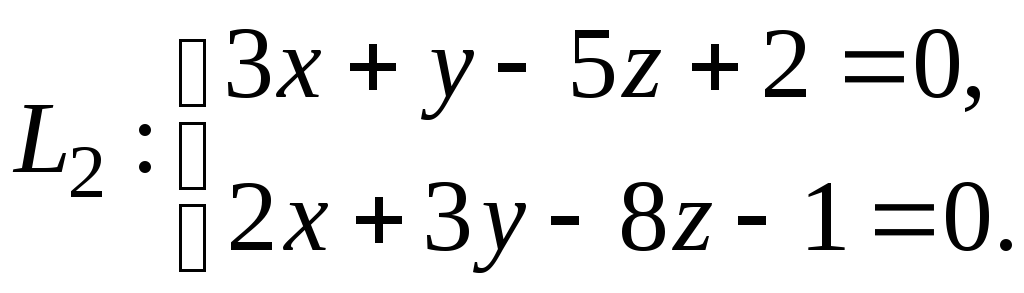
Задача 84.
Вычислить расстояние точки
![]() от прямой:
от прямой:
1)
![]() ;
;
2)![]() .
.
Задача 85.
Вычислить расстояние между параллельными
прямыми:
![]() и
и
![]() .
.
Задача 86.
В уравнениях прямой
![]() определить параметр
определить параметр![]() так, чтобы эта прямая пересекалась с
так, чтобы эта прямая пересекалась с
прямой и найти точку их пересечения.
Задача 87.
Показать, что прямая
![]() параллельна плоскости
параллельна плоскости![]() ,
,
а прямая![]() лежит в этой плоскости.
лежит в этой плоскости.
Задача 88.
Найти точку
![]() симметричную точке
симметричную точке![]() относительно плоскости
относительно плоскости![]() ,
,
если:
1)
![]() ,
,
![]() ;
;
2)
![]() ,
,
![]() ;.
;.
Задача 89.
Написать уравнение перпендикуляра,
опущенного из точки
![]() на прямую
на прямую![]() .
.
Задача 90.
Найти точку
![]() симметричную точке
симметричную точке![]() относительно прямой
относительно прямой![]() .
.
ОТВЕТЫ
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
плоскости
прямая
пересечения прямой и плоскости:
канонические уравнения прямой, проходящей через
точку М0(2; -4; -1) и
середину отрезка прямой
уравнение прямой, проходящей через точку М0(2; -3; -5) перпендикулярно
к плоскости
уравнение плоскости, проходящей через точку М0(1; -1; -1) перпендикулярно
к прямой
уравнение плоскости, проходящей через точку М0(1; -2; 1) перпендикулярно
к прямой
прямая
С прямая
A и D прямая
в плоскости
А и В плоскость
прямой
l и C прямая
плоскости
точки Р(2; -1; 3) на прямую
симметричную точке Р(4; 1; 6) относительно прямой
симметричную точке Р(2; -5; 7) относительно прямой,
проходящей через точки М1(5; 4; 6) и М2(-2; -17; -8).
точки Р(5; 2; -1) на плоскость
симметричную точке Р(1; 3; -4) относительно
плоскости
найти такую точку Р, сумма расстояний которой до
точек А(-1; 2; 5) и В(11; -16; 10) была бы наименьшей.
найти такую точку Р, разность расстояний которой
до точек M1(3; 2; -5), М2(8; -4; -13) была
бы наибольшей.
расстояний которой до точек А(3; -4; 7) и В(-5; -14; 17)
была бы наименьшей.
расстояний которой до точек М1(5; 2; -7) и М2(7; -25; 10) была
бы наибольшей.
движется прямолинейно и равномерно из
начального положения М0(15; -24; -16)
со скоростью v=12 в направлении
вектора s={-2; 2; 1}. Убедившись, что траектория точки
М пересекает плоскость
пересечения;
на движение точки М от М0 до Р;
движется прямолинейно и равномерно из
начального положения М0(28; -30; -27)
со скоростью v=12,5 по
перпендикуляру, опущенного из точки М0 на плоскость
уравнения движения точки М и определить:
ее траектории с этой плоскостью;
на движение точки М от М0 до Р;
движется прямолинейно и равномерно из
начального положения М0(11; -21; 20) в направлении вектора s={-1; 2; -2} со
скоростью v=12. Определить, за какое время она
пройдет отрезок своей траектории, заключенный
между параллельными плоскостями
расстояние d точки Р(1; -1; -2) от прямой
расстояние d от точки Р(2; 3; -1) до следующих прямых:
прямые
вычислить расстояние d между ними.
уравнение плоскости, проходящей через точку М1(1; 2; -3) параллельно
прямым
Доказать,
что уравнение плоскости, проходящей через точку
М0(x0; y0; z0) параллельно прямым ![]() ,
, ![]() , может быть
, может быть
представлено в следующем виде:
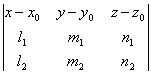 .
.
Доказать,
чо уравнение плоскости, проходящей через точки М1(x1; y1; z1) и М2(x2; y2; z2)
паралелльно прямой ![]() , может
, может
быть представлено в следующем виде:
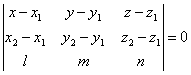 .
.
уравнение плоскости, проходящей через прямую
-2; 1).
Доказать,
что уравнение плоскости, проходящей через прямую
![]() ,
, ![]() ,
, ![]() и точку М1(x1;
и точку М1(x1;
y1; z1), может быть
представлено в следующем виде:
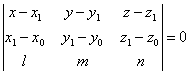 .
.
прямые
плоскости, и составить уравнение этой плоскости.
Доказать,
что если две прямые ![]() ,
, ![]() пересекаются, то уравнение
пересекаются, то уравнение
плоскости, в которой они лежат, может быть
представлено в следующем виде:
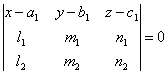 .
.
уравнение плоскости, проходящей через две
параллельные прямые
Доказать,
что уравнение плоскости, проходящей через две
параллельные прямые ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
,
![]() ,
, ![]() , может быть
, может быть
представлено в следующем виде:
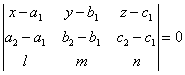 .
.
точки С(3; -4; -2) на плоскость, проходящую через
параллельные прямые
симметричную точке Р(3; -4; -6) относительно
плоскости, проходящей через М1(-6;
1; -5), М2(7; -2; -1) и М3(10; -7; 1).
симметричную точке Р(-3; 2; 5) относительно
плоскости, проходящей через прямые
уравнение плоскости, проходящей через прямую
Доказать,
что уравнение плоскости, проходящей через прямую
![]() параллельно прямой
параллельно прямой ![]() ,
, ![]() ,
, ![]() , может быть представлено в следующем
, может быть представлено в следующем
виде:
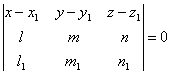 .
.
уравнение плоскости, проходящей через прямую
Доказать,
что уравнение плоскости, проходящей через прямую
![]() ,
, ![]() ,
, ![]() перпендикулярно к
перпендикулярно к
плоскости ![]() , может быть представлено в следующем
, может быть представлено в следующем
виде:
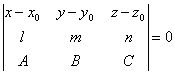 .
.
канонические уравнения прямой, которая проходит
через точку М0(3; -2; -4) параллельно плоскости
пересекает прямую
1082
проходит параллельно плоскостям
пересекает прямые
кратчайшее расстояние между двумя прямыми в
каждом из следующих случаев:
