Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
I. Две точки A(xA;yA) и B(xB;yB) симметричны относительно точки O(xO;yO), если точка O является серединой отрезка AB.
По формулам координаты середины отрезка получаем связь координат этих точек:
![]()
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
Примеры.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Решение:
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: (13;15).
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Решение:
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
Ответ: (-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Пример
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Решение:
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
5=-0,5·(-4)+b, откуда b=3.
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Найдём координаты точки пересечения прямых:
![]()
![]()
![]()
![]()
![]()
![]()
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Ответ: (3,2;1,4).
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
| для точки A(x;y) | |
| симметрия относительно: | |
| оси Ox | A1(x;-y) |
| оси Oy | A2(-x;y) |
|
биссектрисы I и II координатных четвертей (прямой y=x) |
A3(y;x) |
|
биссектрисы I b II координатных четвертей (прямой y= -x) |
A4(-y;-x) |
Как найти точку, симметричную относительно прямой
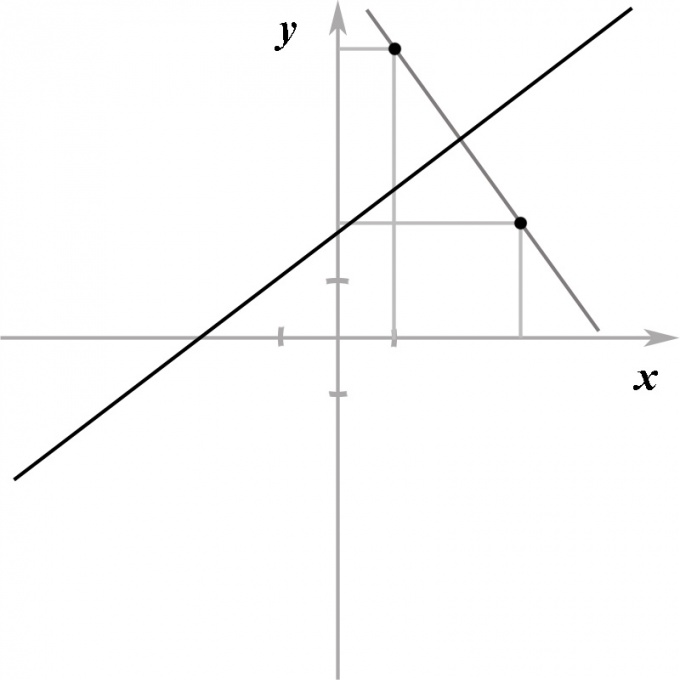
Пусть даны некоторая прямая, заданная линейным уравнением, и точка, заданная своими координатами (x0, y0) и не лежащая на этой прямой. Требуется найти точку, которая была бы симметрична данной точке относительно данной прямой, то есть совпадала бы с ней, если плоскость мысленно согнуть пополам вдоль этой прямой.
Инструкция
Ясно, что обе точки — заданная и искомая — должны лежать на одной прямой, причем эта прямая должна быть перпендикулярна данной. Таким образом, первая часть задачи заключается в том, чтобы найти уравнение прямой, которая была бы перпендикулярна некоторой данной прямой и при этом проходила бы через данную точку.
Прямая может быть задана двумя способами. Каноническое уравнение прямой выглядит так: Ax + By + C = 0, где A, B, и C — константы. Также прямую можно определить при помощи линейной функции: y = kx + b, где k — угловой коэффициент, b — смещение.
Эти два способа взаимозаменяемы, и от любого можно перейти к другому. Если Ax + By + C = 0, то y = – (Ax + C)/B. Иными словами, в линейной функции y = kx + b угловой коэффициент k = -A/B, а смещение b = -C/B. Для поставленной задачи удобнее рассуждать, исходя из канонического уравнения прямой.
Если две прямые перпендикулярны друг другу, и уравнение первой прямой Ax + By + C = 0, то уравнение второй прямой должно выглядеть Bx – Ay + D = 0, где D — константа. Чтобы найти конкретное значение D, нужно дополнительно знать, через какую точку проходит перпендикулярная прямая. В данном случае это точка (x0, y0).
Следовательно, D должно удовлетворять равенству: Bx0 – Ay0 + D = 0, то есть D = Ay0 – Bx0.
После того как перпендикулярная прямая найдена, нужно вычислить координаты точки ее пересечения с данной. Для этого требуется решить систему линейных уравнений:
Ax + By + C = 0,
Bx – Ay + Ay0 – Bx0 = 0.
Ее решение даст числа (x1, y1), служащие координатами точки пересечения прямых.
Искомая точка должна лежать на найденной прямой, причем ее расстояние до точки пересечения должно быть равно расстоянию от точки пересечения до точки (x0, y0). Координаты точки, симметричной точке (x0, y0), можно, таким образом, найти, решив систему уравнений:
Bx – Ay + Ay0 – Bx0 = 0,
√((x1 – x0)^2 + (y1 – y0)^2 = √((x – x1)^2 + (y – y1)^2).
Но можно поступить проще. Если точки (x0, y0) и (x, y) находятся на равных расстояниях от точки (x1, y1), и все три точки лежат на одной прямой, то:
x – x1 = x1 – x0,
y – y1 = y1 – y0.
Следовательно, x = 2×1 – x0, y = 2y1 – y0. Подставив эти значения во второе уравнение первой системы и упростив выражения, легко убедиться, что правая его часть становится идентична левой. Дополнительно учитывать первое уравнение уже нет смысла, поскольку известно, что точки (x0, y0) и (x1, y1) ему удовлетворяют, а точка (x, y) заведомо лежит на той же прямой.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Простейшие задачи аналитической геометрии на плоскости

1. Расстояние между двумя точками.
Теорема
1.
Для любых двух точек
 и
и плоскости расстояние
плоскости расстояние между ними выражается формулой:
между ними выражается формулой:
 .
.
(1.1)
Например,
если
даны точки
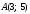 и
и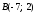 ,
,
то расстояние между ними:
 .
.
2. Площадь треугольника.
Теорема
2.
Для любых точек 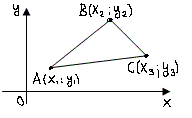
 ,
,
не лежащих на одной прямой, площадь
треугольника
 выражается формулой:
выражается формулой:
 .
.
(1.2)
Например,
найдем площадь треугольника, образованного
точками
 ,
, и
и .
.
 .
.
Замечание.
Если площадь треугольника равна нулю,
это означает, что точки лежат на одной
прямой.
3. Деление отрезка в заданном отношении.
Пусть
на плоскости дан произвольный отрезок
![]()
и
пусть
 –любая
–любая
точка этого отрезка, отличная от точек
концов. Число
 ,
,
определенное равенством ,
,
называетсяотношением,
в
котором точка
 делит отрезок
делит отрезок![]() .
.
Задача
о делении отрезка в данном отношении
состоит в том, чтобы по данному отношению
![]() и данным координатам точек
и данным координатам точек
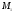 и
и
 найти координаты точки
найти координаты точки .
.
Теорема
3.
Если
точка
![]() делит отрезок
делит отрезок![]()
в
отношении 
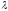 ,
,
то
координаты этой точки определяются
формулами:
 (1.3), где
(1.3), где – координаты точки
– координаты точки ,
, – координаты точки
– координаты точки .
.
Следствие:
Если
![]() – середина отрезка
– середина отрезка
 ,
,
где
 и
и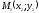 ,
,
то (1.4) (т.к.
(1.4) (т.к. ).
).
Например.
Даны точки
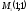 и
и .
.
Найти координаты точки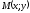 ,
,
которая в два раза ближе к ,
,
чем к
![]()
Решение:
Искомая точка
![]() делит
делит
отрезок
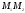 в
в
отношении
 так как
так как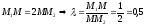 ,
,
тогда ,
,![]() ,
,
получили
 .
.
Полярные координаты
Наиболее
важной после прямоугольной системы
координат является полярная система
координат. Она состоит из некоторой
точки
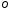 ,
,
называемойполюсом,
и исходящего из нее луча
 –полярной
–полярной
оси.
Кроме того, задается единица масштаба
для измерения длин отрезков.
Пусть
задана полярная система координат и
пусть
 – произвольная точка плоскости. Пусть
– произвольная точка плоскости. Пусть![]()
–
расстояние от точки
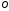 до
до
точки
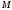 ;
; – угол, на который нужно повернуть
– угол, на который нужно повернуть
полярную ось для совмещения с лучом .
.
Полярными
координатами точки
 называются числа
называются числа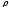 и
и .
.
При этом число считается первой координатой и называетсяполярным
считается первой координатой и называетсяполярным
радиусом,
число
 – второй координатой и называетсяполярным
– второй координатой и называетсяполярным
углом.
Обозначается
 .
.
Полярный радиус может иметь любое
неотрицательное значение:
 .
.
Обычно считают, что полярный угол
изменяется в следующих пределах: .
.
Однако в ряде случаев приходится
определять углы, отсчитываемые от
полярной оси по часовой стрелке.
Связь между полярными координатами точки и ее прямоугольными координатами.
Будем
считать, что начало прямоугольной
системы координат находится в полюсе,
а положительная полуось абсцисс совпадает
с полярной осью.
Пусть
 – в прямоугольной системе координат и
– в прямоугольной системе координат и – в полярной системе координат. Определен
– в полярной системе координат. Определен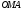 – прямоугольный треугольник с
– прямоугольный треугольник с .
.
Тогда![]() (1.5).
(1.5).
Эти формулы выражают прямоугольные
координаты через полярные.
С
другой стороны, по теореме Пифагора
 и
и![]()
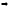
![]() (1.6)
(1.6)
– эти формулы, выражают полярные
координаты через прямоугольные.
Заметим,
что формула
 определяет два значения полярного угла
определяет два значения полярного угла ,
,
так как .
.
Из этих двух значений угла выбирают тот, при котором удовлетворяются
выбирают тот, при котором удовлетворяются
равенства .
.
Например,
найдем полярные координаты точки

 .
. .
. или
или ,
,
т.к. I
I
четверти .
.
Пример
1:
Найти точку, симметричную точке 

относительно
биссектрисы первого координатного
угла.
Решение:
Проведем
через точку А
прямую l1,
перпендикулярную биссектрисе l
первого координатного угла. Пусть
 .
.
На прямой
l1
отложим отрезок
СА1,
равный
отрезку
АС.
Прямоугольные треугольники
АСО
и
А1СО
равны
между собой (по двум катетам). Отсюда
следует, что |ОА|
= |OA1|.
Треугольники
ADO
и
ОЕА1
также равны между собой (по гипотенузе
и острому углу). Заключаем, что
|AD|
= |ОЕ|
= 4,
|OD| = |EA1|
=
2, т.е. точка имеет координаты х
= 4, у = -2,
т.е. А1(4;-2).
Отметим,
что имеет место общее утверждение: точка
A1,
симметричная точке

относительно биссектрисы первого и
третьего координатных углов, имеет
координаты
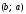 ,
,
то есть .
.
Пример
2:
Найти точку, в которой прямая, проходящая
через точки
 и
и
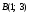 ,
,
пересечет ось
Ох.
Решение:
Координаты
искомой точки
С
есть (x;
0). А так как точки
А,
В и
С
лежат на одной прямой, то должно
выполняться условие (x2-x1)(y3-y1)-(x3-x1)(y2-y1)=0
(формула (1.2), площадь треугольника ABC
равна
нулю!), где

–
координаты точки А,
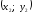 – точкиВ,
– точкиВ,
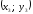 – точкиС.
– точкиС.
Получаем
 ,
,
т.е.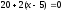 ,
,
 ,
,
 .
.
Следовательно, точка
С
имеет координаты
 ,
, ,
,
т.е. .
.
Пример
3: В
полярной системе координат заданы точки
 ,
, .
.
Найти:
а)
расстояние между точками

и
 ;
;
б)
площадь треугольника
ОМ1М2
(О
– полюс).
Решение:
а)
Воспользуемся формулами (1.1) и (1.5):

 ,
,
то
есть,
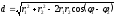 .
.
б)
пользуясь формулой для площади
треугольника со сторонами
а
и
b
и углом
 между ними (
между ними ( ),
),
находим площадь треугольника
ОМ1М2.
 .
.
Оборудование:
- SMART-BOARD.
- ПК “КМ-школа”.
- Мультимедийный проектор.
- Индивидуальные планшетки, маркер, ватный диск
(для удаления и исправления записей). - Два листа А4 на каждой парте для работы в группах
и в парах. - Изображение парусника на миллиметровой бумаге
для самостоятельной работы в двух вариантах.
Основные цели урока: тренировать
способность к определению координат точек и
построению точек по их координатам; выявить
взаимосвязь между координатами точек
симметричных относительно начала координат и
повторить взаимосвязь между координатами точек
симметричных относительно координатных осей.
Перед началом урока учитель собирает
творческое домашнее задание: на альбомных листах
учащиеся оформляли свои рисунки по координатам.
Ход урока
1. Самоопределение к деятельности.
– Здравствуйте, ребята!
– Я вижу у вас хорошее настроение и
боевой настрой. Они нам очень пригодятся. Сегодня
у нас пройдёт необычный урок – Морское
путешествие. Дело в том, что вчера на сайте нашей
школы появился сигнал бедствия от Робинзона
Крузо. Он просит помочь ему построить парусник,
на котором он смог бы вернуться домой. Чтобы
спасти его, нам надо преодолеть большое
расстояние. Давайте посмотрим на карту нашего
путешествия.
Маршрут: Бухта знаний – Залив
Исторический – Остров сокровищ – Школа
Робинзона Крузо – Мыс Настроения – Бухта знаний.
– Итак, мы отправляемся в путь, но
чтобы не сбиться с маршрута, преодолеть все рифы
и подводные течения, нам необходимо внимательно
следить за координатами нашего корабля. Давайте
вспомним, какую тему мы недавно начали изучать?
(Координатная плоскость).
– Чтобы преодолеть залив Исторический
и не разбиться о его скалистые берега, давайте
вспомним как давно появилось понятие
координатной плоскости, и кто впервые ввёл его? (
Рене Декарт.)
– Что вам о нём известно? Тогда давайте
обратимся к нашей энциклопедии.
– Из чего же состоит координатная
плоскость?
Вызвать ученика. (Весь класс помогает:
две пересекающиеся под прямым углом прямые – оси
абсцисс и ординат, точка их пересечения – начало
отсчёта, стрелочки – указывают положительное
направление осей, единичный отрезок.) Ученик
заполняет маркером пустые места на координатной
плоскости. Оценка.
– Сколько углов образовалось при
построении координатной плоскости? (четыре) Как
они называются? (координатные углы или
координатные четверти). Покажите, как они
расположены.
Ученик нумерует маркером углы и
указывает координаты точек в этих углах
схематично с помощью знаков “+” и “-”.
– Как с помощью неравенств записать
знаки координат точек в каждом из углов? Ученики
обсуждают в парах и предлагают свои варианты, из
которых выбирается верный.
I. x>0, y>0
II. x<0, y>0
III. x<0, y<0
IV. x>0, y<0.
– А каким углам принадлежат точки,
лежащие на осях координат? (Никаким)
– Молодцы! А кто знает третье название
координатных углов? (?)
– Ответить на этот вопрос нам поможет
ребус:
– Какое слово зашифровано? (Квадрант).
Что оно означает? (?) Снова обратимся к
энциклопедии.
Записать новое слово в словарик.
– Мы много говорим о координатной
плоскости. А для чего нужна координатная
плоскость? (Строить точки по координатам и
наоборот – находить координаты точек.)
– Назовите алгоритм построения точки
в координатной плоскости. ( На оси абсцисс найти
число х и провести через неё вертикальную
пунктирную линию, отметить на оси ординат число у
и провести через неё горизонтальную пунктирную
линию; точка их пересечения и есть искомая точка,
которая обозначается заглавной латинской
буквой.)
– Молодцы. Я вижу вы хорошо усвоили
теоретический материал. Давайте проверим ваши
знания на практике. Тем временем мы приплыли к
острову сокровищ, где спрятаны сокровища
капитана Флинта. С их помощью мы добудем средства
на строительство парусника. Приготовьте
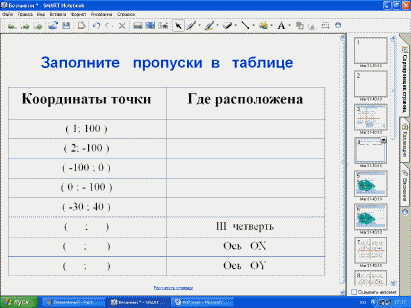
планшетки и маркеры. Устная работа (фронтально).
- Заполните пропуски в таблице. (дети пишут
ответы на планшетках, учитель проверяет и
записывает правильные ответы в таблицу на доске)
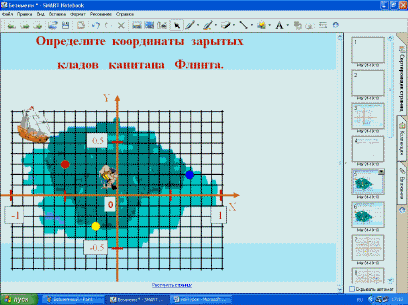
- Запишите координаты точек, в которых зарыты
сокровища капитана Флинта и координатные
четверти, в которых они расположены в порядке:
синяя, красная, жёлтая.
(Ответы будут поочерёдно появляться на
доске)
- Не выполняя построения, запишите координаты
точек симметричных данным относительно:
оси абсцисс (синяя)
оси ординат (красная)
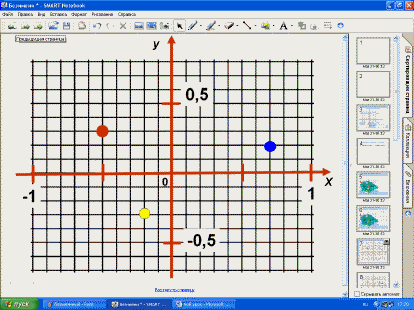
– Проверим.
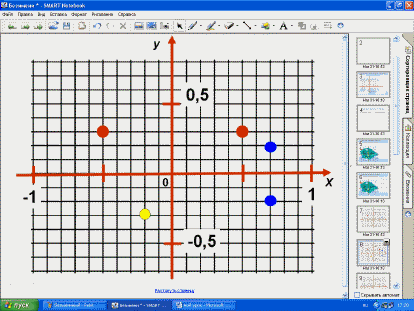
– Относительно начала координат
(жёлтая)
Последнее задание вызовет
затруднение.
– Почему возникло затруднение? (Не
умеем строить точки симметричные относительно
начала координат)
– Давайте попробуем выйти из этого
затруднительного положения.
– Как вы думаете, над какой темой мы сегодня
будем работать? (Симметрия на координатной
плоскости относительно начала координат).
– Откройте тетради, запишите число, классная
работа и тема урока “Симметрия на координатной
плоскости относительно начала координат”.
– Как расположены на оси абсцисс числа
0,2 и -0,2? (Равноудалены от начала координат и
симметричны относительно начала координат).
– Как расположены на оси ординат числа
0,3 и -0,3? (Равноудалены от начала координат и
симметричны относительно начала координат).
– Какой можно сделать вывод? (Точки
симметричны относительно начала координат).
– На чём основывался ваш вывод? (Так
как первые и вторые координаты симметричны
относительно начала координат, то точки
симметричны относительно начала координат).
– Чем отличаются координаты точек
симметричных относительно начала координат? (Они
являются противоположными числами)
– Как в общем виде записать координаты
точек симметричных относительно начала
координат? Работа в группах – 1 минута.
Учитель выборочно опрашивает
учащихся.
В результате приходят к выводу: (x; y)
и (– x; – y).
Вывод появляется на доске в виде слайда.
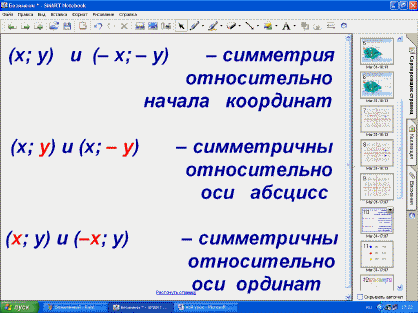
– Запишите их в тетрадь.
– Давайте вернёмся к нашим кладам и отметим
координаты точек, симметричных для них.
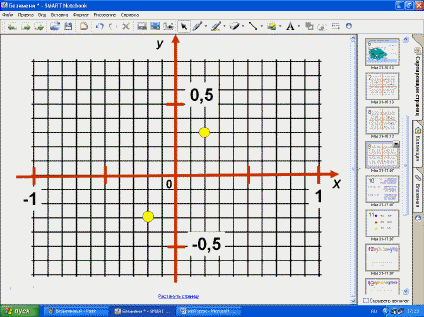
– Поднимите руку, кто построил верно? Кто
допустил ошибку? В чём причина ошибки? (……)
Запишите координаты точек в тетрадь:
– Мы хорошо потрудились, но нам предстоит
выполнить очень ответственное задание
–строительство парусника. Давайте физически к
этому подготовимся.
Физкультминутка.
Расправьте плечи. Вдох. Выдох.
Да – опустить голову вниз, нет – голову назад.
Точка (6;0) – лежит на оси абсцисс – да.
Точка (0; -2) –лежит на оси абсцисс – нет.
Точка (0;0) –начало координат – да.
Ось абсцисс лежит в первой четверти – нет.
Ось ординат лежит в четвёртой четверти – нет.
Да –голову вправо, нет – голову влево.
Сегодня мы изучаем симметрию – да.
Абсциссу точки записывают второй координатой
– нет.
Ординату точки записывают первой координатой
– нет.
Координаты точки записывают в круглых скобках,
через точку с запятой – да.
Мы приближаемся к острову Робинзона Крузо, где
нам предстоит построить для него парусник.
– Запишите в тетрадях – самостоятельная
работа ( Работа выполняется на миллиметровой
бумаге – по вариантам. На листочках изображён
один парусник, но в разных координатных
четвертях: первый вариант – в первой
координатной четверти, второй вариант – во
второй).
Самостоятельная работа ( 8-10 мин.):
1. Постройте точки парусника, симметричные
данному по заданным координатам
относительно оси ординат.
2. Запишите точки, симметричные точкам флага
исходного парусника относительно начала
координат в тетрадь.
– Сдайте работу на миллиметровой бумаге.
– Давайте сверим результаты.
– Поднимите руки, у кого такой же рисунок?
– У кого другой? Почему?
– Сравните координаты флага.
Вопросы рефлексии:
- Что нового узнали?
- На каких знаниях вы основывались для открытия
нового знания? - Как же записать координаты симметричных точек
относительно начала координат? - Кто считает, что хорошо усвоил тему?
- Кому ещё надо поработать дома?
Домашнее задание:
Учебник Математика 5 Петерсон Л.Г. Глава 3, ![]() параграф 4, п.1 № 177 (а) –
параграф 4, п.1 № 177 (а) –
построить четырёхугольник по координатам и
построить ему симметричный относительно оси
абсцисс; № 201 (а или б).
Презентация
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Координаты на плоскости
- Осевая и центральная симметрии
Осевая симметрия
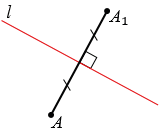
Рассмотрим построение точки, симметричной данной точке А относительно данной прямой  .
.
Пусть дана точка А и прямая  .
.
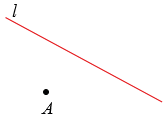
Точку симметричную точке А относительно прямой  , можно построить так. Проведем через точку А прямую
, можно построить так. Проведем через точку А прямую  , перпендикулярную прямой
, перпендикулярную прямой  . Для этого используем чертежный угольник. Прикладываем чертежный угольник так, как показано на рисунке ниже и проводим прямую
. Для этого используем чертежный угольник. Прикладываем чертежный угольник так, как показано на рисунке ниже и проводим прямую  через точку А.
через точку А.
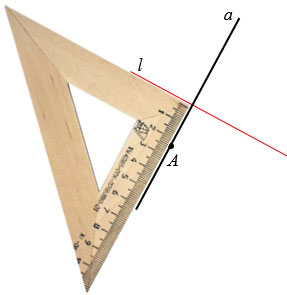
Пусть прямые  и
и  пересекаются в точке О. Отложим при помощи линейки на прямой
пересекаются в точке О. Отложим при помощи линейки на прямой  отрезок ОА1, равный отрезку ОА.
отрезок ОА1, равный отрезку ОА.
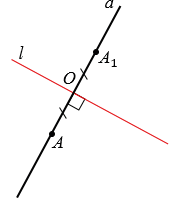
Получаем точки А и А1, которые симметричны относительно прямой  .
.
Также можно построить фигуры, симметричные относительно прямой.
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой  .
.
Пусть дан треугольник АВС и прямая  .
.
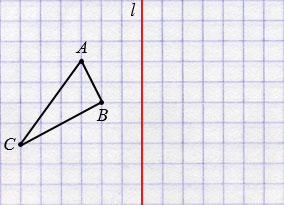
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно прямой  (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой
(алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой  .
.
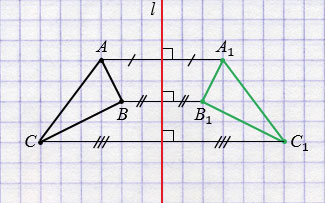
Обратите внимание, любые две фигуры, симметричные относительно прямой, равны.
Если фигура имеет ось симметрии (прямая  ) то, все точки этой фигуры, не принадлежащие этой оси, можно разделить на пары симметричных точек.
) то, все точки этой фигуры, не принадлежащие этой оси, можно разделить на пары симметричных точек.
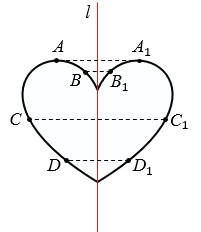
Центральная симметрия
Точки М и М1 называют симметричными относительно точки О, если точка О является серединой отрезка ММ1 (смотри рисунок ниже).
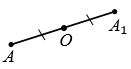
Рассмотрим построение точки, симметричной данной точке М относительно данной точки О.
Пусть даны точки М и О. Точку, симметричную точке М относительно точки О, можно построит так. Проведем луч МО.
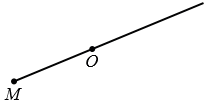
На луче МО отложим отрезок ОN , равный отрезку ОМ.
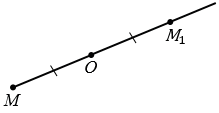
Точки М и М1, которые симметричны относительно точки О.
Также можно построить фигуры, симметричные относительно точки.
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
Пусть дан треугольник АВС и точки О.
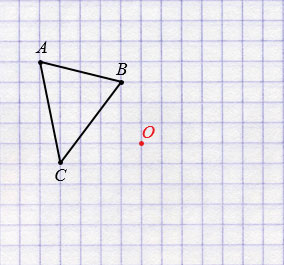
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно точки О (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
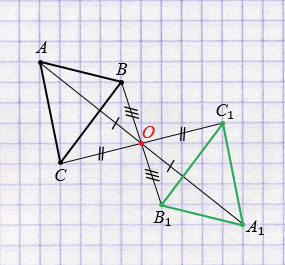
Обратите внимание, любые две фигуры, симметричные относительно точки, равны.
Рассмотрим окружность с центром в точке О. Все точки окружности можно разбить на пары точек, симметричных относительно точки О.
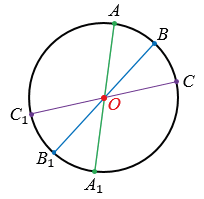
В таком случае говорят, что окружность имеет центр симметрии – точку О.
Также центр симметрии имеют такие фигуры, как отрезок, прямоугольник, эллипс.
Советуем посмотреть:
Перпендикулярные прямые
Параллельные прямые
Координатная плоскость
Координаты на плоскости
Правило встречается в следующих упражнениях:
6 класс
Номер 1248,
Мерзляк, Полонский, Якир, Учебник
Номер 1249,
Мерзляк, Полонский, Якир, Учебник
Номер 1260,
Мерзляк, Полонский, Якир, Учебник
Номер 1263,
Мерзляк, Полонский, Якир, Учебник
Номер 1272,
Мерзляк, Полонский, Якир, Учебник
Номер 1273,
Мерзляк, Полонский, Якир, Учебник
Номер 1316,
Мерзляк, Полонский, Якир, Учебник
Номер 1318,
Мерзляк, Полонский, Якир, Учебник
Номер 1334,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник