Как найти симметрию двух окружностей

Осевая и центральная симметрия

О чем эта статья:

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.
2. Проводим через точку В прямую, перпендикулярную прямой l.
3. Измеряем расстояния от точек А и В до прямой l.
4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Две окружности на плоскости.
Общие касательные к двум окружностям

Взаимное расположение двух окружностей

Взаимное расположение на плоскости двух окружностей радиусов r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

r₁ – r₂ лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов

d r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

r₁ – r₂ лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов

d r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей меньше разности их радиусов

d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.

Каждая из окружностей лежит вне другой

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Фигура	Рисунок	Свойства
Две окружности на плоскости
Каждая из окружностей лежит вне другой
Внешнее касание двух окружностей
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Каждая из окружностей лежит вне другой
Внешнее касание двух окружностей
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Каждая из окружностей лежит вне другой
Расстояние между центрами окружностей больше суммы их радиусов
Внешнее касание двух окружностей
Расстояние между центрами окружностей равно сумме их радиусов
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой
Внутренняя касательная к двум окружностям
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Внешнее касание двух окружностей

Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Внутреннее касание двух окружностей

Окружности пересекаются в двух точках

Внешнее касание двух окружностей

Каждая из окружностей лежит вне другой

Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Формулы для длин общих касательных и общей хорды двух окружностей

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Внутреннее касание двух окружностей

Окружности пересекаются в двух точках

Внешнее касание двух окружностей

Каждая из окружностей лежит вне другой

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

Фигура	Рисунок	Формула
Внешняя касательная к двум окружностям
Внутренняя касательная к двум окружностям
Общая хорда двух пересекающихся окружностей

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Общая хорда двух пересекающихся окружностей

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Общая хорда двух пересекающихся окружностей

Длина общей хорды двух окружностей вычисляется по формуле Доказательства формул для длин общих касательных и общей хорды двух окружностей Утверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Взаимное расположение окружностей Выясним, каким может быть взаимное расположение двух окружностей. Две окружности могут пересекаться, не пересекаться либо касаться друг друга. I. Пересекающиеся окружности имеют две общие точки. Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов: II. Не пересекающиеся окружности не имеет общих точек. Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов: Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов: R + r]” title=”Rendered by QuickLaTeX.com”/> III. Касающиеся окружности имеют одну общую точку — точку касания. При внешнем касании расстояние между центрами окружностей равно сумме их радиусов: При внутреннем касании расстояние между центрами равно разности радиусов: Концентрические окружности разного радиуса не пересекаются. Расстояние между центрами концентрических окружностей равно нулю: O1O2=0. [spoiler title=”источники:”] http://www.resolventa.ru/demo/him/demohim.htm Взаимное расположение окружностей [/spoiler]

ЭСТЕТИЧЕСКАЯ ГЕОМЕТРИЯ

---

УЧЕБНИК. ОГЛАВЛЕНИЕ: Введение.    Часть 1. Понятие о симметрии. Взаиморасположение окружностей. Определение симметрии. Перпендикулярные окружности. Касание. Медитации. Окружности, касающиеся двух данных. Серединная окружность и биссектрисы. Симметрия двух пар точек. Теоремы о разбиении четырех точек на пары. Теоремы о касающихся окружностях. Симметрия трех окружностей.    Часть 2. Основные фигуры. Трехокружник как треугольник. Биссектрисы и высоты. Гармония шести биссектрис. Задача Аполлония. Неевклидовы геометрии. Симметрия трехокружника. 4 взаимокасающиеся окружности. Построение биссектрис.    Часть 3. Динамика геометрии или инженерия эстетики. Композиция. Коммутативность. Траектории и пучки. Гармоническая мельница, спирали. Трехмерное: узлы, рога и раковины. Три взаимоперпендикулярные окружности, биплетная симметрия. Симметрия, коммутирующая с тремя данными. Фракталы, “DDU-венок”

Что общего между орбитами планет и узлами, неевклидовыми геометриями, фракталами и орнаментами? Их всех объединяет симметрия относительно окружности, систематическое изучение которой я называю “Эстетической геометрией”. Надеюсь, что читатели получат хотя бы часть того удовольствия и удивления, которое испытал я, изучая ее. Я постарался разместить в этом учебнике много интересных иллюстраций,но любые иллюстрации, сделанные вами самостоятельно, помогут понять геометрию лучше, чем прекрасные чертежи, сделанные кем-то другим.

---

Взаимное расположение точек и окружностей: пересечение и разделение.

  


  


Пусть окружность B лежит внутри окружности А. Будем “выносить” окружность В из А.
В начале – окружности не имеют общих точек, затем касаются, затем пересекаются,
а точка касания “раздваивается” и превращается в пару точек пересечения А и В (точки x, y),
затем А и В снова касаются, а точки их пересечения сливаются в одну. Затем окружности не имеют общих точек. Касание окружностей
есть промежуточное или переходное положение окружностей.
Промежуточное между окружностями, не имеющих общих точек и пересекающимися окружностями.

---

Окружность В разделяет окружности А и С (они лежат по разные стороны от В. Окружность А не разделяет окружности В и С
(они лежат по одну сторону от А).
Любые две не пересекающиеся окружности можно разделить третьей окружностью. Никакая окружность не может разделить две пересекающиеся
окружности. Любые две точки можно разделить окружностью. А существует ли окружность, разделяющая две касающиеся окружности? Как она проходит?

---

  
  
  

Свойство окружности разделять точки и другие окружности очень важно для классификации трех взаимопересекающихся окружностей.
Если одна из трех окружностей разделяет точки пересечения двух других, то: 1. она обязательно с ними пересекается;
2. любая из этих окружностей разделяет точки пересечения двух других.

---

Симметрия между окружностями или инверсия. Примеры.

  
   


В динамике: чем дальше голубая окружность от синей, тем меньше и ближе к центру синей симметричная ей.
Если мы приближаем голубую окружность к синей, то симметричная ей будет увеличиваться и также приближаться к границе синей.
Когда голубая коснется синей, то симметричная ей – коснется синей в той же точке.
На этом и следующих рисунках окружности одного цвета симметричны относительно синей.

---

   


Геометрия окружности трактует прямые, как частный случай окружностей. И не знает, что такое “центр” окружности, как это ни странно.
Но мы-то различаем, или думаем что умеем различать прямую от окружности. Для связи с привычным миром укажем и эти свойства.

---

Симметрия между окружностями сохраняет свойства расположения окружностей.

 

Пересекающиеся окружности симметричны пересекающимся, касающиеся – касающимся, разделенные – снова окажутся разделены.
А симметричные – снова будут симметричны. Свойства, сохраняющиеся при симметрии называются инвариантными.
Не все привычные свойства окружностей сохраняются при симметрии. Например: центр окружности не перейдет в центр окружности.
Большая окружность может перейти в маленькую. А если одна окружность лежит внутри другой –
обязательно ли сохранится эта их особенность после симметрии относительно третьей окружности?

---

Определение симметрии точек относительно окружности.

  

Внутренности окружности симметрична ее внешность. Окружность всегда разделяет пару симметричных относительно нее точек.

Чтобы точно определить симметрию окружностей – достаточно определить симметрию точек. Но для этого нам пока
надо пользоваться расстояниями и прямыми. Геометрия окружности их не знает, но мы знаем, и не будем педантами, а воспользуемся этим.
Позднее, мы научимся определять симметрию точек не пользуясь ни прямыми, ни длинами.
Достаточно уметь проводить окружность через три точки.
Что означает “симметрия между окружностями?” Как связать симметрию точек и симметрию окружностей?
Если при симметрии точек, точки, лежащие на одной окружности, переходят в точки, снова лежащие на одной окружности,
мы и говорим, что есть симметрия окружностей, т.к. окружностям оказываются симметричны окружности, а не какие-либо другие фигуры.
Доказательство, что при симметрии точек, описанной здесь, окружности переходят в окружности есть во многих учебниках.

---

Определение А-отображений

А-отображения отображают окружность в окружность. Для того, чтобы задать А-отображение данной окружности,
надо выбрать произвольную точку плоскости, не лежащую на данной окружности и провести через эту точку секущие к окружности.
А-отображение меняет местами точки пересечения секущей с окружностью. Если проводить секущие из бесконечно далекой точки,
то они будут представляться нам пучком параллельных прямых. А-отображения окружности легко обобщаются
на отображения сфер в пространстве и позволяют определить инвесию (симметрию окружностей) на сфере. Подумайте, как это сделать?

А-отображения теснейше связаны с геометрией окружностей, хотя и основаны прямых линиях.
Пользуясь то геометрией окружностей,
то прямолинейными А-отображениями мы обогащаем наше понимание и геометрии прямых и геометрии окружностей.

Здесь мы не будем пользоваться этими определениями. Для нас важно, что существует преобразование I, при котором все точки
окружности I остаются неподвижными, окружности переходят в окружности и симметричное переходит в симметричное.

---

Перпендикулярные окружности. Определение.

  
  

Окружности А и В называются перпендикулярными,
если при симметрии относительно одной – другая остается на месте: А(В)=В.

При симметрии относительно А, точки на В меняются местами. Не остаются неподвижны.
Но окружность В, как целое, – остается на своем месте. Если точка x лежит на В, то и А(x) обязательно лежит на В.
Точно также обстоит дело в привычной геометрии с перпендикулярными прямыми.

Точки, лежащие внутри В, симметричны точкам, снова лежащим внутри В, точки лежащие вне В симметричны точкам, лежащим
вне В. Точнее говоря: точки, симметричные относительно А, всегда лежат по одну сторону от В.

---

ОСНОВНОЕ СВОЙСТВО
перпендикулярных окружностей:

если две точки x и y симметричны относительно I,
то ЛЮБАЯ окружность, проходящая через эти точки – перпендикулярна I.

I(x)=y и А, В, С проходят через точки x, y следовательно I(A)=A, I(B)=B, I(C)=C, A(D)=D

Мы не доказываем основное свойство, а используем его как аксиому.

---

ПЕРВАЯ ТЕОРЕМА эстетической геометрии:
две пары симметричных точек обязательно лежат на одной окружности.

ПЕРВАЯ ТЕОРЕМА следует из основного свойства: по основному свойству всякая окружность, проходящая через x и I(x) перпендикулярна I,
следовательно, окружность S, проходящая через x, I(x) и y – тоже перпендикулярна I, следовательно I(y) лежит на на S.
Из теоремы понятно, что если даны две точки x и y, и окружность I, то есть единственная перпендикулярная I окружность S,
проходящая через данные точки. Чтобы построить S достаточно отразить
одну из данных точек относительно I, и через полученную точку и две исходных провести окружность S. Она и будет искомой.

---

Построение перпендикуляра

В геометрии прямых из данной точки на данную прямую можно опустить единственный перпендикуляр. В геометрии окружности – не так.
Из одной точки можно провести сколько угодно окружностей, перпендикулярных данной. Все они, по основному свойству,
проходят через точку
симметричную данной относительно окружности. Первая теорема гарантирует нам, что есть единственная окружность,
проходящая через две данные точки и перпендикулярная данной окружности. А сейчас мы видим, что существует единственная окружность S,
проходящая через данную точку p и перпендикулярная ДВУМ данным окружностям А и В.
Чтобы построить S надо отразить точку p относительно
данных окружностей. И через p и полученные точки провести S – по основному свойству эта окружность перпендикулярна и А и В
(т.к. на ней есть пара точек, симметричных относительно А и пара точек, симметричных относительно В).

Что будет, если точка p лежит на пересечении окружностей А и В?
При симметрии относительно А и В мы не получим новых точек, в этом случае А(p)=B(p)=p, и наше построение не получается.
Если две окружности пересекаются,
то ни одна окружность, проходящая через точку их пересечения не будет перпендикулярна им обеим. Если не считать… если не считать
такой окружностью саму точку их пересечения.

---

Три перпендикулярные друг другу окружности.

  

На плоскости нельзя провести три перпендикулярные друг другу прямые. А три взаимоперпендикулярные окружности – можно.
Пользуясь основным свойством, построим окружность B, перпендикулярную A.
Затем, как было только что показано, построим третью окружность С, перпендикулярную первым двум.

На правом рисунке выделены 8 участков (один из которых неограничен), на которые разделяют плоскость А, В и С.
Попробуйте проследить, какие участки плоскости симметричны друг другу относительно А? Относительно В? Относительно С?

---

Перпендикулярные и касающиеся окружности.

  
  

Перпендикулярные и касающиеся окружности тесно связаны между собой.
Аналогично связаны между собой параллельные и перпендикулярные прямые: если первая прямая перпендикулярна к другой прямой,
а та к третьей, то первая и третья прямые – параллельны. Подобным образом можно построить окружность,
касающуюся данной окружности I в данной точке x.
Мы берем произвольную точку p, не лежащую на данной окружности I, проводим окружность А через точки x, p, I(p).
По основному свойству А перпендикулярна I. Теперь мы построим окружность В, перпендикулярную А и проходящую через x. Для этого
возмем произвольную точку q и проведем В через x, q, B(q). По перпендикулярно-касательном признаку В – касается I в
точке x, что и требовалось.

Если нам надо построить окружность, перпендикулярную I и проходящую через точки x, y лежащие на I, то прием,
использованный в основной теореме не работает. В этом случае I(x)=x, I(y)=y,
и у нас не появляется новой точки, через которую можно провести искомую окружность.
Поступим так: мы только что построили окружность В, касающуюся I в точке x. Проведем окружность S через точки x, y, B(y).
По основному свойству она перпендикулярна В, отсюда, по перпендикулярно-касательному признаку она перпендикулярна I. Следовательно –
S и является искомой окружностью. Прием, использованный для ее построения назовем “двойным перпендикулированием“.

---

Медитация о перпендикулярных и касающихся окружностях

Подумайте, как можно продолжать рисунок, добавляя новые окружности?
И как “работает” с новыми окружностями симметрия относительно пунктирной окружости?
А можно в этом рисунке найти и новые симметрии. Для этого рассмотрим две голубые окружности и большую желтую.
Через точки их касания можно провести окружность. Она будет перпендикулярна выбранным.
Куда, при симметрии относительно построенной окружности, перейдет ближайший к ней синий круг?

---

Медитация о касающихся окружностях и фрактале

Система касающихся окружностей. Ее можно продолжать: внутрь каждого небольшого желтого круга поместить то,
что изображено на экране. И так далее.
То, что получается – называется фракталом. А сейчас мы видим синие круги на желтом, или желтые на сннем фоне?

---

Свойства окружностей, касающихся двух данных.

Начнем с простейшего.

---

Если А и В пересекаются, то мы точно также раздуваем маленькую окружность 1. Она увеличивается, совпадает с А, затем “перегибается”
(по дороге побывав прямой), уменьшается, сворачиваясь в точку q. При этом, окружность эта, как и в прошлом случае,
сначала не имеет общих точек с В, затем касается, В, затем пересекает В, затем снова касается В,
затем же – опять не имеет с В общих точек. Окружности 1 и 8 касаются А и В. Обратим внимание: ни одна из них не разделяет А и В.
Пересекающиеся окружности вообще невозможно разделить.

А что будет, если А и В касаются друг друга? Если точка их касания отличается от q, то существует всего одна искомая окружность,
касающаяся А и В одновременно. Почему?

Если же А и В сами касаются друг друга в точке q, то искомых окружностей – бесчисленное множество.

---

Серединная окружность

Окружности, касающиеся одновременно двух не имеющих общих точек окружностей А и В распадаются на два семейства.
Семейство “лепестков” и семейство “обручей“.

На этом рисунке хорошо видны свойства симметрии относительно окружности I. Внутренность малинового круга А, симметрична
неограниченной внешности малиновой окружности B. Голубые круги-лепестки симметричны сами себе. Точка, лежащая внутри
такого круга симметрична точке, снова лежащей внутри этого круга. Границы этих кругов (окружности) переходят в себя.
Точки касания голубых кругов друг с другом
остаются неподвижны. Каждый светлозеленый трехдужник симметричен такому же треждужнику, лежащему напротив него. Точка касания голубого
круга с окружностью А симметрична точке касания этого же круга с окружностью В.

---

Семейство лепестков определяет серединную окружность и симметрию окружностей I,
при которой все точки серединной окружности неподвижны, а окружности А и В меняются местами: I(A)=B, I(B)=A.
Семейство обручей тоже задает такую симметрию. Но не задает никакой “серединной окружности”,
точки которой неподвижны при симметрии I.

---

Если окружности А и В пересекаются, то окружности касающиеся их одновременно также распадаются на два семейства.
Среди эти семейств нет ни “лепестков”, ни обручей”, каждое семейство располагается в своей “зоне” на плоскости.
Каждое из двух семейств определяет свою серединную окружность между А и В.

В этом случае аналогия между серединными окружностями и биссектрисами между прямыми видна особенно ясно. Между двумя пересекающимися
прямыми есть две биссектрисы. Одна лежит в основном угле между прямыми, другая – в дополнительном угле.
Обе прямые симметричны друг другу относительно каждой своей биссектрисы.
А что будет, если исходные окружности А и В касаются? В этом случае, есть всего одно семейство окружностей,
касающихся их одновременно. Почему?
Это семейство позволяет построить единственную симметрию между А и В и серединную окружность между ними.
Что это напоминает в мире прямых? Параллельные прямые. Почему?

---

Медитация о композиции.

Именно композиция симметрий превращает геометрию окружности в эстетическую геометрию.
С помощью композиции симметрий относительно окружностей можно строить художественные объекты. А что такое композиция?
Последовательное применение симметрий, сначала относительно Р, затем относительно Q. Как это проследить на рисунке?

---

Примеры построения симметрии с помощью проведения окружностей, касающихся двух данных.

  
   
   

Пусть мы знаем, что симметрия I меняет местами А и В: I(A)=B. Как найти точку, симметричную x относительно I?
Проведем через x одну окружность, касающуюся А и В одновременно, затем, другую окружность также касающуюся А и В и лежащую в том же
семействе, что и первая проведенная окружность. y, вторая точка пересечения проведенных окружностей
(первая точка пересечения – сама x) и будет симметрична x относительно I. y=I(x). Почему?


Окружности одного семейства, касающихся данных двух А и В остаются неподвижны при симметрии, относительно биссектрисы между А и В
(биссектрисы, связанной с этим семейством). Точки лежащие на А и В одновременно будут лежать на I(A) и I(B) одовременно, но т.к.
I(A)=A, I(B)=B, то точки пересечения А и В оказываются симметричны точкам пересечения А и В. Значит I(x)=x или I(x)=y. Но первое
невозможно, значит, остается второе: I(x)=y. Что и требовалось. Если же проведенные окружности касаются друг друга в точке x, то x
симметрична сама себе или, что тоже самое, неподвижна при симметрии I.
При такой симметрии точка касания проведенной вспомогательной окружности с А симметрична точке касания этой окружности с В.

Не для всякой точки x такое построение удастся выполнить. Почему? Потому что есть такие точки x, через
которые нельзя провести ни одной окружности, касающейся А и В одновременно. Попробуйте привести примеры.
В каких случаях через x можно провести ровно две такие окружности? А в каких четыре?

Симметрия точек была определена с помощью прямых и расстояний. Сейчас мы научились находить симметричные точки не используя этих,
инородных для геометрии окружности понятий. Мы находим нужные точки с помощью проведения касательных окружностей. Это уже – шаг вперед
в развитии геометрии окружности. Но – шаг недостаточный. Во-первых, как было замечено, не для всякой точки x удается построить
симметричную ей точку таким образом. Во-вторых, провести окружность через данную точку и касающихся двух данных не очень просто. Скоро
мы сделаем следующий шаг и удобно определим симметрию по двум парам симметричных точек.

---

Теорема о цепочке четырех касающихся окружностей.

      

---

В теореме участвует 6 касающихся окружностей: 4 из них касаются друга по цепочке, а две (А и B) вплетены между ними. Если А и В
пересекаются, то теорема получает интересное развитие, приведенное в разделе о построении биссектрис (ч.2).

---

Новое определение симметрии между окружностями.

ДВЕ ПАРЫ ТОЧЕК (a, b) и (c, d) лежащих на одной окружности S

определяют симметрию окружностей I при которой точки каждой пары симметричны друг другу: I(a)=b, I(c)=d.
Проведем две окружности: одну через точки a и b, другую через c и d. Если эти окружности пересекаются – точки их пересечения симметричны друг другу относительно I. Если эти окружности касаются – точка касания неподвижна (переходит в себя) при симметрии I.
Двигаясь из точек чертежа x, y, z, t по окружностям одного цвета, мы придем в симметричную точку.

  

Мы удобно и просто определили симметрию между окружностями не меряя длин и не проводя прямых. Единственное, что нам нужно для нахождения точки I(x)
– уметь проводить окружность через три данные точки. Благодаря этому и можно говорить о геометрии окружности,
и об эстетической геометрии, как о самостоятельном разделе знаний. Иначе бы геометрия окружности
оставалась частью евклидовой геометрии прямых. Заметим, что подобного простого построения симметрии относительно прямой в геометрии
Евклида – нет. Там нужно измерять длины, откладывать прямые углы. А здесь – достаточно провести две окружности.

Почему это построение дает тоже, что было показано при определении симметрии точек относительно окружности? Попробуйте разобраться
самостоятельно, используя свойства перпендикулярных окружностей.

---

Важные свойства окружностей, следующие из нового определения симметрии.

Эти свойства можно обобщить на трехмерный случай. Подумайте, как это сделать.

Если мы немного обработаем чертеж к теореме (опция Combine в Corledraw), то получим интересный рисунок.
Попробуйте проследить, какие непрерывные цветные области симметричны друг другу. А какие из этих областей симметричны сами себе
(то есть точка лежащая внутри такой области симметрична точке, снова лежащей в этой области)?

Две пары точек, лежащие на одной окружности, определяют важное семейство окружностей (и семейство пар точек).
В семейство окружностей мы включаем:
все окружности, проходящие через одну пару точек, все окружности, проходящие через другую пару точек. Если две окружности семейства
пересекаются в какой-то паре точек, то мы включаем и все окружности, проходящие через эту пару точек. В семейство пар точек мы включаем все
пары точек, в которых пересекаются включенные окружности. Любые две пары точек семейства обязательно лежат на одной окружности.
Как можно охарактеризовать построенные семейства с помощью понятия симметрии?

Если две исходные пары точек разделяют друг друга, то все окружности семейства – пересекаются между собой. И любые две пары
точек – разделяют друг друга (на той окружности, на которой они лежат).

---

ТЕОРЕМА о разбиении четырех точек, лежащих на одной окружности на пары двумя способами.

Эта теорема связана с понятием коммутативности или “перестановочности”.
Два преобразования, две функции, две операции f и g называются коммутирующими, если не важно,
в каком порядке их применять: для любого x –
f(g(x))=g(f(x)). Симметрии относительно перпендикулярных прямых –
коммутируют между собой. Почему? Также коммутируют симметрии
между перпендикулярными окружностями. Это будет разъяснено позднее.

Из чертежа к теореме нетрудно “извлечь” интересные рисунки.

---

ТЕОРЕМА о разбиении четырех точек, лежащих на одной окружности на пары тремя способами.
Теорема позволяет осуществлять симметрию точки относительно окружности, не считая расстояния, не меряя углы, не проводя прямых.

Ранее было показано, как зная две пары симметричных точек: (а, b=S(a)), (c, d=S(c)) находить для любой точки х симметричную ей точку
S(x)=y. Но как быть, если мы не знаем двух таких пар, а знаем лишь окружность S, относительно которой осуществляется симметрия? ТЕОРЕМА
о разбиении четырех точек на пары тремя способами – дает ответ на этот вопрос. Нужно выбрать на S какие-то четыре точки и
осуществить построение на рисунке. Понадобиться провести 6 вспомогательных окружностей.
Вспомним: ранее мы умели делать такую симметрию только с помощью длин и прямых.
Доказательство этой и предыдущей теоремы основано на понятии композиции преобразований.

---

Теоремы о касающихся окружностях.

Почему так происходит? Точки касания – неподвижны при симметрии I, при которой I(a)=b, I(c)=d.
А такие точки лежат на одной окружности. По основному свойству перпендикулярных окружностей все окружности проходящие через
a и b – перпендикулярны I, окружности, проходящие через c и d – тоже. По перпендикулярно-касателному признаку такие окружности
могут касаться только в точках, лежащих на I. Попробуйте на следующем рисунке найти симметричные друг другу точки и области.

Если точки a и b близки друг к другу, то окружность, проходящая через них, почти касается окружности S. Когда они совпадут – эта
окружность касается S. Поэтому точки касания окружностей, одна из которых касается S в точке a, другая же проходит через c и d –
сами лежат на одной окружности I. I(c)=d, I(a)=a. Обратите внимание – таким образом мы сумели определить симметрию I, используя всего
три точки: a, c, d.

А теперь соединились не только точки a и b, но и точки c и d. И все интересующие нас окружности стали касаться S в точках a и c.
Точки касания этих окружностей, сами лежат на одной окружности I, которая перпендикулярна им всем.

И на этом рисунке попробуйте найти симметричные точки и области: двух и трехдужники.

---

Еще два свойства касающихся окружностей:

Почему? Можно мыслить предельный переход: когда-то были точки b и d, две пары точек (a, b) и (с, d) задавали симметрию.
Но точка b приблизилась к точке a, точка d тоже приблизилась неотличимо к с. Тогда окружности,
проходящие через a и b стали окружностями касающимися S, также и окружности, проходящие через с и d стали касаться S.
Теперь пара точек задает симметрию окружностей. Потому, что на самом деле в каждой точке пары скрывается еще одна точка,
очень близкая к первой. Обозначим эту симметрию I. Тогда I(e)=h, I(f)=q, I(a)=a, I(b)=b.
Из первой теоремы эстетической геометрии следует первое утверждение. Из того, что при симметрии точки,
лежащие на окружности переходят в точки, лежащие на окружности – второе.

Можно же не искать “совпавшие точки” а заметить, что симметрия относительно окружности, перпендикулярной S
и проходящей через a и c и нужна, для доказательства обоих утверждений.

---

Теорема о трех пересекающихся окружностях.

Еще одно определение симметрии между окружностями.

ТЕОРЕМА позволяет по трем пересекающимся окружностям определить одну симметрию. Произвольной точке х
симметрична точка пересечения двух окружностей, одна из которых проходит через одну пару точек пересечения
данных окружностей, а вторая – через другую пару.
Но у нас три пары точек пересечения, а для этого построения надо выбрать две пары. Как выбрать? ТЕОРЕМА гарантирует, что это не имеет
значения – результат (симметричная x точка y) будет тем же самым.

На рисунке точки одного цвета симметричны друг другу, I(x)=y.
Точки пересечения окружностей между собой меняются местами, отсюда, по основному свойству перпендикулярных окружностей: I(A)=A,
I(B)=B, I(C)=C. Симметрия I может быть и определена, как такая симметрия,
при которой все три окружности А, В, С – переходят в себя, неподвижны.

  

Присмотримся: мы видим цветные участки плоскости, ограниченные двумя, тремя или четыремя дугами. На правом рисунке “трехдужники”
симметричны другим трехдужникам, оранжевые – оранжевые, белые – белым. Верхние “паруса” переворачиваются,
и чем выше парус, тем ниже симметричный ему трехдужник. А области, ограниченные двумя или четыремя дугами – остаются на месте.
Это означает, что точке, лежащей внутри какого-нибудь цветного двухдужника или четырехдужника, симметрична точка,
тоже лежащая внутри этого же двухдужника (или четырехдужника).
Какие точки при этой симметрии I остаются неподвижны (симметричны сами себе)? Понять помогают теоремы
о касающихся окружностях, показанные ранее.

---

Другое расположение исходных пересекающихся окружностей A, B, C.

На первом рисунке точки пересечения А и В лежали по одну сторону от С. Ранее мы назвали три такие окружности окружностями
Лобачевского. Теперь рассмотрим случай, когда окружность С разделяет точки пересечения А и В. Такие три окружности названы Римановыми
окружностями. Теорема о трех окружностях верна и в этом случае. Но свойства симметрии, определенной такими тремя окружностями –
резко отличаются. В этом случае пара точек пересечения одной окружности также обязательно
разделяет любую другую пару точек пересечения. У симметрии I между окружностями, определенной тремя окружностями
Римана нет неподвижных точек. Подобная симметрия появилась первый раз, когда мы изучали симметрию, определенную семейством
окружностей-обручей. Неподвижных точек нет, потому что любые две окружности, одна из которых проходит через пару
точек пересечения А и В, а вторая – через пару точек пересечения В и С – пересекаются. Точки пересечения этих двух окружностей
и будут симметричны друг другу: I(x)=y, все точки одного цвета симметричны друг другу.

Из верхнего чертежа, как и в прошлом случае – мы извлекли рисунок. Он сильно отличается от предыдущего,
хотя и получен тем же способом. Теперь все непрерывные области плоскости ограничены ровно тремя дугами, и проследить симметричные
друг другу трехдужники сложнее, чем в прошлый раз. Попробуйте это сделать хотя бы для пары областей.

Хотя теорема о трех окружностях формулируется для плоскости, проще и изящней всего ее

СТЕРЕОДОКАЗАТЕЛЬСТВО:

Вспомним, что три сферы в общем случае пересекаются в двух точках: две сферы пересекаются по окружности,
а сфера с окружностью – в двух точках. Проведем сферу Хa через точку Х и окружность А, сферу Хb через точку Х и
окружность В, сферу Хс через точку Х и окружность С. Окружность, проведенная через Х и пару точек пересечения окружностей
А и В будет линией пересечения сфер Ха и Хв. Окружность, проведенная через Х и пару точек пересечения окружностей В и С
будет линией пересечения сфер Хв и Хс. По условию, точка Y лежит на пересечении этих двух окружностей.
Но точки пересечения этих двух окружностей есть пересечение всех трех проведенных нами сфер: Ха, Хв, Хс.
Точки Х и Y по условию лежат на пересечении этих окружностей, следовательно – они есть точки пересечения этих трех сфер.
Окружность, проходящая через Х и пару точек пересечения окружностей А и С есть линия пересечения Ха и Хс, и пара точек
пересечения этих трех сфер обязательно лежит на ней. Что и требовалось доказать.
В плоском же случае сфера все три сферы Ха, Хв, Хс совпадают между собой, поэтому доказательство не работает.

---

Мы рассмотрели два случая расположения исходных пересекающихся окружностей. Осталась третья возможность: все три исходные окружности
А, В, С пересекаются в одной точке. Ранее такой случай расположения окружностей был назван Евклидовым. В этом случае теорема
о трех окружностях также верна, но она становится бессодержательной. Почему?

А определяют ли три Евклидовых окружности какую-либо симметрию?
Выполнить построение, аналогичное предыдущим случаям
увидим, что всякой точке плоскости соответствует одна и та же точка: точка пересечения всех трех окружностей.
При таком отображении вся плоскость как бы стягивается или засовывается в эту точку. Но если мы будем считать, что точка есть
очень маленькая окружность, что точку можно “раскрыть” или “развернуть” (так поступают в анализе, когда у точки обнаруживают
“бесконечно-малую окрестность”) – то мы можем полагать, что имеем дело с отображением всей плоскости в бесконечно малую окрестность
точки, и обратно: этой малой окрестности во всю оставшуюся плоскость.

---

Конец первой части.

////////////////////////////////////////////////////////ЧАСТЬ 2///////////////////////////////////////

---

Трехокружник как треугольник.

В геометрии Евклида изучается треугольник: фигуру, образованную тремя пересекающимися прямыми.
В геометрии окружности подобную фигуру образуют три пересекающиеся
окружности. Назовем эту фигуру трехокружником, окружности, образующие трехокружник можно называть сторонами,
а пары точек их пересечения – вершинами трехокружника.

Сразу видно, какие точки лежат внутри треугольника, а какие вне. Про трехокружник этого не скажешь.

Трехокружник задает симметрию окружностей между собой (это было показано в пред. разделе). А треугольник никакой симметрии не задает.

---

Присмотримся: на какие части и как разделяет плоскость трекохружник.

Трехокружник, образованный тремя римановыми окружностями:


Плоскость разделена на 8 областей. Каждая из них ограничена тремя дугами (одна из областей простирается неограниченно).
При симметрии, определенной исходными окружностями, точки, лежащие в одном трехдужнике переходят в точки трехдужника,
не имеющего с первым общих точек (не граничащий с ним, не имеющий общих вершин). эти трехдужники имеют разный цвет на рисунке.
Например, внутренний синий трехдужник симметричен внешней белой области.

Точки внутри одного трехдужника можно отличить от точек другого трехдужника по окружностям, в которых эти точки лежат.

Трехокружники, образованные тремя окружностями Лобачевского могут выглядеть по-разному.

Трехокружник Лобачевского также как и трехокружник Римана, разделяет плоскость на восемь областей. Но эти области
устроены по-другому. Некоторые ограничены двумя дугами, другие – тремя или четыремя.
Точки, лежащие внутри области, ограниченной двумя или четыремы дугами, симметричны точкам внутри той же самой области.
А трехдужники – симметричны друг другу. Обратите внимание, на нижнем рисунке точки внутри маленького белого трехдужника в центре
симметричны точкам неограниченной внешней белой области. Заметим, и точки центрального трехдужника,
и точки неограниченной внешней белой области лежат ВНЕ всех окружностей. Или: ни одна окружность среди трех исходных не разделяет
точки внутри этих областей друг от друга.

Какой случай расположения трех пересекающихся окружностей не был рассмотрен?

---

Биссектрисы и высоты трехокружника. Определения.

Перпендикуляр (или высота) треугольника определяется как прямая,проходящая через одну из вершин треугольника
и перпендикулярная противоположной стороне треугольника. Аналогично определяется высота (или перпендикуляр) трехокружника:

Перпендикуляром трехокружника называется окружность, проходящая через одну из вершин трехокружника
и перпендикулярная противоположной стороне.

Вершина трехокружника это – пара точек. Чтобы провести через нее перпендикуляр
достаточно отразить симметрично одну из этих точек относительно А и провести через три эти точки окружность.
Она, по основному свойству перпендикулярных окружностей и будет искомым перпендикуляром на А.

---

Биссетрисой треугольника называется биссектриса его угла. Между двумя прямыми есть два угла (основной и дополнительный),
поэтому у двух прямых
– две биссектрисы. Биссектрисой треугольника называют обычно ту биссектрису его сторон,
которая проходит внутри треугольника.

Не ясно, что называть внутренностью трехокружника. Поэтому биссектрисой трехокружника называют ОБЕ биссектрисы между двумя его
сторонами.

---

Теорема о высотах трехокружника.

Все три высоты треугольника пересекаются в одной точке. Аналогичная теорема есть и про высоты трехокружника.

Мы видим, что три перпендикуляра трехокружника пересекаются в двух точках. Это естественно: вершина треугольника – одна
точка, а вершина трехокружника – пара точек. Сформулируем иначе: окружность, проведенная
через вершину трехокружника, и через пару точек пересечения двух перпендикуляров этого трехокружника, сама является
перпендикуляром трехокружника.
Что можно сказать о двух точках пересечения перпендикуляров? Они симметричны друг другу при симметрии I, определенной
трехокружником A, B, C. Точки одного цвета на рисунке (пары точек пересечения окружностей) – также симметричны друг другу при I.

Есть существенное отличие геометрии трехокружника от геометрии треугольника. Перпендикуляры трехокружника Лобачевского могут не иметь
общих точек. Перпендикуляры (и не только перпендикуляры) трехокружника Римана – пересекаются всегда.

В общем случае теорема о перпендикулярах трехокружника звучит кратко:
три перпендикуляра трехокружника всегда лежат в одном пучке. Но мы еще не ввели
понятие пучка окружностей. Поэтому сформулируем так: если два перпендикуляра трехокружника имеют общие точки, то третий
перпендикуляр всегда проходит через их общие точки. Отсюда следует, что если два перпендикуляра не пересекаются, то и третий не
пересекается ни с одним из них.

В геометрии окружности реализуются промежуточные случаи. Если возможно, что перпендикуляры пересекаются, и возможно, что они
не имеют общих точек,то возможно и то, что они касаются.

Теорема о перпендикулярах треугольника оказывается частным случаем теоремы о перпендикулярах трехокружника.

Не так-то просто среди “птиц”, получившихся из перпендикуляров риманова трехокружника, найти сами перпендикуляры и три
исходные окружности.

А в случае трехокружника Лобачевского мы сразу видим трехдужник и криволинейные перпендикуляры в нем. Точнее – мы видим два
симметричных трехдужника.

Маленький трехдужник, образованный тремя исходными окружностями Лобачевского очень похож на треугольник, а окружности-перпендикуляры
на прямые. Это происходит от того, что все окружности на рисунке велики, а вторая точка пересечения перпендикуляров находится далеко.
А чему будет симметричен этот маленький трехдужник (при симметрии, определенной исходным трехокружником)? Как, примерно, пройдет
неподвижная окружность этой симметрии?

---

Теорема о биссектрисах (серединных окружностях) трехокружника.

Все три биссектрисы треугольника пересекаются в одной точке. Аналогичная теорема есть и про биссектрисы трехокружника. Поскольку
у двух сторон трехокружника – две биссектрисы (всего у трехокружника 6 биссектрис), то придется немного уточнять. Теорема звучит так: возьмем две биссектрисы трехокружника,
проходящие через разные его вершины. Среди двух биссектрис, проходящих через оставшуюся вершину,
одна обязательно лежит в том же пучке,
что и две, выбранные ранее. Определение пучка еще не дано. Переформулируем так: если две биссектрисы (выходящие из разных вершин)
имеют общие точки, то одна из двух биссектрис, проходящих через оставшуюся вершину обязательно проходит через все эти точки.
В трехокружнике Римана биссектрисы обязательно пересекаются.

В этом и следующем рисунке попробуйте найти исходный трехокружник и его биссектрисы. А какие области симметричны каким (при симметрии
определенной исходным трехокружником)? Если ли у этой симметрии неподвижные точки?

Здесь найти симметричные области проще. Можно примерно представить, как проходит окружность точек,
неподвижных при симметри, определенной трехокружником Лобачевского. В центре просматривается симпатичная рыбка. Куда она переходит
при симметрии?

---

Гармония биссектрис:

6 биссектрис малинового трехокружника Римана группируются на 4 тройки биссектрис, пересекающихся в двух точках. Каждая точка пересечения
лежит в своей непрерывной области (трехдужнике). В симметричном трехдужнике лежит вторая точка пересечения тех же биссектрис.
Нам “мешали” лишние биссектрисы сформулировать теорему об их точках пересечения. Но когда мы видим сразу все биссектрисы,
ясно – “лишних” биссектрис нет.

6 биссектрис трехокружника Лобачевского также группируются на тройки биссектрис. Одна тройка биссектрис не пересекается.
Эти три биссектрисы лежат в одном пучке. Внутри четырехдужников лежат по две точки пересечения биссектрис, внутри трехдужников –
по одной. Разумеется, на этом и предыдущем рисунке каждая биссектриса входит в несколько троек, иначе бы шести биссектрис хватило
бы всего на две тройки.

---

Попробуйте в этом “витраже” найти три римановы окружности и 6 их биссектрис. Указать несколько симметричных фрагментов.

Тоже самое для случая Лобачевского.

Видны две пары симпатичных ног и даже торс. Голову и руки надо пририсовывать.

---

Задача Аполлония.

Древнегреческий математик Аполлоний Пергский поставил задачу о построении окружности, касающейся трех данных. Если данные окружности
пересекаются между собой, то они образуют трехокружник и искомую окружность можно назвать
окружностью, вписанной в трехокружник.
Решим задачу, по аналогии с задачей о построении окружности, вписанной в треугольник. Чтобы найти центр такой окружности,
надо провести биссектрисы треугольника, точка их пересечения и будет центром вписанной окружности.
В геометрии окружности центр – неизвестное понятие. Чтобы приспособить решение к трехокружнику, мы найдем точки касания
вписанной окружности со сторонами. Для этого мы опустим перпендикуляры из точки пересечения биссектрис на стороны треугольника.
Точка пересечения стороны с опущенным на нее перпендикуляром – лежит на вписанной окружности, тем самым мы находим три точки искомой
окружности. Окружность по трем точкам геометрия окружности строить умеет.
Это рассуждение без помех переносится на трехокружник. Мы разберем случай риманова трехокружника.

Риманов трехокружник разбивает плоскость на 8 частей. В каждой из них можно постоить окружность, касающуюся сторон трехокружника.
В каждой такой области на рисунке есть цветная точка. Это – точки пересечения шести биссектрис, которые были на рисунке о
гармонии.
Выберем какую-нибудь область из 8. Проведем биссектрисы трехокружника, проходящие через эту область. На риснуке это область, где
лежит красная точка p. По теореме о биссектрисах все три выбранные биссектрисы пересекутся в двух точках p и q. Из этих точек проведем
окружности перпендикулярные сторонам трехокружника А, В, С и отметим точки пересения стороны с опущенным на нее перпендикуляром
(в отличие от треугольника, таких точек сейчас по две на каждой стороне)

Упростим чертеж, удалив с него биссектрисы и раскрасив каждый перпендикуляр в свой цвет, чтобы легко видеть точки его пересечения
со стороной, на которую он опущен.

Мы имеем три пары точек пересечения. Выберем из каждой пары ту точку, которая лежит на границе выбранной ранее области. Через
три выбранные точки проведем окружность. Она и будет искомой. Через три невыбранные точки можно также провести окружность. Она
также касается трех исходных окружностей A, B, C. Эта окружность лежит в области, симметричной выбранной области (при симетрии
относительно трехокружника А, В, С).

Выполним такое построение для всех областей (его нужно выполнять не 8 раз, а всего 4, т.к. каждый раз мы будем получать сразу
две окружности, симметричные относительно симметрии трехокружника А, В, С). Раскрасим полученные окружности. Круги одного цвета
симметричны друг другу, а белесая окружность симметрична внешней белой области.

Двухцветная раскраска хорошо показывает динамику.

Как доказать, что построение дает нужный результат? Вернемся к рисунку, где есть и три биссектрисы F, G, H, и опущенные из
пары точек их пересечения p и q перпендикуляры L, M, K. F(A)=B. При симметрии относительно F, точки p и q неподвижны
(т.к. лежат на F). Поэтому L, перпендикуляр на А, опущенный из p и q будет симметричен K, перпендикуляру, опущенному на B.
Поэтому пара точек пересечения L и A симметрична паре точек пересечения K и B (зеленые точки симметричны оранжевым относительно F)
Какая именно зеленая точка из двух симметрична какой именно оранжевой? Симметричны точки, лежащие на границе выбранной нами области.

Поэтому, всякая окружность, проходящая через выбранные зеленые и оранжевые точки перпендикулярна F (по основному свойству).
Аналогичное рассуждение можно провести и для биссектрис G и H. Отсюда следует, что
окружность, проходящая через три выбранные нами точки – перпендикулярна всем трем биссектрисам F, G, H. А отсюда следует,
что проведенная окружность перпендикулярна и всем трем перпендикулярам K, L, M (т.к. все эти перпендикуляры проходят через p и q –
точки пересечения F, G, H). А отсюда, по перпендикулярно-касательному признаку
следует, что проведенная окружность касается А, В, С. Что и требовалось доказать.

Аналогичное построение действует и для случая, когда три исходные малиновые окружности A, B, C – окружности Лобачевского.

Но в этом случае есть важные отличия. Получается 8 окружностей, как и в прошлом случае, но расположены они несколько иначе. Но,
как и в прошлом случае – найденные окружности симметричны друг другу при симметрии трехокружника.
Сравните рисунок с чертежом всех 6 биссектрис трехокружника Лобачевского.
Самое важное отличие: мы видели, что биссектрисы трехокружника Лобачевского могут не пересекаться. И как тогда провести окружности,
перпендикулярные сторонам трехокружника из отсутствующих точек пересечения? Никак не провести. Но можно провести окружность,
лежащую в том же самом пучке, что и три непересекающиеся биссектрисы и перпендикулярную стороне трехокружника. Точки ее
пересечения со стороной и будут искомыми точками касания. Определение пучка окружностей будет в третьей части.

Мы научились строить окружности, вписанные в трехокружник А, В, С. А если А, В С – не образуют трехокружник, не пересекаются
между собой? Нужно применить тот же самый метод: провести биссектрисы, опустить перпендикуляры из точек пересечения биссектрис,
выбрать из пар точек пересечения перпендикуляров со сторонами по точке и провести окружность через три выбранные точки. Она и будет
искомой. В общем случае получается 8 окружностей, касающихся трех данных. Но тут есть много тонкостей. Например, если А и В не имеют
общих точек, то между ними есть одна биссектриса. Есть между ними еще и симметрия, у которой нет неподвижных точек. Но как такую
симметрию использовать для нашего построения? Для этого надо расширить понятия пучка и включать в пучок не только окружности,
но и симметрии, при которых нет неподвижных точек. Но это мы забегаем слишком далеко вперед.

А при каком расположении А, В, С – нет ни одной окружности, касающейся их всех? А при каком – таких окружностей бесконечно много?

---

Три сокасающиеся окружности и три их биссектрисы.

Применим изложенный метод к интересному случаю: найдем окружность, касающуюся трех, которые сами уже касаются друг друга.
Три такие окружности A, B, C строго говоря нельзя называть трехокружником, т.к. они касаются, а не пересекаются. Но мы – назовем.
Что считать вершиной такого трехокружника? Вершина трехокружника это – пара точек, а здесь есть всего ода точка на эту роль, точка
касания. Что такое вершина пока не ясно, а биссектрису и высоту в этом случае легко определить по аналогии.
Биссектриса, как обычно – окружность, относительно которой две стороны трехокружника симметричны. Между двумя касающимися окружностями
есть всего одна симметрия, меняющая их местами. Так что у такого трехокружника всего три биссектрисы, как и у треугольника.
Биссектриса проходит через одну из точек касания окружностей
и меняет местами две оставшиеся точки касания. Высотой
такого трехокружника естественно назвать окружность, перпендикулярную одной из окружностей А, В, С, проходящую через точку касания
двух других и касающуюся двух других в этой точке. Высота лежит в одном пучке с ними.

Трехокружник А, В, С напоминает равноугольный треугольник. Ведь углы между касающимися окружностями равны между собой и равны нулю.
Среди трехокружников много равноугольных – например трехокружник из трех взаимоперпендикулярных окружностей тоже – равноугольный.
Прежде, чем применять метод, заметим: в нашем трехокружнике высота совпадает с биссектрисой, как происходит и в равнобедренном
треугольнике (и тем более в равностороннем). Это доказыается просто: биссектриса или серединная окружность к А и В перпендикулярна
окружности С, касающейся одновременно их обеих. Это сильно упрощает метод. Достаточно просто провести три биссектрисы трехокружника
А, В, С и взять точки их пересечения со сторонами, лежащие во внутренней области. Через три выбранные точки проведем окружность. Она и
будет искомой. Окружность, проведенная через три оставшиеся точки касается трехокружника А, В, С извне.
Доказательство нетрудно. Достаточно заметить, что, например, F меняет местами на только окружности А и В, но и точки пересечения этих
окружностей с опущенными на А и В высотами. Отсюда следует, что проведенная малиновая окружность перпендикулярна F, G, H и потому –
касается А, B, С.

Результат:

Первая медитация о тройственной симметрии.

Тройная симметрия возникает при рассмотрении симметрий, относительно биссектрис А, В, С. Каждая такая симметрия меняет местами
две окружности и точки касания, а одну окружность и одну точку касания оставляет неподвижной. Что будет, если последовательно
применять симметрии: вначале относительно одной биссектрисы, затем относительно другой? Точки касания будут меняться местами,
их можно переставить в каком угодно порядке. Сами биссектрисы – симметричны друг относительно друга, они являются образующими в группе
перестановок трех элементов. Подробней об этом – в
третьей части.

---

Моделирование геометрий трехокружником.

Остановимся и осмыслим сделанное. Мы видим, что трехокружник является “обобщенным треугольником”: у него есть вершины, высоты, биссектрисы,
медианы, вписанные окружности. И многие утверждения о треугольнике оказываются верны и для трехокружника. Есть и некоторые
особенности, главная из которых:
всюду, где в треугольнике мы говорим про одну точку, в трехокружнике мы говорим о паре точек.
Вершина трехокружника – пара точек, биссектрисы пересекаются – в одной паре точек, при построении вписанной окружности, решая задачу
Аполлония – мы также оперировали с парами точек. В чем же дело? В том, что трехокружник моделирует свойства неевклидовых
геометрий. Риманов трехокружник моделирует треугольник римановой геометрии, а трехокружник Лобачевского моделирует
свойства треугольника геометрии Лобачевского. Евклидов трехокружник (образующие его окружности все пересекаются в одной точке) –
моделирует свойства обычного, евклидова треугольника. И если нам удается доказать какую-то теорему о произвольном
трехокружнике – значит мы доказали теорему о треугольнике, верную и для геометрии Евклида, и для геометрии Римана, и для
геометрии Евклида одновременно. А пара точек геометрии окружности играет роль одной точки в геометрии прямых.

Чтобы яснее это видеть, свяжем с каждым трехокружником семейство окружностей и семейство пар точек. Мы уже делали подобное в ч.1,
рассматривая семейства, возникающие из двух пар точек, лежащих на одной окружности. Теперь мы получим те же семейства, но немного
другим способом.

Мы включим в наше семейство окружностей три исходные окружности, образующие трехокружник (стороны трехокружника). Затем мы включим все
окружности, проходящие через пары точек их пересечения (вершины трехокружника). Если две окружности семейства пересекаются, мы включим
в семейство все окружности, проходящие через пару точек их пересечения. Все пары точек пересечения окружностей семейства мы включим
в семейство пар точек.
Прежде всего отметим: любые две пары точек семейства – лежат на одной окружности. Это можно вывести из теоремы о трех пересекающихся
окружностях. А можно доказать иначе, рассматривая симметрию I, определенную исходным трехокружником. Легко видеть, что любая окружность
построенного семейства остается неподвижной при симметрии относительно I. Поэтому точки в любой паре точек из семейства – симметричны
друг другу относительно I. По первой теореме эстетической геометрии любые две пары
симметричных точек лежат на одной окружности. что и требовалось доказать. Мы видим, что наши семейства окружностей и пар точек можно
определить как семейство окружностей, неподвижных при I и семейство пар точек, симметричных относительно I.
Заметим, что все окружности, входящие в семейство, созданное римановым трехокружником – обязательно пересекаются между собой.
И любая пара точек семейства – разделяется любой окружностью семейства. Окружности же, входящие в семейство, порожденное трехокружником
Лобачевского – могут и не пересекаться друг с другом. Окружность этого семейства никогда не разделяет пару точек семейства.

Сделаем следующий шаг. Назовем окружности, входящие в семейство прямыми, а пары точек – точками. Раньше мы изучали
трехокружник по аналогии с треугольником, теперь мы и называть будем его треугольником.
Несложно показать, что если исходный трехокружник Риманов, то возникающая после такого определения “прямых” и “точек” геометрия
оказывается геометрией Римана. Сразу видно, что в такой геометрии все прямые пересекаются
(т.к. все окружности риманова семейства пересекаются). Если исходный трехокружник – трехокружник Лобачевского, то не все “прямые”
пересекаются. Очень много непересекающихся “прямых”. А параллельными среди них называют те “прямые”, которые представлены касающимися
окружностями семейства.
Если исходный трехокружник Евклидов, то семейство окружностей состоит просто из всех окружностей плоскости, проходящих через общую
точку всех сторон исходного трехокружника. А семейство пар точек состоит из таких пар, где одна точка – точка пересечения исходных
трех окружностей, а вторая точка может быть произвольной точкой плоскости. Разумеется, в этом случае у всех пар – одна точка совпадает
и о ней можно просто не говорить. Если мы осуществим инверсию с центром в этой точке, то все окружности семейства перейдут в прямые,
а центр инверсии симметричен бесконечно удаленной точке – вспомните формулу для расстояний в начале ч.1, там возникает деление на ноль.
Таким образом, евклидов трехокружник порождает обычную Евклидову геометрию.

Мы не будем подробно рассматривать модели, это намечено в другом месте в статьях на сайте. Здесь мы отметим
предельные свойства. Если мы находимся очень далеко от исходного трехокружника, то окружности, образующие его и он сам (каким
бы он ни был: Римановым, Лобачевского, Евклидовым) будет казаться нам очень малыми, почти точкой. А все окружности семейства, проходящие вблизи нас
станут очень велики,
практически неотличимы от прямых (т.к. все они проходят и вблизи нас и вблизи исходного трехокружника,
а между нами и трехокружником расстояние очень велико). Поэтому, на большом расстоянии
от трехокружника геометрии Римана и Лобачевского неотличимы от геометрии Евклида. Это можно видеть на некоторых иллюстрация ч. 2, где
и некоторые трехдужники издалека видны как маленькие треугольники. Также видно, что геометрия Евклида занимает промежуточное
положение между геометриями Лобачевского и Римана: ведь трехокружник Евклида получается из треокружника Римана, если выносить одну
из окружностей трехокружника так, чтобы она перестала разделять точки пересечения двух других.

Мы изучали трехокружник, не очень обращая внимания на симметрию I, определенную его сторонами. Хотя порой мы следили, как эта эта
симметрия действует на те или другие области плоскости. Теперь мы изучим ее основные свойства.

---

Симметрия трехокружника.

Каждый не Евклидов трехокружник А, В, С определяет симметрию окружностей I. Эту симметрию можно определить, используя любые две пары точек
пересечения окружностей А, В и С, т.к. две пары точек, лежащих на одной окружности, также определяют симметрию. Можно выбирать
эти пары точек по разному: пары точек пересечения А с В и С или В с С и А, или С с В и А. Симметрия при этом определяется одна и
таже, что гарантирует теорема о трех пересекающихся окружностях. Свойства этой симметрии определяются тем,
каков исходный трехокружник. В первую очередь изучая любую симметрию, интересно узнать есть ли у нее неподвижные точки.

Трехокружник Лобачевского.

Образом точки v при симметрии I будет вторая точка пересечения окружностей, проходящих через v и пары точек перечения трех окружностей
(вершин трехокружника). Если проведенные окружности касаются друг друга в точке v, то I(v)=v, v – неподвижная точка
(точки пересечения совпадают друг с другом). Можно
сформулировать добавление к теореме о трех окружностях: если две окружности, проведенные через произвольную точку v и
две пары точек пересечения трех окружностей касаются друг друга, то окружность, проведенная через v и оставшуюся пару точек
пересечения также касается их. Из ч. 1 легко понять, что неподвижные при I точки лежат на одной окружности. Как построить эту
окружность неподвижных точек? Для этого надо найти 3 точки, лежащие на ней. В этом нам помогут окружности,
построенные на точках пересечения А, В, С между собой, мы уже упоминали о таких окружностях, когда искали аналог “окружности описанной
вокруг треугольника” в трехокружнике.

Bыберем из каждой пары точек пересечения по одной точке и проведем через них окружность D. Через оставшиеся
точки проведем окружность E. Т.к. при симметрии трехокружника точки в паре пересечения окружностей меняются местами, то I(D)=E. Если
две окружности симметричны друг другу, то точки их пересечения (или касания) – остаются неподвижны. Это – интересная лемма, попробуйте
доказать ее. Отсюда следует, что точки пересечения E и D – неподвижны при симметрии I.

Двух точек найденных пересечения недостаточно, чтобы определить окружность. Поэтому мы повторим процедуру: выберем из трех пар
точек пересечения другие точки, проведем одну окружность через них, а другую – через оставшиеся, обе окружности симметричны
относительно I, следовательно точки их пересечения неподвижны при симметрии I. Всего можно выбрать по одной точке из каждой пары точек
пересечения (всего пар 3) 8 (2х2х2) способами, каждая выборка позволяет провести окружность через выбранные точки. На чертеже эти окружности
показаны пунктиром. Получившиеся окружности разбиваются на 4 пары симметричных друг другу окружностей. Заметим, что из этих четырех
пар одна пара окружностей может не пересекаться. А три пары – обязательно пересекаются. Это можно доказать, рассматривая какие пары
точек разделяют друг друга. Таким образом мы получаем 6 неподвижных точек. Для построения окружности неподвижных точек
достаточно каких-то трех из них. То, что все полученные описанным образом 6 точек лежат на одной окружности можно сформулировать
как новую теорему о трехокружнике Лобачевского. Проведенная окружность I – перпендикулярна всем трем исходным окружностям A, B,C.

На рисунке хорошо видна окружность I. А вот найти исходные окружности A, B, C – не очень просто.

Мы смогли построить окружность, перпендикулярную трем окружностям Лобачевского, причем в ходе построения мы пользовались лишь двумя
приемами: находили точки пересечения окружностей и проводили окружность через три точки. В этом проявилось
очень важное отличие геометрии окружности от геометрии прямых. В рамках геометрии прямых НЕВОЗМОЖНО выполнить подобное построение.
Мы не можем провести прямую, перпендикулярную данной, какие бы вспомогательные прямые мы не проводили через точки пересечения других
прямых. Свойство прямых “быть перпендикулярными” НЕВОЗМОЖНО описать через свойства прямых, связанные только со свойствами точек
пересечения прямых (афинными свойствами). Чтобы построить перпендикулярные прямые – нам недостаточно
одной линейки, нам понадобится и угольник. А, проводя одни окружности через точки пересечения других, мы только что определили
перпендикулярные окружности.

---

Трехокружник Римана.

У симметрии, определенной трехокружником Римана не может быть неподвижных точек. Потому что любые две окружности, проходящие через
пары точек пересечения риманова трехокружника (вершины трехокружника) – пересекаются. А неподвижная точка появляется, только если эти
эти окружности касаются.

Поэтому любые две окружности, построенные описанным ранее способом на точках пересечения исходных А, В, С – не пересекаются.
Если бы они пересеклись – точки их пересечения были бы неподвижны при симметрии I, а неподвижных точек быть не может.

Более того, если I – симметрия риманова трехокружника, то никакие две симметричные окружности не могут пересекаться между собой:
X и I(X) не могут имть общих точек, какова бы ни была окружность X (за одним исключением I(X)=X). Ведь если бы такие точки нашлись,
то они были бы неподвижны при I,
а неподвижных точек у I нет. Есть и другое интересное свойство у симметрии риманова трехокружника: если какая-то окружность Х
неподвижна под действием I (то самое исключение X=I(X)), то точки, симметричные друг другу относительно I всегда лежат по разные
стороны от X. Например: каждая окружность из трех исходных A, B, C разделяет точки пересечения двух других.
В случае трехокружника Лобачевского дело обстоит противоположным образом: окружность, переходящая в себя при симметрии I (перпендикулярная
I окружность) никогда не разделяет пару симметричных относительно I точек. Мы сталкивались с этим при осбуждении свойств семейств
окружностей и пар точек, порожденных трехокружником.

---

4 взаимокасающиеся и 3 взаимоперпендикулярные окружности.

Великолепная шестерка точек.

Когда видишь три окружности A, B, C, касающиеся друг друга, то рука тянется дорисовать четвертую D, касающуюся их всех.
Обычно хочется
поместить ее внутрь, внешнюю окружность, охватывающую их всех часто и не замечаешь. Как построить такую окружность мы уже разобрали.
Теперь мы изучим свойства точек касания четырех взаимокасающихся окружностей.
Сколько их: можно просто подсчитать на рисунке – 6. А можно воспользоваться комбинаторикой: любые две окружности касаются
друг друга в одной точке, всего пар окружностей 4*3/2=6. Кстати, можно построить 5 взаимокасающихся сфер, точек их касания –
5*4/2=10.

Обозначим каждую точку касания двумя буквами: ab, ac, ad, bc,bd, cd. Каждая буква в названии точки означает одну из двух касающихся
в этой точке окружностей. У этих шести точек много интереснейших свойств, они пронизаны двойной, тройной и четверной симметриями,
они определяют соотношение, называемое в геометрии “гармоническим соотношением”, их с полным основанием следует называть ВЕЛИКОЛЕПНОЙ
ШЕСТЕРКОЙ ТОЧЕК. Здесь мы видим, открывающуюся в этой шестерке точек, четверку новых окружностей.

Если мы сгруппируем эти шесть точек иначе, то получим другую четверку окружностей P, Q, S, T,
касающихся друг друга и проходящую через те же самые шесть точек.
Докажем, например, что окружности S и P касаются друг друга. Для этого покажем, что они обе перпендикулярны окружности А.
Окружность S проходит через точки касания А, В, С, следовательно она перпендикулярна им всем, в том числе и А.
Окружность Р проходит через точки касания A, C, D, следовательно она тоже перпендикулярна А.
По построению P и S обе проходят через точку AC, из перпендикулярно-касательного признака следует,
что P и S касаются друг друга в этой точке (т.к. они перпендикулярны одной и той же окружности А).
Аналогично доказывается, что и другие построенные окружности касаются друг друга.
Четыре построенные взаимокасающиеся окружности P, Q, S, T называются дополнительными к исходным окружностям A, B, C, D.
Легко видеть, что окружности дополнительные к дополнительным – это исходные окружности.

Вторая медитация о тройственной гармонии


Хотя мы видим тройственную гармонию, в ней участвуют четверки взаимокасающихся окружностей и потому здесь присутствует
не только тройная, но и четверная симметрия. Есть и двойная симметрия – она обеспечивает переход от одной четверки взаимокасающихся
окружностей к дополнительной. Как проследить эту симметрию?

Мы группируем точки великолепной шестерки
еще раз и обнаруживаем, что через них можно провести 3 окружности так, чтобы на каждой окружности было по четыре точки из шести.
Проведенные окружности F, G, H все обязательно перпендикулярны друг другу.

Докажем, что, например, точки ac, bd, cd, ab – лежат на одной окружности.
Для это рассмотрим пару окружностей В и С. Окружности A и D – касаются их обеих.
Следовательно, точки касания А и D с B и С – сами лежат на одной окружности
(перпендикулярной биссектрисе А и D) по теореме о касающихся друг друга по цепочке окружностях.


Рассмотрим трехокружник F, G, H. Он определяет симметрию окружностей, при которой точки пересечения F, G, H
между собой меняются местами, а сами окружности F, G, H – переходят в себя.
При этом четыре исходные взаимокасающиеся окружности переходят в дополнительные к ним окружности

Как доказать, что например G и F перпендикулярны? Для этого, по основному свойству перпендикулярных окружностей,
достаточно доказать, что G(ab)=bd. Воспользуемся теоремой о разбиении четырех точек
на пары тремя способами (ч.1) и найдем образ точки ab при симметрии относительно G. Четыре, нужные для теоремы точки – ac, ad, cd, bc.
Попробуйте проследить это, используя метод “путешествия по парам окружности” указанной теоремы.

Третья медитация о тройственной симметрии.

Великолепная шестерка точек была определена как шестерка точек касания четырех окружностей. Мы видим,
что ее же можно определить через три взаимоперпендикулярные окружности. Это шесть точек пересечения их всех между собой.
Для построения великолепной шестерки удобней пользоваться именно этим определением: перпендикулярные окружности построить проще,
чем касающиеся. Если нам надо построить 4 взаимокасательные окружности также удобней вначале построить 3 взаимоперпендикулярные,
сгруппировать нужным образом точки их пересечения и провести через них окружности, которые и будут искомыми.

---

Задачи на построение в геометрии окружности.

---

Построение биссектрис.

Мы использовали биссектрисы для решения самых разных задач. Но про сами биссектрисы мы пока знаем довольно мало. Как их
построить? Какие у них свойства? Будем искать биссектрисы между двумя окружностями А и В. Для этого проведем окружность I, перпендикулярную
А и В. Пусть она пересекает А в точках s и h, В – в точках f и g. Есть ровно два отображения пары точек (s, h) и (f, g)
друг в друга. Обозначим эти отображения W и V. V(s)=f, V(f)=s, V(h)=g, V(g)=h; W(s)=g, W(h)=g, W(h)=f, W(f)=h. Из ч.1 мы знаем, что
любые две пары точек, лежащих на одной окружности (в данном случае это окружность I) определяют симметрию окружностей. Следовательно,
W и V определяют такие симметрии. Легко видеть, что W(I)=V(I)=I, W(A)=V(A)=B. Последнее равенство и означает, что W и V меняют местами
А и В. Поэтому, если у этих отображений есть неподвижные точки, то W и V – являются биссектрисами между А и В. Если же у одного из
этих отображений нет неподвижных точек (при каком условии это возможно?), то А и В не могут иметь общих точек. Сейчас мы рассматриваем
случай, когда А и В пересекаются.

Мы нашли симметрии, определяемые биссектрисами. Образ каждой точки мы можем найти, использую симметрию двух пар точек.
Но как провести сами биссектрисы? Две точки, через которые обе они проходят мы знаем. Это точки пересечения А и В.
Поэтому нам достаточно найти еще одну точку, лежащую на биссектрисе: три точки определяют окружность однозначно. Если нам
удастся построить окружность, перпендикулярную одной из биссектрис, например биссектрисе V, то мы отобразим относительно
построенной окружности известную нам точку, лежащую на V (одну из точек p или q) и проведем через p, q, и новопостроенную точку
окружность, она и будет искомой биссектрисой V. Окружностей, перпендикулярных V много, например, это окружности. касающиеся
А и В одновременно. Но как их построить? Проще выбрать окружность, проходящую через s и f. V(s)=f, следовательно любая такая
окружность перпендикулярна V. Для определенности проведем ее через p. Это окружность К на чертеже. Окружность, проходящая через
p, q, K(q) и будет искомой биссектрисой V. Аналогично проведена окружность L ортогональная W и с ее помощью проведена W.
W и V перпендикулярны друг другу. Это связано с теоремой о разбиении четырех точек (s, h, f, g)
на пары двумя способами, ч.1.
Биссектрисы между двумя прямыми также перпендикулярны друг другу.
Почему биссектрис две? Мы получили это, потому что пару точек пересечения окружности I с А, можно отобразить в пару точек пересечения
I с B ровно двумя способами. Есть и другое объяснение, оно становится наглядным, если мыслить круги, границами которых являются
окружности А и В. При одном отображении А в В внутренность А переходит во внутренность В и внешность А во внешность В,
при другом – внутренность А переходит во внешность В и внешность А во внутренность В. Несмотря на логичность этого
объяснения – оно неверно. Попробуйте разобраться с тем, как обстоит дело с внутренностью ивнешностью отображаемых окружностей самостоятельно.

Построение позволяет сформулировать интересную теорему про точки s, h, f, g. Окружность, проходящая через s, f, p всегда касается
окружности, проходящей через h, g, p. Ведь они обе перпендикулярны V и все три окружности проходят через p
(перпендикулярно-касательный признак). Также они касаются и W. Аналогично и окружности, проходящие через s, g, p и f, h, p
касаются друг друга и V. Кроме того, мы можем построить окружности через эти четыре точки и вторую точку пересечения А и В – q,
соответственные окружности также будут касаться друг друга.


Удобней формулировать эту теорему, используя окружность I, перпендикулярную А и В. Если мы выберем одну точку из пары точек
пересечения I
c A, одну точку из пары точек пересечения I с B и через выбранные точки и одну из точек пересечения А и В проведем окружность, то она
обязательно касается окружности, проведенной через оставшиеся точки пересечения I с А и В и выбранную точку пересечения А и В.

Нужные для теоремы точки s, h, f, g можно получить не проводя окружность I, а рассматривая систему из четырех окружностей, последовательно
касающихся А и В. Выберем две точки, лежащие на одной из четырех таких окружностей, и проведем окружность через них и точку пересечения
А и В. Затем проведем окружность через оставшиеся две точки касания окружностей системы и выбранную точку пересечения А и В.
Эти две окружности обязательно касаются.

Чертеж, содержащий все рассматриваемые окружности получается громоздкий. Но из него можно извлечь интересный рисунок.
Попробуйте найти в нем какие-то элементы рассматриваемой теоремы. Окружности I, А и В были удалены, а вот все касающиеся
окружности на нем есть.

Мы подробно рассмотрели построение биссектрис для случая пересекающихся А и В и даже получили интересную теорему. Если
А и В не имеют общих точек, то пара точек пересечения I с A не разделяет пару точек пересечения I с В. Как разбиралось при
определении симметрии двумя парами симметричных точек (ч.1), свойства симметрии зависят от того, разделяет ли одна пара симметричных
точек другую. Четыре точки можно разбить на пары тремя способами, и при одном, и только одном способе – пары точек будут разделять
друг друга. В данном случае эта возможность обязательно будет реализована в симметрии W или V. Такая симметрия – симметрия “обручей”, у нее нет
окружности неподвижных точек. Другая же симметрия имеет неподвижные точки, и ее биссектрису можно построить. Мы не пользовались
во второй части биссектрисами между окружностями, не имеющими общих точек, поэтому не будем пока разбирать этот случай.

Мы пользовались биссектрисами между касающимися окружностями. В этом случае все наше построение не работает. Окружность I,
перпендикулярная касающимся друг друга А и В обязательно проходит через точку их касания. Поэтому среди двух пар точек пересечения
есть общая точка – точка касания А и В. Попробуйте разобрать этот случай самостоятельно.

---

Конец второй части. Револьт Пименов, С-Петербург, 2012, revoltp@mail.ru

---

Композиция.

В первой части, например при изложении теорем о разбиении 4 точек на пары мы уже пользовались композицией симметрий,
сейчас мы будем делать это систематически. Композиция может быть не только у симметрий, а у любый действий, функций, операций,
и означает просто их последовательное примение. Скажем композиция четырех операций: зажечь горелку, налить воду в чайник, поставить его
на плиту, дождаться кипения, выключить горелку – есть новая операция, назовем ее “вскипятить воду в чайнике”.
Операцию “налить воду в чайник”
также можно представить композицией более простых операций: открыть кран, открыть чайник, поставить чайник под струю воды, закрыть
кран, закрыть чайник. В математике композиция применяется постоянно, скажем композиция “икс плюс пять” и “возведение в квадрат”
есть функция “икс плюс пять возведенное в квадрат”. Обратите внимание: в квадрат возводится не 5, а икс плюс 5.

Именно благодаря применению композиции симметрий относительно окружности геометрия окружности и превращается в эстетическую
геометрию. Всмотритесь в мешанину стрелок. Даны окружности S, T, V, I, а изображается,
как композиция симметрий относительно них действуют на оранжевые точки: a (слева), k (справа) и круг G.

Отражая объект (точку или окружность, круг) мы всякий раз окрашиваем его в тот же цвет, которым окрашена окружность,
отражающая объект. Продвигаясь по стрелке, мы каждый раз продвигаемся в композиции симметрий, подробности записаны на рисунке.
Разберем, например запись I(V(T(S(k))))=p. Мы видим, что в отличие от словесного описания, когда мы вначале указываем симметрию,
которую делаем первой, затем второй, а в заключение – ту симметрию. которую делаем последней, в математической записи
поступают наоборот. Первой слева стоит та операция, которая делается последней, а последней мы пишем операцию, которую надо делать
первой. В самом же конце мы указываем объект, с которым эти операции (в данном случае – симметрии) совершаются.

Для композиции произвольных преобразований вводят специальный знак: “*”. h=f*g означает, что “преобразование h есть результат
последовательного применения преобразований f и g, причем первым выполняется преобразование, указанное справа (в нашем случае – g).
Что означает “знать преобразование h” или “вычислить композицию”? Это означает, уметь по каждому объекту x
определять результат преобразования h. h=f*g означает, что для любого x: h(x)=f(g(x)).

Вернемся к иллюстрации с мешаниной стрелок. На ней изображена композиция преобразований f= I*V*T*S. Пользуясь стрелками, мы видим
значения f на точках a и k и на круге G. Еще быстрее мы видим значение преобразований f1=T*S и f2= V*T*S. Мы можем записать и так:
f=I*V*f1=I*f2. Если это неясно – попробуйте проследить по стрелкам. Есть замечательное свойство у композиции
преобразований – ассоциативность. Обратите внимание, в наших записях со знаком “*” – нет скобок! Если f, g, h –
произвольные преобразования то всегда f*(g*h)= (f*g)*h. Попробуйте самостоятельно разобраться, почему это так.

Есть еще одно важное свойство выражений о композиции преобразований. Равенства можно домножать справа и слева. Если f=I*V*T*S, то
верно и f*S=I*V*T и f*S*T=I*V (домножение справа) и I*f=V*T*S и V*I*f=T*S (домножение слева).
точно также мы поступаем при умножении чисел, когда “звездочка” означает знак умножения. Правда, при обычном умножении чисел нет
разницы справа или слева умножать, умножение чисел коммутативно: 5*7=7*5, а операция композиции преобразования в общем случае –
некоммутативна. f*g обычно не равно g*f (f(g(x)) не равно g(f(x))). поэтому умножая числа все равно – домножать справа или слева,
а работая с композицие преобразований надо это различать.

Оперируя с чем-либо, нам часто хочется “вернуть все обратно”. В математике вводят понятие “обратного преобразования” или “обратной
функции”. Операции “открыть кран” обратна операция “закрыть кран” операции “одеть носки” обратна операция “снять носки”.
Функции “умножить на пять” обратна функция “разделить на пять”. Операции “включить свет” обратна операция “выключить свет”. Причем
часто “включить” и “выключить” свет – одна и таже на самом деле операция: на один и тот же выключатель нажимаем. Точно также функции
“умножить на минус единицу” обратна функция “умножить на минус единицу”, т.е. функция может быть обратна самой себе: чтобы вернуться
в исходное состояние надо просто сделать тоже самое, что мы уже сделали.
Такие операции, такие функции называются инволютивными.
Все симметрии по своему определению инволютивны. I(I(x))=x так можно выразить инволютивность произвольной операции I.
В общем случае g будет обратным преобразованием к f, если для любого x: x=g(f(x)). Чтобы это выразить с помощью знака для композиции, надо
ввести обозначение, для такого преобразования, которое ничего не меняет или оставляет все на своих местах. Как это делает прибавление
нуля, или умножение на единицу. Такое преобразование называют “единичным” или “тождественным” преобразованием и обозначают буквой
e или E. Для любого x, e(x)=x. Можно записать: e*e=e, для любого преобразования f: f*e=e*f=f,
если f обратно g то f*g=e. Заметим: если f обратно g, то и g обратно f. А для каких операций, для каких функций –
нет обратных преобразований?

Не все симметрии окружностей коммутативны. Если S и Т коммутируют, то S*T=T*S. Коммутативность произвольных операций или
преобразований означает, что неважно в каком порядке их применять. Обычно важно: насыпать сахар в кофе и затем выпить, или в начале
выпить кофе, а потом насыпать сахар – разницу мы сразу почувствуем. А что одеть в начале: рубашку или носки – не имеет значения.
Эти две операции коммутируют. Какие симметрии коммутируют между собой? Легко видеть, что симметрии относительно двух перпендикулярных
прямых – коммутируют между собой. Композиция симметрий относительно двух перпендикулярных прямых – симметрия относительно точки их
пересечения. Коммутируют между собой и композиция симметрий относительно двух перпендикулярных окружностей. Ниже мы это объясним.
А сейчас заметим, что если две симметрии S и T коммутируют между собой, то их композиция сама является некоторой симметрией.
Ведь если S*T=T*S, то S*T*S*T=e (мы домножили справа на S*T и воспользовались тем, что S*S=T*T=e т.к. все симметрии инволютивны.
Обозначим S*T=f. Т.к. S*T*S*T=e, то и (S*T)*(S*T)=e (скобки можно ставить как удобно – ассоциативность!) Мы доказали. что f*f=e, т.е.
что композиция двух коммутирующих симметрий обязательно инволютивна т.е. если мы исполним эту композицию второй раз,
то вернемся в исходную точку. Поэтому ее и можно назвать симметрией. Но относительно чего? Это мы узнаем позже.

---

Траектории и пучки окружностей.

Теперь мы следим за движением точек b, c, d. Они кружатся, каждая по своей окружности, причем кружатся они против часовой
стрелке и внутри окружности кружения (перпендикулярной S и T) теперь лежит другая точка пересечения S и T – точка q. Мы видим,
что вся плоскость под действием преобразования h “расслаивается” на линии, которые прорисовывают точки x, h(x), h(h(x)), h(h(h(x)))…
эти линии не могут пересекаться между собой (подумайте, почему?). Эти линии движения точки х называют траекторией точки x при
преобразовании h. В данном случае эти линии устроены просто – это окружности, перпендикулярные S и T одновременно.

Рассмотрим второй случай расположения окружностей S и T, когда они не имеют общих точек. Обратите внимание: хотя рисунок создан
исходя из законов плоской геометрии, цветные точки кажутся расположенными объемно: они вылетают, или влетают в одну точку. Самой этой
точки на чертеже нет: они бы заслоняла собой другие (или бы была заслонена ими).

Это означает, что под действием преобразования h любая точка x окажется сколь угодно близко к точке w, что вся плоскость под действием
этого преобразования окажется в сколь угодно малой окрестности точки w (внутри сколь угодно малой окружности с цетром в w, или, говоря
языком геометрии окружности, которая не знает ни центров ни расстояний – под действием h любая точка x рано или поздно окажется по ту
же сторону от любой окружности, что и точка w). Заметим, что точки не так быстро стягиваются к w, как они стягивались к p на
предыдущем чертеже. Что означает, что точки вытягиваются из w? То, что если мы рассмотрим преобразование g, обратное к h, g=T*S, то
оно втягивает все точки в ту же точку w. Мы можем представлять w необычной воронкой, откуда точки втекают и вытекают и оба этих потока
не мешают друг другу. Если мы действуем преобразованием h на точку сколь угодно близкую к w вполне может быть, что она удалится от w
сколь угодно далеко, но потом точка обязательно снова приблизится к w сколь угодно близко.

Почему так происходит? Потому что “точки втягивания и вытягивания” обязательно должны быть корнями уравнения h(x)=x, а в данном случае
есть всего один корень этого уравнения x=w. Как и в прошлых случаях, точки двигаются по окружностям, перпендикулярным S и T и легко
доказать, что все эти окружности касаются друг друга в точке w.

Вариант, когда S и T касаются друг друга можно представить себе как предельный случай. Пусть S и T пересекаются в двух точках p и q.
Если мы будем приближать точки p и q друг к другу, то S и T будут напоминать касающиеся окружности и действие h=S*T будет напоминать
случай касания S и T. Еще наглядней переход если S и T не имеют общих точек. Будем приближать окружности S и T друг другу. В этом случае
точка втягивания p будет приближаться к точке вытягивания q пока они не совпадут в момент касания S и T. Совпадут они, разумеется,
в точке w – точке касания S и T.

Мы видим, что во всех трех возможных случаях расположения окружностей S и T, точки плоскости под действием h=S*T сами двигаются по
окружностям, перпендикулярным S и T. Эти окружности-траектории (как мы видели, в двух случаях траектория это не вся окружность,
а некоторая дуга, но сейчас мы говорим именно об окружностях) – и называются пучками окружностей. Каждая пара окружностей S и T
однозначно задает пучок окружностей, сейчас мы и будем изучать пучки.

---

Пучки окружностей

Начнем с того, что приведем все три возможных типа пучков:

Пучки были определены через перпендикулярность. Действительный пучок представляет траекторию движения точек под действием двух
окружностей не имеющих общих точек. Касающийся пучок – движение точек под действием двух касающихся окружностей, Мнимый пучок – позднее
мы скажем откуда берется столь странное название – представляет движение точек под действием двух пересекающихся окружностей.

Пучки можно определить по разному. Можно просто описать три типа пучков, как это было только что сделано. Можно дать одно общее
определение: пучок окружностей есть совокупность окружностей, перпендикулярных двух данным (в зависимости от этих “двух данных” мы
получаем три возможных типа пучка). Можно определить пучок окружностей отталкиваясь от двух окружностей А и В, входящих в пучок.
Для этого надо включить в пучок все окружности, получающиеся при симметриях А и В друг относительно друга, все биссектрисы между
А и В и окружностями, полученными в результате симметрий и все окружности, к которым можно таким образом приблизиться сколь угодно
близко. Это напоминает получение всех действительных чисел исходя из 0 и 1. Прибавлением и
вычитанием единицы и делением на два мы получаем новые числа.
Так даже дробь “одна треть”, тем более иррациональное выражение “корень из двух” мы никогда не получим. Но мы приближаемся к этим числам
сколь угодно близко.
Еще одно определение пучка: пучок это совокупность окружностей, таких, что композиция симметрий относительно любых трех из них
инволютивна. Иными словами, если А, В, С лежат в одном пучке, то композиция симметрий g=A*B*C сама есть некоторая симметрия
относительно окружности и g*g=e. Подумайте, как это связано с предыдущим построением пучка из двух его окружностей А и В?
Правда, это определение неточно: если А, В, С все перпендикулярны друг другу, то они не лежат в одном пучке, но их композиция –
инволютивна и есть симметрия окружностей, не имеющая неподвижных точек.

“Симметрии окружностей, не имеющие неподвижных точек” врываются в наши рассуждения порой неожиданно и на первый взгляд
представляют собой какие-то досадные исключения. Вот и сейчас: мы включали в пучок биссектрисы между окружностями пучка. Но ведь
между двумя окружностями есть симметрия, меняющая их местами и не имеющая неподвижных точек. Как ее включать в пучок? Ведь мы говорим
о пучке окружностей, а никакая окружность такой симметрии не сопоставляется? Именно из-за этого вопроса этот
пучок и называют “мнимым”.
Выход из положения – говорить о “пучке симметрий“. Определение пучка симметрий будет таким: любые две симметрии
S и T задают пучок симметрий: это совокупность всех симметрий. коммутирующих с ними обеими. Это обобщение оказывается очень полезно.
С его помощью, например, можно найти все решения задачи Аполлония (о построении окружности, касающейся трех данных), для того
случая, когда три исходные окружности не имеют общих точек.

Теперь о свойствах пучков. У пучков есть центры (центр). Это точки точки P и Q. Центры действительного пучка –
точки, через которые
проходят все окружности пучка. Центры мнимого пучка – точки, симметричные друг другу относительно любой окружности пучка. Центр
касающегося пучка – точка касания всех окружностей пучка. Все три случая могут быть описаны одним уравнением h(x)=x, где h –
композиция симметрий относительно любых двух окружностей рассматриваемого пучка. Решения этого уравнения и есть центры пучка.
Если у уравнения всего одно решение – мы имеем дело с касающимся пучком.

Часто возникает задача проведения окружности, лежащей в данном пучке и проходящей через данную точку x. Если пучок действительный,
то решение – окружность I, проходящая через x и центры пучка p и q. Если пучок касающийся, то задача сводится к нахождению окружности
проходящей через данную точку и касающихся двух данных в точке их касания между собой. Мы рассматривали мельком в ч.2 этот случай,
сейчас мы дадим решение, пригодное для всех трех типов пучков одновременно.
Проведем две окружности S и T, перпендикулярные двум каким-то окружностям пучка. Проводить перпендикулярные окружности несложно.
Проведем из точки x перпендикулярную S и T окружность. Она и будет искомой, поскольку одно из определений пучка: совокупность
окружностей, перпендикулярных двум данным (в нашем случае S и T). Этот прием проведения окружности пучка через данную точку есть
обобщение “двойного перпендикулирования” с которым мы столкнулись в ч.1 рассматривая связь касающихся и перпендикулярных
окружностей.
Прием корректен из-за следующего свойства перпендикулярных окружностей: если три окружности все перпендикулярны каким-то двум другим
(лежат в одном пучке), то любая окружность, перпендикулярная двум из этих трех – обязательно перпендикулярна и третьей из них.
Докажите это свойство самостоятельно. Но есть исключение, когда из точки x нельзя провести ни одной окружности данного пучка.
Когда это происходит?

Обратим внимание на проведение окружности I через данную точку x, лежащую в мнимом пучке с центрами P и Q. Фактическим мы здесь
решаем систему простых уравнений: I(x)=x, I(p)=q. Решение оказывается единственным. А когда мы проводим окружность по трем точкам,
мы решаем систему уравнений: I(x)=x, I(p)=p, I(q)=q. Мы видим, что три точки х, p, q однозначно определяют четыре окружности:
окружность, проходящую через них и три окружности, каждая из которых меняет местами пару точек (I меняет местами p и q), а
оставшаяся точка – неподвижна. Эти три окружности появлялись у нас при изучении биссектрис трех сокасающихся окружностей и между ними
есть тройственные симметрии, которые можно изучать методами, аналогичными изучению разбиения четырех точек на пары разными способами
в ч.1

Описанный прием двойного перпендикулирования позволяет строить пары “двойственных пучков”. Совокупность окружностей,
перпендикулярных всем окружностям данного пучка, сама образут пучок. Если исходный пучок – действительный, то ему двойственен
мнимый пучок причем центры пучков совпадают, а если исходный пучок касающийся, то ему двойственен также касающийся пучок.

Голубые окружности образуют действительный пучок, золотые – мнимый, каждая золотая окружность перпендикулярна каждой голубой.
Совместное изображение двух таких пучков напоминает искривленную шахматную доску. Оно имеет значение для электромагнетизма: если
ток движется по золотым окружностям, то силовый линии магнитного поля – по голубым. Правда, там рисунок должен быть трехмерным и чуть
более сложным, здесь мы видим проекцию.

Посмотрим на пучки разных типов, после небольшой их раскраски:

Как строились эти изображения? Во всех случаях, мы взяли две окружности А и В пучка (недалеко отстоящие друг от друга), и стали
действовать на одну из них, например на А, композицией h=A*B. получается ряд окружностей А, h(A), h(h(A)), h(h(h(A)))… и так далее,
все они лежат в одном пучке.
Ранее мы изучали действие h на точки, сейчас мы продемонстрировали действие h на окружности. Изучением такого действия мы займемся
в следующем разделе об однолопастной гармонической мельнице.

Сейчас же мы свяжем пучки окружности со свойствами геометрии Евклида. Осуществим инверсию с центром в одном из центров пучка. Тогда
действительный пучок превратится в пучок прямых (все окружности, проходящие через центр инверсии превращаются в прямые, а все
окружности пучка по определению проходят через центр пучка). Итак, действительный пучок имеет те же свойства, что и пучок прямых,
проходящих через одну точку. Касающийся пучок при такой инверсии превратится в пучок параллельных прямых. Мнимый пучок при инверсии
с центром в одном из центров пучка превратится в совокупность концентрических окружностей. Какая точка будет центром всех этих окружностей?

Построенные выше на основании пучков фигуры имеют эстетическое значение. И сами по себе и в различных сочетаниях. Например, если мы
сделаем две одинаковых черно-белых фигуры (мнимый пучок), совместим их, а затем начнем одну из них сдвигать, то увидим много
интересных эффектов, сопровождающихся различными иллюзиями.
Посмотрим теперь на несколько “искривленных шахматных досок”

У этой доски 10 “вертикалей, то есть в действительном пучке – 10 окружностей. Просматриваются верхняя и нижняя точки их пересечения –
центры пучка. Двойственный ему пучок – мнимый пучок “горизонталей”. Горизонталей в таких досках может быть любое количество,
мы теряем им счет, т.к они стягиваются вокруг центров пучка. Действительный пучок построен с помощью h –
композиции симметрий относительно окружностей A и B. h=A*B, причем A и B были выбраны не случайно, а так, чтобы десятикратное
применение их композиции дало бы тождественное движение E. Это выражают так: “h в десятой степени тождественно” или “порядок h в группе
преобразований равен 10” В этом случае действие h зацикливается, на десятом шаге все объекты возвращаются на свое место. Действие
h напоминает поворот на 360:10=36 градусов.

А в этом случае порядок h был выбран равным 99. h напоминает поворот на небольшой угол (360:99). Между двумя
пересекающимися окружностями можно ввести понятие угла. Между перпендикулярными окружностям он равен 90 градусам. Рассмотрим
h=A*B где A и B перпендикулярны, тогда последовательность x, h(x), h(h(x)), h(h(h(x)))… зацикливается уже на третьем шаге:
ее третий член всегда равен первому, второй четвертому и так далее, поскольку h(h(x))=x. В этом случае порядок h равен двум. Можно определить
угол между окружностями, исследуя композиции симметрий относительно пересекающихся окружностей с помощью понятия порядок элемента,
а можно непосредственно: углом между окружностями называют угол между касательными к ним прямыми в точке их пересечения.

Горизонтали в этом и прошлом случае были выбраны неслучайно. В кажду “клетку” доски можно вписать окружность так, чтобы она касалась
границ клетки. Теперь мы убрали границы, и оставили только вписанные окружности.

С такими “шахматными досками” связано много интересных эстетических эффектов и иллюзий. Стоит вернуться к ним и осмысливая
двухлопастную гармоническую мельницу.

---

Гармоническая мельница.

Гармонической мельницей я называют алгоритм или метод, или “двигатель”, позволяющий создавать красивые и
разнообразные образы на основе симметрии
относительно окружности. Он основывается на композиция симметрий относительно окружности, и действия полученного преобразования
на одну или несколько окружностей. Я полагаю, что этот метод важен не только для эстетики, но и в других областях, особенно для
биологии. Гармоническая мельница может быть плоской или объемной. Гармоническая мельница состоит из лопастей. Лопастью
гармонической мельницы я называю пару окружностей, не очень далеко расположенных друг от друга.
Работа лопасти – действие композиции
симметрий относительно входящих в нее окружностей. Лопасти в гармонической
мельнице должны быть перпендикулярны друг другу: обе окружности одной лопасти должны быть перпендикулярны обеим окружностям
другой лопасти. В плоской и трехмерной гармонической мельнице может быть одна или две лопасти. В этом разделе будет изучена
плоская гармоническая мельница, а следующем – показаны результаты работы объемной.
Разумеется, двухлопастная мельница
создает более разнообразные картины, чем однолопастная. Однолопастная гармоническая мельница работает просто, мы отчасти изучили
ее, исследуя траектории точек под действием композиции двух окружностей. Но мельница двигает не
только точки – она может двигать или преобразовывать окружность, несколько окружностей, круги, произвольные фигуры. Сейчас
мы изучим, как однолопастная мельница действует на окружность.

Однолопастная мельница.

---

Крутящая лопасть.

Крутящей лопастью называется лопасть, состоящая из двух пересекающихся окружностей S и T. На рисунке мы видим
результат работы нескольких тактов лопасти над окружностями A, B и зеленым кругом. Обратите внимание: ни одна окружность
не разделяет точки пересечения S и T (они же – центры пучка, в котором лежат S и T). Другой случай мы рассмотрим
позже.

Обратите внимание на сходство чертежа с изображением окружностей, касающихся двух данных из ч.1. Окружность А касается L и M и лежит
в семействе лепестков. Окружность W, перпендикулярная S, T, A – серединная окружность или биссектриса окружностей L и M. А
сам рисунок поясняет “медитацию о композиции” предложенную в первой части. Мы видим, что окружность под действием преобразования h
кружится, плавно меняясь в размерах. Окружность А не пересекается с h(A), если мы уменьшим радиус А – h(A) отдалится от A, если мы
сделаем радиус А бесконечно малым, то движение А под действием h совпадет с разобранным ранее движением точки. Обратите внимание:
если А не имеет общих точек c h(A) то никакие две соседние окружности из ряда А, h(A), h(h(A))… не имеют общих точек, а если
бы две какие-то соседние окружности из этого ряда пересекались, то пересекались бы
все соседние окружности в ряду. Мы видим этот случай на примере работы лопасти с окружностью B. Если
сильно уменьшить радиус B, то за один такт работы лопасти она перейдет в окружность, не имеющую с В общих точек. Значит, плавно
уменьшая радиус B и воздействуя на получающуюся окружность преобразованием h в какой-то момент мы получим касающиеся окружности,
а продолжая работу лопасти – целое ожерелье.

Вернемся к окружности A. Все изображенные окружности, полученные из А за несколько тактов работы лопасти – не пересекаются друг
с другом. Но если мы продолжим работу лопасти – ситуация изменится. Окружность А за один такт работы лопасти смещается против часовой
стрелки. Под воздействием h мы получаем последовательность лепестков, приближающихся к А с другой стороны. Через достаточное
количество тактов один из лепестков пересечется с А или совпадет с ней. Если совпадение случится и на энном такте лопасть
вернет A туда же, где окружность находилась в начальный момент, то дальнейшая работа однолопастной мельницы не имеет смысла:
ничего нового не появится, А перемещается только по своим следам. Если преобразование h подействовало на A N раз подряд, и
результат совпал с A, то на энном такте работы лопасти любая окружность вернется на свое место (а не только окружность
А). Это обозначают так: порядок преобразования h равен N, или так: “h в степени N есть тождественное
преобразование E”. Преобразования конечного порядка удобно использовать, например, для построения ожерелий, бусины которых плавно
меняют свой размер. Количество бусин равно порядку преобразования h.
Подобное замыкание может случиться не сразу, не за одну проходку (движение A вокруг W), а за несколько проходок. Если же замыкание
никогда не происходят – говорят, что “порядок h бесконечен“.


Ниже мы видим, какой образ создает окружность B, если лопасть сделает
еще несколько десятков тактов: похоже на обмотку тора. Если продолжить работу мельницы, то В зарисует всю
область между двумя окружностями, каждая из ограничивающих окружностей касается всех появившихся в ходе работы. Уточним – это
произойдет, если h имеет бесконечный порядок, в противном случае чертеж замкнется и В с каждым тактом будет идти в точности по
своим следам. Справа рисунок с обмоткой немного обработан. Мы видим на нем сочетание лепестков и искривленных шахматных досок.

Вернемся к чертежу, изображающую крутящую лопасть. Она действовала и на зеленый круг. Размеры этого круга не велики. Попробуем
понять, что происходит с кругом при следующих тактах лопасти. Представим себе окружности, касающиеся всех зеленых кругов, как
окружности L и M касаются всех окружностей производимых лопастью из А. Такие окружности существуют, одна, расположенная выше,
охватывает верхнюю точку пересечения (центр пучка) S и T, вторая, нижняя, охватывает нижнюю точку пересечения S и T. Зеленый
круг двигается между этими окружностями. Область, по которой он двигается – не ограничена, поэтому при следующих тактах лопасти
круг резко увеличивается. Ограничивающая его окружность станет почти прямой линией (а сам круг превратится в почти полуплоскость).
Круг может накрыть собой все, изображенное на чертеже. Именно поэтому работа лопасти была оборвана – в противном случае чертеж стал
бы неинтересен – зеленый круг на следующих тактах все накрывает. По другой причине не показаны окружности, касающиеся всех зеленых
кругов. Сейчас мы можем видеть неожиданный эффект: последовательность зеленых кругов кажется не лежащей в плоскости чертежа,
а объемной, падающей или взлетающей с нее. Эффект менее заметен, если огибающие касательные окружности нарисованы.
Изучая крутящую лопасть мы не интересовались объемом и действовали в рамках плоской геометрии. Меж тем и зеленые круги и
“обмотка тора”, произведенная из окружности B – воспринимаются объемно. Почему? Видимо, ответ на этот вопрос следует искать в
психологии, в восприятии нами трехмерного пространства, которое судя по приведенным здесь и далее примерам,
– связано с симметрией относительно окружности.

Ниже мы видим результат работы мельницы с окружностью, расположенной аналогично зеленому кругу: область, по которой лопасть перемещает
желтую окружность неограниченна, поэтому и размеры производимых желтых окружностей – неограничены. Результат работы немного обработан,
тем же способом, что и обычно.

А это желтое ожерелье сделано с помощью преобразования h двадцатого порядка, в нем ровно 20 касающихся кругов. Оно сделано на
другой однолопастной мельнице.


Ранее была показана укладка синего круга по клеткам искривленной шахматной доски. Из того рисунка можно извлечь множество
подобных друг другу (изоморфных) ожерелий из 99 касающихся кругов.

---

Теперь мы разберем случай, когда преобразумая окружность A разделяет точки пересечения S и T.
Именно в этом случае не существует окружности W, перпендикулярной ей, S и T одновременно (т.к. эти три окружности образуют
риманов трехокружник). Но существуют окружности L и M, перпендикулярные S и T и касающиеся A. В этом случае, все окружности, производимые
крутящей лопастью из А: h(A), h(h(A)),h(h(h(A)))… и так далее – касаются L и M и лежат в семействе обручей, как
описано в первой части. Все окружности этого семейства пересекаются друг с другом. Сравните картину с предыдущим случаем.

Когда мельница сделает еще несколько десятков тактов, мы получим такую картину. Обратите внимание: производимые окружности
располагаются не равномерно. Чтобы описать эту неравномерность надо углубляться в теорию чисел. Из-за неравномерности
рисунок обогащается звездообразной структурой вокруг внутренней касающейся окружности и искривленными шахматными досками. Если
совершить еще сотню-другую тактов – окружности начнут сливаться, заштриховав практически всю область между L и M, как это
было и в предыдущем случае. Справа – обработка рисунка.

---

С точки зрения геометрии окружности этот случай ничем не отличается от предыдущего: окружность A не разделяет точки пересечения
S и T. Но теперь область, по которой движется A – между небольшими окружностями L и M неограниченна, радиус производимых из А
окружностей может быть сколь угодно велик, а сами они могут быть малоотличимы от прямых.
Поэтому визуальные и эстетические свойства получающегося рисунка – другие. Аналогичная
ситуация была в предыдущем случае, когда мы обсуждали движение зеленых кругов.

После нескольких десятков тактов лопасти получится такая картина. Мы снова видим неравномерность
– но и ритмичность этой неравномерности – расположения произведенных из А окружностей. Звездовидные структуры вокруг L и M сейчас
видны очень отчетливо, “шахматные доски” искривились и уже напоминают скорее лучи или мечи. Они образованы пересечениями наборов
окружностей или сплетением их.

Рисунок после обработки.

Ниже – результат работы крутящей лопасти состоящей из другими окружностей, расположенных друг к другу ближе, чем S и T
в прошлом примере. Но движимая окружность A расположена аналогично только что разобранному случаю: разделяя точки пересечения окружностей
лопасти, касающиеся ее окружности L и M не охватывают одна другую. Поэтому производимые из А окружности часто неотличимы
от прямых. Присмотритесь к рисунку. его структура очень отличается в разных местах, он воспринимается как некая поверхность, хотя
и создан по законам плоской геометрии окружности.

---

Мы рассмотрели случаи, когда А разделяет или не разделяет точки пересечения S и T.
Возможны еще два варианта: А проходит через одну из этих точек, А проходит через обе эти точки.
В последнем случае А лежит в том же пучке, что и S, и T, и все производимые из А лопастью окружности также лежат в этом
пучке. Как выглядят окружности, лежащие в таком пучке уже было показано в разделе о пучках. Поэтому здесь мы разберем только первый
вариант. В этом случае одна из окружностей L и M (касающихся А) превращается в точку. Все окружности, произведенные из А лежат по
одну сторону от второй касающейся А окружности, вне, или внутри ее. И все они, а не только A, проходят через точку пересечения S и T.
Ниже показан случай, когда все окружности лежат внутри. Рисунок
уже обработан.

Выше мы видим получающуюся картину в целом. Весь рисунок, состоящий из многих окружностей, расположен внутри огибающей окружности,
касающейся их всех. Но если мы приблизимся к точке пересечения S и T (через которую проходят все окружности, входящие в образ), картина
резко меняется, как под микроскопом. Внизу мы увеличили масштаб, перекрасили элементы рисунка и подошли ближе к точке пересечения.

Мы подошли еще ближе к точке пересечения и снова увеличили масштаб.

---

Стягивающая лопасть.

Мы видим действие лопасти, состоящей из окружностей S и T на окружности А, В, круги С и D, и на зеленый безымянный круг.
Как и во многих разобранных ранее случаях – результат работы однолопастной мельницы представляется нам объемным,
хотя и порожден плоской геометрией. Зеленый круг оставлен безымянным, потому что его движения начинается с очень маленького
круга, расположенного вблизи верхнего центра пучка S и T – точки p. В дальнейшем, мы часто будем говорить не “центры пучка”, а
“центры лопасти“, имея в виду те же самые точки p и q. Этот первый зеленый круг, из которого лопасть производит
все остальные зеленые круги столь мал, а его сосед тоже мал и так близко к нему расположен, что просто некуда было бы написать его
обозначение. Наблюдая за ним можно проще представить, как, как все вытягивается из верхнего центра пучка и втягивается в нижний.
Разумеется, без обозначений не ясно – из какого центра вытягиваются, а в какой втягиваются, откуда взлетают, а куда падают.

Окружности А и B расположены не случайно. Они перпендикулярны одной окружности W и лежат в одном
семействе касающихся L и M окружностей. Если мы дадим лопасти обратный ход, т.е. будем действовать на
A и B преобразованием g=S*T к образу будут добавляться новые окружности: g(A), g(B), g(g(A)), g(g(B)) и так далее. Все эти окружности
будут из того же семейства касающихся L и M окружностей, и будут перпендикулярны серединной между L и M окружности W. Добавляющиеся
окружности втягиваются в точку p. При перемене хода мельницы с прямого на обратный точки втягивания и вытягивания
меняются местами – обратный ход вытягивает оттуда, куда было втянуто прямым прямым ходом, втягивает туда, откуда было вытянуто прямым
ходом.. А при перемене хода крутящей лопасти все начинало кружиться в другую сторону.

Работа с крутящей лопастью почти не требовала обратного хода. Не так со стягивающей лопастью: для того, чтобы проследить
втягивание окружности или круга X, надо в начале прямым ходом втянуть его к одному из центров лопасти, а затем, обратным ходом – втянуть
к другом центру лопасти. В результате мы получим цельную картину, наподобие той, что изображена была выше с зеленым кругом.
Если отразить все, произведенное прямым и обратным ходом, относительно окружности, проходящей через центры пучка и
перпендикулярную W, то все полученное будет целостным рисунком, все окружности будут касаться двух, уменьшаться с одной стороны
точки пересечения этих двух окружностей, “гаснуть”, появляться с другой стороны. Внизу слева мы видим непересекающиеся зеленые
круги, созданные таким способом, а справа – ожерелье, бусины которого вспыхивают из двух точек. Обратите внимание: правому рисунку
тоже присущ объем, нижняя и верхняя его части кажутся лежащими в разных плоскостях.

Нижний рисунок получен аналогично верхним. Но круг, произведенный из малинового круга лопастью за один такт, пересекается с исходным
кругом, поэтому стягивающая лопасть в данном случае создает последовательность пересекающихся кругов. Думаю, объемность
получающегося образа наглядней, чем в прошлом примере.



Какой случай расположения движимой окружности Х, не разделяющей центры стягивающей лопасти, не был рассмотрен?

Если движимая окружность Х разделяет центры стягивающей лопасти, то – интересный момент – все произведенные лопастью из нее окружности
не имеют общих точек между собой, каждая из получаемых окружностей разделяет не только центры пучка, но и те окружности, которые были
получены до нее, от тех, которые будут получены после. Получающийся образ напоминает геодезические линии холма.
После обработки получается рисунок ниже. Был использован обратный ход, поэтому мы имеем два косоглазых холма,с вершинами
в центрах лопасти. Рассматривая образ подольше, вместо холма можно увидеть воронку, впадину.

Заметим противоположность крутящей и стягивающей лопасти: если окружность Х разделяет центры крутящей лопасти, то все производимые
из Х окружности пересекаются. Если X разделяет центры стягивающей лопасти, то все производимые окружности не имеют общих точек
между собой.

Остались случаи, когда движимая окружность X проходит через один или оба центра лопасти. Во втором варианте лопасть производит мнимый
пучок окружностей, а первый вариант дает неожиданный результат, который я предлагаю обнаружить самостоятельно.

---

Касающаяся лопасть.

Этот случай мы рассмотрим коротко. Он получается из предыдущего совмещением начала и конца: центры стягивающей лопасти стали приближаться
друг к другу и в момент их совпадения лопасть из стягивающей стала касающейся. Эта лопасть имеет всего один центр, из которого
все вытягивается и в который все втягивается: ведь в нем совпали втягивающий и вытягивающий центры стягивающей лопасти.
Слева мы видим работу лопасти с синим и красными кругами. При прямом ходе эти круги втягиваются в точку касания окружностей лопасти,
двигаясь при этом по часовой стрелке. При обратном ходе они втягиваются в эту же точку но, с другой стороны, двигаясь против часовой
стрелки. В результате голубые круги создают ожерелье, растущее из w.

Справа мы видим окружности возникшие после многих тактов работы лопасти над небольшой окружность, охватывающей w. Если продолжить
работу мельницы, то окружность, уже похожая на точку, будет втягиваться к w, при обратном ходе – она будет втягиваться с другой
стороны. Мы видим “отростки” этого втягивания. Как и в прошлых случаях – прорисовываются две огибающие окружности, касающиеся
всех окружностей, произведенных мельницей. В отличие от прошлых случаев, огибающие окружности сами обязательно касаются друг
друга. Почему?

Увеличим и обработаем получившийся рисунок.

Еще раз увеличим масштаб и понаблюдаем, что происходит вблизи единственного центра касающейся лопасти.

---

Изменение скорости лопасти.

Кружением и стягиванием можно управлять: менять их скорость. Как увеличить скорость в два раза? В исходной лопасти две окружности
S и T, один такт лопасти – преобразование h=T*S. В новой, “удвоенной”, лопасти будут окружности S и M, M=T(S), тактом новой лопасти будет преобразование
f, равное композиции симметрий относительно S и новой окружности M=T(S). Симметрия относительно T(S) равна T*S*T, поэтому
f=M*S=(T*S*T)*S=(T*S)*(T*S)=h*h. Один такт работы новой лопасти делает то же, что два такта работы старой. Преобразуемый объект X
преобразуется новой лопастью в два раза быстрей, а получающийся образ оказывается частью образа, создаваемого
исходной, медленной лопастью. Первая лопасть создает образ, элементы которого: X, h(X), h(h(X)), h(h(h(X))), h(h(h(h(X))))…
и так далее, “удвоенная лопасть” создает образ из: X, f(X)=h(h(X)), f(f(X))=h(h(h(h(X)))), f(f(f(X)))=h(h(h(h(h(h(X))))))… и
так далее. Мы видим, что каждый второй элемент первого образа является частью второго.

А как замедлить работу лопасти? Проведем биссектрису между S и T, лежащую ближе к S чем T, лопасть из S и биссектрисы
будет работать в два раза медленней исходной, и все создаваемое исходной лопастью будет частью того, что создаст новая. Но
построение биссектрисы требует времени. Если мы хотим замедлить работу лопасти, и нам не важно во сколько точно раз, то проще
поступить так: выбрать какую-то точку v, лежащую ближе
к S чем окружность T, и провести через v окружность K из пучка,
в котором лежат S и T. Лопасть, состоящая из S и K, будет работать медленней, чем исходная, чем ближе v и K, тем медленней
работа лопасти. Аналогично можно и ускорять работу мельницы, если нам не важна точная скорость: точку v теперь надо выбрать
дальше от S , чем T. А как ускорить работу лопасти точно в три раза?

На рисунках ниже показано изменение скорости для крутящей и стягивающей лопасти. Круг А преобразуется исходной лопастью,
круг B – движется в два раза быстрей: на него действует “удвоенная лопасть”,
а окружность С – преобразуется очень медленно, “ползет” почти не изменяясь за один такт: на нее действует замедленная лопасть,
построенная с помощью точки v.
Обратим внимание, на правом чертеже стягивающей лопасти есть две зеленые окружности. Это – вспомогательные окружности, проходящие,
через центры лопасти, перпендикулярные S и T. Они
нужны для удобства проведения новой, замедляющей окружности K. Выбрав точку v ближе к S, мы отражаем v относительно
зеленых окружностей и проводим K через v и две новопостроенные точки. А на левом чертеже крутящей лопасти мы просто проводим
окружность через v, и центры лопасти и получаем искомый “замедлитель” K.

Две безымянные зеленые окружности на правом рисунке подсказывает идею: совместить действие двух лопастей. Ведь сами зеленые
окружности образуют крутящую лопасть, а стягивающая была дана исходно. Что будет, если объект преобразуется одновременно двумя лопастями,
крутящей и стягивающей? Будет – двухлопастная мельница, о ней речь дальше.

---

Двухлопастная мельница.

“Червяк” созданный на двухлопастной мельнице. Мельница работает не только с окружностями: “червяк” был создан из пятиконечной
звезды. А вот и сама мельница:

Двухлопастная мельница состоит из четырех окружностей: S, T; L, M. Первая пара окружностей, S и Т, образует крутящую лопасть,
а вторая пара, L и M – стягивающую лопасть мельницы. p и q, точки пересечения первой пары окружностей и центры пучка второй пары
называются центрами мельницы. Окружности крутящей лопасти, S и T перпендикулярны обеим окружностям стягивающей лопасти L и M:
S(L)=L, S(M)=M, T(L)=L, T(M)=M. Что происходит за один такт работы двухлопастной мельницы? Произвольный объект X преобразуется
в объект T(S(M(L(X)))) и добавляется к образу. Работает пребразование h=T*S*M*L=(T*S)*(M*L)=f*g где f – преобразование крутящей лопасти
из T и S, а g – преобразование стягивающей лопасти из M и L. Т.к. пара окружностей S и T перпендикулярна окружностям M и L, то
соответствующие симметрии коммутируют и коммутируют преобразования f и g. h=f*g =(T*S)*(M*L)=M*T*S*L=M*L*T*S=(M*L)*(T*S)=g*f=h.
Не важно, в каком порядке действуют лопасти, но важно, в каком порядке работают окружности составляющие
каждую лопасть. Посмотрим, как действует двухлопастная мельница на окружность или круг.

Еще раз увеличиваем скорость крутящей лопасти в два раза. В результате круги разбегаются так далеко, что рисунок приходится уменьшить
и повернуть. Мы видим уже два витка. Правда, спираль разрывается, один такт лопасти очень далеко уносит преобразумый объект

А сейчас преобразуеся не круг, а окружность А. Причем окружность А разделяет центры мельницы p и q.
Лопасти мельницы выделены оранжевым и зеленым цветом.
В этом случае мы можем быть уверены
на каком-то такте работы мельницы А превратится в окружность очень большого радиуса. Как обычно, мы даем мельнице прямой ход, обрывая ее работу,
когда окружности будут близки к нижнему центру мельницы, затем даем мельнице обратный ход, спираль закручивается в обратную сторону,
к верхнему центру мельницы, получающиеся окружности пересекаются между собой. Пересечение окружностей не создает хаос. В нем – есть
закономерности. Спиралевидная структура образуется из точек пересечения окружностей между собой и огибающих линий. На рисунке не выделена
стартовая окружность А – она может любой окружностью, из имеющихся на чертеже, результат, т.е. совокупный образ от этого не меняется.

На прошлом рисунке мы видели кусок спирали в натуральную величину. Ниже
та же спираль, но с “птичьего полета”, уменьшенная в 10 раз. Все равно: мы видим ее не целиком, две окружности не уместились.

Мы приблизились к центру мельницы и увеличили спираль в три раза.

Так обрабатывает мельница круги. Они накладываются друг друга.

Обработанная спираль.

Увеличенная в три раза, у центра мельницы.

С птичьего полета, уменьшенная в 10 раз.

---

Уже разбирая крутящую и стягивающие лопасти, мы не рассмотрели всех случаев расположения одной-единственной окружности или круга.
Разбирая двухлопастную мельницу это тем более невозможно. А ведь эстетическое значение имеют случаи, когда преобразовывается
несколько разноцветных окружностей или кругов одновременно, и когда преобразуются не круги, а другие фигуры. Некоторые примеры
возникающих образов есть на этом сайте, сотни примеров на сайте
http://revolt33.narod.ru/oldpicture.
Здесь мы покажем несколько выразительных пиктограмм разных типов образов, сделанных на двухлопастной гармонической
мельнице.

Несколько приемов обработки возникающих образов.

1. Выбор фрагмента и масштабирование. Образ, созданный после нескольких сотен
(а иногда и нескольких десятков) тактов работы мельницы обычно
значителен по размеру. В первую очередь следует поглядеть на образ в целом, для этого обычно нужно его уменьшить. Затем следует
поглядеть на фрагмент образа вблизи центра мельницы. Для этого надо его увеличить: то, что казалось “грязью” после увеличения
может выглядеть очень красиво. Порой и серединные участки образа заслуживают внимания, хотя сразу это и не видно: после
увеличения, то, что раньше казалось хаосом приобретает структуру, обнаруживается орнамент. Места сгущения окружностей создают
повторяющийся (хотя и немного меняющийся с каждым шагом) элемент этого орнамента.

2. Подбор параметров мельницы. Регулируя скорости лопастей мы регулируем скорость закручивания спирали. Увеличивая скорость
крутящей лопасти мы увеличиваем число витков спирали, увеличивая скорость стягивающей лопасти мы уменьшаем число витков. Чем
больше скорости лопастей, тем менее тщательно прорисовываются спирали. Если окружности крутящей лопасти имеют
конечный порядок – образ может иметь симметрию: тройную, четверную и т.п.

3. Если мы построим образ на двухлопостной мельнице, а потом дадим обратный ход только одной лопасти, то взаимодействие
двух получающихся спиралей создает неожиданные эффекты. Совокупно они напоминают серде, повторяющееся раз от раза.

4. Компановка. Выбрав какой-то интересный фрагмент образа, мы можем создать его копию (второй экземпляр). Если второй экземпляр
отразить симметрично по вертикали и горизонтали и удачно совместить с первым можно получить интересный орнамент или фигуру.
Неожиданно среди таких фигур могут оказаться зооморфные.

---

Мы исследовали движение окружностей под действием композиции симметрий относительно двух данных, заинтересовшись
разнообразыми эстетическими эффектами. Но изучение этого преобразования важно не только для эстетики, у него много и других
приложений. Например, оно позволяет моделировать движение планет.
Когда мы используем геометрию окружности в других разделах: эстетике, математике, физике – нам снова надо отличать прямую
от окружности, интересоваться центром окружности, возвращать понятия, ранее изгнанные. Чтобы промоделировать движение планет
с помощью геометрии окружности надо вспомнить про центр окружности.
Пусть окружность А преобразуется под действием лопасти, состоящей из окружностей S и T, такт лопасти – работа преобразования h=T*S.
Рассмотрим появляющийся ряд окружностей: A, h(A), h(h(A)), h(h(h(A)))… и так далее. Что можно сказать о центрах
этих окружностей? Оказывается, все они лежат или на эллипсе, или на параболе, или на гиперболе, или на прямой. Будем внимательны:
под действием h центр А не перейдет в центр h(A). Но у всех этих окружностей есть центр и именно его расположение
нас сейчас интересует. Чтобы доказать это свойство центров окружностей, надо рассмотреть окружности L и M, касающиеся A и
перпендикулярные S и T. Они будут огибающими всего ряда полученных окружностей. Пользуясь L и M нетрудно найти и фокусы.
Подробно это продемонстрировано во флеш-программах DodecaTeach. Таким образом, однолопастная мельница моделирует движение планет.
Можно сделать и большее: промоделировать с помощью геометрии окружности движение планеты со спутником вокруг Солнца.
И тут уже возникнет связь эстетики и движения небесных тел.

Другая связь однолопастной мельницы с физикой – электромагнетизм. Мы уже указывали на это: пучок и двойственный ему пучок иллюстрируют
линии тока и силовые линии магнитного поля. Но, как и было сказано: электромагнитное поле связано с трехмерным пространством, а все
наши преобразования происходят на плоскости. В следующем разделе коротко рассказывается о трехмерной эстетической геометрии.

---

Преобразование сфер.

В трехмерном пространстве также можно установить гармоническую мельницу. Что будет ее лопастью? Две пары расположенных
недалеко друг от друга сфер. Обозначим их S и T. Один такт работы лопасти состоит в применении преобразования h=T*S где T и S – симметрии
относительно одноименных сфер. Свойства трехмерной однолопастной мельницы очень похожи на свойства плоской
однолопастной мельницы: лопасть может быть крутящей (если сферы S и T пересекаются), стягивающей (если S и T не имеют общих точек)
или касающейся (если S и T касаются). Точки под действием лопасти движутся по окружностям (или их дугам). Эти окружности перпендикулярны
исходным сферам S и T, а проводятся они также, как и в двумерном случае: окружность перпендикулярная S и T и проходящая через точку x
проходит через x, S(x) и T(x). Обозначим эту окружность W. Стягивающая трехмерная лопасть стягивает все пространство к одной точке
p и вытягивает пространство из некоей точки q. Траектории точек лежат на всех окружностях, проходящих через p и q. Касающаяся
лопасть, как и в плоском случае, все стягивает и все вытягивает из одной точки: точки касания сфер S и T. Траектории движения точек
в этом случае – не все окружности проходящие через точку касания, а только перпендикулярные S и T. Все они касаются прямой, проходящей
через центры S и T. Точнее, как и в прошлом случае – точка двигается по дуге такой окружности
Если лопасть крутящая, то X кружится по всей окружности W, причем движение может и зациклиться. Если h имеет конечный порядок N,
то на энном такте точка Х вернется на свое место и далее с каждым тактом лопасти Х перемещается по своим собственным следам. Какие точки
неподвижны в этом случае? Точки, лежащие на окружности пересечения S и T. Траектории движения точек под действием крутящей лопасти
окружности, обвивающие окружность пересечения S и T (в плоском случае вместо окружности пересечения сфер была пара точек пересечения окружностей).
Картины рассмотренных траекторий удивительным образом совпадает с картиной силовых линий электромагнитного поля.

Что можно сказать о движении сферы X под действием лопасти, состоящей из S и T? Во многих случаях помогает тот же прием, что и в
плоском случае: надо провести окружность W, перпендикулярную сферам S, T, X. W остается на своем месте при каждом такте лопасти,
h(W)=W, поэтому на каждом такте лопасти образ X будет перпендикулярен W. Представим себе совокупность окружностей, перпендикулярных
S и T и перескающих X. Именно по таким окружностям двигаются точки лежащие на X, поэтому Х всегда лежит внутри области пространства,
заштрихованной этими окружностями. В случае крутящей лопасти эта область напоминает бублик или тор. В плоском случае разобраться с
движением окружности нам помогли окружности L и M касающиеся ее и перпендикулярные окружностям плоской лопасти. Похожий прием помогает
и при изучении движения сферы. Теперь возникают изменения и новые закономерности. Обычно существует 4 сферы, касающиеся данной сферы
Х и перпендикулярные сферам лопасти S и T. Причем эти сферы симметричны друг другу относительно окружности W – сравните с плоским
случаем, когда L и M также симметричны относительно W. Область пространства, ограниченная этими сферами и заполняется образами
Х при работе лопасти, на любом такте работы лопасти образ Х касается этих четырех огибающих, сферических стенок.
Более подробное изучение свойств однолопастной мельницы связано с развитием теории пучков сфер (и окружностей) в пространстве. Мы
не будем этого делать, тем более что эстетические свойства образов сделанных однолопастной мельницей в пространстве
вряд ли кардинально отличаются от свойств плоской однолопастной мельницы.
Перейдем к возведению двухлопастной пространственной
мельницы.

Как мы возводим плоскую двухлопастную гармоническую мельницу? Мы выбираем две пересекающиеся окружности S и T и называем их крутящей
лопастью. Затем мы проводим две окружности L и M, перпендикулярные S и T. L и M не имеют общих точек и поэтому образуют стягивающую
лопасть. Тактом лопасти мы называем действие преобразования h=T*S*M*L=(T*S)*(M*L). Точно также мы поступаем при возведении трехмерной
двухлопастной гармонической мельницы. Вместо окружностей – мы проводим сферы. При этом появляется одна существеннейшая разница:
окружности M и L не могли пересекаться между собой. А сферы M и L, перпендикулярные пересекающимся сферам S и T – могут пересекаться,
а могут и не пересекаться. Таким образом,
трехмерная двухлопастная гармоническая мельница может состоять из двух крутящих лопастей.
В плоском случае такое невозможно – если одна лопасть мельницы крутящая, то вторая – обязательно стягивающая. Также трехмерная
двухлопастная гармоническая мельница может состоять из крутящей и стягивающей лопасти, как это бывает и в плоском случае.
Двухлопастную гармоническую мельницу из двух крутящих лопастей назовем римановой мельницей, преобразование
h=T*S*M*L=(T*S)*(M*L) назовем римановым преобразованием, а мельницу, состоящую
из крутящей и стягивающей лопасти – мельницей Лобачевского, преобразование h=T*S*M*L=(T*S)*(M*L) –
преобразованием Лобачевского.
С чем связаны такие названия? Вспомним определение риманова
трехокружника: третья окружность разделяет точки пересечения двух других. Четыре сферы будут римановыми,
если четвертая сфера разделяет пару точек пересечения трех других. Рассмотрим четыре сферы,
входящие в двухлопастную мельницу: T, S, M, L. Если обе лопасти крутящие, то эти четыре сферы обязательно римановы: любая сфера
разделяет точки пересечения трех других. Интересно отметить и расположение окружностей пересечения в этом случае: окружность
пересечения S и T зацепляет (проходит сквозь, как звено в цепочке) окружность пересечения M и L.
Если же в мельнице одна лопасть из S и T крутящая, а вторая стягивающая – то сферы L и M не имеют общих точек, и
разумеется точки пересечения S, T, L лежат по одну сторону от M. Есть и другие интересные причины называть эти типы
трехмерных двухлопастных гармонических мельниц именно так. Но о них нет места говорить.

Познакомимся с типами объемных фигур, которые ообразует трехмерная двухлопастная гармоническая мельница. Начнем со случая
римановой мельницы.

---

Риманово преобразование.

Пусть у нас обе лопасти трехмерной мельницы – крутящие. В этом случае преобразование h=T*S*M*L риманово и впервые мы
сталкиваемся с ситуацией, когда у преобразования гармонической мельницы – нет неподвижных точек. Нет
и точек втягивания или вытягивания, впрочем, это следует из отсутствия неподвижных точек. Работа мельницы создает
образ, элементы которого X, h(X), h(h(X)), h(h(h(X)))… и так далее, где Х – исходный движимый объект. Если Х – точка, то
все получаемые в ходе работы мельницы точки лежат на некоей кривой (траектории), а все пространство
расслаивается на такие, непересекающиеся кривые (траектории). Такты работы обеих крутящих лопастей можно выбрать так,что
каждая траектория – замкнется. Сделаем это, и посмотрим, что происходит, если исходная преобразуемый объект X – не точка, а сфера.

В этом примере есть 10 кратная симметрия. А ниже мы немного изменяем такты работы крутящих лопастей.

В результате траектория сохранила десятикратную симметрию, заузлилась и стала звездообразной. Обратите внимание – вся фигура
делается “одним росчерком” – замкнутой непрерывной линией.
Свойствами этого “звездовидного узла” можно управлять, настраивая такты одной и второй крутящей лопасти. Именно: можно указать
параметр, фиксирующей число вершин (в данном случае их десять) и параметр, фиксирующий порядок обхода этих вершин. На первой картинке
от одной вершины кривая переходила к следующей, на второй – от вершины кривая переходит к третьей вершине (если считать вершины по
часовой стрелке).

Обратите внимание – в плоском случае гармоническая мельница могла создать только один тип замкнутых фигур (траекторий) – ожерелья,
с бусинами плавно меняющимися в размерах. В объемном случае типов фигур очень много, ожерелье превращается в “звездовидные узлы”,
простейший из которых – трилистник. А сферы-бусины также плавно меняют размер. Но траектория движения не обязательно замыкается,
создаваемое римановой мельницей может лежать на некоей торовидной поверхности. И если один такт мельницы
(риманово преобразование h) не сильно преобразует объект (X и h(X) близки друг к другу) то возникающий образ постепенно и создает
эту поверхность. На нижнем рисунке мы и видим тот момент, когда торовидная поверхность создана примерно наполовину.

Порядок обхода и формирование поверхности бывает весьма оригинален. Нижний рисунок напоминает ухо, сделанное
из ленты Мебиуса, причем возникает подозрение, что это “ухо” доформируется до “Бутылки Клейна”.

Во всех примерах соседние элементы образа (X и h(X)) пересекались. Можно увеличить скорость работы обеих крутящих лопастей
мельницы, тогда X и h(X) уже не будут пересекаться. Этого же можно достичь и уменьшив сферу X. Это создает новые
эстетические и и геометрические эффекты. Эстетическое и архитектурное значение имеет и случай, когда преобразуется не сфера X, а,
например: куб Х, тетраэдр Х. Трехмерная гармоническая мельница порой предлагает готовые архитектурные проекты. А проекции узлов,
созданных на мельнице Римана дают интереснейшие плоские орнаменты.

---

Преобразование Лобачевского.

Мельница Лобачевского состоит из двух лопастей: крутящей и стягивающей. Крутящая лопасть кружит, но как бы быстро она не кружила,
стягивающая лопасть, состоящая из двух сфер L и M не имеющих общих точек, все стянет в одну точку.
Какую? Это будет центр пучка, в котором лежат сферы L и M. У пучка два центра, найти их приближенно очень просто. Отразим L
относительно M, а M – относительно L. получим две новые сферы. Отразим полученные сферы друг относительно друга. Получим
две новые сферы. Еще раз отразим. И так далее. Очень быстро получаемые сферы будут мало отличаться от точек. Обе предельные точки,
к которым сходится описанный процесс симметрий-отражений и будут центрами пучка, в котором лежат L и M. Аналогично, разумеется,
можно поступать и в случае, когда L и M – окружности на плоскости. Заметим, что описанный процесс стягивается к точкам значительно
быстрее чем последовательность M, L(M), M(L(M)), L(M(L(M)… и так далее: сейчас мы
отражаем сферу (или окружность) M относительно L, полученное
относительно M, затем относительно L… Можно найти центры пучка в коотором лежат две сферы и совершенно точно.
Достаточно провести две какие-нибудь окружности, обозачим их А и В, перпендикулярные M и L. Они обе обязательно проходят через оба
центра пучка. Сейчас мы это докажем. Вернемся к какой-нибудь из построенных ранее последовательности сфер, стягивающихся к искомым
центрам пучка. Каждая сфера этой последовательности перпендикулярна окружностям А и В (т.к. они перпендикулярны исходным сферам L
и M), а перпендикулярные друг друг окружность и сфера обязательно пересекаются, поэтому все сферы последовательности
пересекаются с окружностями А и B. Следовательно окружности
А и В обязательно проходят через центры пучка (в противном случае они бы не пересекались с очень маленькой сферой последовательности,
неотличимой почти
от центра пучка). Что и требовалось доказать. Обозначим центры пучка p и q.

Как и плоская двухлопастная мельница, трехмерная двухлопастная мельница Лобачевского вытягивает точки из одного центра пучка
и втягивает их в другой центр. При этом точки двигаются по спирали, и управлять развитием спирали можно меняя такты крутящей
и стягивающей лопастей мельницы. Для создания целостного образа надо использовать и прямой и обратный ход мельницы. В этом случае
могут получиться “рога”,подобные изображеным слева. Если такт мельницы преобразует сферу немного, то возникающий образ может
прорисовывать некую поверхность, во многих случаях напоминающую простую раковину, наподобие рисунка справа.

Возможен случай, когда точки p и q совпадает. Все пространство под действием такой мельницы (Это уже не будет мельница Лобачевского,
ее вторая лопасть будет не стягивающей, а касающейся) – втягивается и вытягивается из одной и той же точки по спиралевидной траектории.

Мы исследовали плоскую двухлопастную мельницу и очень бегло познакомились с объемной. Все образы получаются последовательным
применением одного и того же преобразования h к какому-то объекту. Чтобы убедиться, что мы не пропутили ничего важного,
надо исследовать преобразования, которые можно получить композицией симметрий относительно окружностей (сфер).
Можно доказать, что любая композиция симметрий относительно пяти окружностей на плоскости равна композиции симметрий относительно
каких-то трех окружностей. Следовательно, композиция симметрий относительно шести окружностей равна композиции симметрий
относительно четырех каких-то окружностей. В двухлопастной мельнице участвует именно 4 окружности и поэтому ничего важного мы
не пропускаем.

В объемном случае любая композиция симметрий относительно сфер равна композиции симметрий относительно не более чем пяти сфер.
А в двухлопастной мельнице участвует всего четыре сферы. Тем не менее, для изучения геометрии образов композиции относительно
четырех сфер оказывется достаточно. Но вполне возможно, что для изучения приложений: в архитектуре, биологии, физике – существенно
рассмотреть особенности, связанные с добавлением пятой сферы. Здесь нет места обсуждать это подробней.

---

Три взаимоперпендикулярных окружности, биплетная симметрия и гармоническое отношение.

На плоскости композиция симметрий относительно двух перпендикулярных прямых есть симметрия относительно точки их пересечения.
В пространстве перпендикулярных объектов больше. Композиция
симметрий относительно двух перпендикулярных плоскостей – симметрия относительно прямой, по которой эти плоскости пересекаются.
Композиция симметрий относительно трех взаимоперпендикулярных плоскостей – симметрия относительно точки их пересечения. Композиция
симметрий относительно плоскости и перпендикулярной ей прямой – симметрия относительно точки их пересечения. Композиция симметрий
относительно двух перпендикулярных прямых – симметрия относительно третьей прямой, перпендикулярной им обеим и проходящей через точку
их пересечения. Мы видим, что композиция симметрий относительно перпендикулярных друг другу объектов – снова симметрия.
Относительно чего? Относительно чего-то лежащего в обоих перпендикулярных объектах или относительно чего-то перпендикулярного
им обоим. Тут есть странная связь между соотношением “лежать на” и “быть перпендикулярным”. Обобщение понятия перпендикулярности,
как мы видели – коммутативность симметрий. Посмотрим на простое уравнение A*B=B*A. Пусть мы находимся на обычной евклидовой плоскости.
А – некоторая прямая. Тогда симметрии А и В коммутируют в двух случаях.
Если В – симметрия относительно прямой, перпендикулярной А или если B – симметрия относительно точки
лежащей на A. Чему в последнем случае равно А*В?

Биплетная симметрия и гармоническое отношение.

Попробуем перенести эти идеи в геометрию окружностей. Первый возникающий вопрос: что можно сказать о композиции симметрий,
относительно двух перпендикулярных окружностей S и T? Пусть h=S*T. Легко видеть, что h*h=e т.к. S*T=T*S. Или h(h(x))=x. Поэтому
h может быть симметрией. По самой сути своей симметрия – инволютивное преобразование: если x симметрично y (h(x)=y), то у
симметрично x (h(y)=x). Но симметрия относительно чего, что остается неподвижным при преобразовании h? Неподвижны остаются точки
пересечения S и T: p и q. h(p)=S(T(p))=S(p)=p тоже и про q. На рисунке ниже мы видим последовательное действие на зеленые точки
симметрии T, а затем – симметрии S. Малиновая стрелка и изображает симметрию h. Кстати, заметим, что окружность, проходящая через
x, y=T(x), p – касается S, а окружность, проходящая через y=T(x), z=S(T(y)), p – касается T.
Назовем отображение h – биплетной симметрией и будем изучать свойства этой новой симметрии. В начале сравним ее с симметрией
относительно точки.

Докажем, что какова бы ни была окружность A, проходящая через точки пересечения S и T, h(A)=A. Рассмотрим окружности A и S(A).
Очевидно, S – биссектриса между ними. Мы знаем, что у двух пересекающихся окружностей есть ровно две биссектрисы и они перпендикулярны
друг другу. Одна биссектриса, S – нам известна. Вторая – окружность, перпендикулярная S и проходящая через p и q. Такая окружность
только одна – окружность T. Следовательно T – также биссектриса между А и S(A), поэтому T(S(A)=A. Но T*S=S*T=h, и h(A)=A, что
и требовалось доказать.

Теперь нетрудно для любой точки a построить h(a). Проведем через a, p, q окружность W. По доказанному h(W)=W, поэтому h(a) снова
лежит на W. С другой стороны h(a)=S(T(A)) и обязательно лежит на окружности V мнимого пучка с центрами p и q (V
перпендикулярна S и T одновременно). Строить окружность V, перпендикулярную двум данным мы умеем. Одна точка пересечения V и W – а,
вторая – h(a). Что и требовалось: зная точки p и q мы умеем научились находить точку h(a). Отметим, что наше построение зависит
только от точек p и q, т.к. окружности V и W однозначно строятся по этим точкам (W проходит через них и a, V меняет их местами
и проходит через a). Поэтому биплетная симметрия h зависит только от точек пересечения S и T, но не зависит от того, какие
именно перпендикулярные окружности в этих точках пересекаются. Аналогично и композиция симметрий относительно перпендикулярных прямых
зависит исключительно от точки их пересечения.

Удаляем лишнее. А на правом чертеже мы добавили еще точки с и k и нашли h(c) и h(k). Окружности, проходящие через p и q показаны
пунктиром, все они лежат в одном действительном пучке с центрами p и q. Окружности,
показанные непрерывной линией – лежат в двойственном ему мнимом
пучке также с центрами в p и q, эта пара точек симметричны друг другу относительно любой непрерывной окружности.

Попробуйте разобраться, какие биплеты, с концами в точках m, n, k, r перпендикулярны биплетам f, g, w.
А чему равна композиция биплетных симметрий относительно двух перпендикулярных биплетов? Легко видеть, что такая композиция снова
инволютивна, поэтому она может являться какой-то симметрией. Она – симметрия относительно биплета, перпендикулярного двум исходным.
На чертеже взаимоперпендикулярны биплеты f, g, w и имеют место три соотношения: f*g=w, g*w=f, w*f=g, которые можно выразить
одним тождеством f*g*w=e. Точно такие же соотношение связывают симметрии относительно трех взаимоперпендикулярных прямых.
Заметим: если два биплета f и g перпендикулярны, то их концы находятся в гармоническом отношении. Концы трех
взаимоперпендикулярных биплетов образуют великолепную шестерку точек, на которых можно построить четыре
взаимокасательные окружности или три взаимоперпендикулярные.

---

Три взаимоперпендикулярные окружности.

Типы симметрий между окружностями и взаимоотношения между ними ясно видны при рассмотрении трех взаимоперпендикулярных окружностей.

---

Окружность, перпендикулярная трем данным окружностям,
или симметрия, коммутирующая с тремя данными. Предельные свойства.

Мы искали окружность, перпендикулярную трем данным, в ч.2, когда изучали симметрию трехокружника и узнали, как построить окружность,
перпендикулярную всем трем взаимопересекающимся окружностям Лобачевского. Также было показано, что не существует окружности
перпендикулярной одновременно трех римановым окружностям A, B, C. Прежде всего укажем: окружности-то такой нет. Но симметрия,
коммутирующая с тремя римановыми окружностями всегда существует. Это симметрия, определенная римановым трехокружником A, B, C, меняющая
местами точки пересечения этих окружностей.
Итак, для любых трех взаимопересекающихся окружностей существует симметрия, коммутирующая со всеми ними (точнее говоря, коммутирующая
с симметриями относительно трех данных окружностей). Если эти три окружности Римановы, то это симметрия без неподвижных точек, а если
это окружности Лобачевского – это симметрия относительно окружности. А что происходит, если среди трех окружностей A, B, C есть
непересекающиеся?

На рисунках рассмотрены разные случаи расположения A, B, C и указываются методы построения окружности, перпендикулярной им всем.
Попутно доказано, что все шесть центров трех пучков, созданными окружностями А, B, C лежат на одной окружности. Мы не рассматривали
случай когда среди А, B, C есть касающиеся окружности, попробуйте сделать это самостоятельно. Итак, три непересекающиеся окружности
с этой точки зрения ведут себя как и окружности Лобачевского: существует одна и только одна окружность, перпендикулярная
им всем. Они и во многих других случаях ведут себя подобно трехокружнику Лобачевского, за одним исключением: у этого трехокружника
нет вершин. Но две окружности всегда создают пучок, благодаря этому можно определить высоту и многие другие понятие
взятые из геометрии треугольника. Например, высотой трехокружника, опущенную на сторону С, в случае, когда А и B не пересекаются, мы
называем окружность лежащую в том же пучке, что и окружности A и B и перпендикулярную C. Как мы построим такую высоту? Мы проведем
две какие-нибудь окружности, перпендикулярные A и B и проведем окружность, перпендикулярную новопроведенным и С. А вдруг С разделяет
центры пучка, в котором лежат A и B? В этом случае нет такой окружности. т.к. образовывается риманов трехокружник. Не беда – нет
окружности, но есть – симметрия без неподвижных точек, коммутирующая со всеми ними. Эта-то симметрия и будет называться высотой в таком
случае. Как мы указывали во “мнимом” пучке могут лежать не только окружности, но и симметрии без неподвижных точек.

Итак мы показали, что для любых трех окружностей существует симметрия, коммутирующая с симметриями относительно них. Если эти
три окружности Римановы – это симметрия без неподвижных точек, в противном случае – это симметрия относительно окружности, перпендикулярной
им всем. Попробуйте найти неточность в этом утверждении, какой случай расположения трех исходных окружностей A, B, C – не был рассмотрен.
Раз мы стали рассматривать симметрии без неподвижных точек равноправно с окружностями, то можно расширить вопрос: если нам даны
не три окружности, а три какие-то симметрии, всегда ли существует симметрия, коммутирующая со всеми ними. Ответ – да, существует,
и если три исходные симметрии не лежат в одном пучке, симметрия коммутирующая со всеми ними – единственна. Этот факт весьма важен,
для построения разнообразных моделей на основании геометрии окружности. Например, на его основе можно определить проективную
геометрию исходя из геометрии окружности. Но мы не будем в это вдаваться. Вместо этого мы укажем неточность в наших рассуждениях.
Если три исходные окружности евклидовы, то есть все пересекаются в одной точке, то ни окружности, перпендикулярной им всем, ни симметрии
коммутирующей с ними – нет. Она появится, только если мы будем считать точку “очень маленькой окружностью”. Так можно поступать,
но это разговор долгий и я не вполне к нему готов.

Рассмотрим теперь композицию преобразований h=A*B*C. Оказывается, некоторые свойства окружностей A, B, С можно установить
не глядя на них, а изучая преобразование h. Рассмотрим уравнение h(x)=x, где x означает какую-либо точку. Иными
словами: мы ищем неподвижные точки преобразования h. Оказывается, если уравнение h(x)=x не имеет решений, то окружности
A, B, C – римановы. Если у этого уравнения одно решение, то окружности A, B, C – евклидовы. В противном случае уравнение имеет два решения
и существует окружность, перпендикулярная им всем. Разумеется, возможны всякие исключительные случаи расположения A, В, С, например –
они все могут совпадать, тогда h=A*A*A=A и уравнение имеет бесчисленное количество решений: любая точка на А. Но исключения мы сейчас
не рассматриваем, они возможны если все три окружности лежат в одном пучке, а это простой и неинтересный случай.
Итак, мы многое можем сказать уже исходя из решений уравнения h(x). но как его решать? Для этого можно рассмотреть действие
преобразования h. То есть рассмотреть последовательность точек q, h(q), h(h(q))… Его предельные точки и дадут решение.
А предельные точки действия обратного к h преобразования дадут второе решение. Не удивительно, что эти решения лежат на окружности,
перпендикулярной A, B и C. Отсюда возникает приближенный способ построения этой окружности: как найти приближенно найти две точки
мы показали, а как найти третью? Рассмотреть преобразование g=B*A*C и предельные точки его действия. Через три полученные точки
мы проведем окружность, и она будет лежать очень близко к окружности, перпендикулярной А, B, C.
Но еще интересней другое. Мы можем начать инвертировать окружности А, В, С друг в друга. Т.е. получать окружности: А(В), В(A), C(B),
A(C), C(A), B(C), A(B(C), C(A(B), C(A(B(A(C)… и так далее, всеми мыслимыми способами. Заметим. что все получающиеся окружности –
перпендикулярны окружности, перпендикулярной А, В, С. Почему? Это следует из замечания о подгруппах в пред. разделе.
Довольно быстро окружности будут становиться очень малыми (особенно если исходные окружности не пересекаются). И вот эти маленькие
окружности будут прижиматься или “налепляться” на окружность перпендикулярную А, В, С.
Если мы будем следить за происходящим “размножением
окружностей” на дисплее, то область вблизи этой окружности будет ярче, плотней зарисованней. Это верно и для случая, когда
среди исходных окружностей А, В, С – есть пересекающиеся.


Начав рассматривать подобное размножение окружностей мы вступили в область фрактальной геометрии.

---

Фракталы

Мост.

Фрактал возникает постепенно. Как картинка в калейдоскопе: он возникает из отражений самого себя в своих частях.
Фрактал “Мост” возникает всего из четырех окружностей A, B, C, D, показанных на первом рисунке. Мы строим их отражения
друг в друга, т.е. окружности А(B), B(A), C(B) и так далее. На рисунках показаны последовательные этапы. Мы видим, как постепенно
прорисовывается одна “опора” моста, затем другая, и, наконец – третья тянется им навстречу. “Опоры” возникают из мест сгущения
окружностей: точек к которым они в ходе симметрий стягиваются и из точек, около которых пересекается много окружностей.

Можно описывать возникающий фрактал в терминах теории групп. Образующими “группы фрактала МОСТ” будут четыре
исходные окружности A, B, C, D, элементами группы – все преобразования, которые можно получить с помощью композиции симметрий
относительно образующих. На рисунках мы видим не все элементы группы. Скажем элемент A*B – преобразование, которое не рисуется,
а вот элемент A*B*A=A(B) – есть симметрия относительно окружности и эта окружность нарисована, является частью фрактала.
Каждый элемент “группы фрактала” выражается последовательностью четырех букв (при этом две одинаковые буквы не должны стоять рядом),
а рисуются только такие элементы, которые одинаково читаются слева направо и справа налево.

---

Петляющая линия.

А здесь мы строим фрактал, стартуя с шести красных и синих кругов. Они отражаются друг в друга. С каждым шагом круги становятся все
меньше, при этом если красный круг отражается в красный – ничего видимым образом не меняется. Или если синий – в синий. Рисунок
уточняется с каждым шагом, просматривается петляющая линия, которая образуется из все уменьшающихся разноцветных кругов. Но эту
линию заслоняют большие круги.

---

Синее дерево, растующее во все стороны.

Часть предыдущего фрактала. Синий круг, “размножаясь” проростает в корнями (или ветвится) в три красных круга. С последующими итерациями
рисунок мало меняется, система корней-ветвей становится все детальней, но на глаз это не видно – уточнения слишком мелки.

---

Возникновение витража.

Если исходные окружности пересекаются между собой, то растущий из них фрактал постепенно заполняет всю плоскость. Это
происходит уже и с фракталом “Мост”, но не так быстро, как здесь. Обратите внимание: исходные 12 окружностей расположены
не случайным, а симметричным образом. И все симметрии, которые есть на первом рисунке присущи и образам-фракталам, возникающим на следующих
итерациях.

---

Черное на белом или белое на черном?

За этим фракталом мы следим не с самого начала, не с первого шага итерации, а с середины. В начале мы видим
черный рисунок из множества окружностей на белом фоне. Разрастаясь и уточняя детали черные окружности заполняют плоскость.
на последнем рисунке мы видим уже белое на черном фоне. Если дать фракталу разрастаться далее, он просто заштрихует весь экран.

Примеры демонстрируют возникновение фракталов из геометрии окружности. Изучение
точек и линий сгущения, симметрий, связанных с ними, их “площадей” и “длин” лежит на стыке многих математических дисциплин, об этом
много литературы, на мой взгляд: геометрия окружности – царский путь во фрактальную геомерию.

---

Построение венка.

Есть и другой, может быть более простой способ строить фракталы на основе геометрии окружности. Для его объяснения
даже не нужно говорить о симметрии между окружностями. Мы впервые его коснулись в “медитации о фрактале” из части 1. Здесь
с помощью скриншотов программы DodecaTeach рассказывается как сплести огромный ДДУ-венок. Все построения несложно
выполнить в графических редакторах. Можно начать с CorelDraw, а продолжить в Photoshop.

Конец.

Симметричные окружности

Как найти уравнение окружности, симметричной данной?

Симметричные окружности имеют равные радиусы. Следовательно, остаётся найти координаты центра симметричной окружности (как точки, симметричной данной).

1) Окружность задана уравнением (x-3)²+(y+2)²=16. Составить уравнение окружности, симметричной данной относительно точки (7; 10).

Центр окружности (x-3)²+(y+2)²=16 — точка с координатами (3;-2). Найдём точку, симметричную ей относительно точки (7; 10).

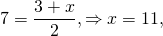
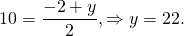
Таким образом, центр окружности, симметричной данной, — точка с координатами (11;22). Подставляем в формулу уравнения окружности a=11, b=22, R²=16:

2) Окружность задана уравнением (x+5)²+(y+1)²=9. Составить уравнение окружности, симметричной данной относительно начала координат.

Центром данной окружности является точка (-5;-1). Точка, симметричная данной относительно начала координат — (5;1). Таким образом, для окружности, симметричной данной относительно точки O(0;0) a=5, b=1, R²=9:

3) Окружность задана уравнением (x-7)²+(y-2)²=12. Составить уравнение окружности, симметричной данной относительно прямой y=x.

Центр окружности (x-7)²+(y-2)²=12 — точка (7;2) — при симметрии относительно прямой y=x переходит в точку (2;7). Следовательно, a=2, b=7, R²=12 и искомое уравнение окружности:

4) Окружность задана уравнением (x+4)²+(y-5)²=19. Составить уравнение окружности, симметричной данной относительно прямой y=2x+4.

Центр окружности (x+4)²+(y-5)²=19 — точка (-4;5). Точку, симметричную точке (-4;5) относительно прямой y=2x+4, нашли в прошлый раз — (3,2; 1,4). Таким образом, a=3,2, b=1,4, R²=19 и уравнение симметричной окружности

5) Окружность задана уравнением (x+8)²+(y+3)²=4. Составить уравнение окружности, симметричной данной относительно прямой y= -1.

Центр окружности (x+8)²+(y+3)²=4 — (-8; -3). Точка, симметричная точке (-8; -3) относительно прямой y= -1, имеет такую же абсциссу, x= -8. Расстояние от точки (-8; -3) до прямой y= -1 равно -1-(-3)=2. Расстояние от прямой y= -1 до центра симметричной окружности также равно 2, отсюда -1+2=1 — это ордината центра. Таким образом, точка (-8; 1) — центр окружности, симметричной данной, а R²=4.

Следовательно, искомое уравнение окружности

Составьте уравнение окружности, симметричной окружности (х — 10)2 + (у + 8)2 = 49 относительно точки (-1; 5).

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,292
• гуманитарные 33,622
• юридические 17,900
• школьный раздел 607,160
• разное 16,830

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Найти уравнение окружности симметричной с окружностью

Симметричные окружности

Как найти уравнение окружности, симметричной данной?

Симметричные окружности имеют равные радиусы. Следовательно, остаётся найти координаты центра симметричной окружности (как точки, симметричной данной).

1) Окружность задана уравнением (x-3)²+(y+2)²=16. Составить уравнение окружности, симметричной данной относительно точки (7; 10).

Центр окружности (x-3)²+(y+2)²=16 — точка с координатами (3;-2). Найдём точку, симметричную ей относительно точки (7; 10).

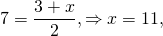
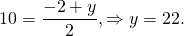
Таким образом, центр окружности, симметричной данной, — точка с координатами (11;22). Подставляем в формулу уравнения окружности a=11, b=22, R²=16:

2) Окружность задана уравнением (x+5)²+(y+1)²=9. Составить уравнение окружности, симметричной данной относительно начала координат.

Центром данной окружности является точка (-5;-1). Точка, симметричная данной относительно начала координат — (5;1). Таким образом, для окружности, симметричной данной относительно точки O(0;0) a=5, b=1, R²=9:

3) Окружность задана уравнением (x-7)²+(y-2)²=12. Составить уравнение окружности, симметричной данной относительно прямой y=x.

Центр окружности (x-7)²+(y-2)²=12 — точка (7;2) — при симметрии относительно прямой y=x переходит в точку (2;7). Следовательно, a=2, b=7, R²=12 и искомое уравнение окружности:

4) Окружность задана уравнением (x+4)²+(y-5)²=19. Составить уравнение окружности, симметричной данной относительно прямой y=2x+4.

Центр окружности (x+4)²+(y-5)²=19 — точка (-4;5). Точку, симметричную точке (-4;5) относительно прямой y=2x+4, нашли в прошлый раз — (3,2; 1,4). Таким образом, a=3,2, b=1,4, R²=19 и уравнение симметричной окружности

5) Окружность задана уравнением (x+8)²+(y+3)²=4. Составить уравнение окружности, симметричной данной относительно прямой y= -1.

Центр окружности (x+8)²+(y+3)²=4 — (-8; -3). Точка, симметричная точке (-8; -3) относительно прямой y= -1, имеет такую же абсциссу, x= -8. Расстояние от точки (-8; -3) до прямой y= -1 равно -1-(-3)=2. Расстояние от прямой y= -1 до центра симметричной окружности также равно 2, отсюда -1+2=1 — это ордината центра. Таким образом, точка (-8; 1) — центр окружности, симметричной данной, а R²=4.

Следовательно, искомое уравнение окружности

Уравнение с двумя переменными и его график. Уравнение окружности

п.1. Понятие уравнения с двумя переменными

Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm ) – гипербола.

Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.

Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm ) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график — ниже).

п.2. Обобщенные правила преобразования графика уравнения

Пусть F(x; y) = 0 – исходный график некоторой функции

Симметричное отображение относительно оси OY

Симметричное отображение относительно оси OX

Центральная симметрия относительно начала координат

Параллельный перенос графика на a единиц вправо

Параллельный перенос графика на a единиц влево

Параллельный перенос графика на b единиц вниз

Параллельный перенос графика на b единиц вверх

Сжатие графика к оси OY в a раз

Сжатие графика к оси OX в b раз

F(x; by) = 0
0 Например:

Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm $$

п.4. Примеры

Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm =-frac + 2 > ) – это прямая

б) xy + 4 = 0
Выразим y из уравнения: ( mathrm > ) – это гипербола

в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm =2> )

г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm > ) – это парабола

Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm =-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.

б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.

в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.

г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).

д) (mathrm +2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.

Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.

Уравнения прямых и кривых на плоскости с примерами решения

Содержание:

Уравнения прямых и кривых на плоскости

Уравнения кривых в большом количестве встречаются при чтении экономической литературы. Укажем некоторые из этих кривых.

Кривая безразличия — кривая, показывающая различные комбинации двух продуктов, имеющих одинаковое потребительское значение, или полезность, для потребителя.

Кривая потребительского бюджета — кривая, показывающая различные комбинации количеств двух товаров, которые потребитель может купить при данном уровне его денежного дохода.

Кривая производственных возможностей — кривая, показывающая различные комбинации двух товаров или услуг, которые могут быть произведены в условиях полной занятости и полного объема производства в экономике с постоянными запасами ресурсов и неизменной технологией.

Кривая инвестиционного спроса — кривая, показывающая динамику процентной ставки и объем инвестиций при разных процентных ставках.

Кривая Филлипса — кривая, показывающая существование устойчивой связи между уровнем безработицы и уровнем инфляции.

Кривая Лаффера — кривая, показывающая связь между ставками налогов и налоговыми поступлениями, выявляющая такую налоговую ставку, при которой налоговые поступления достигают максимума.

Уже простое перечисление терминов показывает, как важно для экономистов умение строить графики и анализировать уравнения кривых, каковыми являются прямые линии и кривые второго порядка — окружность, эллипс, гипербола, парабола. Кроме того, при решении большого класса задач требуется выделить на плоскости область, ограниченную какими-либо кривыми, уравнения которых заданы. Чаще всего эти задачи формулируются так: найти наилучший план производства при заданных ресурсах. Задание ресурсов имеет обычно вид неравенств, уравнения которых даны. Поэтому приходится искать наибольшее или наименьшее значения, принимаемые некоторой функцией в области, заданной уравнениями системы неравенств.

В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению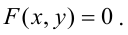

Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:

1. Общее уравнение прямой:

Вектор 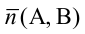ортогонален прямой, числа А и В одновременно не равны нулю.

2. Уравнение прямой с угловым коэффициентом:

где 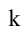— угловой коэффициент прямой, то есть 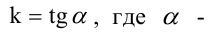величина угла, образованного прямой с осью 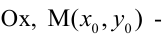некоторая точка, принадлежащая прямой.

Уравнение (2.2) принимает вид 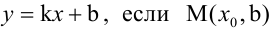есть точка пересечения прямой с осью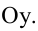

3. Уравнение прямой в отрезках:

где а и b — величины отрезков, отсекаемых прямой на осях координат.

4. Уравнение прямой, проходящей через две данные точки —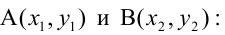

5. Уравнение прямой, проходящей через данную точку 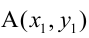параллельно данному вектору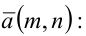

6. Нормальное уравнение прямой:

где 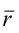— радиус-вектор произвольной точки 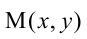этой прямой, 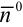— единичный вектор, ортогональный этой прямой и направленный от начала координат к прямой; 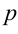— расстояние от начала координат до прямой.

Нормальное уравнение прямой в координатной форме имеет вид:

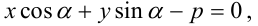где 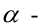величина угла, образованного прямой с осью Ох.

Уравнение пучка прямых с центром в точке 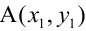имеет вид: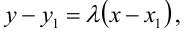

где 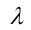— параметр пучка. Если пучок задается двумя пересекающимися прямыми 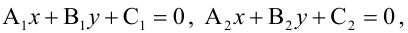то его уравнение имеет вид:

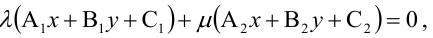где 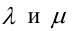— параметры пучка, не обращающиеся в 0 одновременно.

Величина угла между прямыми 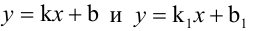задается формулой:

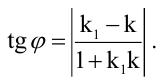
Равенство 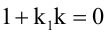есть необходимое и достаточное условие перпендикулярности прямых.

Для того, чтобы два уравнения

задавали одну и ту же прямую, необходимо и достаточно, чтобы их коэффициенты были пропорциональны:

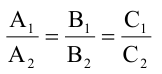
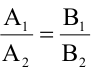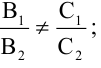Уравнения (2.7), (2.8) задают две различные параллельные прямые, если и прямые пересекаются, если 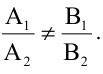Расстояние d от точки 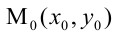до прямой есть длина перпендикуляра, проведенного из точки 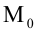к прямой. Если прямая задана нормальным уравнением, то 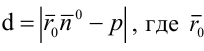— радиус-вектор точки или, в координатной форме,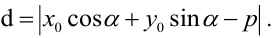

Общее уравнение кривой второго порядка имеет вид:

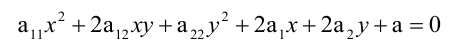
Предполагается, что среди коэффициентов уравнения 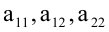есть отличные от нуля.

Уравнение окружности с центром в точке 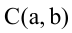и радиусом, равным R: Эллипсом называется геометрическое место точек, сумма расстояний которых от двух данных точек 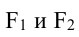(фокусов) есть величина постоянная, равная 2а. Каноническое (простейшее) уравнение эллипса:

Эллипс, заданный уравнением (2.10), симметричен относительно осей координат.

Параметры а и b называются полуосями эллипса.

Пусть 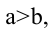тогда фокусы 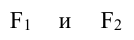и находятся на оси Ох на расстоянии 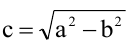от начала координат. Отношение 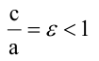называется эксцентриситетом эллипса.

Расстояния от точки 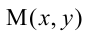эллипса до его фокусов (фокальные радиусы-векторы) определяются формулами:

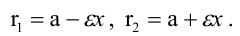
Если же 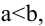то фокусы находятся на оси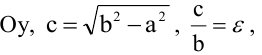

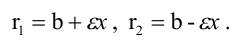
Если а=b, то эллипс является окружностью с центром в начале координат радиуса а.

Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек (фокусов) равна по абсолютной величине данному числу 2а.

Каноническое уравнение гиперболы:

Гипербола, заданная уравнением (2.11), симметрична относительно осей координат. Она пересекает ось 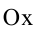в точках 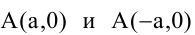— вершинах гиперболы и не пересекает ось 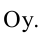Параметр а называется вещественной полуосью, b — мнимой полуосью. Параметр 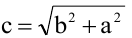есть, расстояние от фокуса до начала координат. Отношение 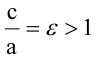называется эксцентриситетом гиперболы. Прямые, уравнения которых 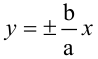называются асимптотами гиперболы.

Расстояния от точки 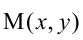гиперболы до ее фокусов (фокальные радиусы-векторы) определяются формулами: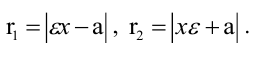

Гипербола, у которой а=b, называется равносторонней, ее уравнение 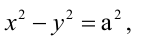а уравнение асимптот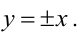

Гиперболы 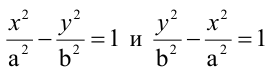называются сопряженными. Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы).

Каноническое уравнение параболы имеет два вида:

1. 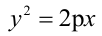— парабола симметрична относительно оси Ох. 2. 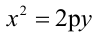— парабола симметрична относительно оси Оy. В обоих случаях 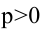и вершина параболы, то есть точка, лежащая на оси симметрии, находится в начале координат.

Парабола, уравнение которой 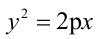имеет фокус 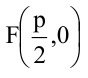и директрису 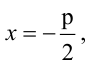фокальный радиус-вектор точки 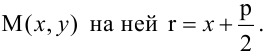Парабола, уравнение которой 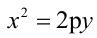имеет фокус 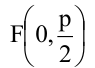и директрису 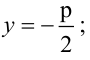фокальный радиус-вектор точки 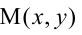параболы равен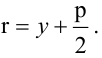

Уравнение 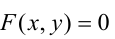задает линию, разбивающую плоскость на две или несколько частей. В одних из этих частей выполняется неравенство 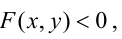а в других — неравенство 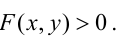Иными словами, линия 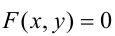отделяет часть плоскости, где 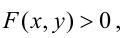от части плоскости, где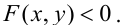

Прямая, уравнение которой 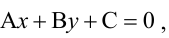разбивает плоскость на две полуплоскости. На практике для выяснения того, в какой полуплоскости мы имеем 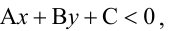а в какой 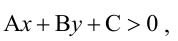применяют метод контрольных точек. Для этого берут контрольную точку (разумеется, не лежащую на прямой, уравнение которой 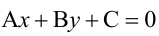) и проверяют, какой знак имеет в этой точке выражение 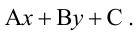Тот же знак имеет указанное выражение и во всей полуплоскости, где лежит контрольная точка. Во второй полуплоскости 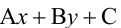имеет противоположный знак.

Точно так же решаются и нелинейные неравенства с двумя неизвестными.

Например, решим неравенство 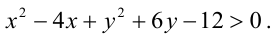Его можно переписать в виде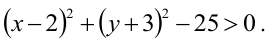

Уравнение 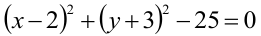задает окружность с центром в точке С(2,-3) и радиусом 5. Окружность разбивает плоскость на две части — внутреннюю и внешнюю. Чтобы узнать, в какой из них имеет место данное неравенство, возьмем контрольную точку во внутренней области, например, центр С(2,-3) нашей окружности. Подставляя координаты точки С в левую часть неравенства, получаем отрицательное число -25. Значит, и во всех точках, лежащих внутри окружности, выполняется неравенство 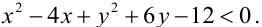Отсюда следует, что данное неравенство имеет место во внешней для окружности области.

Пример:

Составьте уравнения прямых, проходящих через точку А(3,1) и наклоненных к прямой 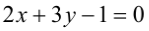под углом 45°.

Решение:

Будем искать уравнение прямой в виде 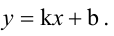Поскольку прямая проходит через точку А, то ее координаты удовлетворяют уравнению прямой, т.е.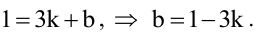

Величина угла между прямыми 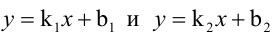определяется формулой 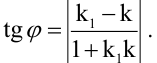Так как угловой коэффициент 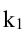исходной прямой 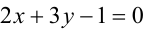равен 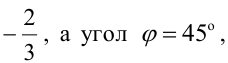то имеем уравнение для определения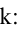

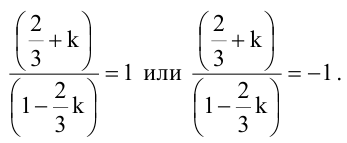
Имеем два значения 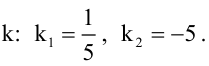Находя соответствующие значения b по формуле 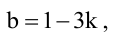получим две искомые прямые, уравнения которых: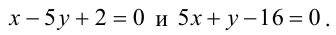

Пример:

При каком значении параметра t прямые, уравнения которых 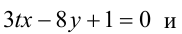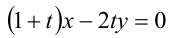параллельны ?

Решение:

Прямые, заданные общими уравнениями, параллельны, если коэффициенты при x и y пропорциональны, т.е. 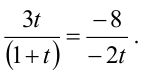Решая полученное уравнение, находим t:

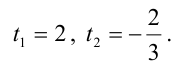
Пример:

Найти уравнение общей хорды двух окружносте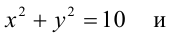й: и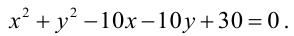

Решение:

Найдем точки пересечения окружностей, для этого решим систему уравнений: 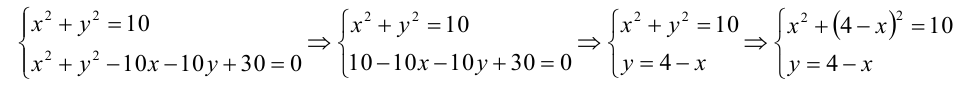Решая первое уравнение, находим значения 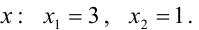Из второго уравнения -соответствующие значения 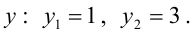Теперь получим уравнение общей хорды, зная две точки А(3,1) и В(1,3), принадлежащие этой прямой: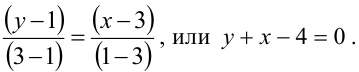

Пример:

Как расположены на плоскости точки, координаты которых удовлетворяют условиям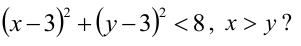

Решение:

Первое неравенство системы определяет внутренность круга, не включая границу, т.е. окружность с центром в точке (3,3) и радиуса 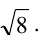Второе неравенство задает полуплоскость, определяемую прямой, уравнение которой х = у, причем, так как неравенство строгое, точки самой прямой не принадлежат полуплоскости, а все точки ниже этой прямой принадлежат полуплоскости. Поскольку мы ищем точки, удовлетворяющие обоим неравенствам, то искомая область — внутренность полукруга.

Пример:

Вычислить длину стороны квадрата, вписанного в эллипс, уравнение которого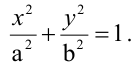

Решение:

Пусть 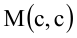— вершина квадрата, лежащая в первой четверти. Тогда сторона квадрата будет равна 2с. Т.к. точка М принадлежит эллипсу, ее координаты удовлетворяют уравнению эллипса 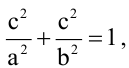откуда 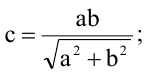значит, сторона квадрата —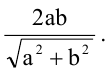

Пример:

Зная уравнение асимптот гиперболы 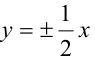и одну из ее точек 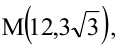составить уравнение гиперболы.

Решение:

Запишем каноническое уравнение гиперболы: 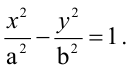Асимптоты гиперболы задаются уравнениями 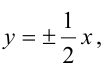значит, 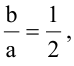откуда 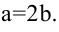Поскольку М — точка гиперболы, то ее координаты удовлетворяют уравнению гиперболы, т.е. 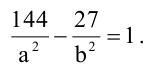Учитывая, что а=2b , найдем b: 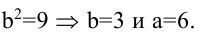Тогда уравнение гиперболы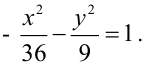

Пример:

Вычислить длину стороны правильного треугольника АВС, вписанного в параболу с параметром р, предполагая, что точка А совпадает с вершиной параболы.

Решение:

Каноническое уравнение параболы с параметром р имеет вид 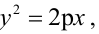вершина ее совпадает с началом координат, и парабола симметрична относительно оси абсцисс. Так как прямая АВ образует с осью Оx угол в 30°, то уравнение прямой имеет вид: 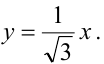Следовательно, мы можем найти координаты точки В, решая систему уравнений 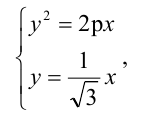откуда 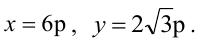Значит, расстояние между точками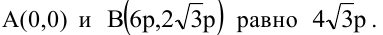

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Плоскость и прямая в пространстве
• Определитель матрицы
• Критерий совместности Кронекера-Капелли
• Формулы Крамера
• Производные тригонометрических функции
• Производная сложной функции
• Пределы в математике
• Функции многих переменных

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Задача

Найти уравнение окружности, симметричной с окружностью (x^2+y^2=2x+2y-4) относительно прямой (x-y-3=0).

Решение

Приведем уравнение данной окружности к каноническому виду ((x-1)^2+(y-2)^2=1); центр окружности находится в точке (C(1;2)) и ее радиус равен (1). Найдем координаты центра (C_1(x_1;y_1)) симметричной окружности, для чего через точку (C(1;2)) проведем прямую, перпендикулярную прямой (x-y-3=0); ее уравнение (y-2=k(x-1)), где (k=-1/1=-1), откуда (y-2=-x+1), или (x+y-3=0).
Решая совместно уравнения (x-y-3=0) и (x+y-3=0), получим (x=3), (y=0), т.е. проекция точки (C(1;2)) на данную прямую – точка (P(3;0)). Координаты же симметричной точки получим по формулам координат середины отрезка: (3=(1+x_1)/2),(0=(2+y_1)/2;); таким образом, (x_1=5, y_1=-2). Значит точка (C_1(5;-2)) – центр окружности, а уравнение окружности имеет вид ((x-5^2)+(y+2)^2=1).

---

2011-07-23 • Просмотров [ 7288 ]

UCHEES.RU – помощь студентам и школьникам

Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.

---

2020 – 2023 – UCHEES.RU