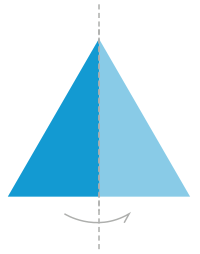
Равнобедренный треугольник с зеркальной симметрией. Пунктирная линия является осью симметрии

Рисунок бабочки с двусторонней симметрией
(др.-греч. συμμετρία = «соразмерность»; от συν- «совместно» + μετρέω «мерю»), в широком смысле — соответствие, неизменность (инвариантность), проявляемые при каких-либо изменениях, преобразованиях (например: положения, энергии, информации, другого). Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя центр на месте и если поверхность тела однородна). Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.
Симметрия — основополагающий принцип самоорганизации материальных форм в природе и формообразования в искусстве[1]. Отсутствие или нарушение симметрии называется асимметрией или диссимметрией[2].
Общие симметрийные свойства описываются с помощью теории групп.
Симметрии могут быть точными или приближёнными.
Симметрия в геометрии[править | править код]
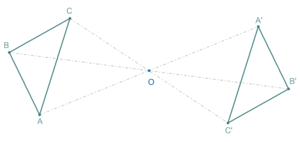
Два треугольника с точечной симметрией отражения в плоскости. Треугольник А’В’С может быть получен из треугольника ABC поворотом на 180 ° вокруг точки O.
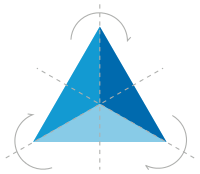
Геометрическая симметрия — это наиболее известный тип симметрии для многих людей. Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства. Например, круг, повёрнутый вокруг своего центра, будет иметь ту же форму и размер, что и исходный круг. Поэтому круг называется симметричным относительно вращения (имеет осевую симметрию).
Виды симметрий, возможных для геометрического объекта, зависят от множества доступных геометрических преобразований и того, какие свойства объекта должны оставаться неизменными после преобразования.
Виды геометрических симметрий:
- Зеркальная симметрия
- Осевая симметрия
- Вращательная симметрия
- Центральная симметрия
- Скользящая симметрия
- Винтовая симметрия
Зеркальная симметрия[править | править код]
Зеркальная симметрия или отражение— движение евклидова пространства, множество неподвижных точек которого является гиперплоскостью (в случае трехмерного пространства — просто плоскостью). Термин зеркальная симметрия употребляется также для описания соответствующего типа симметрии объекта, то есть, когда объект при операции отражения переходит в себя. Это математическое понятие в оптике описывает соотношение объектов и их (мнимых) изображений при отражении в плоском зеркале. Проявляется во многих законах природы (в кристаллографии, химии, физике, биологии и т. д., а также в искусстве и искусствоведении).
Осевая симметрия[править | править код]
Фигура называется симметричной относительно прямой А, если для каждой точки фигуры симметричная ей точка относительно прямой А также принадлежит этой фигуре.
Вращательная симметрия[править | править код]
Вращательная симметрия — термин, означающий симметрию объекта относительно всех или некоторых собственных вращений m-мерного евклидова пространства. Собственными вращениями называются разновидности изометрии, сохраняющие ориентацию. Таким образом, группа симметрии, отвечающая вращениям, есть подгруппа группы E+(m) (см. Евклидова группа).
Трансляционная симметрия может рассматриваться как частный случай вращательной — вращение вокруг бесконечно-удалённой точки. При таком обобщении группа вращательной симметрии совпадает с полной E+(m). Такого рода симметрия неприменима к конечным объектам, поскольку делает всё пространство однородным, однако она используется в формулировке физических закономерностей.
Совокупность собственных вращений вокруг фиксированной точки пространства образуют специальную ортогональную группу SO(m) — группу ортогональных матриц m×m с определителем, равным 1. Для частного случая m = 3 группа носит специальное название — группа вращений.
В физике инвариантность относительно группы вращений называется изотропностью пространства (все направления в пространстве равноправны) и выражается в инвариантности физических законов, в частности, уравнений движения, относительно вращений. Теорема Нётер связывает эту инвариантность с наличием сохраняющейся величины (интеграла движения) — углового момента.

Симметрия относительно точки[править | править код]
Центра́льной симме́трией (иногда центра́льной инве́рсией) относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через 

Скользящая симметрия[править | править код]
Скользящая симметрия — изометрия евклидовой плоскости.
Скользящей симметрией называют композицию симметрии относительно некоторой прямой 

Симметрии в физике[править | править код]
| Симметрия в физике | ||
|---|---|---|
| Преобразование | Соответствующая инвариантность |
Соответствующий закон сохранения |
| ↕ Трансляции времени | Однородность времени |
…энергии |
| ⊠ C, P, CP и T-симметрии | Изотропность времени |
…чётности |
| ↔ Трансляции пространства | Однородность пространства |
…импульса |
| ↺ Вращения пространства | Изотропность пространства |
…момента импульса |
| ⇆ Группа Лоренца (бусты) | Относительность Лоренц-ковариантность |
…движения центра масс |
| ~ Калибровочное преобразование | Калибровочная инвариантность | …заряда |
В теоретической физике поведение физической системы описывается некоторыми уравнениями. Если эти уравнения обладают какими-либо симметриями, то часто удаётся упростить их решение путём нахождения сохраняющихся величин (интегралов движения). Так, уже в классической механике формулируется теорема Нётер, которая каждому типу непрерывной симметрии сопоставляет сохраняющуюся величину. Из неё, например, следует, что инвариантность уравнений движения тела с течением времени приводит к закону сохранения энергии; инвариантность относительно сдвигов в пространстве — к закону сохранения импульса; инвариантность относительно вращений — к закону сохранения момента импульса.
Суперсимметрия[править | править код]
Суперсимме́трия или симме́трия Ферми́ — Бозе́ — гипотетическая симметрия, связывающая бозоны и фермионы в природе. Абстрактное преобразование суперсимметрии связывает бозонное и фермионное квантовые поля, так что они могут превращаться друг в друга. Образно можно сказать, что преобразование суперсимметрии может переводить вещество во взаимодействие (или в излучение), и наоборот.
По состоянию на начало 2009 года суперсимметрия является физической гипотезой, не подтверждённой экспериментально. Совершенно точно установлено, что наш мир не является суперсимметричным в смысле точной симметрии, так как в любой суперсимметричной модели фермионы и бозоны, связанные суперсимметричным преобразованием, должны обладать одинаковыми массой, зарядом и другими квантовыми числами (за исключением спина). Данное требование не выполняется для известных в природе частиц. Предполагается, тем не менее, что существует энергетический лимит, за пределами которого поля подчиняются суперсимметричным преобразованиям, а в рамках лимита — нет. В таком случае частицы-суперпартнёры обычных частиц оказываются очень тяжёлыми по сравнению с обычными частицами. Поиск суперпартнёров обычных частиц — одна из основных задач современной физики высоких энергий. Ожидается, что Большой адронный коллайдер[3] сможет открыть и исследовать суперсимметричные частицы, если они существуют, или поставить под большое сомнение суперсимметричные теории, если ничего не будет обнаружено.
Трансляционная симметрия[править | править код]
Трансляционная симметрия — тип симметрии, при которой свойства рассматриваемой системы не изменяются при сдвиге на определённый вектор, который называется вектором трансляции. Например, однородная среда совмещается сама с собой при сдвиге на любой вектор, поэтому для неё свойственна трансляционная симметрия.
Трансляционная симметрия свойственна также для кристаллов. В этом случае векторы трансляции не произвольны, хотя их существует бесконечное число. Среди всех векторов трансляций кристаллической решётки можно выбрать 3 линейно независимых таким образом, что любой другой вектор трансляции был бы целочисленно-линейной комбинацией этих трёх векторов. Эти три вектора составляют базис кристаллической решётки.
Теория групп показывает, что трансляционная симметрия в кристаллах совместима только с поворотами на углы θ=2π/n, где n может принимать значения 1, 2, 3, 4, 6.
При повороте на углы 180, 120, 90, 60 градусов положение атомов в кристалле не меняется. Говорят, что кристаллы имеют ось вращения n-го порядка.[уточнить]
Перенос в плоском четырёхмерном пространстве-времени не меняет физических законов. В теории поля трансляционная симметрии, согласно теореме Нётер, соответствует сохранению тензора энергии-импульса. В частности, чисто временные трансляции соответствуют закону сохранения энергии, а чисто пространственные сдвиги — закону сохранения импульса.
Симметрии в биологии[править | править код]
Сложные узоры на крыльях бабочки являются одним из примеров двусторонней симметрии
Симметрия в биологии — это закономерное расположение подобных (одинаковых, равных по размеру) частей тела или форм живого организма, совокупности живых организмов относительно центра или оси симметрии. Тип симметрии определяет не только общее строение тела, но и возможность развития систем органов животного. Строение тела многих многоклеточных организмов отражает определённые формы симметрии. Если тело животного можно мысленно разделить на две половины, правую и левую, то такую форму симметрии называют билатеральной. Этот тип симметрии свойственен подавляющему большинству видов, а также человеку. Если тело животного можно мысленно разделить не одной, а несколькими плоскостями симметрии на равные части, то такое животное называют радиально-симметричным. Этот тип симметрии встречается значительно реже.
Асимметрия — отсутствие симметрии. Иногда этот термин используется для описания организмов, лишённых симметрии первично, в противоположность диссимметрии — вторичной утрате симметрии или отдельных её элементов.
Понятия симметрии и асимметрии обратны. Чем более симметричен организм, тем менее он асимметричен и наоборот. Небольшое количество организмов полностью асимметричны. При этом следует различать изменчивость формы (например у амёбы) от отсутствия симметрии. В природе и, в частности, в живой природе симметрия не абсолютна и всегда содержит некоторую степень асимметрии. Например, симметричные листья растений при сложении пополам в точности не совпадают.
У биологических объектов встречаются следующие типы симметрии:
- сферическая симметрия — симметричность относительно вращений в трёхмерном пространстве на произвольные углы.
- аксиальная симметрия (радиальная симметрия, симметрия вращения неопределённого порядка) — симметричность относительно поворотов на произвольный угол вокруг какой-либо оси.
- симметрия вращения n-го порядка — симметричность относительно поворотов на угол 360°/n вокруг какой-либо оси.
- двусторонняя (билатеральная) симметрия — симметричность относительно плоскости симметрии (симметрия зеркального отражения).
- трансляционная симметрия — симметричность относительно сдвигов пространства в каком-либо направлении на некоторое расстояние (её частный случай у животных — метамерия (биология)).
- триаксиальная асимметрия — отсутствие симметрии по всем трём пространственным осям.
Радиальная симметрия[править | править код]
В биологии о радиальной симметрии говорят, когда через трёхмерное существо проходят одна или более осей симметрии. При этом радиальносимметричные животные могут и не иметь плоскостей симметрии. Так, у сифонофоры Velella имеется ось симметрии второго порядка и нет плоскостей симметрии[4]
Обычно через ось симметрии проходят две или более плоскости симметрии. Эти плоскости пересекаются по прямой — оси симметрии. Если животное будет вращаться вокруг этой оси на определённый градус, то оно будет отображаться само на себе (совпадать само с собой). Таких осей симметрии может быть несколько (полиаксонная симметрия) или одна (монаксонная симметрия). Полиаксонная симметрия распространена среди протистов (например, радиолярий).
Как правило, у многоклеточных животных два конца (полюса) единственной оси симметрии неравноценны (например, у медуз на одном полюсе (оральном) находится рот, а на противоположном (аборальном) — верхушка колокола. Такая симметрия (вариант радиальной симметрии) в сравнительной анатомии называется одноосно-гетеропольной. В двухмерной проекции радиальная симметрия может сохраняться, если ось симметрии направлена перпендикулярно к проекционной плоскости. Иными словами, сохранение радиальной симметрии зависит от угла наблюдения.
Радиальная симметрия характерна для многих стрекающих, а также для большинства иглокожих. Среди них встречается так называемая пентасимметрия, базирующаяся на пяти плоскостях симметрии. У иглокожих радиальная симметрия вторична: их личинки двустороннесимметричны, а у взрослых животных наружная радиальная симметрия нарушается наличием мадрепоровой пластинки.
Кроме типичной радиальной симметрии существует двулучевая радиальная симметрия (две плоскости симметрии, к примеру, у гребневиков). Если плоскость симметрии только одна, то симметрия билатеральная (такую симметрию имеют животные из группы Bilateria).
У цветковых растений часто встречаются радиальносимметричные цветки: 3 плоскости симметрии (водокрас лягушачий), 4 плоскости симметрии (лапчатка прямая), 5 плоскостей симметрии (колокольчик), 6 плоскостей симметрии (безвременник). Цветки с радиальной симметрией называются актиноморфные, цветки с билатеральной симметрией — зигоморфные.
Билатеральная симметрия[править | править код]
Билатера́льная симме́трия (двусторонняя симметрия) — симметрия зеркального отражения, при которой объект имеет одну плоскость симметрии, относительно которой две его половины зеркально симметричны. Если на плоскость симметрии опустить перпендикуляр из точки A и затем из точки О на плоскости симметрии продолжить его на длину AО, то он попадёт в точку A1, во всём подобную точке A. Ось симметрии у билатерально симметричных объектов отсутствует. У животных билатеральная симметрия проявляется в схожести или почти полной идентичности левой и правой половин тела. При этом всегда существуют случайные отклонения от симметрии (например, различия в папиллярных линиях, ветвлении сосудов и расположении родинок на правой и левой руках человека). Часто существуют небольшие, но закономерные различия во внешнем строении (например, более развитая мускулатура правой руки у праворуких людей) и более существенные различия между правой и левой половиной тела в расположении внутренних органов. Например, сердце у млекопитающих обычно размещено несимметрично, со смещением влево.
У животных появление билатеральной симметрии в эволюции связано с ползанием по субстрату (по дну водоема), в связи с чем появляются спинная и брюшная, а также правая и левая половины тела. В целом среди животных билатеральная симметрия более выражена у активно подвижных форм, чем у сидячих.
Билатеральная симметрия свойственна всем достаточно высокоорганизованным животным, кроме иглокожих. В других царствах живых организмов билатеральная симметрия свойственна меньшему числу форм. Среди протистов она характерна для дипломонад (например, лямблий), некоторых форм трипаносом, бодонид, раковинок многих фораминифер. У растений билатеральную симметрию имеет обычно не весь организм, а его отдельные части — листья или цветки. Билатерально симметричные цветки ботаники называют зигоморфными.
Симметрия в химии[править | править код]
Симметрия важна для химии, так как она объясняет наблюдения в спектроскопии, квантовой химии и кристаллографии.
Кристаллографическая точечная группа симметрии — это точечная группа симметрии, которая описывает макросимметрию кристалла. Поскольку в кристаллах допустимы оси (поворотные и несобственного вращения) только 1, 2, 3, 4 и 6 порядков, из всего бесконечного числа точечных групп симметрии только 32 относятся к кристаллографическим.
Анизотропия (от др.-греч. ἄνισος — неравный и τρόπος — направление) — различие свойств среды (например, физических: упругости, электропроводности, теплопроводности, показателя преломления, скорости звука или света и др.) в различных направлениях внутри этой среды; в противоположность изотропии. Причиной анизотропности кристаллов является то, что при упорядоченном расположении атомов, молекул или ионов силы взаимодействия между ними и межатомные расстояния (а также некоторые не связанные с ними прямо величины, например, поляризуемость или электропроводность) оказываются неодинаковыми по различным направлениям. Причиной анизотропии молекулярного кристалла может быть также асимметрия его молекул. Макроскопически эта неодинаковость проявляется, как правило, лишь если кристаллическая структура не слишком симметрична.

Симметрия в религии и культуре[править | править код]
Предполагается, что тенденция людей видеть цель в симметрии, является одной из причин, почему симметрия часто является неотъемлемой частью символов мировых религий. Вот лишь некоторые из многих примеров, изображённые на рисунке справа.
Люди наблюдают симметричную природу (также включающую асимметричный баланс) социального взаимодействия в различных контекстах. Они включают оценки взаимности, эмпатии, извинения, диалога, уважения, справедливости и мести. Симметричные взаимодействия посылают сигналы «мы одинаковые», а асимметричные взаимодействия выражают мысль «я особый, лучше, чем ты». Взаимоотношения со сверстниками строятся на основе симметрии, а властные отношения — на асимметрии[5].
Другие виды симметрий[править | править код]
Типы симметрий, встречающиеся в математике и в естественных науках:

Краб-скрипач, Uca pugnax

Камбала
Асимметрия[править | править код]
Асимметрией (др.-греч. ασυμμετρία «несоразмерность» от μετρέω «измеряю») можно считать любое нарушение симметрии. Чаще всего термин употребляется в отношении зрительных объектов и в изобразительном искусстве. В художественном творчестве асимметрия может выступать (и очень часто выступает) в качестве одного из основных средств формообразования (или композиции). Одно из близких понятий в искусстве — аритмия.
В связи с постоянным делением клеток в организме асимметрия в организмах является обычным явлением по крайней мере в одном измерении наравне с биологической симметрией (также см. Межполушарная асимметрия). Луи Пастер полагал, что биологические молекулы асимметричны из-за космических [то есть физических] сил, которые осуществляют контроль над их формированием, закладывая свойства (асимметричность), аналогичные своим. Хоть и в его время, и даже сейчас, симметрии в физических процессах придаётся большее значение, так же известны фундаментальные физические асимметрии, начиная с времени.
Существует понятие «преобладающая рука», означающее асимметрию в развитии навыков людей и животных. Тренировка нервных путей во время обучения навыку с одной рукой (лапой) занимает меньше времени, чем та же тренировка с двумя.[6]
Понятие асимметрии существует также в физике (Барионная асимметрия Вселенной, Омическая асимметрия, Ёмкостная асимметрия), математике (Коэффициент асимметрии, Асимметричное отношение, Асимметрический атом, Асимметричная криптография) архитектуре и т. д.
Примечания[править | править код]
- ↑ В. Г. Власов. Новый энциклопедический словарь изобразительного искусства. В 10 т. СПб.: Азбука-Классика. Т. VIII, 2008. C.793-802
- ↑ В. Г. Власов.Тектоника и диссимметрия архитектурной композиции Архивная копия от 10 января 2020 на Wayback Machine // Электронный научный журнал «Архитектон: известия вузов». — УралГАХУ, 2016. — № 4 (56)
- ↑ Официальный короткий технический отчёт CERN от 2 июля 2008 года (недоступная ссылка) (англ.)
- ↑ Беклемишев В. Н. Основны сравнительной анатомии беспозвоночных. (в 2-х томах). Т.1. М., «Наука», 1964.
- ↑ Emotional Competency. Дата обращения: 14 марта 2012. Архивировано 4 декабря 2017 года.
- ↑ Martin Gardner. The New Ambidextrous Universe: Symmetry and Asymmetry from Mirror Reflections to Superstrings. — 3. — New York: W.H.Freeman & Co Ltd., 1990. — 416 p. — ISBN 0486442446. — ISBN 978-0486442440. Архивная копия от 18 февраля 2019 на Wayback Machine
Литература[править | править код]
- Урманцев Ю. А. Симметрия природы и природа симметрии. — М., Мысль, 1974.
- Вигнер Е. Этюды о симметрии. — М., Мир, 1971. — 320 с.
- Нокс Р., Голд А. Симметрия в твердом теле. — М., Наука, 1970. — 424 с.
- Шубников А. В., Копцик В. А. Симметрия в науке и искусстве. — М., Наука, 1972. — 340 с.
- Вернадский В. И. Химическое строение биосферы Земли и её окружения. — М., Наука, 1965. — 373 с.
- Болтянский В. Г., Виленкин Н. Я. Симметрия в алгебре. — М., Наука, 1967. — 284 с.
- Под ред. Сенешаль М., Флека Дж. Узоры симметрии. — М., Мир, 1980. — 269 с.
- Ю. К. Егоров-Тисменко, Г. П. Литвинская Теория симметрии кристаллов, ГЕОС, 2000.
- П. М. Зоркий Симметрия молекул и кристаллических структур, МГУ, 1986.
- А. В. Шубников Симметрия и антисимметрия конечных фигур, Изд-во АН СССР, 1951
- И. Харгиттаи, М. Харгиттаи Симметрия глазами химика. – М., Мир, 1989. – 494 с.
Ссылки[править | править код]
- Симметрия — статья из Большой советской энциклопедии.
- Симметрия — статья из Физической энциклопедии.
Симметрия — соразмерность, соответствие, сходность, порядок в расположении частей. Это слово, как и многие другие математические понятия, произошли от греческих слов.
Смотря на объекты вокруг, мы не раз восклицаем: «Какая симметрия!»

Рис. (1). Симметрия в архитектуре.
Люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре, художестве, строительстве.
Но симметрия широко распространена и в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, морской звезде.

Рис. (2). Симметрия в природе.
Пока рассмотрим две симметрии на плоскости: относительно точки и прямой.
Симметрию относительно точки называют центральной симметрией.
Точки
M
и
M1
симметричны относительно некоторой точки (O), если точка (O) является серединой отрезка
MM1
.

Рис. (3). Центральная симметрия.
Точка (O) называется центром симметрии.
Алгоритм построения центрально-симметричных фигур.

Рис. (4). Треугольники симметричны относительно точки (O).
Построим треугольник
A1B1C1
, симметричный треугольнику (ABC) относительно центра (точки) (O).
1. Для этого соединим точки (A), (B), (C) с центром (O) и продолжим эти отрезки.
2. Измерим отрезки (AO), (BO), (CO) и отложим с другой стороны от точки (O) равные им отрезки
AO=OA1;BO=OB1;CO=OC1
;
3. Соединим получившиеся точки отрезками и получим треугольник
A1B1C1
, симметричный данному треугольнику (ABC).
Фигуры, симметричные относительно некоторой точки, равны.
Фигура симметрична относительно центра симметрии, если для каждой точки этой фигуры симметричная ей точка также лежит на этой фигуре. Такая фигура имеет центр симметрии (фигура с центральной симметрией).
Есть фигуры с центральной симметрией, это, например, окружность и параллелограмм. У окружности центр симметрии — это её центр, у параллелограмма центр симметрии — это точка, в которой пересекаются его диагонали. Есть очень много фигур, у которых нет центра симметрии.
Осевая симметрия
Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Точки
M
и
M1
симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.

Рис. (5). Осевая симметрия.
Алгоритм построения фигуры, симметричной относительно некоторой прямой.

Рис. (6). Треугольники симметричны относительно прямой.
Построим треугольник
A1B1C1
, симметричный треугольнику (ABC) относительно красной прямой.
1. Для этого проведём из вершин треугольника (ABC) прямые, перпендикулярные оси симметрии, и продолжим их дальше на другой стороне оси.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками и получим треугольник
A1B1C1
, симметричный данному треугольнику (ABC).
Фигуры, симметричные относительно прямой, равны.
Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.
Иногда у фигур несколько осей симметрии:
- для неразвёрнутого угла существует единственная ось симметрии — это биссектриса данного угла.
- Для равнобедренного треугольника есть единственная ось симметрии.
- Для равностороннего треугольника — три оси.
- Для прямоугольника и ромба существуют две оси симметрии.
- Для квадрата — целых четыре.
- Для окружности осей симметрии бесчисленное множество — это каждая прямая, которая проходит через центр этой фигуры.
- Есть фигуры без осей симметрии — это параллелограмм и треугольник, все стороны которого различны.
Источники:
Рис. 1 Симметрия в архитектуре. Указание авторства не требуется, 2021-06-02, Архитектура/Здания, бесплатно для коммерческого использования, https://clck.ru/VFC5B.
Рис. 2. Симметрия в природе. Указание авторства не требуется, 2021-06-02, бесплатно для коммерческого использования, https://clck.ru/VFECn.
Рис. 3. Центральная симметрия, © ЯКласс.
Рис. 4. Треугольники симметричны относительно точки O, © ЯКласс.
Рис. 5. Осевая симметрия, © ЯКласс.
Рис. 6. Треугольники симметричны относительно прямой, © ЯКласс.
Правильные многогранники своей симметрией с древних времён привлекали к себе внимание учёных, архитекторов, художников. Их по праву называют самыми симметричными из всех
многогранников.
Подробно описал свойства правильных многогранников древнегреческий учёный Платон. Поэтому их называют телами Платона. Правильным многогранникам посвящена 13 книга “Начал”
Евклида.
Очень симметричной фигурой является, например, куб. Центром симметрии куба является точка пересечения его диагоналей. Через центр симметрии проходят 9 осей
симметрии. Плоскостей симметрии у куба также 9 и проходят они либо через противоположные ребра (6), либо через середины противоположных ребер (3).
Через центр симметрии проходят 9 осей симметрии. Плоскостей симметрии у куба также 9 и проходят они либо через противоположные ребра (6), либо через середины противоположных
ребер (3).
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Симметрия геометрических фигур и тел
Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.
А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника — также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно — длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.

Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых — бесконечное множество.
У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии — диагонали, а во втором — средние линии. Множество таковых осей только у квадрата.
Видео
Центральная симметрия
Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.

Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.
Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.
Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.

Рис. 2 Графическое представление центральной симметрии
Фигуры, имеющие несколько осей симметрии
Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.
Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.

То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.
Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.

Рис. 5 Оси симметрии ромба
Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.

Рис. 6 Оси симметрии равностороннего треугольника
В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.

Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.
Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.
Теги
Что называется осевой симметрией
Содержание:
- Что такое осевая симметрия в геометрии
- Свойства осевой симметрии
- Теорема и доказательство
- Фигуры, обладающие симметрией
- Симметрия в повседневной жизни
Что такое осевая симметрия в геометрии
Симметрия – это свойство геометрических фигур отражаться. Симметрия относительно точки называется центральной. Осевая симметрия – это симметрия относительно прямой.
Если точка A и точка B симметричны относительно прямой n, то прямая называется осью симметрии n и проходит через середину отрезка AB. Обозначение осевой симметрии – Sn, таким образом симметрия точек A и B обозначается так:
Sn (А) = В.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Другое название осевой симметрии – вращательная – применяется в естественных науках. Данное понятие означает отражение предметов касательно поворотов вокруг прямой.
Свойства осевой симметрии
- Осевая симметрия переводит прямую в прямую, луч – в луч, отрезок – в отрезок, плоскость в плоскость.
- Неподвижными являются: ось симметрии и все точки на ней, все прямые и плоскости, перпендикулярные оси симметрии.
- Обратное преобразование осевой симметрии есть та же осевая симметрия.
- Осевая симметрия – это поворот относительно оси симметрии на 180°.
Теорема и доказательство
Теорема
Осевая симметрия – это движение, то есть при преобразовании осевой симметрии расстояние между точками сохраняется.
Если отрезок MN симметричен отрезку M1N1 относительно прямой a, то MN = M1N1.
Чтобы доказать, что MN = M1N1, сделаем дополнительные построения:
- P – это точка пересечения MM1 и прямой a;
- Q – это точка пересечения NN1 и прямой a;
- построим отрезок MK, перпендикулярный NN1;
- тогда точка K отразится в точку K1.
Докажем, что прямоугольные треугольники MNK и M1N1K1 равны. Стороны MN и M1N1 являются гипотенузами данных треугольников, поэтому, нужно доказать равенство катетов.
МК = М1К1 , так как перпендикулярны к параллельным прямым.
По построению:
NK = NQ – KQ,
N1K1 = N1Q – K1Q.
Точка N отобразилась в точку N1, значит:
NK = N1K1.
Итак, треугольники равны по двум катетам, следовательно, их гипотенузы равны, то есть MN = M1N1, что и требовалось доказать.
Фигуры, обладающие симметрией
Осевой симметрией обладает угол, а биссектриса является осью симметрии.
Пример №1
Из произвольной точки одной стороны угла опустим перпендикуляр к биссектрисе и продлим его до другой стороны угла:
Рассмотрим Δ KAO и Δ MAO:
- AO – общая сторона
- Из свойства биссектрисы: ∠ MAO = ∠KAO
- Треугольники KAO и MAO прямоугольные,
Отсюда следует, что KO = OM, поэтому точки K и M симметричны касательно биссектрисы угла.
Следовательно, равнобедренный треугольник тоже симметричен относительно биссектрисы, проведенной к основанию.
Пример №2
Равносторонний треугольник имеет три оси симметрии – биссектрисы, медианы, высоты каждого угла:
Пример №3
У прямоугольника две оси симметрии. Каждая из них проходит через середины противоположных сторон.
Пример №4
Ромб обладает двумя осями симметрии – это прямые, содержащие его диагонали.
Пример №5
Квадрат имеет 4 оси симметрии, так как он одновременно и ромб, и прямоугольник.
Пример №6
У окружности бесконечное множество осей симметрии – это все прямые, проведенные через центр круга.
Симметрия в повседневной жизни
Симметрия стала частью жизни человека уже в древние времена. Орнаменты с признаками зеркального отражения встречаются на античных зданиях, древнегреческих вазах. Свойство пропорционального расположения заимствовано в науку из природы.
Зеркальное отражение часто встречается в живой и неживой природе. Этой характеристикой обладают снежинки. В растительном мире одинаково расположены противоположные элементы растений: большинство листьев зеркально отражаются сравнительно среднего стебля. В животном мире законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны обладает парными частями тела: уши, лапы, глаза, крылья, рога. Ярким образцом зеркальной симметрии считается бабочка. Прямая, условно проведенная вдоль туловища насекомого по центру, является осью симметрии.
Поскольку человек – это часть природы, в своем творчестве он использует принцип симметрии. В искусстве свойство отражения применяется для создания красоты и гармонии. В архитектуре пропорциональность выполняет практическую функцию – придает зданиям устойчивость и надежность. В предметах быта можно встретить одинаковость в расположении частей узоров на коврах, принтов на ткани, рисунков обоев.
Стремление к созданию симметричного, предположительно, связано с притяжением Земли – гравитацией. Человек интуитивно считает симметрию формулой устойчивости. Принцип зеркального отражения играет важную роль в человеческой жизни. Тяга к гармонии и красоте побуждает человечество придерживаться правил пропорциональности.

