В данной таблице приведены значения синусов и косинусов для углов от 0 до 359 градусов. Но если Вам нужно рассчитать значения тригонометрических функций
для более точных углов (с минутами и секундами) или углов больше 360 градусов или углов с отрицательными значениями (например 8° 5′ 53″
или -1775° 15′ 22″ ), то можно воспользоваться тригонометрическим калькулятором.
Таблица углов от 0 до 179 градусов
| Угол (градусы) | Синус (Sin) | Косинус (Cos) |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0.01745241 | 0.9998477 |
| 2 | 0.0348995 | 0.99939083 |
| 3 | 0.05233596 | 0.99862953 |
| 4 | 0.06975647 | 0.99756405 |
| 5 | 0.08715574 | 0.9961947 |
| 6 | 0.10452846 | 0.9945219 |
| 7 | 0.12186934 | 0.99254615 |
| 8 | 0.1391731 | 0.99026807 |
| 9 | 0.15643447 | 0.98768834 |
| 10 | 0.17364818 | 0.98480775 |
| 11 | 0.190809 | 0.98162718 |
| 12 | 0.20791169 | 0.9781476 |
| 13 | 0.22495105 | 0.97437006 |
| 14 | 0.2419219 | 0.97029573 |
| 15 | 0.25881905 | 0.96592583 |
| 16 | 0.27563736 | 0.9612617 |
| 17 | 0.2923717 | 0.95630476 |
| 18 | 0.30901699 | 0.95105652 |
| 19 | 0.32556815 | 0.94551858 |
| 20 | 0.34202014 | 0.93969262 |
| 21 | 0.35836795 | 0.93358043 |
| 22 | 0.37460659 | 0.92718385 |
| 23 | 0.39073113 | 0.92050485 |
| 24 | 0.40673664 | 0.91354546 |
| 25 | 0.42261826 | 0.90630779 |
| 26 | 0.43837115 | 0.89879405 |
| 27 | 0.4539905 | 0.89100652 |
| 28 | 0.46947156 | 0.88294759 |
| 29 | 0.48480962 | 0.87461971 |
| 30 | 0.5 | 0.8660254 |
| 31 | 0.51503807 | 0.8571673 |
| 32 | 0.52991926 | 0.8480481 |
| 33 | 0.54463904 | 0.83867057 |
| 34 | 0.5591929 | 0.82903757 |
| 35 | 0.57357644 | 0.81915204 |
| 36 | 0.58778525 | 0.80901699 |
| 37 | 0.60181502 | 0.79863551 |
| 38 | 0.61566148 | 0.78801075 |
| 39 | 0.62932039 | 0.77714596 |
| 40 | 0.64278761 | 0.76604444 |
| 41 | 0.65605903 | 0.75470958 |
| 42 | 0.66913061 | 0.74314483 |
| 43 | 0.68199836 | 0.7313537 |
| 44 | 0.69465837 | 0.7193398 |
| 45 | 0.70710678 | 0.70710678 |
| 46 | 0.7193398 | 0.69465837 |
| 47 | 0.7313537 | 0.68199836 |
| 48 | 0.74314483 | 0.66913061 |
| 49 | 0.75470958 | 0.65605903 |
| 50 | 0.76604444 | 0.64278761 |
| 51 | 0.77714596 | 0.62932039 |
| 52 | 0.78801075 | 0.61566148 |
| 53 | 0.79863551 | 0.60181502 |
| 54 | 0.80901699 | 0.58778525 |
| 55 | 0.81915204 | 0.57357644 |
| 56 | 0.82903757 | 0.5591929 |
| 57 | 0.83867057 | 0.54463904 |
| 58 | 0.8480481 | 0.52991926 |
| 59 | 0.8571673 | 0.51503807 |
| 60 | 0.8660254 | 0.5 |
| 61 | 0.87461971 | 0.48480962 |
| 62 | 0.88294759 | 0.46947156 |
| 63 | 0.89100652 | 0.4539905 |
| 64 | 0.89879405 | 0.43837115 |
| 65 | 0.90630779 | 0.42261826 |
| 66 | 0.91354546 | 0.40673664 |
| 67 | 0.92050485 | 0.39073113 |
| 68 | 0.92718385 | 0.37460659 |
| 69 | 0.93358043 | 0.35836795 |
| 70 | 0.93969262 | 0.34202014 |
| 71 | 0.94551858 | 0.32556815 |
| 72 | 0.95105652 | 0.30901699 |
| 73 | 0.95630476 | 0.2923717 |
| 74 | 0.9612617 | 0.27563736 |
| 75 | 0.96592583 | 0.25881905 |
| 76 | 0.97029573 | 0.2419219 |
| 77 | 0.97437006 | 0.22495105 |
| 78 | 0.9781476 | 0.20791169 |
| 79 | 0.98162718 | 0.190809 |
| 80 | 0.98480775 | 0.17364818 |
| 81 | 0.98768834 | 0.15643447 |
| 82 | 0.99026807 | 0.1391731 |
| 83 | 0.99254615 | 0.12186934 |
| 84 | 0.9945219 | 0.10452846 |
| 85 | 0.9961947 | 0.08715574 |
| 86 | 0.99756405 | 0.06975647 |
| 87 | 0.99862953 | 0.05233596 |
| 88 | 0.99939083 | 0.0348995 |
| 89 | 0.9998477 | 0.01745241 |
| 90 | 1 | 0 |
| 91 | 0.9998477 | -0.01745241 |
| 92 | 0.99939083 | -0.0348995 |
| 93 | 0.99862953 | -0.05233596 |
| 94 | 0.99756405 | -0.06975647 |
| 95 | 0.9961947 | -0.08715574 |
| 96 | 0.9945219 | -0.10452846 |
| 97 | 0.99254615 | -0.12186934 |
| 98 | 0.99026807 | -0.1391731 |
| 99 | 0.98768834 | -0.15643447 |
| 100 | 0.98480775 | -0.17364818 |
| 101 | 0.98162718 | -0.190809 |
| 102 | 0.9781476 | -0.20791169 |
| 103 | 0.97437006 | -0.22495105 |
| 104 | 0.97029573 | -0.2419219 |
| 105 | 0.96592583 | -0.25881905 |
| 106 | 0.9612617 | -0.27563736 |
| 107 | 0.95630476 | -0.2923717 |
| 108 | 0.95105652 | -0.30901699 |
| 109 | 0.94551858 | -0.32556815 |
| 110 | 0.93969262 | -0.34202014 |
| 111 | 0.93358043 | -0.35836795 |
| 112 | 0.92718385 | -0.37460659 |
| 113 | 0.92050485 | -0.39073113 |
| 114 | 0.91354546 | -0.40673664 |
| 115 | 0.90630779 | -0.42261826 |
| 116 | 0.89879405 | -0.43837115 |
| 117 | 0.89100652 | -0.4539905 |
| 118 | 0.88294759 | -0.46947156 |
| 119 | 0.87461971 | -0.48480962 |
| 120 | 0.8660254 | -0.5 |
| 121 | 0.8571673 | -0.51503807 |
| 122 | 0.8480481 | -0.52991926 |
| 123 | 0.83867057 | -0.54463904 |
| 124 | 0.82903757 | -0.5591929 |
| 125 | 0.81915204 | -0.57357644 |
| 126 | 0.80901699 | -0.58778525 |
| 127 | 0.79863551 | -0.60181502 |
| 128 | 0.78801075 | -0.61566148 |
| 129 | 0.77714596 | -0.62932039 |
| 130 | 0.76604444 | -0.64278761 |
| 131 | 0.75470958 | -0.65605903 |
| 132 | 0.74314483 | -0.66913061 |
| 133 | 0.7313537 | -0.68199836 |
| 134 | 0.7193398 | -0.69465837 |
| 135 | 0.70710678 | -0.70710678 |
| 136 | 0.69465837 | -0.7193398 |
| 137 | 0.68199836 | -0.7313537 |
| 138 | 0.66913061 | -0.74314483 |
| 139 | 0.65605903 | -0.75470958 |
| 140 | 0.64278761 | -0.76604444 |
| 141 | 0.62932039 | -0.77714596 |
| 142 | 0.61566148 | -0.78801075 |
| 143 | 0.60181502 | -0.79863551 |
| 144 | 0.58778525 | -0.80901699 |
| 145 | 0.57357644 | -0.81915204 |
| 146 | 0.5591929 | -0.82903757 |
| 147 | 0.54463904 | -0.83867057 |
| 148 | 0.52991926 | -0.8480481 |
| 149 | 0.51503807 | -0.8571673 |
| 150 | 0.5 | -0.8660254 |
| 151 | 0.48480962 | -0.87461971 |
| 152 | 0.46947156 | -0.88294759 |
| 153 | 0.4539905 | -0.89100652 |
| 154 | 0.43837115 | -0.89879405 |
| 155 | 0.42261826 | -0.90630779 |
| 156 | 0.40673664 | -0.91354546 |
| 157 | 0.39073113 | -0.92050485 |
| 158 | 0.37460659 | -0.92718385 |
| 159 | 0.35836795 | -0.93358043 |
| 160 | 0.34202014 | -0.93969262 |
| 161 | 0.32556815 | -0.94551858 |
| 162 | 0.30901699 | -0.95105652 |
| 163 | 0.2923717 | -0.95630476 |
| 164 | 0.27563736 | -0.9612617 |
| 165 | 0.25881905 | -0.96592583 |
| 166 | 0.2419219 | -0.97029573 |
| 167 | 0.22495105 | -0.97437006 |
| 168 | 0.20791169 | -0.9781476 |
| 169 | 0.190809 | -0.98162718 |
| 170 | 0.17364818 | -0.98480775 |
| 171 | 0.15643447 | -0.98768834 |
| 172 | 0.1391731 | -0.99026807 |
| 173 | 0.12186934 | -0.99254615 |
| 174 | 0.10452846 | -0.9945219 |
| 175 | 0.08715574 | -0.9961947 |
| 176 | 0.06975647 | -0.99756405 |
| 177 | 0.05233596 | -0.99862953 |
| 178 | 0.0348995 | -0.99939083 |
| 179 | 0.01745241 | -0.9998477 |
Таблица углов от 180 до 359 градусов
| Угол (градусы) | Синус (Sin) | Косинус (Cos) |
|---|---|---|
| 180 | 0 | -1 |
| 181 | -0.01745241 | -0.9998477 |
| 182 | -0.0348995 | -0.99939083 |
| 183 | -0.05233596 | -0.99862953 |
| 184 | -0.06975647 | -0.99756405 |
| 185 | -0.08715574 | -0.9961947 |
| 186 | -0.10452846 | -0.9945219 |
| 187 | -0.12186934 | -0.99254615 |
| 188 | -0.1391731 | -0.99026807 |
| 189 | -0.15643447 | -0.98768834 |
| 190 | -0.17364818 | -0.98480775 |
| 191 | -0.190809 | -0.98162718 |
| 192 | -0.20791169 | -0.9781476 |
| 193 | -0.22495105 | -0.97437006 |
| 194 | -0.2419219 | -0.97029573 |
| 195 | -0.25881905 | -0.96592583 |
| 196 | -0.27563736 | -0.9612617 |
| 197 | -0.2923717 | -0.95630476 |
| 198 | -0.30901699 | -0.95105652 |
| 199 | -0.32556815 | -0.94551858 |
| 200 | -0.34202014 | -0.93969262 |
| 201 | -0.35836795 | -0.93358043 |
| 202 | -0.37460659 | -0.92718385 |
| 203 | -0.39073113 | -0.92050485 |
| 204 | -0.40673664 | -0.91354546 |
| 205 | -0.42261826 | -0.90630779 |
| 206 | -0.43837115 | -0.89879405 |
| 207 | -0.4539905 | -0.89100652 |
| 208 | -0.46947156 | -0.88294759 |
| 209 | -0.48480962 | -0.87461971 |
| 210 | -0.5 | -0.8660254 |
| 211 | -0.51503807 | -0.8571673 |
| 212 | -0.52991926 | -0.8480481 |
| 213 | -0.54463904 | -0.83867057 |
| 214 | -0.5591929 | -0.82903757 |
| 215 | -0.57357644 | -0.81915204 |
| 216 | -0.58778525 | -0.80901699 |
| 217 | -0.60181502 | -0.79863551 |
| 218 | -0.61566148 | -0.78801075 |
| 219 | -0.62932039 | -0.77714596 |
| 220 | -0.64278761 | -0.76604444 |
| 221 | -0.65605903 | -0.75470958 |
| 222 | -0.66913061 | -0.74314483 |
| 223 | -0.68199836 | -0.7313537 |
| 224 | -0.69465837 | -0.7193398 |
| 225 | -0.70710678 | -0.70710678 |
| 226 | -0.7193398 | -0.69465837 |
| 227 | -0.7313537 | -0.68199836 |
| 228 | -0.74314483 | -0.66913061 |
| 229 | -0.75470958 | -0.65605903 |
| 230 | -0.76604444 | -0.64278761 |
| 231 | -0.77714596 | -0.62932039 |
| 232 | -0.78801075 | -0.61566148 |
| 233 | -0.79863551 | -0.60181502 |
| 234 | -0.80901699 | -0.58778525 |
| 235 | -0.81915204 | -0.57357644 |
| 236 | -0.82903757 | -0.5591929 |
| 237 | -0.83867057 | -0.54463904 |
| 238 | -0.8480481 | -0.52991926 |
| 239 | -0.8571673 | -0.51503807 |
| 240 | -0.8660254 | -0.5 |
| 241 | -0.87461971 | -0.48480962 |
| 242 | -0.88294759 | -0.46947156 |
| 243 | -0.89100652 | -0.4539905 |
| 244 | -0.89879405 | -0.43837115 |
| 245 | -0.90630779 | -0.42261826 |
| 246 | -0.91354546 | -0.40673664 |
| 247 | -0.92050485 | -0.39073113 |
| 248 | -0.92718385 | -0.37460659 |
| 249 | -0.93358043 | -0.35836795 |
| 250 | -0.93969262 | -0.34202014 |
| 251 | -0.94551858 | -0.32556815 |
| 252 | -0.95105652 | -0.30901699 |
| 253 | -0.95630476 | -0.2923717 |
| 254 | -0.9612617 | -0.27563736 |
| 255 | -0.96592583 | -0.25881905 |
| 256 | -0.97029573 | -0.2419219 |
| 257 | -0.97437006 | -0.22495105 |
| 258 | -0.9781476 | -0.20791169 |
| 259 | -0.98162718 | -0.190809 |
| 260 | -0.98480775 | -0.17364818 |
| 261 | -0.98768834 | -0.15643447 |
| 262 | -0.99026807 | -0.1391731 |
| 263 | -0.99254615 | -0.12186934 |
| 264 | -0.9945219 | -0.10452846 |
| 265 | -0.9961947 | -0.08715574 |
| 266 | -0.99756405 | -0.06975647 |
| 267 | -0.99862953 | -0.05233596 |
| 268 | -0.99939083 | -0.0348995 |
| 269 | -0.9998477 | -0.01745241 |
| 270 | -1 | 0 |
| 271 | -0.9998477 | 0.01745241 |
| 272 | -0.99939083 | 0.0348995 |
| 273 | -0.99862953 | 0.05233596 |
| 274 | -0.99756405 | 0.06975647 |
| 275 | -0.9961947 | 0.08715574 |
| 276 | -0.9945219 | 0.10452846 |
| 277 | -0.99254615 | 0.12186934 |
| 278 | -0.99026807 | 0.1391731 |
| 279 | -0.98768834 | 0.15643447 |
| 280 | -0.98480775 | 0.17364818 |
| 281 | -0.98162718 | 0.190809 |
| 282 | -0.9781476 | 0.20791169 |
| 283 | -0.97437006 | 0.22495105 |
| 284 | -0.97029573 | 0.2419219 |
| 285 | -0.96592583 | 0.25881905 |
| 286 | -0.9612617 | 0.27563736 |
| 287 | -0.95630476 | 0.2923717 |
| 288 | -0.95105652 | 0.30901699 |
| 289 | -0.94551858 | 0.32556815 |
| 290 | -0.93969262 | 0.34202014 |
| 291 | -0.93358043 | 0.35836795 |
| 292 | -0.92718385 | 0.37460659 |
| 293 | -0.92050485 | 0.39073113 |
| 294 | -0.91354546 | 0.40673664 |
| 295 | -0.90630779 | 0.42261826 |
| 296 | -0.89879405 | 0.43837115 |
| 297 | -0.89100652 | 0.4539905 |
| 298 | -0.88294759 | 0.46947156 |
| 299 | -0.87461971 | 0.48480962 |
| 300 | -0.8660254 | 0.5 |
| 301 | -0.8571673 | 0.51503807 |
| 302 | -0.8480481 | 0.52991926 |
| 303 | -0.83867057 | 0.54463904 |
| 304 | -0.82903757 | 0.5591929 |
| 305 | -0.81915204 | 0.57357644 |
| 306 | -0.80901699 | 0.58778525 |
| 307 | -0.79863551 | 0.60181502 |
| 308 | -0.78801075 | 0.61566148 |
| 309 | -0.77714596 | 0.62932039 |
| 310 | -0.76604444 | 0.64278761 |
| 311 | -0.75470958 | 0.65605903 |
| 312 | -0.74314483 | 0.66913061 |
| 313 | -0.7313537 | 0.68199836 |
| 314 | -0.7193398 | 0.69465837 |
| 315 | -0.70710678 | 0.70710678 |
| 316 | -0.69465837 | 0.7193398 |
| 317 | -0.68199836 | 0.7313537 |
| 318 | -0.66913061 | 0.74314483 |
| 319 | -0.65605903 | 0.75470958 |
| 320 | -0.64278761 | 0.76604444 |
| 321 | -0.62932039 | 0.77714596 |
| 322 | -0.61566148 | 0.78801075 |
| 323 | -0.60181502 | 0.79863551 |
| 324 | -0.58778525 | 0.80901699 |
| 325 | -0.57357644 | 0.81915204 |
| 326 | -0.5591929 | 0.82903757 |
| 327 | -0.54463904 | 0.83867057 |
| 328 | -0.52991926 | 0.8480481 |
| 329 | -0.51503807 | 0.8571673 |
| 330 | -0.5 | 0.8660254 |
| 331 | -0.48480962 | 0.87461971 |
| 332 | -0.46947156 | 0.88294759 |
| 333 | -0.4539905 | 0.89100652 |
| 334 | -0.43837115 | 0.89879405 |
| 335 | -0.42261826 | 0.90630779 |
| 336 | -0.40673664 | 0.91354546 |
| 337 | -0.39073113 | 0.92050485 |
| 338 | -0.37460659 | 0.92718385 |
| 339 | -0.35836795 | 0.93358043 |
| 340 | -0.34202014 | 0.93969262 |
| 341 | -0.32556815 | 0.94551858 |
| 342 | -0.30901699 | 0.95105652 |
| 343 | -0.2923717 | 0.95630476 |
| 344 | -0.27563736 | 0.9612617 |
| 345 | -0.25881905 | 0.96592583 |
| 346 | -0.2419219 | 0.97029573 |
| 347 | -0.22495105 | 0.97437006 |
| 348 | -0.20791169 | 0.9781476 |
| 349 | -0.190809 | 0.98162718 |
| 350 | -0.17364818 | 0.98480775 |
| 351 | -0.15643447 | 0.98768834 |
| 352 | -0.1391731 | 0.99026807 |
| 353 | -0.12186934 | 0.99254615 |
| 354 | -0.10452846 | 0.9945219 |
| 355 | -0.08715574 | 0.9961947 |
| 356 | -0.06975647 | 0.99756405 |
| 357 | -0.05233596 | 0.99862953 |
| 358 | -0.0348995 | 0.99939083 |
| 359 | -0.01745241 | 0.9998477 |
Другие таблицы
Синус 135 градусов
Синус 135 градусов найдем по формуле приведения для синуса тупого угла от 90 до 180 градусов.
Синус угла альфа на единичной окружности — это ордината точки, полученной из точки (1;0) при повороте на угол альфа вокруг точки O.
Для синуса тупого угла (от 90º до 180º) имеет место следующая формула приведения:
то воспользовавшись этой формулой приведения и значением синуса 45º, получаем:
Как найти синус и косинус углов в градусах без тригонометрической таблицы?
В статье мы расскажем, как находить значения:
и других тригонометрических выражений без тригонометрической таблицы .
Как вычисляются синусы и косинусы углов?
Чтобы вычислить косинус и синус некоторого угла нужно:
1. Отложить этот угол на тригонометрическом круге и определить какая точка соответствует этому углу;
2. Найти абсциссу и ординату этой точки. Косинус угла равен – абсциссе, а синус угла – ординате.
Предположим, стоит задача найти косинус и синус угла (30^°). Отложим на круге угол в (30^°) и найдем какая точка соответствует этому углу.
Если построить все точно, то видно, что абсцисса точки равна (0,866)… , что равно числу (frac<sqrt<3>><2>) , а ордината равна (0,5), то есть (frac<1><2>).
Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:
В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».
Обычно на осях не отмечают (0,1); (0,2); (0,3) и т.д., а сразу наносят стандартные значения для синуса и косинуса: (±frac<1><2>=±0,5); (±frac<sqrt<2>> <2>≈±0,707); (±frac<sqrt<3>> <2>≈±0,866).
Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.
Как отметить любой угол на тригонометрическом круге?
Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;
Градусная мера окружности равна (360^°), полуокружности (180^°), а четверти (90^°);
Углы в (0^°), (30^°), (45^°) и (60^°) выглядят так:
- Одна точка может соответствовать разным углам;
- Угол может быть больше (360^°). В этом случае он просто сделает полный оборот и пойдет дальше. Фактически, можно (360^°) просто отбросить и откладывать тот угол, который останется – в итоге вы всё равно окажетесь в той же точке.
Задание 1 . Отметьте на окружности точки соответствующие углам: (720^°), (225^°), (300^°), (870^°), (900^°), (-330^°), (-630^°), (-210^°).
Как находить синус и косинус любого угла?
- Начертите тригонометрический круг и оси косинусов и синусов (не обязательно рисовать прям аккуратно, как на картинке ниже, можно и некрасиво – главное не запутаться какая точка к какому значению относится).
- Отложите на круге угол, синус и косинус которого надо найти, и определите точку на круге, соответствующую этому углу.
- Найдите координаты точки, используя картинку ниже.
(-540^°) на тригонометрическом круге совпадает с (-1) на оси косинусов. То есть, координаты этой точки: ((-1;0)). Значит, (cos(-540^°)=-1), а (sin(-540^° )=0).
Да, имея перед глазами тригонометрический круг, вычислять синусы и косинусы любых углов легко. Возможно, у вас возник вопрос: «а что делать, если круга нет? Как делать такие вычисления на ЕГЭ?». Ответ очевиден – нарисовать круг самому! Для этого надо понять, как располагаются значения на нем. Подробную методику того, как это делается я рассказывала в этой статье .
Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).
Примеры вычисления синуса и косинуса из ЕГЭ
В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.
Пример . Найдите значение выражения (54sqrt<3>cos(510^°)).
Решение. (510^°=360^°+150^°=360^°+180^°-30^°.)
Тригонометрические функции на единичной окружности. Тангенс и котангенс

Тригонометрический круг
Углы в радианах
Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан.
Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π .
Например, для угла 90° будет 90°180°· π = 12π
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
Видео
Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике
Прямоугольный вид треугольника — это тот, у которого один из углов равен 90°. Он образован катетами и гипотенузой со всеми значениями тригонометрии. Катеты две стороны треугольника, которые прилегают к углу 90°, а третья гипотенуза, она всегда длиннее катетов.

Синусом называется отношение одного из катетов к гипотенузе, косинусом отношение другого катета к ней, а тангенсом отношение двух катетов. Отношение символизирует деление. Также тангенсом является деление острого угла на синус с косинусом. Котангенсом является противоположное тангенсу отношение.
Формулы последних двух отношений выглядят следующим образом: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a).
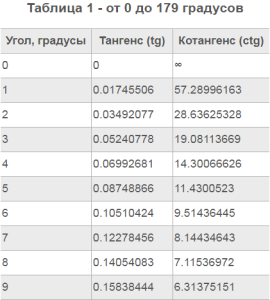
Тангенс угла
Синус и косинус являются основными, или, как говорят математики, прямыми тригонометрическими ф-циями. Однако есть ещё две производных тригонометрических ф-ций – тангенс и котангенс. Напомним, что тангенс угла в прямоугольном треугол-ке – это отношение противолежащего катета к прилежащему. Однако в тригонометрии куда удобнее пользоваться другим его определением. Тангенс – это отношение синуса угла к его косинусу:


Для получения тангенса на единичной окружности необходимо продолжить прямую, образующую угол α, до её пересечения с прямой х = 1. Точка их пересечения будет иметь координаты (1; tgα):

Заметим, что если α относится ко второй четверти, то тангенс получится отрицательным. Действительно, с одной стороны, соответствующая прямая пересечет линию х = 1 в точке, лежащей ниже оси Ох:

С другой стороны, мы знаем, что во второй четверти синус положителен, а косинус – отрицателен. Тогда их отношение, то есть тангенс, должно быть отрицательным:

Очевидно, что тангенс должен быть периодической ф-цией. Однако его период вдвое меньше 2π и составляет π. Действительно, углы, отличающиеся на π, будут иметь одинаковое значение тангенса, что видно из построения:

Это значит, что справедлива формула:

С другой стороны, это означает, что тангенсы углов из III четверти положительны, ведь они равны тангенсам углов из I четверти. Аналогично можно утверждать, что тангенсы углов из IV четверти отрицательны:

Также тангенс является нечетной ф-цией. Чтобы убедиться в этом, найдем с помощью единичной окружности tgα и tg (– α):

Из построения видно, что tg (– α) = tgα, поэтому тангенс попадает под определение нечетной ф-ции.

Доказать этот факт можно и иначе. Вспомним, что синус – это нечетная ф-ция, а косинус – четная. Тогда, используя определение тангенса, можно записать:

Для вычисления тангенса проще всего использовать его определение. Мы знаем синусы и косинусы стандартных углов, а потому, деля их друг на друга, сможем найти и тангенсы стандартных углов:

Ещё раз отметим, что важнее всего запомнить значения синусов и косинусов стандартных углов. Зная их, школьник всегда сможет самостоятельно вычислить тангенс.
Можно ли вычислить тангенс для угла π/2, то есть для 90°? Сделать это не получится, ведь cosπ/2 равен нулю. Если подставить cosπ/2 в формулу для вычисления тангенса, то получится деление на ноль! Так как тангенс – периодическая ф-ция, то его нельзя вычислить и в тех точках, которые отличаются от π/2 на целое число π.

В частности, тангенс не определен при х = – π/2.
Определение знака синуса, косинуса, тангенса и котангенса
Вообще, этот вопрос заслуживает особого внимания, но здесь все просто: у угла ( displaystyle 30) градусов и синус и косинус положительны (смотри рисунок), тогда берем знак «плюс».
( displaystyle cos 30<>^circ =frac<sqrt<3>><2>)Теперь попробуй на основе вышеизложенного найти синус и косинус углов: ( displaystyle 60<>^circ ) и ( displaystyle 45<>^circ )
Можно схитрить: в частности для угла в ( displaystyle 60<>^circ ) градусов. Так как если один угол прямоугольного треугольника равен ( displaystyle 60<>^circ ) градусам, то второй – ( displaystyle 30<>^circ ) градусам. Теперь вступают в силу знакомые тебе формулы:( displaystyle sin 30<>^circ =cos 60<>^circ )( displaystyle sin 60<>^circ =cos 30<>^circ )Тогда так как ( displaystyle sin 30<>^circ =0,5), то и ( displaystyle cos 60<>^circ =0,5). Так как ( displaystyle cos 30<>^circ =frac<sqrt<3>><2>), то и ( displaystyle sin 60<>^circ =frac<sqrt<3>><2>).
C ( displaystyle 45) градусами все еще проще: так если один из углов прямоугольного треугольника равен ( displaystyle 45) градусам, то и другой тоже равен ( displaystyle 45) градусам, а значит такой треугольник равнобедренный.
Значит, его катеты равны. А значит равны его синус и косинус.
Тогда:( displaystyle si<^<2>>45<>^circ +co<^<2>>45<>^circ =2si<^<2>>45<>^circ =1)( displaystyle si<^<2>>45<>^circ =co<^<2>>45<>^circ =1/2)Откуда: ( displaystyle sin 45<>^circ =cos 45<>^circ =sqrt<1/2>=frac<sqrt<2>><2>)
Теперь найди сам по новому определению (через икс и игрек!) синус и косинус углов в ( displaystyle 0) градусов и ( displaystyle 90) градусов. Здесь уже никакие треугольники нарисовать не получится! Уж слишком они будут плоские!
У тебя должно было получиться:
( displaystyle sin 0<>^circ =0), ( displaystyle cos 0<>^circ =1), ( displaystyle sin 90<>^circ =1), ( displaystyle cos 90<>^circ =0).Тангенс и котангенс ты можешь отыскать самостоятельно по формулам:
( displaystyle textg alpha =frac<sin alpha ><cos alpha >), ( displaystyle ctg alpha =frac)Обрати внимание, что на ноль делить нельзя!!
Теперь все полученные числа можно свести в таблицу:

Здесь приведены значения синуса, косинуса, тангенса и котангенса углов I четверти.
Для удобства углы приведены как в градусах, так и в радианах (но ты-то теперь знаешь связь между ними!). Обрати внимание на 2 прочерка в таблице: а именно у котангенса нуля и тангенса ( displaystyle 90) градусов. Это неспроста!
( displaystyle ctg 0=frac<cos 0><sin 0>=frac<1><0>=. )Поэтому мы с тобой будем считать, что тангенс ( displaystyle 90) градусов и котангенс нуля просто-напросто не определены!
Теперь давай обобщим понятие синус и косинус на совсем произвольный угол. Я рассмотрю здесь два случая:
- Угол лежит в пределах от ( displaystyle 0) до ( displaystyle 360) градусов;
- Угол больше ( displaystyle 360) градусов.
Честно говоря, я скривил немного душой, говоря про «совсем все» углы. Они бывают также и отрицательными! Но этот случай мы с тобой рассмотрим чуть позже. Вначале остановимся на первом случае.
Если угол лежит в 1 четверти – то тут все понятно, мы этот случай уже рассмотрели и даже таблицы нарисовали.
Теперь же пусть наш угол больше ( displaystyle 90) градусов и не больше чем ( displaystyle 360).
Это значит, что он расположен либо во 2, либо в 3 или же в 4 четверти.
Как мы поступаем? Да точно так же!
Давай рассмотрим вместо вот такого случая…

…вот такой:

То есть рассмотрим угол ( displaystyle alpha ), лежащий во второй четверти. Что мы можем сказать про него?
У точки ( displaystyle <_<1>>), которая является точкой пересечения луча и окружности по-прежнему имеет 2 координаты (ничего сверхъестественного, правда?). Это координаты ( displaystyle <_<1>>) и ( displaystyle <_<1>>).
Причем первая координата отрицательная, а вторая – положительная! Это значит, что у углов второй четверти косинус отрицателен, а синус – положителен!
Удивительно, правда? До этого мы еще ни разу не сталкивались с отрицательным косинусом.
Да и в принципе этого не могло быть, когда мы рассматривали тригонометрические функции как отношения сторон треугольника.
Кстати, подумай, у каких углов косинус равен ( displaystyle -1)? А у каких ( displaystyle -1) равен синус?
Аналогично можно рассмотреть углы во всех остальных четвертях. Я лишь напомню, что угол отсчитывается против часовой стрелки! (так, как это показано на последнем рисунке!).
Конечно, можно и отсчитывать в другую сторону, но вот подход к таким углам будет уже несколько другой.
Исходя из приведенных выше рассуждений, можно расставить знаки у синуса, косинуса, тангенса (как синус деленный на косинус) и котангенса (как косинус деленный на синус) для всех четырех четвертей.

Но еще раз повторюсь, нет смысла запоминать этот рисунок. Все, что тебе нужно знать:
Синус – это игрек. Косинус – это икс. Тангенс – это синус деленный на косинус. Котангенс – это косинус деленный на синус.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Два случая, когда тригонометрическая окружность может пригодиться для решения уравнений
- В ответе у нас не получается «красивый» угол, но тем не менее надо производить отбор корней
- В ответе получается уж слишком много серий корней
Никаких специфических знаний тебе не требуется, кроме знания темы: «Тригонометрические уравнения»
Тему «тригонометрические уравнения» я старался писать, не прибегая к окружности. Многие бы меня за такой подход не похвалили.
Но мне милее формулы, уж что тут поделать. Однако в некоторых случаях формул оказывается мало. Например здесь:
Решите уравнение: ( displaystyle 8co<^<4>>x-10co<^<2>>x+3=0)
Решение:
Ну что же. Решить само уравнение несложно.
Замена ( displaystyle t=co<^<2>>x).
( displaystyle cosx=frac<sqrt<3>><2>) или ( displaystyle cosx=-frac<sqrt<3>><2>)
Отсюда наше исходное уравнение равносильно аж четырем простейшим уравнениям!
Неужели нам нужно будет записывать 4 серии корней?!
[spoiler title=”источники:”]
http://cos-cos.ru/ege/zadacha209/357/
http://naiti-ludei.ru/posts/trigonometricheskie-funkcii-na-edinichnoy-okruzhnosti-tangens-i-kotangens/
[/spoiler]
Полные таблицы косинусов и синусов (cos и sin), а также значений тангенсов (tg), котангенсов (ctg) – это мощный и полезный инструмент, помогающий решать множество задач, как теоретического, так и прикладного характера. В этой статье мы приведем некоторые главные таблицы значений тригонометрических функций (таблицу синусов, таблицу косинусов, таблицу тангенсов и котангенсов) для углов 0, 30, 45, 60, 90, …, 360 градусов (0, π6, π3, π2, … , 2π радиан). Также здесь будут встречаться отдельные таблицы Брадиса для синусов и косинусов, тангенсов и котангенсов с пояснением, как их использовать для нахождения значений основных тригонометрических функций.
Таблица основных тригонометрических функций для углов 0, 30, 45, 60, 90, …, 360 градусов
Исходя из определений синуса, косинуса, тангенса и котангенса можно найти значения этих функций для углов 0 и 90 градусов
sin 0=0, cos 0=1, tg 0=0, котангенс нуля – не определен,
sin 90°=1, cos 90°=0, сtg 90°=0, тангенс дявяноста градусов не определен.
Значения синусов, косинусов, тангенсов и котангенсов в курсе геометрии определяются как соотношения сторон прямоугольного треугольника, углы которого равны 30, 60 и 90 градусов, и также 45, 45 и 90 градусов.
Синус (син) – отношение противолежащего катета к гипотенузе.
Косинус (кос) – отношение прилежащего катета к гипотенузе.
Тангенс (танг) – отношение противолежащего катета к прилежащему.
Котангенс (котанг) – отношение прилежащего катета к противолежащему.
В соответствии с определениями находятся значения функций:
sin 30°=12, cos 30°=32, tg 30°=33, ctg 30°=3,sin 45°=22, cos 45°=22, tg 45°=1, ctg 45°=1,sin 60°=32, cos 45°=12, tg 45°=3, ctg 45°=33.
Сведем эти значения в таблицу и назовем ее таблицей основных значений косинуса и синуса, тангенса и котангенса.
| α° | 0 | 30 | 45 | 60 | 90 |
| sin α | 0 | 12 | 22 | 32 | 1 |
| cos α | 1 | 32 | 22 | 12 | 0 |
| tg α | 0 | 33 | 1 | 3 | не определен |
| ctg α | не определен | 3 | 1 | 33 | 0 |
| α, радиан | 0 | π6 | π4 | π3 | π2 |
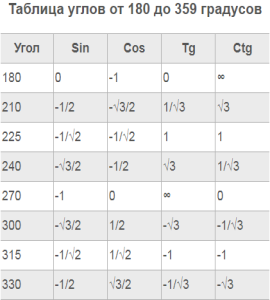
Одно из важных свойств тригонометрических функций, представленное в таблице в тригонометрии и важное для изучения – периодичность. На основе этого свойства данную таблицу можно расширить,используя формулы приведения. Ниже представим расширенную таблицу значений основных тригонометрических функций для углов 0, 30, 60, … ,120, 135, 150, 180, … , 360 градусов ( 0 , π 6 , π 3 , π 2 , . . . , 2 π радиан).
| α° | 0 | 30 | 45 | 60 | 90 | 120 | 135 | 150 | 180 | 210 | 225 | 240 | 270 | 300 | 315 | 330 | 360 |
| sin α | 0 | 12 | 22 | 32 | 1 | 32 | 22 | 12 | 0 | -12 | -22 | -32 | -1 | -32 | -22 | -12 | 0 |
| cos α | 1 | 32 | 22 | 12 | 0 | -12 | -22 | -32 | -1 | -32 | -22 | -12 | 0 | 12 | 22 | 32 | 1 |
| tg α | 0 | 33 | 1 | 3 | – | -1 | -33 | 0 | 0 | 33 | 1 | 3 | – | -3 | -1 | 0 | |
| ctg α | – | 3 | 1 | 33 | 0 | -33 | -1 | -3 | – | 3 | 1 | 33 | 0 | -33 | -1 | -3 | – |
| α, радиан | 0 | π6 | π4 | π3 | π2 | 2π3 | 3π4 | 5π6 | π | 7π6 | 5π4 | 4π3 | 3π2 | 5π3 | 7π4 | 11π6 | 2π |
Периодичность синуса, косинуса, тангенса и котангенса позволяет расширять табличные значения углов сколько угодно. Значения, собранные в таблице, часто используются при решении задач (чаще всего), поэтому их рекомендуется запоминать и выучивать наизусть.
Как пользоваться таблицей основных значений тригонометрических функций
Принцип пользования таблицей значений тангенсов и котангенсов, а также синусов и косинусов, понятен на интуитивном уровне (но это не означает, что их не стоит изучать и заучивать). Пересечение строки и столбца дает значение функции для конкретного угла.
Нужно узнать, чему равен sin 7π6
Находим в таблице столбец, значение последней ячейки которого равно 7π6 радиан – то же самое, что 210 градусов. Затем выбираем сроку таблицы, в которой представлены значения синусов. На пересечении строки и столбца будем находить искомое значение:
sin 7π6=-12
Таблицы Брадиса
Таблица Брадиса позволяет вычислить значение синуса, косинуса, тангенса или котангенса с точностью до 4-х знаков после запятой без использования вычислительной техники (как и в решении предыдущего уравнения). Это своего рода замена инженерному калькулятору.
Владимир Модестович Брадис (1890 – 1975) – советский математик-педагог, с 1954 года член-корреспондент АПН СССР. Таблицы четырёхзначных логарифмов и натуральных тригонометрических величин, разработанные Брадисом, впервые вышли в 1921 году.
Сначала приведем таблицу Брадиса для синусов и косинусов. Она позволяет достаточно точно вычислять приближенные значения этих функций для углов, содержащих целое количество градусов и минут. В крайнем левом столбце таблицы представлены градусы, а в верхней строке – минуты. Отметим, что все значения углов таблицы Брадиса кратны шести минутам.
Таблица Брадиса для синусов и косинусов
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | cos | 1′ | 2′ | 3′ |
| 0.0000 | 90° | ||||||||||||||
| 0° | 0.0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0.0872 | 85° | 3 | 6 | 9 |
| 5° | 0.0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 82° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 0.1736 | 80° | 3 | 6 | 9 |
| 10° | 0.1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 77° | 3 | 6 | 9 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 0.2588 | 75° | 3 | 6 | 8 |
| 15° | 0.2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 74° | 3 | 6 | 8 |
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 72° | 3 | 6 | 8 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0.3420 | 70° | 3 | 5 | 8 |
| 20° | 0.3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0.4226 | 65° | 3 | 5 | 8 |
| 25° | 0.4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 63° | 3 | 5 | 8 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0.5000 | 60° | 3 | 5 | 8 |
| 30° | 0.5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 59° | 3 | 5 | 8 |
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0.5736 | 55° | 2 | 5 | 7 |
| 35° | 0.5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0.5878 | 54° | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52° | 2 | 5 | 7 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0.6428 | 50° | 2 | 4 | 7 |
| 40° | 0.6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 47° | 2 | 4 | 6 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 8909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0.7071 | 45° | 2 | 4 | 6 |
| 45° | 0.7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0.7660 | 40° | 2 | 4 | 6 |
| 50° | 0.7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 38° | 2 | 4 | 5 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 36° | 2 | 3 | 5 |
| 54° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0.8192 | 35° | 2 | 3 | 5 |
| 55° | 0.8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 34° | 2 | 3 | 5 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 32° | 2 | 3 | 5 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0.8660 | 30° | 1 | 3 | 4 |
| 60° | 0.8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| 61° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 27° | 1 | 3 | 4 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0.9063 | 25° | 1 | 3 | 4 |
| 65° | 0.9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9256 | 9272 | 22° | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9383 | 9391 | 0.9397 | 20° | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0.9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0.9659 | 15° | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0.9848 | 10° | 1 | 1 | 2 |
| 80° | 0.9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 5° | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0.9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0° | 0 | 0 | 0 |
| 90° | 1.0000 | ||||||||||||||
| sin | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | 1′ | 2′ | 3′ |
Для нахождения значений синусов и косинусов углов, не представленных в таблице, необходимо использовать поправки.
Теперь приведем таблицу Брадиса для тангенсов и котангенсов. Она содержит значения тангенсов углов от 0 до 76 градусов, и котангенсов углов от 14 до 90 градусов.
Таблица Брадиса для тангенса и котангенса
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | ctg | 1′ | 2′ | 3′ |
| 0 | 90° | ||||||||||||||
| 0° | 0,000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87° | 3 | 6 | 9 |
| 3° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86° | 3 | 6 | 9 |
| 4° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 0,0875 | 85° | 3 | 6 | 9 |
| 5° | 0,0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84° | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 83° | 3 | 6 | 9 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 82° | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 81° | 3 | 6 | 9 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0,1763 | 80° | 3 | 6 | 9 |
| 10° | 0,1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 79° | 3 | 6 | 9 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78° | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 77° | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76° | 3 | 6 | 9 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0,2679 | 75° | 3 | 6 | 9 |
| 15° | 0,2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 74° | 3 | 6 | 9 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 73° | 3 | 6 | 9 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 72° | 3 | 6 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71° | 3 | 6 | 10 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0,3640 | 70° | 3 | 7 | 10 |
| 20° | 0,3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69° | 3 | 7 | 10 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 68° | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67° | 3 | 7 | 10 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 66° | 3 | 7 | 10 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0,4663 | 65° | 4 | 7 | 11 |
| 25° | 0,4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 64° | 4 | 7 | 11 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63° | 4 | 7 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 62° | 4 | 7 | 11 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 61° | 4 | 8 | 11 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0,5774 | 60° | 4 | 8 | 12 |
| 30° | 0,5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 59° | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 58° | 4 | 8 | 12 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 57° | 4 | 8 | 12 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 56° | 4 | 8 | 13 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0,7002 | 55° | 4 | 9 | 13 |
| 35° | 0,7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54° | 4 | 8 | 13 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 53° | 5 | 9 | 14° |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52° | 5 | 9 | 14 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 51° | 5 | 9 | 14 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0,8391 | 50° | 5 | 10 | 15 |
| 40° | 0,8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0,8693 | 49° | 5 | 10 | 15 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 48° | 5 | 10 | 16 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 47° | 6 | 11 | 16 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0,9657 | 46° | 6 | 11 | 17 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1,0000 | 45° | 6 | 11 | 17 |
| 45° | 1,0000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 0355 | 44° | 6 | 12 | 18 |
| 46° | 0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 0724 | 43° | 6 | 12 | 18 |
| 47° | 0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 1106 | 42° | 6 | 13 | 19 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 41° | 7 | 13 | 20 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1,1918 | 40° | 7 | 14 | 21 |
| 50° | 1,1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 39° | 7 | 14 | 22 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 38° | 8 | 15 | 23 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 37° | 8 | 16 | 24 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 36° | 8 | 16 | 25 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1,4281 | 35° | 9 | 17 | 26 |
| 55° | 1,4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 34° | 9 | 18 | 27 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 33° | 10 | 19 | 29 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 32° | 10 | 20 | 30 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 31° | 11 | 21 | 32 |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1,7321 | 30° | 11 | 23 | 34 |
| 60° | 1,732 | 1,739 | 1,746 | 1,753 | 1,760 | 1,767 | 1,775 | 1,782 | 1,789 | 1,797 | 1,804 | 29° | 1 | 2 | 4 |
| 61° | 1,804 | 1,811 | 1,819 | 1,827 | 1,834 | 1,842 | 1,849 | 1,857 | 1,865 | 1,873 | 1,881 | 28° | 1 | 3 | 4 |
| 62° | 1,881 | 1,889 | 1,897 | 1,905 | 1,913 | 1,921 | 1,929 | 1,937 | 1,946 | 1,954 | 1,963 | 27° | 1 | 3 | 4 |
| 63° | 1,963 | 1,971 | 1,980 | 1,988 | 1,997 | 2,006 | 2,014 | 2,023 | 2,032 | 2,041 | 2,05 | 26° | 1 | 3 | 4 |
| 64° | 2,050 | 2,059 | 2,069 | 2,078 | 2,087 | 2,097 | 2,106 | 2,116 | 2,125 | 2,135 | 2,145 | 25° | 2 | 3 | 5 |
| 65° | 2,145 | 2,154 | 2,164 | 2,174 | 2,184 | 2,194 | 2,204 | 2,215 | 2,225 | 2,236 | 2,246 | 24° | 2 | 3 | 5 |
| 66° | 2,246 | 2,257 | 2,267 | 2,278 | 2,289 | 2,3 | 2,311 | 2,322 | 2,333 | 2,344 | 2,356 | 23° | 2 | 4 | 5 |
| 67° | 2,356 | 2,367 | 2,379 | 2,391 | 2,402 | 2,414 | 2,426 | 2,438 | 2,450 | 2,463 | 2,475 | 22° | 2 | 4 | 6 |
| 68° | 2,475 | 2,488 | 2,5 | 2,513 | 2,526 | 2,539 | 2,552 | 2,565 | 2,578 | 2,592 | 2,605 | 21° | 2 | 4 | 6 |
| 69° | 2,605 | 2,619 | 2,633 | 2,646 | 2,66 | 2,675 | 2,689 | 2,703 | 2,718 | 2,733 | 2,747 | 20° | 2 | 5 | 7 |
| 70° | 2,747 | 2,762 | 2,778 | 2,793 | 2,808 | 2,824 | 2,840 | 2,856 | 2,872 | 2,888 | 2,904 | 19° | 3 | 5 | 8 |
| 71° | 2,904 | 2,921 | 2,937 | 2,954 | 2,971 | 2,989 | 3,006 | 3,024 | 3,042 | 3,06 | 3,078 | 18° | 3 | 6 | 9 |
| 72° | 3,078 | 3,096 | 3,115 | 3,133 | 3,152 | 3,172 | 3,191 | 3,211 | 3,230 | 3,251 | 3,271 | 17° | 3 | 6 | 10 |
| 73° | 3,271 | 3,291 | 3,312 | 3,333 | 3,354 | 3,376 | 3 | 7 | 10 | ||||||
| 3,398 | 3,42 | 3,442 | 3,465 | 3,487 | 16° | 4 | 7 | 11 | |||||||
| 74° | 3,487 | 3,511 | 3,534 | 3,558 | 3,582 | 3,606 | 4 | 8 | 12 | ||||||
| 3,630 | 3,655 | 3,681 | 3,706 | 3,732 | 15° | 4 | 8 | 13 | |||||||
| 75° | 3,732 | 3,758 | 3,785 | 3,812 | 3,839 | 3,867 | 4 | 9 | 13 | ||||||
| 3,895 | 3,923 | 3,952 | 3,981 | 4,011 | 14° | 5 | 10 | 14 | |||||||
| tg | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | 1′ | 2′ | 3′ |
Как пользоваться таблицами Брадиса
Рассмотрим таблицу Брадиса для синусов и косинусов. Все, что относится к синусам, находится вверху и слева. Если нам нужны косинусы – смотрим на правую сторону внизу таблицы.
Для нахождения значений синуса угла нужно найти пересечение строки, содержащей в крайней левой ячейке необходимое количество градусов, и столбца, содержащего в верхней ячейке необходимое число минут.
Если точного значения угла нет в таблице Брадиса, прибегаем к помощи поправок. Поправки на одну, две и три минуты даны в крайних правых столбцах таблицы. Для нахождения значения синуса угла, которого нет в таблице, находим самое близкое к нему значение. После этого прибавляем или отнимаем поправку, соответствующую разнице между углами.
В случае, если мы ищем синус угла, который больше 90 градусов, сначала нужно воспользоваться формулами приведения, а уже потом – таблицей Брадиса.
Пусть нужно найти синус угла 17°44′. По таблице находим тождество синус 17°42′ и прибавляем к его значению поправку на две минуты:
17°44′-17°42’=2′ (необходимая поправка)sin 17°44’=0.3040+0.0006=0.3046
Принцип работы с косинусами, тангенсами и котангенсами аналогичен. Однако, важно помнить о знаке поправок.
При вычислении значений синусов поправка имеет положительный знак, а при вычислении косинусов поправку необходимо брать с отрицательным знаком.
