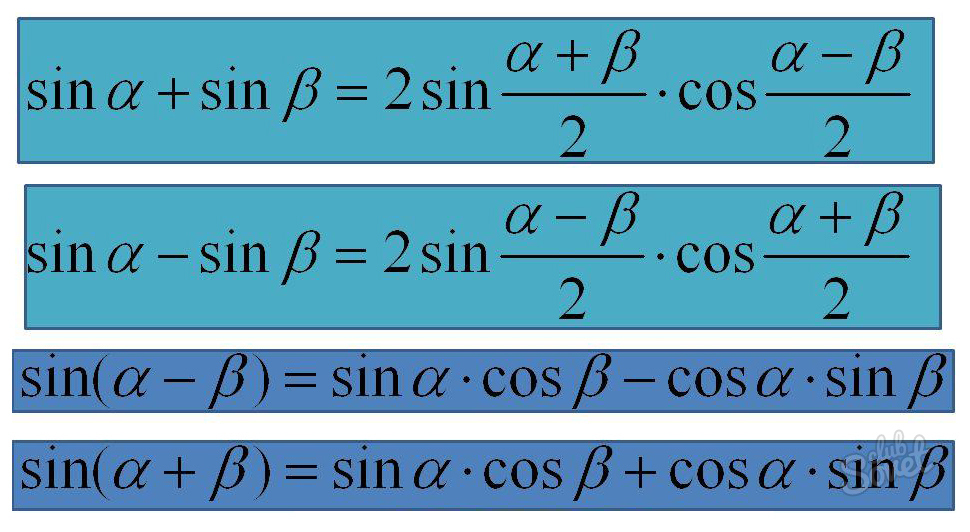Содержание материала
- Синус, косинус, тангенс и котангенс. Определения
- Видео
- Теорема косинусов
- Формула Герона
- Решение треугольников
- Пример (решение треугольника по двум сторонам и углу между ними).
- Пример (решение треугольника по стороне и двум прилежащим к ней углам).
- Пример (решение треугольника по трем сторонам).
- Пример
- Пример
- Примеры решения задач с использованием теоремы синусов и теоремы косинусов
- Пример
- Пример
- Пример
- Теорема Стюарта
- Пример
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cosα) — отношение прилежащего катета к гипотенузе.
Тангенс угла (tg α) — отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Видео
Теорема косинусов
Теорема косинусов позволяет выразить длину любой стороны треугольника через длины двух других его сторон и косинус угла между ними (например, длину стороны  треугольника АВС (рис. 165) через длины сторон
треугольника АВС (рис. 165) через длины сторон  ). Теорему косинусов можно назвать самой «работающей» в геометрии. Она имеет многочисленные следствия, которые часто используются при решении задач.
). Теорему косинусов можно назвать самой «работающей» в геометрии. Она имеет многочисленные следствия, которые часто используются при решении задач.

Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними, т. е.


Доказательство:
Докажем теорему для случая, когда в треугольнике АВС угол А и угол С острые (рис. 166). Проведем высоту ВН к стороне АС. Из  находим
находим  откуда
откуда  Из
Из  по теореме Пифагора
по теореме Пифагора 

По основному тригонометрическому тождеству  Тогда
Тогда 
Справедливость теоремы для случаев, когда  или
или  тупой или прямой, докажите самостоятельно. Теорема доказана. Для сторон
тупой или прямой, докажите самостоятельно. Теорема доказана. Для сторон  теорема косинусов запишется так:
теорема косинусов запишется так:
 Замечание. Если
Замечание. Если  , то по теореме Пифагора
, то по теореме Пифагора  Так как
Так как  то
то  Таким образом, теорема Пифагора — частный случай теоремы косинусов. С помощью теоремы косинусов можно решить следующие задачи:
Таким образом, теорема Пифагора — частный случай теоремы косинусов. С помощью теоремы косинусов можно решить следующие задачи:
• зная две стороны и угол между ними, найти третью сторону треугольника;
• зная две стороны и угол, противолежащий одной из этих сторон, найти третью сторону (рис. 167) (в этом случае возможны два решения).

Рассмотрим следствия из теоремы косинусов, которые дают возможность решить еще целый ряд задач.
Следствие:
Теорема косинусов позволяет, зная три стороны треугольника, найти его углы (косинусы углов). Из равенства  следует формула
следует формула

Для углов  получим:
получим:

Пример:
В треугольнике АВС стороны АВ = 8, ВС = 5, АС = 7. Найдем ZB (рис. 168).

По теореме косинусов

Используя записанную выше формулу, можно сразу получить:

Следствие:
С помощью теоремы косинусов можно по трем сторонам определить вид треугольника: остроугольный, прямоугольный или тупоугольный.
Так, из формулы  с учетом того, что
с учетом того, что  следует:
следует:
- если
 то
то  и угол
и угол  острый;
острый; - если
 то
то  и угол
и угол  тупой;
тупой; - если
 то
то  и угол
и угол  прямой.
прямой.
При определении вида треугольника достаточно найти знак косинуса угла, лежащего против большей стороны, поскольку только больший угол треугольника может быть прямым или тупым.
Пример:
Выясним, каким является треугольник со сторонами a = 2, 6 = 3 и с = 4. Для этого найдем знак косинуса угла у, лежащего против большей стороны с. Так как  то
то  угол
угол  тупой и данный треугольник тупоугольный.
тупой и данный треугольник тупоугольный.
Сформулируем правило определения вида треугольника (относительно углов). Треугольник является:
- остроугольным, если квадрат его большей стороны меньше суммы квадратов двух других его сторон:

- тупоугольным, если квадрат его большей стороны больше суммы квадратов двух других его сторон:

- прямоугольным, если квадрат его большей стороны равен сумме квадратов двух других его сторон:

Следствие:
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: 

Доказательство:
Пусть в параллелограмме ABCD  — острый, откуда
— острый, откуда  — тупой (рис. 169). По теореме косинусов из
— тупой (рис. 169). По теореме косинусов из 
 (1) Из
(1) Из  Поскольку cos
Поскольку cos  то
то
 (2)
(2)
Сложив почленно равенство (1) и равенство (2), получим  что и требовалось доказать.
что и требовалось доказать.
Данная формула дает возможность:
- • зная две соседние стороны и одну из диагоналей параллелограмма, найти другую диагональ;
- • зная две диагонали и одну из сторон параллелограмма, найти соседнюю с ней сторону.
Следствие:
Медиану  треугольника со сторонами а, b и с можно найти по формуле
треугольника со сторонами а, b и с можно найти по формуле 

Доказательство:
Рассмотрим 
 — медиана треугольника (рис. 170). Продлим медиану AM за точку М на ее длину:
— медиана треугольника (рис. 170). Продлим медиану AM за точку М на ее длину: 
Проведем отрезки BD и DC. Так как у четырехугольника ABDC диагонали AD и ВС точкой пересечения делятся пополам, то он — параллелограмм. По свойству диагоналей параллелограмма 
 Отсюда следует, что
Отсюда следует, что  Утверждение доказано.
Утверждение доказано.
Аналогично: 
Формула медианы позволяет:
- зная три стороны треугольника, найти любую из его медиан;
- зная две стороны и медиану, проведенную к третьей стороне, найти третью сторону;
- зная три медианы, найти любую из сторон треугольника.
Пример:
а) Дан треугольник АВС, а = 5, 5 = 3,  Найти сторону с. б) Дан треугольник АВС, а = 7, с = 8, а = 60°. Найти сторону Ь.
Найти сторону с. б) Дан треугольник АВС, а = 7, с = 8, а = 60°. Найти сторону Ь.
Решение:
а) По теореме косинусов 
 Отсюда
Отсюда  б) Пусть
б) Пусть  По теореме косинусов
По теореме косинусов  то есть
то есть 
 Отсюда
Отсюда  или
или  так как для наборов длин отрезков 7, 3, 8 и 7, 5, 8 выполняется неравенство треугольника. Ответ: а) 7; б) 3 или 5.
так как для наборов длин отрезков 7, 3, 8 и 7, 5, 8 выполняется неравенство треугольника. Ответ: а) 7; б) 3 или 5.
Пример:
Две стороны треугольника равны 6 и 10, его площадь —  Найти третью сторону треугольника при условии, что противолежащий ей угол — тупой.
Найти третью сторону треугольника при условии, что противолежащий ей угол — тупой.

Решение:
Пусть в  стороны АВ = 6, ВС = 10 и
стороны АВ = 6, ВС = 10 и  (рис. 171). Поскольку
(рис. 171). Поскольку  то
то  откуда
откуда  Так как
Так как  и по условию
и по условию  — тупой, то
— тупой, то  . Для нахождения стороны АС применим теорему косинусов:
. Для нахождения стороны АС применим теорему косинусов:
Ответ: 14.
Пример:
Найти площадь треугольника, две стороны которого равны 6 и 8, а медиана, проведенная к третьей стороне, равна 5.

Решение:
Обозначим стороны треугольника 
 Пусть
Пусть  — медиана (рис. 172). По формуле медианы
— медиана (рис. 172). По формуле медианы  откуда
откуда 

 По обратной теореме Пифагора данный треугольник со сторонами 6, 8 и 10 — прямоугольный, его площадь равна половине произведения катетов:
По обратной теореме Пифагора данный треугольник со сторонами 6, 8 и 10 — прямоугольный, его площадь равна половине произведения катетов: Ответ: 24.
Ответ: 24.
Формула Герона
Мы знаем, как найти площадь треугольника по основанию и высоте, проведенной к этому основанию:  а также по двум сторонам и углу между ними:
а также по двум сторонам и углу между ними:  Теперь мы выведем формулу нахождения площади треугольника по трем сторонам.
Теперь мы выведем формулу нахождения площади треугольника по трем сторонам.
Теорема (формула Герона).
Площадь треугольника со сторонами  можно найти по формуле
можно найти по формуле  где
где  — полупериметр треугольника.
— полупериметр треугольника.

Доказательство:
 (рис. 183). Из основного тригонометрического тождества
(рис. 183). Из основного тригонометрического тождества  следует, что
следует, что  Для
Для  синус положительный. Поэтому
синус положительный. Поэтому  Из теоремы косинусов
Из теоремы косинусов  откуда
откуда 
Тогда 

Так как
 Теорема доказана.
Теорема доказана.
Решение треугольников
Решением треугольника называется нахождение его неизвестных сторон и углов (иногда других элементов) по данным, определяющим треугольник.
Такая задача часто встречается на практике, например в геодезии, астрономии, строительстве, навигации.
Рассмотрим алгоритмы решения трех задач.
Пример (решение треугольника по двум сторонам и углу между ними)

Дано:  (рис. 184).
(рис. 184).
Найти : 
Решение:
Рис. 184 1) По теореме косинусов 
2) По следствию из теоремы косинусов 
3) Угол  находим при помощи калькулятора или таблиц.
находим при помощи калькулятора или таблиц.
4) Угол  Замечание. Нахождение угла
Замечание. Нахождение угла  по теореме синусов
по теореме синусов  требует выяснения того, острый или тупой угол
требует выяснения того, острый или тупой угол 
Пример (решение треугольника по стороне и двум прилежащим к ней углам)

Дано:  (рис. 185).
(рис. 185).
Найти: 
Решение:
1) Угол 
2) По теореме синусов  (sin
(sin  и sin
и sin  находим при помощи калькулятора или таблиц).
находим при помощи калькулятора или таблиц).
3) Сторону с можно найти с помощью теоремы косинусов или теоремы синусов:  или
или  (cos
(cos  и sin
и sin  находим при помощи калькулятора или таблиц).
находим при помощи калькулятора или таблиц).
Пример (решение треугольника по трем сторонам)
Дано:  (рис. 186).
(рис. 186).

Найти:  и радиус R описанной окружности.
и радиус R описанной окружности.
Решение:
1) По следствию из теоремы косинусов

2) Зная  угол
угол  находим при помощи калькулятора или таблиц.
находим при помощи калькулятора или таблиц.
3) Аналогично находим угол 
4) Угол 
5) Радиус R описанной окружности треугольника можно найти по формуле  где
где 
Замечание*. Вторым способом нахождения R будет нахождение косинуса любого угла при помощи теоремы косинусов  затем нахождение по косинусу угла его синуса
затем нахождение по косинусу угла его синуса  и, наконец, использование теоремы синусов
и, наконец, использование теоремы синусов  для нахождения R.
для нахождения R.
Пример
Найти площадь S и радиус R описанной окружности треугольника со сторонами 9, 12 и 15.
Решение:
Способ 1. Воспользуемся формулой Герона. Обозначим а = 9, b = 12, с = 15. Получим: 

 Тогда
Тогда 
 Радиус R описанной окружности найдем из формулы
Радиус R описанной окружности найдем из формулы  Имеем:
Имеем:  Ответ:
Ответ:  Способ 2. Так как
Способ 2. Так как  поскольку
поскольку  то треугольник — прямоугольный по обратной теореме Пифагора. Его площадь равна половине произведения катетов:
то треугольник — прямоугольный по обратной теореме Пифагора. Его площадь равна половине произведения катетов:  а радиус описанной окружности равен половине гипотенузы:
а радиус описанной окружности равен половине гипотенузы: 
Пример
Найти площадь трапеции с основаниями, равными 5 и 14, и боковыми сторонами, равными 10 и 17.

Решение:
Пусть в трапеции ABCD основания AD = 14 и ВС = 5, боковые стороны АВ = 10 и  Проведем
Проведем  (рис. 187). Так как АВСК — параллелограмм, то СК = АВ = 10, АК = ВС = 5, откуда KD = AD — АК = 9. Найдем высоту СН треугольника KCD, которая равна высоте трапеции. Площадь треугольника KCD найдем по формуле Герона, обозначив его стороны а = 10, b = 17, с = 9. Получим:
(рис. 187). Так как АВСК — параллелограмм, то СК = АВ = 10, АК = ВС = 5, откуда KD = AD — АК = 9. Найдем высоту СН треугольника KCD, которая равна высоте трапеции. Площадь треугольника KCD найдем по формуле Герона, обозначив его стороны а = 10, b = 17, с = 9. Получим:


 Так как
Так как  СН = 8. Площадь трапеции
СН = 8. Площадь трапеции 
Ответ: 76.
Примеры решения задач с использованием теоремы синусов и теоремы косинусов
Пример:
Внутри угла А, равного 60°, взята точка М, которая находится на расстоянии 1 от одной стороны угла и на расстоянии 2 от другой стороны. Найти расстояние от точки М до вершины угла А (рис. 189, а).

Решение:
Пусть 
 Найдем длину отрезка AM. Сумма углов четырехугольника АВМС равна 360°. Поэтому
Найдем длину отрезка AM. Сумма углов четырехугольника АВМС равна 360°. Поэтому  Так как в четырехугольнике АВМС
Так как в четырехугольнике АВМС  , то около него можно описать окружность по признаку вписанного четырехугольника (рис. 189, б). Поскольку прямой вписанный угол опирается на диаметр, то отрезок AM — диаметр этой окружности, т. е.
, то около него можно описать окружность по признаку вписанного четырехугольника (рис. 189, б). Поскольку прямой вписанный угол опирается на диаметр, то отрезок AM — диаметр этой окружности, т. е.  где R — радиус. Из
где R — радиус. Из  по теореме косинусов
по теореме косинусов 
 Из
Из  по теореме синусов
по теореме синусов  откуда
откуда 

Ответ:  Замечание. Вторым способом решения будет продление отрезка ВМ до пересечения с лучом АС и использование свойств полученных прямоугольных треугольников. Рассмотрите этот способ самостоятельно.
Замечание. Вторым способом решения будет продление отрезка ВМ до пересечения с лучом АС и использование свойств полученных прямоугольных треугольников. Рассмотрите этот способ самостоятельно.
Пример
В прямоугольном треугольнике АВС известно: 
 высота СН = 2 (рис. 190). Найти гипотенузу АВ.
высота СН = 2 (рис. 190). Найти гипотенузу АВ.

Решение:
Построим  симметричный
симметричный  относительно прямой АВ (см. рис. 190). Поскольку
относительно прямой АВ (см. рис. 190). Поскольку  то вокруг четырехугольника
то вокруг четырехугольника  можно описать окружность, где АВ — диаметр этой окружности (прямой вписанный угол опирается на диаметр). Треугольник
можно описать окружность, где АВ — диаметр этой окружности (прямой вписанный угол опирается на диаметр). Треугольник  вписан в эту окружность,
вписан в эту окружность,  По теореме синусов
По теореме синусов  откуда
откуда  Ответ: 8.
Ответ: 8.
Пример
Дан прямоугольный треугольник АВС с катетами ВС = а и АС =  На гипотенузе АВ как на стороне построен квадрат ADFB (рис. 191). Найти расстояние от центра О этого квадрата до вершины С прямого угла, т. е. отрезок СО.
На гипотенузе АВ как на стороне построен квадрат ADFB (рис. 191). Найти расстояние от центра О этого квадрата до вершины С прямого угла, т. е. отрезок СО.

Решение:
Способ 1. Так как  (диагонали квадрата ADFB взаимно перпендикулярны), то
(диагонали квадрата ADFB взаимно перпендикулярны), то  поэтому четырехугольник АОВС является вписанным в окружность, ее диаметр
поэтому четырехугольник АОВС является вписанным в окружность, ее диаметр  Тогда
Тогда 
Пусть СО = х. По теореме косинусов из  находим
находим 
из  находим
находим 
По свойству вписанного четырехугольника  Поскольку
Поскольку  то
то  откуда находим
откуда находим  Тогда
Тогда  .
.
Способ 2. Используем теорему Птолемея, которая гласит: «Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон». Для нашей задачи получаем (см. рис. 191):



Способ 3. Достроим  до квадрата CMNK, как показано на рисунке 192. Можно показать, что центр квадрата CMNK совпадет с центром квадрата ADFB, т. е. с точкой О (точки В и D симметричны относительно центров обоих квадратов). Тогда
до квадрата CMNK, как показано на рисунке 192. Можно показать, что центр квадрата CMNK совпадет с центром квадрата ADFB, т. е. с точкой О (точки В и D симметричны относительно центров обоих квадратов). Тогда  Ответ:
Ответ: 
Пример
Точка О — центр окружности, вписанной в треугольник АВС,  Найти стороны треугольника (см. задачу 232*).
Найти стороны треугольника (см. задачу 232*).

Решение:
Пусть  и
и  — радиус вписанной окружности (рис. 193). Тогда
— радиус вписанной окружности (рис. 193). Тогда 
Отсюда 
 Применим формулу Герона:
Применим формулу Герона:


С другой стороны,  Из уравнения
Из уравнения  находим
находим  = 2. Откуда
= 2. Откуда  (см),
(см),  (см),
(см),  (см). Ответ: 15 см; 20 см; 7 см.
(см). Ответ: 15 см; 20 см; 7 см.
Теорема Стюарта
Следующая теорема позволяет найти длину отрезка, соединяющего вершину треугольника с точкой на противоположной стороне.
Теорема Стюарта. «Если а, b и с — стороны треугольника и отрезок d делит сторону с на отрезки, равные х и у (рис. 194), то справедлива формула


Доказательство:
По теореме косинусов из  и
и  (см. рис. 194) следует:
(см. рис. 194) следует:
 (1)
(1)
 (2)
(2)
Умножим обе части равенства (1) на у, равенства (2) — на 

Сложим почленно полученные равенства:  Из последнего равенства выразим
Из последнего равенства выразим 
 Теорема доказана.
Теорема доказана.
Следствие:
Биссектрису треугольника можно найти по формуле (рис. 195)


Доказательство:
По свойству биссектрисы треугольника  Разделив сторону
Разделив сторону  с в отношении
с в отношении  получим:
получим:
 По теореме Стюарта
По теореме Стюарта 

Пример
Доказать, что если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера—Лемуса).

Доказательство:
Пусть дан треугольник АВС,  — биссектрисы, проведенные к сторонам ВС = а и АС = b соответственно, и
— биссектрисы, проведенные к сторонам ВС = а и АС = b соответственно, и  (рис. 196). Нужно доказать, что
(рис. 196). Нужно доказать, что  Выразим
Выразим  и через
и через  и приравняем полученные выражения. Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Поэтому
и приравняем полученные выражения. Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Поэтому  откуда
откуда 
 откуда
откуда 
По формуле биссектрисы треугольника 

Из условия  следует:
следует:  Перенеся слагаемые в одну сторону равенства и разложив на множители (проделайте это самостоятельно), получим:
Перенеся слагаемые в одну сторону равенства и разложив на множители (проделайте это самостоятельно), получим:  Отсюда
Отсюда  (второй множитель при положительных
(второй множитель при положительных  больше нуля). Утверждение доказано.
больше нуля). Утверждение доказано.
Теги
Как найти синус?
Решение многих как алгебраических, так и геометрических задач невозможно без использования такой тригонометрической функции как синус. Для нахождения величины синуса можно использовать как собственно определение функции, так и соотношения тождеств тригонометрии, формулы приведения, а также теорему синусов. С каждым из данных способов более подробно и познакомит данная статья.
1
Нахождение величины синуса по определению
Формулировка термина “синус” определяет данную тригонометрическую величину как соотношение определенных сторон прямоугольного треугольника – отношение катета, лежащего против искомого угла, к гипотенузе.
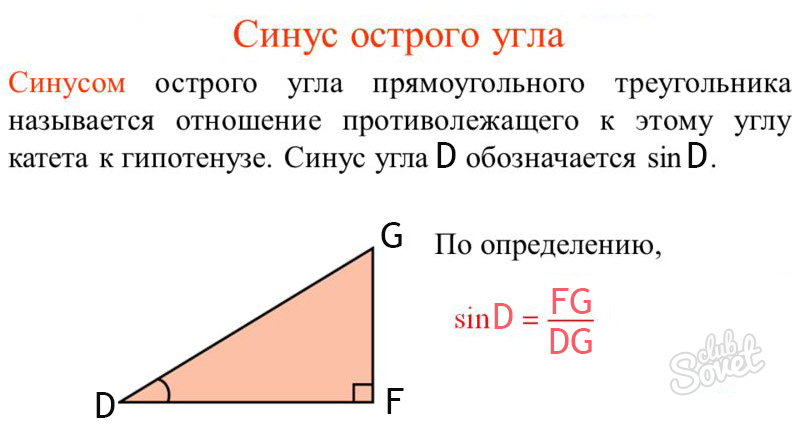
Рассмотрим ΔDFG, ∠DFG = 90°. Тогда:
- sinD = FG / DG,
- FG — противолежащий катет,
- DG — гипотенуза представленного треугольника.
2
Нахождение величины синуса через формулу теоремы синусов
Данная теорема является универсальной, т.к. позволяет установить соотношение между углами и сторонами не только прямоугольного, то и произвольного треугольника.
Рассмотрим ΔLMN,
- MN = l, NL = m, ML = n.
- ∠M = η, ∠N = μ, ∠L = γ.
Для произвольного треугольника ΔLMN верно соотношение l / sinL = m / sinM = n / sinN – каждая сторона треугольника пропорциональна синусу угла, напротив которого она располагается.
Обозначив радиус описанной около треугольника окружности через R, соотношение теоремы синусов справедливо в следующей форме:
l / sinL = m / sinM = n / sinN = 2R.
Из соотношения следует:
sinL = l / 2R,
sinM = m / 2R,
sinN = n / 2R.
3
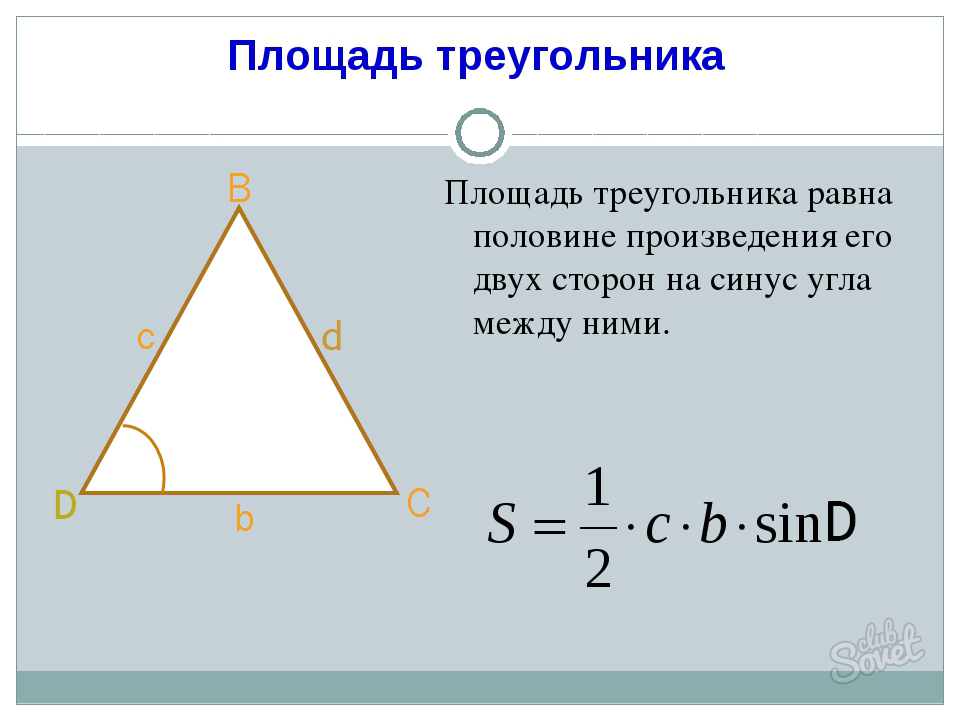
Нахождение величины синуса через площадь треугольника
Перед вами ΔDBC со сторонами
DB = c,
BC = d,
DC = b.
Для нахождения площади треугольника можно воспользоваться соотношением S = bc / 2sinD (или S = cd / 2sinB, или S = bd / 2sinC). Из этого следует, что:
- sinD = bc / 2S,
- sinB = cd / 2S,
- sinC = bd / 2S.
4
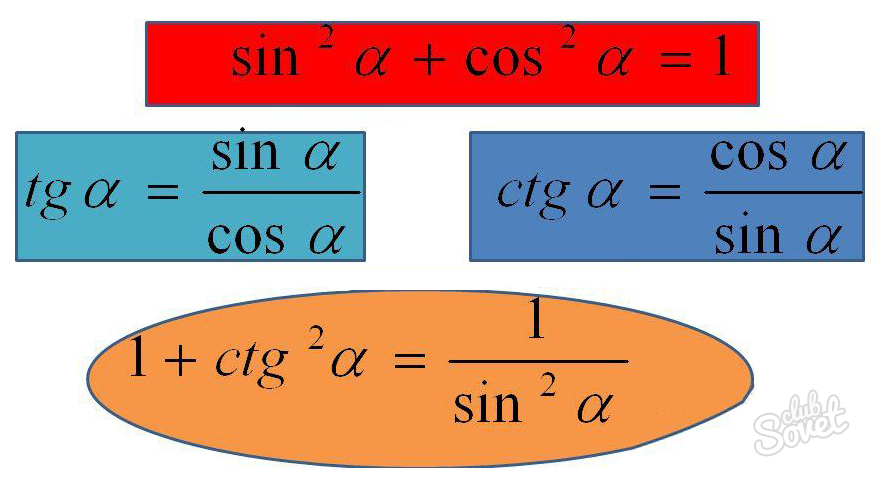
Нахождение величины синуса через тождества тригонометрии
Тождественные выражения справедливы для угла любой градусной меры.
- cos2φ + sin2φ = 1 ⇒ sin2φ = 1 — cos2φ ⇒ ΙsinφΙ = √ 1 — cos2φ ⇒ sinφ = ±√ 1 — cos2φ.
- tgφ = sinφ / cosφ ⇒ sinφ = cosφ * tgφ.
- ctgφ = cosφ / sinφ ⇒ sinφ = cosφ / ctgφ.
- 1/sin2φ = ctg2φ + 1 ⇒ sin2φ = 1 / (ctg2φ + 1) ⇒ ΙsinφΙ = 1 / √ctg2φ + 1 ⇒ sinφ = ± 1 / √ctg2φ + 1.
5
Нахождение величины синуса через формулы преобразования
- sin(η + μ) = sinη * cosμ + cosη * sinμ,
- sin(η – μ) = sinη * cosμ – cosη * sinμ,
- sinη + sinμ = 2sin((η + μ)/2) * cos((η – μ)/2),
- sinη – sinμ = 2cos((η + μ)/2) * sin((η – μ)/2)
- sinη * sinμ = (cos(η – μ) – cos(η + μ))/2,
- sinη = 2tg(η/2) / (1 + tg2(η/2)).
- sin2η =2sinη * cosη,
- sin3η =3sinη – 4sin3η.
6
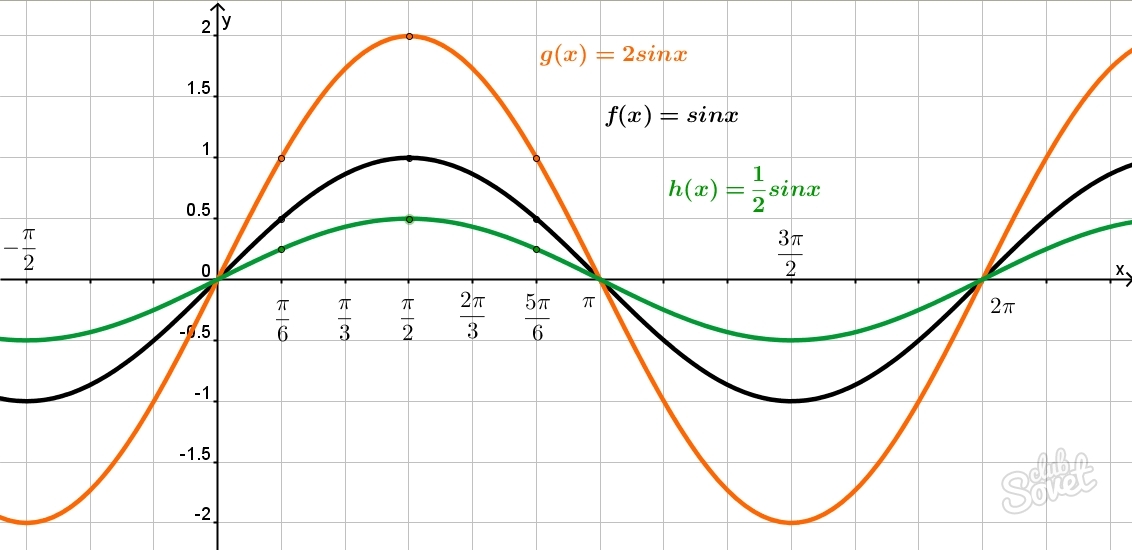
Нахождение синуса угла – табличные величины
Воспользовавшись таблицей Брадиса, можно определить значение синуса для каждого угла в промежутке от 0° до 360°. Наиболее часто при решении задач школьного курса геометрии используются следующие табличные величины:
- sin0° = 0, sin90° = 1,
- sin30° = 1/2, sin180° = 0,
- sin60° = √3/2, sin270° = -1,
- sin45° = √2/2, sin360° = 0.
Содержание:
- Формулировка теоремы синусов
- Расширенная теорема синусов
- Примеры решения задач
- Историческая справка
Формулировка теоремы синусов
Теорема
Стороны треугольника пропорциональны синусам противолежащих углов.
$frac{a}{sin alpha}=frac{b}{sin beta}=frac{c}{sin gamma}$
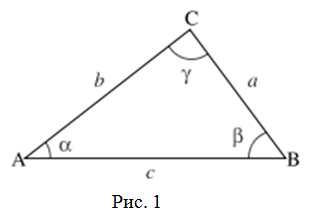
Теорема синусов устанавливает зависимость между сторонами треугольника и противолежащими им углами.
Расширенная теорема синусов
Теорема
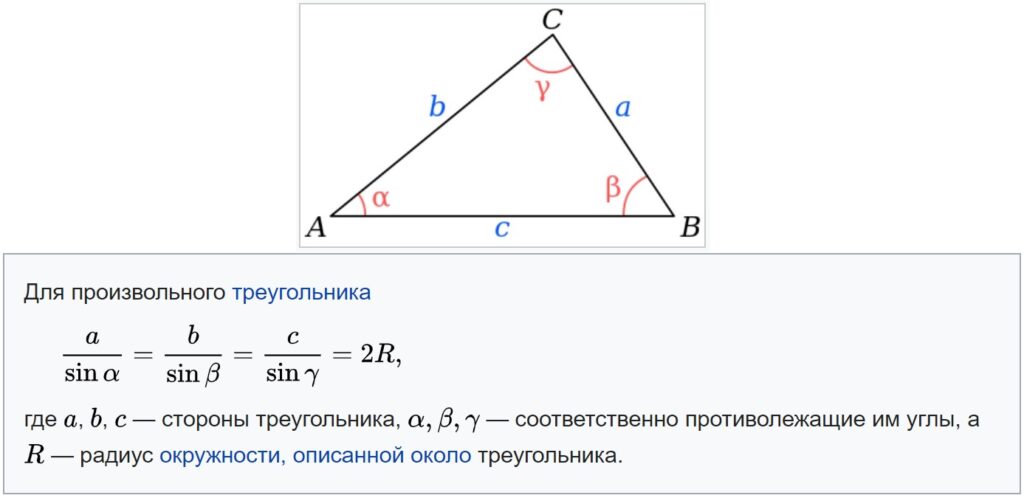
Для произвольного треугольника имеет место соотношение:
$frac{a}{sin alpha}=frac{b}{sin beta}=frac{c}{sin gamma}=2 R$
Здесь $R$ – радиус окружности, описанной около рассматриваемого треугольника.
Примеры решения задач
Пример
Задание. Основание треугольника равно 10 см, один из углов при основании равен
$45^{circ}$, а противолежащий основанию угол равен $60^{circ}$. Найдите сторону, противолежащую углу в
$45^{circ}$.
Решение. Пусть искомая сторона – $x$ см. Тогда по теореме синусов имеем:
$$frac{10}{sin 60^{circ}}=frac{x}{sin 45^{circ}} Rightarrow x=frac{10 cdot frac{sqrt{2}}{2}}{frac{sqrt{3}}{2}}=frac{10 sqrt{2}}{sqrt{3}}=frac{10 sqrt{6}}{3} (mathrm{см})$$
Ответ.$frac{10 sqrt{6}}{3}(mathrm{см})$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В треугольнике $A B C quad angle A=45^{circ}, angle C=15^{circ},$
$B C=4 sqrt{6}$. Найти $A C$ .
Решение. Согласно
теореме о сумме углов треугольника
$$angle A+angle B+angle C=180^{circ} Rightarrow angle B=180^{circ}-45^{circ}-15^{circ}=$$
Сторону $AC$ найдем по теореме синусов:
$$frac{A C}{sin angle B}=frac{B C}{sin angle A} Rightarrow frac{A C}{sin angle 120^{circ}}=frac{4 sqrt{6}}{sin angle 45^{circ}} Rightarrow$$
$$Rightarrow frac{A C}{frac{sqrt{3}}{2}}=frac{4 sqrt{6}}{frac{sqrt{2}}{2}} Rightarrow A C=frac{4 sqrt{18}}{sqrt{2}}=4 cdot sqrt{9}=12$$
Ответ. $A C=12$
Историческая справка
Самое древнее доказательство для теоремы синусов на плоскости описано в книге “Трактат о полном четырёхстороннике” персидского математика,
механика и астронома Насира ад-Дина Ат-Туси (1201 – 1274), которая была написана в 13 веке. Теорема синусов для сферического треугольника
была доказана математиками средневекового Востока ещё в 10 веке. В труде западноарабского математика, астронома и законоведа
Ал-Джайяни (989 – 1050) 11 века “Книга о неизвестных дугах сферы” приводилось общее доказательство теоремы синусов на сфере.
Теорема синусов. Доказательство
Тебе уже известно, что около каждого треугольника можно описать окружность. Мы это и сделаем. А потом проведём диаметр ( displaystyle BO).
Пусть этот диаметр пересекает окружность в точке ( displaystyle K). Давай рассмотрим ( displaystyle Delta BKC).
Что же это за треугольник?
Ну, конечно же, прямоугольный, ведь в ( displaystyle Delta BKC) угол ( displaystyle C) опирается на диаметр ( displaystyle BKquadRightarrow quadangle C=90{}^circ ) (вспоминаем тему «Вписанный и центральный угол окружности»).
Но и кроме того, ( displaystyle angle K) в ( displaystyle Delta BKC) равен ( displaystyle angle A) в ( displaystyle Delta ABC), потому что эти углы опираются на одну дугу ( displaystyle BC) (опять вспоминаем ту же тему).
А теперь просто запишем выражение для синуса ( displaystyle angle K) в прямоугольном ( displaystyle Delta BKC) ( displaystyle sin angle K=frac{a}{BK}).
Но ведь ( displaystyle BK) – диаметр ( displaystyle quadRightarrowquad BK=2R), и ( displaystyle sin angle K=frac{a}{2R}).
Вспомним, что ( displaystyle angle K=angle A) и получим ( displaystyle sin angle A=frac{a}{2R}quadRightarrowquad frac{a}{sin angle A}=2R).
Вот и всё! Провели одну линию, рассмотрели один прямоугольный треугольник – и доказательство готово.
Но как же быть с углами ( displaystyle B) и ( displaystyle C)? – спросишь ты.
Да, точно также. Давай рассмотрим ( displaystyle angle B).
Теперь проведём диаметр ( displaystyle AO) и соединим точки ( displaystyle K) и ( displaystyle C).
Как-то тут немного по-другому получается, ты заметил? ( displaystyle Delta AKC), конечно, прямоугольный, так как ( displaystyle angle C) опирается на диаметр ( displaystyle AK).
Но теперь ( displaystyle angle K+angle B=180{}^circ ), потому что четырехугольник ( displaystyle ABCK) – вписанный. (Надеюсь, ты ещё помнишь, что для угла ( displaystyle A) у нас было ( displaystyle angle A=angle K).) В чём же дело?
Ну, просто ( displaystyle angle B) – тупой, поэтому и получилось такое различие. Но, к счастью, для теоремы синусов это различие не играет роли. Сейчас мы в этом убедимся.
Итак, запишем выражение для синуса ( displaystyle angle K) в прямоугольном ( displaystyle Delta AKC).
( displaystyle sin angle K=frac{b}{AK}); то есть ( displaystyle sin angle K=frac{b}{2R})
Но ( displaystyle angle B=180{}^circ -angle KRightarrow sin angle B=sin angle K) (читаем или вспоминаем формулы приведения в тригонометрии.)
Значит, ( displaystyle sin angle B=frac{b}{2R}quadRightarrowquad frac{b}{sin angle B}=2R).
Ну вот, мы рассмотрели и острый, и тупой угол. Если ты все ещё беспокоишься об угле ( displaystyle C), то проделай все те же действия самостоятельно и убедись, что все получается.
Обрати внимание, что мы доказали «четверное равенство».
( displaystyle frac{a}{sin angle A}=frac{b}{sin angle B}=frac{c}{sin angle C}=2R)
в такой последовательности:
( displaystyle left{ begin{array}{l}frac{a}{sin angle A}=2R\frac{b}{sin angle B}=2Rhspace{13mm}Rightarrowquad frac{a}{sin angle A}=frac{b}{sin angle B}=frac{c}{sin angle C}=2R\frac{c}{sin angle C}=2Rend{array} right.)
А теперь внимание! Обсудим пользу этой теоремы
Понимаешь, теорема синусов – единственный разумный способ для нахождения радиуса описанной окружности.
Почему я так говорю? А ты вспомни сам: ну где ещё в формулах участвует ( displaystyle R)?! Возможно, правда, ты знаком с формулой ( displaystyle S=frac{abc}{4R}), то есть ( displaystyle R=frac{abc}{4S}quad), но!
Давай – ка сравним:
Из теоремы синусов: ( displaystyle R=frac{a}{2sin angle A})
Из формулы площади: ( displaystyle R=frac{abc}{4S}).
Чувствуешь разницу? В первой формуле нужно знать только одну сторону и один угол, а во второй формуле – все стороны, да ещё и площадь! Ну и какую формулу легче применить?
А кроме того, открою тебе маленький секрет: формула ( displaystyle S=frac{abc}{4R}) как раз и доказывается именно с применением теоремы синусов.
Чтобы убедиться в этом, читай темы «Площадь круга», «Площадь треугольника и четырехугольника».
Итак, теорема синусов бывает полезна и для нахождения синуса какого – то угла, если известны две стороны и один угол.
Но в основном теорема синусов – главный инструмент для нахождения радиуса описанной окружности.
Запомни это очень хорошо!
Расширенная синусов теорема с примерами
Добавлено: 5 ноября 2021 в 18:07

При подготовке к ЕГЭ по математике одиннадцатиклассник должен помнить базовый набор формул, которые помогут решать задачи. Одной из них является синусов теорема, которая отражает взаимосвязь между сторонами и углами треугольника.
Напомним, доказательство теоремы учить не нужно, поскольку экзамен ориентирован на проверку практических навыков. Лучше посвятить время разбору примеров, в которых можно применить указанную математическую закономерность.
Теорема синусов с примерами
Человечество знакомо с теоремой синусов довольно давно — еще в начале XXI века ее доказательство приводил в своей работе «Книга о неизвестных дугах сферы» западноарабский астроном и математик Ибн Муаз аль-Джайяни.
Существует два варианта теоремы синусов:
- обычный — устанавливает соотношения между сторонами треугольника и синусами его углов;
- расширенный — связывает соотношение сторон треугольника с радиусами описанной окружности.
Формулировка обычной синусов теоремы: отношение сторон треугольника к синусам противолежащих углов равны или стороны пропорциональны синусам противолежащих углов.
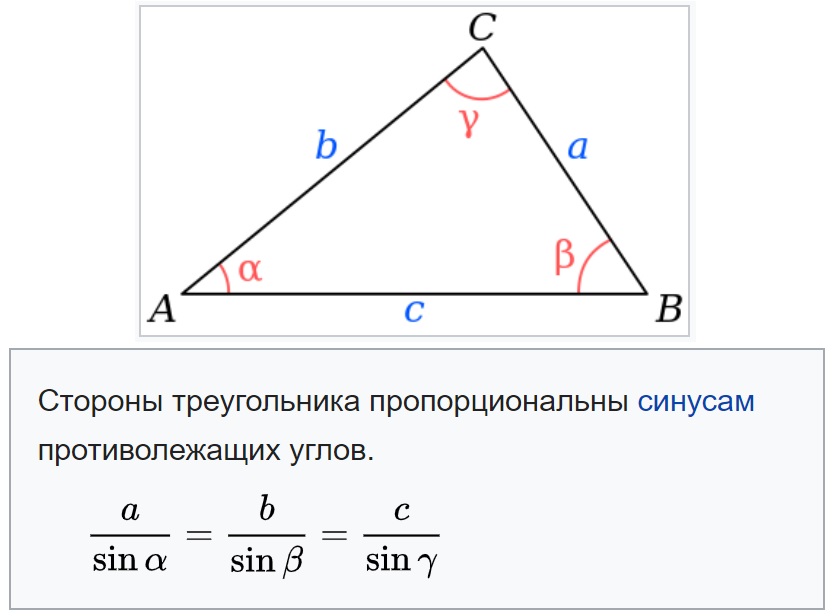
Теорема синусов с примерами: классика и расширенная
Пример 1. В треугольнике АВС сторона АВ равна 5 см, а синус противолежащего угла АСВ = 3/5. Найти сторону ВС, если синус угла САВ, прилежащего к стороне АВ, равен 1/2.
Решение
Составим соотношение фигурирующих в условии сторон и синусов их углов:
АВ : sin ∠АСВ = ВС : sin ∠САВ.
Подставим известные значения:
5 : 3/5 = ВС : 1/2.
Выразим из этого выражения ВС:
ВС = (5 : 3/5) : 1/2 = 5 : 1/2 = 10 см.
Ответ: ВС = 10 см.
Пример 2. В треугольнике АВС сторона АВ равна 10 см, а противолежащий угол АСВ = 30°. Найти остальные стороны, если угол САВ равен 60°.
Решение
Для решения этой задачи воспользуемся прилагаемой таблицей, в которой указаны значения синусов основных углов. В остальном ход решения будет аналогичен предыдущему примеру за исключением одного маленького хода. Для начала составим соотношение сторон и синусов противолежащих углов:
АВ : sin ∠АСВ = ВС : sin ∠САВ = АС : sin ∠ВАС.
На первом этапе нам известны только три из шести членов этого равенства, причем два из них в косвенном виде:
10 : sin 30° = ВС : sin 60° = АС : sin ∠ВАС.
Если вспомнить, что сумма углов треугольника равна 180°, то легко найти оставшийся угол:
∠ВАС = 180° – (∠АСВ + ∠САВ) = 180° – (30° + 60°) = 90°.
Мы уже знаем и третий угол, поэтому уравнение приобретет следующий вид:
10 : sin 30° = ВС : sin 60° = АС : sin 90°.
Дальше поступаем, как в предыдущей задаче, выразив стороны через известные члены выражений:
ВС = sin 60° ∙ 10 : sin 30°,
АС = sin 90° ∙ 10 : sin 30°.
Обратимся к таблице, приведенной выше и выберем из нее соответствующие синусы известных углов:
ВС = √3/2∙ 10 : 1/2 = 10√3 см,
АС = 1 ∙ 10 : 1/2 = 20 см.
Ответ: ВС = 10√3 см; АС = 20 см.

Теорема синусов с примерами: классика и расширенная
Расширенная синусов теорема с примерами
Формулировка расширенной теоремы синусов: отношение сторон треугольника к синусам противолежащих углов равны друг другу и удвоенному радиусу окружности, описанной вокруг него.
Пример 3. Найти площадь треугольника, если диаметр описанной окружности D равен 20 см. Угол АСВ = 30°, а угол САВ = 60°.
Решение
Для решения воспользуемся расширенной формулировкой теоремы синусов:
АВ : sin ∠АСВ = ВС : sin ∠САВ = АС : sin ∠ВАС = 2R.
В этой формулировке нам известны два из семи компонентов и еще лва мы можем определить из базовых знаний по геометрии:
- R = ½ D, следовательно 2 R = D = 20 см;
- ∠ВАС = 180° – (∠АСВ + ∠САВ) = 180° – (30° + 60°) = 90°.
Подставим в исходное выражение известные величины и получим соотношение:
АВ : sin 30° = ВС : sin 60° = АС : sin 90° = 20.
Основным отличием от предыдущей задачи является то, что нам неизвестна сторона АВ, зато известен удвоенный радиус описанной окружности. Это позволяет составить выражения для нахождения всех сторон треугольника:
ВС = 20 ∙ sin 60°
АС = 20 ∙ sin 90°,
АВ = 20 ∙ sin 30°.
Выберем из таблицы значения синусов углов и вычитаем стороны треугольника:
ВС = 20 ∙ sin 60° = 20 ∙ √3/2 = 10√3 см,
АС = 20 ∙ sin 90° = 20 ∙ 1 = 20 см,
АВ = 20 ∙ sin 30° = 20 ∙ 1/2 = 10 см.
Теорема синусов с примерами: классика и расширенная
Внимательный читатель заметил, что мы «зашифровали» в этой задаче треугольник из предыдущего примера. Теперь осталось найти его площадь. Для этого берем стандартную формулу площади произвольного треугольника, которая равна половине произведения сторон на синус угла между ними
S = ½ ∙ a ∙ b ∙ sin α
Поскольку нам известны все стороны и все углы, то мы можем выбрать любые из них. Возьмем стороны АС и АВ, а также угол САВ между ними:
S = ½ ∙ АС ∙АВ ∙ sin 60° = ½ ∙ 20 ∙10 ∙ √3/2 = 50√3 см2.
Примечание: внимательный читатель заметил, что наш треугольник — прямоугольный, так как один из его углов равен 90°. В таком случае можно обойтись без знания синуса угла, вычислив площадь треугольника как половину площади прямоугольника, длина и ширина которого равна катетам треугольника.
S = ½ ∙ ВС ∙АВ = ½ ∙ 10√3 ∙ 10 = 50√3 см2.
Ответ: S = 50√3 см2.
Занимайтесь на курсах ЕГЭ и ОГЭ в паре TwoStu и получите максимум баллов на экзамене:

Эксперт по подготовке к ЕГЭ, ОГЭ и ВПР
Задать вопрос
Закончил Московский физико-технический институт (Физтех) по специальности прикладная физика и математика. Магистр физико-математических наук. Преподавательский стаж более 13 лет. Соучредитель курсов ЕГЭ и ОГЭ в паре TwoStu.