Как найти sin внешнего угла при вершине

Внешний угол треугольника. Синус и косинус внешнего угла

В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?

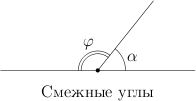
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна .

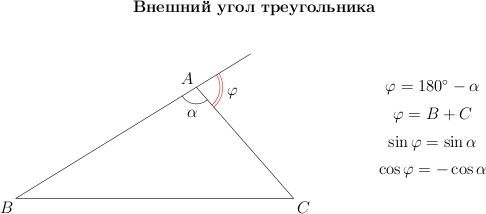
Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом . Если угол острый, то смежный с ним угол — тупой, и наоборот.

Обратите внимание, что:

Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.

Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

1. В треугольнике угол равен , . Найдите тангенс внешнего угла при вершине .

Пусть — внешний угол при вершине .

Зная , найдем по формуле:

Получим:

2. В треугольнике угол равен , . Найдите синус внешнего угла при вершине .

Задача решается за четыре секунды. Поскольку сумма углов и равна , . Тогда и синус внешнего угла при вершине также равен .

Как найти синус внешнего угла

По определению любой угол составляют два несовпадающих луча, которые выходят из единственной общей точки – вершины. Если один из лучей продолжить за вершину, это продолжение вместе со вторым лучом образует еще один угол – он называется смежным. Смежный угол в вершине любого выпуклого многоугольника называют внешним, так как он лежит вне участка поверхности, ограниченного сторонами этой фигуры.

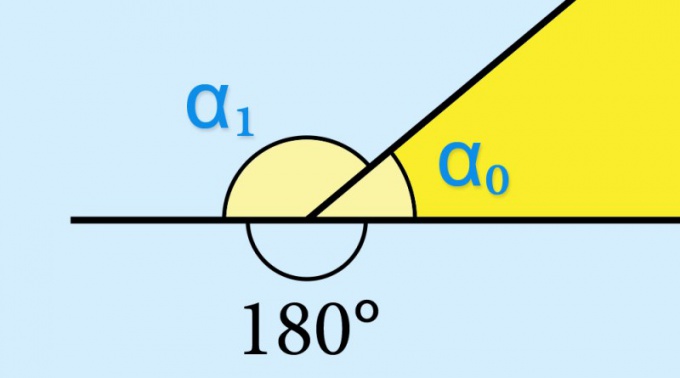
Инструкция

Если вам известно значение синуса внутреннего угла (α₀) геометрической фигуры, вычислять что-либо нет необходимости – синус соответствующего ему внешнего угла (α₁) будет иметь точно такое же значение: sin(α₁) = sin(α₀). Это определяется свойствами тригонометрической функции sin(α₀) = sin(180°-α₀). Если бы требовалось узнать, например, значение косинуса или тангенса внешнего угла, эту величину нужно было бы брать с противоположным знаком.

Существует теорема о том, что в треугольнике сумма величин двух любых внутренних углов равна величине внешнего угла третьей вершины. Используйте ее в том случае, если величина внутреннего угла, соответствующего рассматриваемому внешнему (α₁), неизвестна, а углы (β₀ и γ₀) в двух других вершинах приведены в условиях. Найдите синус от суммы известных углов: sin(α₁) = sin(β₀+γ₀).

Задача с теми же исходными условиями, что и в предыдущем шаге, имеет и другое решение. Оно вытекает из другой теоремы – о сумме внутренних углов треугольника. Так как эта сумма, согласно теореме, должна быть равна 180°, величину неизвестного внутреннего угла можно выразить через два известных (β₀ и γ₀) – она будет равна 180°-β₀-γ₀. Это означает, что вы можете использовать формулу из первого шага, заменив в нем величину внутреннего угла этим выражением: sin(α₁) = sin(180°-β₀-γ₀).

В правильном многоугольнике величина внешнего угла при любой вершине равна величине центрального угла, а значит, может быть рассчитана по той же формуле, что и он. Поэтому, если в условиях задачи дано число сторон (n) многоугольника, при вычислении синуса любого внешнего угла (α₁) исходите из того, что его величина равна полному обороту, поделенному на число сторон. Полный оборот в радианах выражается удвоенным числом Пи, поэтому формула должна иметь такой вид: sin(α₁) = sin(2*π/n). При расчетах в градусах удвоенное Пи замените на 360°: sin(α₁) = sin(360°/n).

Источники:

• найти sin угла

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Внешний угол треугольника. Синус и косинус внешнего угла

В некоторых
задачах ЕГЭ требуется найти синус,
косинус или тангенс внешнего
угла
треугольника. А что такое внешний
угол треугольника?

Давайте
вспомним сначала, что такое смежные
углы.
Вот они, на рисунке. У смежных углов
одна сторона общая, а две другие лежат
на одной прямой. Сумма смежных углов
равна

.

Возьмем
треугольник и продолжим одну из его
сторон. Внешний угол

при
вершине

 —
это угол, смежный с углом

. Если
угол 

острый, то смежный с ним угол —
тупой, и наоборот.

Обратите
внимание, что:

Запомните
эти важные соотношения. Сейчас мы берем
их без доказательств. В разделе
«Тригонометрия», в теме «Тригонометрический
круг»,
мы вернемся к ним.

Легко
доказать, что внешний
угол треугольника равен сумме двух
внутренних углов, не смежных с ним.

1.
В треугольнике

угол 

равен

,

.
Найдите тангенс внешнего угла при
вершине

.

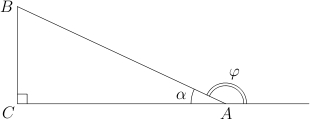
Пусть

—
внешний угол при вершине

.
Имеем:

Зная

,
найдем

 по формуле

Получим:

2.
В треугольнике

угол 

равен

,

.
Найдите синус внешнего угла при вершине

.

Задача
решается за четыре секунды. Поскольку
сумма углов 

и 

равна 
,

.
Тогда и синус внешнего угла при
вершине 

также равен

.

Высота в прямоугольном треугольнике

Вспомним,
что высота
треугольника —
это перпендикуляр, опущенный из его
вершины на противоположную сторону.

В
прямоугольном треугольнике катеты
являются высотами друг к другу. Главный
интерес представляет высота, проведённая
к гипотенузе.

Один
из типов экзаменационных задач В6 в
банке заданий ФИПИ — такие, где
в прямоугольном треугольнике высота
проведена из вершины прямого угла.
Посмотрим, что получается:

Высота
проведена к гипотенузе

.
Она делит треугольник

на два
прямоугольных треугольника —

и 
.
Смотрим внимательно на рисунок
и находим на нем равные
углы.
Это и есть ключ к задачам по геометрии,
в которых высота опущена на гипотенузу.

Мы помним,
что сумма двух острых углов прямоугольного
треугольника равна

.
Значит,

,
то есть угол

равен
углу

.
Аналогично, угол

.

Иными
словами, каждый из трех углов
треугольника

равен
одному из углов треугольника

и треугольника

.
Треугольники

,

и 

называются подобными.
Давайте нарисуем их рядом друг
с другом.

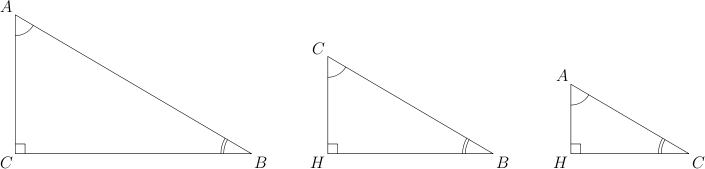
Они
отличаются только размерами. Стороны
подобных треугольников пропорциональны.
Что это значит?

Возьмем
треугольники

и 
.
Стороны треугольника

длиннее,
чем стороны треугольника

,
в  некоторое число

 раз:

При
решении задач нам пригодится равенство
углов треугольников

,

и 
,
а также пропорциональность их сторон.
Обратите также внимание, что площадь
треугольника

можно
записать двумя разными способами: как
половину произведения катетов и как
половину произведения гипотенузы
на проведенную к ней высоту.

1.
В треугольнике

угол 

равен

,

 —
высота,

,

.
Найдите

.

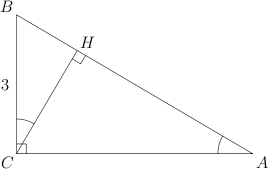
Рассмотрим
треугольник

.
В нем известны косинус угла 

и противолежащий катет

.
Зная синус угла 
,
мы могли бы найти гипотенузу

.
Так давайте найдем

:

(поскольку
значение синуса острого угла положительно).
Тогда:

Рассмотрим
прямоугольный треугольник

,

.
Имеем:

Отсюда,
поскольку

:

и
тогда

Ответ:

.

2.
В треугольнике

угол 

равен

,

,

.
Найдите высоту

.

Сделайте
чертеж и рассмотрите прямоугольный
треугольник

.

Ответ:

.

3.
В треугольнике

угол 

равен

,

,

.
К гипотенузе проведена высота

.
Найдите

.

Это
чуть более сложная задача. Ведь вам
неизвестны катеты

 и 
.

Зато
можно записать теорему Пифагора:

Нам
известно также, что

Решая
эту систему из двух уравнений, найдем:

Запишем
площадь треугольника

двумя
способами:

и найдем

.

Найти
высоту, проведенную из вершины прямого
угла, можно было и другим способом.
Мы выбрали самый короткий путь —
составили и решили систему уравнений.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #

  30.03.201540.15 Mб22спицын мартыненко.djvu

• #
• #
• #
• #
• #
• #
• #
• #

Please wait.

We are checking your browser. mathvox.ru

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6dc5226e5c2b00a5 • Your IP : 85.95.188.35 • Performance & security by Cloudflare

Найдите синус внешнего угла треугольника

27359. Найдите синус внешнего угла треугольника АВС при вершине А, угол С равен 90 0 , sin A=0,1.

Углы ∠ВАС и ∠ВАD смежные, значит

По свойству синуса:

Ответ: 0,1

27445. В треугольнике АВС угол С равен 90 0 , угол А равен 30 0 . Найдите синус угла BAD.

Углы BAD и BAC смежные, значит ∠ВАD=180 0 –30 0 =150 0 .

Известно, что значения синусов смежных углов равны, то есть:

sin BAD=sin BAC = sin 30 0 =0,5

27378. В треугольнике АВС угол С равен 90 0 , АВ=25, ВС=20. Найдите косинус внешнего угла при вершине А.

Углы ∠ВАС и ∠BAD смежные. Это значит, что

По свойству косинуса cos BAD=cos (180 0 –∠ВАС)=–cos ВАС.

Найдём cos ВАС Для этого найдём сторону АС. По теореме Пифагора:

По определению косинуса в прямоугольном треугольнике:

Таким образом, cos BAD = – cos BAС = –0,6.

27381. В треугольнике АВС угол С равен 90 0 , АВ=8, АС=4. Найдите косинус внешнего угла при вершине А.

Углы ∠ВАС и ∠ВАD и смежные. Это значит, что

По свойству косинуса cos BAD = cos (180 0 –∠ВАС)=–cos ВАС. Найдём cos BAC. По определению косинуса в прямоугольном треугольнике:

Таким образом, cos BAD=–cos BAС=–0,5. Косинус внешнего угла при вершине A равен –0,5.

Внешний угол треугольника. Задание В7

Если в геометрической задаче присутствуют слова “внешний угол треугольника“, нам надо вспомнить несколько фактов:

1. Внешним углом треугольника называется угол, смежный с каким-либо углом треугольника:

2. Сумма смежных углов равна 180°

3. Внешний угол треугольника равен сумме двух углов, не смежных с ним:

Чтобы найти синус, косинус или тангенс внешнего угла треугольника, нужно найти эту функцию соответствующего внутреннего угла, а затем воспользоваться следующим формулами приведения:

(1)

(2)

(3)

Необходимо также вспомнить, как тригонометрические функции острого угла выражаются одна через другую:

Прежде чем приступать к разбору решений задач, рекомендую вам прочитать статью о соотношении сторон и углов в прямоугольном треугольнике.

Рассмотрим решение задач из Открытого банка заданий для подготовки к ЕГЭ по математике: .

1 . Задание B7 (№ 27382)

В треугольнике ABC угол C равен , , . Найдите тангенс внешнего угла при вершине A.

Найдем тангенс угла А, а затем воспользуемся формулой приведения.

АС=4, ВС найдем по теореме Пифагора:

Отсюда . Соответственно, по формуле приведения (3), тангенс внешнего угла при вершине А равен -0,25.

Ответ: -0,25

2 . Задание B7 (№ 27386)

В треугольнике ABC угол C равен , синус внешнего угла при вершине A равен 0,1. Найдите .

Воспользуемся формулой приведения (2): sinA=0,1

Ответ: 0,1.

3 . Задание B7 (№ 27387)

В треугольнике ABC угол C равен , синус внешнего угла при вершине A равен . Найдите .

Найдем сначала sin A. Он равен синусу внешнего угла треугольника при вершине А. То есть .

Найдем cosA c помощью основного тригонометрического тождества:

Ответ: 0,96

4. Задание B7 (№ 27389)

В треугольнике ABC угол C равен , синус внешнего угла при вершине A равен . Найдите .

Найдем сначала sin A. Он равен синусу внешнего угла треугольника при вершине А. То есть .

Сумма острых углов прямоугольного треугольника равна 90°, поэтому

Ответ: 0,96

5 . Задание B7 (№ 27392)

В треугольнике ABC угол C равен , косинус внешнего угла при вершине A равен . Найдите .

Если косинус внешнего угла при вершине A равен , то cos A=. Отсюда sinA=0,96

Ответ: 0,96

И.В. Фельдман, репетитор по математике.

Купить видеокурс “ВСЯ ГЕОМЕТРИЯ. Часть В”

[spoiler title=”источники:”]

http://matematikaege.ru/treugolniki/27359-najdite-sinus-vneshnego-ugla-treugolnika.html

http://ege-ok.ru/2012/03/24/vneshniy-ugol-treugolnika-zadanie-v6

[/spoiler]

Задания

Версия для печати и копирования в MS Word