Как найти синдром ошибки

Как найти синдром ошибки

Вычисление
синдрома для циклических кодов является
довольно простой процедурой.

Пусть
U(x)
и r(х)
‑
полиномы, соответствующие переданному
кодовому слову и принятой последовательности.

Разделив
r(x)
на g(x),
получим

r(x)
= q(x)
g(x)
+ s(x),
(1.73)

где
– q(x)
— частное от деления, s(x)
— остаток от деления.

Если
r(x)
является кодовым полиномом, то он делится
на g(x)
без остатка, то есть s(x)
= 0.

Следовательно,
s(x)

0
является условием наличия ошибки в
принятой последовательности, то есть
синдромом принятой последовательности.

Синдром
s(x)
имеет в общем случае вид

S(x)
= S0
+ S1

x + … + Sn-
k-1
xn-k-1
. (1.74)

Очевидно,
что схема вычисления синдрома является
схемой деления, подобной схемам
кодирования рис. 1.10 или 1.11 .

При
наличии в принятой последовательности
r

хотя бы одной ошибки вектор синдрома S
будет иметь, по крайней мере, один
нулевой элемент, при этом факт наличия
ошибки легко обнаружить, объединив по
ИЛИ
выходы всех ячеек регистра синдрома.

Покажем,
что синдромный многочлен S(x)
однозначно связан с многочленом ошибки
e(x),
а
значит, с его помощью можно не только
обнаруживать, но и локализовать ошибку
в принятой последовательности.

Пусть

e(x)
= e0
+ e1

x
+ e2

x2
+ … + en-1

x
n-1
(1.75)

— полином
вектора ошибки.

Тогда
полином принятой последовательности

r(x)
= U(x)
+ e(x).
(1.76)

Прибавим
в этом выражении слева и справа U(x),
а также учтем, что

r(x)
= q(x)
g(x) + S(x), U(x) = m(x)
g(x), (1.77)

тогда


,
(1.78)

то
есть синдромный
полином S(x)
есть
остаток от
деления полинома ошибки e(x)
на порождающий полином g(x).

Отсюда следует, что по синдрому S(x)
можно однозначно определить вектор
ошибки e(x), а следовательно,
исправить эту ошибку.

На рис. 1.14 приведена схема синдромного
декодера с исправлением однократной
ошибки для циклического (7,4)-кода.
По своей структуре она подобна схеме,
приведенной на рис. 1.6, с той лишь разницей,
что вычисление синдрома принятой
последовательности производится здесь
не умножением на проверочную матрицу,
а делением на порождающий полином. При
этом она сохраняет и недостаток, присущий
всем синдромным декодерам: необходимость
иметь запоминающее устройство, ставящее
в соответствие множеству возможных
синдромов S множество векторов
ошибок e. Цикличность структуры
кода в этом случае не учитывается.

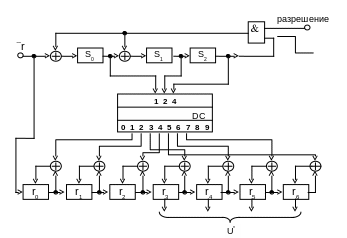
Рис.
1.14

1.3.4. Неалгебраические методы декодирования циклических кодов

Все
методы декодирования линейных блочных
кодов можно разбить на две группы:
алгебраические
и неалгебраические.

В
основе алгебраических методов лежит
решение систем уравнений, задающих
значение и расположение ошибок.
Рассмотренные синдромные декодеры
относятся именно к этой группе методов.

При
неалгебраических методах та же цель
достигается с помощью простых структурных
понятий теории кодирования, позволяющих
находить комбинации ошибок более простым
путем.

Одним
из неалгебраических методов является
декодирование с использованием алгоритма
Меггитта,
пригодного для исправления как одиночных,
так и l-кратных
ошибок (на практике l

3).

При
декодировании в соответствии с алгоритмом
Меггитта также вычисляется синдром
принятой последовательности S(x),
однако используется он иначе, нежели в
рассмотренных ранее синдромных декодерах.

Идея,
лежащая в основе декодера Меггитта,
очень проста и основывается на следующих
свойствах циклических кодов:

–
существует взаимно-однозначное
соответствие между множеством всех
исправляемых ошибок и множеством
синдромов;

–
если S(x)
— синдромный многочлен, соответствующий
многочлену ошибок е(x),

то xS(x)
mod
g(x)
— синдромный многочлен, соответствующий
x
e(x) mod (xn
+ 1).

Равенство
а(x)
= b(x) mod p(x)
читается как “а(x),
сравнимо с b(x)
по модулю р(x)”
и означает, что а(x)
и b(x)
имеют одинаковые остатки от деления на
полином p(x).

Таким
образом, второе
условие
означает, что если
комбинация ошибок циклически сдвинута
на одну позицию вправо, то для получения
нового синдрома нужно сдвинуть содержимое
регистра сдвига с обратными связями,
содержащего S(x),

также на одну позицию вправо.

Следовательно,
основным
элементом декодера Меггитта является
сдвиговый регистр. Структурная схема
декодера Меггитта для циклических кодов
произвольной длины приведена
на рис. 1.15.

Рис.
1.15

Декодер
работает следующим образом. Перед
началом работы содержимое всех разрядов
регистров равно нулю. Принимаемая
последовательность r
в
течение первых n
тактов вводится в буферный регистр и
одновременно с этим в (n–k)-разрядном
сдвиговом регистре с обратными связями
производится ее деление на порождающий
полином g(x).

Через
n
тактов
в буферном регистре оказывается принятое
слово r
,
a в регистре синдрома — остаток от
деления вектора ошибки на порождающий
полином.

Вычисленный
синдром сравнивается со всеми табличными
синдромами, и в случае совпадения с
одним из них старший разряд буферного
регистра исправляется путем прибавления
к его значению единицы.

После
этого синдромный и буферный регистры
один раз циклически сдвигаются. Это
реализует умножение S(x)
на
x
и деление на g(x).
Содержимое ячеек синдромного регистра
теперь равно остатку от деления xS(x)
на g(x)
или синдрому ошибки x
е(x) mod (Хn
+ 1).

Если
новый синдром совпадает с одним их
табличных, то исправляется очередная
ошибка и т.д. Через n
тактов
все позиции будут, таким образом,
исправлены.

Рассмотрим
работу декодера Меггитта для циклического
(7,4)-кода,
исправляющего одиночную ошибку. Схема
декодера изображена на рис. 1.16.

Рис.
1.16

Принцип
работы декодера заключается в том, что
независимо
от того, в какой позиции произошла
ошибка, осуществляется ее сдвиг в
последнюю ячейку буферного регистра с
соответствующим пересчетом синдрома
и ее исправление в этой позиции.

Полином
ошибки в старшем разряде для (7,4)-кода
Хемминга имеет вид е6
(x)
= x6,
соответствующий ему синдромный полином
S6
(x)
= 1 + x3
(
S
= (101)),
детектор ошибки настроен на это значение
синдрома.

Пусть,
например, передана последовательность
U
= (1001011),
ей соответствует кодовый полином U(x)
= 1 + x3
+ x5
+ x6.
Произошла ошибка в третьей позиции е(x)
= x3,
принятый вектор имеет вид r
= (1000011),
его полином r(x)
= 1 + x5
+ x6.

Kогда
принятая последовательность полностью
входит в буферный регистр, в регистре
синдрома оказывается синдром,
соответствующий ошибке е(x)
= x3
S3
= (110).
Поскольку он не совпадает с табличным
для е6,
на выходе детектора ошибок будет 0
и исправления не происходит.

Далее
производятся однократный циклический
сдвиг принятой последовательности в
буферном регистре, однократное деление
синдрома x∙S3
на порождающий полином в регистре с
обратными связями и проверка на совпадение
синдрома с заданным.

Последовательность
состояний регистров декодера в процессе
декодирования показана на рис. 1.17.

Рис.
1.17

Т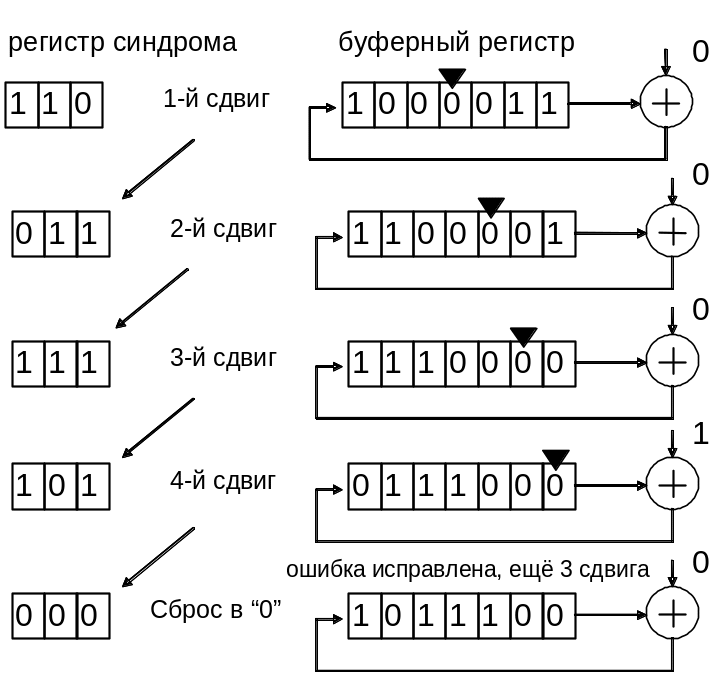
аким
образом, исправление ошибки в декодере
Меггитта осуществляется за 2n
тактов: в течение n
тактов производится ввод принятой
последовательности в буферный регистр,
в течение l
тактов
— исправление ошибки, и еще в течение
n
– l
– восстановление
буферного регистра в исходное состояние
с исправленным словом. Простота декодера
достигается увеличением времени
декодирования.

Следует
отметить, что в связи с успехами в
разработке БИС и устройств памяти в
значительной степени снимается вопрос
о размерах таблиц, связывающих значения
синдрома и вектора ошибки (для синдромных
декодеров) и даже значения кодовых слов
и принятых последовательностей (для
декодера максимального правдоподобия).
Поэтому в перспективе возможно снижение
интереса к кодам, обладающим специальной
структурой, и к методам их декодирования.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #

    10.06.2015684.82 Кб14P4.pdf

  • #
  • #
  • #
  • #
Источник

В силу первого предположения, а -1 принадлежит Н и а _1 *а = е. Тогда а- 1 *а*Ь -1 = а _1 *с или Ь -1 = а _1 *с, что означает существование обратного элемента любого элемента Н.

Таким образом, необходимым и достаточным условием того, что непустое подмножество Н элементов группы G образует подгруппу, является выполнение для любых двух элементов а и Ь из Н следующих условий:

Кроме того, следует отметить, что единичный элемент подгруппы всегда совпадает с единичным элементом исходной группы [8].

Очевидно, что подмножество <е>любой группы G, состоящее только из единичного элемента, а также сама группа G удовлетворяют условиям образования подгруппы. Такие подгруппы называются тривиальными подгруппами.

Пусть Н – подгруппа группы G, a g – произвольный фиксированный элемент G. Множество

называется правым смежным классом группы G по подгруппе Н, порождаемым элементом g. Аналогично множество

называется левым смежным классом группы G по подгруппе Н, порождаемым элементом g.

В случае некоммутативной группы G число левых смежных классов группы G по подгруппе Н совпадает с числом правых смежных классов. При этом в общем случае никакой левый смежный класс не совпадает ни с каким правым смежным классом. Исключение составляют так называемые нормальные делители – подгруппы, для любого элемента которых H*g = g*H [10].

Очевидно, что если G – абелева группа, то ее левые смежные классы по подгруппе Н совпадают с правыми. Условимся в случае абелевой группы обозначать смежные классы группы G по подгруппе Н в форме соотношения (2.14).

Пусть Н – подгруппа некоторой конечной группы G.

по подгруппе Н равны: gi*hj = gi*hk. Тогда умножение слева на g;

1 дает равенство hj = hk. Но это противоречит определению подгруппы.

равны: gi*hj = gk*hs. Умножение справа на hj– 1 дает равенство g; = gk*hs*hj

Пусть Н = hn> – подгруппа конечной группы G. Пусть g n ) как векторном пространстве GF n (q).

Таким образом, векторное подпространство GF k (q) кода С разбивает исходное векторное пространство GF n (q) на непересекающиеся смежные классы, определяемые следующим образом:

где а – элемент GF n (q), порождающий смежный класс.

Как было показано в предыдущем пункте этого подпараграфа, число элементов каждого смежного класса совпадает с числом кодовых слов кода С. Иными словами, каждый смежный класс а + С содержит q k элементов. Число всех непересекающихся смежных классов определяется соотношением (2.15) и имеет значение q n

Таким образом, векторное пространство GF n (q) можно представить как объединение множеств:

где a s ), s = 0,1. q n


k – 1 – элементы GF n (q), образующие все различные

(не пересекающиеся) смежные классы.

Будем считать, что в соотношении (2.16) а(°) = 0. Тогда смежный класс а(°) + + С совпадает с кодом С.

Как было показано в предыдущем пункте этого подпараграфа, каждый смежный класс вида (2.16) может быть порожден q k различными элементами (векторами) векторного пространства GF n (q).

Пример 2.1.7. Рассмотрим построение отличных от исходного кода смежных классов двоичного линейного (6, 3)-кода С из примера 2.1.4.

Множество всех кодовых слов в данном случае содержит восемь элементов (векторов) векторного пространства GF 6 (2), которые можно представить в виде двоичных последовательностей длиной не более шести двоичных символов:

Число элементов (векторов) каждого смежного класса соответствует числу q k = 8 кодовых слов кода С.

Пусть, например, а = 000001. Тогда смежный класс а + С будет состоять из следующих элементов (векторов):

Нетрудно проверить, что то же множество векторов может быть получено при а = 001100, 010010, 011111, 100111,101010,110100,111001. То есть при любом другом отличном от исходного порождающего элемента а значении, принадлежащем указанному смежному классу.

Согласно соотношению (2.16), число не пересекающихся смежных классов в этом случае: q n


k = 8 (в следующем примере мы укажем их все). Все остальные (отличные от самого кода С) смежные классы могут быть получены, например, при следующих значениях порождающего элемента а:

При этом каждый смежный класс может быть образован, помимо указанных, семью другими значениями вектора а из GF 6 (2), принадлежащими тому же смежному классу.

Любой элемент (вектор) каждого смежного класса, как и сам смежный класс, может быть получен восемью различными способами как а + с для восьми различных значений порождающего элемента а и всех восьми кодовых слов с кода С. Например, элемент 111001 рассмотренного выше в этом примере смежного класса, порожденного элементом а = 000001, может быть получен как а + с для значений а = 000001, 001100, 010010, 011111, 100111, 101010, 110100, 111001 и с = 111000, 110101, 101011, 100110, 011110, 010011, 001101, 000000 соответственно.

4. Пусть С – линейный (л, к)-код над GF(q) и v = с + е – вектор принятого сообщения.

Как было показано выше в этом подпараграфе, вектор v всегда принадлежит одному из q n


k не пересекающихся смежных классов вида (2.16). При отсутствии ошибок вектор v принадлежит смежному классу, совпадающему с кодом С. При ненулевом векторе ошибок вектор i/оказывается в другом смежном классе а + С (пока будем считать, что вес вектора ошибок не превосходит максимального числа t исправляемых кодом ошибок).

Принимая вектор е за порождающий элемент смежного класса е + С, по известному вектору v мы можем определить q k возможных значений вектора е. Очевидно, наиболее вероятным является значение е наименьшего веса.

Элемент (вектор) минимального веса в смежном классе а + С называется лидером смежного класса а + С.

Если в смежном классе а + С несколько векторов имеют минимальный вес, то в качестве лидера смежного класса выбирается любой из них. Таким образом, вектор ошибок принимается равным лидеру смежного класса, которому принадлежит принятый вектор v.

В этом случае аппаратная реализация декодера основана на так называемом табличном методе и требует хранения в памяти устройства всех смежных классов и их лидеров. Подобного рода декодер даже при небольшой длине кода требует значительных аппаратных затрат. Например, для рассмотренного в примерах 2.1.4 и 2.1.7 двоичного линейного (6, 3)-кода требуется хранить в памяти декодера q n


k = 8 смежных классов по q k = 8 двоичных векторов длины п = 6 символов.

Однако табличный декодер может быть несколько упрощен.

Пусть Н – проверочная матрица линейного (л, /с)-кода С. Тогда матрица-строка s(y) = у-Н т размера 1 х к называется синдромом вектора у.

Пусть у = v = с + е – вектор принятого сообщения. Тогда, в силу соотношения (2.10), s(y) = s(e) и, стало быть, равенство нулю s(v) означает принадлежность вектора v коду С. Это в свою очередь означает отсутствие ошибок вектора v. Пока будем считать, что вес вектора ошибок не превосходит максимального числа t исправляемых кодом ошибок. К этому вопросу мы еще вернемся ниже, в конце этого подпараграфа.

Пусть С – линейный (л, к)-код над GF(q), а у и z – два вектора векторного пространства GF n (q).

Очевидно, что s(y) = s(z) тогда и только тогда, когда у-Н т = z-H T или (у – z) х х Н т = 0. Это означает, что вектор у – z принадлежит С. Тогда y-z = Ck- некоторое кодовое слово кода С. Последнее равенство выполняется и в том случае,

если у = а + CiVz = а + Cj, где с,- – су = с*, а – некоторый вектор GF n (q). Равенство синдромов векторов у и z означает принадлежность обоих векторов одному смежному классу.

Таким образом, в силу равенства синдромов s(v) и s(e), вектор v принятого сообщения и вектор ошибок е всегда принадлежат одному смежному классу и по известному синдрому s(v) можно однозначно определить лидер соответствующего смежного класса.

Теперь мы можем описать один из возможных алгоритмов декодирования линейных кодов.

  • 1. Определить синдром s(v) принятого сообщения v.
  • 2. По известному синдрому s[v) определить соответствующий лидер смежного класса, синдром которого совпадает с s(v).
  • 3. Определить исходное кодовое слово с согласно соотношению (2.13) как c-v-e.

Аппаратная реализация декодера в этом случае требует хранения q k синдромов длины п – к (/-ичных символов и q k соответствующих им лидеров смежных классов длины п q-ичных символов в памяти устройства.

Такой метод декодирования называется декодированием линейных кодов по лидерам смежных классов.

Пример 2.1.8. Рассмотрим снова двоичный линейный (6, 3)-код из примеров 2.1.4 и 2.1.7.

В таблице 2.1 показаны смежные классы, лидеры смежных классов и соответствующие им синдромы рассматриваемого кода. Во избежание громоздкости элементы смежных классов представлены соответствующими десятичными значениями. Жирным шрифтом выделены значения лидеров смежных классов.

Лидер смежного класса

< 1, 12, 18,31,39, 42, 52, 57 >

< 2, 15, 17, 28, 36,41,55, 58 >

< 4, 9, 23, 26, 34,47, 49, 60 >

  • 001010
  • 010100
  • 100001

Нетрудно убедиться в том, что синдром любого элемента каждого смежного класса совпадает с синдромом лидера этого смежного класса.

Как видно из таблицы 2.1, в данном случае лидеры смежных классов представлены всеми возможными двоичными векторами веса 1. Эти векторы определены однозначно (в каждом смежном классе только один такой вектор). Таким образом, в случае одиночной ошибки существует единственным образом определяемый синдром, позволяющий однозначно определить вектор ошибки. Поэтому рассмотренный линейный (6,3)-код позволяет гарантированно исправлять одиночную ошибку.

Кроме того, в одном (последнем) смежном классе три лидера веса 2. Это позволяет с небольшой (1/3) вероятностью декодировать двойную ошибку (при условии, что вероятности всех векторов принимаемых сообщений с двойной ошибкой равны).

Очевидно, избыточность рассмотренного в примерах 2.1.4, 2.1.7 и 2.1.8 двоичного линейного (6, 3)-кода немного превышает накладываемые на него корректирующие свойства, так как помимо достаточных для декодирования лидеров смежных классов веса 1 в одном из смежных классов имеют место лидеры веса 2.

Если в качестве лидеров q n


k смежных классов кода удается взять векторы веса t и менее и только их, то код называется совершенным кодом. Если же в качестве лидеров q n


k смежных классов кода удается взять все необходимые для исправления не менее t ошибок векторы веса t и менее, а также несколько векторов веса t + 1, то код называется квазисовершенным кодом.

Проще говоря, у совершенных кодов избыточности «ровно столько, сколько нужно» для исправления не менее чем t ошибок кодового слова.

Возвращаясь к примеру 2.1.4, отметим, что в случае двоичного линейного

  • (5,3)-кода вообще нельзя определить однозначно лидеры смежных классов веса
  • 1. Пусть, например, проверочная матрица (5,3)-кода имеет вид:

Тогда порождающая матрица:

В этом случае лидер смежного класса веса 1 будет однозначно определен только в одном смежном классе, отличном от смежного класса самого кода. В двух других смежных классах будет по два лидера веса 1. В смежном классе, совпадающем с кодом, также будут два лидера веса 2. Таким образом, данный код не может исправлять одиночную ошибку кодового слова.

Этот вывод подтверждается неравенством (2.5), так как минимальное расстояние (5, 3)-кода равно двум и, следовательно, ни одно целое положительное значение t исправляемых кодом ошибок данному неравенству не удовлетворяет.

Таким образом, при длине информационного сообщения к = 3 двоичных символа и длине проверочной последовательности г=п-к = 2 символа код вообще не позволяет исправлять одиночную ошибку кодового слова, а при длине г – 3 символа уже оказывается не совершенным (хотя и квазисовершенным).

Следует отметить, что совершенные коды, равно как и квазисовершенные, для некоторых значений п и к вообще могут не существовать [10]. Далее мы рассмотрим несколько видов кодов из класса линейных кодов, конструкция которых часто позволяет получить квазисовершенный или даже совершенный код.

Выше мы считали, что вес вектора ошибок не превосходит значение t исправляемых кодом ошибок, так как восстановление исходного кодового слова возможно только в этом случае. В противном случае исходное кодовое слово и принятый вектор могут попасть в один смежный класс, и восстановление кодового слова будет невозможно. Таким образом, число ошибок, превышающее корректирующую способность кода, приводит к ошибочному декодированию.

Если же число ошибок превосходит t и принятый вектор попадает в смежный класс, отличный от смежного класса кода, то декодирование возможно лишь с некоторой (обычно небольшой) вероятностью. При этом возможны два способа декодирования:

  • – декодирование любого полученного кодового слова в ближайшее кодовое слово;
  • – декодирование только кодовых слов, число ошибок которых не превосходит максимально возможное для данного кода число ошибок t, если число ошибок превышает t, происходит отказ от декодирования.

В первом случае декодер называется полным декодером, а во втором – неполным декодером.

Очевидно, что по сравнению с неполным декодером полный декодер чаще декодирует неправильно. Поэтому полный декодер используется обычно только в тех случаях, когда лучше «угадывать» сообщение, чем вообще не иметь никакой оценки.

В силу указанных особенностей мы будем рассматривать только неполные декодеры.

Метод декодирования линейных кодов по лидерам смежных классов является общим для всех линейных кодов. При этом вполне очевидно, что этот метод связан с трудоемким процессом определения лидеров смежных классов.

Например, для линейного (31, 26)-кода над GF(2) требуется определить 32 смежных класса по 67108864 вектора длины 31 в каждом и найти лидеры каждого смежного класса.

Таким образом, метод декодирования линейных кодов по лидерам смежных классов в общем случае не является приемлемым.

Однако мы можем заранее определить некоторый удобный метод декодирования и на его основе построить линейный код специального вида.

Корректирующие коды «на пальцах»

Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.

Давайте же разберёмся, что это такое.

Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.

Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.

Каналы с ошибкой

Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.

Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем ошибок. Это будет характеристикой канала связи.

Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами (, , , …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.

Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (). Ошибки при передаче будем подчёркивать.

Например, пусть мы хотим передавать только сообщения и . В простейшем случае их можно закодировать нулём и единицей (сюрприз!):

Передача по каналу, в котором возникла ошибка будет записана так:

Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это и .

Код с утроением

Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:

Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:

Какие выводы мы можем сделать, когда получили ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква . А может, во втором, и была передана .

То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.

Проверим в деле:

Получили . Тут у нас есть две возможности: либо это и было две ошибки (в крайних цифрах), либо это и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква . Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.

Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква .

Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.

Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.

Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.

Расстояния между кодами

Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.

И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.

Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.

Пусть мы передавали , а получили . Видно, что эта цепочка больше похожа на исходные , чем на . А так как других кодовых слов у нас нет, то и выбор очевиден.

Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.

Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек и . Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.

Например, , так как все цифры в соответствующих позициях равны, а вот .

Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:

  1. Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
  2. Расстояние в обе стороны одинаково.
  3. Путь через третью точку не короче, чем прямой путь.

Достаточно разумные требования.

Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):

  3. .

Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.

Окрестности

Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.

Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.

Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.

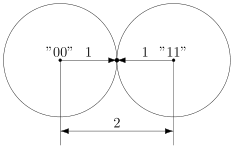
Так, скажем, окрестность кодового слова радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:

Да, вот так странно выглядят шары в пространстве кодов.

А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.

Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение , мы получим один из кодов, который принадлежит окрестности радиусом 2.

Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.

Сколько ошибок может исправить код?

Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.

В коде с удвоением между кодовыми словами и расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.

Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.

Что интересно, точек касания в нашем странном пространстве у шаров две — это коды и . Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.

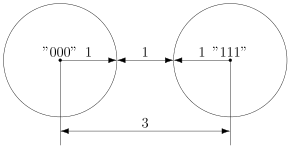
В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).

В общем случае получаем следующее.

Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием будет успешно работать в канале с ошибками, если выполняется соотношение

Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса других кодовых слов. Математически это записывается так:

Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.

Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.

A B C D
A — 3 3 4
B 3 — 4 3
C 3 4 — 3
D 4 3 3 —

Минимальное расстояние , а значит , откуда получаем, что такой код может исправить до ошибок. Обнаруживает же он две ошибки.

Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.

Минимальное расстояние получилось для символа , значит вероятнее всего передавался именно он:

Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.

Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.

Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.

Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.

Интерлюдия: поле GF(2)

Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.

Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):

Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.

Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.

У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.

Это свойство прямо следует из определения.

А в этом можно убедиться, прибавив к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.

Проверяем корректность

Вернёмся к коду с утроением.

Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.

Пусть мы приняли вектор-строку из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)

Математически равенство всех трёх цифр можно записать как систему:

Или, если воспользоваться свойствами сложения в GF(2), получаем

В матричном виде эта система будет иметь вид

Транспонирование здесь нужно потому, что — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.

Будем называть матрицу проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.

Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.

Кодирование

Итак, у нас есть система для проверки

Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице ) найдём кодовые слова.

Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:

Соответствующая система имеет вид:

Чтобы найти кодовые слова соответствующего кода нужно её решить.

В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если и — решения системы, то для их суммы верно

что означает, что она тоже — решение.

Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.

Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .

Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.

Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.

Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:

где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно сочетания.

Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.

Строчки здесь — линейно независимые решения, которые мы получили. Матрица называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:

Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)

Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?

А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!

Для кода с утроением, кстати, порождающая матрица выглядит очень просто:

Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.

Ошибка по синдрому

Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!

Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение , а было отправлено кодовое слово . Тогда вектор ошибки по определению

Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:

В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.

Как мы уже говорили раньше, если мы получили сообщение с ошибкой, то . Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?

Назовём результат умножения на проверочную матрицу синдромом:

И заметим следующее

Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.

Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?

А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.

Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.

В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.

Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.

Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.

Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.

Ура, всё работает!

Что же дальше?

Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.

Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.

Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.

Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.

[spoiler title=”источники:”]

http://studref.com/365851/tehnika/dekodirovanie_lineynyh_kodov

http://habr.com/ru/post/328202/

[/spoiler]

Источник

Корректирующие коды «на пальцах»

Время на прочтение
11 мин

Количество просмотров 62K

Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.

Давайте же разберёмся, что это такое.

Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.

Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.

Каналы с ошибкой

Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.

Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем $k$ ошибок. Это будет характеристикой канала связи.

Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами ($A$, $B$, $C$, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.

Кодирование и декодирование будем обозначать прямой стрелкой ($rightarrow$), а передачу по каналу связи — волнистой стрелкой ($rightsquigarrow$). Ошибки при передаче будем подчёркивать.

Например, пусть мы хотим передавать только сообщения $A=0$ и $B=1$. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):

$ begin{aligned} A &to 0,\ B &to 1. end{aligned} $

Передача по каналу, в котором возникла ошибка будет записана так:

$ A to 0 rightsquigarrow underline{1} to B. $

Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это $0$ и $1$.

Код с утроением

Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:

$ begin{aligned} A &to 00,\ B &to 11. end{aligned} $

Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:

$ A to 00 rightsquigarrow 0underline{1} to ?. $

Какие выводы мы можем сделать, когда получили $01$? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква $B$. А может, во втором, и была передана $A$.

То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.

$ begin{aligned} A &to 000,\ B &to 111. end{aligned} $

Проверим в деле:

$ A to 000 rightsquigarrow 0underline{1}0 to A?. $

Получили $010$. Тут у нас есть две возможности: либо это $B$ и было две ошибки (в крайних цифрах), либо это $A$ и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква $A$. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.

Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква $A$.

Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.

Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.

Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.

Расстояния между кодами

Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.

И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.

Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.

Пусть мы передавали $000$, а получили $001$. Видно, что эта цепочка больше похожа на исходные $000$, чем на $111$. А так как других кодовых слов у нас нет, то и выбор очевиден.

Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.

Можно ввести некоторую величину $d(alpha, beta)$, равную количеству различающихся цифр в соответствующих разрядах цепочек $alpha$ и $beta$. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.

Например, $d(010, 010) = 0$, так как все цифры в соответствующих позициях равны, а вот $d(010101, 011011) = 3$.

Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:

  1. Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
  2. Расстояние в обе стороны одинаково.
  3. Путь через третью точку не короче, чем прямой путь.

Достаточно разумные требования.

Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):

  1. $d(x, y) geqslant 0,quad d(x, y) = 0 Leftrightarrow x = y;$
  2. $d(x, y) = d(y, x);$
  3. $d(x, z) + d(z, y) geqslant d(x, y)$.

Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.

Окрестности

Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.

Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.

Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.

Так, скажем, окрестность кодового слова $000$ радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:

$ {000, 100, 010, 001}. $

Да, вот так странно выглядят шары в пространстве кодов.

А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим $000$! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.

Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение $x$, мы получим один из кодов, который принадлежит окрестности $x$ радиусом 2.

Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.

Сколько ошибок может исправить код?

Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.

В коде с удвоением между кодовыми словами $00$ и $11$ расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.

Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.

Что интересно, точек касания в нашем странном пространстве у шаров две — это коды $01$ и $10$. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.

В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).

В общем случае получаем следующее.

Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием $d_{min}$ будет успешно работать в канале с $k$ ошибками, если выполняется соотношение

$ d_{min} geqslant 2k+1. $

Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает $k$ ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса $k$ других кодовых слов. Математически это записывается так:

$d_{min}geqslant k + 1.$

Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.

$ begin{aligned} A to 10100,\ B to 01000,\ C to 00111,\ D to 11011.\ end{aligned} $

Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.

A B C D
A — 3 3 4
B 3 — 4 3
C 3 4 — 3
D 4 3 3 —

Минимальное расстояние $d_{min}=3$, а значит $3geqslant2k+1$, откуда получаем, что такой код может исправить до $k=1$ ошибок. Обнаруживает же он две ошибки.

Рассмотрим пример:

$ A to 10100 rightsquigarrow 101underline{1}0. $

Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.

$ begin{aligned} A:, d(10110, 10100) &= 1,\ B:, d(10110, 01000) &= 4,\ C:, d(10110, 00111) &= 2,\ D:, d(10110, 11011) &= 3. end{aligned} $

Минимальное расстояние получилось для символа $A$, значит вероятнее всего передавался именно он:

$ A to 10100 rightsquigarrow 101underline{1}0 to A?. $

Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.

Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.

Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы $2^5 = 32$ варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.

Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.

Интерлюдия: поле GF(2)

Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.

Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):

$ begin{aligned} 0 + 0 &= 0,\ 0 + 1 &= 1,\ 1 + 0 &= 1,\ 1 + 1 &= 0. end{aligned} $

Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.

Множество из двух элементов ${0, 1}$ с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.

У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.

$ x + x = 0. $

Это свойство прямо следует из определения.

$ x + y = x - y. $

А в этом можно убедиться, прибавив $y$ к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.

Проверяем корректность

Вернёмся к коду с утроением.

$ begin{aligned} A &to 000,\ B &to 111. end{aligned} $

Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.

Пусть мы приняли вектор-строку $x$ из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)

$dots rightsquigarrow x = (x_1, x_2, x_3). $

Математически равенство всех трёх цифр можно записать как систему:

$ left{ begin{aligned} x_1 &= x_2,\ x_2 &= x_3. end{aligned} right. $

Или, если воспользоваться свойствами сложения в GF(2), получаем

$ left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right. $

Или

$ left{ begin{aligned} 1cdot x_1 + 1cdot x_2 + 0cdot x_3 &= 0,\ 0cdot x_1 + 1cdot x_2 + 1cdot x_3 &= 0. end{aligned} right. $

В матричном виде эта система будет иметь вид

$ Hx^T = 0, $

где

$ H = begin{pmatrix} 1 & 1 & 0\ 0 & 1 & 1 end{pmatrix}. $

Транспонирование здесь нужно потому, что $x$ — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.

Будем называть матрицу $H$ проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.

Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.

Кодирование

Итак, у нас есть система для проверки

$ left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right. $

Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице $H$) найдём кодовые слова.

Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:

$ H = begin{pmatrix} 1 & 0 & 1 & 0 & 0 \ 0 & 1 & 1 & 0 & 1\ 0 & 0 & 0 & 1 & 1 end{pmatrix}. $

Соответствующая система имеет вид:

$ left{ begin{aligned} x_1 + x_3 &= 0,\ x_2 + x_3 + x_5 &= 0,\ x_4 + x_5 &= 0. end{aligned} right. $

Чтобы найти кодовые слова соответствующего кода нужно её решить.

В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если $a$ и $b$ — решения системы, то для их суммы верно

$H(a+b)^T=Ha^T+Hb^T=0+0=0,$

что означает, что она тоже — решение.

Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.

Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить $x_1, x_2, x_4$.

Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.

Итак, получаем:

$ left{ begin{aligned} x_1 &= x_3,\ x_2 &= x_3 + x_5,\ x_4 &= x_5. end{aligned} right. $

Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.

$ begin{aligned} x_3=1, x_5=0:quad x_1=1, x_2=1, x_4=0 Rightarrow x^{(1)} = (1, 1, 1, 0, 0),\ x_3=0, x_5=1:quad x_1=0, x_2=1, x_4=1 Rightarrow x^{(2)} = (0, 1, 0, 1, 1). end{aligned} $

Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:

$ a_1 x^{(1)}+a_2 x^{(2)}, $

где $a_1, a_2$ равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно $2^2=4$ сочетания.

Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.

$ (a_1, a_2)cdot begin{pmatrix} 1 & 1 & 1 & 0 & 0 \ 0 & 1 & 0 & 1 & 1 end{pmatrix} = aG. $

Строчки здесь — линейно независимые решения, которые мы получили. Матрица $G$ называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:

$ a to aG. $

Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)

$ begin{aligned} 00 &to 00000,\ 01 &to 01011,\ 10 &to 11100,\ 11 &to 10111. end{aligned} $

Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?

$ a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to Hx^T = (110)^T neq 0. $

А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!

Для кода с утроением, кстати, порождающая матрица выглядит очень просто:

$G=begin{pmatrix}1&1&1end{pmatrix}.$

Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.

Ошибка по синдрому

Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!

Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение $x$, а было отправлено кодовое слово $v$. Тогда вектор ошибки по определению

$ e = x - v. $

Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:

$ begin{aligned} v &= x + e,\ x &= v + e. end{aligned} $

В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.

Как мы уже говорили раньше, если мы получили сообщение $x$ с ошибкой, то $Hx^Tneq 0$. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?

Назовём результат умножения на проверочную матрицу синдромом:

$ s(x)=Hx^T.$

И заметим следующее

$ s(x) = Hx^T = H(v+e)^T = He^T = s(e). $

Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.

Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?

А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.

Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.

$s(x)$ $x$
$000$ $underline{00000}, 11100, 01011, 10111$
$001$ $underline{00010}, 11110, 01001, 10101$
$010$ $underline{01000}, 10100, 00011, 11111$
$011$ $01010, 10110, underline{00001}, 11101$
$100$ $underline{10000}, 01100, 11011, 00111$
$101$ $underline{10010}, 01110, 11001, underline{00101}$
$110$ $11000, underline{00100}, 10011, 01111$
$111$ $11010, underline{00110}, underline{10001}, 01101$

В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.

Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.

Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.

$ a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to s(x)=Hx^T = (110)^T to e=(00100). $

Вектор ошибки равен $(00100)$, а значит ошибка в третьем разряде. Как мы и загадали.

Ура, всё работает!

Что же дальше?

Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.

Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.

Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.

Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.

Источник
  • Авторы
  • Резюме
  • Файлы
  • Ключевые слова
  • Литература


Барсагаев А.А.

1

Калмыков М.И.

1

1 Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Северо-Кавказский федеральный университет»

В работе рассмотрены вопросы, связанные с анализом корректирующих способностей модулярных полиномиальных кодов (МПК). Данные коды позволяют осуществлять обработку данных в реальном масштабе времени за счет использования малоразрядных данных. При этом обработка информации осуществляется параллельно по вычислительным трактам и независимо друг от друга. Такое свойство МПК позволяет осуществлять процедуры поиска и коррекции ошибок. Для повышения корректирующих способностей кодов в МПК вводят дополнительные контрольные основания. С целью определения местоположения и глубины ошибки используются позиционные характеристики. В статье представлен алгоритм поиска и коррекции ошибок с использованием псевдоортогональных базисов модулярных полиномиальных кодов.

модулярные полиномиальные коды

параллельные вычисления

остатки

псевдоортогональные базисы

коррекция ошибок.

1. Бережной В.В., Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Шилов А.А. Нейросетевая реализация в полиномиальной системе классов вычетов операций ЦОС повышенной разрядности // Нейрокомпьютеры: разработка и применение. – 2004. – № 5-6. – С. 94.

2. Бережной В.В., Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Шилов А.А. Архитектура отказоустойчивой нейронной сети для цифровой обработки сигналов // Нейрокомпьютеры: разработка и применение. – 2004. – № 12. – С. 51-57.

3. Емарлукова Я.В., Калмыков И.А., Зиновьев А.В. Высокоскоростные систолические отказоустойчивые процессоры цифровой обработки сигналов для инфотелекоммуникационных систем // Инфокоммуникационные технологии. Самара. – 2009. – №2. – С. 31-37.

4. Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Шилов А.А. Нейросетевая реализация в полиномиальной системе классов вычетов операций ЦОС повышенной разрядности // Нейрокомпьютеры: разработка и применение. – 2004. – № 5-6. – С. 94.

5. Калмыков И.А., Чипига А.Ф. Структура нейронной сети для реализации цифровой обработки сигналов повышенной разрядности // Вестник Ставропольского государственного университета. – 2004. – Т.38. – С. 46.

6. Калмыков И.А., Петлеванный С.В., Сагдеев А.К., Емарлукова Я.В. Устройство для преобразования числа из полиномиальной системы классов вычетов в позиционный код с коррекцией ошибки // Патент России № 2309535. 31.03.2006. Бюл. № 30 от 27.10.2007.

7. Калмыков И.А., Гахов В.Р., Емарлукова Я.В. Устройство обнаружения и коррекции ошибок в кодах полиномиальной системы классов вычетов // Патент России № 2300801. 30.06.2005. Бюл. № 16 от 10.06.2007.

8. Хайватов А.Б., Калмыков И.А. Математическая модель отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов // Инфокоммуникационные технологии. – 2007. – Т.5. – №3. – С.39-42.

9. Червяков Н.И., Калмыков И.А., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронной сети для коррекции ошибок в непозиционном коде расширенного поля Галуа // Нейрокомпьютеры: разработка и применение. – 2003. – № 8-9. – С. 10-17.

10. Чипига А.А., Калмыков И.А., Лободин М.В. Устройство спектрального обнаружения и коррекции в кодах полиномиальной системы классов вычетов // Патент России № 2301441. Бюл. № 17 от 20.06.2007.

Введение

В последние годы цифровая обработка сигналов (ЦОС) занимает доминирующее положение в системах и средствах передачи и обработки информации в связи с неоспоримыми достоинствами – точность, гибкость и высокая скорость обработки. Кроме того, с развитием средств вычислительной техники системы ЦОС становятся все дешевле и компактнее. Эффективность ЦОС полностью определяется объемом вычислений, которые получаются при реализации математической модели процесса цифровой обработки сигнала с помощью специализированного процессора (СП). Снижение объема вычислений приводит к уменьшению аппаратурных затрат при реализации систем ЦОС или к повышению производительности вычислительного устройства. Таким образом, выбор алгебраической системы оптимальной с точки зрения минимума объема вычислений при реализации методов ЦОС является актуальной и важной.

Постановка задачи исследований. Как правило, в подавляющем большинстве приложений задачи ЦОС сводится к нахождению значений ортогонального преобразования конечной реализации сигнала для большого числа точек, что предопределяет повышенные требования к скорости обработки и разрядности вычислительного устройства. Решить данную проблему можно за счет перехода от одномерных вычислений к многомерным. В основу данного преобразования положена китайская теорема об остатках (КТО) [1-5].

Особое место среди таких систем занимает модулярная полиномиальная система класса вычетов, с помощью которых возможна организация ортогональных преобразований сигналов в расширенных полях Галуа . Если исходное число А представить в полиномиальной форме, а в качестве оснований выбрать минимальные многочлены поля Галуа, то справедливо

A (z) = (α1 (z), α2 (z).., αn (z)), (1)

где αi (z) ≡ A (z mod pi(z); pi (z) – минимальный многочлен.

Применение модулярных полиномиальных кодов позволяет свести операции в кольце полиномов к соответствующим операциям над остатками [1-6]. В этом случае

, (1)

где и – модулярный код в кольце полиномов; ; ; – операции сложения, вычитания и умножения в GF(p); l = 1, …,n.

Таким образом, основным достоинством непозиционных кодов является, то, что данные представляются в виде малоразрядных остатков, которые обрабатываются по параллельным вычислительным трактам. Это позволяет повысить скорость вычислений, что и предопределяет интерес к полиномиальным непозиционным кодам в различных областях применения [1-6].

В работах [1-5] предлагается для эффективной реализации ортогональных преобразований с высокой точностью и скоростью вычислений реализация дискретного преобразования Фурье (ДПФ) в кольце полиномов. В этом случае, если имеется кольцо полиномов P(z), с коэффициентами в виде элементов поля GF(p), то данное кольцо разлагается в сумму

, (2)

где Pl(z) – локальное кольцо полиномов, образованное неприводимым полиномом pl(z) над полем GF(p); l=1, …, n.

При этом в кольце полиномов можно организовать ортогональное преобразование, представляющее собой полиномиальное ДПФ, вида

, (3)

где , l=1,2,…,m; k=0,1,…d-1.

При этом должны выполняться следующие условия:

1. – первообразный элемент порядка d для локального кольца Pl(z).

2. d имеет мультипликативный обратный элемент d*.

Если отмеченные условия выполняются, то получается циклическая группа, которая имеет порядок d. В этом случае ортогональное преобразование является полиномиальным ДПФ для кольца вычетов P(z) если существуют преобразования над конечным кольцом Pl(z)

Поэтому ДПФ над Pl(z) можно обобщить над кольцом P(z), если конечное кольцо Pl(z) содержит корень d-ой степени из единицы и d имеет мультипликативный обратный элемент d*, такой что справедливо

. (4)

Основным достоинством системы класса вычетов является сравнительная простота выполнения модульных операций (сложения, вычитания, умножения). Формальные правила выполнения таких операций в МПК позволяют существенно повысить скорость вычислительных устройств ЦОС [5].

Кроме модульных операций, позволяющих повысить скорость обработки информации, модулярные коды позволяют обнаруживать и исправлять ошибки, возникающие в процессе функционирования СП. Если в качестве рабочих оснований выбрать k минимальных многочленов МПК (k<n), то данные основания определяют рабочий диапазон

. (5)

Если , то такой полином считается разрешенным и не содержит ошибок. В противном случае, полином, представленный в модулярном полиномиальном коде, содержит ошибки [6-10].

Для определения местоположения и глубины ошибки в полиномиальной системе классов вычетов используются позиционные характеристики. В работе [9] представлен алгоритм вычисления такой характеристики как интервальный номер. Синдром ошибки для полиномиального кода вычисляется в работе [8]. В работе [7] показана математическая модель поиска ошибочного основания с использованием алгоритма нулевизации. Структура устройства спектрального обнаружения и коррекции в кодах полиномиальной системы классов вычетов приведена в работе [10].

Одной из характеристик, использующемой при выполнении процедур поиска и коррекции ошибок в модулярных кодах, является след полинома. Для получения данной характеристики используются псевдоортогональные полиномы. Они представляют собой ортогональные полиномы, у которых нарушена ортогональность по нескольким основаниям. Известно, что если в псевдоортогональных полиномах нарушена ортогональность по контрольным основаниям, то данные полиномы являются ортогональными полиномами безизбыточной системы оснований полиномиальной системы классов вычетов.

Для получения псевдоортогональных полиномов проведем расширение системы оснований p1(z), …, pk(z) на r контрольных оснований pk+1(z), …, pk+r(z) и представим ортогональные полиномы в виде:

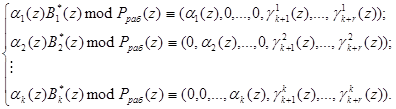(6)

Выражение (6) определяет значения псевдоортогональных полиномов, у которых нарушена ортогональность по контрольным основаниям.

Согласно китайской теореме об остатках

, (7)

полином можно представить в виде:

. (8)

Тогда каждое слагаемое выражения (4) представляет собой

, (9)

где Bi*(z) – ортогональный базис безизбыточной системы оснований МПК.

Подставив выражение (6) в равенство (8), и учитывая, что в процессе выполнения операции не бывает выход за пределы Pраб(z), получаем

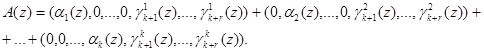
Следовательно, справедливо

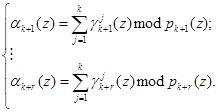(9)

Таким образом, на основании (9) и воспользовавшись значениями псевдоортогональных полиномов, определяемых равенством (6), можно вычислить значения остатков по контрольным основаниям согласно

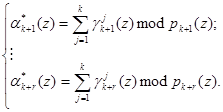. (10)

Затем на основании полученных значений и значений, поступающих на вход устройства коррекции ошибок, можно определить синдром ошибки согласно выражения

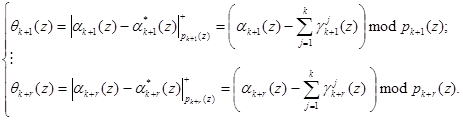(11)

Если разность равна нулю, т.е. , то исходный полином является разрешенным и не содержит ошибки. В противном случае модулярная комбинация является запрещенной. Тогда в зависимости от величины синдрома ошибки осуществляется коррекция ошибки, т.е.

(12)

где– вектор ошибки модулярного кода; – глубина ошибки по i-му модулю МПК.

В работе [6] представлена структура устройства для преобразования числа из полиномиальной системы классов вычетов в позиционный код с коррекцией ошибки, в процессе функционирования которого используется данный алгоритм. Следует отметить, что этот алгоритм поиска и коррекции ошибок позволяет осуществить поиск и коррекцию всех однократных ошибок с использованием двух контрольных оснований и 90 процентов двоичных ошибок.

Вывод. В работе показана возможность осуществления цифровой обработки сигналов с использованием математической модели ЦОС, обладающей свойством кольца и поля. Применение полиномиальных кодов позволяет повысить скорость обработки данных за счет применения малоразрядных остатков и их параллельной архитектуре вычислений. Кроме того, МПК могут использоваться для повышения отказоустойчивости вычислительных систем. В работе рассмотрен алгоритм вычислений позиционной характеристики на основе ортогональных базисов, у которых нарушена ортогональность по контрольным основаниям.

Патент России № 2301441. Бюл. № 17 от 20.06.2007.

Библиографическая ссылка

Барсагаев А.А., Калмыков М.И. АЛГОРИТМЫ ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В МОДУЛЯРНЫХ ПОЛИНОМИАЛЬНЫХ КОДАХ // Международный журнал экспериментального образования. – 2014. – № 3-1.
– С. 103-106;

URL: https://expeducation.ru/ru/article/view?id=4672 (дата обращения: 21.05.2023).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Источник

Добавить комментарий