Найдем синус 120 градусов, пользуясь формулой приведения для синуса тупого угла от 90º до 180º.
Утверждение:
![]()
Доказательство:

Синус угла альфа на единичной окружности — это ордината точки, полученной из точки (1;0) поворотом на угол альфа вокруг точки O.
Для синуса тупого угла (от 90 до 180 градусов) имеет место следующая формула приведения:
![]()
Представим
![]()
Воспользуемся данной формулой приведения и значением синуса 60º:
![]()
Что и требовалось доказать.
Если перевести 120 градусов в радианы, получим:
![]()
Отсюда, синус 2П/3 равен
![]()
|
Как найти синус 120 градусов
Если ответить совсем кратко: то синус ста двадцати градусов равен корню из трех, разделить пополам. А записать выражение можно так:
А можно записать в числовом значении, тогда синус 120 равен 0, 8660. Ниже пояснительный наглядный рисунок, почему все именно так:
автор вопроса выбрал этот ответ лучшим Rafail 4 года назад Если уж Вам знакомо слово синус, то наверное знакомы и формулы приведения. Нужная Вам формула sin(a)= sin(180°-a). Таким образом sin(120)= sin(180°-120°)=sin(60°)= (√3)/2. Ещё одна “очень полезная” формула приведения sin(a)= cos(90°-a).
zanoza-1952 3 года назад Вопрос некорректен, так как тригонометрические функции, к которым относятся синус, косинус, тангенс, котангенс, имеют место в прямоугольном треугольнике. Синус угла, это отношение противополжного катета прямоугольного треугольника к гипотенузе.
Степан БВ 2 месяца назад Синус 120 градусов равен -0,5. Это можно проверить, используя тригонометрическую таблицу или настроив калькулятор. Для решения задачи можно использовать также тригонометрические формулы и рассчитать синус угла самостоятельно. Знаете ответ? |
Синус 120 градусов
Найдем синус 120 градусов, пользуясь формулой приведения для синуса тупого угла от 90º до 180º.
Синус угла альфа на единичной окружности — это ордината точки, полученной из точки (1;0) поворотом на угол альфа вокруг точки O.
Для синуса тупого угла (от 90 до 180 градусов) имеет место следующая формула приведения:
Воспользуемся данной формулой приведения и значением синуса 60º:
Что и требовалось доказать.
Если перевести 120 градусов в радианы, получим:
Синус, косинус и тангенс угла 120 градусов
Синус, косинус и тангенс угла 2π/3 радиан
Напомним себе, что 2π/3 в градусах – это 120 градусов. ( 2 * 180 / 3 = 120 ). Таким образом, найти значение тригонометрической функции для угла 2π/3 и для ула 120 градусов – это одно и то же.
Как найти значения тригонометрических функций для угла 120 градусов
Найдем значения синуса, косинуса и тангенса для угла 120 градусов аналитическим способом.
На первый взгляд, нахождение значений синуса, косинуса и тангенса для угла 120 градусов – задача сложная. Однако, это не совсем так.
Прежде всего, мы должны обратить внимание, что для углов, значения которых превышают 90 градусов, у нас есть формулы приведения к углу, меньшему 90 градусов.
Поэтому, для начала, представим себе угол в 120 градусов как (90 + 30)
Тогда
sin ( 90 + α ) = cos α
sin 120 = sin( 90 + 30 ) = cos 30
cos ( 90 + α ) = – sin α
cos 120 = cos( 90 + 30 ) = -sin 30
tg ( 90 + α ) = -ctg α
tg 120 = tg( 90 + 30 ) = -ctg 30
Теперь можно посмотреть значения в таблицах синуса, косинуса и тангенса 120 градусов, который преобразован в значения тригонометрических функций синуса, косинуса и тангенса угла 30 градусов.
В уроке по ссылке можно посмотреть как вычислить значения тригонометрических функций для угла 30 градусов.
В итоге получаем:
Как видно из примера, значения тригонометрических функций углов синуса, косинуса и тангенса 120 градусов могут быть получены путем несложных тригонометрических преобразований с использованием тригонометрических тождеств.
См. также полную таблицу значений тригонометрических функций (таблицу синусов, косинусов и тангенсов).
Ниже приведены также значения тригонометрических функций для угла 120 градусов в виде десятичной дроби с четырьмя знаками после запятой.
Таблица СИНУСОВ для углов от 0° до 360° градусов
СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| SIN α (СИНУС) | 0 | 1/2 | √ 2/2 | √3 /2 | 1 | 0 | -1 | 0 |
Малая таблица значений тригонометрических функций (в радианах и градусах)
| Угол в градусах | Sin (Синус) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0523 |
| 4° | 0.0698 |
| 5° | 0.0872 |
| 6° | 0.1045 |
| 7° | 0.1219 |
| 8° | 0.1392 |
| 9° | 0.1564 |
| 10° | 0.1736 |
| 11° | 0.1908 |
| 12° | 0.2079 |
| 13° | 0.225 |
| 14° | 0.2419 |
| 15° | 0.2588 |
| 16° | 0.2756 |
| 17° | 0.2924 |
| 18° | 0.309 |
| 19° | 0.3256 |
| 20° | 0.342 |
| 21° | 0.3584 |
| 22° | 0.3746 |
| 23° | 0.3907 |
| 24° | 0.4067 |
| 25° | 0.4226 |
| 26° | 0.4384 |
| 27° | 0.454 |
| 28° | 0.4695 |
| 29° | 0.4848 |
| 30° | 0.5 |
| 31° | 0.515 |
| 32° | 0.5299 |
| 33° | 0.5446 |
| 34° | 0.5592 |
| 35° | 0.5736 |
| 36° | 0.5878 |
| 37° | 0.6018 |
| 38° | 0.6157 |
| 39° | 0.6293 |
| 40° | 0.6428 |
| 41° | 0.6561 |
| 42° | 0.6691 |
| 43° | 0.682 |
| 44° | 0.6947 |
| 45° | 0.7071 |
| 46° | 0.7193 |
| 47° | 0.7314 |
| 48° | 0.7431 |
| 49° | 0.7547 |
| 50° | 0.766 |
| 51° | 0.7771 |
| 52° | 0.788 |
| 53° | 0.7986 |
| 54° | 0.809 |
| 55° | 0.8192 |
| 56° | 0.829 |
| 57° | 0.8387 |
| 58° | 0.848 |
| 59° | 0.8572 |
| 60° | 0.866 |
| 61° | 0.8746 |
| 62° | 0.8829 |
| 63° | 0.891 |
| 64° | 0.8988 |
| 65° | 0.9063 |
| 66° | 0.9135 |
| 67° | 0.9205 |
| 68° | 0.9272 |
| 69° | 0.9336 |
| 70° | 0.9397 |
| 71° | 0.9455 |
| 72° | 0.9511 |
| 73° | 0.9563 |
| 74° | 0.9613 |
| 75° | 0.9659 |
| 76° | 0.9703 |
| 77° | 0.9744 |
| 78° | 0.9781 |
| 79° | 0.9816 |
| 80° | 0.9848 |
| 81° | 0.9877 |
| 82° | 0.9903 |
| 83° | 0.9925 |
| 84° | 0.9945 |
| 85° | 0.9962 |
| 86° | 0.9976 |
| 87° | 0.9986 |
| 88° | 0.9994 |
| 89° | 0.9998 |
| 90° | 1 |
Полная таблица синусов для углов от 0° до 360° с шагом всего в 1°
| Угол в градусах | Sin (Синус) |
|---|---|
| 91° | 0.9998 |
| 92° | 0.9994 |
| 93° | 0.9986 |
| 94° | 0.9976 |
| 95° | 0.9962 |
| 96° | 0.9945 |
| 97° | 0.9925 |
| 98° | 0.9903 |
| 99° | 0.9877 |
| 100° | 0.9848 |
| 101° | 0.9816 |
| 102° | 0.9781 |
| 103° | 0.9744 |
| 104° | 0.9703 |
| 105° | 0.9659 |
| 106° | 0.9613 |
| 107° | 0.9563 |
| 108° | 0.9511 |
| 109° | 0.9455 |
| 110° | 0.9397 |
| 111° | 0.9336 |
| 112° | 0.9272 |
| 113° | 0.9205 |
| 114° | 0.9135 |
| 115° | 0.9063 |
| 116° | 0.8988 |
| 117° | 0.891 |
| 118° | 0.8829 |
| 119° | 0.8746 |
| 120° | 0.866 |
| 121° | 0.8572 |
| 122° | 0.848 |
| 123° | 0.8387 |
| 124° | 0.829 |
| 125° | 0.8192 |
| 126° | 0.809 |
| 127° | 0.7986 |
| 128° | 0.788 |
| 129° | 0.7771 |
| 130° | 0.766 |
| 131° | 0.7547 |
| 132° | 0.7431 |
| 133° | 0.7314 |
| 134° | 0.7193 |
| 135° | 0.7071 |
| 136° | 0.6947 |
| 137° | 0.682 |
| 138° | 0.6691 |
| 139° | 0.6561 |
| 140° | 0.6428 |
| 141° | 0.6293 |
| 142° | 0.6157 |
| 143° | 0.6018 |
| 144° | 0.5878 |
| 145° | 0.5736 |
| 146° | 0.5592 |
| 147° | 0.5446 |
| 148° | 0.5299 |
| 149° | 0.515 |
| 150° | 0.5 |
| 151° | 0.4848 |
| 152° | 0.4695 |
| 153° | 0.454 |
| 154° | 0.4384 |
| 155° | 0.4226 |
| 156° | 0.4067 |
| 157° | 0.3907 |
| 158° | 0.3746 |
| 159° | 0.3584 |
| 160° | 0.342 |
| 161° | 0.3256 |
| 162° | 0.309 |
| 163° | 0.2924 |
| 164° | 0.2756 |
| 165° | 0.2588 |
| 166° | 0.2419 |
| 167° | 0.225 |
| 168° | 0.2079 |
| 169° | 0.1908 |
| 170° | 0.1736 |
| 171° | 0.1564 |
| 172° | 0.1392 |
| 173° | 0.1219 |
| 174° | 0.1045 |
| 175° | 0.0872 |
| 176° | 0.0698 |
| 177° | 0.0523 |
| 178° | 0.0349 |
| 179° | 0.0175 |
| 180° | 0 |
Полная таблица синусов для углов от 91° до 180°
| Угол | Sin (Синус) |
|---|---|
| 181° | -0.0175 |
| 182° | -0.0349 |
| 183° | -0.0523 |
| 184° | -0.0698 |
| 185° | -0.0872 |
| 186° | -0.1045 |
| 187° | -0.1219 |
| 188° | -0.1392 |
| 189° | -0.1564 |
| 190° | -0.1736 |
| 191° | -0.1908 |
| 192° | -0.2079 |
| 193° | -0.225 |
| 194° | -0.2419 |
| 195° | -0.2588 |
| 196° | -0.2756 |
| 197° | -0.2924 |
| 198° | -0.309 |
| 199° | -0.3256 |
| 200° | -0.342 |
| 201° | -0.3584 |
| 202° | -0.3746 |
| 203° | -0.3907 |
| 204° | -0.4067 |
| 205° | -0.4226 |
| 206° | -0.4384 |
| 207° | -0.454 |
| 208° | -0.4695 |
| 209° | -0.4848 |
| 210° | -0.5 |
| 211° | -0.515 |
| 212° | -0.5299 |
| 213° | -0.5446 |
| 214° | -0.5592 |
| 215° | -0.5736 |
| 216° | -0.5878 |
| 217° | -0.6018 |
| 218° | -0.6157 |
| 219° | -0.6293 |
| 220° | -0.6428 |
| 221° | -0.6561 |
| 222° | -0.6691 |
| 223° | -0.682 |
| 224° | -0.6947 |
| 225° | -0.7071 |
| 226° | -0.7193 |
| 227° | -0.7314 |
| 228° | -0.7431 |
| 229° | -0.7547 |
| 230° | -0.766 |
| 231° | -0.7771 |
| 232° | -0.788 |
| 233° | -0.7986 |
| 234° | -0.809 |
| 235° | -0.8192 |
| 236° | -0.829 |
| 237° | -0.8387 |
| 238° | -0.848 |
| 239° | -0.8572 |
| 240° | -0.866 |
| 241° | -0.8746 |
| 242° | -0.8829 |
| 243° | -0.891 |
| 244° | -0.8988 |
| 245° | -0.9063 |
| 246° | -0.9135 |
| 247° | -0.9205 |
| 248° | -0.9272 |
| 249° | -0.9336 |
| 250° | -0.9397 |
| 251° | -0.9455 |
| 252° | -0.9511 |
| 253° | -0.9563 |
| 254° | -0.9613 |
| 255° | -0.9659 |
| 256° | -0.9703 |
| 257° | -0.9744 |
| 258° | -0.9781 |
| 259° | -0.9816 |
| 260° | -0.9848 |
| 261° | -0.9877 |
| 262° | -0.9903 |
| 263° | -0.9925 |
| 264° | -0.9945 |
| 265° | -0.9962 |
| 266° | -0.9976 |
| 267° | -0.9986 |
| 268° | -0.9994 |
| 269° | -0.9998 |
| 270° | -1 |
Таблица синусов для углов 181° — 270°
| Угол | Sin (Синус) |
|---|---|
| 271° | -0.9998 |
| 272° | -0.9994 |
| 273° | -0.9986 |
| 274° | -0.9976 |
| 275° | -0.9962 |
| 276° | -0.9945 |
| 277° | -0.9925 |
| 278° | -0.9903 |
| 279° | -0.9877 |
| 280° | -0.9848 |
| 281° | -0.9816 |
| 282° | -0.9781 |
| 283° | -0.9744 |
| 284° | -0.9703 |
| 285° | -0.9659 |
| 286° | -0.9613 |
| 287° | -0.9563 |
| 288° | -0.9511 |
| 289° | -0.9455 |
| 290° | -0.9397 |
| 291° | -0.9336 |
| 292° | -0.9272 |
| 293° | -0.9205 |
| 294° | -0.9135 |
| 295° | -0.9063 |
| 296° | -0.8988 |
| 297° | -0.891 |
| 298° | -0.8829 |
| 299° | -0.8746 |
| 300° | -0.866 |
| 301° | -0.8572 |
| 302° | -0.848 |
| 303° | -0.8387 |
| 304° | -0.829 |
| 305° | -0.8192 |
| 306° | -0.809 |
| 307° | -0.7986 |
| 308° | -0.788 |
| 309° | -0.7771 |
| 310° | -0.766 |
| 311° | -0.7547 |
| 312° | -0.7431 |
| 313° | -0.7314 |
| 314° | -0.7193 |
| 315° | -0.7071 |
| 316° | -0.6947 |
| 317° | -0.682 |
| 318° | -0.6691 |
| 319° | -0.6561 |
| 320° | -0.6428 |
| 321° | -0.6293 |
| 322° | -0.6157 |
| 323° | -0.6018 |
| 324° | -0.5878 |
| 325° | -0.5736 |
| 326° | -0.5592 |
| 327° | -0.5446 |
| 328° | -0.5299 |
| 329° | -0.515 |
| 330° | -0.5 |
| 331° | -0.4848 |
| 332° | -0.4695 |
| 333° | -0.454 |
| 334° | -0.4384 |
| 335° | -0.4226 |
| 336° | -0.4067 |
| 337° | -0.3907 |
| 338° | -0.3746 |
| 339° | -0.3584 |
| 340° | -0.342 |
| 341° | -0.3256 |
| 342° | -0.309 |
| 343° | -0.2924 |
| 344° | -0.2756 |
| 345° | -0.2588 |
| 346° | -0.2419 |
| 347° | -0.225 |
| 348° | -0.2079 |
| 349° | -0.1908 |
| 350° | -0.1736 |
| 351° | -0.1564 |
| 352° | -0.1392 |
| 353° | -0.1219 |
| 354° | -0.1045 |
| 355° | -0.0872 |
| 356° | -0.0698 |
| 357° | -0.0523 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° | 0 |
Таблица синусов для углов от 271° до 360°
Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.
Чему равен синус 45? …
– А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071
[spoiler title=”источники:”]
http://profmeter.com.ua/communication/learning/course/course7/lesson1077/
http://kvn201.com.ua/table-of-sines.htm
[/spoiler]
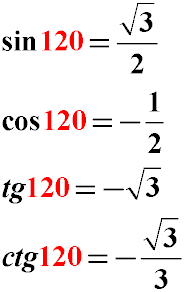
Синус, косинус и тангенс угла 2π/3 радиан
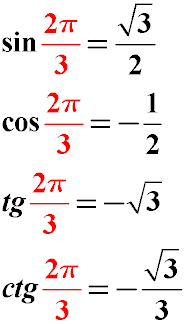
Напомним себе, что 2π/3 в градусах – это 120 градусов. ( 2 * 180 / 3 = 120 ). Таким образом, найти значение тригонометрической функции для угла 2π/3 и для ула 120 градусов – это одно и то же.
Как найти значения тригонометрических функций для угла 120 градусов
Найдем значения синуса, косинуса и тангенса для угла 120 градусов аналитическим способом.
На первый взгляд, нахождение значений синуса, косинуса и тангенса для угла 120 градусов – задача сложная. Однако, это не совсем так.
Прежде всего, мы должны обратить внимание, что для углов, значения которых превышают 90 градусов, у нас есть формулы приведения к углу, меньшему 90 градусов.
Поэтому, для начала, представим себе угол в 120 градусов как (90 + 30)
Тогда
sin ( 90 + α ) = cos α
sin 120 = sin( 90 + 30 ) = cos 30
cos ( 90 + α ) = – sin α
cos 120 = cos( 90 + 30 ) = -sin 30
tg ( 90 + α ) = -ctg α
tg 120 = tg( 90 + 30 ) = -ctg 30
Теперь можно посмотреть значения в таблицах синуса, косинуса и тангенса 120 градусов, который преобразован в значения тригонометрических функций синуса, косинуса и тангенса угла 30 градусов.
В уроке по ссылке можно посмотреть как вычислить значения тригонометрических функций для угла 30 градусов.
В итоге получаем:
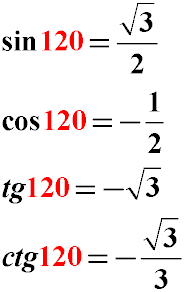
Как видно из примера, значения тригонометрических функций углов синуса, косинуса и тангенса 120 градусов могут быть получены путем несложных тригонометрических преобразований с использованием тригонометрических тождеств.
См. также полную таблицу значений тригонометрических функций (таблицу синусов, косинусов и тангенсов).
Ниже приведены также значения тригонометрических функций для угла 120 градусов в виде десятичной дроби с четырьмя знаками после запятой.
|
2π/3 |
синус 120 sin 120 |
косинус 120 cos 120 |
тангенс 120 tg 120 |
котангенс 120 ctg 120 |
| Значение | 0,8660 | -0,5000 | -1,7321 | -0,5774 |
0
Синус, косинус, тангенс угла 105 градусов (sin 105 cos 105 tg 105) |
Описание курса
| Тригонометрические тождества и преобразования

evadima0912
+10
Решено
5 лет назад
Геометрия
5 – 9 классы
Найдите синус 120 градусов
Смотреть ответ
2
Ответ проверен экспертом
5
(1 оценка)
3

Andr1806
5 лет назад
Светило науки – 4084 ответа – 52605 раз оказано помощи
По формуле приведения
Sin120 = Sin(180-60) = Sin60 =√3/2 ≈ 0,8660.
(1 оценка)
Ответ
5
(1 оценка)
1

Mamedov12
5 лет назад
Светило науки – 1006 ответов – 5391 помощь
sin120град=0,8660254038
примерно 0.87
(1 оценка)
https://vashotvet.com/task/1720847



