Синус угла. Таблица синусов.
Синус угла через градусы, минуты и секунды
Синус угла через десятичную запись угла
Как найти угол зная синус этого угла
У синуса есть обратная тригонометрическая функция – arcsin(y)=x
Пример sin(30°) = 1/2; arcsin(1/2) = 30°
Определение синуса
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
Периодичность синуса
Функция y = sin(x) периодична, с периодом 2π
Таблица СИНУСОВ для углов от 0° до 360° градусов
СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| SIN α (СИНУС) | 0 | 1/2 | √ 2/2 | √3 /2 | 1 | 0 | -1 | 0 |
Малая таблица значений тригонометрических функций (в радианах и градусах)
| Угол в градусах | Sin (Синус) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0523 |
| 4° | 0.0698 |
| 5° | 0.0872 |
| 6° | 0.1045 |
| 7° | 0.1219 |
| 8° | 0.1392 |
| 9° | 0.1564 |
| 10° | 0.1736 |
| 11° | 0.1908 |
| 12° | 0.2079 |
| 13° | 0.225 |
| 14° | 0.2419 |
| 15° | 0.2588 |
| 16° | 0.2756 |
| 17° | 0.2924 |
| 18° | 0.309 |
| 19° | 0.3256 |
| 20° | 0.342 |
| 21° | 0.3584 |
| 22° | 0.3746 |
| 23° | 0.3907 |
| 24° | 0.4067 |
| 25° | 0.4226 |
| 26° | 0.4384 |
| 27° | 0.454 |
| 28° | 0.4695 |
| 29° | 0.4848 |
| 30° | 0.5 |
| 31° | 0.515 |
| 32° | 0.5299 |
| 33° | 0.5446 |
| 34° | 0.5592 |
| 35° | 0.5736 |
| 36° | 0.5878 |
| 37° | 0.6018 |
| 38° | 0.6157 |
| 39° | 0.6293 |
| 40° | 0.6428 |
| 41° | 0.6561 |
| 42° | 0.6691 |
| 43° | 0.682 |
| 44° | 0.6947 |
| 45° | 0.7071 |
| 46° | 0.7193 |
| 47° | 0.7314 |
| 48° | 0.7431 |
| 49° | 0.7547 |
| 50° | 0.766 |
| 51° | 0.7771 |
| 52° | 0.788 |
| 53° | 0.7986 |
| 54° | 0.809 |
| 55° | 0.8192 |
| 56° | 0.829 |
| 57° | 0.8387 |
| 58° | 0.848 |
| 59° | 0.8572 |
| 60° | 0.866 |
| 61° | 0.8746 |
| 62° | 0.8829 |
| 63° | 0.891 |
| 64° | 0.8988 |
| 65° | 0.9063 |
| 66° | 0.9135 |
| 67° | 0.9205 |
| 68° | 0.9272 |
| 69° | 0.9336 |
| 70° | 0.9397 |
| 71° | 0.9455 |
| 72° | 0.9511 |
| 73° | 0.9563 |
| 74° | 0.9613 |
| 75° | 0.9659 |
| 76° | 0.9703 |
| 77° | 0.9744 |
| 78° | 0.9781 |
| 79° | 0.9816 |
| 80° | 0.9848 |
| 81° | 0.9877 |
| 82° | 0.9903 |
| 83° | 0.9925 |
| 84° | 0.9945 |
| 85° | 0.9962 |
| 86° | 0.9976 |
| 87° | 0.9986 |
| 88° | 0.9994 |
| 89° | 0.9998 |
| 90° | 1 |
Полная таблица синусов для углов от 0° до 360° с шагом всего в 1°
| Угол в градусах | Sin (Синус) |
|---|---|
| 91° | 0.9998 |
| 92° | 0.9994 |
| 93° | 0.9986 |
| 94° | 0.9976 |
| 95° | 0.9962 |
| 96° | 0.9945 |
| 97° | 0.9925 |
| 98° | 0.9903 |
| 99° | 0.9877 |
| 100° | 0.9848 |
| 101° | 0.9816 |
| 102° | 0.9781 |
| 103° | 0.9744 |
| 104° | 0.9703 |
| 105° | 0.9659 |
| 106° | 0.9613 |
| 107° | 0.9563 |
| 108° | 0.9511 |
| 109° | 0.9455 |
| 110° | 0.9397 |
| 111° | 0.9336 |
| 112° | 0.9272 |
| 113° | 0.9205 |
| 114° | 0.9135 |
| 115° | 0.9063 |
| 116° | 0.8988 |
| 117° | 0.891 |
| 118° | 0.8829 |
| 119° | 0.8746 |
| 120° | 0.866 |
| 121° | 0.8572 |
| 122° | 0.848 |
| 123° | 0.8387 |
| 124° | 0.829 |
| 125° | 0.8192 |
| 126° | 0.809 |
| 127° | 0.7986 |
| 128° | 0.788 |
| 129° | 0.7771 |
| 130° | 0.766 |
| 131° | 0.7547 |
| 132° | 0.7431 |
| 133° | 0.7314 |
| 134° | 0.7193 |
| 135° | 0.7071 |
| 136° | 0.6947 |
| 137° | 0.682 |
| 138° | 0.6691 |
| 139° | 0.6561 |
| 140° | 0.6428 |
| 141° | 0.6293 |
| 142° | 0.6157 |
| 143° | 0.6018 |
| 144° | 0.5878 |
| 145° | 0.5736 |
| 146° | 0.5592 |
| 147° | 0.5446 |
| 148° | 0.5299 |
| 149° | 0.515 |
| 150° | 0.5 |
| 151° | 0.4848 |
| 152° | 0.4695 |
| 153° | 0.454 |
| 154° | 0.4384 |
| 155° | 0.4226 |
| 156° | 0.4067 |
| 157° | 0.3907 |
| 158° | 0.3746 |
| 159° | 0.3584 |
| 160° | 0.342 |
| 161° | 0.3256 |
| 162° | 0.309 |
| 163° | 0.2924 |
| 164° | 0.2756 |
| 165° | 0.2588 |
| 166° | 0.2419 |
| 167° | 0.225 |
| 168° | 0.2079 |
| 169° | 0.1908 |
| 170° | 0.1736 |
| 171° | 0.1564 |
| 172° | 0.1392 |
| 173° | 0.1219 |
| 174° | 0.1045 |
| 175° | 0.0872 |
| 176° | 0.0698 |
| 177° | 0.0523 |
| 178° | 0.0349 |
| 179° | 0.0175 |
| 180° | 0 |
Полная таблица синусов для углов от 91° до 180°
| Угол | Sin (Синус) |
|---|---|
| 181° | -0.0175 |
| 182° | -0.0349 |
| 183° | -0.0523 |
| 184° | -0.0698 |
| 185° | -0.0872 |
| 186° | -0.1045 |
| 187° | -0.1219 |
| 188° | -0.1392 |
| 189° | -0.1564 |
| 190° | -0.1736 |
| 191° | -0.1908 |
| 192° | -0.2079 |
| 193° | -0.225 |
| 194° | -0.2419 |
| 195° | -0.2588 |
| 196° | -0.2756 |
| 197° | -0.2924 |
| 198° | -0.309 |
| 199° | -0.3256 |
| 200° | -0.342 |
| 201° | -0.3584 |
| 202° | -0.3746 |
| 203° | -0.3907 |
| 204° | -0.4067 |
| 205° | -0.4226 |
| 206° | -0.4384 |
| 207° | -0.454 |
| 208° | -0.4695 |
| 209° | -0.4848 |
| 210° | -0.5 |
| 211° | -0.515 |
| 212° | -0.5299 |
| 213° | -0.5446 |
| 214° | -0.5592 |
| 215° | -0.5736 |
| 216° | -0.5878 |
| 217° | -0.6018 |
| 218° | -0.6157 |
| 219° | -0.6293 |
| 220° | -0.6428 |
| 221° | -0.6561 |
| 222° | -0.6691 |
| 223° | -0.682 |
| 224° | -0.6947 |
| 225° | -0.7071 |
| 226° | -0.7193 |
| 227° | -0.7314 |
| 228° | -0.7431 |
| 229° | -0.7547 |
| 230° | -0.766 |
| 231° | -0.7771 |
| 232° | -0.788 |
| 233° | -0.7986 |
| 234° | -0.809 |
| 235° | -0.8192 |
| 236° | -0.829 |
| 237° | -0.8387 |
| 238° | -0.848 |
| 239° | -0.8572 |
| 240° | -0.866 |
| 241° | -0.8746 |
| 242° | -0.8829 |
| 243° | -0.891 |
| 244° | -0.8988 |
| 245° | -0.9063 |
| 246° | -0.9135 |
| 247° | -0.9205 |
| 248° | -0.9272 |
| 249° | -0.9336 |
| 250° | -0.9397 |
| 251° | -0.9455 |
| 252° | -0.9511 |
| 253° | -0.9563 |
| 254° | -0.9613 |
| 255° | -0.9659 |
| 256° | -0.9703 |
| 257° | -0.9744 |
| 258° | -0.9781 |
| 259° | -0.9816 |
| 260° | -0.9848 |
| 261° | -0.9877 |
| 262° | -0.9903 |
| 263° | -0.9925 |
| 264° | -0.9945 |
| 265° | -0.9962 |
| 266° | -0.9976 |
| 267° | -0.9986 |
| 268° | -0.9994 |
| 269° | -0.9998 |
| 270° | -1 |
Таблица синусов для углов 181° — 270°
| Угол | Sin (Синус) |
|---|---|
| 271° | -0.9998 |
| 272° | -0.9994 |
| 273° | -0.9986 |
| 274° | -0.9976 |
| 275° | -0.9962 |
| 276° | -0.9945 |
| 277° | -0.9925 |
| 278° | -0.9903 |
| 279° | -0.9877 |
| 280° | -0.9848 |
| 281° | -0.9816 |
| 282° | -0.9781 |
| 283° | -0.9744 |
| 284° | -0.9703 |
| 285° | -0.9659 |
| 286° | -0.9613 |
| 287° | -0.9563 |
| 288° | -0.9511 |
| 289° | -0.9455 |
| 290° | -0.9397 |
| 291° | -0.9336 |
| 292° | -0.9272 |
| 293° | -0.9205 |
| 294° | -0.9135 |
| 295° | -0.9063 |
| 296° | -0.8988 |
| 297° | -0.891 |
| 298° | -0.8829 |
| 299° | -0.8746 |
| 300° | -0.866 |
| 301° | -0.8572 |
| 302° | -0.848 |
| 303° | -0.8387 |
| 304° | -0.829 |
| 305° | -0.8192 |
| 306° | -0.809 |
| 307° | -0.7986 |
| 308° | -0.788 |
| 309° | -0.7771 |
| 310° | -0.766 |
| 311° | -0.7547 |
| 312° | -0.7431 |
| 313° | -0.7314 |
| 314° | -0.7193 |
| 315° | -0.7071 |
| 316° | -0.6947 |
| 317° | -0.682 |
| 318° | -0.6691 |
| 319° | -0.6561 |
| 320° | -0.6428 |
| 321° | -0.6293 |
| 322° | -0.6157 |
| 323° | -0.6018 |
| 324° | -0.5878 |
| 325° | -0.5736 |
| 326° | -0.5592 |
| 327° | -0.5446 |
| 328° | -0.5299 |
| 329° | -0.515 |
| 330° | -0.5 |
| 331° | -0.4848 |
| 332° | -0.4695 |
| 333° | -0.454 |
| 334° | -0.4384 |
| 335° | -0.4226 |
| 336° | -0.4067 |
| 337° | -0.3907 |
| 338° | -0.3746 |
| 339° | -0.3584 |
| 340° | -0.342 |
| 341° | -0.3256 |
| 342° | -0.309 |
| 343° | -0.2924 |
| 344° | -0.2756 |
| 345° | -0.2588 |
| 346° | -0.2419 |
| 347° | -0.225 |
| 348° | -0.2079 |
| 349° | -0.1908 |
| 350° | -0.1736 |
| 351° | -0.1564 |
| 352° | -0.1392 |
| 353° | -0.1219 |
| 354° | -0.1045 |
| 355° | -0.0872 |
| 356° | -0.0698 |
| 357° | -0.0523 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° | 0 |
Таблица синусов для углов от 271° до 360°
Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.
Чему равен синус 45? …
– А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии “на пальцах”.
Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
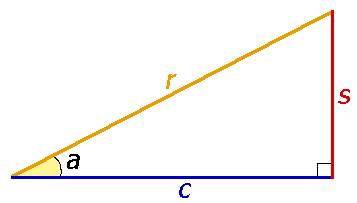
Или в виде формул:
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
| 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|
| sin | 0 | 1 | √3 | – |
| ctg | – | √3 | 1 |
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно. Тригонометрический кругУглы в радианахДля математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π . Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций. [spoiler title=”источники:”] http://kvn201.com.ua/table-of-sines.htm http://matematika.club/articles/trigonometry/ [/spoiler] |
Вообще то синус 60 градусов это число, которое легче всего ассоциировать с длиной отрезка.
Возможны два варианта.
Первый, на единичной окружности.
Где синус 60 градусов, это отрезок от точки с пометкой 60(pi/3) до горизонтальной оси Х
Второй вариант, на синусоиде.
Где показано, что sin(60)= √3/2=0,866
Другими словами, это коэффициент, который определяет, что отрезок от точки до оси Х в 0,866 раз меньше радиуса единичной окружности.
Обратимся, еще раз, к первому рисунку и рассмотрим треугольник, определенный тремя точками. Началом координат, точкой с пометкой “60” и ее проекцией на ось Х. Гипотенуза этого треугольника, есть радиус окружности, а вертикальный катет наш синус. Это значит, что каким бы не был размер треугольника, его вертикальный катет будет в 0,866 раз меньше гипотенузы.
Аналогично рассматривается косинус, только это будет горизонтальный катет данного треугольника и он будет в 0,5 раза меньше гипотенузы. Так как cos(60)=0,5
Найдем синус 60 градусов, пользуясь определением синуса в прямоугольном треугольнике.
Утверждение.
![[sin {60^0} = frac{{sqrt 3 }}{2}]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-20945f18cb5be7c605177adb93ca1d34_l3.png "Rendered by QuickLaTeX.com")
Доказательство:
Рассмотрим прямоугольный треугольник ABC с острым углом 60 градусов:
∠C=90º, ∠A=60º.
Так как сумма острых углов прямоугольного треугольника равна 90º, то
∠B=90º-60º=30º.
Катет, лежащий напротив угла 30 градусов, равен половине гипотенузы, поэтому
![[AC = frac{1}{2}AB.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-12a7f528eacb30840dd510c080f5cb73_l3.png "Rendered by QuickLaTeX.com")
Обозначим AC=a, тогда AB=2a.
По теореме Пифагора
![[A{B^2} = A{C^2} + B{C^2}]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-3336516ea5280cb10d81ff464a2712cc_l3.png "Rendered by QuickLaTeX.com")
![[{(2a)^2} = {a^2} + B{C^2}]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-656353b30509b5d2ec1d9560ae011fad_l3.png "Rendered by QuickLaTeX.com")
![[B{C^2} = 4{a^2} - {a^2} = 3{a^2}]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-295aafb07d6430026921d68e842ddd78_l3.png "Rendered by QuickLaTeX.com")
![[BC = sqrt {3{a^2}} = asqrt 3 .]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-6a6f492f443ce86b4eca2e0f53cb571d_l3.png "Rendered by QuickLaTeX.com")
По определению синуса острого угла прямоугольного треугольника,
![[sin angle A = frac{{BC}}{{AB}}.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-14a613e58eba1591fd036c9ed6cd783b_l3.png "Rendered by QuickLaTeX.com")
Отсюда,
![[sin {60^o} = frac{{asqrt 3 }}{{2a}} = frac{{sqrt 3 }}{2}.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-8207edf71d6fe34ede58cce322ab17a5_l3.png "Rendered by QuickLaTeX.com")
Что и требовалось доказать.
Если перевести 60 градусов в радианы:
![[{60^o} = frac{pi }{3},]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-bc553e50540543097eda70a70f10e2f7_l3.png "Rendered by QuickLaTeX.com")
то получим, что синус пи на три равен
![[sin frac{pi }{3} = frac{{sqrt 3 }}{2}.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-492357694aa567096ceaf9a1ef74903a_l3.png "Rendered by QuickLaTeX.com")
Александр Титов
Гений
(50749)
9 лет назад
Вспомним, что синус острого угла в прямоугольном треугольнике – это отношение катета, противолежащего этому углу к гипотенузе.
Далее рассмотрим равносторонний треугольник со стороной, равной 1. В таком треугольнике все стороны равны, а против равных сторон лежат и равные углы, значит все углы тоже равны, а поскольку сумма углов в любом треугольнике равна 180 градусов и всего три угла, то каждый из них равен 60 градусов.
Теперь из какой-нибудь вершины опускаем медиану на противоположную сторону, т.е. соединяем вершину с серединой противоположной стороны. Равносторонний треугольник – частный случай равнобедренного – эта медиана является также высотой, так что она перпендикулярна соответствующей стороне.
Таким образом, медиана делит равносторонний треугольник на два равных прямоугольных треугольника. Рассмотрим один такой треугольник. В нём известен острый угол – это угол исходного равностороннего треугольника – 60 градусов. Гипотенуза – это сторона равностороннего треугольника, она по договору равна 1.
Прилежащий к этому острому углу катет равен половине стороны равностороннего треугольника (т.к. основание высоты-медианы делит сторону пополам), эта половина равна 1/2.
Оставшийся катет – противолежащий. Его находим по теореме Пифагора, как корень квадратный из разности квадратов гипотенузы и известного катета. Получится (корень из 3) / 2.
Разделив этот противолежащий катет на гипотенузу, равную 1, получим всё равно (корень из 3) / 2. Это и есть синус 60 градусов.
Вероятно, справа – ты
Оракул
(69070)
9 лет назад
из формулы двойного угла
sin(2*30) =2sin30cos30=2sin30sin60
получаем, что
sin(2*30) =2sin30sin60
или
1=2sin30
опираясь на него, сразу находим значение корень из (1-1/4)= cos30=sin60
всё, и не надо городить такой огород, как ответчик выше
Владимир Ильин
Мастер
(1146)
2 года назад
Я уже использовал в одном из ответов, что sin^2(x)+cos^2(x)=1. Для х=60 (градусов), cos(60)=1/2 (это известно), тогда легко получить, что sin(60)=(корень кв. из 3)/2
Многих девятиклассников и восьмиклассников кидает в дрожь, когда учитель спрашивает чему равен косинус 60 градусов и строго наказывает учить “табличку”. А для того чтобы ее выучить, достаточно один раз понять, откуда берутся эти значения в табличке.
Начнем с определений. Без них конечно вообще невозможно понять, что такое синус, косинус и тангенс. На то они и определения…
Вспомним как называются стороны прямоугольного треугольника, а также понятия противолежащая и прилежащая стороны.
Выходит, что синус и косинус это отношения, т.е. безразмерный числовой коэффициент. Этот числовой коэффициент является связующим звеном между сторонами и углами в прямоугольном треугольнике.
Аналогично, тангенс является отношением сторон прямоугольного треугольника, а также отношением синуса к косинусу одного и того же угла.
Из определений синуса и косинуса острого угла прямоугольного треугольника можно заметить:
Это нам понадобится для вывода синуса и косинуса углов 30 и 60 градусов.
А теперь посмотрим, откуда берутся значения синуса и косинуса для углов 30, 60, 45 градусов…
Итак, во-первых, вспоминаем, что против угла 30° в прямоугольном треугольнике лежит катет равный половине гипотенузы (1/2с). Далее выражаем второй катет через “с” по теореме Пифагора. Найденные значения подставляем в определение синуса и косинуса. “с” сокращается и остаются числовые значения.
Угол 60° является вторым острым углом прямоугольного треугольника с углом 30°, а значит его косинус равен синусу 30°, аналогично синус 60° равен косинусу 30°.
Далее по определению находим тангенс этих углов.
Не трудно догадаться, если синус и косинус 45° равны, то тангенс 45° равен 1 🙂
Вывод этих формул поможет не только запомнить значения синуса и косинуса основных углов, но и научит решать простейшие задачи.
Сами задачи посмотрим в следующей статье завтра
А пока…
Продолжение следует…
