Как найти синус 7пи 6

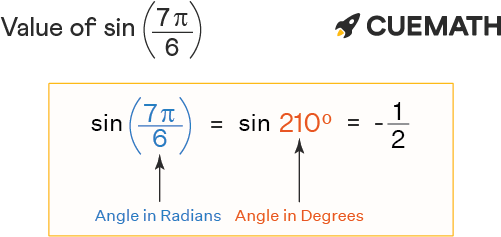
The value of sin 7pi/6 is -0.5. Sin 7pi/6 radians in degrees is written as sin ((7π/6) × 180°/π), i.e., sin (210°). In this article, we will discuss the methods to find the value of sin 7pi/6 with examples.

• Sin 7pi/6: -(1/2)
• Sin 7pi/6 in decimal: -0.5
• Sin (-7pi/6): 0.5 or 1/2
• Sin 7pi/6 in degrees: sin (210°)

What is the Value of Sin 7pi/6?

The value of sin 7pi/6 in decimal is -0.5. Sin 7pi/6 can also be expressed using the equivalent of the given angle (7pi/6) in degrees (210°).

We know, using radian to degree conversion, θ in degrees = θ in radians × (180°/pi)
⇒ 7pi/6 radians = 7pi/6 × (180°/pi) = 210° or 210 degrees
∴ sin 7pi/6 = sin 7π/6 = sin(210°) = -(1/2) or -0.5

Explanation:

For sin 7pi/6, the angle 7pi/6 lies between pi and 3pi/2 (Third Quadrant). Since sine function is negative in the third quadrant, thus sin 7pi/6 value = -(1/2) or -0.5
Since the sine function is a periodic function, we can represent sin 7pi/6 as, sin 7pi/6 = sin(7pi/6 + n × 2pi), n ∈ Z.
⇒ sin 7pi/6 = sin 19pi/6 = sin 31pi/6 , and so on.
Note: Since, sine is an odd function, the value of sin(-7pi/6) = -sin(7pi/6).

Methods to Find Value of Sin 7pi/6

The sine function is negative in the 3rd quadrant. The value of sin 7pi/6 is given as -0.5. We can find the value of sin 7pi/6 by:

• Using Unit Circle
• Using Trigonometric Functions

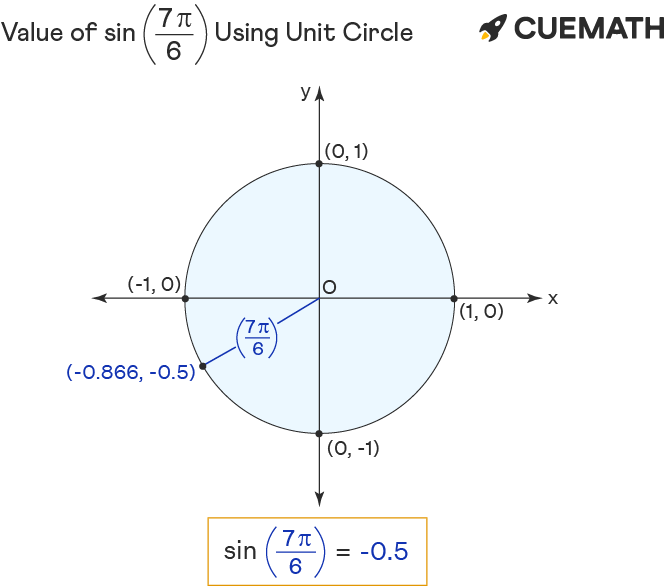
Sin 7pi/6 Using Unit Circle

To find the value of sin 7π/6 using the unit circle:

• Rotate ‘r’ anticlockwise to form 7pi/6 angle with the positive x-axis.
• The sin of 7pi/6 equals the y-coordinate(-0.5) of the point of intersection (-0.866, -0.5) of unit circle and r.

Hence the value of sin 7pi/6 = y = -0.5

Sin 7pi/6 in Terms of Trigonometric Functions

Using trigonometry formulas, we can represent the sin 7pi/6 as:

• ± √(1-cos²(7pi/6))
• ± tan(7pi/6)/√(1 + tan²(7pi/6))
• ± 1/√(1 + cot²(7pi/6))
• ± √(sec²(7pi/6) – 1)/sec(7pi/6)
• 1/cosec(7pi/6)

Note: Since 7pi/6 lies in the 3rd Quadrant, the final value of sin 7pi/6 will be negative.

We can use trigonometric identities to represent sin 7pi/6 as,

• sin(pi – 7pi/6) = sin(-pi/6)
• -sin(pi + 7pi/6) = -sin 13pi/6
• cos(pi/2 – 7pi/6) = cos(-2pi/3)
• -cos(pi/2 + 7pi/6) = -cos 5pi/3

☛ Also Check:

• cos pi/3
• cos 5pi/3
• cos pi/4
• cos pi/6
• cot pi
• tan pi/8

FAQs on Sin 7pi/6

What is Sin 7pi/6?

Sin 7pi/6 is the value of sine trigonometric function for an angle equal to 7pi/6 radians. The value of sin 7pi/6 is -(1/2) or -0.5.

How to Find the Value of Sin 7pi/6?

The value of sin 7pi/6 can be calculated by constructing an angle of 7π/6 radians with the x-axis, and then finding the coordinates of the corresponding point (-0.866, -0.5) on the unit circle. The value of sin 7pi/6 is equal to the y-coordinate (-0.5). ∴ sin 7pi/6 = -0.5.

How to Find Sin 7pi/6 in Terms of Other Trigonometric Functions?

Using trigonometry formula, the value of sin 7π/6 can be given in terms of other trigonometric functions as:

• ± √(1-cos²(7pi/6))
• ± tan(7pi/6)/√(1 + tan²(7pi/6))
• ± 1/√(1 + cot²(7pi/6))
• ± √(sec²(7pi/6) – 1)/sec(7pi/6)
• 1/cosec(7pi/6)

☛ Also check: trigonometry table

What is the Value of Sin 7pi/6 in Terms of Cosec 7pi/6?

Since the cosecant function is the reciprocal of the sine function, we can write sin 7pi/6 as 1/cosec(7pi/6). The value of cosec 7pi/6 is equal to -2.

What is the Value of Sin 7pi/6 in Terms of Tan 7pi/6?

We know, using trig identities, we can write sin 7pi/6 as -tan(7pi/6)/√(1 + tan²(7pi/6)). Here, the value of tan 7pi/6 is equal to 0.577350.

В статье мы рассмотрим, как найти значения:

(cosfrac{π}{6}),       (sin⁡(-frac{7π}{3})),     (cosfrac{3π}{4}),     (sin⁡(-frac{27π}{2}))

и других тригонометрических выражений без тригонометрической таблицы.

Для начала внимательно прочтите статью о числовой окружности. Вы должны научиться находить точки на окружности в числах с Пи.

Уже умеете? Тогда два ключевых утверждения:

Например, пусть нам нужно найти синус и косинус числа (frac{π}{6}). Обозначим на числовой окружности точку со значением (frac{π}{6}).

Если построить все точно и крупно, то можно убедиться, что абсцисса этой точки будет равна (0,866…) , что соответствует числу (frac{sqrt{3}}{2}) , а ордината равна (0,5), то есть (frac{1}{2}).

Значит, что (cos⁡(frac{π}{6}) = frac{sqrt{3}}{2}), а (sin(frac{π}{6}) ⁡=frac{1}{2}).

Аналогично и для любой другой точки: значение абсциссы совпадает со значением косинуса, а ординаты – синуса. Поэтому:

И обычно на них не наносят значения в десятичных ((0,1); (0,2); (0,3) и т.д.), а сразу отмечают стандартные значения для синуса и косинуса: (frac{1}{2} =0,5); (frac{sqrt{2}}{2} ≈0,707); (frac{sqrt{3}}{2}≈0,866), причем, как со знаком плюс, так и минус. Почему стандартные значения синуса и косинуса именно (frac{1}{2}),(frac{sqrt{2}}{2}) и (frac{sqrt{3}}{2}) вы можете узнать из этого видео.

Как находить значения синуса и косинуса без таблицы, а только с помощью круга?

Алгоритм прост:

1. Начертите круг и оси косинусов и синусов.
2. Отметьте на круге число, синус и косинус которого надо найти. Если с этим возникают проблемы, прочитайте здесь о том, как расставлять числа на числовой окружности. 
3. Найдите координаты точки, используя картинку ниже.

Пример. Найдите синус и косинус для числа (-frac{7π}{6}).
Решение:(-frac{7π}{6}=-frac{6π}{6}-frac{π}{6}=-π-frac{π}{6}) , то есть, чтобы отметить на окружности точку (-frac{7π}{6}) сначала находим число (-π) и от него в отрицательную сторону откладываем дугу длиной (frac{π}{6}).

Отмечаем число, синус и косинус которого надо найти:

Получается, что (sin⁡(-frac{7π}{6})=frac{1}{2}), (cos⁡(-frac{7π}{6})=-frac{sqrt{3}}{2}).

Пример. Вычислите (sinfrac{5π}{2}) и (cosfrac{5π}{2}).
Решение:  (frac{5π}{2}=frac{4π+π}{2}=frac{4π}{2}+frac{π}{2}=2π+frac{π}{2}).

Точка (frac{5π}{2}) совпадает с (1) на оси синусов, значит (sin⁡frac{5π}{2}=1). А если провести перпендикуляр из точки (frac{5π}{2}) до оси косинусов, то можно убедиться, что он попадет в (0). Поэтому (cosfrac{5π}{2}=0).

И тут некоторые из вас подумали: «с кругом, на котором подписаны числа, каждый дурак сможет посчитать, а что делать, когда его под рукой нет? Что делать на ЕГЭ?» Ответ прост – нарисуйте круг сами! Для этого вам будет нужно понять логику расположения чисел на осях (подробнее об этом читайте в статье «Как запомнить тригонометрический круг»).

Пример. Найдите а) (sin⁡frac{3π}{2}), б) (cos⁡frac{3π}{4}), в) (sin⁡(-frac{π}{3})) .
Решение: а) Чертим круг, оси и отмечаем число (frac{3π}{2}). Обращаем внимание на ось синусов и понимаем, что точка совпала с (-1), получается (sin⁡frac{3π}{2}=-1).
б) (frac{3π}{4}=frac{4π}{4}-frac{π}{4}=π-frac{π}{4}) – отмечаем число на круге. Проводим перпендикуляр до оси косинусов и вспоминаем, что точки со знаменателем (4) находятся посередине. Мы еще попали и в отрицательную часть оси косинусов, получается (cos⁡frac{3π}{4}=-frac{sqrt{2}}{2}).
в) (-frac{π}{3}) – отмечаем число на круге. Видим, что перпендикуляр к оси синусов попал в точку близкую к (-1), значит (sin⁡(-frac{π}{3})=-frac{sqrt{3}}{2}).

Как видите не обязательно рисовать, очень красивую или очень большую окружность – вы можете определить нужное вам значение, быстро набросав круг. И ничего не надо учить!

Если вы хотите еще примеров с вычислением синусов и косинусов без тригонометрической таблицы, то прочтите эту статью.

Пример (ЕГЭ). Найдите значение выражения (frac{8}{sin⁡(-frac{27π}{4}) cos⁡(frac{31π}{4})}) .
Решение.    (-frac{27π}{4}=-frac{28π}{4}+frac{π}{4}=-7π+frac{π}{4}).
(frac{31π}{4}=frac{32π}{4}-frac{π}{4}=8π-frac{π}{4}).

(sin⁡(-frac{27π}{4})=-frac{sqrt{2}}{2}),      (cos⁡(frac{31π}{4})=frac{sqrt{2}}{2}).

(frac{8}{sin⁡(-frac{27π}{4}) cos⁡(frac{31π}{4})})(=) (frac{ 8}{-frac{sqrt{2}}{2}cdotfrac{sqrt{2}}{2}})(=-8:frac{2}{4}=-8cdotfrac{2}{1}=-16).

Ответ: (-16).

Смотрите также:
Как найти синус и косинус углов в градусах без тригонометрической таблицы?
Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?

Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов