Для решения задачи следует воспользоваться основным тригонометрическим тождеством: сумма квадратов синуса и косинуса одного и того же угла равна 1.
Отсюда синус угла равен плюс минус корню квадратному из разности 1 и квадрата косинуса угла.

Какой знак перед корнем квадратным брать зависит от того, где находится угол, косинус которого известен.
Если в условии задачи значение косинуса больше нуля (равенство нулю рассмотрено, как частный случай, ниже, хотя применимы рассуждения и для нуля), то угол находится либо в 1-й, либо в 4-й четверти.
Для определенности в условии задачи обычно дается ограничение для угла.
Если указано, что 0< a< 90 (1 четверть), то значение синуса тоже следует брать со знаком плюс.
Если же 270< a< 360 (4 четверть), то значение синуса следует брать со знаком минус.
Если значение косинуса угла меньше нуля, то это означает, что угол может находиться во 2-й или 3-й четверти.
1) 90< a< 180 (2 четверть).
Тогда синус угла будет положительным и равняется корню квадратному из разности 1 и квадрата косинуса угла.
2) 180< a< 270 (3 четверть).
В этом случае синус угла будет отрицательным и равняется тому же значению, что и в первом случае, только со знаком минус.
Частные случаи: Если cos a = 0, то sina=1; если cos a = 1, то sina=0; cos a = -1, то sina=0. Эти значения также легко находятся из основного тригонометрического тождества.
Приведем примеры.
Пример 1. Найти синус угла, если cos a = -0,8. 180<a<270 (в градусах)
Решение. Находим разность 1 и квадрата значения cos a, т.е. квадрата (-0,8).
-0,8 возводим в квадрат, получим (-0,8)*(-0,8) = 0, 64. Подставим его в искомую разность:
1-0,64=0,36
Получили квадрат значения синуса. Для нахождения значения самого синуса, извлечем корень квадратный из 0,36 и возьмем его со знаком + и со знаком – (см. картинку). Получим 0,6 или -0,6.
Так как по условию угол находится в 3 четверти, то искомое значение синуса будет отрицательным. Значит выбираем -0,6.
Ответ: sina=-0,6.
Рассмотрим для краткости изложения этот же пример для случая, когда угол находится во второй четверти:
Пример 2. Найти синус угла, если cos a = -0,8. 90<a<180 (в градусах)
Решение будет точно таким же, как для примера 1.
Изменится лишь выбор ответа. Рассуждения будут следующими:
Так как по условию угол находится во 2 четверти, то искомое значение синуса будет положительным. Значит выбираем 0,6.
Ответ: sina=0,6.
Тригонометрия — это раздел математики, в котором изучаются тригонометрические функции, их свойства, взаимосвязи и применение.
Слово «тригонометрия» образовано от греческих слов «trigonom» (треугольник) и «metreo» (измерять).
Возникновение и развитие тригонометрии связаны с практическими потребностями в измерении и вычислении сначала элементов треугольников на местности, а позднее — в строительстве, мореплавании и астрономии. Современная тригонометрия широко применяется в разных областях математики, в частности в геометрии, других науках, в технике. Например, тригонометрические функции используются при решении задач оптики, задач кинематического анализа и синтеза механизмов, гармонического анализа и других.
Cинус, косинус, тангенс, котангенс острого угла прямоугольного треугольника
Нет понятий «просто синус» или «просто косинус», не имеют смысла записи типа «sin» и «cos» сами по себе, они сами по себе никакой величины не обозначают (точно так же, как и, например, значок квадратного корня сам по себе). Те, кто этого не понимает, часто делает грубую ошибку типа: sin x /cos x = in /co
Есть понятие синуса, косинуса, тангенса, котангенса как тригонометрических функций угла. Здесь угол — аргумент функции. Он может обозначаться «х», «а», «альфа», «бета», «гамма», «фи», «дельта» или ещё какой-нибудь буквой. Суть от этого не меняется.
Для того, чтобы более наглядно представить приведенные ниже определения, начертите прямоугольный треугольник. Это треугольник, один из углов которого — прямой (т.е. один из углов равен 90 градусов). Стороны, прилежащие к прямому углу (перпендикулярные друг другу стороны) — это катеты данного прямоугольного треугольника. Противолежащая прямому углу сторона — это гипотенуза.
Теперь выберите любой из двух других (острых) углов треугольника и обозначьте его, например, альфа. Один из катетов будет примыкать к вершине этого угла (и, собственно, образовывать этот угол вместе с гипотенузой). Это — прилежащий катет. Другой катет не примыкает к вершине этого угла, он находится как бы напротив данной вершины. Это — противолежащий катет.
Кстати, почему-то не все представляют, что такое угол треугольника при данной вершине. У треугольника (обозначим его ABC) есть три вершины: А, В и С. Когда говорят об угле А треугольника, то подразумевают угол, образованный сторонами ВА и АС. Это и есть угол при вершине А.
Итак,
Синусом острого угла называется отношение противолежащего этому углу катета к гипотенузе.
Косинусом острого угла называется отношение прилежащего к этому углу катета к гипотенузе.
Тангенсом острого угла называется отношение противолежащего этому углу катета к прилежащему катету.
Котангенсом острого угла называется отношение прилежащего этому углу катета к противолежащему катету.
Секансом острого угла называется отношение гипотенузы к прилежащему к этому углу катету. Обозначается: sec x.
Косекансом острого угла называется отношение гипотенузы к противолежащему этому углу катету. Обозначается: cosec x.
Как найти углы в прямоугольном треугольнике, если известны стороны?
Дан треугольник АВС, угол С — прямой.
Стороны АВ, АС и ВС известны.
Т.к. угол С — прямой, он равен 90 градусам.
Другие углы можно найти, например, так:
если известен катет и гипотенуза
sinA = BC / AB,
sinB = AC / AB,
если известны два катета
tg A = BC / AC
tg B = AC / BC
Предположим, получили, что sin A = ½. По таблице смотрим, что такому значению sin x соответствует величина угла 30 градусов.
Или, к примеру, получили, что tg B = 1. Значит, угол В равен 45 градусов.
Или, к примеру, мы получили, что sin B = 0,259. По таблице Брадиса или с помощью калькулятора находим, что угол В равен 15 градусов.
sin 15° = 0,259
arcsin0,259 = 15°
Как найти углы в прямоугольном треугольнике, если известен один угол?
Поскольку треугольник прямоугольный, то один из его углов равен 90 градусов. Величина второго угла известна (по условию задачи, обозначим её альфа). В сумме углы треугольника составляют 180 градусов. Значит, третий угол равен 180—90—альфа.
Еединичная окружность (единичный круг)
Единичный круг — это круг с центром в начале координат и радиусом, равным единице (R = 1).
Единичная окружность — это окружность единичного круга (т.е. окружность с центром в начале координат и с радиусом, равным единице).
Единичный радиус-вектор — это вектор, начало которого совпадает с началом координат, а его длина равна единице.
Углы отсчитывают от начального положения подвижного радиуса-вектора (совпадает с положением Ох).
Координатные четверти отсчитываются так:
y
|
|
(II четверть) | (I четверть)
|
________________________ x
|0
|
(III четверть) | (IV четверть)
|
|
Угол первой четверти — от 0 до 90 градусов (от 0 до пи/2).
Угол второй четверти — от 90 до 180 градусов (от пи/2 до пи).
Угол третьей четверти — от 180 до 270 градусов (от пи до 2пи/3).
Угол четвертой четверти — от 270 до 360 градусов (от 2пи/3 до 2пи).
Например:
- углы первой четверти: 30 градусов, 85 градусов, пи/4;
- углы второй четверти: 120 градусов, 178 градусов;
- углы третьей четверти: 205 градусов, 260 градусов;
- углы четвертой четверти: 272 градуса, 305 градусов.
Тригонометрические функции
К тригонометрическим функциям относятся функции:
y = sin x;
y = cos x;
y = tg x;
y = ctg x;
y = sec x;
y = cosec x.
Синусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его длине.
Косинусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его длине.
Тангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его проекции на ось Ох.
Котангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его проекции на ось Оу.
Секансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Ох.
Косекансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Оу.
Тригонометрические функции связаны между собой, и этим можно воспользоваться для нахождения синуса угла по его косинусу или котангенсу или косинуса угла по его синусу или тангенсу.
Как найти синус угла, если известен косинус?
Нужно воспользоваться основным тригонометрическим тождеством:
sin2a + cos2a = 1
sin2a = 1 − cos2a
|sin a| = КОРЕНЬ(1 − cos2a)
sin a = ± КОРЕНЬ(1 − cos2a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)
Как найти косинус угла, если известен синус?
Нужно воспользоваться основным тригонометрическим тождеством:
sin2a + cos2a = 1
cos2a = 1 − sin2a
|cos a| = КОРЕНЬ(1 − sin2a)
cos a = ± КОРЕНЬ(1 − sin2a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)
Как найти синус угла, если известен котангенс?
Нужно воспользоваться тригонометрическим тождеством
1 + ctg2 a = 1/sin2 a
sin2 a = 1 / (1 + ctg2 a)
|sin a| = 1/ КОРЕНЬ(1 + ctg2 a)
sin a = ±1/ КОРЕНЬ(1 + ctg2 a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, котангенс положительный в I и III четвертях)
Как найти косинус угла, если известен тангенс?
Нужно воспользоваться тригонометрическим тождеством
1 + tg2 a = 1/cos2 a
cos2 a = 1 / (1 + tg2 a)
|cos a| = 1/ КОРЕНЬ(1 + tg2 a)
cos a = ±1/ КОРЕНЬ(1 + tg2 a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (косинус положительный в I и IV четвертях, тангенс положительный в I и III четвертях)
Тригонометрическое тождество
Тригонометрическим тождеством называется равенство, в которое входят тригонометрические функции и которое удовлетворяется произвольным допустимым значением угла — аргумента тригонометрических функций, но не удовлетворяется, если каждую в отдельности тригонометрическую функцию заменить произвольной величиной.
Основные тригонометрические тождества:
sin2a + cos2a = 1
tg a = sin a / cos a
ctg a = cos a / sin a
sec a = 1 / cos a
cosec a = 1 / sin a
Arcsin, arcos, arctg, arcctg (обратные тригонометрические функции)
- arcsin — читается: арксинус;
- arcos — читается: арккосинус;
- arctg — читается: арктангенс;
- arcctg — читается: арккотангенс.
arcsin, arcos, arctg, arcctg — это обратные тригонометрические функции.
Обратной тригонометрической функцией y = arcsin x называют угол у, взятый на отрезке от –пи/2 до +пи/2, синус которого равен х:
y = arcsin x sin y = x
Обратной тригонометрической функцией y = arccos x называют угол у, взятый на отрезке от –пи до +пи, косинус которого равен х:
y = arccos x cos y = x
Обратной тригонометрической функцией y = arctg x называют угол у, взятый на промежутке от –пи/2 до +пи/2 (исключая концы), тангенс которого равен х:
y = arctg x tg y = x
Обратной тригонометрической функцией y = arcctg x называют угол у, взятый на промежутке от 0 до пи (исключая концы), котангенс которого равен х:
y = arctg x tg y = x
Например,
sin 30° = 0,5
arcsin0,5 = 30°
Синусоида и косинусоида
График функции y = sin x называется синусоидой.
График функции y = cos x называется косинусоидой.
Источники информации:
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра. Под редакцией П.Ф. Фильчакова. —К.: Наукова думка, 1967. — 442 с.
- В.Д. Гетманцев, О.Ф. Саушкiн. Математика: Тригонометрiя: Посiбник для слухачiв пiдотовчих вiддiлень, вступникiв до вищих навчальних закладiв, студентiв педагогiчних iнститутiв (на укр.). —К.: Либiдь, 1994. — 144 с.
- docme.ru — зачем нужна тригонометрия?
- ru.wikipedia.org — Википедия — тригонометрия;
- ru.wikihow.com — как изучать тригонометрию?
Синусом угла в прямоугольном треугольнике называют отношение противолежащего катета к гипотенузе.
Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.
Для простоты запоминания можно дать такое определение: синус угла — это отношение дальнего от рассматриваемого угла катета к гипотенузе.
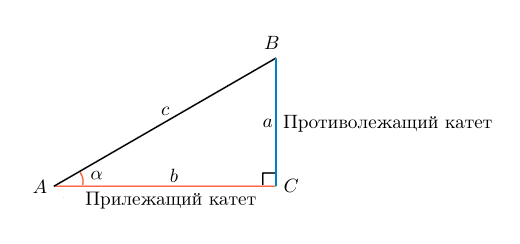
В случае с рисунком, описанным выше: sinα=acsinalpha=frac{a}{c}
В треугольнике, один из углов которого равен 90 градусам, известен катет при угле αalpha и равен он 3 см3text{ см}. Также дано произведение длин катетов и равно 12 см212text{ см}^2. Найдите синус угла αalpha.
Решение
Сначала нужно найти длину неизвестного нам катета. Для этого воспользуемся данным нам произведением. Обозначим неизвестный катет за xx. Тогда, по условию задачи:
3⋅x=123cdot x=12
x=123=4x=frac{12}{3}=4
a=x=4a=x=4
По теореме Пифагора найдем гипотенузу:
a2+b2=c2a^2+b^2=c^2
42+32=c24^2+3^2=c^2
25=c225=c^2
c=5c=5
sinα=ac=45=0.8sinalpha=frac{a}{c}=frac{4}{5}=0.8
Ответ
0.80.8
Вычислите синус 45 градусов.
Решение
Для этого воспользуемся тригонометрической таблицей углов. Находим, что:
sin45∘=π4=0.785sin 45^circ=frac{pi}{4}=0.785
Ответ
0.7850.785
Если в задаче известен косинус угла и нужно найти его синус, то наличие известных длин катетов и гипотенузы не обязательны. Достаточно просто воспользоваться основным тригонометрическим тождеством, которое имеет следующий вид:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
αalpha — любой угол.
Квадрат косинуса угла в треугольнике равен 0.8. Найдите синус данного угла.
Решение
Воспользуемся основным тригонометрическим тождеством:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
sin2α+0.8=1sin^2alpha+0.8=1
sin2α=0.2sin^2alpha=0.2
sinα=0.2sinalpha=sqrt{0.2}
sinα≈0.447sinalphaapprox0.447
Ответ
0.4470.447
Испытываете проблемы с вычислением синуса? Оформите задачу по математике на заказ у наших экспертов!
