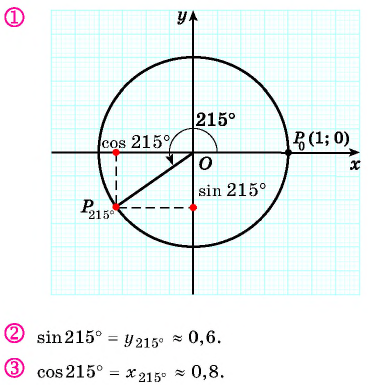
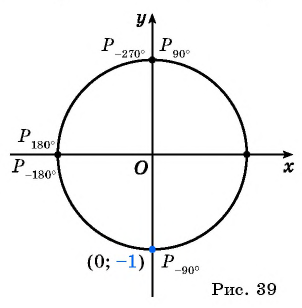
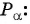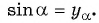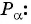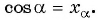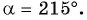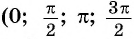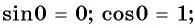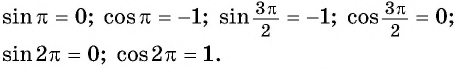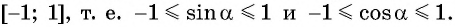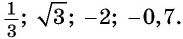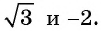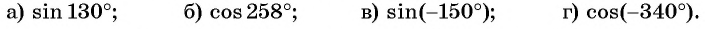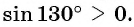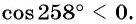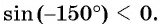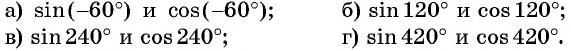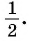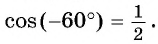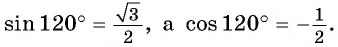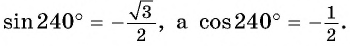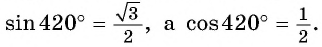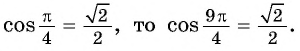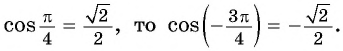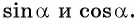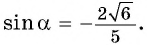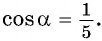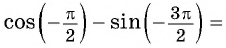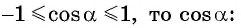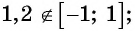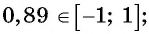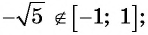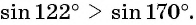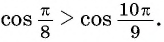План урока:
Синус и косинус угла на единичной окружности
График синуса и косинуса
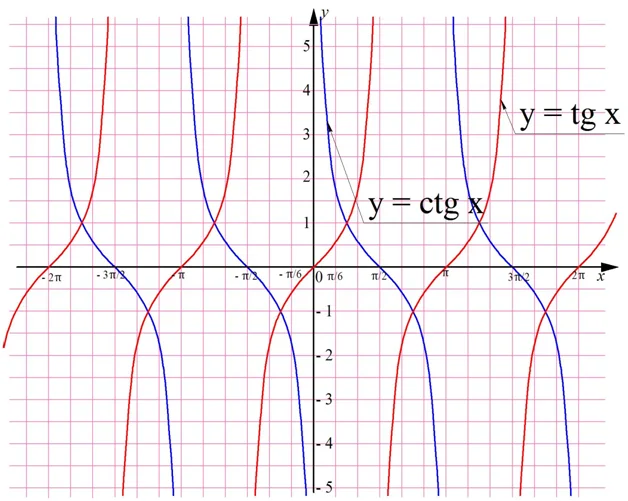
Тангенс угла
График тангенса
Котангенс угла
Синус и косинус угла на единичной окружности
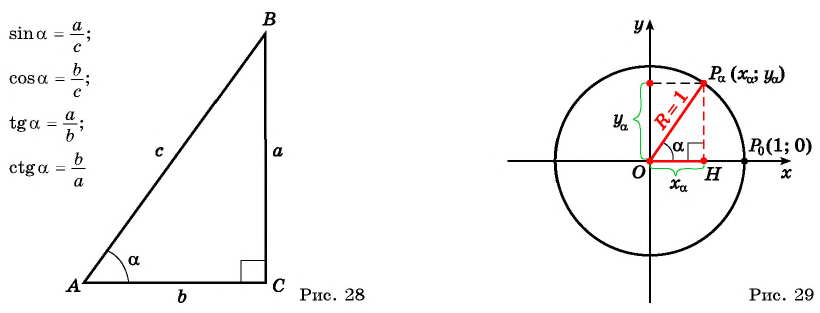
Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:
С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что
ВС = АВ•sinα = 5•0,8 = 4
Если известно, что cosα = 0,6, то мы сможем найти и второй катет:
cosα = АС/АВ
АС = АВ•cosα = 5•0,6 = 3
Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:
tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)
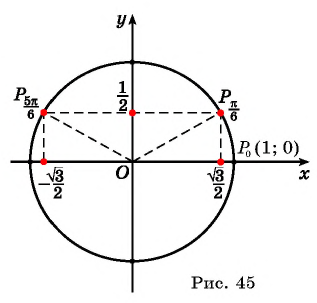
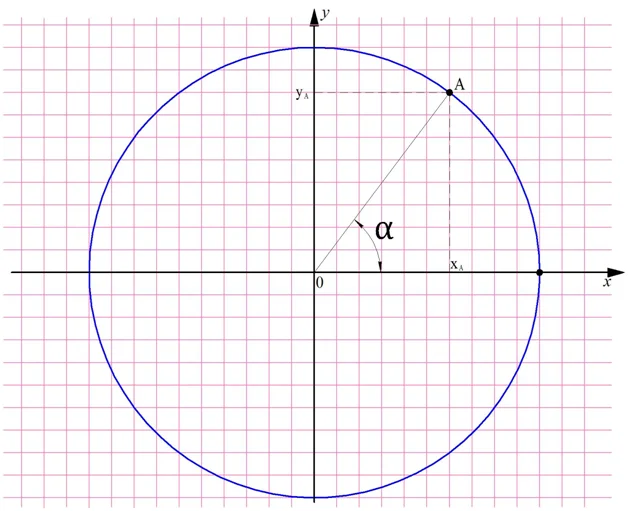
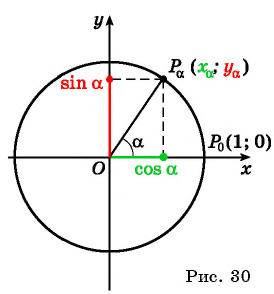
Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты хА и уА:
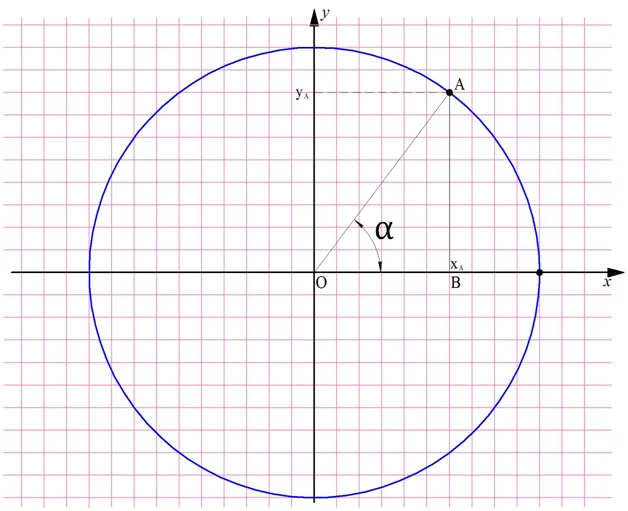
Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:
Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле
АВ = sinα•ОА
Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда
АВ = sinα•ОА = sinα•1 = sinα
С другой стороны, видно, что величина отрезка АВ равна координате уА. Получается, что уА = АВ = sinα, или
уА = sinα
Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:
ОВ = cosα•ОА
Учитывая, что ОА = 1, а длина ОВ равна координате хА, мы получим следующее:
хА = ОВ = cosα•ОА = cosα•1 = cosα
то есть координата хА равна cos α:
хА = cosα
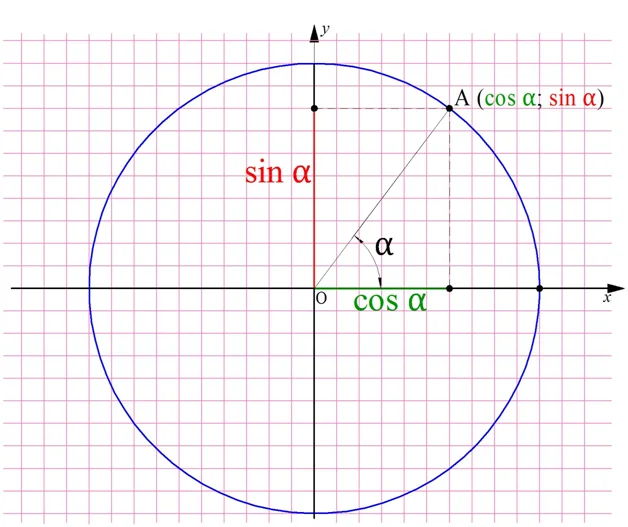
Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.
Таким образом, нам удалось дать новое определение синусу и косинусу угла:
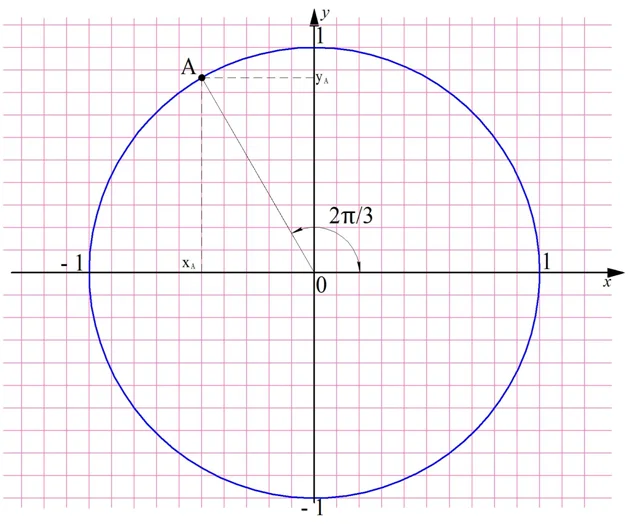
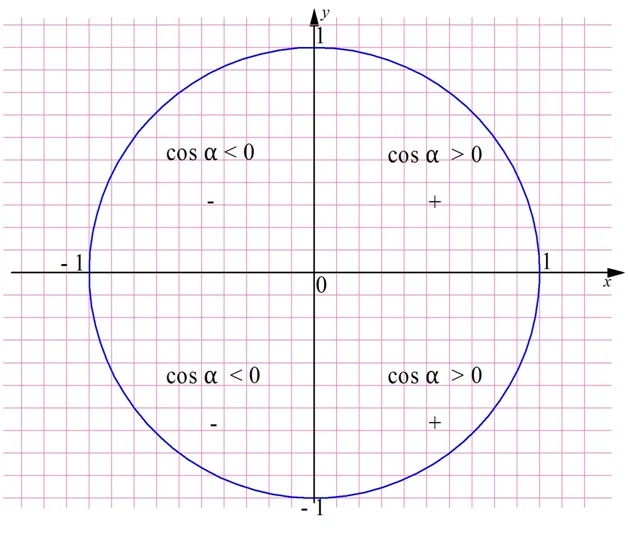
Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 <α < 90°. На единичной окружности можно отложить любой угол, то есть теперь мы можем вычислять тригонометрические ф-ции для произвольных значений α. При этом синус и косинус могут оказаться отрицательными величинами. Например, для угла α = 2π/3 косинус окажется отрицательным, ведь координата хА соответствующей ему точки окажется левее нуля на горизонтальной оси Ох:
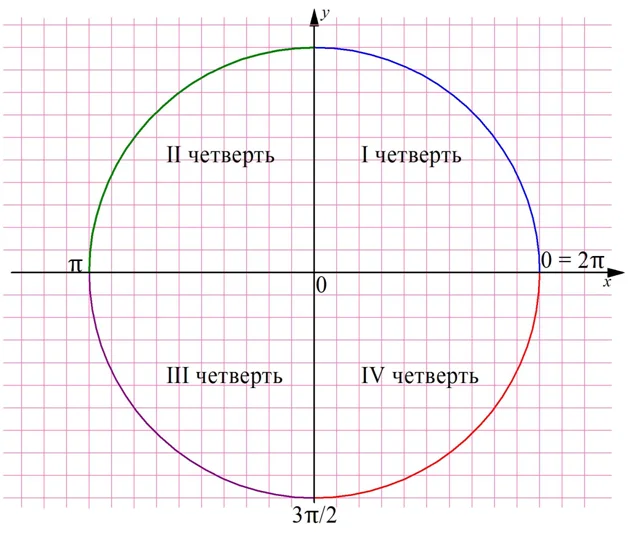
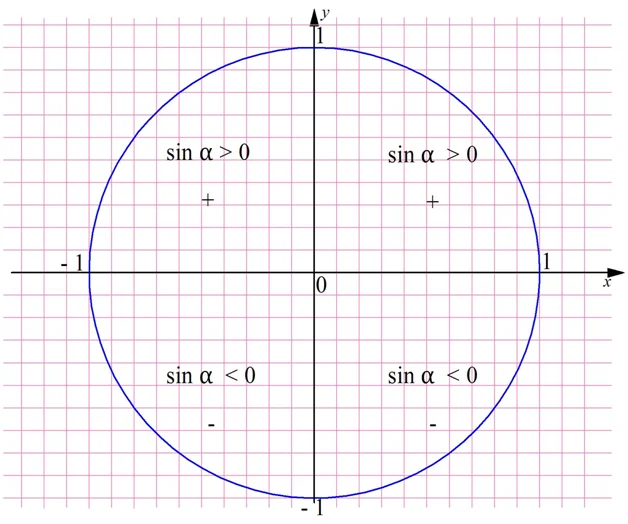
Заметим, что знак синуса и косинуса определяется той четвертью, в которой будет располагаться точка на окружности. Углам в диапазоне 0 <α<π/2 соответствует I четверть, здесь все тригонометрические ф-ции принимают положительные значения. Ко II четверти относятся углы из промежутка π/2 <α<π. Здесь косинус становится меньше нуля, а синус остается положительным. В III четверти будут располагаться точки, соответствующие углам из интервала π <α< 3π/2, у них отрицательны и синус, и косинус. Наконец, к IV четверти относят углы из диапазона 3π/2 <α< 2π. Здесь отрицателен синус, а косинус больше нуля.
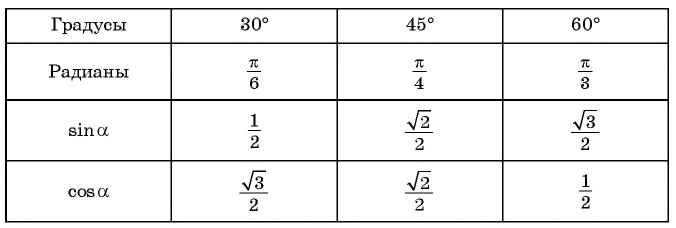
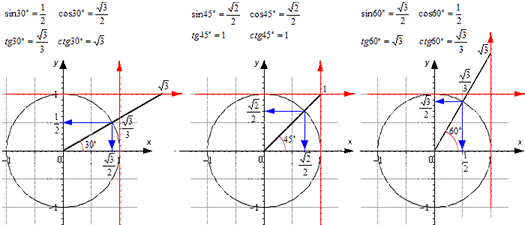
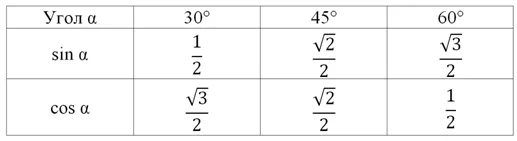
Как же определять значение синуса угла и его косинуса? Из геометрии нам уже известны их значения для трех углов: 30°, 45° и 60°:
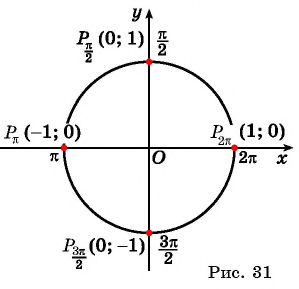
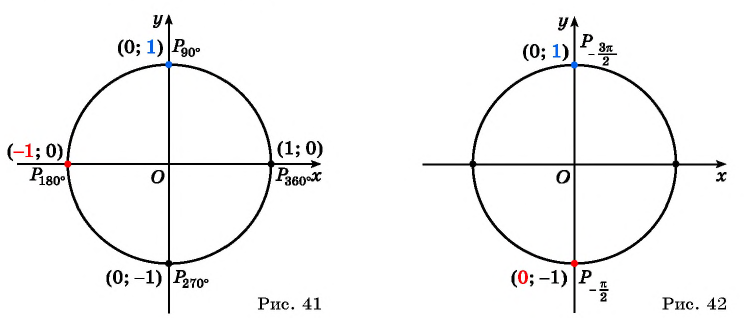
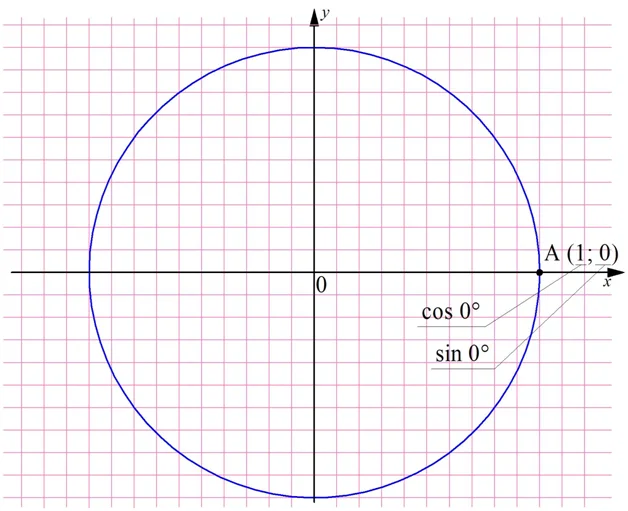
Далее определим тригонометрические ф-ции угла, равного нулю. Если такой угол отложить на единичной окружности, то ему будет соответствовать точка А с координатами (1; 0). Поэтому
sin 0° = уА = 0
cos 0° = xА = 1
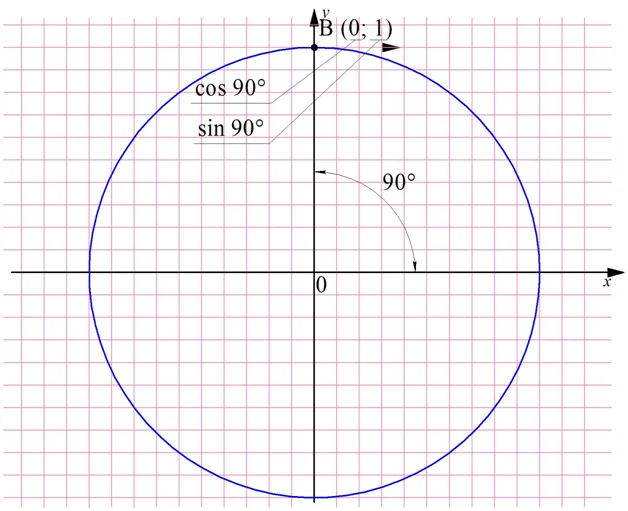
Аналогичным образом можно найти значение этих ф-ций и для угла 90°. Прямому углу на единичной окружности соответствует точка В с координатами (0; 1). Поэтому
sin90° = уВ = 1
cos90° = xВ = 0
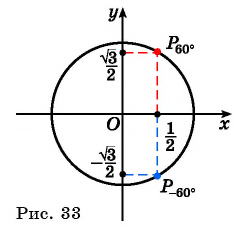
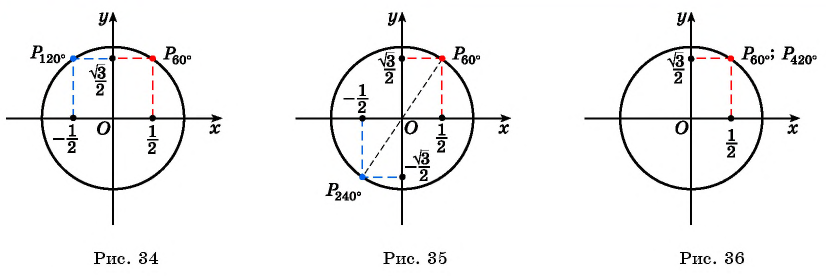
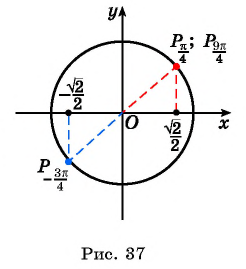
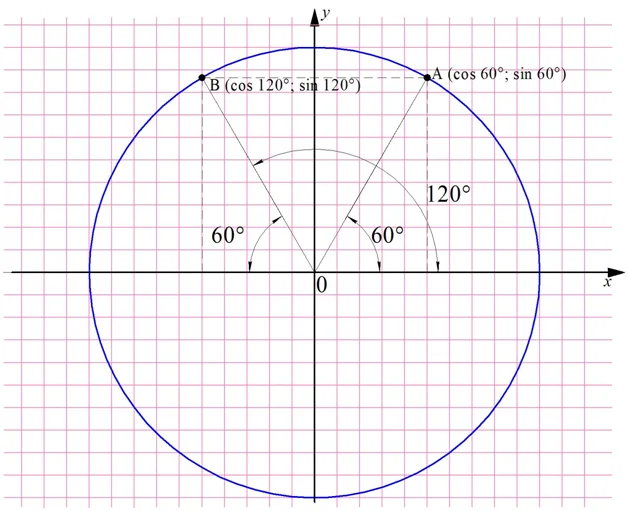
Для определения тригонометрических ф-ций у углов, больших 90°, удобно использовать симметрию. Например, пусть необходимо вычислить синус для угла 120°. Отложим на окружности две точки, В и А. Первая будет соответствовать 120°, а вторая 60°:
Видно, что эти точки находятся на одном горизонтальном уровне, то есть их ординаты (координаты у) одинаковы. При этом абсциссы у них противоположны, ведь точки симметричны относительно оси Оу. Отсюда можно сделать вывод, что
уВ = уА
хВ = – хА
Но координаты А – это синус и косинус 60°, а координаты В являются тригонометрическими ф-циями угла 120°. То есть можно записать
sin 120° = sin 60°
cos 120° = – cos 60°
Так как для угла 60° значения синуса и косинуса нам уже известны, то можно записать:
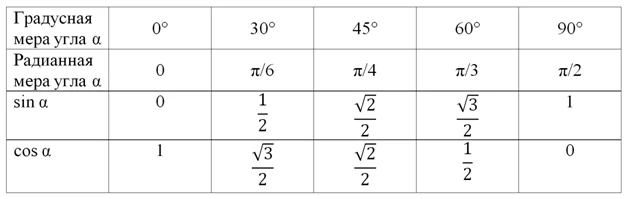
В будущем мы изучим более простые способы вычисления синуса и косинуса углов, больших 90°, когда построения нам уже не потребуются. Однако сразу заметим, что в первую очередь необходимо запомнить значения синуса и косинуса для пяти углов: 0°, 30°, 45°, 60°, 90°. Приведем таблицу значений тригонометрических функций:
Некоторые люди испытывают проблемы с запоминанием этой таблицы. Однако ее можно представить в более простом виде. Заменим числа 0, 1 и 1/2 следующими выражениями с корнями:
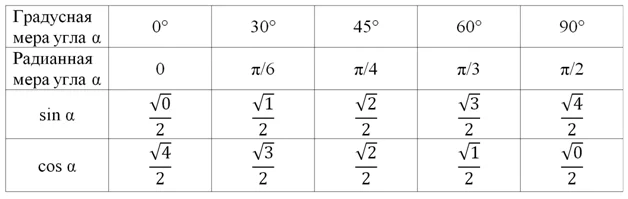
С учетом этого таблицу тригонометрических функций можно переписать так:
Теперь в каждой ячейке стоит дробь, у которой знаменатель равен двум. В числителе же стоит корень. Обратите внимание, что у синуса под корнем последовательно стоят числа 0, 1, 2, 3, и 4. У косинуса эти же числа идут в обратном порядке – от четверки до нуля. В таком виде таблицу запомнить проще.
Для вычисления тригонометрических ф-ций углов, не попадающих в диапазон 0 ⩽ α < 2π их надо привести к этому самому диапазону. Напомним, что для этого можно просто добавить к углу несколько полных оборотов, или отнять их.
Задание. Вычислите cos 7π/3.
Решение. Угол 7π/3 равен углу π/3:
7π/3 = 6π/3 + π/3 = 2π + π/3 = π/3
Значит, и косинус у угла 7π/3 будет равен косинусу угла π/3:
cos 7π/3 = cosπ/3 = 1/2
Ответ: 1/2.
График синуса и косинуса
Заметим, что координаты точек, лежащей на единичной окружности, варьируются в пределах от – 1 до 1. Это означает, что значение синуса и косинуса также может находиться только в интервале между этими числами. Получается, что область значения этих ф-ций – это промежуток [– 1; 1].
Вычислить синус и косинус можно для абсолютно любого угла поворота, поэтому область определения этих тригонометрических ф-ций – вся числовая прямая, то есть промежуток (– ∞; + ∞).
Изучение графиков тригонометрических функций начнем с синуса. В тригонометрии при построении графика синуса принято по оси Ох откладывать значение угла в радианах, а не в градусах. Из-за этого в школьной тетради тяжело точно отметить точки, через которые проходит этот график. Например, возьмем угол, равный 90°. Его величина в радианах π/2, а sinπ/2 = 1. Получается, график должен пройти через точку (π/2; 1). Однако число π/2 – иррациональное, равное примерно 1,5708…, и точно отложить отрезок длиной π/2 невозможно.
Поэтому в учебных целях график строят приближенно (естественно, что на практике точный график можно построить с помощью компьютера с любой требуемой точностью). Считают, что величина π/2 примерно равна 1,5, то есть дроби 3/2. Если выбрать масштаб, при котором единице равны 2 клеточки, то π/2 – это 3 клеточки. Тогда π/6 – это одна клеточка, а π/3 – две.
Мы знаем, что
sin 0 = 0
sin π/6 = 1/2
sin π/2 = 1
Значит, график синуса должен проходить через точки (0; 0), (π/6; 1/2) и (π/2; 1). Отметим их на координатной плоскости:
С помощью некоторых соображений симметрии можно вычислить ещё несколько точек в диапазоне от 0 до 2π. Не будем перечислять их координаты, а просто отметим их на рисунке:
Теперь соединим их плавной кривой:
Мы получили график синуса на промежутке от 0 до 2π. Но ведь мы можем вычислить синус для любого другого угла! При этом мы используем тот факт, что углам, отличающимся на 2π (на один полный оборот), на единичной окружности соответствует одинаковая точка. То есть этим двум углам будут соответствовать точки на графике с одинаковой ординатой (координатой у), но абсциссами, отличающимися на 2π. Другими словами, точку графика можно перенести на 2π (то есть 12 клеточек) влево или вправо:
Перенести можно не одну точку, а сразу всё множество точек, лежащих между 0 и 2π:
Получили ещё два участка графика, на промежутках [– 2π; 0] и [2π; 4π]. Эти участки также можно переместить влево и вправо. Продолжая этот процесс бесконечно, мы получим весь график у = sinx:
В результате мы получили кривую, которую называют синусоидой.
Теперь построим график косинуса. Мы знаем что
cos 0 = 1
cos π/3 = 1/2
cos π/2 = 1
Получается, что график должен проходить через точки (0;1), (π/3; 1/2) и (π/2; 0). Отметим их на плоскости:
Можно вычислить, используя симметрию на единичной окружности, ещё несколько точек, которые должны лежать на графике. Не приводя этих вычислений, просто отметим эти точки на плоскости:
Соединяем эти точки плавной линией:
Как и в случае с синусом, участок графика косинуса можно перенести на 2π (12 клеточек влево и вправо). В результате таких действий получим окончательный вид ф-ции у = cosх:
Можно заметить несколько особенностей полученных графиков. Во-первых, все точки обоих графиков лежат в «полосе» между прямыми у = 1 и у = – 1. Это следствие того, что и у синуса, и у косинуса область значений – это промежуток [– 1; 1]:
Во-вторых, график косинуса очень похож на синусоиду. Он имеет такую же форму, но просто смещен на π/2 (3 клеточки) влево. Это не случайно, в будущих уроках мы узнаем причину этого явления. Но, так как график косинуса – это просто смещенная синусоида, то термин «косинусоида» для его обозначения почти не используется – он просто избыточен.
В-третьих, графики обладают периодичностью. Они «повторяются» с периодом 2π. Дело в том, что углам, отличающимся друг от друга на 2π (то есть ровно на один полный поворот в 360°), на единичной окружности соответствует одна и та же точка. То есть справедливы формулы:
sin (x+ 2π) = sinx
cos (x+ 2π) = sinx
В-четвертых, можно заметить, что график косинуса симметричен относительно оси Ох, а график синуса симметричен относительно начала координат. Это значит, что синус является нечетной функцией, а косинус – четной функцией. Напомним, что ф-ция f(x) является нечетной, если справедливо условие
f(x) = – f(– x)
Если f(x) – четная ф-ция, то должно выполняться условие:
f(x) = f(– x)
Действительно, если отложить на единичной окружности углы α и (– α), то можно заметить, что их косинусы будут равны друг другу, и синусы окажутся противоположными:
Поэтому верны формулы:
sin (– α) = – sinα
cos (– α) = cosα
Тангенс угла
Синус и косинус являются основными, или, как говорят математики, прямыми тригонометрическими ф-циями. Однако есть ещё две производных тригонометрических ф-ций – тангенс и котангенс. Напомним, что тангенс угла в прямоугольном треугол-ке – это отношение противолежащего катета к прилежащему. Однако в тригонометрии куда удобнее пользоваться другим его определением. Тангенс – это отношение синуса угла к его косинусу:
Для получения тангенса на единичной окружности необходимо продолжить прямую, образующую угол α, до её пересечения с прямой х = 1. Точка их пересечения будет иметь координаты (1; tgα):
Заметим, что если α относится ко второй четверти, то тангенс получится отрицательным. Действительно, с одной стороны, соответствующая прямая пересечет линию х = 1 в точке, лежащей ниже оси Ох:
С другой стороны, мы знаем, что во второй четверти синус положителен, а косинус – отрицателен. Тогда их отношение, то есть тангенс, должно быть отрицательным:
Очевидно, что тангенс должен быть периодической ф-цией. Однако его период вдвое меньше 2π и составляет π. Действительно, углы, отличающиеся на π, будут иметь одинаковое значение тангенса, что видно из построения:
Это значит, что справедлива формула:
tg(α + π) = tg α
С другой стороны, это означает, что тангенсы углов из III четверти положительны, ведь они равны тангенсам углов из I четверти. Аналогично можно утверждать, что тангенсы углов из IV четверти отрицательны:
Также тангенс является нечетной ф-цией. Чтобы убедиться в этом, найдем с помощью единичной окружности tgα и tg (– α):
Из построения видно, что tg (– α) = tgα, поэтому тангенс попадает под определение нечетной ф-ции.
Доказать этот факт можно и иначе. Вспомним, что синус – это нечетная ф-ция, а косинус – четная. Тогда, используя определение тангенса, можно записать:
Для вычисления тангенса проще всего использовать его определение. Мы знаем синусы и косинусы стандартных углов, а потому, деля их друг на друга, сможем найти и тангенсы стандартных углов:
Ещё раз отметим, что важнее всего запомнить значения синусов и косинусов стандартных углов. Зная их, школьник всегда сможет самостоятельно вычислить тангенс.
Можно ли вычислить тангенс для угла π/2, то есть для 90°? Сделать это не получится, ведь cosπ/2 равен нулю. Если подставить cosπ/2 в формулу для вычисления тангенса, то получится деление на ноль! Так как тангенс – периодическая ф-ция, то его нельзя вычислить и в тех точках, которые отличаются от π/2 на целое число π.
В частности, тангенс не определен при х = – π/2.
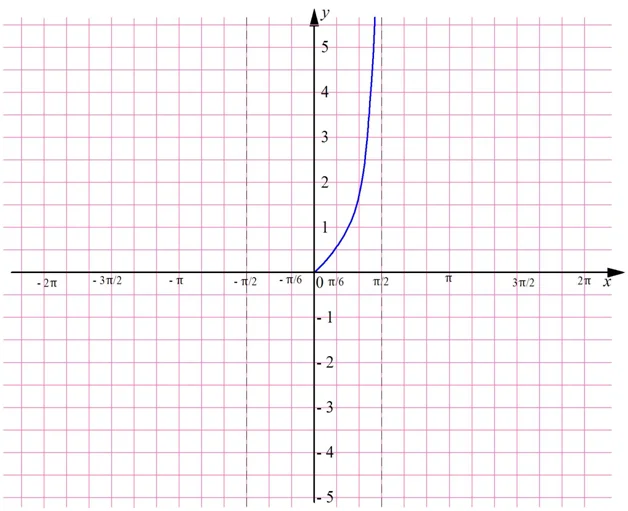
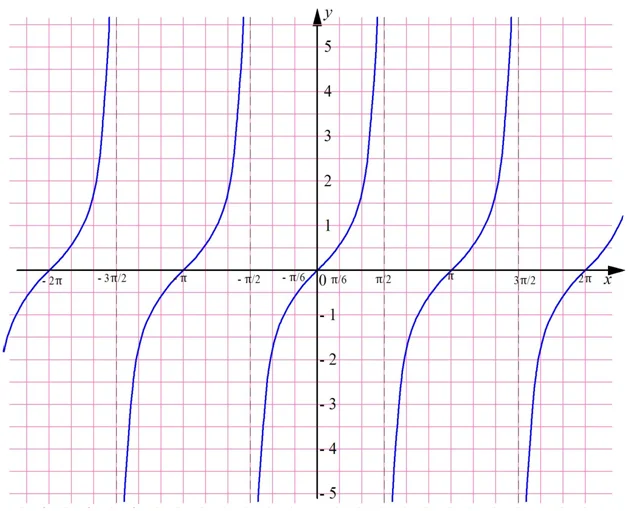
График тангенса
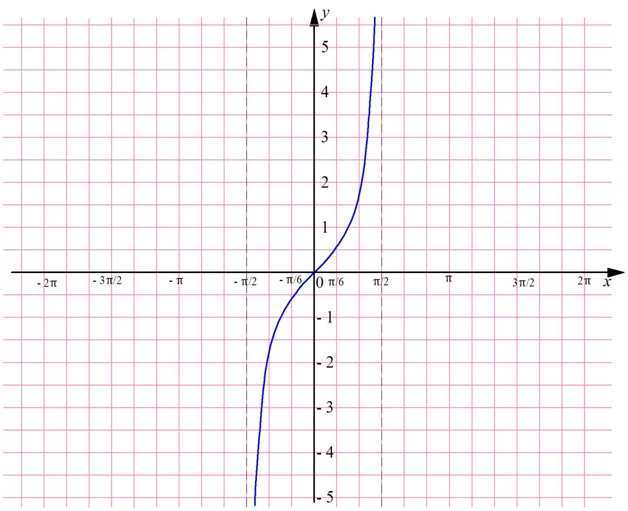
Так как тангенс обладает периодом, равным π, достаточно построить его график на каком-нибудь промежутке длиной π. Далее его можно будет просто перенести на π единиц влево и вправо. Удобно выбрать промежуток от – π/2 до π/2. Дело в том, что на нем она определена во всех точках, кроме его концов.
Через точки х = – π/2 и х = π/2 проведем штриховые линии – они означают, что график НЕ должен пересекать их. Ясно, что график проходит через точку (0; 0), ведь tg 0 = 0. Тангенс представляет собой дробь sinx/cosx. При увеличении х от 0 до π/2 знаменатель возрастает, а числитель убывает, стремясь к нулю. Поэтому вся дробь неограниченно растет, и график тангенса возрастает до бесконечности:
Так как мы строим график нечетной ф-ции, то мы можем полученную ветвь отобразить симметрично относительно начала координат:
Полученный график называют тангенсоидой. Осталось воспользоваться тем, что мы рассматриваем периодическую ф-цию с периодом π, и перенести тангенсоиду влево и вправо:
Котангенс угла
Помимо тангенса в тригонометрии выделяют ещё одну производную ф-цию – котангенс. Он представляет отношение косинуса к синусу:
Видно, что определение котангенса очень похоже определение тангенса. В принципе, удобней использовать несколько другую формулу:
Почти во всех задачах с помощью формулы
можно избавиться от котангенса, заменив его дробью 1/tgα. Поэтому мы вкратце расскажем об основных особенностях котангенса, ведь он очень редко используется на практике.
Значения этой ф-ции рассчитываются так:
При х = 0 значение котангенса не определено, так как в этой точке косинус становится равным нулю, а деление на ноль невозможно.
График котангенса – это тангенсоида, которая отображена симметрично относительно оси Ох и смещена на π/2:
Можно заметить, что вертикальные штриховые линии (асимптоты) графика проходят через точки, кратные π: –2π, – π, 0, π, 2π… Они разбивают координатную прямую на интервалы (– 2π; – π), (– π; 0), (0; π), (π; 2π), на каждом из которых ф-ция у = ctgx убывает. Видно, что котангенс – это периодическая ф-ция с периодом π.
Для сравнения покажем на одной плоскости графики тангенса и котангенса:
Котангенс, как и тангенс – нечетная ф-ция, то есть
ctg (– x) = – ctgx
Теперь у нас есть представление об основных тригонометрических ф-циях. Важнейшими из них являются синус и косинус. Тангенс является производной ф-цией от них и рассчитывается как отношение синуса к косинусу. Редко используемый котангенс, наоборот, представляет собой отношение косинуса к синусу.
Впервые элементы тригонометрии стали использовать ещё древние греки, которые производили с их помощью астрономические расчеты. В XVIII веке Эйлер сформулировал определения тригонометрических функций с помощью единичной окружности, благодаря которым стало возможным вычислять их значение для любых углов. Изначально тригонометрия использовалась для географических расчетов и навигации, однако со временем область ее применения расширилась. Оказалось, что без неё не обойтись в анализе финансовых рынков и биологических процессов, архитектуре, акустике и оптике, теории вероятностей.
Содержание:
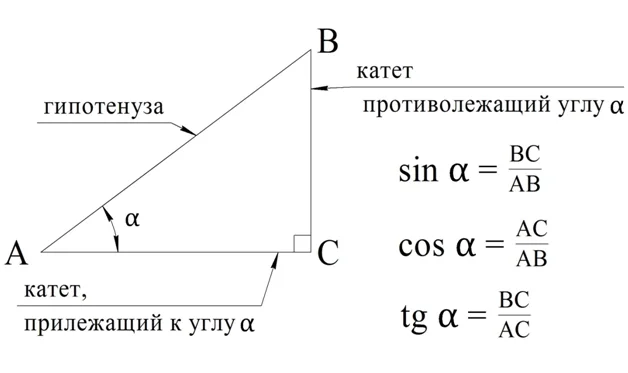
При изучении геометрии вы рассматривали отношения сторон в прямоугольном треугольнике и познакомились с понятиями синуса, косинуса, тангенса и котангенса острого угла (рис. 28).
Построение синуса и косинуса произвольного угла
Построим точку
Рассмотрим прямоугольный треугольник 
Таким образом, синус угла 
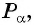
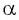
Поскольку в тригонометрии рассматриваются углы 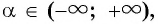
Определение синуса произвольного угла
Определение:
Синусом угла 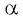
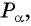
Определение косинуса произвольного угла
Определение:
Косинусом угла 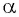
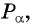
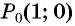
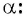
Для того чтобы найти синус и косинус произвольного угла 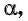
- Построить точку
единичной окружности.
- Найти ординату точки
- Найти абсциссу точки
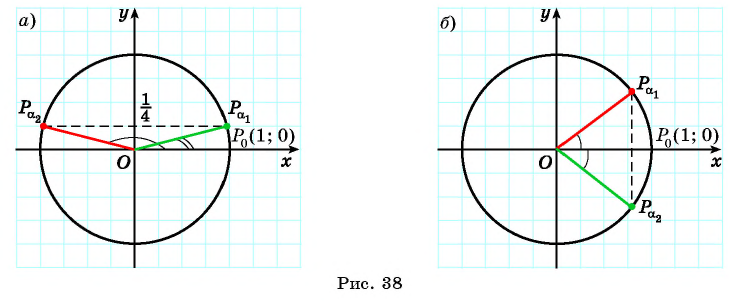
Найдите синус и косинус угла
Значения синуса и косинуса произвольного угла с помощью единичной окружности в основном можно указать только приближенно.
Однако для некоторых углов значения синуса и косинуса можно указать точно. Определим значения синуса и косинуса для углов, которые соответствуют точкам пересечения окружности с осями координат 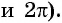
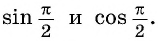
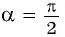
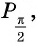
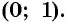
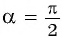
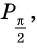
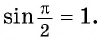
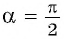
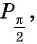
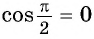
Пользуясь определением синуса и косинуса угла 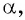
Так как ординаты и абсциссы точек единичной окружности изменяются от -1 до 1, то значения синуса и косинуса произвольного угла принадлежат промежутку
Например, выясним, может ли 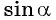
Значения синуса произвольного угла принадлежат отрезку 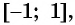
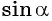
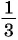
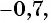
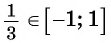
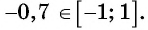
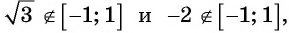
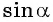
По определению синуса и косинуса угла 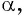
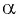
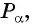
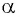
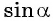
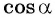
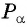
Пример №1
Определите знак выражения:
Решение:
а) Так как 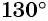
б) Так как 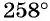
в) Так как 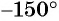
г) Так как 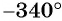
Из геометрии нам известны значения синусов и косинусов острых углов (см. табл.).
С помощью этих значений можно находить значения синусов и косинусов некоторых других углов
Пример №2
Вычислите:
Решение:
а) Отметим на единичной окружности точку 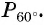
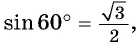
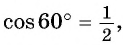
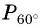
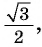
Точки 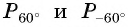
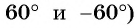
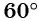
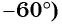
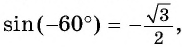
б) Так как 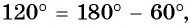
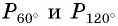
в) Точки 
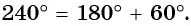
г) Поскольку 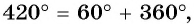
Пример №3
Вычислите:
Решение:
а) Так как 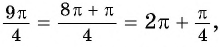
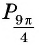
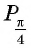
Поскольку
б) Точки 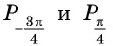
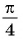
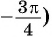
Пример №4
Постройте один из углов, если:
Решение:
а) Так как 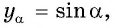
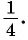
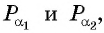
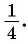
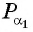
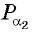
б) Так как 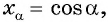
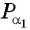
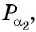
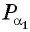
- Заказать решение задач по высшей математике
Примеры заданий и их решения:
Пример №5
Точка 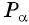
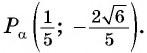
Решение:
Синусом угла 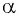
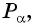
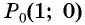
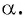
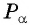
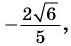
Косинусом угла 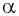
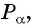
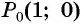
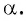
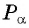
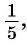
Пример №6
Если 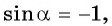
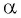
Выберите правильный ответ.
Решение:
Так как синусом угла 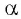
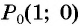
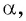
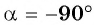
Пример №7
Если 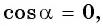
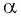
Выберите правильный ответ.
Решение:
Так как косинусом угла 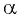
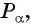
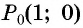
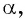
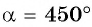
Пример №8
Найдите значение выражения:
Решение:
а) Абсцисса точки 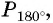
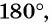
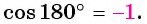
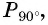
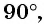

б) 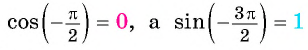
Может ли 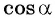
Решение:
Поскольку
а) не может быть равным 1,2, так как
б) может быть равным 0,89, так как
в) не может быть равным 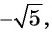
г) может быть равным 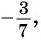
Пример №9
Определите знак выражения:
Решение:
а) 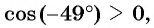
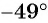
б) 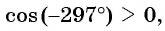
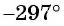
в) 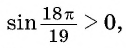
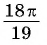
г) 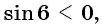
Пример №10
Сравните:
Решение:
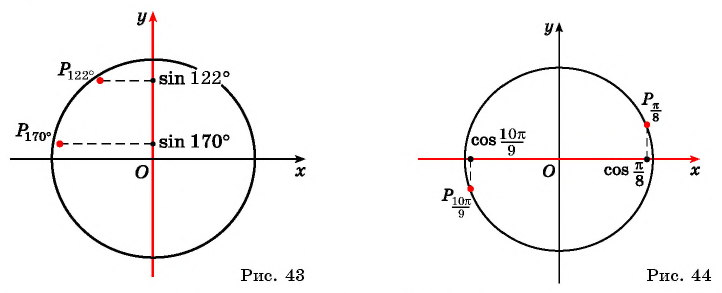
а) Отметим на единичной окружности точки, соответствующие углам 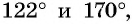
б) Сравним абсциссы точек единичной окружности 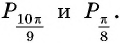
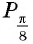
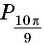
Пример №11
С помощью единичной окружности найдите значение:
Решение:
а) Ордината точки 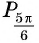
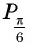
б) Абсцисса точки 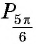
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
- Прогрессии в математике – арифметическая, геометрическая
- Единичная окружность – в тригонометрии
Нахождение значений синуса, косинуса, тангенса и котангенса
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30 ° , 45 ° , 60 ° . Если угол выходит за пределы 90 ° , то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α , можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45 ° , мы сможем определить значение синуса 30 ° , воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
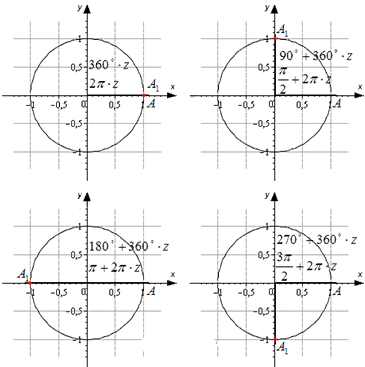
Если взять за основу определения, возможно определить значения для определенного угла α . Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0 ° , 90 ° , 180 ° , 270 ° , 360 ° .
Разобьем эти углы на четыре группы: 360 · z градусов ( 2 π · z рад), 90 + 360 · z градусов ( π 2 + 2 π · z рад), 180 + 360 · z градусов ( π + 2 π · z рад) и 270 + 360 · z градусов ( 3 π 2 + 2 π · z рад), где z – любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
При повороте из точки A на 360 · z ° , она переходит в себя. А 1 ( 1 , 0 ) . Синус 0 ° , 360 ° , 720 ° равен 0 , а косинус равен 1 . Представим это в виде формулы: sin ( 360 ° · z ) = 0 и cos ( 360 ° · z ) = 1 .
Можно определить, что t g ( 360 ° · z ) = 0 1 = 0 , а котангенс не определен.
Если А ( 1 , 0 ) повернуть на 90 + 360 · z ° , то она перейдет в А 1 ( 0 , 1 ) . По определению: sin ( 90 ° + 360 ° · z ) = 1 и cos ( 90 ° + 360 ° · z ) = 0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: c t g ( 90 ° + 360 ° · z ) = 0 1 = 0 .
Рассмотрим особенности для третьей группы углов. После поворота точки А ( 1 , 0 ) на любой из углов 180 + 360 · z ° , она перейдет в A 1 ( − 1 , 0 ) . Мы находим значения функций кроме тангенса.
Рассмотрим правила для четвертой группы углов. При повороте точки на 270 + 360 · z ° мы попадем в A 1 ( 0 , − 1 ) . Мы находим значения всех функций кроме тангенса.
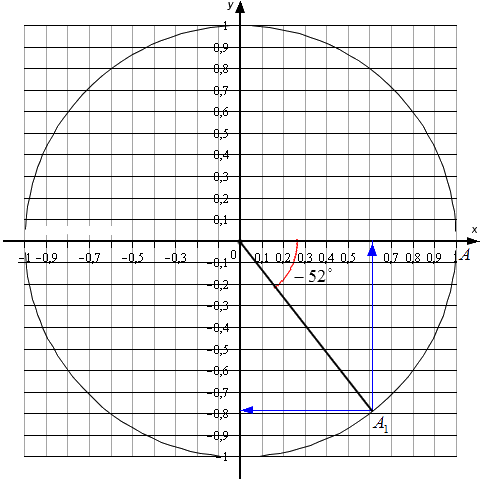
Для углов, которые не относятся к перечню от 0 ° , 90 ° , 180 ° , 270 ° , 360 ° … , точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла − 52 ° . Выполним построения.
Согласно рисунку, абсцисса А 1 ≈ 0 , 62 , а ордината ≈ − 0 , 78 . Соответственно, sin ( – 52 ° ) ≈ – 0 , 78 и cos ( – 52 ° ) ≈ 0 , 62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: t g ( – 52 ° ) ≈ – 0 , 78 0 , 62 ≈ – 1 , 26 и c t g ( – 52 ° ) ≈ 0 , 62 – 0 , 78 ≈ – 0 , 79 .
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
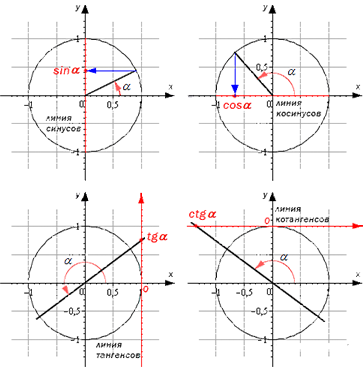
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α , cos α , t g α , c t g α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1 . Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 1 2 – 1 2 2 = 3 2 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30 ° = 1 2 1 = 1 2 и sin 60 ° = 3 2 1 = 3 2 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30 ° = 3 2 1 = 3 2 и cos 60 ° = 1 2 1 = 1 2 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: t g 30 ° = 1 2 3 2 = 1 3 = 3 3 и t g 60 ° = 3 2 1 2 = 3 . Находим котангенс по подобной схеме: с t g 30 ° = 3 2 1 2 = 3 и с t g 60 ° = 1 2 3 2 = 1 3 = 3 3 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45 ° и гипотенузой, которая равна 1 . Используем теорему Пифагора. Согласно формуле, длины катетов равны 2 2 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: c t g 45 ° = 2 2 2 2 = 1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α , cos α , t g α , c t g α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin 2 α + cos 2 α = 1 .
Тангенс по известному косинусу t g 2 α + 1 = 1 cos 2 α .
Котангенс по известному синусу или наоборот 1 + c t g 2 α = 1 sin 2 α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: t g α · c t g α = 1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Необходимо найти значение синуса угла π 8 , если t g π 8 = 2 – 1 .
Сначала найдем котангенс угла: c t g π 8 = 1 t g π 8 = 1 2 – 1 = 2 + 1 ( 2 – 1 ) · ( 2 + 1 ) = 2 + 1 ( 2 ) 2 – 1 2 = 2 + 1 Воспользуемся формулой 1 + c t g 2 α = 1 sin 2 α . Благодаря этому мы вычисляем значение синуса. Имеем
sin 2 π 8 = 1 1 + c t g 2 π 8 = 1 1 + ( 2 + 1 ) 2 = 1 4 + 2 2 = 1 2 · ( 2 + 2 ) = 2 – 2 2 · ( 2 + 2 ) · ( 2 – 2 ) = = 2 – 2 2 · ( 2 2 – ( 2 ) 2 ) = 2 – 2 4
Для завершения необходимо определить значение синуса. Угол π 8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π 8 = sin 2 π 8 = 2 – 2 4 = 2 – 2 2 . sin π 8 = 2 – 2 2 .
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 ° . Сведение к углу из интервала от 0 до 90 ° . Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210 ° . Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30 ° : sin 210 ° = sin ( 180 ° + 30 ° ) = – sin 30 ° = – 1 2 , или косинуса 60 ° sin 210 ° = sin ( 270 ° – 60 ° ) = – cos 60 ° = – 1 2 .
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π 8 , который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение t g π 8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства t g 2 π 8 = 1 – cos π 4 1 + cos π 4 . Значения косинуса угла π 4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
t g 2 π 8 = 1 – cos π 4 1 + cos π 4 = 1 – 2 2 1 + 2 2 = 2 – 2 2 + 2 = = ( 2 – 2 ) 2 ( 2 + 2 ) · ( 2 – 2 ) = ( 2 – 2 ) 2 2 2 – ( 2 ) 2 = ( 2 – 2 ) 2 2
Угол π 8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: t g π 8 = t g 2 π 8 = ( 2 – 2 ) 2 2 = 2 – 2 2 = 2 – 1
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Узнать ещё
Знание — сила. Познавательная информация
Синус 1, sin 2, sin 3
Единичная окружность помогает понять, чему равны sin 1, sin 2, sin 3, sin 4, sin 5, sin 6.
Итак, речь идет об углах в радианах. 1 радиан — это угол, длина дуги которого равна радиусу окружности. Соответственно, определяем приблизительное местонахождение на единичной окружности углов в 2, 3, 4, 5 и 6 радиан, отмечая каждую следующую точку через дугу, длина которой равна радиусу. Впрочем, если вспомнить, что п приближенно равно 3,14, задача существенно упростится.
Рисунок позволяет наглядно определять приблизительные значения sin 1, sin 2, sin 3, sin 4, sin 5, sin 6, а также сравнивать их.
Поскольку синус — это ордината соответствующей точки на единичной окружности (как это легко запомнить — здесь ), то для нахождения sin 1, sin 2, sin 3, sin 4, sin 5, sin 6 достаточно определить значение y в точках 1, 2, 3, 4, 5 и 6 радиан.
Поскольку синус — это y, то вверху, над осью x, синус принимает положительные значения. Поэтому sin 1>0, sin 2>0, sin 3>0.
Соответственно внизу синус отрицателен: sin 4 sin4, ведь любое положительное число больше любого отрицательного.
Если требуется сравнить значения синуса одного знака, например, sin2 и sin3, то исходя из геометрических соображений, sin2>sin3.
Если нужно уточнить, чему равен 1 радиан, 2, 3, 4, 5 и 6 радиан в градусах, то приближенные значения таковы:
Приближенно чему равен синус 1, синус 2 и синус 3, можно узнать по таблицам Брадиса:
Используя геометрические соображения, можно найти и приблизительные значения углов, больших 6 радиан.
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Координата по оси x – косинус угла , координата по оси y – синус угла .
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
0 °
30 °
45 °
60 °
90 °
sin α
0
1 2
2 2
3 2
1
cos α
1
3 2
2 2
1 2
0
tg α
0
3 3
1
3
нет
ctg α
нет
3
1
3 3
0
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
[spoiler title=”источники:”]
[/spoiler]
Синус и косинус на единичной числовой окружности
- Синус и косинус острого угла в прямоугольном треугольнике
- Основное тригонометрическое тождество
- Синус и косинус угла на числовой окружности
- Знаки синусов и косинусов
- Синусы и косинусы углов πk/2
- Синусы и косинусы углов π/4+πk/2
- Синусы и косинусы углов π/6+πk/2
- Синусы и косинусы углов π/3+πk/2
- Примеры
п.1. Синус и косинус острого угла в прямоугольном треугольнике
 |
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. sinα=$frac{a}{c} $ Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. cosα=$frac{b}{c} $ |
Например:
B ΔABC, ∠C = 90°, a = 2, b = 4. Найдем синус и косинус ∠A.
По теореме Пифагора гипотенуза равна (c=sqrt{a^2+b^2}=sqrt{2^2+4^2}=2sqrt{5})
Получаем: $$ sinA=frac{a}{c}=frac{2}{2sqrt{5}}=frac{1}{sqrt{5}}, cosA=frac{b}{c}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}} $$
п.2. Основное тригонометрическое тождество
Из теоремы Пифагора следует: $$ a^2+b^2=c^2Rightarrow frac{a^2+b^2}{c^2}=1Rightarrowleft(frac{a}{c}right)^2+left(frac{b}{c}right)^2=1Rightarrow sin^2alpha+cos^2alpha=1 $$
Сумма квадратов синуса и косинуса одного и того же угла равна единице: $$ sin^2alpha+cos^2alpha=1 $$
п.3. Синус и косинус угла на числовой окружности
 |
Числовая окружность расположена в декартовой прямоугольной системе координат. Отметим на числовой окружности точку M, где луч OM составляет с положительным направлением оси OX угол α. Найдем координаты точки M. Рассмотрим ΔMOK. ∠MKO=90°, ∠MOK=α OM=1 – гипотенуза По определению синуса и косинуса острого угла в прямоугольном треугольнике получаем: begin{gather*} cosalpha=frac{OK}{OM}=frac{x}{1}=x\ sinalpha=frac{MK}{OM}=frac{y}{1}=y end{gather*} |
Каждому углу α на числовой окружности соответствует точка, координаты которой: $$ x=cosalpha, y=sinalpha $$
Уравнение числовой окружности по определению: x2 + y2 = 1
Откуда снова получаем основное тригонометрическое тождество:
sin2α + cos2α = 1
п.4. Знаки синусов и косинусов
п.5. Синусы и косинусы углов (frac{pi k}{2})
 |
Базовыми точками на числовой окружности для углов, кратных прямому углу (углы (frac{pi k}{2})), будут четыре точки: 0°, 90°, 180°, 270° (left(0, frac{pi}{2}, pi, frac{3pi}{2}right)). Все остальные точки (например, 360°, 900° или –540°) будут отличаться от базовых точек на один или несколько полных периодов 2πk, т.е. будут совпадать с ними на окружности. Синусы и косинусы для совпадающих точек равны. Косинус – это координата x, синус – координата y. |
| α | 0° | 90° | 180° | 270° | |
| 0 | π/2 | π | 3π/2 | ||
| x | cosα | 1 | 0 | –1 | 0 |
| y | sinα | 0 | 1 | 0 | –1 |
п.6. Синусы и косинусы углов (frac{pi}{4}+frac{pi k}{2})
 |
Базовыми точками на числовой окружности для угла 45° и всех отстоящих от него на углы, кратные прямому (углы (frac{pi}{4}+frac{pi k}{2})), будут четыре точки: 45°, 135°, 225°, 315° (left(frac{pi}{4}, frac{3pi}{4}, frac{5pi}{4}, frac{7pi}{4}right)). Все остальные точки (например, 405°, 945° или –585°) будут отличаться от базовых точек на один или несколько полных периодов 2πk, т.е. будут совпадать с ними на окружности. Синусы и косинусы для совпадающих точек равны. Косинус – это координата x, синус – координата y. |
Как видно из чертежа, для этих углов синус и косинус по модулю равны и отличаются только по знаку. Найдем модуль из тригонометрического тождества.
Обозначим для угла (45^{circ} sin45^{circ}=cos45^{circ}=mgt 0.) Тогда
$$ sin^2 45^{circ}+cos^2 45^{circ}=1Rightarrow m^2+m^2=1Rightarrow 2m^2=1Rightarrow m^2=frac12 overset{mgt 0}{Rightarrow} m=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} $$ Все исследуемые точки на числовой окружности будут иметь пару координат (frac{sqrt{2}}{2} text{и} frac{sqrt{2}}{2}), только с разными знаками.
| α | 45° | 135° | 225° | 315° | |
| π/4 | 3π/4 | 5π/4 | 7π/4 | ||
| x | cosα | (frac{sqrt{2}}{2}) | (-frac{sqrt{2}}{2}) | (-frac{sqrt{2}}{2}) | (frac{sqrt{2}}{2}) |
| y | sinα | (frac{sqrt{2}}{2}) | (frac{sqrt{2}}{2}) | (-frac{sqrt{2}}{2}) | (-frac{sqrt{2}}{2}) |
п.7. Синусы и косинусы углов π/6+πk/2
 |
Базовыми точками на числовой окружности для угла 30° и всех отстоящих от него на углы, кратные прямому (углы (frac{pi}{6}+frac{pi k}{2})), будут четыре точки: 30°, 120°, 210°, 300° (left(frac{pi}{6}, frac{2pi}{3}, frac{7pi}{6}, frac{5pi}{3}right)). Все остальные точки (например, 390°, 960° или –420°) будут отличаться от базовых точек на один или несколько полных периодов 2πk, т.е. будут совпадать с ними на окружности. Синусы и косинусы для совпадающих точек равны. Косинус – это координата x, синус – координата y. |
Известно, что (sin 30^{circ}=frac12). Тогда из основного тригонометрического тождества: $$ cos30^{circ}=sqrt{1-sin^230^{circ}}=sqrt{1-frac14}=frac{sqrt{3}}{2}. $$ Все исследуемые точки на числовой окружности будут иметь пару координат из чисел (frac12 text{и} frac{sqrt{3}}{2}) в разном порядке и с разными знаками. Чтобы различать их «на глаз», заметим, что (frac{sqrt{3}}{2}approx 0,87gtfrac12). Т.е, отрезок короче будет равен по модулю (frac12), а длиннее (frac{sqrt{3}}{2}).
| α | 30° | 120° | 210° | 300° | |
| π/6 | 2π/3 | 7π/6 | 5π/3 | ||
| x | cosα | (frac{sqrt{3}}{2}) | (-frac12) | (-frac{sqrt{3}}{2}) | (frac12) |
| y | sinα | (frac12) | (frac{sqrt{3}}{2}) | (-frac12) | (-frac{sqrt{3}}{2}) |
п.8. Синусы и косинусы углов π/3+πk/2
 |
Базовыми точками на числовой окружности для угла 60° и всех отстоящих от него на углы, кратные прямому (углы (frac{pi}{3}+frac{pi k}{2})), будут четыре точки: 60°, 150°, 240°, 330° (left(frac{pi}{3}, frac{5pi}{6}, frac{4pi}{3}, frac{11pi}{6}right)). Все остальные точки (например, 390°, 960° или –420°) будут отличаться от базовых точек на один или несколько полных периодов 2πk, т.е. будут совпадать с ними на окружности. Синусы и косинусы для совпадающих точек равны. Косинус – это координата x, синус – координата y. |
Известно, что (cos60^{circ}=sin 30^{circ}=frac12). Тогда из основного тригонометрического тождества: $$ sin60^{circ}=sqrt{1-cos^2 60^{circ}}=sqrt{1-frac14}=frac{sqrt{3}}{2}. $$ Все исследуемые точки на числовой окружности будут иметь пару координат из чисел (frac12 text{и} frac{sqrt{3}}{2}) в разном порядке и с разными знаками. Чтобы различать их «на глаз», заметим, что (frac{sqrt{3}}{2}approx 0,87gtfrac12). Т.е, отрезок короче будет равен по модулю (frac12), а длиннее (frac{sqrt{3}}{2}).
| α | 60° | 150° | 240° | 330° | |
| π/3 | 5π/6 | 4π/3 | 11π/6 | ||
| x | cosα | (frac12) | (-frac{sqrt{3}}{2}) | (-frac12) | (frac{sqrt{3}}{2}) |
| y | sinα | (frac{sqrt{3}}{2}) | (frac12) | (-frac{sqrt{3}}{2}) | (-frac12) |
п.9. Примеры
Пример 1.
а) Найдите косинус угла α, если известно, что (sinalpha=0,8, fracpi2 lt alpha lt pi)
Угол находится во второй четверти, значит, косинус отрицательный:
(cosalpha=-sqrt{1-sin^2alpha}=-sqrt{1-0,8^2}=-sqrt{0,36}=-0,6)
б) Найдите синус угла, если известно, что (cosalpha=frac{5}{13}, -fracpi2 lt alpha lt 0)
Угол находится в четвертой четверти, значит синус отрицательный:
(sinalpha=-sqrt{1-cos^2alpha}=-sqrt{1-frac{5}{13}^2}=-sqrt{frac{144}{169}}=-frac{12}{13})
Пример 2. Сравните числа
а) sin10° и sin320°
Угол 10° находится в 1-й четверти, sin10° > 0
Угол 320° находится в 4-й четверти, sin320° < 0
Получаем: sin320° < 0 < sin10°
sin10° > sin320°.
б) cos115° и sin85°
Угол 85° находится в 1-й четверти, sin85° > 0
Угол 115° находится во 2-й четверти, cos115° < 0
Получаем: cos115° < 0 < sin85°
cos115° < sin85°.
в) (sinfrac{8pi}{7}) и (cosfrac{11pi}{25})
(pilt frac{8pi}{7}lt frac{3pi}{2}Rightarrow) угол (frac{8pi}{7}) находится в 3-й четверти, (sinfrac{8pi}{7}lt 0)
(0lt frac{11pi}{25}lt frac{pi}{2}Rightarrow) угол (frac{11pi}{25}) находится в 1-й четверти, (cosfrac{11pi}{25}gt 0)
Получаем: (sinfrac{8pi}{7} lt 0lt cosfrac{11pi}{25})
(sinfrac{8pi}{7}lt cosfrac{11pi}{25})
Пример 3. Заданы точки на числовой окружности. Найдите их координаты
Пример 4. Найти sint,cost для данных t.
(a) t=frac{13pi}{4})
 |
Отнимем полный оборот: (frac{13pi}{4}-2pi=frac{13-8}{4}pi=frac{5pi}{4}) Угол кратный (fracpi4), его синус и косинус по модулю равны (frac{sqrt{2}}{2}), знаки определяются расположением угла. (piltfrac{5pi}{4}ltfrac{3pi}{2}Rightarrow) угол находится в 3-й четверти, синус и косинус отрицательные. Получаем: begin{gather*} sinfrac{13pi}{4}=sinfrac{5pi}{4}=-frac{sqrt{2}}{2}\ cosfrac{13pi}{4}=cosfrac{5pi}{4}=-frac{sqrt{2}}{2} end{gather*} |
(б) t=frac{11pi}{2})
 |
Отнимем 2 полных оборота: (frac{11pi}{2}-2cdot 2pi=frac{11-8}{2}pi=frac{3pi}{2}) Угол кратный (fracpi2), находится на оси Y, в нижней точке числовой окружности. Получаем: begin{gather*} sinfrac{11pi}{2}=sinfrac{3pi}{2}=-1\ cosfrac{11pi}{2}=cosfrac{3pi}{2}=0 end{gather*} |
(в) t=frac{17pi}{6})
 |
Отнимем полный оборот: (frac{17pi}{6}-2pi=frac{17-12}{6}pi=frac{5pi}{6}) Угол типа (fracpi6), в котором синус и косинус – это пара из (frac12) и (frac{sqrt{3}}{2}), фактическое значение определяется по чертежу, исходя из того, что (frac{sqrt{3}}{2}approx 0,87gtfrac12). Знаки определяются по расположению угла в четверти: (fracpi2ltfrac{5pi}{6}ltpiRightarrow) угол находится во 2-й четверти. Из чертежа получаем: Косинус – длинный отрицательный Синус – короткий положительный Таким образом: begin{gather*} sinfrac{17pi}{6}=sinfrac{5pi}{6}=frac12\ cosfrac{17pi}{6}=cosfrac{5pi}{6}=-frac{sqrt{3}}{2} end{gather*} |
(г) t=-frac{4pi}{3})
 |
Добавим полный оборот: (-frac{4pi}{3}+2pi=frac{-4+6}{3}pi=frac{2pi}{3}) Угол типа (fracpi3), в котором синус и косинус – это пара из (frac12) и (frac{sqrt{3}}{2}), фактическое значение определяется по чертежу, исходя из того, что (frac{sqrt{3}}{2}approx 0,87gtfrac12). Знаки определяются по расположению угла в четверти: (fracpi2ltfrac{2pi}{3}ltpiRightarrow) угол находится во 2-й четверти. Из чертежа получаем: Косинус – короткий отрицательный Синус – длинный положительный Таким образом: begin{gather*} sinleft(-frac{4pi}{3}right)=sinfrac{2pi}{3}=frac{sqrt{3}}{2}\ cosleft(-frac{4pi}{3}right)=cosfrac{2pi}{3}=-frac12 end{gather*} |
урок 2. Математика ЕГЭ
Тригонометрическая окружность
В этой статье мы поговорим об основах тригонометрии – о тригонометрической окружности. С нее начинается изучение тригонометрии в 10-м классе.
Именно тригонометрические уравнения, как правило, попадаются в самом легком задании второй части ЕГЭ по профильной математике. А умение преобразовывать тригонометрические выражения часто бывают и в первой части. Без этой важной темы на ЕГЭ никак не обойтись.
Тригонометрия очень непривычная тема для школьников. А единичная окружность – это основа, если вы разберетесь с ней, то все остальное не будет казаться таким сложным.
Единичная окружность
Чтобы начать пользоваться тригонометрической окружностью, ее нужно построить.
Для начала нарисуем обычную прямоугольную декартову систему координат – ту, в которой вы должны были в младших классах строить различные графики прямых, парабол и т.д. Горизонтальную ось (ось абсцисс), как обычно, обозначим за (x), а вертикальную (ось ординат) за (y). И нарисуем в этой системе координат обыкновенную окружность единичного радиуса с центром в точке с координатами ((0;0)) – начало координат.
Пусть наша единичная окружность пересекает оси абсцисс и ординат в точках (A,B,C,D), как показано на рисунке. Центр окружности обозначим за точку (O).
Тригонометрическая окружность
Сразу обратите внимание, что оси (x) и (y) делят наш круг на четыре части, их называют четвертями. А еще каждой четверти присвоили свой номер так же, как пронумеровано римскими цифрами на рисунке. В школе часто мучают этими четвертями.
Как считать углы на единичной окружности
А теперь мы подобрались к самому главному: будем рисовать углы на окружности. Все углы отсчитываются, начиная с отрезка (OA) ПРОТИВ часовой стрелки. Например, давайте повернем отрезок (OA) против часовой стрелки на угол (30^o) (как стрелку часов) и получим некоторую точку (M), лежащую на окружности. На рисунке хорошо видно, как мы получили угол (angle{AOM}).
Острый угол на единичной окружности
Таким образом, можно получать любые углы, просто поворачивая отрезок (OA). На рисунке 3 кроме угла (angle{AOM}=30^o) я нарисовал углы: (angle{AON}=45^o), (angle{AOK}=60^o), (angle{AOB}=90^o), (angle{AOF}=120^o), (angle{AOL}=135^o), (angle{AOT}=150^o), (angle{AOC}=180^o).
Рис.3. Углы на тригонометрической окружности
Обратите внимание на углы (angle{AOB}=90^o) и (angle{AOC}=180^o): прямой и развернутый углы соответственно. Они нам понадобятся чуть позже.
Но и это еще не все! Оказывается, бывают углы больше чем (180^o). Например, на нашей окружности такими углами будут (angle{AOW}=210^o), (angle{AOQ}=315^o).
Есть даже угол, который соответствует полному обороту (angle{AOA}=360^o) (см. Рис. 4)
Рис.4. Развернутые углы на тригонометрической окружности
Обратите внимание, что абсолютно все углы отсчитываются от отрезка (OA). И каждому углу соответствует своя точка на окружности. В тригонометрии принято все углы на единичной окружности обозначать просто точками. Например, точка (K) на рисунке 3 соответствует углу в (60^o), точка (W) соответствует углу (210^o).
Любознательный читатель может спросить: а существуют ли углы большие (360^o)? И ответом будет – конечно, да. Нам ничто не мешает повернуть отрезок (OA) на (360^o), а потом продолжить поворачивать его, например, еще градусов на (30^o). И тогда мы получим прекрасный угол, соответствующий точке (V=390^o).
Угол больше одного оборота на тригонометрической окружности
Кстати, точка (V) совпадет с точкой (M), соответствующей углу в (30^o). Получается, одна и та же точка может соответствовать сразу нескольким углам!
Действительно, если к любому углу прибавить (360^o), то вы попадете опять в ту же самую точку. Аналогично можно обратить внимание, что точка (A) одновременно соответствует как минимум двум углам: (0^o) и (360^o).
Угол в (720^o) будет соответствовать двум полным оборотам.
А ведь можно к любому углу прибавить не (360^o), а (720^o), что соответствует сразу 2-м полным оборотам. И так добавлять обороты можно до бесконечности. Значит, любой точке на единичной окружности соответствует бесконечное количество углов с шагом в (360^o). Например, углы (60^o, , 420^o, , 780^o, , 1140^o) и т.д. все лежат в одной и той же точке на окружности, так как они все отличаются на один полный оборот – на (360^o). Это важная мысль, в дальнейшем она нам пригодится.
В общем, можно отсчитывать углы от отрезка (OA) сколько угодно большие и можно накручивать круги до бесконечности. Причем каждой точке соответствует бесконечное количество углов.
А еще существуют отрицательные углы! Оказывается, если повернуть отрезок (OA) ПО ЧАСОВОЙ стрелке, то мы получим отрицательный угол. Например, на рисунке показан угол в (-30^o).
Отрицательные углы на единичной окружности
Любой угол, получившийся поворотом по часовой стрелке, будет отрицательным.
Кстати, точка (M) на окружности, соответствующая углу в (-30^o), отсчитанному по часовой стрелке, совпадает с точкой, соответствующей углу в (330^o), отсчитанным против часовой.
Как переводить радианы в градусы?
Все знают, чтобы измерить некоторое расстояние, можно воспользоваться несколькими единицами измерения: сантиметрами, метрами, километрами или даже световыми годами. Точно так же углы можно измерять по-разному. Мы всю свою жизнь углы измеряли градусами и интуитивно уже понимаем, сколько градусов соответствует визуально какому углу. Довольно легко представить угол в (30^o) или (90^o).
Но, к большому сожалению, в математике углы часто измеряют не в градусах, а в радианах. Так просто удобно в некоторых случаях. А нам с вами ничего не остается, как привыкнуть к новой единице измерения углов.
Ничего страшного в этом нет. Первое, с чем нам нужно познакомиться – это иррациональное число Пи:
$$pi=3,14…;$$
Это известная константа, которая обладает интересными свойствами и используется во множестве научных областей. Но об этом в другой раз. Сейчас нам нужно запомнить, что угол в (pi) радиан это тоже самое, что и угол равный (180^o).
$$pi , рад=180^o;$$
Из этого факта легко переводить радианы в градусы и наоборот:
$$ frac{pi}{2}=frac{180}{2}^o=90^o;$$
$$ frac{pi}{3}=frac{180}{3}^o=60^o;$$
$$ frac{pi}{4}=frac{180}{4}^o=45^o;$$
$$ frac{pi}{6}=frac{180}{6}^o=30^o;$$
Для того, чтобы перевести абсолютно любой угол в градусы, удобно воспользоваться пропорцией. Для примера переведем (frac{5pi}{6}) радиан:
$$pi , рад=180^o;$$
$$frac{5pi}{6} , рад=x^o;$$
Пропорции решаются перемножением крест на крест:
$$pi*x=frac{5pi}{6}*180;$$
$$x=frac{frac{5pi}{6}*180}{pi}=frac{5}{6}*180=150^o.$$
Теперь отметим на тригонометрической окружности углы в радианах так же, как мы отмечали углы в градусах:
Радианы на тригонометрической окружности
Чтобы интуитивно воспринимать радианы, важно помнить, что (pi , рад=180^o;) – это равно половине окружности. Тогда (2pi=360^o) – это полный круг. Представьте, что перед вами пирог или пицца, которую вы режете на части. Тогда, помня, что (pi) это ровно половина пирога, легко представить, что, например, (frac{pi}{6}) – это мы половину пирога поделили на 6 одинаковых частей и взяли одну. А (frac{5*pi}{6}) – это опять делим половину пирога на 6 частей, только в этот раз берем 5 частей из 6-ти, считая от 0.
Можно пользоваться такой аналогией, а можно решать пропорции, как вам удобнее.
Мы научились отмечать на единичной окружности углы и познакомились с радианами.
Теперь приступаем к самому важному: какое отношение имеет этот круг единичного радиуса к тригонометрическим функциям?
Прямоугольный треугольник в тригонометрии
$$sin(alpha)=frac{a}{c};$$
$$cos(alpha)=frac{b}{c};$$
И из этих формул и теоремы Пифагора следует одна из самых важных тригонометрических формул:
$$sin^2(alpha)+cos^2(alpha)=1.$$
Раз эти определения вводились для прямоугольного треугольника, то у них есть большой недостаток. Они работают только в прямоугольном треугольнике, а значит только для острых углов. (В прямоугольном треугольнике, один угол прямой, а два другие обязательно острые).
Но синус и косинус можно посчитать на калькуляторе от абсолютно любого угла. Тогда определение из 9-го класса нам не годится.
И вот здесь на помощь приходит тригонометрическая окружность. При помощи нее мы сейчас постараемся определить синус и косинус.
Нарисуем единичную окружность (единичного радиуса) и отметим на ней какой-нибудь острый угол (angle{AOM}=alpha). Точка (M) лежит на дуге этой окружности и соответствует углу в (30^o). Посмотрите внимательно на рисунок: у точки (M) мы можем определить координаты. Пусть по оси (x) координата точки (M) будет (M_{x}), а по оси (y) – (M_{y}).
Точка (M):
$$(M_{x};M_{y});$$
Координаты точки на окружности
Опустим из точки (M) перпендикуляры на оси координат. Перпендикуляр к оси (x) попадет в точку (M_{x}), а перпендикуляр к оси (y) попадет в (M_{y}). Строго говоря, в математике (M_{x}) и (M_{y}) называются проекциями точки (M) на оси координат.
Мы получили прямоугольный треугольник (triangle{MOM}_{x}). По определению из 9-го класса синус (angle{alpha}) – это отношение противолежащего катета (MM_{x}) к гипотенузе (MO) в (triangle{MOM_{x}}):
$$sin(alpha)=frac{MM_{x}}{MO};$$
Обратите внимание, что (MO) это радиус нашей единичной окружности, значит он равен единице:
$$sin(alpha)=frac{MM_{x}}{MO}=MM_{x};$$
Из рисунка видно, что (MM_{x}=OM_{y}) или, другими словами, длина отрезка (MM_{x}) – это координата точки (M) по оси (y).
Это важный момент! Получается, что (sin(alpha)) равен координате точки (M) по оси (y).
Аналогичные рассуждения можно провести и для косинуса. Косинус по определению в прямоугольном треугольнике (triangle{MOM_{x}}) – это отношение прилежащего катета к гипотенузе:
$$cos(alpha)=frac{OM_{x}}{MO}=OM_{x}=M_{x};$$
Косинус (angle{alpha}), оказывается, будет равен координате точки (M) по оси (x).
Точно такие же рассуждения можно сделать для любого другого угла (beta). Из рисунка ниже видно, что синус (angle{beta}) – это координата точки (N) по оси (y). А косинус угла (angle{beta}) – это координата точки (N) по оси (x). (Показано фиолетовым цветом).
Координаты точки на окружности
Данная логика будет справедлива и для тупых углов. Посмотрите на угол (gamma). Значение синуса (angle{gamma}) будет соответствовать координате точки (K) по оси (y), а косинуса – по оси (x).
Тупой угол на единичной окружности
Можно сделать вывод, что значения синуса любого угла на окружности лежат на оси (y), а значения косинуса на (x).
А раз такие дела, то давайте обзовем наши оси координат не (x) и (y), а осями (cos) и (sin) соответственно. На этих осях будут лежать значения косинуса и синуса всех углов на окружности. И в дальнейшем на всех рисунках оси мы будем обозначать (cos) и (sin) соотвественно.
Обратите внимание еще на один факт: координаты любой точки на окружности обязательно будут больше минус единицы и меньше единицы. Это значит, что значения синуса и косинуса лежат в этом же промежутке. Синус и косинус – это ограниченные функции.
$$sin(alpha)in[-1;1];$$
$$cos(alpha)in[-1;1];$$
Пример 1
Изобразить на тригонометрической окружности синус и косинус (frac{pi}{3}=60^o).
Повернем отрезок (OA) против часовой стрелки на (frac{pi}{3}), получим точку (W) на окружности, которая соответствует этому углу. Если выполнять все это на миллиметровке и строить очень точно, то вы увидите, что координата точки (W) по (y) будет (W_{y}=frac{sqrt{3}}{2}approx0,87), а по оси (x) координата будет (W_{x}=frac{1}{2}).
Значения косинуса и синуса на тригонометрической окружности
Исходя из сказанного выше, мы делаем вывод:
$$sin(frac{pi}{3})=frac{sqrt{3}}{2};$$
$$cos(frac{pi}{3})=frac{1}{2};$$
Посмотрев в таблицу стандартных углов тригонометрических функций, понимаем, что мы сделали все правильно.
Тригонометрическая таблица стандартных углов
Вам, конечно, не придется сидеть с миллиметровкой и высчитывать значения тригонометрических функций, вы будете пользоваться таблицей стандартных углов. А тригонометрическая окружность нужна как большой помощник. При дальнейшем изучении тригонометрии вы в этом не раз убедитесь.
Кстати, интересно и очень важно отметить, что значение, например, синуса (frac{pi}{2}=(90^o)) будет равно 1, а косинус (frac{pi}{2}) будет равен 0. Чтобы это понять, необязательно смотреть в таблицу стандартных углов, такой вывод можно сделать при помощи тригонометрической окружности.
Прямой угол на единичной окружности
Действительно, обратите внимание: угол в (frac{pi}{2}=(90^o) соответствует на окружности точке (B). Координата точки (B) по оси (x) будет (0), а по оси (y) (1). А так как координаты точек на окружности, согласно сказанному выше, и есть значения косинуса и синуса угла, то:
$$sin(frac{pi}{2})=1;$$
$$cos(frac{pi}{2})=0;$$
Знаки синуса и косинуса в зависимости от угла
В самом начале мы не просто так разбивали нашу окружность на четверти. Дело в том, что в каждой из этих четвертей тригонометрические функции имеют разные знаки. В школе обычно заставляют учить в какой четверти какой знак. Но мы, как всегда, постараемся вникнуть в суть и понять, как это работает. Тем более, что ничего сложного здесь нет, если разобраться в материале выше.
Мы с вами выяснили, что координаты любой точки на окружности – это и есть значения синуса и косинуса. Рассмотрим первую четверть: возьмем произвольную точку (M), лежащую на дуге в этой четверти, координата точки (M) по (x) будет (M_{x}) и она будет обязательно положительной, так как лежит между нулем и единицей! А это значит, что косинус угла, соответствующего точке (M) тоже будет положительным. Аналогично координата точки (M) по оси (y) тоже лежит от 0 до 1, а значит синус (angle{MOA}) тоже положительный.
Знак синуса и косинуса в первой четверти
И какой бы угол мы не нарисовали в первой четверти, у него будут положительные координаты, а значит, и положительные значения косинуса и синуса!
Рассмотрим теперь вторую четверть. Руководствуясь той же логикой: координаты произвольной точки (K), лежащей на дуге из второй четверти по (x) будут отрицательны, а по (y) положительны. Делаем вывод, что косинус любого угла из второй четверти будет отрицательным, а синус положительным.
Точно так же в третьей четверти и косинус, и синус будут отрицательными.
В четвертой четверти косинус положительный, а синус отрицательный.
Тангенс и котангенс на тригонометрической окружности
Теперь разберемся, как пользоваться тригонометрической окружностью в случае тангенса и котангенса.
Опять из программы 9-го класса вы должны помнить, что в прямоугольном треугольнике тангенс – это отношение противолежащего катета к прилежащему. А котангенс – отношение прилежащего к противолежащему.
$$ tg(alpha)=frac{a}{b};$$
$$ctg(alpha)=frac{b}{a};$$
Отсюда, кстати, следуют несколько простейших тригонометрических формул:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)};$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$
$$tg(alpha)*ctg(alpha)=1.$$
Тангенс и котангенс в прямоугольном треугольнике
Тангенс на окружности и его знаки
Чтобы на окружности можно было пользоваться тангенсом, нам понадобится дополнительная ось. Проведем ее перпендикулярно оси (x) (теперь это у нас ось косинусов) через точку (A):
Тангенс на тригонометрической окружности
Эта ось параллельна оси (y) и полностью ее дублирует. В точке (A) будет координата (0). Отметим на окружности в первой четверти произвольную точку (L). Соединим точку (L) с центром окружности и продлим прямую до пересечения с новой осью в точке (F).
Мы получили прямоугольный треугольник (FOA). В этом прямоугольном треугольнике можем расписать тангенс по определению:
$$tg(angle{FOA})=frac{FA}{OA};$$
А так как (OA) это ни что иное, как радиус единичной окружности:
$$tg(angle{FOA})=FA;$$
А (FA) – это координата точки (F) по нашей новой оси.
Значит (tg(angle{FOA})=tg(angle{LOA})) будет равен координате точки (F) по новой оси.
Аналогичным образом я могу выбрать другую произвольную точку (P) на окружности в первой четверти, продлить до пересечения с новой осью, получить некоторую точку (T). И опять, тангенс получившегося угла (angle{TOA}=angle{POA}) будет равен координате точки (T) на новой оси.
Тут все ясно, но возникает справедливый вопрос: а что, если угол лежит не в первой четверти?
Логика рассуждений сохраняется: произвольному углу (angle{QOA}) соответствует своя точка на окружности (Q), соединим точку (Q) с центром окружности и продлим до пересечения с новой осью в точке (H). Оказывается, тангенс (angle{QOA}) будет равен координате точки (H) по новой оси.
Тангенс на тригонометрической окружности от тупого угла
Общая логика простая – берем точку на окружности, соответствующую некоторому углу (alpha), соединяем ее с центром окружности и продляем до пересечения с осью тангенса. Координата точки пересечения с осью тангенса и будет значением тангенса угла (alpha).
Эта ось называется осью тангенсов, так как на ней лежат значения тангенсов всех углов на окружности.
Стоит обратить внимание на знаки тангенса. Если соединять точки на окружности, лежащие в первой и третьей четвертях с центром окружности, то пересекать ось тангенсов эти прямые будут всегда выше (0). Значение тангенса любых углов из первой и третьей четвертей будет положительно.
А если углы лежат во второй и четвёртой четвертях, то их тангенс будет отрицательным.
Котангенс на окружности и его знаки
С котангенсом ситуация очень похожа на тангенс. Только в этот раз мы проводим горизонтальную ось перпендикулярно оси синусов через произвольную точку (B). Эта ось будет параллельна оси (x) и полностью ее дублировать. Сразу назовем эту ось осью котангенса. Ноль на оси котангенса будет совпадать с точкой (B).
Теперь выберем произвольную точку (N) на окружности, этой точке будет соответствовать угол (angle{NOA}). Соединим точку (N) с центром окружности и продлим получившуюся прямую до пересечения с осью котангенса в точке (Q).
Котангенс на тригонометрической окружности
Обратите внимание, что (angle{NOA}=angle{OQB}), как накрест лежащие при параллельных прямых (оси синуса и котангенса). Рассмотрим прямоугольный треугольник (BOQ) и распишем в нем котангенс (angle{OQB}), как отношение прилежащего катета к противолежащему в прямоугольном треугольнике:
$$ctg(angle{NOA})=ctg(angle{OQB})=frac{QB}{OB}=QB;$$
Мы получили, что котангенс (angle{NOA}) равен координате точки (Q) на оси котангенса.
Аналогичным образом можно выбрать произвольную точку на единичной окружности, соединить ее с центром окружности, продлить получившуюся прямую до пересечения с осью котангенса, координата получившейся точки будет значением котангенса угла, соответствующего точке на окружности.
И у внимательного читателя должен возникнуть вопрос! Ведь не любую точку на окружности возможно соединить с центром окружности и продлить до пересечения с осью тангенса или котангенса.
Действительно, если точки (B) и (D) соединить с центром окружности, то получится прямая параллельная оси тангенса, а значит, она никогда не пересчёт ее. Как же тогда найти значения тангенса углов, соответствующих точкам (B) и (D)? А никак, тангенс этих углов не существует. Точкам (B) и (D) соответствуют углы: (frac{pi}{2}=90^o, , frac{3pi}{2}=270^o, , -frac{pi}{2}=-90^o) и т.д. Каждой точке на окружности, как мы помним, соответствует бесконечное количество углов с периодом (2pi=360^o).
Аналогичные рассуждения с котангенсом. Котангенс не будет существовать от углов: (0, , pi=180^o, , -pi=-180^o, , 2pi) и т.д.
Несколько важных свойств тангенса и котангенса.
- Из построения можно заметить, что для любых углов из первой и третьей четвертей котангенс и тангенс будут положительные, а для второй и четвертой – отрицательные;
- Тангенс и котангенс – неограниченные функции. Это значит, что они могут принимать абсолютно любые значения: (tg(alpha)in(-infty;+infty);) и (ctg(alpha)in(-infty;+infty);)
- Тангенс не существует от углов (frac{pi}{2}*n), где (n in Z) ((n) целое число);
- Котангенс не существует от углов (pi*n), где (n in Z) ((n) целое число);
Пример 2
Изобразить на тригонометрической окружности (ctg(frac{pi}{6})).
Котангенс 30 градусов на тригонометрической окружности
- Рисуем единичную окружность;
- Повернем отрезок (OA) на угол (30^o), что то же самое, что и на (frac{pi}{6}) радиан. Пусть угол пересекает нашу окружность в точке (M);
- Нарисуем ось котангенса параллельно оси косинусов через точку (B);
- Продлим (OM) до пересечения с осью котангенсов в точке (E);
- Координата точки (E) будет соответствовать значению котангенса угла (frac{pi}{6});
- Если делать, опять же, по миллиметровке и измерить аккуратно расстояние (BE), то координата точки (E) будет (sqrt{3}approx1,73;)
- Согласно таблице стандартных углов (ctg(frac{pi}{6})=sqrt{3}). Значит все построено верно;
Симметрия тригонометрических функций
При помощи элементарной геометрии и тригонометрической окружности можно вывести несколько очень важных свойств.
Для начала поговорим про синус и косинус некоторого острого угла (angle{alpha}). Посмотрите на рисунок. Как мы с вами выяснили, значение синуса угла (alpha) будет равно координате точки (M) по оси (y).
Симметричные свойства синуса и косинуса на единичной окружности
Проведем из точки (M) перпендикуляр к оси (y) и продлим до пересечения с окружностью в точке (N). Точка (N) будет соответствовать углу (angle{NOA}).
А так как координаты точек (N) и (M) по (y) равны, то и значения синусов углов (angle{NOA}) и (angle{MOA}) будут равны.
Теперь обратите внимание, что получившаяся картинка симметрична относительно вертикальной оси (y). А значит
$$angle{NOC}=angle{MOA}=angle{alpha};$$
$$angle{NOA}=180-angle{NOC}=180-alpha;$$
А сложив вместе два вывода, получаем:
$$sin(angle{MOA})=sin(angle{NOA}) Rightarrow sin(alpha)=sin(180-alpha);$$
Теперь поговорим про косинус. Координаты у точек (M) и (N) по оси (x) будут одинаковы по модулю, но разные по знаку, так как картинка полностью симметрична относительно оси (y). А это означает, что значения косинусов (angle{MOA}) и (angle{NOA}) будут равны по модулю, но противоположны по знаку:
$$cos(angle{MOA})=-cos(angle{NOA});$$
$$cos(angle{alpha})=-cos(180-angle{alpha});$$
Еще раз нарисуем тригонометрическую окружность и отметим произвольный острый угол (alpha), соответствующий точке (P) на окружности.
Симметричные свойства синуса и косинуса на единичной окружности
Проведем перпендикуляр из точки (P) к оси (x) и продлим до пересечения с окружностью в точке (K). Получили два равных геометрически, исходя из горизонтальной симметрии, угла (angle{POA}=angle{KOA}=angle{alpha}).
Но так как на окружности принято углы, отсчитанные по часовой стрелке, брать со знаком минус, то:
$$angle{KOA}=-angle{alpha};$$
$$angle{POA}=angle{alpha};$$
Обратите внимание, что координаты точек (P) и (K) по оси (x) буду одинаковые, а значит и значения косинусов углов, соответствующих этим точкам, будут одинаковы:
$$cos(angle{POA})=cos(angle{KOA});$$
$$cos(alpha)=cos(-alpha);$$
А вот координаты по оси (y) у точек (P) и (K) будут равны по модулю, но противоположны по знаку. Это дает нам следующее соотношение:
$$sin(-alpha)=-sin(alpha).$$
Кстати, из сказанного выше следует важный вывод, который нам пригодится в дальнейшем при решении тригонометрических уравнений. Из тригонометрической окружности видно, что каждому значению синуса и косинуса соответствует как минимум два угла (кроме единицы и минус единицы).
Теперь обсудим некоторые свойства тангенса и котангенса.
Нарисуем единичную окружность и отметим на ней произвольный угол (angle{LOA}=beta). Продлим сторону (LO) угла до пересечения с осью тангенсов в точке (I) и до пересечения с окружностью с другой стороны в точке (S). Обратите внимание, что значение тангенса углов (angle{LOA}) и тупого угла (angle{SOA}) будут равны! Так как ось тангенсов пересекают в одной точке.
Симметричные свойства тангенса на единичной окружности
$$tg(angle{LOA})=tg(angle{SOA});$$
Кроме этого отметим, что, так как углы (angle{LOA}) и (angle{SOA}) лежат на одной прямой:
$$angle{SOA}=angle{LOA}+180^o=beta+180^o;$$
И получаем:
$$tg(beta)=tg(beta+180);$$
А теперь давайте отметим на рисунке угол (angle{TOA}=-beta). Минус появился потому, что угол (beta) посчитан по часовой стрелке. Продлим (TO) до пересечения с осью тангенса в точке (E). Так как картинка абсолютно симметрична относительно оси (x), то (EA=IA), значит координаты точек (I) и (E) на оси тангенса будут равны по модулю, но противоположны по знаку:
Симметричные свойства тангенса на единичной окружности
$$tg(angle{LOA})=-tg(angle{TOA});$$
$$tg(beta)=-tg(-beta);$$
Абсолютно аналогичные рассуждения можно провести и для котангенса. В качестве тренировки попробуйте это сделать сами:
$$ctg(beta)=ctg(beta+180);$$
$$ctg(beta)=-ctg(180-beta);$$
Выпишем еще раз все полученные формулы:
$$sin(alpha)=sin(180-alpha);$$
$$cos(alpha)=-cos(180-alpha);$$
$$cos(alpha)=cos(-alpha);$$
$$sin(-alpha)=-sin(alpha).$$
$$tg(beta)=tg(beta+180);$$
$$tg(beta)=-tg(-beta);$$
$$ctg(beta)=ctg(beta+180);$$
$$ctg(beta)=-ctg(180-beta);$$
В школе заставляют их учить, но, как видите, достаточно научиться пользоваться тригонометрической окружностью и они легко выводятся.
Краткие правила пользования тригонометрической окружностью
- Углы, отсчитываемые против часовой стрелки, положительны, по часовой – отрицательны;
- Каждой точке на окружности соответствует бесконечное количество углов с периодом (360^o) или (2pi);
- Координата по (x) любой точки на окружности – это значение косинуса угла, координата по (y) – синуса;
- Значения косинуса и синуса принадлежат промежутку ([-1;1]);
- Синус положительный в первой и второй четвертях, отрицательный – в третьей и четвертой;
- Косинус положительный в первой и четвертой, отрицательный – во второй и третьей;
- Чтобы найти тангенс угла, нужно нарисовать ось тангенса параллельно оси (y). Соединить точку на окружности, соответствующую углу, с центром окружности и продлить до пересечения с осью тангенса. Координата полученной точки на оси тангенса и будет значением тангенса угла;
- Чтобы найти котангенс угла, нужно нарисовать ось котангенса параллельно оси (x). Соединить точку на окружности, соответствующую углу, с центром окружности и продлить до пересечения с осью котангенса. Координата полученной точки на оси котангенса и будет значением котангенса угла;
- Тангенс и котангенс положительны в первой и третьей четвертях, отрицательны – во второй и четвертой;
- Тангенс и котангенс могут принимать значения из промежутка ((-infty;+infty)).
Урок с подробным разбором тригонометрических уравнений. Рассмотрим основные методы решения простейших уравнений из тригонометрии, метод замены переменной, однородные уравнения и уравнения с обратными тригонометрическими функциями
Как пользоваться формулами приведения? Правило лошади, единичная окружность и формулы суммы и разности для нахождения формул приведения.
Разбираем тригонометрию с нуля. Синус, косинус, тангенс и котангенс в прямоугольном треугольнике. Таблица стандартных углов и свойства тригонометрических функций.
Подробный разбор метода координат в стереометрии. Формулы расстояния и угла между скрещивающимися прямыми. Уравнение плоскости. Координаты вектора. Расстояние от точки до плоскости. Угол между плоскостями. Выбор системы координат.
Как решать уравнения со степенями. Разбираем основные методы и способы решения простейших показательных уравнений.
Урок по теме логарифмы и их свойства. Разбираемся, что такое логарифм и какие у него свойства. Научимся считать выражения, содержащие логарифмы. И рассмотри несколько возможных заданий №4 из ЕГЭ по профильной математике.
Цикл уроков про степени и логарифмы и их свойства. Учимся решать показательные и логарифмические уравнения и неравенства. Задания №9 и №15 ЕГЭ по профильной математике.
Индивидуальные занятия с репетитором для учеников 6-11 классов. Для каждого ученика я составляю индивидуальную программу обучения. Стараюсь заинтересовать ребенка предметом, чтобы он с удовольствием занимался математикой и физикой.


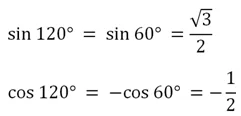
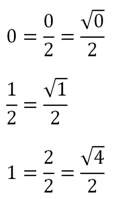

















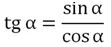












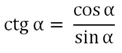

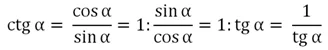
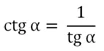
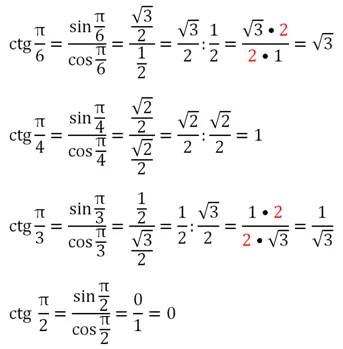
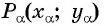
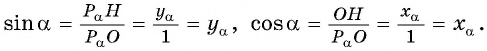
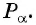
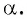
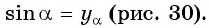
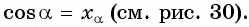
 единичной окружности.
единичной окружности.