Теорема синусов

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, синусы переносим в знаменатели:
bc sinα = ca sinβ
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.
- Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° – α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° – α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° – α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° – 60°) = sin60° = 3/√2;
- sin150° = sin(180° – 30°) = sin30° = 1/2;
- sin135° = sin(180° – 45°) = sin45° = 2/√2.
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° – α)
Так как sin(180° – α) = sinα, то sinγ = sin(180° – α) = sinα
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
-
Согласно теореме о сумме углов треугольника:
∠B = 180° – 45° – 15° = 120°
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
Геометрия. Урок 5. Окружность
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение окружности
- Отрезки в окружности
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности .

Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Часть окружности, заключенная между двумя точками, называется дугой окружности .
Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .
Теорема 4:
Равные хорды стягивают равные дуги.
Если A B = C D , то ∪ A B = ∪ C D
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360 ° .
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.
Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .
Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Длина дуги окружности , на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
Углы, связанные с окружностью
Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).

Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).

Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Теоремы о вписанных и центральных углах
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.
| Фигура | Рисунок | Теорема |
| Вписанный угол |  |
|
| Вписанный угол |  |
Вписанные углы, опирающиеся на одну и ту же дугу равны. |
| Вписанный угол |  |
Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды |
| Вписанный угол |  |
Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды |
| Вписанный угол |  |
Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр |
| Окружность, описанная около прямоугольного треугольника |  |
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу равны.

Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды

Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды

Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Теоремы об углах, образованных хордами, касательными и секущими
| Вписанный угол |
| Окружность, описанная около прямоугольного треугольника |
Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами
Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |
 |
|
| Угол, образованный секущими, которые пересекаются вне круга |  |
 |
|
| Угол, образованный касательной и хордой, проходящей через точку касания |  |
 |
|
| Угол, образованный касательной и секущей |  |
 |
|
| Угол, образованный двумя касательными к окружности |  |
 |
Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.


Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами




| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
|
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
|
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |
|
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).
Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).
В этом случае справедливы равенства
и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).
В этом случае справедливы равенства
что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8.
Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства
что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9.
Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства
что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10.
Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства
что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11.
Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства
что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12.
Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство [spoiler title=”источники:”] http://www.resolventa.ru/spr/planimetry/cangle.htm [/spoiler] |
Как найти синус вписанного угла?
-

1) Величина вписанного угла равна половине центрального угла опирающегося на ту же дугу.
2) Вписанные углы опирающиеся на одну и ту же дугу равны.
3) Вписанный угол опирающийся на диаметр – прямой.
синус угла это отношение противолежащего катета к гипотенузе, построишь треугольник прямо в окружности. Просто нужно видеть само задание из этого решать.
- Комментировать
- Жалоба
- Ссылка
Найди верный ответ на вопрос ✅ «Как найти синус вписанного угла? …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Синусом угла в прямоугольном треугольнике называют отношение противолежащего катета к гипотенузе.
Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.
Для простоты запоминания можно дать такое определение: синус угла — это отношение дальнего от рассматриваемого угла катета к гипотенузе.
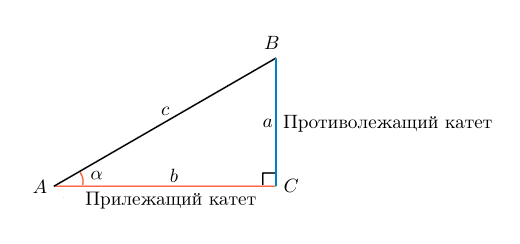
В случае с рисунком, описанным выше: sinα=acsinalpha=frac{a}{c}
В треугольнике, один из углов которого равен 90 градусам, известен катет при угле αalpha и равен он 3 см3text{ см}. Также дано произведение длин катетов и равно 12 см212text{ см}^2. Найдите синус угла αalpha.
Решение
Сначала нужно найти длину неизвестного нам катета. Для этого воспользуемся данным нам произведением. Обозначим неизвестный катет за xx. Тогда, по условию задачи:
3⋅x=123cdot x=12
x=123=4x=frac{12}{3}=4
a=x=4a=x=4
По теореме Пифагора найдем гипотенузу:
a2+b2=c2a^2+b^2=c^2
42+32=c24^2+3^2=c^2
25=c225=c^2
c=5c=5
sinα=ac=45=0.8sinalpha=frac{a}{c}=frac{4}{5}=0.8
Ответ
0.80.8
Вычислите синус 45 градусов.
Решение
Для этого воспользуемся тригонометрической таблицей углов. Находим, что:
sin45∘=π4=0.785sin 45^circ=frac{pi}{4}=0.785
Ответ
0.7850.785
Если в задаче известен косинус угла и нужно найти его синус, то наличие известных длин катетов и гипотенузы не обязательны. Достаточно просто воспользоваться основным тригонометрическим тождеством, которое имеет следующий вид:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
αalpha — любой угол.
Квадрат косинуса угла в треугольнике равен 0.8. Найдите синус данного угла.
Решение
Воспользуемся основным тригонометрическим тождеством:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
sin2α+0.8=1sin^2alpha+0.8=1
sin2α=0.2sin^2alpha=0.2
sinα=0.2sinalpha=sqrt{0.2}
sinα≈0.447sinalphaapprox0.447
Ответ
0.4470.447
Испытываете проблемы с вычислением синуса? Оформите задачу по математике на заказ у наших экспертов!
Тест по теме «Вычисление синуса»
Синус угла. Таблица синусов.
Синус угла через градусы, минуты и секунды
Синус угла через десятичную запись угла
Как найти угол зная синус этого угла
У синуса есть обратная тригонометрическая функция – arcsin(y)=x
sin(arcsin(y))=y
Пример sin(30°) = 1/2; arcsin(1/2) = 30°
Рассчитать арксинус
Определение синуса
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.

sin(α) = BC/AB
sin(-α) = -sin(α)
Периодичность синуса
Функция y = sin(x) периодична, с периодом 2π
sin(α ± 2π) = sin(α)
Пример sin(5π) = sin(4π + π) = sin(π)
Таблица синусов в радианах
sin(0°) = 0sin(π/12) = sin(15°) = 0.2588190451sin(π/6) = sin(30°) = 0.5sin(π/4) = sin(45°) = 0.7071067812sin(π/3) = sin(60°) = 0.8660254038sin(5π/12) = sin(75°) = 0.9659258263sin(π/2) = sin(90°) = 1sin(7π/12) = sin(105°) = 0.9659258263sin(2π/3) = sin(120°) = 0.8660254038sin(3π/4) = sin(135°) = 0.7071067812sin(5π/6) = sin(150°) = 0.5sin(11π/12) = sin(165°) = 0.2588190451sin(π) = sin(180°) = 0sin(13π/12) = sin(195°) = -0.2588190451sin(7π/6) = sin(210°) = -0.5sin(5π/4) = sin(225°) = -0.7071067812sin(4π/3) = sin(240°) = -0.8660254038sin(17π/12) = sin(255°) = -0.9659258263sin(3π/2) = sin(270°) = -1sin(19π/12) = sin(285°) = -0.9659258263sin(5π/3) = sin(300°) = -0.8660254038sin(7π/4) = sin(315°) = -0.7071067812sin(11π/6) = sin(330°) = -0.5sin(23π/12) = sin(345°) = -0.2588190451
Таблица Брадиса синусы
| sin(0) = 0 | sin(120) = 0.8660254038 | sin(240) = -0.8660254038 |
| sin(1) = 0.01745240644 | sin(121) = 0.8571673007 | sin(241) = -0.8746197071 |
| sin(2) = 0.0348994967 | sin(122) = 0.8480480962 | sin(242) = -0.8829475929 |
| sin(3) = 0.05233595624 | sin(123) = 0.8386705679 | sin(243) = -0.8910065242 |
| sin(4) = 0.06975647374 | sin(124) = 0.8290375726 | sin(244) = -0.8987940463 |
| sin(5) = 0.08715574275 | sin(125) = 0.8191520443 | sin(245) = -0.906307787 |
| sin(6) = 0.1045284633 | sin(126) = 0.8090169944 | sin(246) = -0.9135454576 |
| sin(7) = 0.1218693434 | sin(127) = 0.79863551 | sin(247) = -0.9205048535 |
| sin(8) = 0.139173101 | sin(128) = 0.7880107536 | sin(248) = -0.9271838546 |
| sin(9) = 0.156434465 | sin(129) = 0.7771459615 | sin(249) = -0.9335804265 |
| sin(10) = 0.1736481777 | sin(130) = 0.7660444431 | sin(250) = -0.9396926208 |
| sin(11) = 0.1908089954 | sin(131) = 0.7547095802 | sin(251) = -0.9455185756 |
| sin(12) = 0.2079116908 | sin(132) = 0.7431448255 | sin(252) = -0.9510565163 |
| sin(13) = 0.2249510543 | sin(133) = 0.7313537016 | sin(253) = -0.956304756 |
| sin(14) = 0.2419218956 | sin(134) = 0.7193398003 | sin(254) = -0.9612616959 |
| sin(15) = 0.2588190451 | sin(135) = 0.7071067812 | sin(255) = -0.9659258263 |
| sin(16) = 0.2756373558 | sin(136) = 0.6946583705 | sin(256) = -0.9702957263 |
| sin(17) = 0.2923717047 | sin(137) = 0.6819983601 | sin(257) = -0.9743700648 |
| sin(18) = 0.3090169944 | sin(138) = 0.6691306064 | sin(258) = -0.9781476007 |
| sin(19) = 0.3255681545 | sin(139) = 0.656059029 | sin(259) = -0.9816271834 |
| sin(20) = 0.3420201433 | sin(140) = 0.6427876097 | sin(260) = -0.984807753 |
| sin(21) = 0.3583679495 | sin(141) = 0.629320391 | sin(261) = -0.9876883406 |
| sin(22) = 0.3746065934 | sin(142) = 0.6156614753 | sin(262) = -0.9902680687 |
| sin(23) = 0.3907311285 | sin(143) = 0.6018150232 | sin(263) = -0.9925461516 |
| sin(24) = 0.4067366431 | sin(144) = 0.5877852523 | sin(264) = -0.9945218954 |
| sin(25) = 0.4226182617 | sin(145) = 0.5735764364 | sin(265) = -0.9961946981 |
| sin(26) = 0.4383711468 | sin(146) = 0.5591929035 | sin(266) = -0.9975640503 |
| sin(27) = 0.4539904997 | sin(147) = 0.544639035 | sin(267) = -0.9986295348 |
| sin(28) = 0.4694715628 | sin(148) = 0.5299192642 | sin(268) = -0.999390827 |
| sin(29) = 0.4848096202 | sin(149) = 0.5150380749 | sin(269) = -0.9998476952 |
| sin(30) = 0.5 | sin(150) = 0.5 | sin(270) = -1 |
| sin(31) = 0.5150380749 | sin(151) = 0.4848096202 | sin(271) = -0.9998476952 |
| sin(32) = 0.5299192642 | sin(152) = 0.4694715628 | sin(272) = -0.999390827 |
| sin(33) = 0.544639035 | sin(153) = 0.4539904997 | sin(273) = -0.9986295348 |
| sin(34) = 0.5591929035 | sin(154) = 0.4383711468 | sin(274) = -0.9975640503 |
| sin(35) = 0.5735764364 | sin(155) = 0.4226182617 | sin(275) = -0.9961946981 |
| sin(36) = 0.5877852523 | sin(156) = 0.4067366431 | sin(276) = -0.9945218954 |
| sin(37) = 0.6018150232 | sin(157) = 0.3907311285 | sin(277) = -0.9925461516 |
| sin(38) = 0.6156614753 | sin(158) = 0.3746065934 | sin(278) = -0.9902680687 |
| sin(39) = 0.629320391 | sin(159) = 0.3583679495 | sin(279) = -0.9876883406 |
| sin(40) = 0.6427876097 | sin(160) = 0.3420201433 | sin(280) = -0.984807753 |
| sin(41) = 0.656059029 | sin(161) = 0.3255681545 | sin(281) = -0.9816271834 |
| sin(42) = 0.6691306064 | sin(162) = 0.3090169944 | sin(282) = -0.9781476007 |
| sin(43) = 0.6819983601 | sin(163) = 0.2923717047 | sin(283) = -0.9743700648 |
| sin(44) = 0.6946583705 | sin(164) = 0.2756373558 | sin(284) = -0.9702957263 |
| sin(45) = 0.7071067812 | sin(165) = 0.2588190451 | sin(285) = -0.9659258263 |
| sin(46) = 0.7193398003 | sin(166) = 0.2419218956 | sin(286) = -0.9612616959 |
| sin(47) = 0.7313537016 | sin(167) = 0.2249510543 | sin(287) = -0.956304756 |
| sin(48) = 0.7431448255 | sin(168) = 0.2079116908 | sin(288) = -0.9510565163 |
| sin(49) = 0.7547095802 | sin(169) = 0.1908089954 | sin(289) = -0.9455185756 |
| sin(50) = 0.7660444431 | sin(170) = 0.1736481777 | sin(290) = -0.9396926208 |
| sin(51) = 0.7771459615 | sin(171) = 0.156434465 | sin(291) = -0.9335804265 |
| sin(52) = 0.7880107536 | sin(172) = 0.139173101 | sin(292) = -0.9271838546 |
| sin(53) = 0.79863551 | sin(173) = 0.1218693434 | sin(293) = -0.9205048535 |
| sin(54) = 0.8090169944 | sin(174) = 0.1045284633 | sin(294) = -0.9135454576 |
| sin(55) = 0.8191520443 | sin(175) = 0.08715574275 | sin(295) = -0.906307787 |
| sin(56) = 0.8290375726 | sin(176) = 0.06975647374 | sin(296) = -0.8987940463 |
| sin(57) = 0.8386705679 | sin(177) = 0.05233595624 | sin(297) = -0.8910065242 |
| sin(58) = 0.8480480962 | sin(178) = 0.0348994967 | sin(298) = -0.8829475929 |
| sin(59) = 0.8571673007 | sin(179) = 0.01745240644 | sin(299) = -0.8746197071 |
| sin(60) = 0.8660254038 | sin(180) = 0 | sin(300) = -0.8660254038 |
| sin(61) = 0.8746197071 | sin(181) = -0.01745240644 | sin(301) = -0.8571673007 |
| sin(62) = 0.8829475929 | sin(182) = -0.0348994967 | sin(302) = -0.8480480962 |
| sin(63) = 0.8910065242 | sin(183) = -0.05233595624 | sin(303) = -0.8386705679 |
| sin(64) = 0.8987940463 | sin(184) = -0.06975647374 | sin(304) = -0.8290375726 |
| sin(65) = 0.906307787 | sin(185) = -0.08715574275 | sin(305) = -0.8191520443 |
| sin(66) = 0.9135454576 | sin(186) = -0.1045284633 | sin(306) = -0.8090169944 |
| sin(67) = 0.9205048535 | sin(187) = -0.1218693434 | sin(307) = -0.79863551 |
| sin(68) = 0.9271838546 | sin(188) = -0.139173101 | sin(308) = -0.7880107536 |
| sin(69) = 0.9335804265 | sin(189) = -0.156434465 | sin(309) = -0.7771459615 |
| sin(70) = 0.9396926208 | sin(190) = -0.1736481777 | sin(310) = -0.7660444431 |
| sin(71) = 0.9455185756 | sin(191) = -0.1908089954 | sin(311) = -0.7547095802 |
| sin(72) = 0.9510565163 | sin(192) = -0.2079116908 | sin(312) = -0.7431448255 |
| sin(73) = 0.956304756 | sin(193) = -0.2249510543 | sin(313) = -0.7313537016 |
| sin(74) = 0.9612616959 | sin(194) = -0.2419218956 | sin(314) = -0.7193398003 |
| sin(75) = 0.9659258263 | sin(195) = -0.2588190451 | sin(315) = -0.7071067812 |
| sin(76) = 0.9702957263 | sin(196) = -0.2756373558 | sin(316) = -0.6946583705 |
| sin(77) = 0.9743700648 | sin(197) = -0.2923717047 | sin(317) = -0.6819983601 |
| sin(78) = 0.9781476007 | sin(198) = -0.3090169944 | sin(318) = -0.6691306064 |
| sin(79) = 0.9816271834 | sin(199) = -0.3255681545 | sin(319) = -0.656059029 |
| sin(80) = 0.984807753 | sin(200) = -0.3420201433 | sin(320) = -0.6427876097 |
| sin(81) = 0.9876883406 | sin(201) = -0.3583679495 | sin(321) = -0.629320391 |
| sin(82) = 0.9902680687 | sin(202) = -0.3746065934 | sin(322) = -0.6156614753 |
| sin(83) = 0.9925461516 | sin(203) = -0.3907311285 | sin(323) = -0.6018150232 |
| sin(84) = 0.9945218954 | sin(204) = -0.4067366431 | sin(324) = -0.5877852523 |
| sin(85) = 0.9961946981 | sin(205) = -0.4226182617 | sin(325) = -0.5735764364 |
| sin(86) = 0.9975640503 | sin(206) = -0.4383711468 | sin(326) = -0.5591929035 |
| sin(87) = 0.9986295348 | sin(207) = -0.4539904997 | sin(327) = -0.544639035 |
| sin(88) = 0.999390827 | sin(208) = -0.4694715628 | sin(328) = -0.5299192642 |
| sin(89) = 0.9998476952 | sin(209) = -0.4848096202 | sin(329) = -0.5150380749 |
| sin(90) = 1 | sin(210) = -0.5 | sin(330) = -0.5 |
| sin(91) = 0.9998476952 | sin(211) = -0.5150380749 | sin(331) = -0.4848096202 |
| sin(92) = 0.999390827 | sin(212) = -0.5299192642 | sin(332) = -0.4694715628 |
| sin(93) = 0.9986295348 | sin(213) = -0.544639035 | sin(333) = -0.4539904997 |
| sin(94) = 0.9975640503 | sin(214) = -0.5591929035 | sin(334) = -0.4383711468 |
| sin(95) = 0.9961946981 | sin(215) = -0.5735764364 | sin(335) = -0.4226182617 |
| sin(96) = 0.9945218954 | sin(216) = -0.5877852523 | sin(336) = -0.4067366431 |
| sin(97) = 0.9925461516 | sin(217) = -0.6018150232 | sin(337) = -0.3907311285 |
| sin(98) = 0.9902680687 | sin(218) = -0.6156614753 | sin(338) = -0.3746065934 |
| sin(99) = 0.9876883406 | sin(219) = -0.629320391 | sin(339) = -0.3583679495 |
| sin(100) = 0.984807753 | sin(220) = -0.6427876097 | sin(340) = -0.3420201433 |
| sin(101) = 0.9816271834 | sin(221) = -0.656059029 | sin(341) = -0.3255681545 |
| sin(102) = 0.9781476007 | sin(222) = -0.6691306064 | sin(342) = -0.3090169944 |
| sin(103) = 0.9743700648 | sin(223) = -0.6819983601 | sin(343) = -0.2923717047 |
| sin(104) = 0.9702957263 | sin(224) = -0.6946583705 | sin(344) = -0.2756373558 |
| sin(105) = 0.9659258263 | sin(225) = -0.7071067812 | sin(345) = -0.2588190451 |
| sin(106) = 0.9612616959 | sin(226) = -0.7193398003 | sin(346) = -0.2419218956 |
| sin(107) = 0.956304756 | sin(227) = -0.7313537016 | sin(347) = -0.2249510543 |
| sin(108) = 0.9510565163 | sin(228) = -0.7431448255 | sin(348) = -0.2079116908 |
| sin(109) = 0.9455185756 | sin(229) = -0.7547095802 | sin(349) = -0.1908089954 |
| sin(110) = 0.9396926208 | sin(230) = -0.7660444431 | sin(350) = -0.1736481777 |
| sin(111) = 0.9335804265 | sin(231) = -0.7771459615 | sin(351) = -0.156434465 |
| sin(112) = 0.9271838546 | sin(232) = -0.7880107536 | sin(352) = -0.139173101 |
| sin(113) = 0.9205048535 | sin(233) = -0.79863551 | sin(353) = -0.1218693434 |
| sin(114) = 0.9135454576 | sin(234) = -0.8090169944 | sin(354) = -0.1045284633 |
| sin(115) = 0.906307787 | sin(235) = -0.8191520443 | sin(355) = -0.08715574275 |
| sin(116) = 0.8987940463 | sin(236) = -0.8290375726 | sin(356) = -0.06975647374 |
| sin(117) = 0.8910065242 | sin(237) = -0.8386705679 | sin(357) = -0.05233595624 |
| sin(118) = 0.8829475929 | sin(238) = -0.8480480962 | sin(358) = -0.0348994967 |
| sin(119) = 0.8746197071 | sin(239) = -0.8571673007 | sin(359) = -0.01745240644 |
Похожие калькуляторы
что такое? Как найти синус, косинус и тангенс?
Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание – она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза – это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров.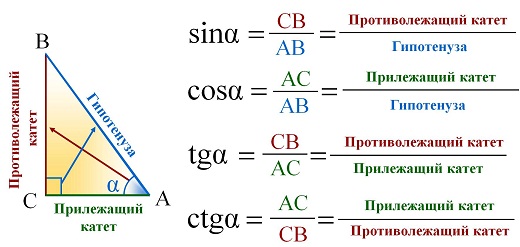 Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза – это по умолчанию самая длинная сторона прямоугольного треугольника. Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях.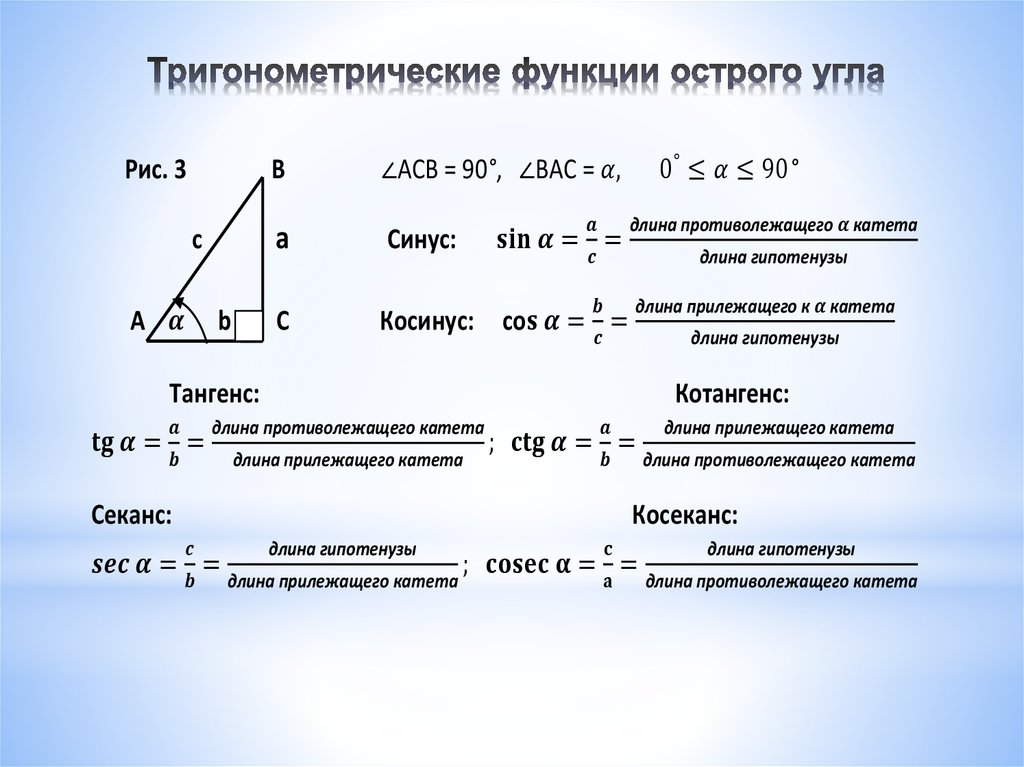 Этот ответ однозначно неверен.
Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии не обойтись без формул – как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.
Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Формулы двойного угла и сложения аргументов
Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.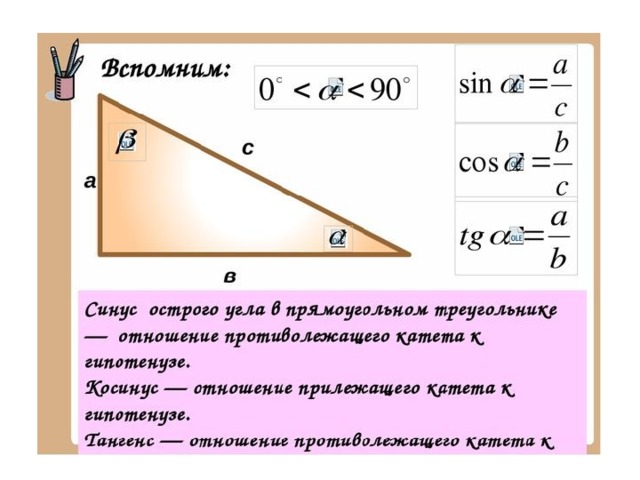
Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих – в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.
Теоремы
Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники.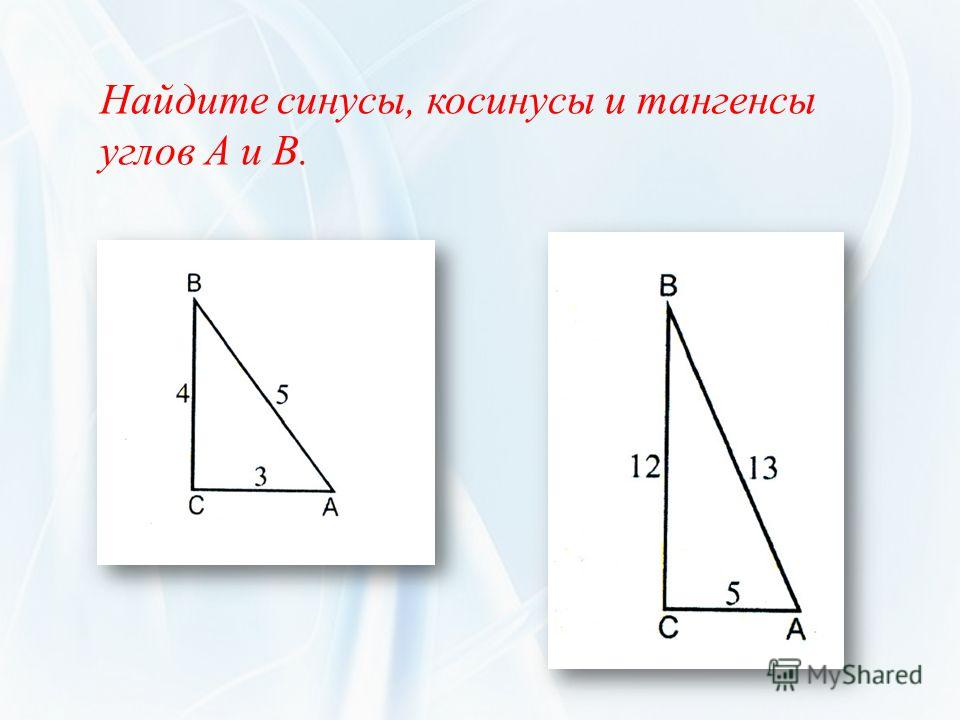 Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата – можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу.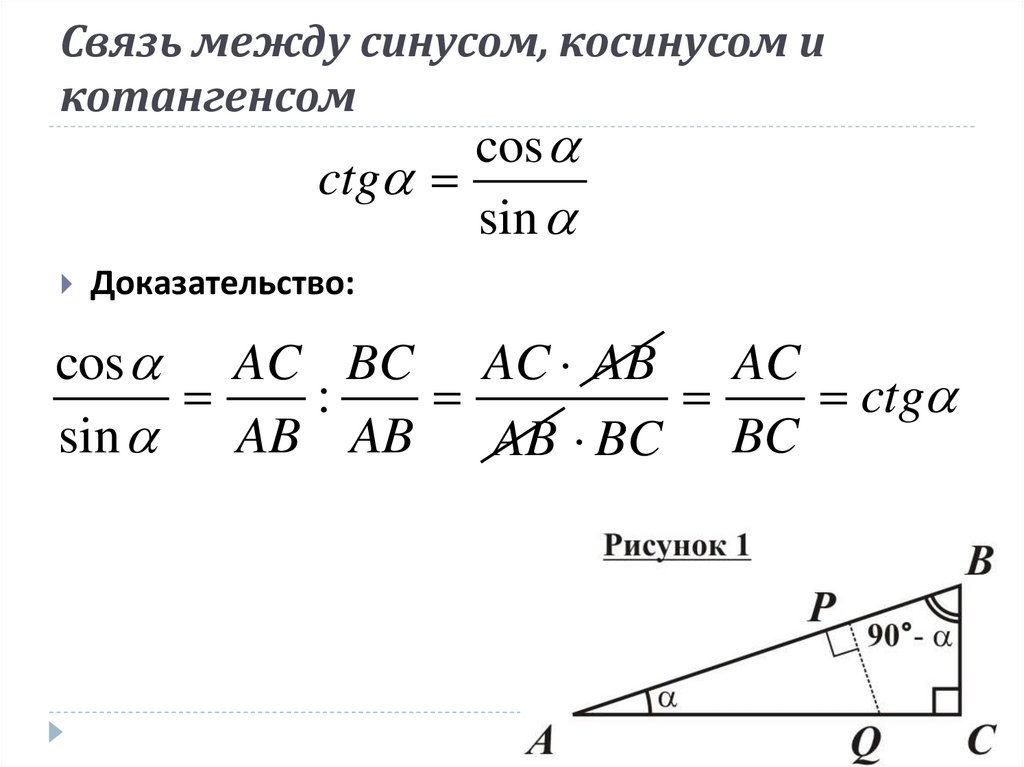 То же касается округлений «некрасивых» чисел.
То же касается округлений «некрасивых» чисел.
Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.
В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
В заключение
Итак, вы знаете, что такое синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение – это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
И здесь вам поможет обычная школьная математика.
Как найти синус зная угол. Нахождение значений синуса, косинуса, тангенса и котангенса
Синус
острого угла α прямоугольного треугольника – это отношение противолежащего
катета к гипотенузе.
Обозначается так: sin α.
Косинус
острого угла α прямоугольного треугольника – это отношение прилежащего
катета к гипотенузе.
Обозначается так: cos α.
Тангенс
острого угла α – это отношение противолежащего катета к прилежащему катету.
Обозначается так: tg α.
Котангенс
острого угла α – это отношение прилежащего катета к противолежащему.
Обозначается так: ctg α.
Синус, косинус, тангенс и котангенс угла зависят только от величины угла.
Правила:
Основные тригонометрические тождества в прямоугольном треугольнике:
(α
– острый угол, противолежащий катету b
и прилежащий к катету a
. Сторона с
– гипотенуза. β
β
– второй острый угол).
|
b |
sin 2 α + cos 2 α = 1 |
|
|
a |
1 |
|
|
b |
1 |
|
|
a |
1 1 |
|
|
sin α |
При возрастании острого угла
sin α и
tg α возрастают, а
cos α убывает.
Для любого острого угла α:
sin (90° – α) = cos α
cos (90° – α) = sin α
Пример-пояснение
:
Пусть в прямоугольном треугольнике АВС
АВ = 6,
ВС = 3,
угол А = 30º.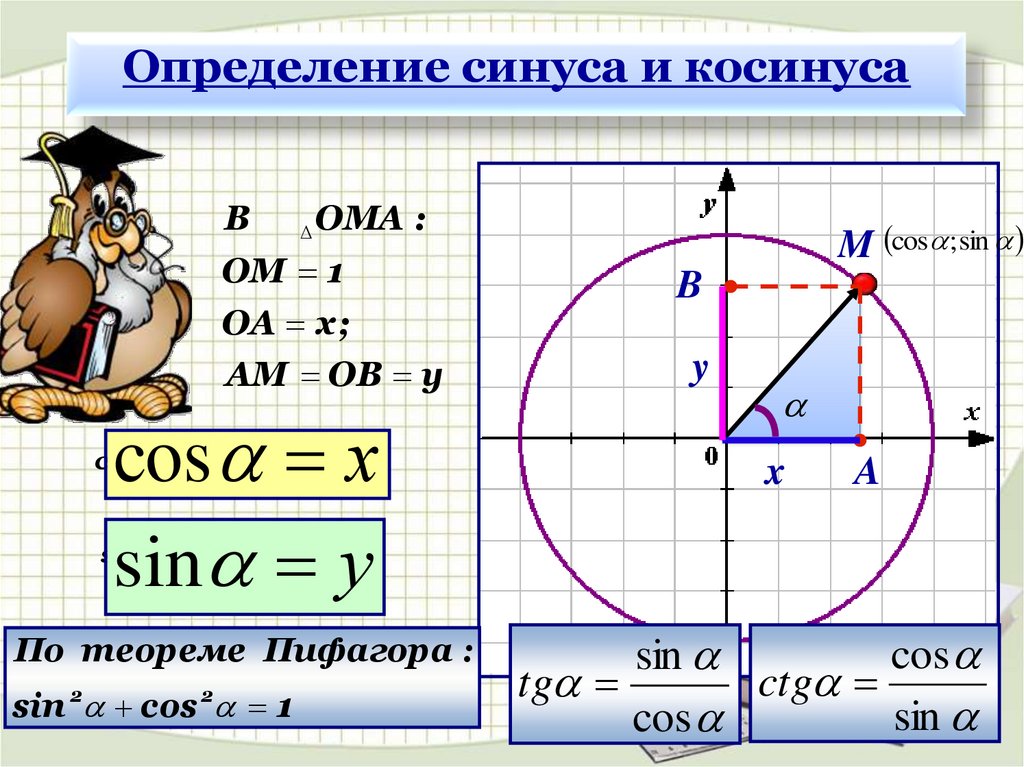
Выясним синус угла А и косинус угла В.
Решение
.
1) Сначала находим величину угла В. Тут все просто: так как в прямоугольном треугольнике сумма острых углов равна 90º, то угол В = 60º:
В = 90º – 30º = 60º.
2) Вычислим sin A. Мы знаем, что синус равен отношению противолежащего катета к гипотенузе. Для угла А противолежащим катетом является сторона ВС. Итак:
BC 3 1
sin A = — = — = —
AB 6 2
3) Теперь вычислим cos B. Мы знаем, что косинус равен отношению прилежащего катета к гипотенузе. Для угла В прилежащим катетом является все та же сторона ВС. Это значит, что нам снова надо разделить ВС на АВ – то есть совершить те же действия, что и при вычислении синуса угла А:
BC 3 1
cos B = — = — = —
AB 6 2
В итоге получается:
sin A = cos B = 1/2.
sin 30º = cos 60º = 1/2.
Из этого следует, что в прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла – и наоборот. Именно это и означают наши две формулы:
sin (90° – α) = cos α
cos (90° – α) = sin α
Убедимся в этом еще раз:
1) Пусть α = 60º. Подставив значение α в формулу синуса, получим:
Подставив значение α в формулу синуса, получим:
sin (90º – 60º) = cos 60º.
sin 30º = cos 60º.
2) Пусть α = 30º. Подставив значение α в формулу косинуса, получим:
cos (90° – 30º) = sin 30º.
cos 60° = sin 30º.
(Подробнее о тригонометрии — см.раздел Алгебра)
Изначально синус и косинус возникли из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было замечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается всегда одинаковым.
Именно так и были введены понятия синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы могут применяться не только в прямоугольных треугольниках. Чтобы найти значение тупого или острого угла, стороны любого треугольника, достаточно применить теорему косинусов и синусов.
Теорема косинусов довольно проста: «Квадрат стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними».
Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему часто расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Производные
Производная — математический инструмент, показывающий, как быстро меняется функция относительно изменения ее аргумента. Производные используются , геометрии, и , ряде технических дисциплин.
При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса. Производной синуса является косинус, а косинуса — синус, но со знаком «минус».
Применение в математике
Особенно часто синусы и косинусы используются при решении прямоугольных треугольников и задач, связанных с ними.
Удобство синусов и косинусов нашло свое отражение и в технике. Углы и стороны было просто оценивать по теоремам косинусов и синусов, разбивая сложные фигуры и объекты на «простые» треугольники. Инженеры и , часто имеющие дело с расчетами соотношения сторон и градусных мер, тратили немало времени и усилий для вычисления косинусов и синусов не табличных углов.
Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов разных углов. В советское время некоторые преподаватели заставляли своих подопечных страницы таблиц Брадиса наизусть.
Радиан — угловая величина дуги, по длине равной радиусу или 57,295779513° градусов.
Градус (в геометрии) — 1/360-я часть окружности или 1/90-я часть прямого угла.
π = 3.141592653589793238462… (приблизительное значение числа Пи).
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам.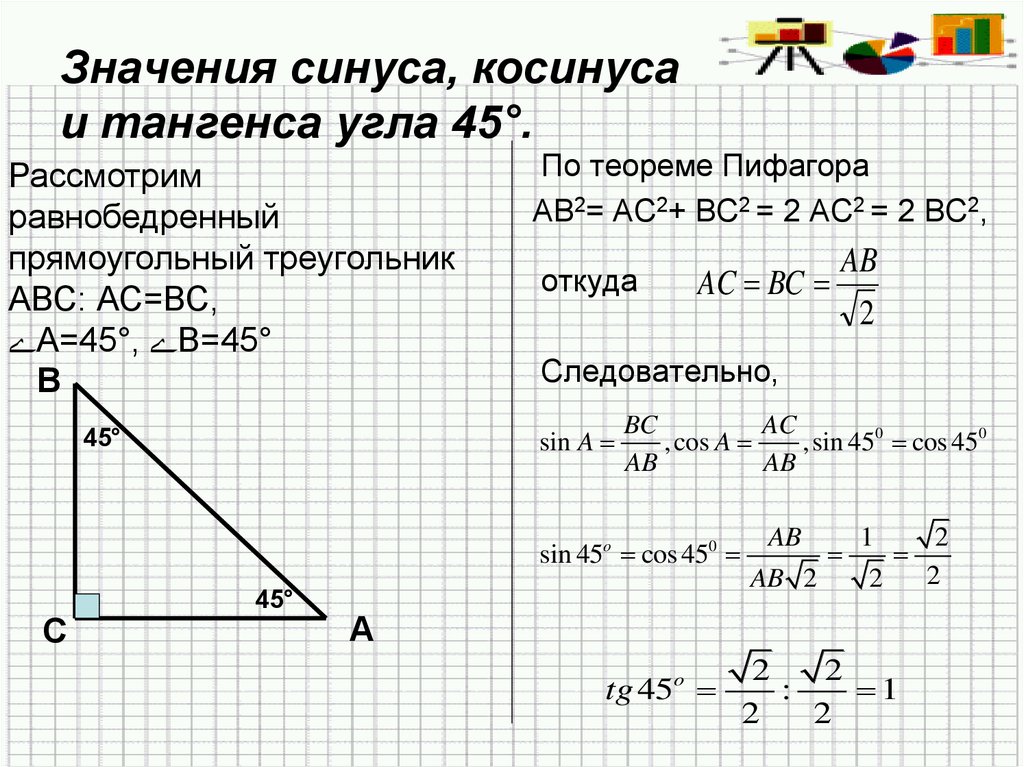 Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.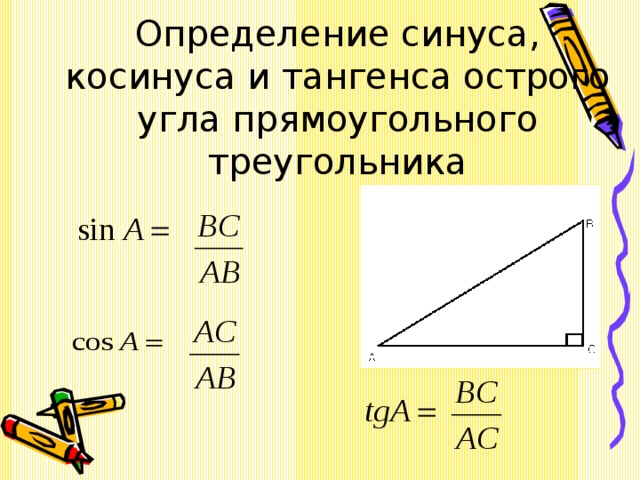
В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла.
Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто.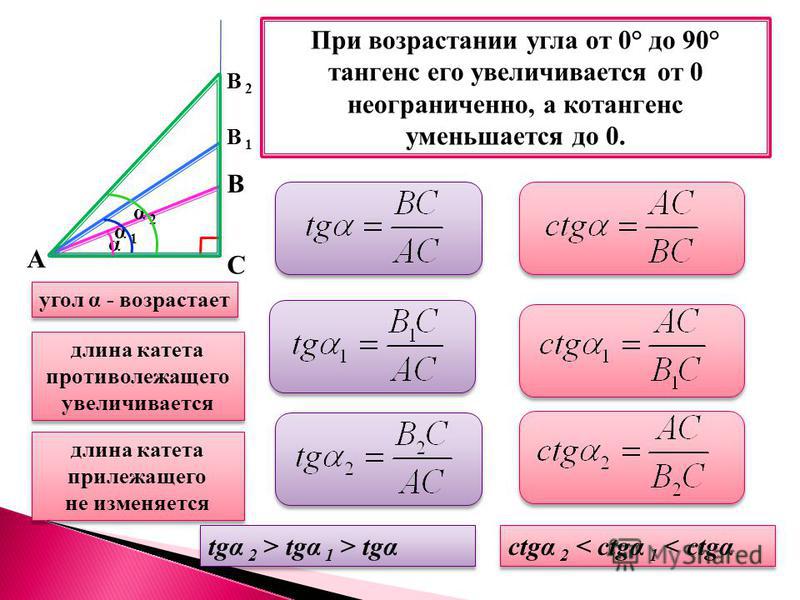
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
- Y = tg x.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.

- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Исправить
Отношение противолежащего катета к гипотенузе называют синусом острого угла
прямоугольного треугольника.
sin alpha = frac{a}{c}
Косинус острого угла прямоугольного треугольника
Отношение близлежащего катета к гипотенузе называют косинусом острого угла
прямоугольного треугольника.
cos alpha = frac{b}{c}
Тангенс острого угла прямоугольного треугольника
Отношение противолежащего катета к близлежащему катету называют тангенсом острого угла
прямоугольного треугольника.
tg alpha = frac{a}{b}
Котангенс острого угла прямоугольного треугольника
Отношение близлежащего катета к противолежащему катету называют котангенсом острого угла
прямоугольного треугольника.
ctg alpha = frac{b}{a}
Синус произвольного угла
Ордината точки на единичной окружности , которой соответствует угол alpha
называют синусом произвольного угла
поворота alpha
.
sin alpha=y
Косинус произвольного угла
Абсцисса точки на единичной окружности, которой соответствует угол alpha
называют косинусом произвольного угла
поворота alpha
.
cos alpha=x
Тангенс произвольного угла
Отношение синуса произвольного угла поворота alpha
к его косинусу называют тангенсом произвольного угла
поворота alpha
.
tg alpha = y_{A}
tg alpha = frac{sin alpha}{cos alpha}
Котангенс произвольного угла
Отношение косинуса произвольного угла поворота alpha
к его синусу называют котангенсом произвольного угла
поворота alpha
.
ctg alpha =x_{A}
ctg alpha = frac{cos alpha}{sin alpha}
Пример нахождения произвольного угла
Если alpha
— некоторый угол AOM
, где M
— точка единичной окружности, то
sin alpha=y_{M}
, cos alpha=x_{M}
, tg alpha=frac{y_{M}}{x_{M}}
, ctg alpha=frac{x_{M}}{y_{M}}
.
Например, если angle AOM = -frac{pi}{4}
, то: ордината точки M
равна -frac{sqrt{2}}{2}
, абсцисса
равна frac{sqrt{2}}{2}
и потому
sin left (-frac{pi}{4} right)=-frac{sqrt{2}}{2}
;
cos left (frac{pi}{4} right)=frac{sqrt{2}}{2}
;
tg
;
ctg
left (-frac{pi}{4} right)=-1
.
Таблица значений синусов косинусов тангенсов котангенсов
Значения основных часто встречающихся углов приведены в таблице:
| 0^{circ} (0) | 30^{circ}left(frac{pi}{6}right) | 45^{circ}left(frac{pi}{4}right) | 60^{circ}left(frac{pi}{3}right) | 90^{circ}left(frac{pi}{2}right) | 180^{circ}left(piright) | 270^{circ}left(frac{3pi}{2}right) | 360^{circ}left(2piright) | |
| sinalpha | 0 | frac12 | frac{sqrt 2}{2} | frac{sqrt 3}{2} | 1 | 0 | −1 | 0 |
| cosalpha | 1 | frac{sqrt 3}{2} | frac{sqrt 2}{2} | frac12 | 0 | −1 | 0 | 1 |
| tg alpha | 0 | frac{sqrt 3}{3} | 1 | sqrt3 | — | 0 | — | 0 |
| ctg alpha | — | sqrt3 | 1 | frac{sqrt 3}{3} | 0 | — | 0 | — |
Тригонометрия является разделом математики, изучающим тригонометрические функции, а также их использование на практике. К таким функциям относятся синус
К таким функциям относятся синус
, косинус, тангенс и котангенс.
Синус – это тригонометрическая функция
, отношение величины противолежащего катета к величине гипотенузы.
Синус в тригонометрии.
Как уже сказано выше, синус имеет непосредственное отношение к тригонометрии и тригонометрическим функциям. Его функция определяется тем, чтобы
- помогать высчитать угол, при условии известности величин сторон треугольника;
- помогать высчитать величины стороны треугольника, при условии известности угла.
Необходимо помнить, что величина синуса будет всегда одинакова для любых размеров треугольника, поскольку синус – это не измерение, а соотношение.
Следовательно, для того чтобы не высчитывать эту постоянную величину при каждом решении той или иной задачи, были созданы специальные тригонометрические таблицы. В них величины синусов, косинусов, тангенсов и котангенсов уже просчитаны и закреплены. Обычно эти таблицы приводятся на форзаце учебников по алгебре и геометрии.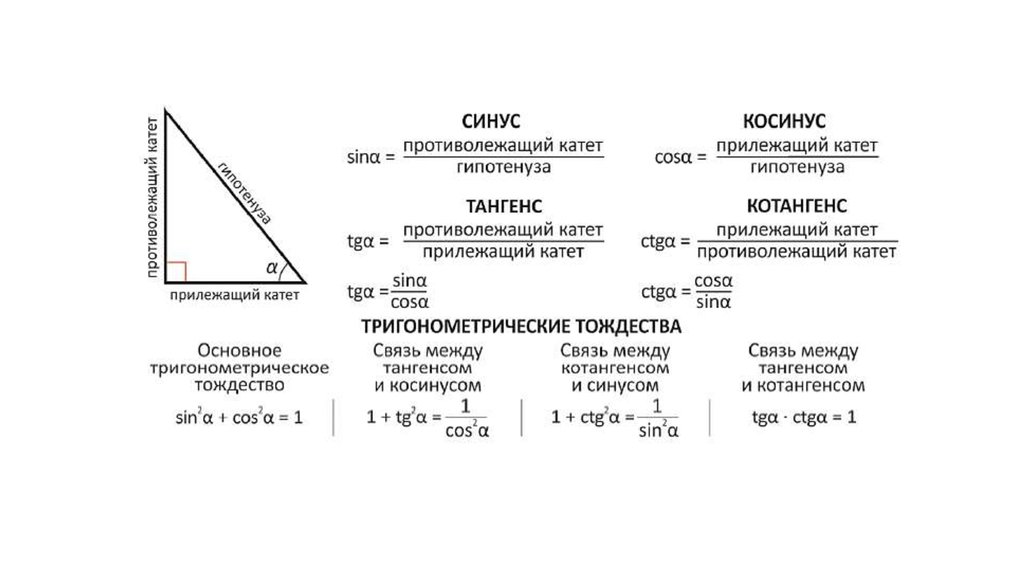 Также их можно найти в Интернете.
Также их можно найти в Интернете.
Синус в геометрии.
Геометрия требует наглядности, поэтому, чтобы понять на практике, что такое синус угла
, нужно нарисовать треугольник с прямым углом.
Допустим, что стороны, образующие прямой угол, названы а, в,
противоположный им угол – х
.
Обычно в заданиях указана длина сторон. Допустим, а=3, в=4
. В таком случае соотношение сторон будет выглядеть как ¾. При этом если удлинить стороны треугольника, прилегающие к острому углу х
, то увеличатся и стороны а
и в
, и гипотенуза – третья сторона прямоугольного треугольника, лежащая не под прямым углом к основанию. Теперь стороны треугольника можно назвать иначе, допустим: m, n, k.
При этом видоизменении сработал закон тригонометрии: длины сторон треугольника изменились, а их отношение – нет.
Тот факт, что при изменении длины сторон треугольника во сколько угодно раз и при сохранении величины угла х, соотношение между его сторонами всё равно останется неизменным, заметили ещё древние ученые. В нашем случае длина сторон могла измениться так: а/в = ¾
В нашем случае длина сторон могла измениться так: а/в = ¾
, при удлинении стороны а
до 6 см, а в
– до 8 см получаем: m/n = 6/8 = 3/4
.
Соотношения сторон в прямоугольном треугольнике в связи с этим получили названия:
- синус угла х – это отношение противолежащего катета к гипотенузе: sinx = а/с;
- косинус угла х – это отношение прилежащего катета к гипотенузе: сosx = в/с;
- тангенс угла х – это отношение противолежащего катета к прилежащему: tgx = а/в;
- котангенс угла х – это отношение прилежащего катета к противолежащему: ctgx = в/а.
Как найти тангенс если известен котангенс
Как найти тангенс и котангенс через косинус?
Итак, читаем внимательно условие вопроса, и вспоминаем, чему нас учили в школе, у нас есть косинус угла, и этого окажется вполне достаточным для того, чтобы мы выполнили задание автора вопроса и нашли тангенс и котангенс данного угла. Вспоминаем, что мы можем найти, зная косинус, конечно-же, мы сразу можем найти синус, это очень легко, и в этом нам поможет вот это волшебное тождество и то, что из него следует, — формула для нахождения синуса:
Теперь, зная чему равен синус угла, через косинус, проще простого решать дальше по известным формулам для нахождения тангенса и котангенса, просто подставляя в них эти формулы для синуса, которые я разместила выше:
Для того, чтобы найти тангенс и котангенс через косинус, достаточно вспомнить тригонометрические формулы:
tgα = sinα / cosα.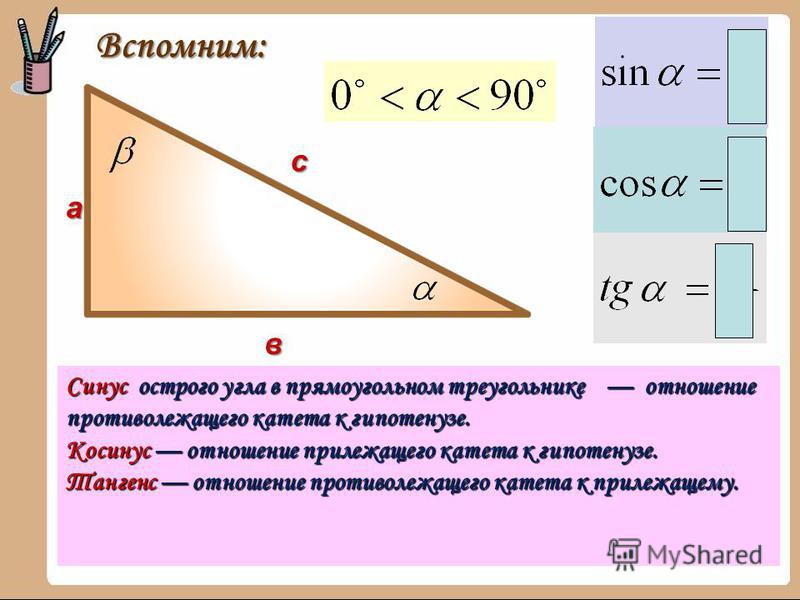
ctgα = cosα / sinα.
Так как косинус известен, то синус можно найти из основного тригонометрического тождества:
sinα = √(1 — cos²α), если угол α находится в 1 и 2 четверти.
sinα = — √(1 — cos²α), если угол α находится в 3 и 4 четверти.
tgα = ± √(1 — cos²α) / cosα.
ctgα = ± cosα / √(1 — cos²α).
Так как произведение тангенса и котангенса = 1, то ctgα также можно найти из формулы: ctgα = 1 / tgα.
Пример
Косинус угла α равен 0,94, при этом α находится в 1 четверти (0 < α < 90). Нужно найти тангенс и котангенс.
tgα = √(1 — cos²α) / cosα.
В первой четверти синус и косинус больше 0, поэтому тангенс и котангенс также будут положительными.
tgα ≈ 0,34 / 0,94 ≈ 0,36.
Соответственно ctgα ≈ 1 / 0,36 ≈ 2,78.
tg а = Sin a/Cos a. Чтобы выразить тангенс через косинус осталось выразить синус через косинус. Для этого воспользуемся основной тригонометрической формулой (Sin a)^2 +/(Cos a)^2 = 1.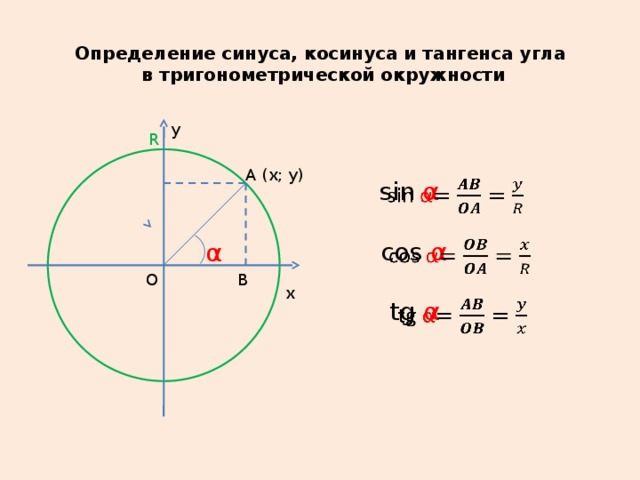 2 =1/0,25 — 1 = 3, tga =корень квадратный из 3, (со знаком + или — в зависимости в какой четверти находится а).
2 =1/0,25 — 1 = 3, tga =корень квадратный из 3, (со знаком + или — в зависимости в какой четверти находится а).
ctga = 1/корень из 3.
Синус, косинус, тангенс и котангенс угла — это тригонометрические функции. Можно сказать, что все они связаны между собой. Часто для нахождения одной из этих функций при условии, что известна другая, приходится вспоминать основные тригонометрические равенства или тождества, а также определение самих этих понятий. Зная все перечисленное выше, несложно выразить одну функцию через другую.
Тангенс угла — это отношение синуса этого угла к его косинусу.
Котангенс угла — это отношение косинуса угла к его синусу.
Нам известен косинус, из основного тригонометрического тождества ( sin²α + cos²α = 1 ) выразим синус:
sinα = √(1 — cos²α) для α из 1 и 2 четвертей,
sinα = -√(1 — cos²α) для α из 3 и 4 четвертей.
Подставив формулу для синуса угла в формулу тангенса и котангенса, получим формулы для вычисления значений этих функций:
tgα = ± √(1 — cos²α) / cosα,
ctgα = ± cosα / √(1 — cos²α).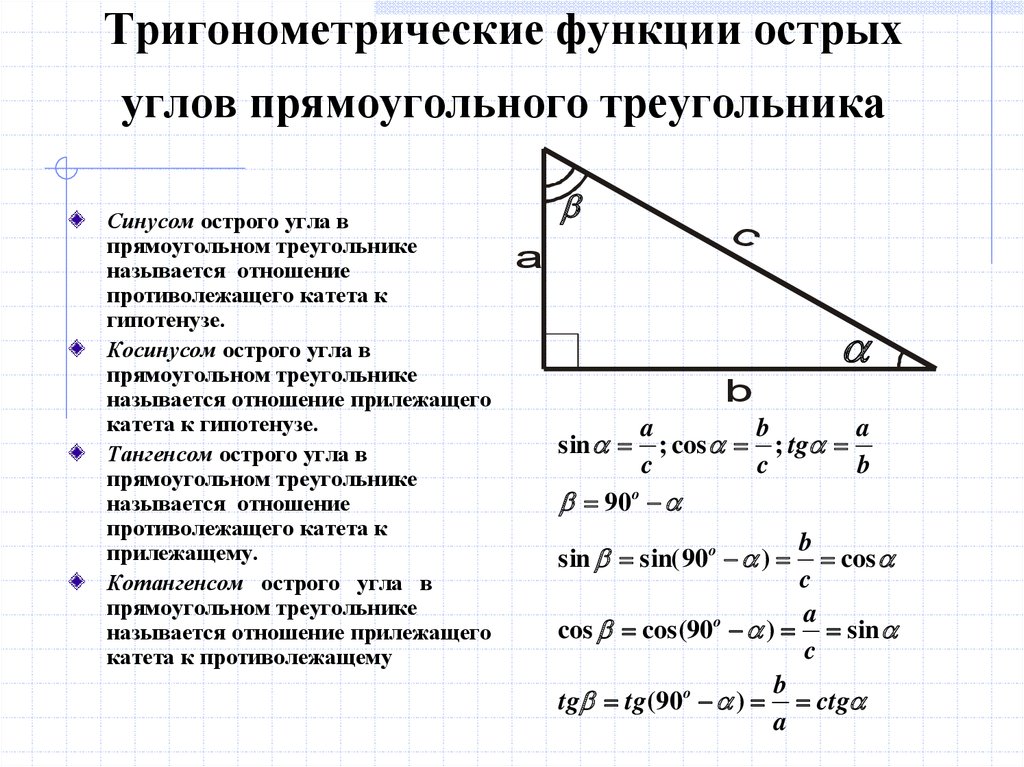 23x≠1)
23x≠1)
(tg, xcdot ctg, y≠1)
Все формулы связи тригонометрических функций учить не надо, потому что они достаточно легко получаются друг из друга несложными преобразованиями (подробности в этих видео). Кроме того, при частом использовании они постепенно запоминаются сами.
Примеры применения формул связи
Зачем нужны формулы связи? Они позволяют найти все тригонометрические функции угла, если известна лишь одна из них, а также дают возможность упрощать выражения, доказывать тождества, решать тригонометрические уравнения , заменяя одну функцию другой и так далее.
Пример. Найдите (5sin,α), если (cos,α=frac>) и (α∈(frac;2π)).
Решение. Нам известен косинус, найти надо синус. А что связывает синус и косинус? Основное тригонометрическое тождество:
Подставим вместо косинуса его значение:
Внимание! Последняя строчка – место, где теряется огромное количество баллов на ЕГЭ! Это одна из самых популярных ошибок – забыть отрицательный корень. 2 β).
2 β).
Решение.
Самое очевидное, что можно сделать – это представить котангенс как отношение косинуса к синусу.
Как найти тангенс через тангенс
Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.
Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.
Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.
Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса, тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.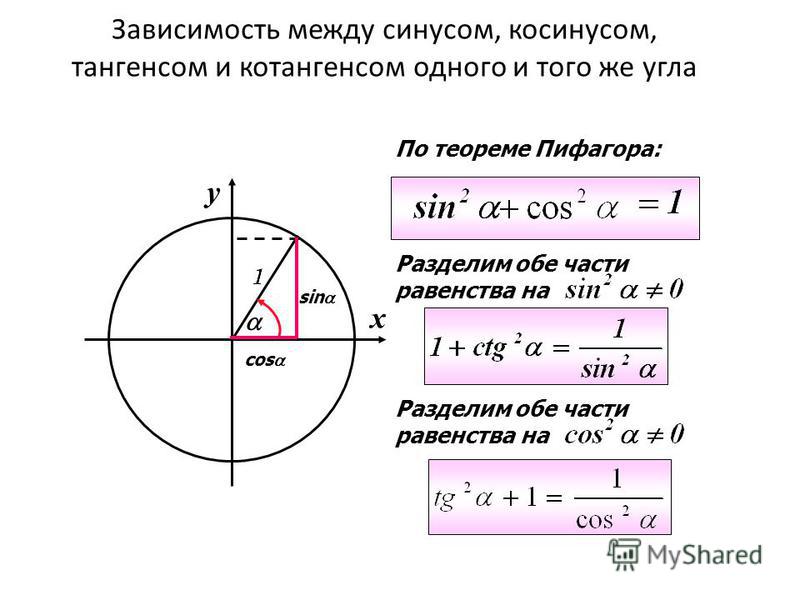
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тангенс — это отношение.
Итак, есть два определения:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Тангенс – это отношение синуса к косинусу.
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Как найти тангенс угла (формулы)
Первое свойство тангенса вытекает из его определения как отношения катетов.
Сумма углов прямоугольного треугольника равна 90º. Поэтому
Так как тангенс – это отношение катетов, то
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.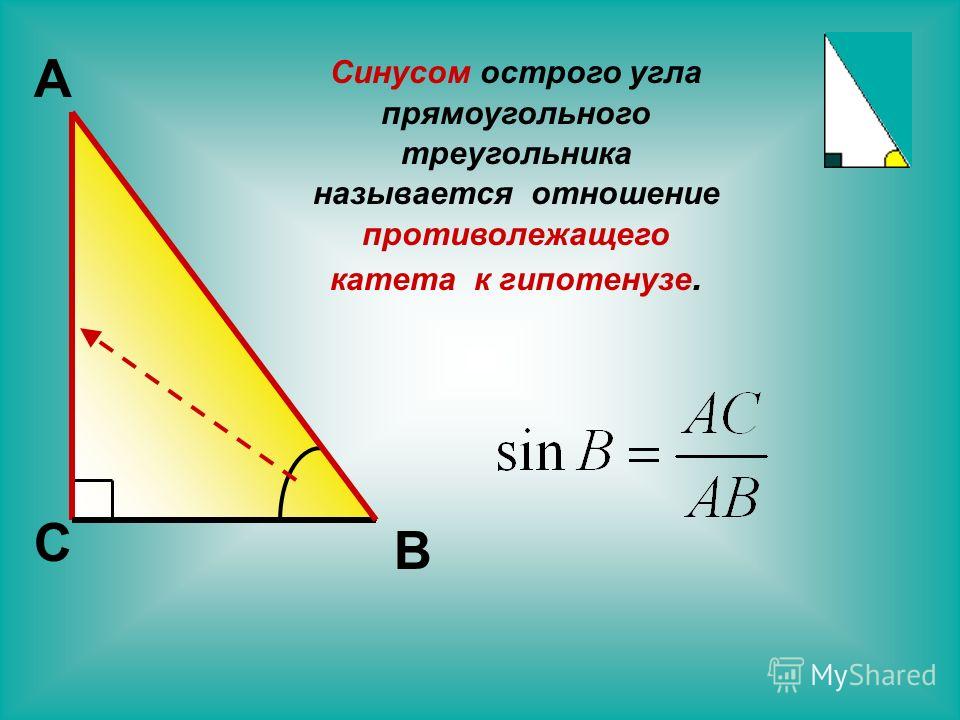
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
Как найти тангенс по клеточкам
Учитывая первое определение, можно определить, как найти тангенс угла по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.
Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:
Из формулы тангенсов, записывающей кратко второе определение
и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.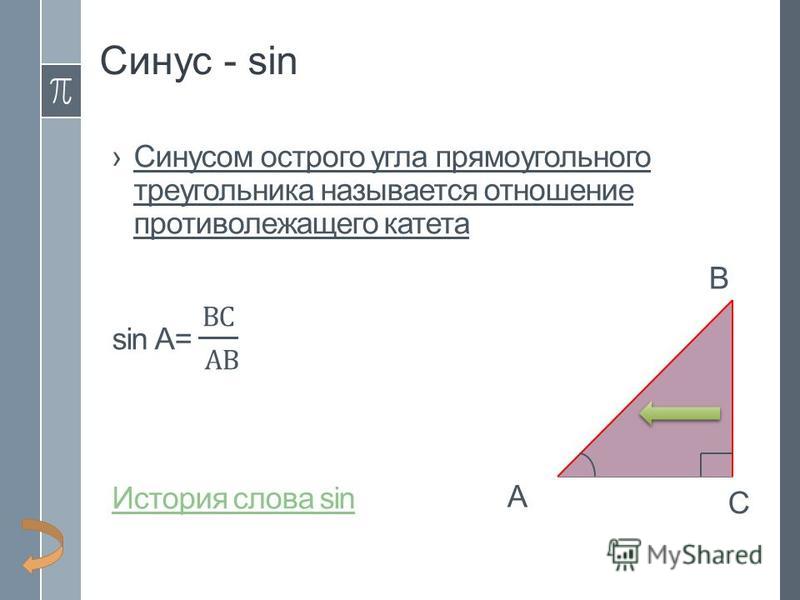
Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится зависимость тангенса и косинуса:
Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:
Тангенс, как отношение катетов в прямоугольном треугольнике, представляет собой функцию которая выглядит как дуга окружности внутри данного треугольника с центром в вершине угла и прилежащим катетом в качестве радиуса.
Значение тангенса показывает не только раскрытие угла α , но и насколько один катет больше другого. При тангенсе угла α , равном 1 , катеты равны друг другу и треугольник считается равнобедренным. Значения всех тангенсов и соответствующих им углов можно найти в таблице, приведенной ниже.
Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) – отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) – отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) – отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) – отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса – вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от – ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).
Определение дается через координаты точки A 1 ( x , y ).
Синус (sin) угла поворота
Синус угла поворота α – это ордината точки A 1 ( x , y ). sin α = y
Косинус угла поворота α – это абсцисса точки A 1 ( x , y ). cos α = х
Тангенс угла поворота α – это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α – это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , – 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат.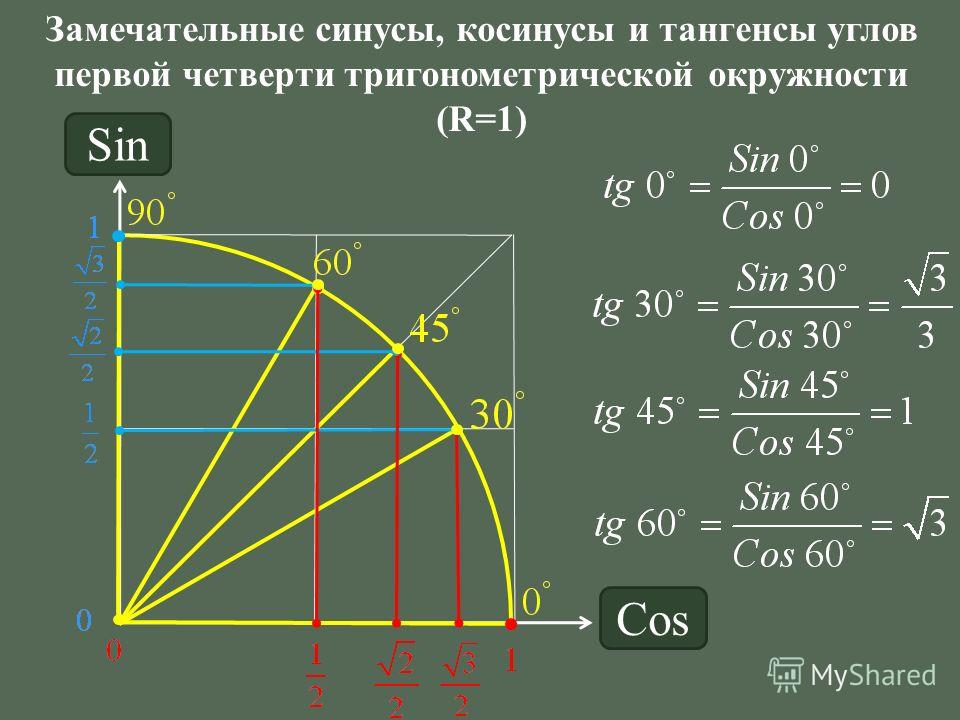 Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности – точка A c координатами ( 1 , 0 ).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t.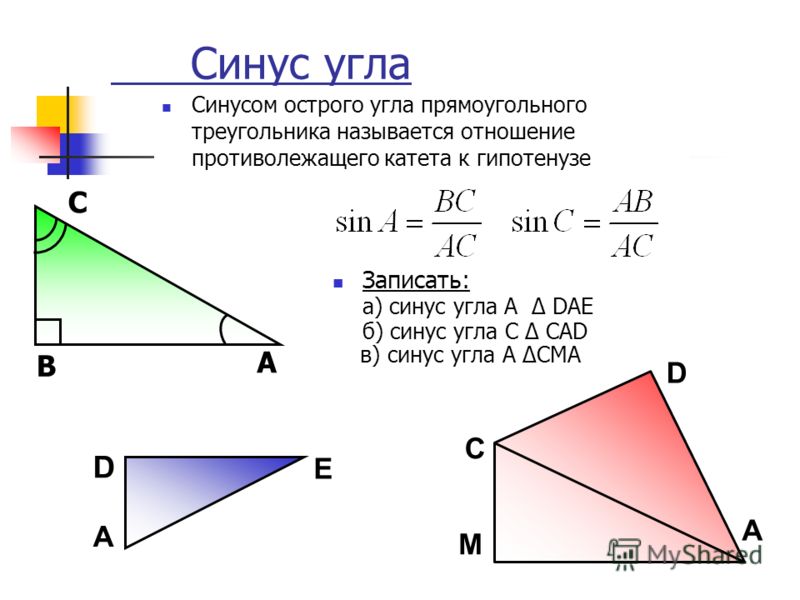 t g t = y x = sin t cos t
t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α , cos α , t g α , c t g α – это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t.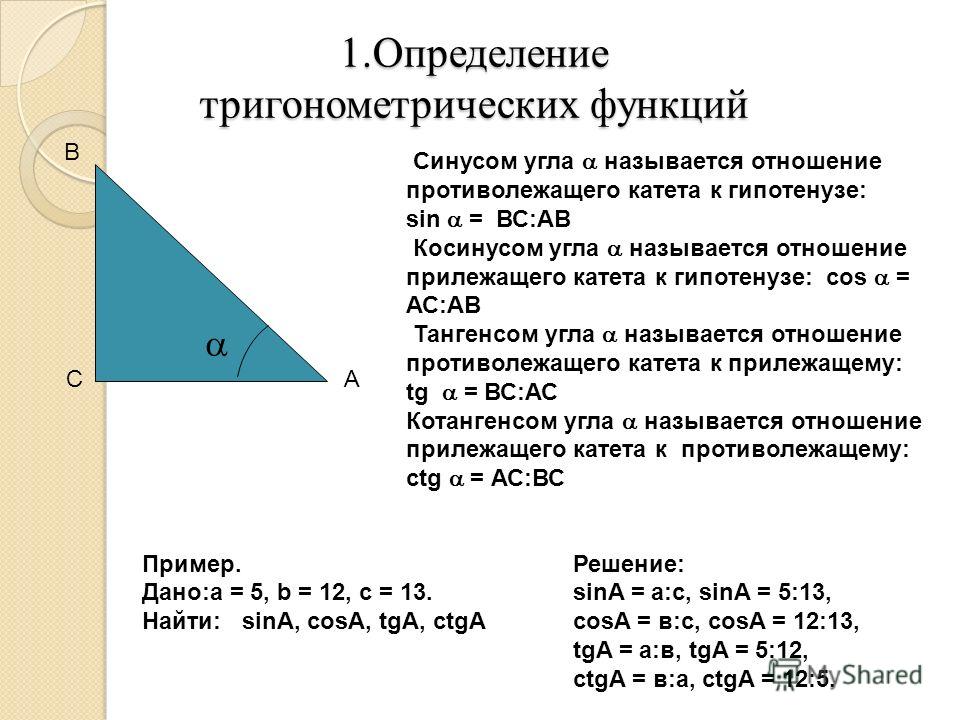 Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс – основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
§ 1. Синус, косинус, тангенс и котангенс любого угла и числа
Тригонометрия
Слово «тригонометрия»
переводится на русский язык как измерение
треугольника. И действительно, в начале
это была наука о треугольниках.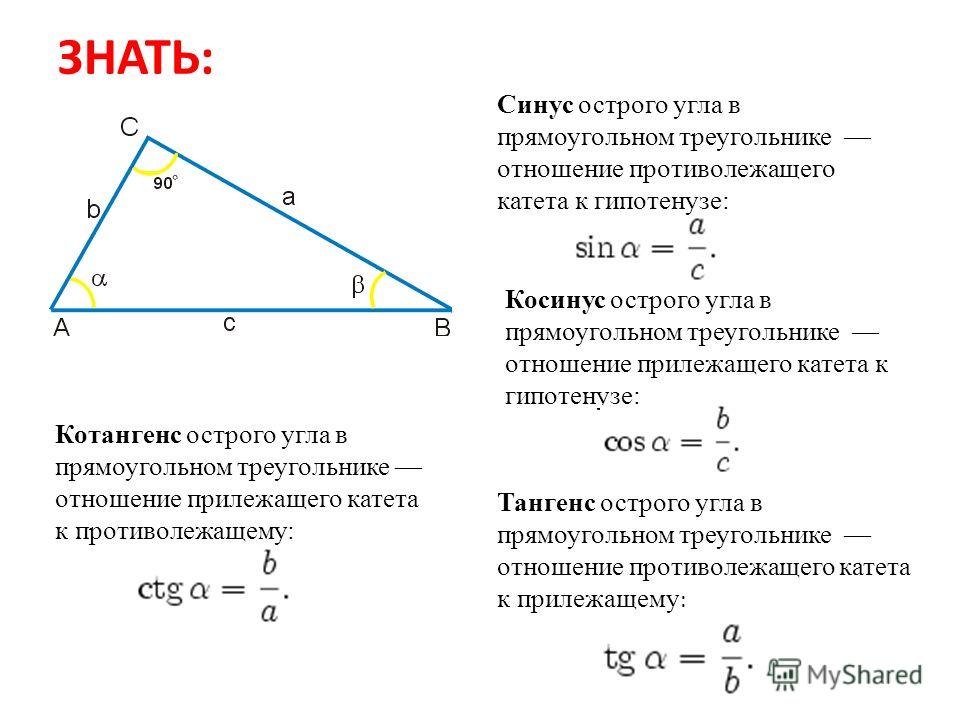 Да и
Да и
ваше знакомство с тригонометрией
началось с определения тригонометрических
функций (синуса, косинуса, тангенса и
котангенса) острого угла прямоугольного
треугольника. Вспомним его.
Определение 1.
Чтобы найти синус, косинус, тангенс или
котангенс острого угла, нужно построить
прямоугольный треугольник, имеющий
данный острый угол, и найти отношение
соответствующих сторон. Именно: синус
равен отношению противолежащего катета
к гипотенузе; косинус равен отношению
прилежащего катета к гипотенузе; тангенс
равен отношению противолежащего катета
к прилежащему катету; котангенс равен
отношению прилежащего катета к
противолежащему катету.
Задание 1. Начертите
АВС
с прямым углом С. Выразите в виде отношения
сторон этого треугольника
все
тригонометрические функции углов A
и В.
Обратите внимание на их попарное
равенство.
Задание 2. Докажите,
что значение той или иной тригонометрической
функции острого угла не зависит от
выбора треугольника, а зависит только
от величины угла.
Задание 3. Вспомните
доказательство шести основных
тригонометрических тождеств, основанное
на только что приведенных определениях.
Задание 4. Пусть
— острый угол. Выразите: а) tg
через ctg;
б) cos
через sin;
в) sin
через ctg
;
г) tg
через cos
.
Задание 5. Вспомните
доказательство четырех формул приведения,
основанное на только что приведенных
определениях.
Задание 6. Используя
таблицы в конце этого пособия, найдите
значения следующих выражений: sin
80o,
cos
56o,
tg
72o,
ctg
46o.
Задание 7. Докажите,
Докажите,
что тригонометрические функции острого
угла
числа положительные, и при этом синус
и косинус меньше 1.
Задание 8.
Докажите, что тангенс и котангенс острого
угла могут быть любыми положительными
числами.
Докажите,
что синус и косинус острого угла могут
быть любыми положительными числами,
меньшими 1.
Задание 9. У
египетского треугольника АВС гипотенуза
АВ равна 5, катет ВС равен 4, катет АС
равен 3. Вычислите sin
A,
cos
B,
ctg
A,
tg
B.
Сделайте чертеж.
Задание 10.
Начертите равнобедренный прямоугольный
треугольник. Обозначьте его катет через
1. Вычислите длину его гипотенузы. Как
с помощью этого чертежа можно определить
величины тригонометрических функций
угла в 450?
Задание 11.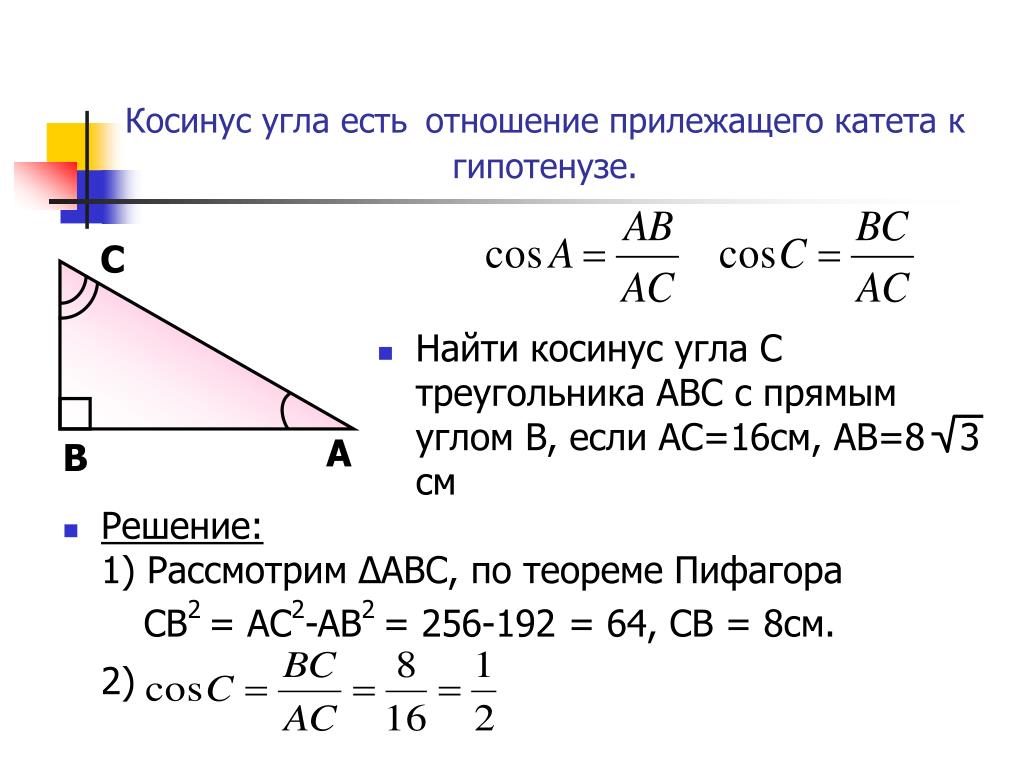
Начертите прямоугольный треугольник
с острыми углами в 30 и 60 градусов.
Обозначьте его меньший катет через 1.
Вычислите длину его гипотенузы и длину
его большего катета. Как с помощью этого
чертежа можно определить величины
тригонометрических функций углов в 300
и в 600?
* * *
Следующим шагом
в вашем ознакомлении с тригонометрией
будет определение синуса, косинуса,
тангенса и котангенса любого
угла.
Под углом теперь
понимается уже не пара лучей, исходящих
из одной точки, а мера поворота луча
относительно некоторого начального
положения. Поворот против часовой
стрелки считается положительными, а
поворот по часовой стрелке
отрицательным. Такой угол может содержать
любое число градусов, например, 1000о
или
2000о.
Определение 2.
Построим в прямоугольной системе
координат окружность с центром в начале
координат и с единичным радиусом –
координатную окружность.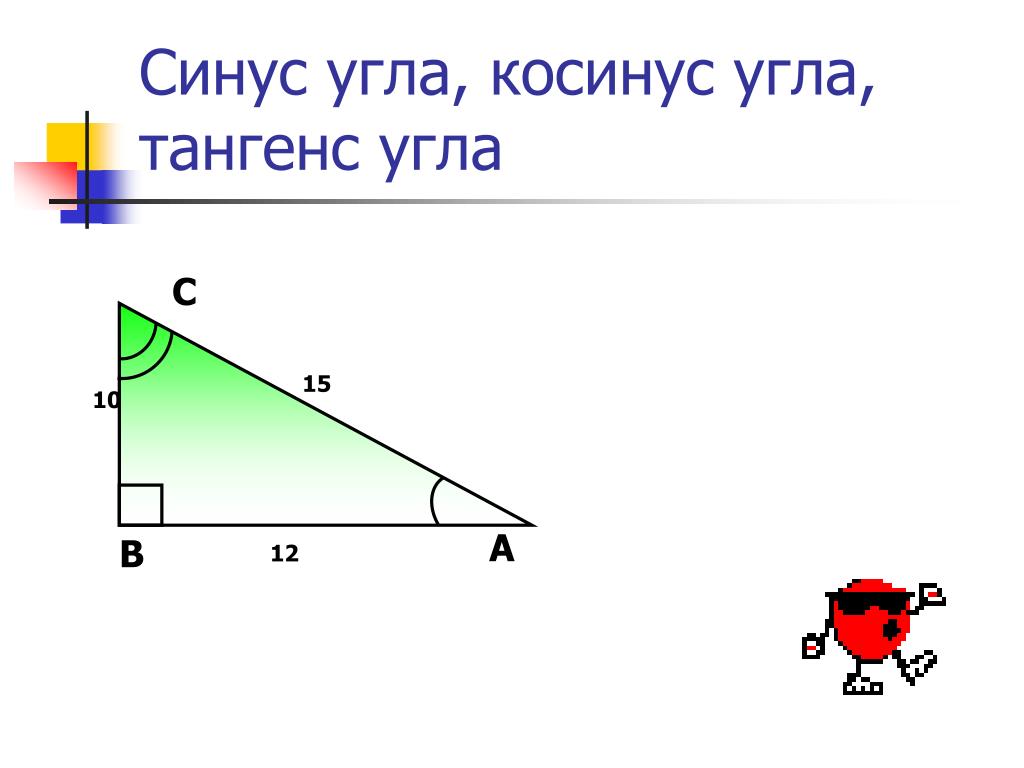 Отложим от
Отложим от
положительного направления оси абсцисс
угол (если он положительный
в направлении против часовой стрелки,
а если отрицательный
в направлении по часовой стрелке). Точку
пересечения второй стороны угла с
окружностью обозначим буквой А.
Синусом отложенного угла называется
ордината точки А,
косинусом
абсцисса точки А,
тангенсом отложенного угла называется
отношение его синуса к его косинусу,
котангенсом
отношение косинуса к синусу.
Задание 12. Выполнив
указанные построения, найдите значения
синуса, косинуса, тангенса и котангенса
угла 2250.
Задание 13.
Докажите, что если углы отличаются друг
от друга на целое число полных оборотов,
то их синусы равны между собой, косинусы
равны между собой, тангенсы равны между
собой, котангенсы равны между собой:
sin(
+360оn)
= sin ,
cos (
+ 360on)
= cos ,
tg(
+ 360on)
= tg,
ctg(
+ 360on)
= ctg,
где
n
любое
целое
число:
n
Z.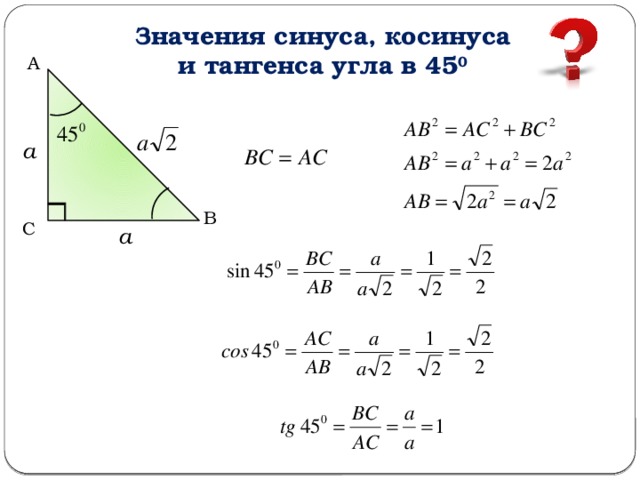
Угол может измеряться
не только в градусной мере. Большую
ценность имеет радианная мера угла:
1 радиан — это
мера центрального угла, соответствующего
дуге, имеющей длину, равную радиусу
окружности;
1 радиан
57о;
1o
0,017 радиана.
Обозначение
радианной меры указывать не принято.
Запись sin 30 читается «синус угла в 30
радиан» (не путать с sin 30о!).
Задание 14.
Вспомните, что такое число ,
и переведите в радианную меру: 360о,
90о,
45о,
60о.
Задание 15.
Переведите в градусную меру: 2,
,
,
1,25.
Задание 16. Сделайте
себе справочную табличку по тригонометрии,
пользуясь черным, синим и красным
цветами. Начертите на клетчатой бумаге
прямоугольную систему координат: ось
абсцисс красного цвета, ось ординат
синего цвета,
взяв единичный отрезок в 5 см (10 клеток).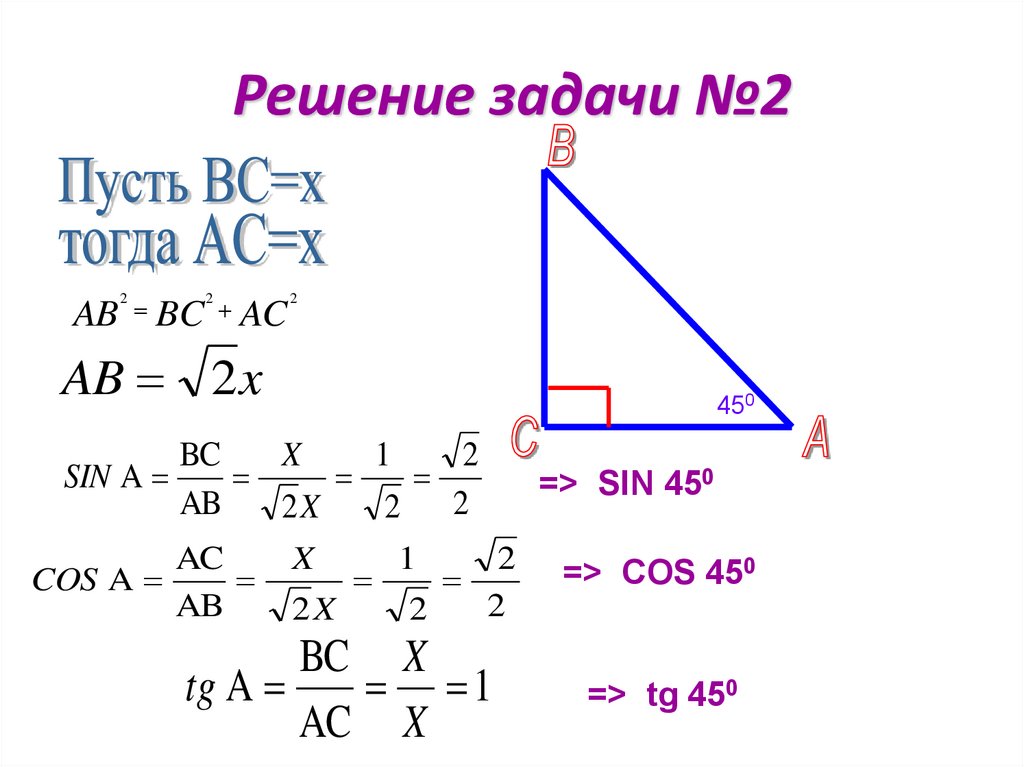
Начертите черным цветом окружность с
центром в начале координат и радиусом
5 см. Ось абсцисс обозначьте не х, а cos x,
ось ординат
не у, а sin x, соответственно красным и
синим цветом. Все обозначения вдоль
осей и вдоль окружности делайте такими
же цветами.
Вдоль
окружности внутри нее отметьте градусные
меры углов: 0, 30, 45, 60, 90, 120, 135, 150, 180, 210, 225,
240, 270, 300, 315, 330, 360 градусов. Вне окружности
рядом с этими метками тоже черным цветом
надпишите радианные меры тех же углов.
Проецируя отмеченные на окружности
точки на оси координат, надпишите
соответствующим цветом значения синусов
и косинусов: 0,
,
,
,
1, ,
,
,
1. На оси абсцисс вашего чертежа будут
отмечаться косинусы, а на оси ординат
синусы углов.
Задание 17.
Потренируйтесь в работе со сделанной
таблицей: 1) переведите в радианную меру
315о
; 2) переведите в градусную меру
;
3) найдите sin 240о
; 4) найдите cos
;
5) найдите tg 150о;
6) найдите ctg
;
7) определите знак косинуса в IV четверти;
8) определите знак котангенса в III
четверти.
Задание 18.
Определите, какие значения могут
принимать sin x и cos x.
Задание 19.
Определите, для каких углов не существует
тангенс или котангенс.
Задание 20. Найдите
корни уравнения 1) sin x = 1; 2) cos x =
1.
Задание 21.
Проведите через точку (1;0) вертикальную
прямую и постройте на ней координатную
прямую с началом в точке (1;0), и положительным
направлением вверх. Докажите, что эта
прямая является линией тангенсов, найдя
правило, по которому можно строить на
ней тангенс любого угла из ()
числовой окружности.
Задание 22. Найдите
с помощью линии тангенсов tg
0,25;
tg
;
tg
1,25;
tg1,75.
Задание 23.
Проведите через точку (0;1) горизонтальную
прямую и постройте на ней координатную
прямую с началом в точке (0;1) и положительным
направлением вправо.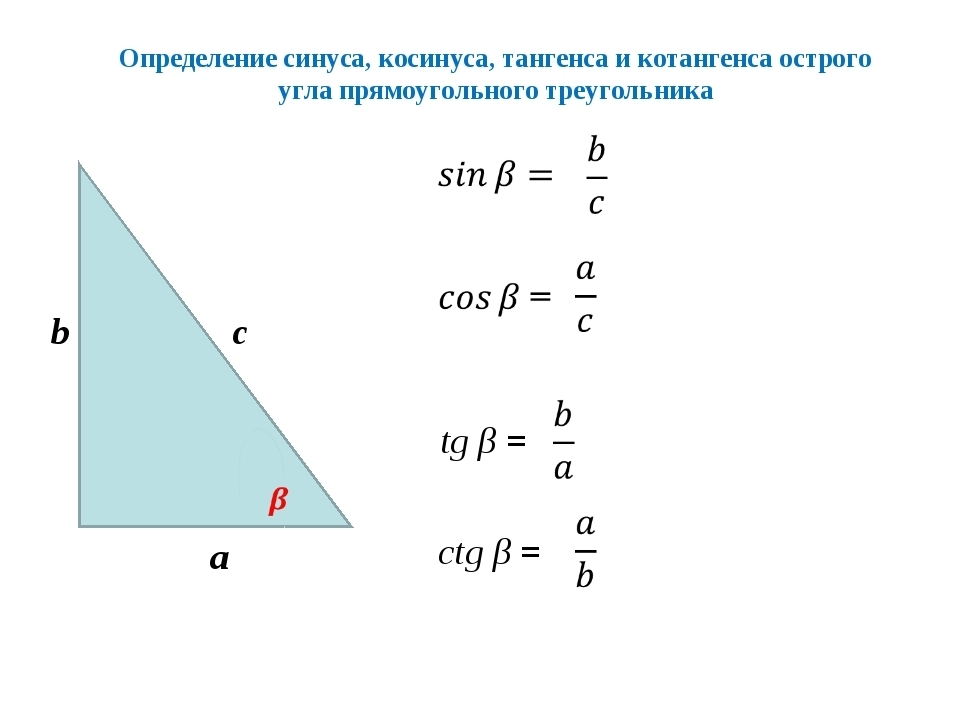 Докажите, что эта
Докажите, что эта
прямая является линией котангенсов,
найдя правило, по которому можно строить
на ней котангенс любого угла из (0;π)
числовой окружности.
Задание 24. С
помощью линии котангенсов найдите ctg
0,5;
ctg
0,75;
ctg
(0,25).
Задача
1. Докажите,
что
sin(x)
=
sin x,
cos(x)
= cos x,
tg(x)
=
tg x,
ctg(x)
=
ctg
x.
Укажите ОДЗ (область допустимых значений
переменных) для каждой из этих формул.
Задача
2. Исходя из
определения синуса и косинуса любого
угла, докажите первое из основных
тригонометрических тождеств. Укажите
ОДЗ для этой формулы.
Задача 3.
Докажите остальные пять основных
тригонометрических тождеств. Укажите
ОДЗ для каждой из этих формул.
* * *
Качественный
рывок, который мы сейчас совершим,
заключается в переходе от синуса,
косинуса, тангенса и котангенса любого
угла к
синусу, косинусу, тангенсу и котангенсу
любого числа.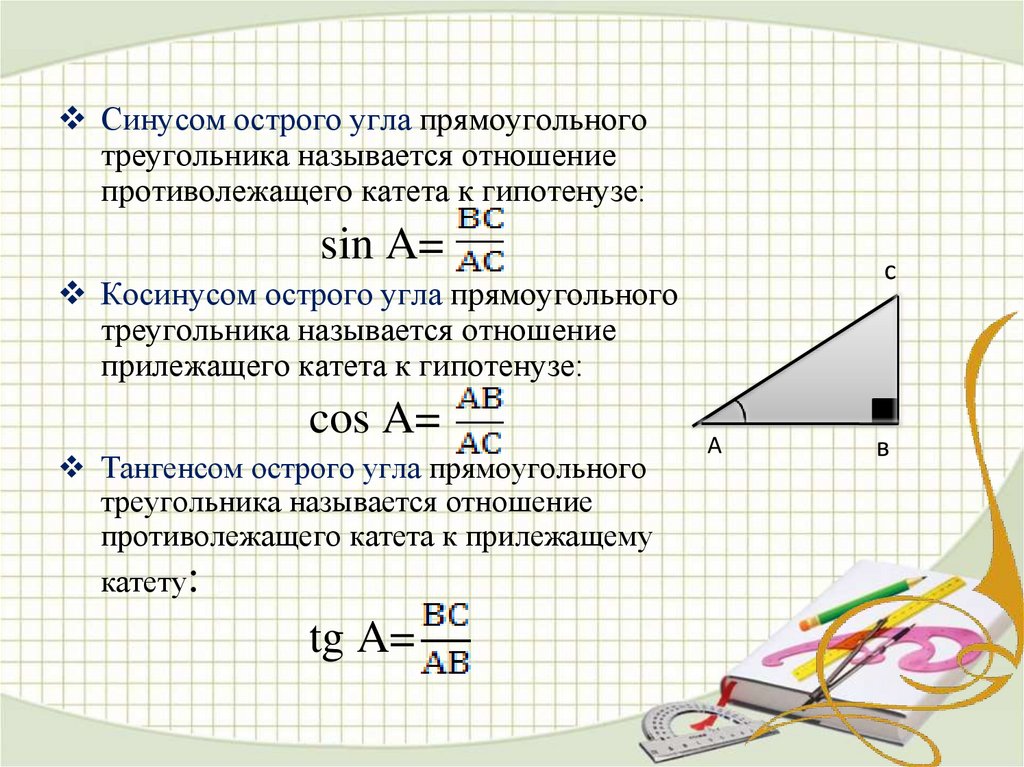
Это раскроет перед нами новые возможности.
Во-первых, станет
возможным рассматривать композицию
тригонометрических функций, например,
такую, как sin
cos
x
или sin
(х2
+ 5).
Задание 25.
Объясните, почему до сих пор было нельзя
рассматривать указанные функции.
Кроме, того, мы
получаем возможность строить графики
синуса, косинуса, тангенса и котангенса.
До сих пор такой возможности у нас не
было. В математике график строят в
прямоугольной системе координат с
одинаковыми координатными осями. Какая
единица выбрана на оси абсцисс, такая
должна быть и на оси ординат. А как можно
построить график у = sin
x,
если х
угол, а у
число? Это физики могут строить графики,
у которых на одной оси
время в секундах, а на другой
путь в метрах. Они так используют
математический
аппарат. Но в математике это не принято.
Определение 3.
Синусом (косинусом, тангенсом, котангенсом)
числа х
называется синус (косинус, тангенс,
котангенс) угла в х
радиан.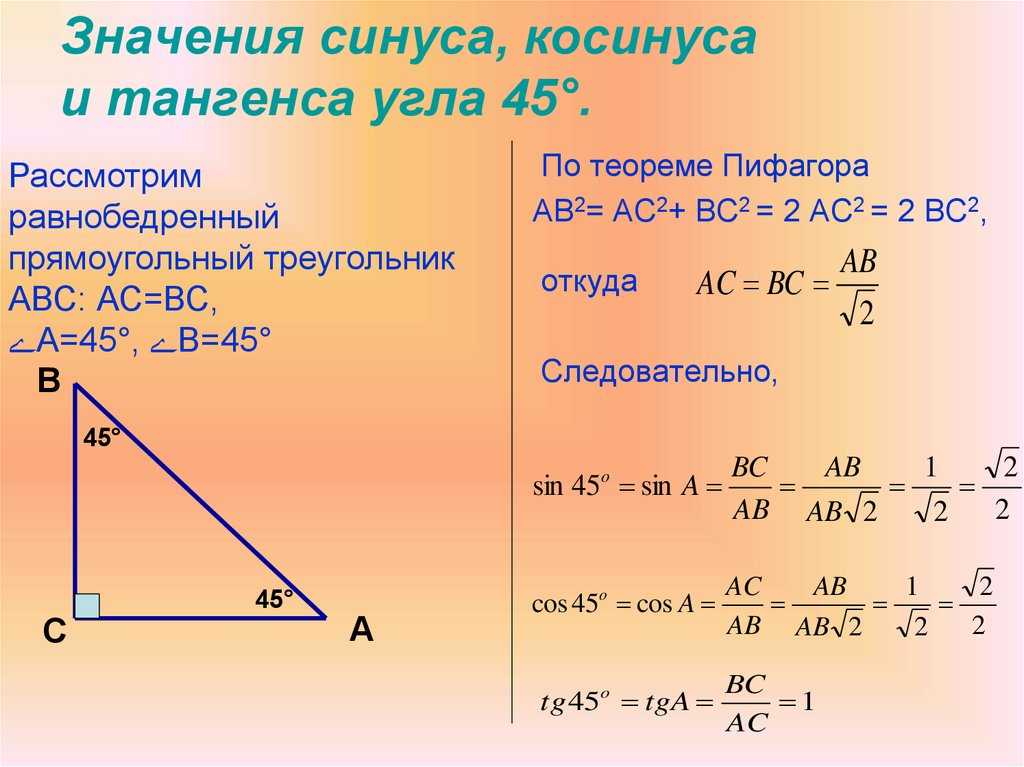
Задание 26. Найдите
синус числа ,
косинус числа 1, тангенс числа 0.
Теперь мы можем
считать синус, косинус, тангенс и
котангенс функциями числового аргумента.
Теперь для нас tg
это не только тангенс развернутого
угла, но и тангенс числа 3,14159… : tg
tg
3,14.
Очень важно, что
ранее
выведенные формулы тригонометрии
остаются верными и в новой ситуации.
Докажем это.
По введенному
определению, синус числа х
равен синусу
угла в х
радиан, аналогично обстоит дело и с
косинусом, тангенсом и котангенсом. Но
если а равно
b,
то взяв верное утверждение, содержащее
а,
мы можем в любом месте заменить а
на b,
и утверждение останется верным (правило
подстановки).
Возьмем любое
доказанное ранее утверждение относительно
синуса, косинуса, тангенса и котангенса
угла в а
радиан и
заменим их на равные
им по определению
синус, косинус, тангенс и котангенс
числа а.
Утверждение останется верным, ч.т.д.
Домашнее задание:
Галицкий, Алгебра 8-9, глава 13, №№ 2, 4-9,
11-14, 17, 20, 27, 30, 31, 33, 36-43, 45-49, 51, 54, 57, 58, 60-62.
Тангенс — что это такое (отношение чего к чему) и как его найти (по формулам и по клеточкам)
Обновлено 23 июля 2021 Просмотров: 63 611 Автор: Дмитрий Петров
Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.
Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.
Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.
Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.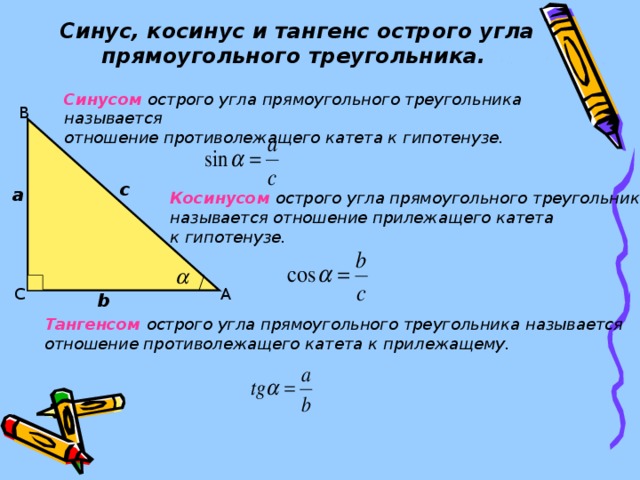
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тангенс — это отношение…
Итак, есть два определения:
-
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
-
Тангенс – это отношение синуса к косинусу.
Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.
Приняты обозначения:
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Как найти тангенс угла (формулы)
Первое свойство тангенса вытекает из его определения как отношения катетов.
Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому
Так как тангенс – это отношение катетов, то
Получается, что
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.
В частности,
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
Как найти тангенс по клеточкам
Учитывая первое определение, можно определить, как найти тангенс угла по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.
Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:
Из формулы тангенсов, записывающей кратко второе определение
и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.
Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится зависимость тангенса и косинуса:
Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
- Математика
Как найти косинус числа
Значения косинуса графически могут быть отображены в виде тригонометрической окружности, на которой угол α образует с осью прямоугольный треугольник. Из этого треугольника, спроецировав точку пересечения угла α с окружностью на ось синуса или косинуса, можно получить его приближенное значение.
Также тригонометрическая окружность показывает знак синуса и косинуса для каждого раскрытия угла α . Поскольку угол начинает раскрываться с правой стороны по оси косинусов, то значения косинуса угла α от 0° до 90° – положительны, так находятся правее нулевой точки отсчета. Угол α от 90° до 270° дает отрицательные значения косинусу, так как точка пересечения его с окружностью расположена левее оси синуса, то есть нуля. Косинус углов от 270° до 360° вновь становится положительным. Точные значения косинусов всех углов от 0° до 360° можно узнать из таблицы косинусов, приведенной ниже.
Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) – отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) – отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) – отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) – отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса – вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов. Угол поворота в градусах или радианах выражается любым действительным числом от – ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).
Синус (sin) угла поворота
Синус угла поворота α – это ордината точки A 1 ( x , y ). sin α = y
Косинус угла поворота α – это абсцисса точки A 1 ( x , y ). cos α = х
Тангенс угла поворота α – это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α – это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , – 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности – точка A c координатами ( 1 , 0 ).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α , cos α , t g α , c t g α – это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс – основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Коcинус – одна из тригонометрических функций. Значение косинуса определяется для угла или для числа (в этом случае используют числовую окружность).
Аргумент и значение
Косинус острого угла
Косинус острого угла можно определить с помощью прямоугольного треугольника – он равен отношению прилежащего катета к гипотенузе.
1) Пусть дан угол и нужно определить косинус этого угла.
2) Достроим на этом угле любой прямоугольный треугольник.
3) Измерив, нужные стороны, можем вычислить косинус.
Косинус острого угла больше (0) и меньше (1)
Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.
Косинус числа
Косинус числа можно определить с помощью числовой окружности – косинус числа равен абсциссе соответствующей точки на ней.
Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи : (frac<π><2>) , (frac<3π><4>) , (-2π).
Например, для числа (frac<π><6>) – косинус будет равен (frac<sqrt<3>><2>) . А для числа (-) (frac<3π><4>) он будет равен (-) (frac<sqrt<2>><2>) (приблизительно (-0,71)).
Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице .
Значение косинуса всегда лежит в пределах от (-1) до (1). При этом вычислен косинус может быть для абсолютно любого угла и числа.
Косинус любого угла
Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем (360°) (полный оборот). Как это делать – проще один раз увидеть, чем (100) раз услышать, поэтому смотрите картинку.
Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в (150°). Совмещаем точку О с центром окружности, а сторону ОК – с осью (x). После этого откладываем (150°) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.
Если же нас интересует угол с градусной мерой, например, в (-60°) (угол КОВ), делаем также, но (60°) откладываем по часовой стрелке.
И, наконец, угол больше (360°) (угол КОС) – всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол (405°) отложен как (360° + 45°).
Несложно догадаться, что для откладывания угла, например, в (960°), надо сделать уже два оборота ((360°+360°+240°)), а для угла в (2640°) – целых семь.
Стоит запомнить, что:
Косинус прямого угла равен нулю. Косинус тупого угла – отрицателен.
Знаки косинуса по четвертям
С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по четвертям числовой (тригонометрической) окружности:
– там, где значения на оси от (0) до (1), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
– там, где значения на оси от (0) до (-1), косинус будет иметь знак минус (II и III четверти – фиолетовая область). 2x>)
– котангенсом и синусом того же угла (или числа): формулой (ctgx=) (frac<cos><sinx>)
Другие наиболее часто применяемые формулы смотри здесь .
Функция (y=cos)
Если отложить по оси (x) углы в радианах, а по оси (y) – соответствующие этим углам значения косинуса, мы получим следующий график:
График данной функции называется косинусоида и обладает следующими свойствами:
– область определения – любое значение икса: (D(cos <x>)=R)
– область значений – от (-1) до (1) включительно: (E(cos )=[-1;1])
– четная: (cos(-x)=cos)
– периодическая с периодом (2π): (cos(x+2π)=cos)
– точки пересечения с осями координат:
ось абсцисс: (() (frac<π><2>) (+πn),(;0)), где (n ϵ Z)
ось ординат: ((0;1))
– промежутки знакопостоянства:
функция положительна на интервалах: ((-) (frac<π><2>) (+2πn;) (frac<π><2>) (+2πn)), где (n ϵ Z)
функция отрицательна на интервалах: (() (frac<π><2>) (+2πn;) (frac<3π><2>) (+2πn)), где (n ϵ Z)
– промежутки возрастания и убывания:
функция возрастает на интервалах: ((π+2πn;2π+2πn)), где (n ϵ Z)
функция убывает на интервалах: ((2πn;π+2πn)), где (n ϵ Z)
– максимумы и минимумы функции:
функция имеет максимальное значение (y=1) в точках (x=2πn), где (n ϵ Z)
функция имеет минимальное значение (y=-1) в точках (x=π+2πn), где (n ϵ Z).
Касательные и наклоны
Касательные и наклоны
Определение касательной
Синус и косинус — не единственные тригонометрические функции, используемые в тригонометрии. Многие другие использовались на протяжении веков, такие как гаверсины и спреды. Наиболее полезным из них является тангенс. С точки зрения диаграммы единичного круга, касательной является длина вертикальной линии ED , касательной к окружности из точки касания E до точки D , где эта касательная пересекает луч AD , образующий угол.
|
Если ваш браузер поддерживает Java, вы можете перетаскивать точку B , чтобы увидеть, как синус, косинус и тангенс изменяются при изменении угла.
(Дополнительную информацию об управлении фигурой см. в разделе Об апплете.) |
Тангенс относительно синуса и косинуса
Поскольку два треугольника ADE и ABC подобны, имеем
ЭД/АЭ = СВ/АС.
Но ED = tan A, AE = 1, CB = sin A, и AC = cos AB. Следовательно, мы получили фундаментальное тождество
Касательные и прямоугольные треугольники
Точно так же, как синус и косинус можно найти как отношение сторон прямоугольного треугольника, можно найти и тангенс.
Мы будем использовать три отношения, которые у нас уже есть. Во-первых, tan A = sin A / cos A. Во-вторых, sin A = a/c. В-третьих, cos A = b/c. Разделив a/c на b/c и убрав появляющиеся c , мы заключаем, что tan A = a/b. Это означает, что касательная – это противолежащая сторона, деленная на прилежащую сторону:
Наклоны линий
Одна из причин, по которой касательные так важны, заключается в том, что они дают наклоны прямых линий. Рассмотрим прямую линию, проведенную в координатной плоскости x-y .
Точка B находится там, где линия пересекает ось y . Мы можем принять координаты B равными (0, b ), так что b, , называемая точкой пересечения y , указывает, насколько выше x -ось B лежит. (Эти обозначения противоречат обозначению сторон треугольника a, b, и c, , поэтому не будем сейчас обозначать стороны.)
Вы можете видеть, что точка на 1 единицу правее начала координат помечена 1, и ее координаты, конечно же, (1,0). Пусть C будет точкой, где эта вертикальная линия пересекает горизонтальную линию через B. Тогда C имеет координаты (1, b ).
Точка A находится там, где вертикальная линия выше 1 пересекает исходную линию. Пусть м обозначает расстояние, на котором А выше С. Тогда А имеет координаты (1, b + м ). Это значение м называется уклоном линии. Если вы переместитесь вправо на одну единицу в любом месте по линии, то вы переместитесь вверх на м единиц.
Теперь рассмотрим угол СВА. Назовем это угол наклона. Тангенс CA/BC = м / 1 = м. Таким образом, наклон представляет собой тангенс угла наклона.
Углы возвышения и депрессии
Термин «угол места» относится к углу над горизонталью от зрителя. Если вы находитесь в точке А, АХ и АХ это горизонтальная линия, то угол возвышения до точки В над горизонтом — угол BAH. Аналогично, «угол депрессии» к точке C ниже горизонта составляет угол CAH.
Касательные часто используются для решения задач, связанных с углами возвышения и депрессии.
Опять общие углы
Мы можем расширить нашу таблицу синусов и косинусов общих углов до тангенсов. Вам не нужно запоминать всю эту информацию, если вы можете просто запомнить отношения сторон 45°-45°-9треугольник 0° и треугольник 30°-60°-90°. Отношения являются значениями триггерных функций.
Обратите внимание, что тангенс прямого угла указан как бесконечность. Это потому, что по мере того, как угол увеличивается до 90°, его тангенс неограниченно растет. Может быть, лучше сказать, что касательная 90 ° не определена, поскольку, используя определение окружности, луч, исходящий из начала координат под углом 90 °, никогда не пересекается с касательной.
| Угол | Градусов | Радиан | cosine | sine | tangent |
|---|---|---|---|---|---|
| 90° | π /2 | 0 | 1 | infinity | |
| 60° | π /3 | 1/2 | √3 / 2 | √3 | |
| 45° | π /4 | √2 / 2 | √2 / 2 | 1 | |
| 30 ° | π /6 | √3 / 2 | 1/2 | 1/√3 | |
| 0° | 0 | 1 | 0 | 0 |
Упражнения
29. В прямоугольном треугольнике a = 30 ярдов и тангенс A = 2. Найдите b и c.
49. cos t = 2 tan t. Найдите значение sin т.р.
Примечание: В следующих задачах расстояние означает расстояние по горизонтали, если не указано иное; под высотой объекта понимается его высота над горизонтальной плоскостью через точку наблюдения. Высота глаза наблюдателя не должна приниматься во внимание, если это специально не оговорено. В задачах, связанных с тенью объекта, предполагается, что тень падает на горизонтальную плоскость через основание объекта, если не указано иное.
151. Угол возвышения дерева на расстоянии 250 футов составляет 16° 13′. Найдите высоту.
152. Найти высоту колокольни на расстоянии 321 фут, угол возвышения 35° 16′.
153. С корабля угол возвышения верхней части маяка на высоте 200 футов над водой составляет 2° 20′. Найдите расстояние.
154. С вершины маяка на высоте 165 футов над водой угол депрессии корабля составляет 3° 50′. Найдите расстояние.
159. Найдите высоту башни на расстоянии 186 футов, угол возвышения 40° 44′.
160. С одной стороны ручья шест высотой 50 футов имеет с противоположной точки угол возвышения 5° 33′. Найдите ширину потока.
164. От одного холма вершина другого на 128 футов выше имеет угол возвышения 2° 40′. Найдите расстояние.
165. С одного холма на вершину другого далекого 6290 футов имеет угол возвышения 4° 9′. Найдите, на сколько высота второго холма больше высоты первого.
189. Фронтон крыши имеет ширину 40 футов у основания и 26 футов от основания до конька. Под каким углом наклон стропил?
Советы
Общий совет для всех этих упражнений: сначала нарисуйте фигуру.
29. Так как вы знаете a и коричневый А, можно найти б. Затем можно определить c по теореме Пифагора, или с помощью синусов, или с помощью косинусов.
49. Вам понадобятся две личности. Во-первых, tan t = sin t /cos t. Во-вторых, тождество Пифагора, sin 2 t + cos 2 t = 1. Тогда вам нужно решить квадратное уравнение.
151. Помните, что тангенс угла прямоугольного треугольника равен противолежащей стороне, деленной на прилежащую сторону. Вы знаете соседнюю сторону (расстояние до дерева) и угол (угол возвышения), поэтому можете использовать касательные для нахождения высоты дерева.
152. Вы знаете угол (опять же, угол возвышения) и примыкающую сторону (расстояние до шпиля), поэтому используйте касательные, чтобы найти противоположную сторону.
153. Используя угол и противоположную сторону, используйте тангенс, чтобы найти соседнюю сторону.
154. Та же подсказка, что и в 153.
159. Та же подсказка, что и в 152.
160. Та же подсказка, что и в 153.
164. Та же подсказка, что и в 153.
165. Та же подсказка, что и в 152.
189. Фронтон крыши представляет собой равнобедренный треугольник. Если провести перпендикулярную линию от хребта, то получится два конгруэнтных прямоугольных треугольника. Вы знаете две стороны треугольников, поэтому можете определить угол наклона стропил с помощью арктангенса.
Ответы
29. b = a /tan A = 30/2 = 15 ярдов. c = 33,5 ярда.
49. Со времен COS T = 2 TAN T, Следовательно, COS T = 2 SIN T /COS T, SO COS 2 T = 2 SIN T, и, как по тождеству Пифагора вы получаете 1 – sin 2 t = 2 sin t. Получается квадратное уравнение sin 2 t + 2 sin t – 1 = 0. Решения: sin t = –1 ± √2. Из этих двух решений единственно возможным является sin t = √2 – 1.
151. Высота = 250 tan 16°13′ = 72,7′ = 72’9″.
152. Высота = 321 tan 35°16′ = 227 футов.
153. Расстояние = 200/тангенс 2°20′ = 4908 футов, почти миля.
154. Расстояние = 165/тангенс 3°50′ = 2462 фута, почти полмили.
159. Высота = 186 tan 40°44′ = 160 футов.
160. Расстояние = 50/тангенс 5°33′ = 515 футов.
164. Расстояние = 128/тангенс 2°40′, около 2750 футов, чуть больше полумили.
165. Высота = 6290 tan 4°9′ = 456,4 фута.
189. тангенс А = 26/20, поэтому А = 52°.
Использование синуса, косинуса и тангенса
Все математические ресурсы SAT
137 Практические тесты
Вопрос дня
Карточки
Learn by Concept
SAT Mathematics Help »
Тригонометрия »
Используя синус, косинус и тангенс
Треугольники ABC и XYZ подобны. Какова ценность?
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку эти треугольники подобны, у них будет точно такое же отношение между их сторонами, а это означает, что синус Z будет таким же, как и синус C. А поскольку синус = противолежащее/гипотенуза, вы можете вычислить это как к .
Сообщить об ошибке
Три угла прямоугольного треугольника имеют размеры , и . Если и , то что?
Возможные ответы:
Правильный ответ:
Объяснение:
Вы, вероятно, знаете SOH-CAH-TOA для синуса, косинуса и тангенса, что, конечно же, является абсолютно необходимым знанием для вопросов по тригонометрии на SAT. Следующим элементом передовых знаний о тригонометрии, который любит проверять SAT, является следующий набор правил:
Вы должны знать эти правила , чтобы иметь возможность решать сложные вопросы тригонометрии SAT!
Вот еще один способ понять эти правила:
В прямоугольном треугольнике всегда есть два меньших угла .
Синус одного угла = косинусу другого угла.
Косинус одного угла = синусу другого угла.
Если вы понимаете SOH-CAH-TOA и прямоугольные треугольники, это логично: Из SOH и CAH вы можете видеть, что единственная разница между синусом и косинусом заключается в том, что у синуса в числителе длина противоположной стороны а косинус имеет длину смежной стороны в числителе. Что ж, в прямоугольном треугольнике, когда вы переключаетесь с одного из меньших углов на другой, вы меняете местами, какая сторона является противоположной, а какая — смежной! (Гипотенуза всегда остается одной и той же стороной.) На основе SOH и CAH, поменяв местами противоположную и смежную стороны означает то же самое, что и перестановка значений синуса и косинуса углов.
Возвращаясь к этому конкретному вопросу, поскольку , и должны быть двумя меньшими углами прямоугольного треугольника. Поэтому, основываясь на правилах, описанных выше, и .
Так как , это означает, что тоже! Таким образом, правильных вариантов ответа — .
Это классический вопрос с подвохом, потому что составители тестовых вопросов знают, что большинство учащихся не ожидают, что правильный ответ будет точно таким же, как другое значение, указанное в вопросе! Таким образом, учащиеся, не знающие правил или не уверенные в своих знаниях на 100%, будут бояться выбрать этот ответ и, скорее всего, предложат другой ответ. Это задача, которую авторы вопросов SAT ставят перед студентами. Вы должны очень хорошо знать эти правила, чтобы успешно пройти это испытание и выбрать правильный ответ!
Сообщить об ошибке
Три угла прямоугольного треугольника имеют меры , и . Подобный треугольник имеет угловые меры , и . Если , и , что такое ?
Возможные ответы:
Правильный ответ:
Пояснение:
Сначала нужно разложить соответствующие углы в подобных треугольниках. Очевидно, так как , и прямые углы. Таким образом, мы знаем, что внутри каждого треугольника и . Ключевой дополнительной информацией в вопросе об углах является то, что . Это означает, что и . Теперь мы точно знаем, какие углы в подобных треугольниках конгруэнтны (равны) друг другу.
Теперь ключевым шагом вопроса является использование значения для нахождения значения . Поскольку теперь мы это знаем, мы это знаем. Теперь мы можем сосредоточиться только на треугольнике с углами , и .
Вы, вероятно, знаете SOH-CAH-TOA для синуса, косинуса и тангенса, что, конечно же, является абсолютно необходимым знанием для вопросов по тригонометрии на SAT. Следующим элементом передовых знаний о тригонометрии, который любит проверять SAT, является следующий набор правил:
Вы должны знать эти правила , чтобы иметь возможность решать сложные вопросы тригонометрии SAT!
Вот еще один способ понять эти правила:
В прямоугольном треугольнике всегда есть два меньших угла .
Синус одного угла = косинусу другого угла.
Косинус одного угла = синусу другого угла.
Если вы понимаете SOH-CAH-TOA и прямоугольные треугольники, это логично: Из SOH и CAH вы можете видеть, что единственная разница между синусом и косинусом заключается в том, что у синуса длина противоположной стороны в числителе а косинус имеет длину смежной стороны в числителе. Что ж, в прямоугольном треугольнике, когда вы переключаетесь с одного из меньших углов на другой, вы меняете местами, какая сторона является противоположной, а какая — смежной! (Гипотенуза всегда остается одной и той же стороной.) На основе SOH и CAH, поменяв местами противоположную и смежную стороны означает то же самое, что и перестановка значений синуса и косинуса углов.
Возвращаясь к этому конкретному вопросу, поскольку , и должны быть двумя меньшими углами прямоугольного треугольника. Поэтому, основываясь на правилах, описанных выше, и .
Так как , это означает, что тоже! Таким образом, правильный выбор ответа равен 0,8.
Это классический вопрос с подвохом, потому что составители тестовых вопросов знают, что большинство учащихся не ожидают, что правильный ответ будет точно таким же, как другое значение, указанное в вопросе! Таким образом, учащиеся, не знающие правил или не уверенные в своих знаниях на 100%, будут бояться выбрать этот ответ и, скорее всего, предложат другой ответ. Это задача, которую авторы вопросов SAT ставят перед студентами. Вы должны очень хорошо знать эти правила, чтобы успешно пройти это испытание и выбрать правильный ответ!
Сообщить об ошибке
Три угла прямоугольного треугольника имеют меры , , и . Какова ценность ?
Возможные ответы:
Ответ не может быть определен на основе информации, указанной в вопросе.
Правильный ответ:
Объяснение:
Прежде всего, следите за выбором ответа-ловушки «Ответ не может быть определен из информации, указанной в вопросе»!! НИКОГДА НЕ УГАДАЙТЕ ЭТОТ ОТВЕТ, если вы не совсем уверены, что он ДОЛЖЕН быть правдой! Чаще всего SAT использует этот вариант ответа как ловушку для студентов, которые не знают расширенный метод, который существует и необходим для поиска правильного ответа, который можно определить из информации, приведенной в вопросе, если вы знаете правильный метод. Если вы не понимаете, как ответить на вопрос, и вам нужно угадать, угадайте один из трех других вариантов ответа!
Вы, вероятно, знаете SOH-CAH-TOA для синуса, косинуса и тангенса, что, конечно же, является абсолютно необходимым знанием для вопросов по тригонометрии на SAT. Следующим элементом передовых знаний о тригонометрии, который любит проверять SAT, является следующий набор правил:
Вы должны знать эти правила , чтобы иметь возможность решать сложные вопросы тригонометрии SAT!
Вот еще один способ понять эти правила:
В прямоугольном треугольнике всегда есть два меньших угла .
Синус одного угла = косинусу другого угла.
Косинус одного угла = синусу другого угла.
Если вы понимаете SOH-CAH-TOA и прямоугольные треугольники, это логично: Из SOH и CAH вы можете видеть, что единственная разница между синусом и косинусом заключается в том, что у синуса длина противоположной стороны в числителе а косинус имеет длину смежной стороны в числителе. Что ж, в прямоугольном треугольнике, когда вы переключаетесь с одного из меньших углов на другой, вы меняете местами, какая сторона является противоположной, а какая — смежной! (Гипотенуза всегда остается одной и той же стороной.) На основе SOH и CAH, поменяв местами противоположную и смежную стороны означает то же самое, что и перестановка значений синуса и косинуса углов.
Возвращаясь к этому конкретному вопросу, и должны быть двумя меньшими углами прямоугольного треугольника. Поэтому, основываясь на правилах, описанных выше, и .
Следовательно, . Таким образом, правильный вариант ответа равен 0.
Сообщить об ошибке
[Примечание. Следующий вопрос может появиться в разделе «С калькулятором», поэтому учащийся может использовать калькулятор для ответа на него.]
Два острых угла имеют размеры и , и . Если и , каково значение ?
Возможные ответы:
Правильный ответ:
Объяснение:
Вы, вероятно, знаете SOH-CAH-TOA для синуса, косинуса и тангенса, что, конечно же, является абсолютно необходимым знанием для вопросов по тригонометрии на SAT. Следующим элементом передовых знаний о тригонометрии, который любит проверять SAT, является следующий набор правил:
Вы должны знать эти правила , чтобы иметь возможность решать сложные вопросы тригонометрии SAT!
Вот еще один способ понять эти правила:
В прямоугольном треугольнике всегда есть два меньших угла .
Синус одного угла = косинусу другого угла.
Косинус одного угла = синусу другого угла.
Если вы понимаете SOH-CAH-TOA и прямоугольные треугольники, это логично: Из SOH и CAH вы можете видеть, что единственная разница между синусом и косинусом заключается в том, что у синуса длина противоположной стороны в числителе и косинус имеет в числителе длину Прилежащей стороны. Что ж, в прямоугольном треугольнике, когда вы переключаетесь с одного из меньших углов на другой, вы меняете местами, какая сторона является противоположной, а какая — смежной! (Гипотенуза всегда остается одной и той же стороной. ) На основе SOH и CAH, поменяв местами противоположную и смежную стороны означает то же самое, что и перестановка значений синуса и косинуса углов.
Возвращаясь к этому конкретному вопросу, мы должны думать о правилах, объясненных выше, по-другому: поскольку правила говорят нам об этом и вопрос говорит нам об этом, мы можем сделать логический вывод, что . [Вопрос также добавляет информацию о том, что оба угла острые, что означает , поэтому мы знаем, что имеем дело с «нормальными» угловыми мерами между и , а не с какими-то более сложными угловыми мерами, большими чем, например.] Теперь мы можем переставить в более простая форма.
Теперь мы можем просто подставить значения и в уравнение . Продолжая добавлять 25 к обеим сторонам, мы получаем . Разделив обе части на 10, получим . Следовательно, правильный выбор ответа равен 11,5.
Если вы ошибочно думаете, что получите неправильный ответ 20.5. Если вы ошибочно полагаете, что получите неправильный ответ 38. 5. Это большое значение 38,5 включено в число вариантов ответа главным образом для того, чтобы сделать более заманчивый неправильный вариант ответа 20,5 более «разумным» по сравнению с ним, чтобы заманить больше учащихся в ловушку неправильного угадывания 20,5.
Сообщить об ошибке
На приведенном выше рисунке отрезки DE и BC параллельны, DE перпендикулярен AB и . Если и , какова площадь трапеции DBCE?
Возможные ответы:
Правильный ответ:
Объяснение:
SAT любит упаковывать множество различных понятий в один вопрос, чтобы заставить вас использовать все свои знания по математике, чтобы ответить на вопрос. Здесь вы должны начать с информации о том, что DE перпендикулярен AB, чтобы установить, что это прямой угол, и поэтому треугольник ADE является прямоугольным. Кроме того, поскольку DE и BC параллельны, это означает, что угол также должен быть прямым, а треугольник ABC прямоугольным.
Так как треугольники ADE и ABC также имеют один и тот же угол A, их третьи углы и также должны быть равны, потому что сумма трех углов каждого треугольника должна быть равна . Теперь, когда вы знаете, что все три угла треугольников ADE и ABC равны, это означает, что они подобны треугольникам.
Следующая ключевая информация в этом вопросе . Зная SOH-CAH-TOA, вы знаете это. В этих треугольниках соседними сторонами к А являются AD в малом треугольнике и АВ в большом треугольнике. Гипотенуза AE в малом треугольнике и AC в большом треугольнике. Следовательно, вы это знаете.
Теперь вы должны распознать числа 12 и 13 в «пифагорейской тройке» прямоугольного треугольника 5-12-13! Напомним, что это длины сторон прямоугольного треугольника, потому что . Однако будьте осторожны! Значение косинуса сообщает вам только отношение длин сторон, а не сами фактические длины сторон. Это могут быть 12 и 13, 24 и 26, 120 и 130, 1,2 и 1,3, 0,12 и 0,13 или любая другая пара длин с соотношением .
Информация в вопросе, которая помогает нам определить фактическую длину сторон. Поскольку BC должна быть кратчайшей стороной прямоугольного треугольника с отношением 5-12-13, вы можете видеть, что фактические длины сторон треугольника ABC должны быть дважды умножены на 5, 12 и 13: Таким образом и . Кроме того, вопрос говорит вам, что . Следовательно, вычитая длину EC из длины AC, вы знаете, что . Это означает, что и . Поскольку и , это означает, что .
Теперь у вас есть все длины сторон трапеции DBCE, и вы готовы вычислить ее площадь. Вам нужно знать формулу площади трапеции: . Это выглядит сложно, но логичный способ понять и запомнить это — осознать, что всего среднее двух оснований трапеции . Всегда помните, что основания — это две стороны, которые параллельны друг другу, независимо от того, в каком направлении они ориентированы на диаграмме. Здесь две базы DE и BC. Их длины равны 5 и 10, поэтому их среднее значение равно 7,5. Высота трапеции — это высота от одного основания до другого, перпендикулярная обоим основаниям. В этом случае, поскольку углы и углы прямые, угол DB перпендикулярен углам DE и BC, а значит, сам угол DB является высотой трапеции. Таким образом, высота равна 12, а площадь трапеции равна , поэтому выбор правильного ответа равен 90.
Сообщить об ошибке
В треугольнике LMN LM перпендикулярен MN. Если , какова ценность ?
Возможные ответы:
Правильный ответ:
Объяснение:
Хотя SAT иногда может задавать такие вопросы по геометрии, как этот, без диаграммы, часто вам следует нарисовать диаграмму самостоятельно, чтобы наглядно представить, что происходит в вопросе!
Здесь вопрос говорит вам, что LM перпендикулярна MN. Перпендикулярные линии встречаются под прямым углом, так что это причудливый скрытый способ сказать вам, что это прямой угол. Теперь вы знаете, что LMN — прямоугольный треугольник, поэтому вам следует нарисовать его собственную диаграмму:
Далее вопрос говорит вам, что . Зная SOH-CAH-TOA, вы знаете, что. Сторона, противоположная L, — это MN, а сторона, примыкающая к L, — это LM, так что теперь вы знаете, что . Технически мы не знаем реальных длин сторон, только отношение одной стороны к другой: они могут быть 4 и 3, или 8 и 6, или 400 и 300, или 0,8 и 0,6, или любые две длины с отношением из . Но в этом конкретном вопросе это не имеет значения, поскольку вопрос требует от вас значения , которое также является отношением длин сторон, как и тангенс L. Таким образом, в этом вопросе вы можете просто не усложнять и принять простейший случай и .
Вы знаете прямоугольный треугольник 3-4-5, так что теперь вы можете предположить .
Снова от SOH-CAH-TOA, вы знаете это. Убедитесь, что вы сейчас переключили перспективу с угла L на угол N! Вопрос просит вас указать значение . С точки зрения угла N прилежащая сторона равна MN, а гипотенуза — LN. Так . Поэтому c выбор правильного ответа равен .
Сообщить об ошибке
Если и , каково значение ?
Возможные ответы:
Ответ не может быть определен на основе информации, указанной в вопросе.
Правильный ответ:
Объяснение:
Прежде всего, следите за выбором ответа-ловушки «Ответ не может быть определен из информации, указанной в вопросе»!! НИКОГДА НЕ УГАДАЙТЕ ЭТОТ ОТВЕТ, если вы не совсем уверены, что он ДОЛЖЕН быть правдой! Чаще всего SAT использует этот вариант ответа как ловушку для студентов, которые не знают расширенный метод, который существует и необходим для поиска правильного ответа, который можно определить из информации, приведенной в вопросе, если вы знаете правильный метод. Если вы не понимаете, как ответить на вопрос, и вам нужно угадать, угадайте один из трех других вариантов ответа!
В этом вопросе SAT пытается запутать вас лишними числами, алгеброй и скобками в первом уравнении, которое они вам дают. Не вводите в заблуждение и не вводите в заблуждение! В скобках нет хитрости: вы можете просто сложить все термины вместе и получить . Теперь просто вычтите 10 с обеих сторон, и вы получите .
Теперь вы можете увидеть связь с вопросом о значениях тангенса: так как , и могут быть двумя меньшими углами прямоугольного треугольника!
Совет профессионала : На этом этапе наиболее опытные студенты-математики уже сразу увидят ответ: Поскольку вы знаете из SOH-CAH-TOA, что , и переход от одного меньшего угла прямоугольного треугольника к другому меньшему углу просто меняет местами противоположные стороны углов и смежные стороны, тангенс одного угла всегда является обратной величиной тангенса другого угла! Таким образом, самые опытные студенты-математики сразу знают, что это правильный вариант ответа .
Если вы не видите этого сразу, другой способ закончить решение вопроса — нарисовать собственную диаграмму: . (Имейте в виду, что на самом деле это могут быть любые длины сторон, имеющие отношение 2:3.) Теперь, переключившись на треугольник с точки зрения угла, вы видите, что теперь противоположная сторона равна , а примыкающая сторона . Итак, что такое выбор правильного ответа .
Сообщить об ошибке
В приведенном выше треугольнике XYZ тангенс равен 1. Чему равно число?
Возможные ответы:
Информация не может быть определена.
Правильный ответ:
Объяснение:
Вопрос говорит вам, что тангенс угла a равен 1. Мы хотим иметь в виду, что тангенс представляет собой отношение: это длина противоположной стороны, деленная на длину соседней стороны. Когда коэффициент равен 1? Когда обе фигуры одинаковы. Итак, сторона XY = сторона YZ, а это означает, что вы имеете дело с равнобедренным прямоугольным треугольником (и именно здесь действительно пригодится обозначение «не в масштабе», поскольку вы бы не подумали, что это правда из рисунка) . Поскольку это равнобедренный прямоугольный треугольник, вы знаете, что отношение сторон равно: . На данный момент, даже если вы не знаете фактических длин, все, что вам нужно сделать, это применить это соотношение. Синус b противоположен гипотенузе, которая является отношением . Отсюда вам нужно «рационализировать знаменатель», умножив его на 1 (в данном случае ). После упрощения остается .
Сообщить об ошибке
В треугольнике ниже тангенс равен . Что такое тангенс?
Возможные ответы:
Информация не может быть определена.
Правильный ответ:
Объяснение:
В этом примере перед нами стоит задача применить наше понимание соотношений, которые мы выражаем с помощью SOH-CAH-TOA, нашего греха, косинуса и тангенса. Имейте в виду, что эти соотношения следующие:
Исходя из этого, если нам говорят, что тангенс ( ) , то тангенс должен быть обратным, так как противоположность а° является прилежащей к Ь°, и наоборот наоборот Во многих случаях понимание того, как SOH-CAH-TOA манипулирует одними и теми же отношениями и сторонами треугольника в вопросах SAT, может упростить ту степень, в которой нам действительно нужно «вычислять». Здесь, признавая, что тангенс является просто величиной, обратной тангенсу , этот вопрос становится чрезвычайно эффективным и позволяет нам сэкономить время для более пошаговых вопросов в других частях экзамена.
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы по математике SAT
137 Практические тесты
Вопрос дня
Карточки
Learn by Concept
Синус, косинус и тангенс » Ярно Воуда
1. Введение
Синус, косинус и тангенс — это функции, которые мы используем в математике для вычисления углов и сторон треугольников. На вашем калькуляторе эти функции записываются сокращенно как «sin», «cos» и «tan»,
Легенда
• = Умножение
∠ = Угол
≈ = Приблизительно равно





























