Ответы Mail.ru
Образование
ВУЗы, Колледжи
Детские сады
Школы
Дополнительное образование
Образование за рубежом
Прочее образование
Вопросы – лидеры.
Помогите инженеры решить данную задачу. Срочно
1 ставка
Начертить фигуру в компасе
1 ставка
Написать уравнение кристаллохимической реакции образования
точечных дефектов
1 ставка
Как найти величину флуктуации сигнала на входе приемника если известно что
1 ставка
Помогите с математикой
Найдите сумму членов ряда
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
upgrade the world
Мастер
(1072),
закрыт
11 лет назад
Лучший ответ
Аркадий Редько
Просветленный
(23856)
13 лет назад
sin(2пи/3)=sin(пи-пи/3)=sin( пи/3)=кв. кор (3)/2
Остальные ответы
Верона
Профи
(799)
13 лет назад
корень из 3/2
светлана гусляева
Профи
(570)
13 лет назад
несомненно, квадратный корень из трёх, делённый на два
Похожие вопросы
The value of sin 2pi/3 is 0.8660254. . .. Sin 2pi/3 radians in degrees is written as sin ((2π/3) × 180°/π), i.e., sin (120°). In this article, we will discuss the methods to find the value of sin 2pi/3 with examples.
- Sin 2pi/3: √3/2
- Sin 2pi/3 in decimal: 0.8660254. . .
- Sin (-2pi/3): -0.8660254. . . or -(√3/2)
- Sin 2pi/3 in degrees: sin (120°)
What is the Value of Sin 2pi/3?
The value of sin 2pi/3 in decimal is 0.866025403. . .. Sin 2pi/3 can also be expressed using the equivalent of the given angle (2pi/3) in degrees (120°).
We know, using radian to degree conversion, θ in degrees = θ in radians × (180°/pi)
⇒ 2pi/3 radians = 2pi/3 × (180°/pi) = 120° or 120 degrees
∴ sin 2pi/3 = sin 2π/3 = sin(120°) = √3/2 or 0.8660254. . .
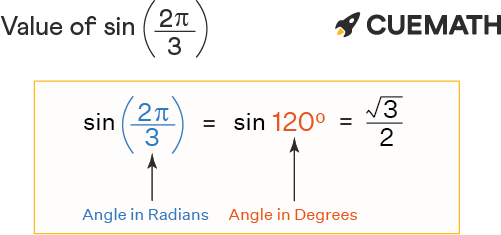
Explanation:
For sin 2pi/3, the angle 2pi/3 lies between pi/2 and pi (Second Quadrant). Since sine function is positive in the second quadrant, thus sin 2pi/3 value = √3/2 or 0.8660254. . .
Since the sine function is a periodic function, we can represent sin 2pi/3 as, sin 2pi/3 = sin(2pi/3 + n × 2pi), n ∈ Z.
⇒ sin 2pi/3 = sin 8pi/3 = sin 14pi/3 , and so on.
Note: Since, sine is an odd function, the value of sin(-2pi/3) = -sin(2pi/3).
Methods to Find Value of Sin 2pi/3
The sine function is positive in the 2nd quadrant. The value of sin 2pi/3 is given as 0.86602. . .. We can find the value of sin 2pi/3 by:
- Using Unit Circle
- Using Trigonometric Functions
Sin 2pi/3 Using Unit Circle
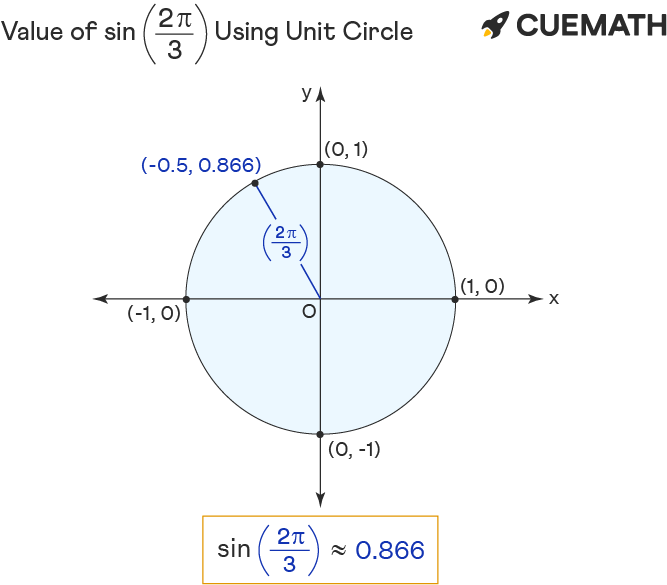
To find the value of sin 2π/3 using the unit circle:
- Rotate ‘r’ anticlockwise to form 2pi/3 angle with the positive x-axis.
- The sin of 2pi/3 equals the y-coordinate(0.866) of the point of intersection (-0.5, 0.866) of unit circle and r.
Hence the value of sin 2pi/3 = y = 0.866 (approx)
Sin 2pi/3 in Terms of Trigonometric Functions
Using trigonometry formulas, we can represent the sin 2pi/3 as:
- ± √(1-cos²(2pi/3))
- ± tan(2pi/3)/√(1 + tan²(2pi/3))
- ± 1/√(1 + cot²(2pi/3))
- ± √(sec²(2pi/3) – 1)/sec(2pi/3)
- 1/cosec(2pi/3)
Note: Since 2pi/3 lies in the 2nd Quadrant, the final value of sin 2pi/3 will be positive.
We can use trigonometric identities to represent sin 2pi/3 as,
- sin(pi – 2pi/3) = sin pi/3
- -sin(pi + 2pi/3) = -sin 5pi/3
- cos(pi/2 – 2pi/3) = cos(-pi/6)
- -cos(pi/2 + 2pi/3) = -cos 7pi/6
☛ Also Check:
- tan 3pi/2
- sin pi/3
- cos 17pi/12
- tan 2pi/3
- sec pi/3
- sin 3pi/2
FAQs on Sin 2pi/3
What is Sin 2pi/3?
Sin 2pi/3 is the value of sine trigonometric function for an angle equal to 2pi/3 radians. The value of sin 2pi/3 is √3/2 or 0.866 (approx).
What is the Value of Sin 2pi/3 in Terms of Cosec 2pi/3?
Since the cosecant function is the reciprocal of the sine function, we can write sin 2pi/3 as 1/cosec(2pi/3). The value of cosec 2pi/3 is equal to 1.15470.
How to Find Sin 2pi/3 in Terms of Other Trigonometric Functions?
Using trigonometry formula, the value of sin 2π/3 can be given in terms of other trigonometric functions as:
- ± √(1-cos²(2pi/3))
- ± tan(2pi/3)/√(1 + tan²(2pi/3))
- ± 1/√(1 + cot²(2pi/3))
- ± √(sec²(2pi/3) – 1)/sec(2pi/3)
- 1/cosec(2pi/3)
☛ Also check: trigonometric table
How to Find the Value of Sin 2pi/3?
The value of sin 2pi/3 can be calculated by constructing an angle of 2π/3 radians with the x-axis, and then finding the coordinates of the corresponding point (-0.5, 0.866) on the unit circle. The value of sin 2pi/3 is equal to the y-coordinate (0.866). ∴ sin 2pi/3 = 0.866.
What is the Value of Sin 2pi/3 in Terms of Tan 2pi/3?
We know, using trig identities, we can write sin 2pi/3 as -tan(2pi/3)/√(1 + tan²(2pi/3)). Here, the value of tan 2pi/3 is equal to -1.732050.
Чтобы найти значение тригонометрического выражения ![]() можно использовать несколько методов.
можно использовать несколько методов.
1-й метод.
Данный метод один из самых простых, но не всегда доступный. Для его использования необходимо, чтобы под рукой была таблица значений основных аргументов тригонометрических функций:
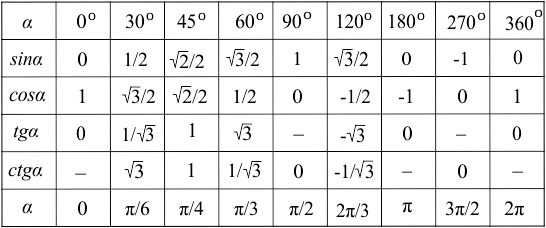
Посмотрев в таблицу, сразу можно определить, что значение ![]() будет равно
будет равно ![]() .
.
2-й метод.
Такой метод подойдет в том случае, если нет возможности воспользоваться таблицей. Метод заключается в использовании тригонометрического круга, с помощью которого можно определить значения тригонометрических функций от множества аргументов.
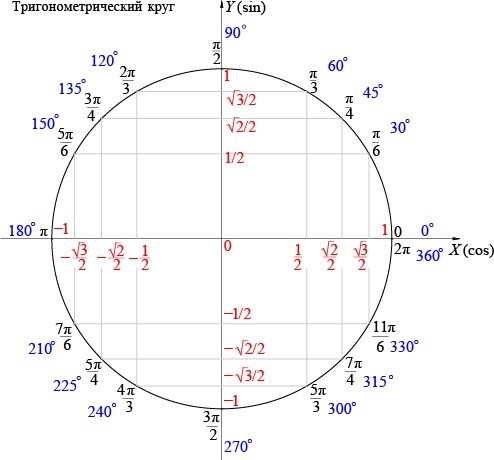
Посмотрев на тригонометрический круг (или окружность), увидим, что значения синуса лежать на оси ординат. Найдем на окружности точку, которая обозначена числом ![]() , соответствующим углу 120 градусов. Спроецируем эту точку на ось ординат, получив при этом значение
, соответствующим углу 120 градусов. Спроецируем эту точку на ось ординат, получив при этом значение ![]() .
.
3-й метод.
Метод могут использовать все, кто не умеет пользоваться тригонометрическим кругом, но помнит, как строится график синуса.
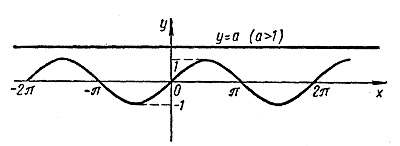
По графику сложнее определить значение такого непростого аргумента, но, опять же, метод подходит для тех, кто хорошо знаком с синусоидой.
Узнать ещё
Знание — сила. Познавательная информация
Синус 1, sin 2, sin 3
Единичная окружность помогает понять, чему равны sin 1, sin 2, sin 3, sin 4, sin 5, sin 6.
Итак, речь идет об углах в радианах. 1 радиан — это угол, длина дуги которого равна радиусу окружности. Соответственно, определяем приблизительное местонахождение на единичной окружности углов в 2, 3, 4, 5 и 6 радиан, отмечая каждую следующую точку через дугу, длина которой равна радиусу. Впрочем, если вспомнить, что п приближенно равно 3,14, задача существенно упростится.
Рисунок позволяет наглядно определять приблизительные значения sin 1, sin 2, sin 3, sin 4, sin 5, sin 6, а также сравнивать их.
Поскольку синус — это ордината соответствующей точки на единичной окружности (как это легко запомнить — здесь ), то для нахождения sin 1, sin 2, sin 3, sin 4, sin 5, sin 6 достаточно определить значение y в точках 1, 2, 3, 4, 5 и 6 радиан.
Поскольку синус — это y, то вверху, над осью x, синус принимает положительные значения. Поэтому sin 1>0, sin 2>0, sin 3>0.
Соответственно внизу синус отрицателен: sin 4 sin4, ведь любое положительное число больше любого отрицательного.
Если требуется сравнить значения синуса одного знака, например, sin2 и sin3, то исходя из геометрических соображений, sin2>sin3.
Если нужно уточнить, чему равен 1 радиан, 2, 3, 4, 5 и 6 радиан в градусах, то приближенные значения таковы:
Приближенно чему равен синус 1, синус 2 и синус 3, можно узнать по таблицам Брадиса:
Используя геометрические соображения, можно найти и приблизительные значения углов, больших 6 радиан.
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Таблица СИНУСОВ для углов от 0° до 360° градусов
СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| SIN α (СИНУС) | 0 | 1/2 | √ 2/2 | √3 /2 | 1 | 0 | -1 | 0 |
Малая таблица значений тригонометрических функций (в радианах и градусах)
| Угол в градусах | Sin (Синус) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0523 |
| 4° | 0.0698 |
| 5° | 0.0872 |
| 6° | 0.1045 |
| 7° | 0.1219 |
| 8° | 0.1392 |
| 9° | 0.1564 |
| 10° | 0.1736 |
| 11° | 0.1908 |
| 12° | 0.2079 |
| 13° | 0.225 |
| 14° | 0.2419 |
| 15° | 0.2588 |
| 16° | 0.2756 |
| 17° | 0.2924 |
| 18° | 0.309 |
| 19° | 0.3256 |
| 20° | 0.342 |
| 21° | 0.3584 |
| 22° | 0.3746 |
| 23° | 0.3907 |
| 24° | 0.4067 |
| 25° | 0.4226 |
| 26° | 0.4384 |
| 27° | 0.454 |
| 28° | 0.4695 |
| 29° | 0.4848 |
| 30° | 0.5 |
| 31° | 0.515 |
| 32° | 0.5299 |
| 33° | 0.5446 |
| 34° | 0.5592 |
| 35° | 0.5736 |
| 36° | 0.5878 |
| 37° | 0.6018 |
| 38° | 0.6157 |
| 39° | 0.6293 |
| 40° | 0.6428 |
| 41° | 0.6561 |
| 42° | 0.6691 |
| 43° | 0.682 |
| 44° | 0.6947 |
| 45° | 0.7071 |
| 46° | 0.7193 |
| 47° | 0.7314 |
| 48° | 0.7431 |
| 49° | 0.7547 |
| 50° | 0.766 |
| 51° | 0.7771 |
| 52° | 0.788 |
| 53° | 0.7986 |
| 54° | 0.809 |
| 55° | 0.8192 |
| 56° | 0.829 |
| 57° | 0.8387 |
| 58° | 0.848 |
| 59° | 0.8572 |
| 60° | 0.866 |
| 61° | 0.8746 |
| 62° | 0.8829 |
| 63° | 0.891 |
| 64° | 0.8988 |
| 65° | 0.9063 |
| 66° | 0.9135 |
| 67° | 0.9205 |
| 68° | 0.9272 |
| 69° | 0.9336 |
| 70° | 0.9397 |
| 71° | 0.9455 |
| 72° | 0.9511 |
| 73° | 0.9563 |
| 74° | 0.9613 |
| 75° | 0.9659 |
| 76° | 0.9703 |
| 77° | 0.9744 |
| 78° | 0.9781 |
| 79° | 0.9816 |
| 80° | 0.9848 |
| 81° | 0.9877 |
| 82° | 0.9903 |
| 83° | 0.9925 |
| 84° | 0.9945 |
| 85° | 0.9962 |
| 86° | 0.9976 |
| 87° | 0.9986 |
| 88° | 0.9994 |
| 89° | 0.9998 |
| 90° | 1 |
Полная таблица синусов для углов от 0° до 360° с шагом всего в 1°
| Угол в градусах | Sin (Синус) |
|---|---|
| 91° | 0.9998 |
| 92° | 0.9994 |
| 93° | 0.9986 |
| 94° | 0.9976 |
| 95° | 0.9962 |
| 96° | 0.9945 |
| 97° | 0.9925 |
| 98° | 0.9903 |
| 99° | 0.9877 |
| 100° | 0.9848 |
| 101° | 0.9816 |
| 102° | 0.9781 |
| 103° | 0.9744 |
| 104° | 0.9703 |
| 105° | 0.9659 |
| 106° | 0.9613 |
| 107° | 0.9563 |
| 108° | 0.9511 |
| 109° | 0.9455 |
| 110° | 0.9397 |
| 111° | 0.9336 |
| 112° | 0.9272 |
| 113° | 0.9205 |
| 114° | 0.9135 |
| 115° | 0.9063 |
| 116° | 0.8988 |
| 117° | 0.891 |
| 118° | 0.8829 |
| 119° | 0.8746 |
| 120° | 0.866 |
| 121° | 0.8572 |
| 122° | 0.848 |
| 123° | 0.8387 |
| 124° | 0.829 |
| 125° | 0.8192 |
| 126° | 0.809 |
| 127° | 0.7986 |
| 128° | 0.788 |
| 129° | 0.7771 |
| 130° | 0.766 |
| 131° | 0.7547 |
| 132° | 0.7431 |
| 133° | 0.7314 |
| 134° | 0.7193 |
| 135° | 0.7071 |
| 136° | 0.6947 |
| 137° | 0.682 |
| 138° | 0.6691 |
| 139° | 0.6561 |
| 140° | 0.6428 |
| 141° | 0.6293 |
| 142° | 0.6157 |
| 143° | 0.6018 |
| 144° | 0.5878 |
| 145° | 0.5736 |
| 146° | 0.5592 |
| 147° | 0.5446 |
| 148° | 0.5299 |
| 149° | 0.515 |
| 150° | 0.5 |
| 151° | 0.4848 |
| 152° | 0.4695 |
| 153° | 0.454 |
| 154° | 0.4384 |
| 155° | 0.4226 |
| 156° | 0.4067 |
| 157° | 0.3907 |
| 158° | 0.3746 |
| 159° | 0.3584 |
| 160° | 0.342 |
| 161° | 0.3256 |
| 162° | 0.309 |
| 163° | 0.2924 |
| 164° | 0.2756 |
| 165° | 0.2588 |
| 166° | 0.2419 |
| 167° | 0.225 |
| 168° | 0.2079 |
| 169° | 0.1908 |
| 170° | 0.1736 |
| 171° | 0.1564 |
| 172° | 0.1392 |
| 173° | 0.1219 |
| 174° | 0.1045 |
| 175° | 0.0872 |
| 176° | 0.0698 |
| 177° | 0.0523 |
| 178° | 0.0349 |
| 179° | 0.0175 |
| 180° | 0 |
Полная таблица синусов для углов от 91° до 180°
| Угол | Sin (Синус) |
|---|---|
| 181° | -0.0175 |
| 182° | -0.0349 |
| 183° | -0.0523 |
| 184° | -0.0698 |
| 185° | -0.0872 |
| 186° | -0.1045 |
| 187° | -0.1219 |
| 188° | -0.1392 |
| 189° | -0.1564 |
| 190° | -0.1736 |
| 191° | -0.1908 |
| 192° | -0.2079 |
| 193° | -0.225 |
| 194° | -0.2419 |
| 195° | -0.2588 |
| 196° | -0.2756 |
| 197° | -0.2924 |
| 198° | -0.309 |
| 199° | -0.3256 |
| 200° | -0.342 |
| 201° | -0.3584 |
| 202° | -0.3746 |
| 203° | -0.3907 |
| 204° | -0.4067 |
| 205° | -0.4226 |
| 206° | -0.4384 |
| 207° | -0.454 |
| 208° | -0.4695 |
| 209° | -0.4848 |
| 210° | -0.5 |
| 211° | -0.515 |
| 212° | -0.5299 |
| 213° | -0.5446 |
| 214° | -0.5592 |
| 215° | -0.5736 |
| 216° | -0.5878 |
| 217° | -0.6018 |
| 218° | -0.6157 |
| 219° | -0.6293 |
| 220° | -0.6428 |
| 221° | -0.6561 |
| 222° | -0.6691 |
| 223° | -0.682 |
| 224° | -0.6947 |
| 225° | -0.7071 |
| 226° | -0.7193 |
| 227° | -0.7314 |
| 228° | -0.7431 |
| 229° | -0.7547 |
| 230° | -0.766 |
| 231° | -0.7771 |
| 232° | -0.788 |
| 233° | -0.7986 |
| 234° | -0.809 |
| 235° | -0.8192 |
| 236° | -0.829 |
| 237° | -0.8387 |
| 238° | -0.848 |
| 239° | -0.8572 |
| 240° | -0.866 |
| 241° | -0.8746 |
| 242° | -0.8829 |
| 243° | -0.891 |
| 244° | -0.8988 |
| 245° | -0.9063 |
| 246° | -0.9135 |
| 247° | -0.9205 |
| 248° | -0.9272 |
| 249° | -0.9336 |
| 250° | -0.9397 |
| 251° | -0.9455 |
| 252° | -0.9511 |
| 253° | -0.9563 |
| 254° | -0.9613 |
| 255° | -0.9659 |
| 256° | -0.9703 |
| 257° | -0.9744 |
| 258° | -0.9781 |
| 259° | -0.9816 |
| 260° | -0.9848 |
| 261° | -0.9877 |
| 262° | -0.9903 |
| 263° | -0.9925 |
| 264° | -0.9945 |
| 265° | -0.9962 |
| 266° | -0.9976 |
| 267° | -0.9986 |
| 268° | -0.9994 |
| 269° | -0.9998 |
| 270° | -1 |
Таблица синусов для углов 181° — 270°
| Угол | Sin (Синус) |
|---|---|
| 271° | -0.9998 |
| 272° | -0.9994 |
| 273° | -0.9986 |
| 274° | -0.9976 |
| 275° | -0.9962 |
| 276° | -0.9945 |
| 277° | -0.9925 |
| 278° | -0.9903 |
| 279° | -0.9877 |
| 280° | -0.9848 |
| 281° | -0.9816 |
| 282° | -0.9781 |
| 283° | -0.9744 |
| 284° | -0.9703 |
| 285° | -0.9659 |
| 286° | -0.9613 |
| 287° | -0.9563 |
| 288° | -0.9511 |
| 289° | -0.9455 |
| 290° | -0.9397 |
| 291° | -0.9336 |
| 292° | -0.9272 |
| 293° | -0.9205 |
| 294° | -0.9135 |
| 295° | -0.9063 |
| 296° | -0.8988 |
| 297° | -0.891 |
| 298° | -0.8829 |
| 299° | -0.8746 |
| 300° | -0.866 |
| 301° | -0.8572 |
| 302° | -0.848 |
| 303° | -0.8387 |
| 304° | -0.829 |
| 305° | -0.8192 |
| 306° | -0.809 |
| 307° | -0.7986 |
| 308° | -0.788 |
| 309° | -0.7771 |
| 310° | -0.766 |
| 311° | -0.7547 |
| 312° | -0.7431 |
| 313° | -0.7314 |
| 314° | -0.7193 |
| 315° | -0.7071 |
| 316° | -0.6947 |
| 317° | -0.682 |
| 318° | -0.6691 |
| 319° | -0.6561 |
| 320° | -0.6428 |
| 321° | -0.6293 |
| 322° | -0.6157 |
| 323° | -0.6018 |
| 324° | -0.5878 |
| 325° | -0.5736 |
| 326° | -0.5592 |
| 327° | -0.5446 |
| 328° | -0.5299 |
| 329° | -0.515 |
| 330° | -0.5 |
| 331° | -0.4848 |
| 332° | -0.4695 |
| 333° | -0.454 |
| 334° | -0.4384 |
| 335° | -0.4226 |
| 336° | -0.4067 |
| 337° | -0.3907 |
| 338° | -0.3746 |
| 339° | -0.3584 |
| 340° | -0.342 |
| 341° | -0.3256 |
| 342° | -0.309 |
| 343° | -0.2924 |
| 344° | -0.2756 |
| 345° | -0.2588 |
| 346° | -0.2419 |
| 347° | -0.225 |
| 348° | -0.2079 |
| 349° | -0.1908 |
| 350° | -0.1736 |
| 351° | -0.1564 |
| 352° | -0.1392 |
| 353° | -0.1219 |
| 354° | -0.1045 |
| 355° | -0.0872 |
| 356° | -0.0698 |
| 357° | -0.0523 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° | 0 |
Таблица синусов для углов от 271° до 360°
Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.
Чему равен синус 45? …
– А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/
http://kvn201.com.ua/table-of-sines.htm
[/spoiler]
|
Чему равен угол пи (сколько градусов)? Чему равен угол пи разделить на 2, 3, 4, 6? Чему равны синусы и косинусы этих углов?
Угол пи равен 180 градусов. Таким образом, угол пи/2 является прямым и равен 180/2 = 90 градусов. Угол пи/3 = 60 градусов (180/3 = 60). Угол пи/4 = 45 градусов (180/4 = 45). Угол пи/6 = 30 градусов (180/6 = 30). В приведенной ниже таблице приведены значения синусов, косинусов, тангенсов и котангенсов этих углов:
Рассмотрев таблицу, мы увидим, что синус угла пи/2= 1, а косинус пи/2 = 0. Синус угла пи/3 = √3/2, а косинус пи/3 = 1/2 или 0,5. Синус угла пи/4 = косинус пи/4 = √2/2. Синус угла пи/6 = 1/2 или 0,5, а косинус пи/6 = √3/2. автор вопроса выбрал этот ответ лучшим Начнем с того, что величина угла Пи радиан равна величине развернутого угла и это 180 градусов
Так, как разделить 180 на 2, 3, 4 и 6 совсем не сложно, получим значения в градусах для этих углов Пи/2=180°/2=90° Пи/3=180°/3=60° Пи/4=180°/4=45° Пи/6=180°/6=30° Что же такое синус? Давайте убедимся, что синус одного и того-же угла в двух разных прямоугольных треугольниках будет одинаковый. рассмотрим прямоугольный треугольник с острым углом альфа, со сторонами а, в и с и другой прямоугольный треугольник с острым углом альфа. По двум соответственно равным углам углам определяем, что они подобны. Следовательно их стороны пропорциональны и всегда при делении противолежащего катета на гипотенузу будем получать один и тот же результат.
исходя из того, что при вычислении синуса длина сторон не имеет значения, решили избавится от знаменателя, придав ему значение равное единице. Тогда в прямоугольном треугольнике, гипотенуза которого равна 1, синус угла равен длине катета напротив этого-же угла. аналогично косинус равен длине прилежащего катета
Нужно также учитывать, что косинус – это синус дополнительного угла. Sin 30° = Cos 60° = 1/2 Sin 60° = Cos 30° = √3/2
Sin 45° = Cos 45° = √2/2 Sin 90° = Cos 0° = 0 Sin 0° = Cos 90° = 1 Зная значения синуса и косинуса, очень просто найти значения тангенса и котангенса этих углов. Чему будут равны значения синуса, косинуса, тангенса и котангенса всех наших углов и других в таблице ниже
88SkyWalker88 5 лет назад Если учесть, что угол пи равняется 180 градусам, получается, что пи на 2 равняется 90 градусам. пи на 3 равняется 60 градусам. пи на 4 равняется 45 градусам. пи на 6 равняется 30 градусам. Sin(Пи) равняется 0. Cos(Пи) равняется -1. Sin(Пи на 2) равняется 1. Cos(Пи на 2) равняется 0. Sin(Пи на 3) равняется √3/2. Cos(Пи на 3) равняется 1/2. Sin(Пи на 4) равняется √2/2. Cos(Пи на 4) равняется √2/2.
moreljuba 5 лет назад В первую очередь необходимо отталкиваться от того факта, что сам угол Пи приравнивается в тригонометрии к 180-ти градусам. И вот уже исходя из этого ясно следующее: Пи/2 будет равняться 90 градусов, Пи/3 будет равняться 60 градусов, Пи/4 будет равняться 45 градусов, Пи/6 будет равняться 30 градусам. А вот информация относительно сунуса и косинуса: 1)Синус Пи/2 будет равняться 0, 2)Косинус Пи/2 будет равняться 1, 3)Синус Пи/3 будет равняться √3/2, 4)Косинус Пи/3 будет равняться 0,5, 5)Синус Пи/4 будет равняться √2/2, 6)Косинус Пи/4 будет равняться √2/2, Синус Пи/6 будет равняться 1/2, Косинус Пи/6 будет равняться √3/2.
владсандрович 5 лет назад Изначальная величина самого угла ПИ равена – ста восьмидесяти градусов – 180 градусов. Производя расчет, Угла пи/2 , есть не что иное как деление 180/2 и в итоге в частном мы получаем – 90 градусов. Теперь по аналогии, давайте разделим каждое цифровое значение угла, требуемые делители и получим правильные отношения: Угол пи/3, мы вычисляем деля 180/3 и в частном получаем 60 гр Угол пи/4 , рассчитываем деля 180/4 и в частном получаем 45 гр Угол пи/6 , рассчитываем деля 180/6 и в частном получаем 30 гр Что касается косинусов и синусов, то это справочные данные и их мы можем всегда просматривать в таблице:
Угол пи равен 180 градусам, соответственно, отсюда можно произвести расчет всех остальных углов, а именно: Пи/2 = 90°, Sin 90° = 0, Cos 90° = 1; Пи/3 = 60°, Sin 60° = √3/2, Cos 60° = 1/2; Пи/4 = 45°, Sin 45° = √2/2, Cos 45° = √2/2; Пи/6 = 30°, Sin 30° = 1/2, Cos 30° = √3/2. При этом значения тригонометрических функция самого угла Пи следующие: Sin 180° = 0°, Cos 180° = -1. дольфаника 5 лет назад Если знаем, сколько градусов составляет число Пи, то некоторые значения можно высчитать самостоятельно, если же значения получаем в результате сложных вычислений, тогда лучше пользоваться таблицей и постепенно запоминать значения. Чем чаще делаешь однотипные задания, тем быстрее запоминается. FantomeRU 5 лет назад В тригонометрии угол Пи равен 180 градусов. Соответственно, угол: Пи/2 = 90 градусов, Пи/3 = 60 градусов, Пи/4 = 45 градусов, Пи/6 = 30 градусам. Синус Пи/2=0, Косинус Пи/2=1, Синус Пи/3=√3/2, Косинус Пи/3=0,5, Синус Пи/4=√2/2, Косинус Пи/4=√2/2, Синус Пи/6=1/2, Косинус Пи/6=√3/2.
Alexgroovy 5 лет назад Переводя Пи в градусную меру получаем 180 градусов. Отсюда получаем:
Значения синусов/косинусов удобно представить в табличном виде
Первые две строчки таблицы содержат искомые значения синусов и косинусов пи на 2, пи на 3, пи на 4.
Zolotynka 5 лет назад Если знать, что угол π равен 180 градусам, то можно легко выстроить следующую логическую цепочку:
И далее:
В приведенной ниже табличке наглядно показаны величины синус и косинус данных углов:
bezdelnik 8 лет назад Угол Пи равен 180°, Sin(Пи) = 0, Cos(Пи) = -1. Пи/2=90° Sin(Пи/2)=1, Cos(Пи/2)=0. Пи/3=60°, Sin(Пи/3)=√3/2, Cos(Пи/3)=1/2. Пи/4=45°, Sin(Пи/4)=√2/2, Cos(Пи/4)=√2/2. Знаете ответ? |












