|
Синус два альфа формула, чему равен?АлексИванов 4 года назад
Как найти синус двойного угла, какая есть формула которая позволяет вычислить синус двойного угла 2α, если известны значения тригонометрический функций для угла α? sin (2α) = ? Rafail 4 года назад Синус двойного угла вычисляется по формуле: sin(2α) = 2*sin(α)*cos(α). комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
|
Есть интересный вопрос? Задайте его нашему сообществу, у нас наверняка найдется ответ! |
Делитесь опытом и знаниями, зарабатывайте награды и репутацию, заводите новых интересных друзей! |
Задавайте интересные вопросы, давайте качественные ответы и зарабатывайте деньги. Подробнее.. |
Статистика проекта за месяц
Новых пользователей: 4390
Создано вопросов: 16462
Написано ответов: 38260
Начислено баллов репутации: 910082
Синус двойного угла
ОПРЕДЕЛЕНИЕ
Формула синуса двойного угла имеет вид
(
sin 2 alpha=2 sin alpha cdot cos alpha
)
Эта формула легко получается из формулы синусоиды.
(
sin (alpha+beta)=sin alpha cdot cos beta+cos alpha cdot sin beta
)
вставляя его (
beta=alpha
)
В самом деле
(
sin 2 alpha=sin (alpha+alpha)=sin alpha cdot cos alpha+cos alpha cdot sin alpha=2 sin alpha cdot cos alpha
)
Синусоидальный угол может все еще выражаться через касательную и кокасательную:
(
sin 2 alpha=frac{2 operatorname{tg} alpha}{1+operatorname{tg}^{2} alpha}
), (
sin 2 alpha=frac{2 operatorname{ctg} alpha}{1+operatorname{ctg}^{2} alpha}
), (
sin 2 alpha=frac{2}{operatorname{tg} alpha+operatorname{ctg} alpha}
)
Примеры решения проблем
ПРИМЕР 1
Упростите выражение:
(
sin frac{alpha}{2} cdot cos frac{alpha}{2} cdot cos alpha
)
Выделите первые два фактора через синус двойного угла:
(
2 sin frac{alpha}{2} cdot cos frac{alpha}{2}=sin left(2 cdot frac{alpha}{2}right) sin frac{alpha}{2} cdot cos frac{alpha}{2}=frac{sin alpha}{2}
)
Тогда исходное выражение принимает вид
(
sin frac{alpha}{2} cdot cos frac{alpha}{2} cdot cos alpha=frac{sin alpha}{2} cdot cos alpha=frac{sin alpha cdot cos alpha}{2}
)
Умножьте числитель и знаменатель наклейки на 2:
(
sin frac{alpha}{2} cdot cos frac{alpha}{2} cdot cos alpha=frac{2 sin alpha cdot cos alpha}{2 cdot 2}
)
давайте применим к числителю формулу синуса двойного угла (
sin 2 alpha=2 sin alpha cdot cos alpha
) и, наконец, получим
(
sin frac{alpha}{2} cdot cos frac{alpha}{2} cdot cos alpha=frac{sin 2 alpha}{4}
)
(
sin frac{alpha}{2} cdot cos frac{alpha}{2} cdot cos alpha=frac{sin 2 alpha}{4}
)
ПРИМЕР 2
Найти значение выражения
(
frac{operatorname{tg} 22^{circ} 30^{prime}}{1+operatorname{tg}^{2} 22^{circ} 30^{prime}}
)
Мы используем формулу с двойным углом синуса (
sin 2 alpha=frac{2 operatorname{tg} alpha}{1+operatorname{tg}^{2} alpha}
) , получаем
(
frac{operatorname{tg} 22^{circ} 30^{prime}}{1+operatorname{tg}^{2} 22^{circ} 30^{prime}}=sin left(2 cdot 22^{circ} 30^{prime}right)=sin 45^{circ}=frac{sqrt{2}}{2}
)
(
frac{operatorname{tg} 22^{circ} 30^{prime}}{1+operatorname{tg}^{2} 22^{circ} 30^{prime}}=frac{sqrt{2}}{2}
)
ПРИМЕР 3
Упростить выражение
(
frac{sin ^{2} 2 alpha-4 sin ^{2} alpha}{sin ^{2} 2 alpha+4 sin ^{2} alpha-4}
)
Запишем в числителе и знаменателе синусов двойного угла, используя формулу (
sin 2 alpha=2 sin alpha cdot cos alpha
) , получим:
(
frac{sin ^{2} 2 alpha-4 sin ^{2} alpha}{sin ^{2} 2 alpha+4 sin ^{2} alpha-4}=frac{(2 sin alpha cdot cos alpha)^{2}-4 sin ^{2} alpha}{(2 sin alpha cdot cos alpha)^{2}+4 sin ^{2} alpha-4}=frac{4 sin ^{2} alpha cdot cos ^{2} alpha-4 sin ^{2} alpha}{4 sin ^{2} alpha cdot cos ^{2} alpha+4 sin ^{2} alpha-4}
)
Мы выставляем скобки в числителе (
4 sin ^{2} alpha
) , а в знаменателе – 4:
(
frac{sin ^{2} 2 alpha-4 sin ^{2} alpha}{sin ^{2} 2 alpha+4 sin ^{2} alpha-4}=frac{4 sin ^{2} alphaleft(cos ^{2} alpha-1right)}{4left(sin ^{2} alpha cdot cos ^{2} alpha+sin ^{2} alpha-1right)}=frac{sin ^{2} alphaleft(cos ^{2} alpha-1right)}{left(sin ^{2} alpha cdot cos ^{2} alpha+sin ^{2} alpha-1right)}
)
В полученном выражении мы используем основное тригонометрическое тождество и представляем единицу как (
1=sin ^{2} alpha+cos ^{2} alpha
), получаем
(
frac{sin ^{2} 2 alpha-4 sin ^{2} alpha}{sin ^{2} 2 alpha+4 sin ^{2} alpha-4}=frac{sin ^{2} alphaleft(cos ^{2} alpha-left(sin ^{2} alpha+cos ^{2} alpharight)right)}{left(sin ^{2} alpha cdot cos ^{2} alpha+sin ^{2} alpha-left(sin ^{2} alpha+cos ^{2} alpharight)right)}==frac{sin ^{2} alphaleft(cos ^{2} alpha-sin ^{2} alpharight)}{left(sin ^{2} alpha cdot cos ^{2} alpha+sin ^{2} alpha-cos ^{2} alpharight)}=frac{sin ^{2} alphaleft(-sin ^{2} alpharight)}{left(sin ^{2} alpha cdot cos ^{2} alpha-cos ^{2} alpharight)}
)
Мы помещаем знаменатель(
cos ^{2} alpha
) для скобок
(
frac{sin ^{2} 2 alpha-4 sin ^{2} alpha}{sin ^{2} 2 alpha+4 sin ^{2} alpha-4}=frac{sin ^{2} alphaleft(-sin ^{2} alpharight)}{left(sin ^{2} alpha cdot cos ^{2} alpha-cos ^{2} alpharight)}=frac{-sin ^{4} alpha}{cos ^{2} alphaleft(sin ^{2} alpha-1right)}
)
Снова в числителе записываем единицу, используя основное тригонометрическое тождество
(
frac{sin ^{2} 2 alpha-4 sin ^{2} alpha}{sin ^{2} 2 alpha+4 sin ^{2} alpha-4}=frac{-sin ^{4} alpha}{cos ^{2} alphaleft(sin ^{2} alpha-1right)}=frac{-sin ^{4} alpha}{cos ^{2} alphaleft(sin ^{2} alpha-left(sin ^{2} alpha+cos ^{2} alpharight)right)}=frac{-sin ^{4} alpha}{cos ^{2} alphaleft(sin ^{2} alpha-sin ^{2} alpha-cos ^{2} alpharight)}=frac{-sin ^{4} alpha}{cos ^{2} alphaleft(-cos ^{2} alpharight)}=frac{-sin ^{4} alpha}{-cos ^{4} alpha}=operatorname{tg}^{4} alpha
)
(
frac{sin ^{2} 2 alpha-4 sin ^{2} alpha}{sin ^{2} 2 alpha+4 sin ^{2} alpha-4}=operatorname{tg}^{4} alpha
)
Чему равен синус двух альфа
Найдите если
и
Поскольку угол лежит в четвёртой четверти, его тангенс отрицателен. Поэтому
тангенс в третьей четверти ведь положительный, получается, в ответе ошибка
Угол принадлежит 4 четверти.
Куда пропала цифра один в числителе?
Найдите если
и
Поскольку угол альфа лежит в третьей четверти, его тангенс положителен. Поэтому
Разве тангенс от 90′ до 135′ не отрицателен?
В третьей четверти тангенс неотрицателен.
Найдите если
и
Поскольку угол α лежит в четвертой четверти, его косинус положителен. Поэтому
В задании дан минус около 2 корня из 2/3. А если ориентироваться на ваш ответ, то минуса не должно быть! Здесь явная опечатка.
,
.
Найдите если
и
Поскольку угол альфа лежит в четвертой четверти, его синус отрицателен. Тогда
Из основного тригонометрического тождества получается
Но, так как речь идет о промежутке, на котором синус отрицателен (четвертая четверт), то из двух возможных значений выбираем отрицательное
Найдите если
Используем формулу косинуса двойного угла Имеем:
Источник
Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Угол поворота
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Синус (sin) угла поворота
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Основные функции тригонометрии
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Источник
Сумма и разность синусов и косинусов: вывод формул, примеры
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
Также представим сами углы в виде суммы полусумм и полуразностей.
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
Вывод формулы суммы косинусов
Вывод формулы разности косинусов
Примеры решения практических задач
Пример 1. Проверка формулы суммы синусов двух углов
Пример 2. Применение формулы разности синусов
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Источник
Тригонометрические формулы. Их вывод
Наиболее часто встречающиеся тригонометрические формулы:
(blacktriangleright) Основные тождества: [begin <|l|l|>hline sin^2 alpha+cos^2 alpha =1& mathrm, alpha cdot mathrm, alpha =1 \ &(sinalphane 0, cosalphane 0)\[0.5ex] hline &\ mathrm, alpha=dfrac<sin alpha> <cos alpha>&mathrm, alpha =dfrac<cos alpha> <sin alpha>\&\ 1+mathrm^2, alpha =dfrac1 <cos^2 alpha>& 1+mathrm^2, alpha=dfrac1<sin^2 alpha>\&\ (cosalphane 0)& (sinalphane 0) \ hline end]
(blacktriangleright) Формулы сложения углов: [begin <|l|r|>hline &\ sin<(alphapm beta)>=sinalphacdot cosbetapm sinbetacdot cosalpha & cos<(alphapm beta)>=cosalphacdot cosbeta mp sinalphacdot sinbeta\ &\ hline &\ mathrm, (alphapm beta)=dfrac<mathrm, alphapm mathrm, beta><1 mp mathrm, alphacdot mathrm, beta> & mathrm, (alphapmbeta)=-dfrac<1mp mathrm, alphacdot mathrm, beta><mathrm, alphapm mathrm, beta>\&\ cosalphacosbetane 0&sinalphasinbetane 0\ hline end]
(blacktriangleright) Формулы понижения степени: [begin <|lc|cr|>hline &&&\ sin^2alpha=dfrac<1-cos<2alpha>>2 &&& cos^2alpha=dfrac<1+cos<2alpha>>2\&&&\ hline end]
(blacktriangleright) Формулы произведения функций: [begin <|c|>hline \ sinalphasinbeta=dfrac12bigg(cos<(alpha-beta)>-cos<(alpha+beta)>bigg)\\ cosalphacosbeta=dfrac12bigg(cos<(alpha-beta)>+cos<(alpha+beta)>bigg)\\ sinalphacosbeta=dfrac12bigg(sin<(alpha-beta)>+sin<(alpha+beta)>bigg)\\ hline end]
(blacktriangleright) Выражение синуса и косинуса через тангенс половинного угла: [begin <|l|r|>hline &\ sin<2alpha>=dfrac<2mathrm, alpha><1+mathrm^2, alpha> & cos<2alpha>=dfrac<1-mathrm^2, alpha><1+mathrm^2, alpha>\&\ cosalphane 0 & sinalphane 0\ hline end]
(blacktriangleright) Формула вспомогательного аргумента: [begin <|c|>hline text<Частный случай>\ hline \ sinalphapm cosalpha=sqrt2cdot sin<left(alphapm dfrac<pi>4right)>\\ sqrt3sinalphapm cosalpha=2sin<left(alphapm dfrac<pi>6right)>\\ sinalphapm sqrt3cosalpha=2sin<left(xpm dfrac<pi>3right)>\\ hline text<Общий случай>\ hline\ asinalphapm bcosalpha=sqrtcdot sin<(alphapm phi)>, cosphi=dfrac a<sqrt>, sinphi=dfrac b<sqrt>\\ hline end]
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
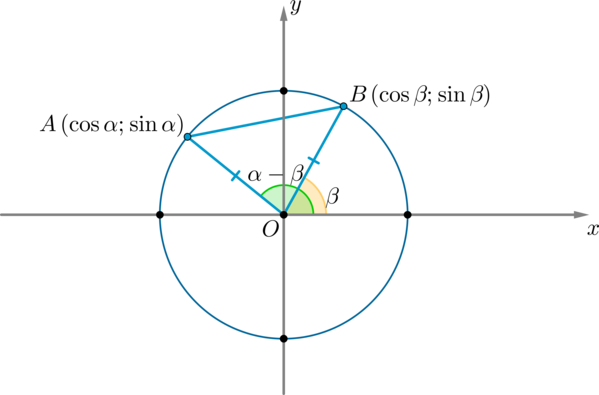
(AB^2=AO^2+BO^2-2AOcdot BOcdot cos(alpha-beta)=1+1-2cos(alpha-beta) (1)) (т.к. (AO=BO=R) – радиус окружности)
По формуле расстояния между двумя точками на плоскости:
Таким образом, сравнивая равенства ((1)) и ((2)) :
Отсюда и получается наша формула.
(blacktriangleright) Вывод остальных формул суммы/разности углов:
Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения (sin x=cos(90^circ-x)) и (cos x=sin (90^circ-x)) :
(blacktriangleright) Вывод формул двойного и тройного углов:
Данные формулы выводятся с помощью предыдущих формул:
1) (sin 2alpha=sin(alpha+alpha)=sinalphacosalpha+sinalphacosalpha=2sinalphacosalpha)
разделим числитель и знаменатель дроби на (cos^2alphane 0) (при (cosalpha=0 Rightarrow mathrm,2alpha=0) ):
5) (sin3alpha=sin(alpha+2alpha)=sinalphacos2alpha+cosalphasin2alpha=sinalpha(1-2sin^2alpha)+cosalphacdot 2sinalphacosalpha=)
6) Аналогично выводится, что (cos3alpha=cos(alpha+2alpha)=4cos^3alpha-3cosalpha)
(blacktriangleright) Вывод формул понижения степени:
Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:
1) (cos2alpha=2cos^2alpha-1 Rightarrow cos^2alpha=dfrac<1+cos2alpha>2)
2) (cos2alpha=1-2sin^2alpha Rightarrow sin^2alpha=dfrac<1-cos2alpha>2)
(blacktriangleright) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
Получим: (cos(alpha+beta)+cos(alpha-beta)=2cosalphacosbeta Rightarrow cosalphacosbeta=dfrac12Big(cos(alpha-beta)+cos(alpha+beta)Big))
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
3) Сложим формулы синуса суммы и синуса разности двух углов:
(blacktriangleright) Вывод формул суммы/разности функций:
Получили формулу суммы косинусов.
Получили формулу разности косинусов.
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
Аналогично выводится формула суммы котангенсов.
(blacktriangleright) Вывод формул выражения синуса и косинуса через тангенс половинного угла:
(разделим числитель и знаменатель дроби на (cos^2alphane 0) (при (cosalpha=0) и (sin2alpha=0) ):)
(blacktriangleright) Вывод формул вспомогательного угла:
Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.
(asin x+bcos x=sqrtleft(dfrac a<sqrt>sin x+ dfrac b<sqrt>cos x right)=sqrtbig(a_1sin x+b_1cos xbig))
(sqrt,big(cos phi sin x+sin phicos xbig)=sqrt,sin (x+phi)) (по формуле синуса суммы двух углов)
Значит, формула выглядит следующим образом: [<large,sin (x+phi),>> quad text <где >cos phi=dfrac a<sqrt>] Заметим, что мы могли бы, например, принять за (cos phi=b_1, sin phi=a_1) и тогда формула выглядела бы как [asin x+bcos x=sqrt,cos (x-phi)]
(blacktriangleright) Рассмотрим некоторые частные случаи формул вспомогательного угла:
(a) sin xpmcos x=sqrt2,left(dfrac1<sqrt2>sin xpmdfrac1<sqrt2>cos xright)=sqrt2, sin left(xpmdfrac<pi>4right))
(b) sqrt3sin xpmcos x=2left(dfrac<sqrt3>2sin xpm dfrac12cos xright)=2, sin left(xpmdfrac<pi>6right))
(c) sin xpmsqrt3cos x=2left(dfrac12sin xpmdfrac<sqrt3>2cos xright)=2,sinleft(xpmdfrac<pi>3right))
Источник
Чему равен синус двух альфа
Развернуть структуру обучения  |
Свернуть структуру обучения  |
Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:
Простейшие тригонометрические тождестваЧастное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств. Преобразование отрицательных углов тригонометрических функций (четность и нечетность)Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.
Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа). Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами: Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам: Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла Формулы универсальной тригонометрической подстановкиДанные формулы называются формулами универсальной тригонометрической подстановки. Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще. Тригонометрические тождества преобразования половины углаТригонометрические формулы сложения углов sin (α + β) = sin α · cos β + sin β · cos α Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций: Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла. Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов. Формулы преобразования суммы или разности тригонометрических функцийФормулы преобразования произведения тригонометрических функцийФормулы приведения тригонометрических функцийИсточник Adblock |
Основные понятия. Тригонометрия довольно древняя наука, и ее первые упоминания связаны с необходимостью в практичной жизни, в земледелии, астрономии и строительстве. Впервые именно астрономы вывели такие понятия как отношение сторон треугольника. А официальные названия функций стали появляться позже, например, синус, который получил свое название первым, получил свое название от греческих математиков уже в третьем веке до н.э.. а косинус является относительно молодым, и был выведен как дополнение к синусу. История тригонометрии обширна и интересна, из древней науки о треугольниках она перешла в известную нам науку о тригонометрических функциях. Для того чтобы разобраться в формулах двойного угла, необходимо вспомнить основные понятия тригонометрии. Начнём:
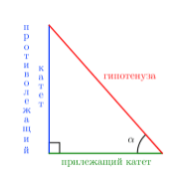
Тригонометрические функции:
- Синус угла — отношение катета напротив угла к гипотенузе:
- Косинус — деление прилежащей стороны треугольника на гипотенузу;
- Тангенс — отношение синуса к косинусу или катета напротив угла к прилежащему;
- Котангенс — деление косинуса на синус, или стороны прилежащей к углу на противолежащую.
Определение
Тригонометрическая окружность — это окружность нанесённая на систему координат, имеющая радиус равный единице и центр в начале координат.
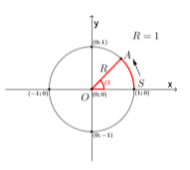
При помощи такой окружность можно наглядно разобраться в тригонометрических формулах и значениях. Например, найти числовые значения функций тригонометрии на системе координат, такие как:
[ sin 60^{circ}=frac{sqrt{3}}{2} ]; [ sin 30^{circ}=frac{1}{2} ]
Данные примеры будут использоваться далее по тексту. Мы можем посмотреть их значение на окружности на рисунке ниже.
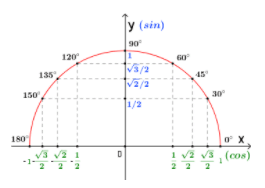
Основное тождество в тригонометрии, звучит так:
- Синус в квадрате угла плюс косинус в квадрате угла равны единице;
- Произведение тангенса и котангенса угла равно единице;
- Тангенс угла равен, делению, синуса этого угла на косинус, а котангенс наоборот косинуса на синус.
Данные тождества также будут применены для выведения формул двойного, тройного и т.д. углов.
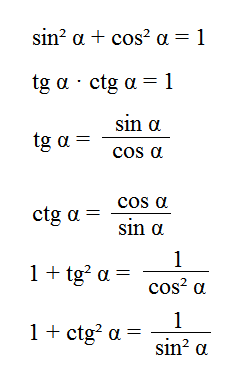
Формулы двойного угла в тригонометрии
Формулы двойного угла тригонометрических функций, необходимы для того чтобы выразить их, при этом угол должен иметь значение 2а, а также используя ТФ этого угла. Для отражения её на графике используют координаты с окружностью.
Список формул двойного угла
Прежде чем преступить к образованию формул двойного угла тригонометрии, давайте вспомним, что в тригонометрии углы принято писать в виде na, в такой записи п — обозначение натурального числа, а а — угол альфа. Обычно такая запись в тригонометрии используется без скобок, значит sin an, это тоже самое что sin (an). А также если рассмотреть запись sinn a, то она тоже имеет аналогичную запись вида (sin а)n . такое правило записи касается всех тригонометрических функций со степенями.
Рассмотрим какие же формулы двойного угла существуют на примерах.
Синус двойного угла формула:
sin 2 α = 2 * sin α * cos α;
Формула косинуса двойного угла:
cos 2 α = cos2α — sin2α, cos 2α = 1 − 2 * sin2α , cos 2α = 2 * cos2α−1;
Тангенс двойного угла формула:
[ operatorname{tg} 2 alpha=frac{2^{*} operatorname{tg} alpha}{1-operatorname{tg}^{2} alpha} ]
Котангенса:
[ operatorname{ctg} 2 alpha=frac{operatorname{ct}^{2} a-1}{2^{*} operatorname{ct} a} ]
Стоит не забывать, что выше приведённые формулы sin и cos, можно применять для любого значения угла. А вот если рассмотреть, формулы для тангенса, то при любых альфа где, tg 2a , имеет смысл, то есть при [a neq frac{pi}{4}+frac{pi}{2} cdot z], где z любое целое число. Что же касается формулы двойного угла котангенса, то при любом a, где ctg 2α определён на α ≠ 2 * z .
Как мы видим косинус с таким видом угла, наделён тремя вариантами записи формул, все они равноправны, а это значит, что результат их применения будет абсолютно одинаковым.
Доказательство формул двойного угла
Для того чтобы, формулы двойного угла были доказаны, вернёмся к истокам, формулам сложения. Сначала рассмотрим формулу синуса суммы, которая выглядит следующим образом:
[ operatorname{Sin}(a+b)=operatorname{Sin} a * cos b+cos a * sin b ]
Косинуса суммы:
[ operatorname{Cos}(a+b)=cos a * cos b-sin a * sin b ]
Если считать что a = b, тогда выходит:
[ operatorname{Sin}(a+a)=sin a * cos a+cos a * sin a=2 * cos a * sin a ]
И также для косинуса:
[ cos (a+a)=cos a * cos a-sin a * sin a=cos ^{2} alpha-sin ^{2} alpha ]
Таким способом мы доказали формулы синуса и косинуса двойного угла.
Формулы которые остались: cos 2α = 1 − 2 * sin2α , cos 2α = 2 * cos2α−1, выразили в таком виде благодаря приведению вместо единицы тождества суммы квадратов, cos2α +sin2α = 1. Поэтому вышло следующее:
Формулы приведения двойного угла: 1 − 2 * sin2α = cos2α +sin2α — 2 * sin2α = cos2α — sin2α.
И так же с третьих примеров формулы двойного угла.
2 * cos2α−1 = 2 * cos2α -( cos2α +sin2α ) = cos2α — sin2α.
Для того, чтобы выполнить доказательство формул для тангенса и котангенса двойного угла тоже применяется равенство следующего вида:
[ operatorname{tg} 2 alpha=frac{sin 2 alpha}{cos 2 alpha} text { и } operatorname{ctg} 2 alpha=frac{cos 2 alpha}{sin 2 alpha} . ]
Сделав замену на данные равенства получим следующие выражения:
[ operatorname{tg} 2 alpha=frac{sin 2 alpha}{cos 2 alpha}=frac{2 cdot sin alpha cdot cos alpha}{cos ^{2} alpha-sin ^{2} alpha} text { и } operatorname{ctg} 2 alpha=frac{cos 2 alpha}{sin 2 alpha}=frac{cos ^{2} alpha-sin ^{2} alpha}{2 cdot sin alpha cdot cos alpha} ]
Представленные выше выражения мы разделим на cos2α, при котором cos2α ≠ 0, а альфа имеет любое значение, когда тангенс угла альфа определён. Со вторым представленным выражением мы также произведём деление, только на sin2α, и он так же не равен нулю, и альфа имеет любое значение, при котором котангенс имеет смысл.
Получим следующие формулы:
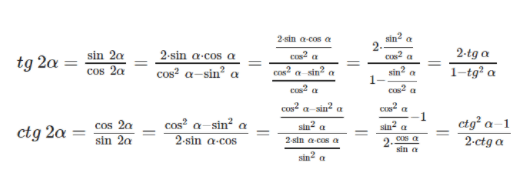
Нет времени решать самому?
Наши эксперты помогут!
Как использовать формулы двойного угла
Рассмотрим, как применяются формулы двойного угла в решении на примерах. Такие примеры помогут закрепить и понять материалы рассмотренный ранее.
Чтобы проверить справедлива ли формула двойного угла для при значении угла альфа в тридцать градусов, необходимо применить функции тригонометрии для этих углов. Если α = 30°, тогда 2α = 60°.
Проверим: sin60° = 2 * sin30° * cos30°cos60° = cos230° — sin230°.
Следующим шагом, подставим эти значения в :
[ operatorname{tg} 60^{circ}=frac{2 cdot operatorname{tg} 30^{circ}}{1-operatorname{tg}^{2} 30^{circ}} text { и } operatorname{ctg} 60^{circ}=frac{operatorname{ctg}^{2} 30^{circ}-1}{2 cdot operatorname{ctg} 30^{circ}} ]
Так как мы знаем, что синус тридцати градусов равен одной второй, косинус этого угла, равен корню из трёх, который поделен на два, тангенс заданного угла это корень из трёх на три, котангенс корень из трёх.
Получается, что синус двойного угла, то есть шестидесяти градусов, равен корню из трёх, который поделен на два; косинус — одной второй; тангенс корню из трёх; а котангенс корню из трёх делённому на три.
Получаем следующие выражения:
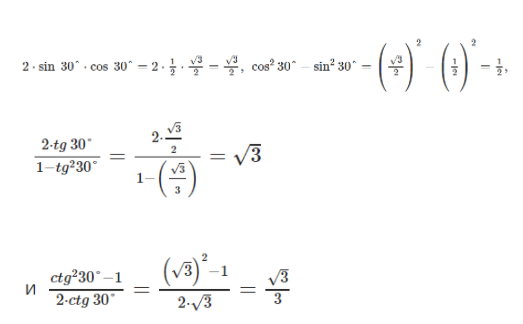
Сделав все операции по вычислению, можно прийти к выводу, что справедливость для угла альфа тридцати градусов, подтверждена.
Теперь мы понимаем, что применение формул тригонометрии двойного угла, это видоизменение тригонометрических выражений. Стоит также рассмотреть пример применения формул двойного угла, в случае, когда угол не равен 2a. К примеру возьмём значение [frac{5 pi}{6}]. Имея такое значение, для решения задания, его необходимо преобразовать, поэтому получаем следующее:
[a=frac{5 pi}{6}: 2=frac{5 pi}{12}], применив данное выражение формула двойного угла для косинуса получит следующий вид:
[ cos frac{5 pi}{6}=cos ^{2} frac{5 pi}{12}-sin ^{2} frac{5 pi}{12} ]
Пример:
Необходимо, через тригонометрические функции представить [sin frac{2 a}{3} text { при } frac{a}{6}].
Решение:
Так как в условии уже [frac{2 a}{3}=4 * frac{a}{6}], то применив дважды выше обозначенную формулу удвоенного угла, что выражая [sin frac{2 a}{3}], через функции угла [frac{a}{6}], с применением формулы двойного угла, выходит , [sin frac{2 a}{3}=2 * sin frac{a}{3} * cos frac{a}{3}], затем к [sin frac{a}{3} text { и } cos frac{a}{3}]в данном примере подставим снова данную формулу удвоенного угла и получим следующее выражение:
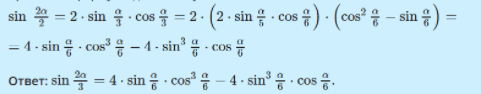
Формулы тройного угла и более углов
Так как зачастую в тригонометрии возникает необходимость вычисления не только двойного угла, но и больше, например тройного, четверного и тд. Стоит рассмотреть примеры их вычисления. Выведение их формул аналогично с выведением формул двойного угла, но для этого будем применять формулы сложения (суммы) двойного угла.
Пример:
sin 3α = sin ( 2 α + α ) = sin 2α * cos α + cos 2 α * sin α = 2 * sin α ⋅ cos α * cos α + ( cos2α — sin2α ) * sin α =
=3 * sin α * cos2α — sin3α
Заменим cos2α, на выражение 1 — sin2α, и теперь получившаяся ранее формула тройного угла sin 3α =3 * sin α * cos2α — sin3α, примет следующий вид: sin 3α = 3 * sin α * cos2α — sin3α = 3 *sin α — 4* sin3α
Аналогично поступим и с формулами cos тройного угла:
cos 3α = cos ( 2 α + α ) = cos 2α * cos α − sin 2α *sin α = ( cos2α — sin2α ) * cos α − 2* sin α * cos α * sin α =
= cos3α − 3* sin2α * cos α
Заменяем sin2α на выражение разности единицы и косинуса, 1 — cos2α, выходит следующая формула : cos 3α =
= -3 * cos α + 4* cos3α
Так как теперь у нас есть формулы тройного угла синуса и косинуса, мы можем вывести формулы тройного угла для тангенса и котангенса, подставив полученные выражения в первичные формулы:

И так далее…
К примеру, чтобы привести формулу угла четыре альфа, для удобства лучше 4а представить, как 2 * 2а, и в результате мы получим, что для выведения формулы для 4а, нужно использовать две формулы двойного угла.
А для выведения формулы угла пятой степени, 5а, необходимо выполнить 5а как сумму тройного и двойного угла, то есть 2а+3а.
В результате мы получим выражение из суммы двух формул двойного и тройного угла. Стоит отметить, что такое же правило будет действовать если необходимо вывести формулу половинного угла.
Область применения
Для того чтобы найти значение тригонометрических функций, берётся окружность на оси координат, у которой радиус равен единице, а диаметры у неё находятся в перпендикулярном положении.
Для такого вычисления нам понадобится отложить от точки, которая принадлежит окружности различные дуги, любой длины. Соответственно если мы отложим их против часовой стрелки они примут положительное значение, а если по часовой, то отрицательное.
Допустим конец дуги имеет некую длину s, в таком случае проекция радиуса в любом выбранном значении диаметра станет значением косинуса данной дуги. Выбранная длина s, или радианная мера угла, будет считаться числом аргумента. А если этот самый аргумент, это тригонометрическая функция угла, то мы знаем, что значение может быть и в градусах.
Мы знаем, что острый угол имеет значения больше нуля, но меньше п2. В таком случае тригонометрическая функция рассматривается как катет делённый на гипотенузу. Такие названия сторон связаны с прямоугольным треугольником, в котором величина угла равна 90 градусов.
Чтобы решить задачи с функциями тригонометрии, используют теорему Пифагора. Такая теорема основана на свойствах того самого прямоугольного треугольника, в котором квадрат гипотенузы равен сумму квадратов катетов.
Так как дуга делит окружность на несколько частей, то мы можем увидеть, что углы лежащие в первой четверти больше нуля. А во второй синус меньше, а косинус больше нуля, а в третьей все функции будут меньше нуля, то есть отрицательными, четвёртая имеет значения противоположные второй. Не стоит забывать, что для построения окружности вам понадобится циркуль.
Как мы видим формулы двойного угла, не так трудно вывести, для этого необходимо знать основные тригонометрические тождества и разобраться в единичной окружности на оси координат. Также необходимо отметить, что формулы двойного угла, как и другие формулы тригонометрии используются в разных сферах жизни:
- В астрономии, учёные с помощью формул вычисляют положение небесных тел, а также расстояние до них;
- Для различного вида навигации, к примеру, морской и воздушной;
- В медицине и биологии, при построении биоритма живых организмов, а также тригонометрия служит основой работы некоторой медицинской техники;
- Архитекторам она важна при создании планов строений;
- но и это не всё, тригонометрия важна и для экономики, в производстве и создании электроники, в различных аналитических вычислениях, акустических построениях и многом другом.
Опубликовано 10.06.2017 по предмету Математика от Гость
>> <<
Найдите синус 2 альфа если известно что синус альфа равен 12/13 и п/2 <-альфа <- п
Ответ оставил Гость
Sin2α= 2*sinα*cosα
cosα=(1-sin^2α) всё это под корнем
cosα = – 5/13
т.к. π/2<-α<-π,значит синус находится во второй четверти и он положителен,а косинус во второй четверти отрицателен!
sin2α= 2*sinα*cosα=2*12/13*(-5/13)= – 120/169
Оцени ответ
Подпишись на наш канал в телеграм. Там мы даём ещё больше полезной информации для школьников!

Найти другие ответы
Загрузить картинку