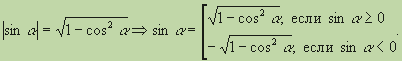Тригонометрия — это раздел математики, в котором изучаются тригонометрические функции, их свойства, взаимосвязи и применение.
Слово «тригонометрия» образовано от греческих слов «trigonom» (треугольник) и «metreo» (измерять).
Возникновение и развитие тригонометрии связаны с практическими потребностями в измерении и вычислении сначала элементов треугольников на местности, а позднее — в строительстве, мореплавании и астрономии. Современная тригонометрия широко применяется в разных областях математики, в частности в геометрии, других науках, в технике. Например, тригонометрические функции используются при решении задач оптики, задач кинематического анализа и синтеза механизмов, гармонического анализа и других.
Cинус, косинус, тангенс, котангенс острого угла прямоугольного треугольника
Нет понятий «просто синус» или «просто косинус», не имеют смысла записи типа «sin» и «cos» сами по себе, они сами по себе никакой величины не обозначают (точно так же, как и, например, значок квадратного корня сам по себе). Те, кто этого не понимает, часто делает грубую ошибку типа: sin x /cos x = in /co
Есть понятие синуса, косинуса, тангенса, котангенса как тригонометрических функций угла. Здесь угол — аргумент функции. Он может обозначаться «х», «а», «альфа», «бета», «гамма», «фи», «дельта» или ещё какой-нибудь буквой. Суть от этого не меняется.
Для того, чтобы более наглядно представить приведенные ниже определения, начертите прямоугольный треугольник. Это треугольник, один из углов которого — прямой (т.е. один из углов равен 90 градусов). Стороны, прилежащие к прямому углу (перпендикулярные друг другу стороны) — это катеты данного прямоугольного треугольника. Противолежащая прямому углу сторона — это гипотенуза.
Теперь выберите любой из двух других (острых) углов треугольника и обозначьте его, например, альфа. Один из катетов будет примыкать к вершине этого угла (и, собственно, образовывать этот угол вместе с гипотенузой). Это — прилежащий катет. Другой катет не примыкает к вершине этого угла, он находится как бы напротив данной вершины. Это — противолежащий катет.
Кстати, почему-то не все представляют, что такое угол треугольника при данной вершине. У треугольника (обозначим его ABC) есть три вершины: А, В и С. Когда говорят об угле А треугольника, то подразумевают угол, образованный сторонами ВА и АС. Это и есть угол при вершине А.
Итак,
Синусом острого угла называется отношение противолежащего этому углу катета к гипотенузе.
Косинусом острого угла называется отношение прилежащего к этому углу катета к гипотенузе.
Тангенсом острого угла называется отношение противолежащего этому углу катета к прилежащему катету.
Котангенсом острого угла называется отношение прилежащего этому углу катета к противолежащему катету.
Секансом острого угла называется отношение гипотенузы к прилежащему к этому углу катету. Обозначается: sec x.
Косекансом острого угла называется отношение гипотенузы к противолежащему этому углу катету. Обозначается: cosec x.
Как найти углы в прямоугольном треугольнике, если известны стороны?
Дан треугольник АВС, угол С — прямой.
Стороны АВ, АС и ВС известны.
Т.к. угол С — прямой, он равен 90 градусам.
Другие углы можно найти, например, так:
если известен катет и гипотенуза
sinA = BC / AB,
sinB = AC / AB,
если известны два катета
tg A = BC / AC
tg B = AC / BC
Предположим, получили, что sin A = ½. По таблице смотрим, что такому значению sin x соответствует величина угла 30 градусов.
Или, к примеру, получили, что tg B = 1. Значит, угол В равен 45 градусов.
Или, к примеру, мы получили, что sin B = 0,259. По таблице Брадиса или с помощью калькулятора находим, что угол В равен 15 градусов.
sin 15° = 0,259
arcsin0,259 = 15°
Как найти углы в прямоугольном треугольнике, если известен один угол?
Поскольку треугольник прямоугольный, то один из его углов равен 90 градусов. Величина второго угла известна (по условию задачи, обозначим её альфа). В сумме углы треугольника составляют 180 градусов. Значит, третий угол равен 180—90—альфа.
Еединичная окружность (единичный круг)
Единичный круг — это круг с центром в начале координат и радиусом, равным единице (R = 1).
Единичная окружность — это окружность единичного круга (т.е. окружность с центром в начале координат и с радиусом, равным единице).
Единичный радиус-вектор — это вектор, начало которого совпадает с началом координат, а его длина равна единице.
Углы отсчитывают от начального положения подвижного радиуса-вектора (совпадает с положением Ох).
Координатные четверти отсчитываются так:
y
|
|
(II четверть) | (I четверть)
|
________________________ x
|0
|
(III четверть) | (IV четверть)
|
|
Угол первой четверти — от 0 до 90 градусов (от 0 до пи/2).
Угол второй четверти — от 90 до 180 градусов (от пи/2 до пи).
Угол третьей четверти — от 180 до 270 градусов (от пи до 2пи/3).
Угол четвертой четверти — от 270 до 360 градусов (от 2пи/3 до 2пи).
Например:
- углы первой четверти: 30 градусов, 85 градусов, пи/4;
- углы второй четверти: 120 градусов, 178 градусов;
- углы третьей четверти: 205 градусов, 260 градусов;
- углы четвертой четверти: 272 градуса, 305 градусов.
Тригонометрические функции
К тригонометрическим функциям относятся функции:
y = sin x;
y = cos x;
y = tg x;
y = ctg x;
y = sec x;
y = cosec x.
Синусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его длине.
Косинусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его длине.
Тангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его проекции на ось Ох.
Котангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его проекции на ось Оу.
Секансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Ох.
Косекансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Оу.
Тригонометрические функции связаны между собой, и этим можно воспользоваться для нахождения синуса угла по его косинусу или котангенсу или косинуса угла по его синусу или тангенсу.
Как найти синус угла, если известен косинус?
Нужно воспользоваться основным тригонометрическим тождеством:
sin2a + cos2a = 1
sin2a = 1 − cos2a
|sin a| = КОРЕНЬ(1 − cos2a)
sin a = ± КОРЕНЬ(1 − cos2a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)
Как найти косинус угла, если известен синус?
Нужно воспользоваться основным тригонометрическим тождеством:
sin2a + cos2a = 1
cos2a = 1 − sin2a
|cos a| = КОРЕНЬ(1 − sin2a)
cos a = ± КОРЕНЬ(1 − sin2a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)
Как найти синус угла, если известен котангенс?
Нужно воспользоваться тригонометрическим тождеством
1 + ctg2 a = 1/sin2 a
sin2 a = 1 / (1 + ctg2 a)
|sin a| = 1/ КОРЕНЬ(1 + ctg2 a)
sin a = ±1/ КОРЕНЬ(1 + ctg2 a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, котангенс положительный в I и III четвертях)
Как найти косинус угла, если известен тангенс?
Нужно воспользоваться тригонометрическим тождеством
1 + tg2 a = 1/cos2 a
cos2 a = 1 / (1 + tg2 a)
|cos a| = 1/ КОРЕНЬ(1 + tg2 a)
cos a = ±1/ КОРЕНЬ(1 + tg2 a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (косинус положительный в I и IV четвертях, тангенс положительный в I и III четвертях)
Тригонометрическое тождество
Тригонометрическим тождеством называется равенство, в которое входят тригонометрические функции и которое удовлетворяется произвольным допустимым значением угла — аргумента тригонометрических функций, но не удовлетворяется, если каждую в отдельности тригонометрическую функцию заменить произвольной величиной.
Основные тригонометрические тождества:
sin2a + cos2a = 1
tg a = sin a / cos a
ctg a = cos a / sin a
sec a = 1 / cos a
cosec a = 1 / sin a
Arcsin, arcos, arctg, arcctg (обратные тригонометрические функции)
- arcsin — читается: арксинус;
- arcos — читается: арккосинус;
- arctg — читается: арктангенс;
- arcctg — читается: арккотангенс.
arcsin, arcos, arctg, arcctg — это обратные тригонометрические функции.
Обратной тригонометрической функцией y = arcsin x называют угол у, взятый на отрезке от –пи/2 до +пи/2, синус которого равен х:
y = arcsin x sin y = x
Обратной тригонометрической функцией y = arccos x называют угол у, взятый на отрезке от –пи до +пи, косинус которого равен х:
y = arccos x cos y = x
Обратной тригонометрической функцией y = arctg x называют угол у, взятый на промежутке от –пи/2 до +пи/2 (исключая концы), тангенс которого равен х:
y = arctg x tg y = x
Обратной тригонометрической функцией y = arcctg x называют угол у, взятый на промежутке от 0 до пи (исключая концы), котангенс которого равен х:
y = arctg x tg y = x
Например,
sin 30° = 0,5
arcsin0,5 = 30°
Синусоида и косинусоида
График функции y = sin x называется синусоидой.
График функции y = cos x называется косинусоидой.
Источники информации:
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра. Под редакцией П.Ф. Фильчакова. —К.: Наукова думка, 1967. — 442 с.
- В.Д. Гетманцев, О.Ф. Саушкiн. Математика: Тригонометрiя: Посiбник для слухачiв пiдотовчих вiддiлень, вступникiв до вищих навчальних закладiв, студентiв педагогiчних iнститутiв (на укр.). —К.: Либiдь, 1994. — 144 с.
- docme.ru — зачем нужна тригонометрия?
- ru.wikipedia.org — Википедия — тригонометрия;
- ru.wikihow.com — как изучать тригонометрию?
Как найти синус угла, если известен косинус, и наоборот?
ОбразованиеМатематика+2
Лилия Туманова
4 февраля 2021 · 1,9 K
ОтветитьУточнить
Игорь Мушников
Топ-автор
3,4 K
Википедист (автор, редактор) с 2008. Интересы широкие – мироустройство – физика, история… · 4 февр 2021
См. тригонометрические тождества.
Сумма квадратов синуса и косинуса равны единице.
Соответственно синус = корень квадратный из (1 – квадрат косинуса)
2,1 K
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30°, 45°, 60°. Если угол выходит за пределы 90°, то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α, можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45°, мы сможем определить значение синуса 30°, воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α. Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0°, 90°, 180°, 270°, 360°.
Разобьем эти углы на четыре группы: 360·z градусов (2π·z рад), 90+360·z градусов (π2+2π·z рад), 180+360·z градусов (π+2π·z рад) и 270+360·z градусов (3π2+2π·z рад), где z- любое целое число.
Изобразим данные формулы на рисунке:
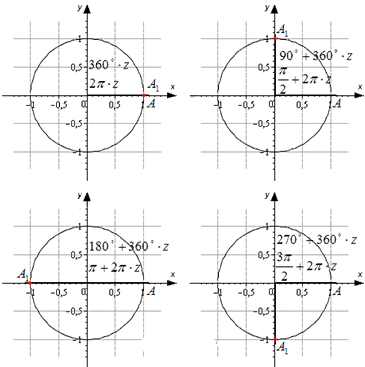
Для каждой группы соответствуют свои значения.
При повороте из точки A на 360·z°, она переходит в себя. А1(1, 0). Синус 0°, 360°, 720° равен 0, а косинус равен 1. Представим это в виде формулы: sin (360°·z)=0 и cos (360°·z)=1 .
Можно определить, что tg (360°·z)=01=0 , а котангенс не определен.
Если А(1, 0) повернуть на 90+360·z°, то она перейдет в А1 (0, 1). По определению: sin (90°+360°·z) =1 и cos (90°+360°·z) =0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: ctg (90°+360°·z) =01=0 .
Рассмотрим особенности для третьей группы углов. После поворота точки А(1, 0) на любой из углов 180+360·z°, она перейдет в A1(−1, 0). Мы находим значения функций кроме тангенса.
Рассмотрим правила для четвертой группы углов. При повороте точки на 270+360·z° мы попадем в A1(0, −1). Мы находим значения всех функций кроме тангенса.
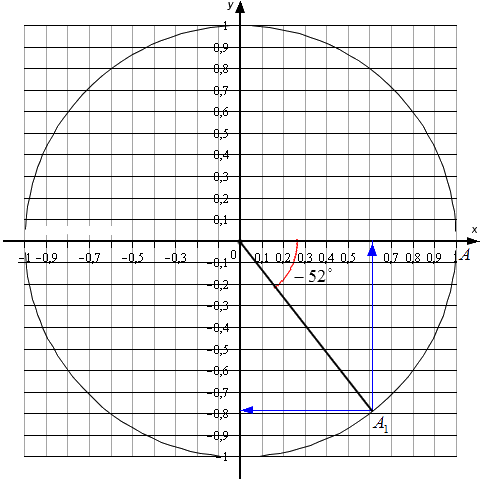
Для углов, которые не относятся к перечню от 0 °, 90 °, 180 °, 270 °, 360 °…, точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла −52 °. Выполним построения.
Согласно рисунку, абсцисса А1 ≈ 0,62, а ордината ≈ −0,78. Соответственно, sin(-52°)≈-0,78 и cos(-52°)≈0,62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: tg(-52°)≈-0, 780, 62≈-1,26 и ctg(-52°)≈0,62-0,78≈-0,79.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
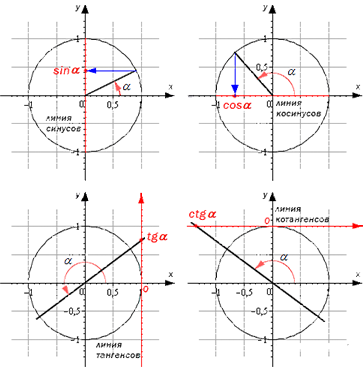
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α, cos α, tg α, ctg α
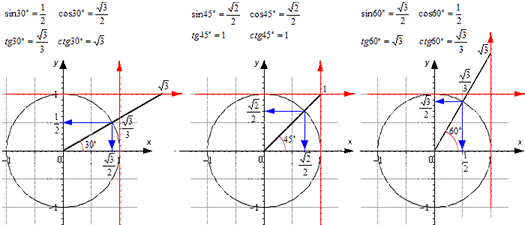
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1. Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 12-122=32 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30°=121=12 и sin 60°=321=32 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30°=321=32 и cos 60°=121=12 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: tg 30°=1232=13=33 и tg 60°=3212=3 . Находим котангенс по подобной схеме: сtg 30°=3212=3 и сtg 60°=1232=13=33 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45° и гипотенузой, которая равна 1. Используем теорему Пифагора. Согласно формуле, длины катетов равны 22 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: ctg 45°=2222=1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α, cos α, tg α, ctg α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin2α+cos2α=1 .
Тангенс по известному косинусу tg2α+1=1cos2α .
Котангенс по известному синусу или наоборот 1+ctg2α= 1sin2α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: tg α·ctg α=1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Необходимо найти значение синуса угла π8, если tg π8=2-1 .
Сначала найдем котангенс угла: ctgπ8=1tgπ8=12-1=2+1(2-1)·(2+1)= 2+1(2)2-12=2+1 Воспользуемся формулой 1+ctg2α=1sin2α . Благодаря этому мы вычисляем значение синуса. Имеем
sin2π8=11+ctg2π8=11+(2+1)2=14+22=12·(2+2)=2-22·(2+2)·(2-2)==2-22·(22-(2)2)=2-24
Для завершения необходимо определить значение синуса. Угол π8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π8=sin2π8=2-24=2-22 . sin π8=2-22.
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 °. Сведение к углу из интервала от 0 до 90 °. Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210°. Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30°: sin 210°=sin(180°+30°)=-sin 30°=-12 , или косинуса 60 ° sin 210°=sin(270°-60°)=-cos 60°=-12.
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π8, который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение tgπ8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства tg2π8=1-cosπ41+cosπ4 . Значения косинуса угла π4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
tg2π8=1-cosπ41+cosπ4=1-221+22=2-22+2==(2-2)2(2+2)·(2-2)=(2-2)222-(2)2=(2-2)22
Угол π8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: tgπ8=tg2π8=(2-2)22=2-22=2-1
tgπ8=2-1.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.

Внимание! Эти формулы работают только если аргументы у тригонометрических функций одинаковые, т.е.
(sin^2 776^° +cos^2 776^° =1)
(tg, 3xcdot ctg, 3x=1)
Но:
(sin^2x+cos^23x≠1)
(tg, xcdot ctg, y≠1)
Все формулы связи тригонометрических функций учить не надо, потому что они достаточно легко получаются друг из друга несложными преобразованиями (подробности в этих видео). Кроме того, при частом использовании они постепенно запоминаются сами.
Примеры применения формул связи
Зачем нужны формулы связи? Они позволяют найти все тригонометрические функции угла, если известна лишь одна из них, а также дают возможность упрощать выражения, доказывать тождества, решать тригонометрические уравнения, заменяя одну функцию другой и так далее.
Пример. Найдите (5sin,α), если (cos,α=frac{2sqrt{6}}{5}) и (α∈(frac{3π}{2};2π)).
Решение. Нам известен косинус, найти надо синус. А что связывает синус и косинус? Основное тригонометрическое тождество:
(sin^2α+cos^2α=1).
Подставим вместо косинуса его значение:
(sin^2α+)((frac{2sqrt{6}}{5}))(^2=1)
(sin^2α+)(frac{4cdot 6}{25})(=1)
(sin^2α+)(frac{24}{25})(=1)
(sin^2α=1-)(frac{24}{25})
(sin^2α=)(frac{1}{25})
(sinα=±)(frac{1}{5})
Внимание! Последняя строчка – место, где теряется огромное количество баллов на ЕГЭ! Это одна из самых популярных ошибок – забыть отрицательный корень. Пожалуйста, раз и навсегда запомните, что у неполного квадратного уравнения вида (x^2=a) (при (a>0)) два корня (x_1=sqrt{a}) и (x_2=-sqrt{a}). Пусть двойка над иксом (та которая «квадрат») будет вам вечным маяком, сигнализирующим: «тут ДВА корня! Два! Не забудь!»
Вернемся к задаче. Получилось, что синус может иметь значение (frac{1}{5}), а может (-)(frac{1}{5}). И какое значение нам надо выбрать – с минусом или плюсом? Тут нам на помощь приходит информация, что (α∈(frac{3π}{2};2π)). Давайте нарисуем числовую окружность и отметим отрезок ((frac{3π}{2};2π)).

Обратите внимание – в этой четверти синус принимает только отрицательные значения (можно провести перпендикуляры до оси синусов и убедиться, что это так).

Значит, в нашем случае (sin,α=-frac{1}{5}) т.е. (5sin,α=5cdot(-frac{1}{5})=-1).
Ответ: (-1).
Пример.Найдите (tg,α), если (cos,α=)(frac{sqrt{10}}{10}) и (α∈(frac{3π}{2};2π)).
Решение. Есть 2 пути решения этой задачи:
– напрямую вычислить тангенс через формулу (tg^2α+1=)(frac{1}{cos^2α});
– сначала с помощью тождества (sin^2α+cos^2α=1) найти (sin,α), а потом через формулу (tg,α=)(frac{sin,α}{cos,α}) получить тангенс.
В учебниках обычно идут первым путем, поэтому мы пойдем вторым.
Вычисляем синус:
(sin^2α+)((frac{sqrt{10}}{10})^2)(=1)
(sin^2α+)(frac{10}{100})(=1)
(sin^2α+)(frac{1}{10})(=1)
(sin^2α=1-)(frac{1}{10})
(sin^2α=)(frac{9}{10});
(sin,α=±)(frac{3}{sqrt{10}})
Опять (α∈(frac{3π}{2};2π)), значит в итоге синус может быть только отрицательным. То есть, (sin,α=-)(frac{3}{sqrt{10}}).
А теперь вычисляем тангенс: (tg,α=-)(frac{3}{sqrt{10}})(:)(frac{sqrt{10}}{10})(=)(-frac{3}{sqrt{10}}cdotfrac{10}{sqrt{10}})(=-)(frac{30}{10})(=-3).
Ответ: (-3).
Пример. Известно, что (tg,α=-frac{3}{4}) и (frac{π}{2}<α<π). Найдите значения трех других тригонометрических функций угла (α).
Решение. Проще всего из тангенса найти котангенс:
(ctg, α=)(frac{1}{tg, α})
(ctg,α=1:(-frac{3}{4})=1cdot(-frac{4}{3})=-frac{4}{3}).
Теперь вычислим косинус по упомянутой выше формуле:
(tg^2 α+1=)(frac{1}{cos^2α})
((-)(frac{3}{4}))(^2+1=)(frac{1}{cos^2α})
(frac{9}{16})(+1=)(frac{1}{cos^2α})
(frac{9+16}{16})(=)(frac{1}{cos^2α})
(frac{25}{16})(=)(frac{1}{cos^2α})
(cos^2α=)(frac{16}{25})
(cosα=±)(frac{4}{5})
Опять перед нами стоит выбор плюс или минус. Отметим отрезок ((frac{π}{2};π)) на тригонометрической окружности и посмотрим какие значения принимает косинус в этой четверти, чтобы определится со знаком.

Очевидно, что косинус отрицателен в этой четверти, а значит (cos,α=-)(frac{4}{5}).
Осталось найти синус:
(sin^2α+cos^2α=1)
(sin^2α+(-)(frac{4}{5})()^2=1)
(sin^2α+)(frac{16}{25})(=1)
(sin^2α=1-)(frac{16}{25})
(sin^2α=)(frac{9}{25})
(sin,α=±)(frac{3}{5})
Опять используем круг, чтобы определить знак.

Получается, что (sin,α=)(frac{3}{5}).
Ответ: (ctg,α=-)(frac{4}{3}); (cos,α=-)(frac{4}{5}); (sin,α=)(frac{3}{5}).
Пример (ЕГЭ). Найдите (tg^2 α), если (5 sin^2α+13 cos^2α=6).
Решение. Давайте пойдем от того, что известно. В равенстве (5 sin^2α+13 cos^2α=6) синус заменим на косинус:
(5(1-cos^2α)+13 cos^2α=6)
(5-5 cos^2α+13 cos^2α=6)
(5+8 cos^2α=6)
(8 cos^2α=1)
(cos^2α=)(frac{1}{8})
Поняли почему именно синус заменили на косинус, а не наоборот? И почему не надо извлекать корень, досчитывая до «чистого» косинуса? Потому что для нахождения (tg^2α) хорошо подходит формула (tg^2α+1=)(frac{1}{cos^2α}) :
(tg^2 α+1=1:)(frac{1}{8})
(tg^2 α+1=1cdot)(frac{8}{1})
(tg^2 α+1=8)
(tg^2 α=7)
Ответ: (7).
Теперь еще одна задача из ЕГЭ, для наглядности мы ее решение оформили картинкой.

Пример. Упростите выражение (frac{1}{sin^2 α})(-ctg^2 α-cos^2 β).
Решение.
|
(frac{1}{sin^2 α})(-ctg^2 α-cos^2 β) |
Самое очевидное, что можно сделать – это представить котангенс как отношение косинуса к синусу. |
|
|
(=)(frac{1}{sin^2 α})(-)(frac{cos^2α}{sin^2 α})(-cos^2 β=) |
Приводим дроби к общему знаменателю. |
|
|
(=)(frac{1-cos^2α}{sin^2 α})(-cos^2 β=) |
(1-cos^2α) можно заменить на (sin^2 α). |
|
|
(=)(frac{sin^2 α}{sin^2 α})(-cos^2 β=) |
Сокращаем синусы. |
|
|
(=1-cos^2 β=sin^2 β). |
Пример. Докажите тождество (frac{cos^4α-sin^4α}{(1-sinα)(1+sinα)})(+2tg^2 α=)(frac{1}{cos^2 α}).
Решение.
|
(frac{cos^4α-sin^4α}{(1-sinα)(1+sinα)})(+2tg^2 α=)(frac{1}{cos^2 α}) |
Чтобы доказать это тождество, будем преобразовывать левую часть, пытаясь свести ее к правой. Поехали. Разложим числитель левой дроби по формуле разности квадратов, а знаменатель, наоборот, соберем по ней же. |
|
|
(frac{(cos^2α-sin^2α )(cos^2 α+sin^2α)}{1-sin^2α})(+2tg^2 α=)(frac{1}{cos^2 α}) |
Очевидно, что вторая скобка числителя равна (1) (по основному тригонометрическому тождеству), а знаменатель можно заменить на (cos^2 α). |
|
|
(frac{cos^2α-sin^2α}{cos^2 α})(+2tg^2 α=)(frac{1}{cos^2 α}) |
Теперь разложим тангенс по формуле (tg, α=)(frac{sin,α}{cos,α}). |
|
|
(frac{cos^2α-sin^2α}{cos^2 α})(+2)(frac{sin^2α}{cos^2α})(=)(frac{1}{cos^2 α}) |
Приводим дроби к общему знаменателю. |
|
|
(frac{cos^2α-sin^2α+2 sin^2α}{cos^2 α})(=)(frac{1}{cos^2 α}) |
Приводим подобные слагаемые. |
|
|
(frac{cos^2α+sin^2α}{cos^2 α})(=)(frac{1}{cos^2 α}) |
И вновь нас выручает основное тригонометрическое тождество |
|
|
(frac{1}{cos^2 α}) (=)(frac{1}{cos^2 α}) |
Левая часть полностью идентична правой, то есть тождество доказано.
Как доказать все формулы связи
Для решения задачи следует воспользоваться основным тригонометрическим тождеством: сумма квадратов синуса и косинуса одного и того же угла равна 1.
Отсюда синус угла равен плюс минус корню квадратному из разности 1 и квадрата косинуса угла.
Какой знак перед корнем квадратным брать зависит от того, где находится угол, косинус которого известен.
Если в условии задачи значение косинуса больше нуля (равенство нулю рассмотрено, как частный случай, ниже, хотя применимы рассуждения и для нуля), то угол находится либо в 1-й, либо в 4-й четверти.
Для определенности в условии задачи обычно дается ограничение для угла.
Если указано, что 0< a< 90 (1 четверть), то значение синуса тоже следует брать со знаком плюс.
Если же 270< a< 360 (4 четверть), то значение синуса следует брать со знаком минус.
Если значение косинуса угла меньше нуля, то это означает, что угол может находиться во 2-й или 3-й четверти.
1) 90< a< 180 (2 четверть).
Тогда синус угла будет положительным и равняется корню квадратному из разности 1 и квадрата косинуса угла.
2) 180< a< 270 (3 четверть).
В этом случае синус угла будет отрицательным и равняется тому же значению, что и в первом случае, только со знаком минус.
<hr />
Частные случаи: Если cos a = 0, то sina=1; если cos a = 1, то sina=0; cos a = -1, то sina=0. Эти значения также легко находятся из основного тригонометрического тождества.
<hr />
Приведем примеры.
Пример 1. Найти синус угла, если cos a = -0,8. 180<a<270 (в градусах)
Решение. Находим разность 1 и квадрата значения cos a, т.е. квадрата (-0,8).
-0,8 возводим в квадрат, получим (-0,8)*(-0,8) = 0, 64. Подставим его в искомую разность:
1-0,64=0,36
Получили квадрат значения синуса. Для нахождения значения самого синуса, извлечем корень квадратный из 0,36 и возьмем его со знаком + и со знаком – (см. картинку). Получим 0,6 или -0,6.
Так как по условию угол находится в 3 четверти, то искомое значение синуса будет отрицательным. Значит выбираем -0,6.
Ответ: sina=-0,6.
Рассмотрим для краткости изложения этот же пример для случая, когда угол находится во второй четверти:
Пример 2. Найти синус угла, если cos a = -0,8. 90<a<180 (в градусах)
Решение будет точно таким же, как для примера 1.
Изменится лишь выбор ответа. Рассуждения будут следующими:
Так как по условию угол находится во 2 четверти, то искомое значение синуса будет положительным. Значит выбираем 0,6.
Ответ: sina=0,6.