Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой нужной науки внесли ученые Ближнего Востока и Индии, которые придумали наиболее важные понятия, объяснили многие свойства, предложили варианты измерения и др.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии без таблиц и графиков.
Синус, косинус, тангенс и котангенс. Определения
Зачем разделять понятия синуса, косинуса, тангенса и котангенса?
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Что такое синус?
Синус угла (sin α) – это отношение противолежащего этому углу катета к гипотенузе.
Что такое косинус?
Косинус угла (cosα) – это отношение прилежащего катета к гипотенузе.
Что такое тангенс?
Тангенс угла (tg α) – это отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) – отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Синус и косинус можно представить через экспоненту (экспоненциальная функция).
Приведем иллюстрацию.

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Означения синуса, косинуса, тангенса и котангенса позволяют вычислять (находить) значения этих функций по известным длинам сторон треугольника.
Что и почему важно и принято помнить в ходе такого нахождения?
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тг и ктг – вся числовая прямая, то есть эти функции могут принимать любые значения.
Как найти синус? Для начала нужно определиться, какой перед нами треугольник: прямоугольный или произвольный. В первом случае можно использовать обычный тригонометрический метод, а во втором – теорему косинусов.
Как найти косинус? Соответственно, нам нужно знать значения прилежающего катета и гипотенузы.
Как найти тангенс? Если треугольник прямоугольный, то тангенс вычисляется при помощи значений противоположного катета и прилежащего (в уравнении нужно поделить одно на другое). Если речь идет о числах, тупых, развернутых углов и углов, превышающих 360 градусов, то тангенс определяется при помощи синуса и косинуса (посредством их отношения и деления).
Теорема синусов и косинусов используется для того чтобы искать элементы в произвольном треугольнике. Такой поиск используется часто.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность (круг) с центром в начале декартовой системы координат.

Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y).
Синус угла поворота α – это ордината точки A1(x , y). sin α=y
Косинус угла поворота α – это абсцисса точки A1(x , y). cos α=икс
Тангенс угла поворота α – это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx
Котанг угла поворота α – это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогична ситуация с котангенсом. Отличие состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Простое правило: синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)
Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)
При решении практических примеров не говорят “синус угла поворота α”. Слова “угол поворота” просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10π равен синусу угла поворота величиной 10π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности – точка A c координатами (1, 0).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t=y
Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t=x
Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α, cos α, tg α, ctg α – это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Синус, косинус, тангенс и котангенс – основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α=A1HOA1=y1=y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Синус, косинус, тангенс и котангенс: основные формулы
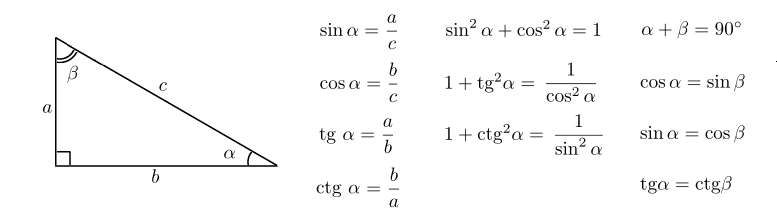
- Определение
- График синуса
- Свойства синуса
- Обратная к синусу функция
- Таблица синусов
Определение
Синус острого угла α (sin α) – это отношение противолежащего катета (a) к гипотенузе (c) в прямоугольном треугольнике.
sin α = a / c

Например:
a = 3
c = 5
sin α = a / c = 3 / 5 = 0.6
График синуса
Функция синуса пишется как y = sin (x). График называется синусоидой и в общем виде выглядит следующим образом:

Синусоида – это периодическая функция с периодом T = 2π.
Свойства синуса
Ниже в табличном виде представлены основные свойства синуса с формулами:
Обратная к синусу функция
Арксинус x – это обратная функция к синусу x, при -1≤x≤1.
Если синус угла у равняется х (sin y = x), значит арксинус x равен у:
arcsin x = sin-1 x = y
Таблица синусов
| x (°) | x (рад) | sin x |
| -90° | -π/2 | -1 |
| -60° | -π/3 | -√3/2 |
| -45° | -π/4 | -√2/2 |
| -30° | -π/6 | -1/2 |
| 0° | 0 | 0 |
| 30° | π/6 | 1/2 |
| 45° | π/4 | √2/2 |
| 60° | π/3 | √3/2 |
| 90° | π/2 | 1 |
microexcel.ru
Что такое синус, косинус, тангенс, котангенс
18 мая 2022
Сегодня мы узнаем, что такое синус, косинус, тангенс и котангенс. Это первый и самый важный урок по тригонометрии на всём сайте.
Содержание:
- Ключевые определения: синус, косинус, тангенс, котангенс.
- Почему эти значения зависят только от углов?
- Стандартные углы: 30°, 45°, 60°.
- Простейшие свойства синуса, косинуса, тангенса, котангенса.
- Тригонометрия на координатной сетке.
Никаких сложных формул и длинных решений. Всё расписано максимально подробно. Изучите этот урок — и никаких проблем с тригонометрией не будет. Погнали!
1. Ключевые определения
Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Мы видим, что острый угол $alpha $ образован гипотенузой $c$ и катетом $b$. Такой катет будем называть прилежащим. А катет $a$, который не участвует в формировании угла $alpha $, назовём противолежащим:
Это общепринятые названия: как только в прямоугольном треугольнике отмечен острый угол, для него немедленно можно указать прилежащий катет и противолежащий. И тут мы переходим к ключевым определениям.
1.1. Синус, косинус, тангенс, котангенс
Итак, пусть дан прямоугольный треугольник с острым углом $alpha $.
Тогда:
Определение 1. Синус угла $alpha $ — это отношение противолежащего катета к гипотенузе:
[sin alpha =frac{text{противолежащий катет}}{text{гипотенуза}}=frac{a}{c}]
Определение 2. Косинус угла $alpha $ — это отношение прилежащего катета к гипотенузе:
[cos alpha =frac{text{прилежащий катет}}{text{гипотенуза}}=frac{b}{c}]
Определение 3. Тангенс угла $alpha $ — это отношение противолежащего катета к прилежащему:
[operatorname{tg}alpha =frac{text{противолежащий катет}}{text{прилежащий катет}}=frac{a}{b}]
Определение 3. Котангенс угла $alpha $ — это отношение прилежащего катета к противолежащему:
[operatorname{ctg}alpha =frac{text{прилежащий катет}}{text{противолежащий катет}}=frac{b}{a}]
Вот так всё просто! Берём один катет, делим его на гипотенузы (или на другой катет) — и получаем выражение для синуса, косинуса, тангенса и котангенса. Все эти выражения называются тригонометрическими («тригонометрия» = «треугольники измеряю»).
Рассмотрим пару примеров.
Задача 1. Дан треугольник $ABC$. Найдите синус, косинус и тангенс угла $alpha $.
Решение. Это классический прямоугольный треугольник с катетами 3 и 4 и гипотенузой 5. Угол $alpha $ (он же — угол $A$ или угол $BAC$) образован прилежащим катетом $AB=3$гипотенузой $AC=5$. Следовательно катет $BC=4$ — противолежащий.
Имеем:
[begin{align}sin alpha& =frac{BC}{AC}=frac{5}{4} \ cos alpha& =frac{AB}{AC}=frac{3}{5} \ operatorname{tg}alpha& =frac{BC}{AB}=frac{4}{3} end{align}]
Далеко не всегда будут получаться такие красивые ответы. Чаще они будут содержать корни — это следствие теоремы Пифагора. Но важно понимать: как только мы находим длины катетов и гипотенузу, мы сразу можем найти и синусы, косинусы, тангенсы.
Далее в примерах мы не будем считать котангенсы, потому что из формулы котангенса очевидно, что они легко выражаются через тангенсы:
[operatorname{ctg}alpha =frac{1}{operatorname{tg}alpha }]
Но об этом чуть позже.
Задача 2. Дан треугольник $ABC$. Найдите синус, косинус и тангенс угла $alpha $.
Это равнобедренный прямоугольный треугольник с катетами $AB=BC=1$. Найдём гипотенузу по теореме Пифагора:
[begin{align}{{ AC}^{2}} & ={{AB}^{2}}+{{BC}^{2}}=1+1=2 \ AC & =sqrt{2} \ end{align}]
Теперь найдём синус, косинус и тангенс:
[begin{align}sin alpha &=frac{BC}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ cos alpha &=frac{AB}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ operatorname{tg}alpha&=frac{BC}{AB}=frac{1}{1}=1 end{align}]
Простое правило, чтобы не запутаться, где прилежащий катет, а где противолежащий. Просто помните: приставка «ко» означает «вместе», «сообща». Поэтому «косинус» — это «катет, лежащий рядом, к гипотенузе», «котангенс» — это «катет, лежащий рядом, к противолежащему». И никак иначе.:)
1.2. Задачи для тренировки
Перед тем как переходить к следующей части урока, предлагаю 4 примера для тренировки.
Задача 3. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Решение.
[begin{align}sin alpha &=frac{5}{13} \ cos alpha &=frac{12}{13} \ operatorname{tg}alpha &=frac{5}{12} \ end{align}]
Задача 4. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Решение.
[begin{align}sin alpha &=frac{8}{17} \ cos alpha &=frac{15}{17} \ operatorname{tg}alpha &=frac{8}{15} \ end{align}]
Задача 5. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Прилежащий катет по теореме Пифагора:
[begin{align}{{l}^{2}}&={{3}^{2}}-{{1}^{2}}=9-1=8 \ l&=sqrt{8}=2sqrt{2} \ end{align}]
Синус, косинус и тангенс:
[begin{align}sin alpha&=frac{1}{3} \ cos alpha&=frac{2sqrt{2}}{3} \ operatorname{tg}alpha&=frac{1}{2sqrt{2}}=frac{sqrt{2}}{4} \ end{align}]
Задача 6. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Прилежащий катет по теореме Пифагора:
[begin{align}{{l}^{2}} &={{2}^{2}}-{{1}^{2}}=4-1=3 \ l &=sqrt{3} \ end{align}]
Синус, косинус и тангенс:
[begin{align}sin alpha&=frac{1}{2} \ cos alpha&=frac{sqrt{3}}{2} \ operatorname{tg}alpha&=frac{1}{sqrt{3}}=frac{sqrt{3}}{3} \ end{align}]
Как видим, считать синусы, косинусы и тангенсы совсем несложно. Перейдём теперь к принципиально важному вопросу: а зачем вообще всё это нужно?
2. Теорема о единственности
Ключевая идея: синус, косинус, тангенс и котангенс зависят только от величины угла $alpha $ и никак не зависят от прямоугольного треугольника, в котором идут вычисления.
Такого не произойдёт. Потому что есть теорема о единственности.
2.1. Формулировка теоремы
Теорема. Значение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике определяются только величиной этого угла и никак не зависят от самого треугольника.
2.2. Доказательство
Рассмотрим произвольный острый угол $alpha $. Для удобства обозначим его вершину буквой $A$:
А затем впишем в него два произвольных прямоугольных треугольника — $ABC$ и $AMN$. Любым удобным способом. Например, можно вписать эти треугольники вот так:
А можно и вот так — это не имеет никакого значения:
Рассмотрим треугольники $ABC$ и $AMN$. Угол $A$ у них общий; углы [angle ABC=angle AMN=90{}^circ ] по условию. Следовательно, треугольники $ABC$ и $AMN$ подобны по двум углам:
[Delta ABCsim Delta AMN]
Из подобия треугольников следует двойное равенство
[frac{AB}{AM}=frac{BC}{MN}=frac{AC}{AN}]
Выпишем второе равенство — получим пропорцию
[frac{BC}{MN}=frac{AC}{AN}]
Попробуем выразить $sin alpha $. Вспомним основное свойство пропорции: произведение крайних членов равно произведению средних. Поэтому
[BCcdot AN=MNcdot AC]
Разделим обе части равенства на длину каждой гипотенузы — $AN$ и $AC$:
[begin{align}frac{BCcdot AN}{ANcdot AC} &=frac{MNcdot AC}{ANcdot AC} \ frac{BC}{AC} &=frac{MN}{AN} end{align}]
Однако по определению синуса имеем:
[begin{align}sin BAC &=frac{BC}{AC} \ sin MAN &=frac{MN}{AN} \ end{align}]
Получается, что $sin BAC=sin MAN$. Другими словами, вне зависимости от выбора треугольника для данного угла $alpha $ мы всегда будем получать одно и то же значение $sin alpha $.
То же самое касается и $cos alpha $, $operatorname{tg}alpha $ и $operatorname{ctg}alpha $ — они зависят лишь от градусной меры угла $alpha $ и никак не зависят от конкретного прямоугольного треугольника, в котором они находятся. Теорема доказана.
3. Стандартные углы
Итак, значения $sin alpha $, $cos alpha $, $operatorname{tg}alpha $ и $operatorname{ctg}alpha $ однозначно определяются величиной угла $alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.
Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:
- Для большинства углов $alpha $ нельзя найти точные значения $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
- Верно и обратное: для большинства «красивых» $sin alpha $, $cos alpha $ и т.д. нельзя подобрать подходящий угол $alpha $.
Звучит немного непонятно, поэтому разберём каждый пункт на конкретных примерах.
3.1. Три стандартных угла
Существует лишь три острых угла, для которых легко считаются синусы, косинусы и т.д. Это 30°, 45°, 60°. Вот их синусы, косинусы и тангенсы:
[begin{array}{c|ccc} alpha& 30{}^circ& 45{}^circ & 60{}^circ \ hlinesin alpha & frac{1}{2} & frac{sqrt{2}}{2} & frac{sqrt{3}}{2} \ cos alpha & frac{sqrt{3}}{2} & frac{sqrt{2}}{2} & frac{1}{2} \ operatorname{tg}alpha& frac{sqrt{3}}{3} & 1 & sqrt{3} \ end{array}]
Чтобы понять, чем эти углы такие особенные, просто посчитаем все эти синусы, косинусы и тангенсы. Начнём с $alpha =45{}^circ $. Для этого рассмотрим равнобедренный прямоугольный треугольник. Мы уже встречались с ним:
Поскольку в равнобедренном треугольнике $angle A=angle B=45{}^circ $, получим:
[begin{align}sin 45{}^circ &=sin A=frac{BC}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ cos 45{}^circ &=sin A=frac{AB}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ operatorname{tg}45{}^circ&=sin A=frac{BC}{AB}=frac{1}{1}=1 end{align}]
Это именно те значения, которые указаны в таблице!
Теперь разберёмся с углами $alpha =30{}^circ $ и $alpha =60{}^circ $. Здесь рассуждения будут чуть сложнее. Сначала рассмотрим равносторонний треугольник $ABC$ со стороной $AB=2$ (просто так удобнее) и проведём высоту $BH$:
Мы знаем, что высота $BH$ — ещё и медиана, и биссектриса. Поэтому $AH=CH=1$, $angle ABH=angle CBH=30{}^circ $.
Следовательно, треугольник $ABH$ — прямоугольный, да ещё и с острыми углами 30° и 60°. По теореме Пифагора легко найти $BH=sqrt{3}$. Нанесём все данные на чертёж:
Разберёмся с углом 60°:
[begin{align} sin{60}^circ &=sin A=frac{BH}{AB}=frac{sqrt{3}}{2} \ cos{60}^circ&=cos A=frac{AH}{AB}=frac{1}{2} \ operatorname{tg}{60}^circ&=operatorname{tg}A=frac{BH}{AH}=sqrt{3} \ end{align}]
И с углом 30°:
[begin{align} sin{30}^circ &=sin ABH=frac{AH}{AB} =frac{1}{2} \ cos{30}^circ &=cos ABH=frac{BH}{AB} =frac{sqrt{3}}{2} \ operatorname{tg}{30}^circ &=operatorname{tg} ABH=frac{AH}{BH} =frac{1}{sqrt{3}} =frac{sqrt{3}}{3} \ end{align}]
Попробуйте повторить все эти рассуждения самостоятельно. Это очень полезное упражнение!
Возникает вопрос: как быть с другими углами? Например, можно ли найти $sin {50}^circ $? Или, быть может, $cos {10}^circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.
Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?
3.2. Что с другими углами?
Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:
Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $alpha $:
[sin alpha =sin A=frac{BC}{AB}=frac{3}{5}=0,6]
Итак, мы знаем синус. Внимание, вопрос: каким должен быть угол $alpha $, чтобы $sin alpha =0,6$? Сколько градусов должно быть в угле $alpha $? Ответ: неизвестно.:)
Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $alpha $, чтобы $sin alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.
Из всех этих рассуждений сделаем важный вывод. В тригонометрии мы:
- Либо берём угол и считаем для него синусы, косинусы и т.д. Но лишь для трёх острых углов — 30°, 45°, 60° — всё будет считаться быстро и красиво. Такие углы называются табличными.
- Либо берём синус, косинус или тангенс и для него пытаемся подобрать острый угол. Но лишь для табличных значений мы сможем подобрать такие углы. И да: это будут углы 30°, 45°, 60°.
Ещё раз:
Мы можем посчитать лишь синус, косинус и тангенс для трёх табличных углов.
Например, $sin 30{}^circ $, $cos 45{}^circ $, $operatorname{tg}60{}^circ $ и т.д. А всякие $sin 15{}^circ $, $cos 25{}^circ $ или $operatorname{tg}89,5{}^circ $ — не сможем. По крайней мере пока.:)
И наоборот:
Зная $sin alpha $, $cos alpha $ или $operatorname{tg}alpha $, мы сможем назвать точный угол $alpha $ только в том случае, если все эти синусы, косинусы и тангенсы — среди табличных значений.
Например, мы точно знаем, что если $sin alpha =frac{sqrt{2}}{2}$, то $alpha =45{}^circ $. Но когда $sin alpha =0,6$, мы уже не можем назвать угол $alpha $ (хотя всегда можем построить такой угол).
С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.
4. Свойства синуса, косинуса, тангенса
Мы разберём три ключевых свойства:
- Связь между синусом, косинусом и тангенсом.
- Связь между острыми углами прямоугольного треугольника.
- Основное тригонометрическое тождество.
Свойствам 2 и 3 далее в курсе будут посвящены отдельные уроки. Но основные идеи полезно взять на вооружение уже сейчас.
4.1. Связь между синусом, косинусом и тангенсом
Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Выразим синус, косинус:
[sin alpha =frac{a}{c};quad cos alpha =frac{b}{c}]
А теперь выразим тангенс и заметим, что
[operatorname{tg}alpha =frac{a}{b}=frac{a}{c}cdot frac{c}{b}=frac{sin alpha }{cos alpha }]
Точно так же можно выразить и котангенс:
[operatorname{ctg}alpha =frac{b}{a}=frac{b}{c}cdot frac{c}{a}=frac{cos alpha }{sin alpha }]
Более того, сам тангенс и котангенс тоже связаны:
[operatorname{tg}alpha cdot operatorname{ctg}alpha =frac{a}{b}cdot frac{b}{a}=1]
Мы получили три важнейших тригонометрических формулы:
Основные формулы тригонометрии:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha };quad operatorname{ctg}alpha =frac{cos alpha }{sin alpha };quad operatorname{tg}alpha cdot operatorname{ctg}alpha =1]
Эти формулы нужно знать наизусть. И понимать, откуда они берутся.
4.2. Связь между острыми углами
Рассмотрим прямоугольный треугольник $ABC$, где $angle C=90{}^circ $. Пусть градусная мера $angle A=alpha $ градусов:
Мы помним, что сумма острых углов прямоугольного треугольника равна 90°. Поэтому если $angle A=alpha $, то угол $angle B=90{}^circ -alpha $. Но тогда:
[sin alpha =sin A=frac{BC}{AB}=cos B=cos left( 90{}^circ -alpha right)]
То же самое и с косинусами:
[cos alpha =cos A=frac{AC}{AB}=sin B=sin left( 90{}^circ -alpha right)]
И даже с тангенсами и котангенсами:
[begin{align} operatorname{tg}alpha&=operatorname{tg}A=frac{BC}{AC} =operatorname{ctg}B=operatorname{ctg}left( {90}^circ -alpharight) \ operatorname{ctg}alpha&=operatorname{ctg}A=frac{AC}{BC} = operatorname{tg}B=tgleft( {90}^circ -alpha right) \ end{align}]
Другими словами, если вместо $alpha $ поставить ${90}^circ -alpha $, то исходная тригонометрическая функция поменяется на ко-функцию:
[begin{align}sin left( {90}^circ-alpharight) &=cos alpha \ cos left( {90}^circ-alpharight) &=sin alpha \ operatorname{tg}left( {90}^circ-alpharight) &=operatorname{ctg}alpha\ operatorname{ctg}left( {90}^circ-alpharight) &=operatorname{tg}alphaend{align}]
Но это ещё не всё. Есть гораздо более интересная формула.
4.3. Основное тригонометрическое тождество
Вновь рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Запишем выражения для $sin alpha $ и $cos alpha $:
[sin alpha =frac{a}{c};quad cos alpha =frac{b}{c}]
Далее заметим, что
[begin{align} {{sin }^{2}}alpha +{{cos }^{2}}alpha&={{left( frac{a}{c} right)}^{2}}+{{left( frac{b}{c} right)}^{2}}= \ & =frac{{{a}^{2}}}{{{c}^{2}}} +frac{{{b}^{2}}}{{{c}^{2}}}= \ & =frac{{{a}^{2}}+{{b}^{2}}}{{{c}^{2}}} end{align}]
В числителе можем применить теорему Пифагора: ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$, поэтому
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =frac{{{c}^{2}}}{{{c}^{2}}}=1]
Правая часть этой формулы вообще не зависит от угла $alpha $.
Основное тригонометрическое тождество:
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =1]
Это равенство связывает синус и косинус одного и того же угла и верно для всех $alpha $.
С помощью основного тригонометрического тождества можно вычислять косинус, зная синус, и наоборот.
Задача 7. Найдите $18cos alpha $ для острого угла $alpha $, если $sin alpha =frac{sqrt{65}}{9}$.
Решение. Запишем основное тригонометрическое тождество:
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =1]
Подставим указанное значение $sin alpha $ и выразим $cos alpha $:
[begin{align}{{left( frac{sqrt{65}}{9} right)}^{2}}+{{cos }^{2}}alpha &=1 \ frac{65}{81}+{{cos }^{2}}alpha &=1 \ {{cos }^{2}}alpha &=frac{16}{81} \ cos alpha&=pm frac{4}{9} end{align}]
Поскольку косинус угла в прямоугольном треугольнике не может быть отрицательным, выбираем вариант $cos alpha ={4}/{9};$. Остаётся сделать финальный шаг:
[18cos alpha =18cdot frac{4}{9}=2cdot 4=8]
Вот и всё! Ответ: 8.
В следующем примере мы уже не будем подробно расписывать каждый шаг. Оформим всё так, как надо оформлять на контрольных и экзаменах.
Задача 8. Найдите $48operatorname{tg}alpha $ для острого угла $alpha $, если $cos alpha =frac{8}{sqrt{113}}$.
Решение. Найдём $sin alpha $:
[begin{align}{{sin }^{2}}alpha &=1-{{cos }^{2}}alpha = \ & =1-{{left( frac{8}{sqrt{113}} right)}^{2}}= \ & =1-frac{64}{113}=frac{49}{113} \ sin alpha&=pm frac{7}{sqrt{113}} end{align}]
Но ${0}^circ lt alpha lt {90}^circ $, поэтому $sin alpha gt 0$. Следовательно
[sin alpha =frac{7}{sqrt{113}}]
Найдём $operatorname{tg}alpha $:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha }=frac{7}{sqrt{113}}cdot frac{sqrt{113}}{8}=frac{7}{8}]
Окончательный ответ:
[48operatorname{tg}alpha =48cdot frac{7}{8}=6cdot 7=42]
Ответ: 42.
Заметка на будущее: замечание о том, что угол $alpha $ острый, весьма существенно. То, как мы сейчас определяем синусы, косинусы и тангенсы (через прямоугольный треугольник), называется геометрической тригонометрией. Её проходят в 8—9 классе.
Но в 10—11 классах появится алгебраическая тригонометрия, где синусы, косинусы и т.д. вполне могут быть отрицательными. И уже не получится просто так избавиться от минуса.
Но всё это будет чуть позже. А сейчас потренируемся.
Задача 9. ►
Найдите $52cos alpha $ для острого угла $alpha $, если $sin alpha =frac{5}{13}$.
Решение. Найдём $cos alpha $:
[begin{align}{{cos }^{2}}alpha &=1-{{sin }^{2}}alpha = \ &=1-frac{25}{169}=frac{144}{169} \ cos alpha&=pm frac{12}{13} end{align}]
Поскольку $cos alpha gt 0$ для острых $alpha $, выбираем $cos alpha ={12}/{13};$. Итого
[52cos alpha =52cdot frac{12}{13}=48]
Ответ: 48.
Задача 10. ►
Найдите $1+2operatorname{tg}alpha $ для острого угла $alpha $, если $cos alpha =frac{1}{sqrt{26}}$.
Решение. Найдём $sin alpha $:
[begin{align}{{sin }^{2}}alpha &=1-{{cos }^{2}}alpha = \ & =1-frac{1}{26}=frac{25}{26} \ sin alpha&=pm frac{5}{sqrt{26}} end{align}]
Поскольку $sin alpha gt 0$ для острых $alpha $, выбираем
[sin alpha =frac{5}{sqrt{26}}]
Считаем $operatorname{tg}alpha $:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha }=frac{5}{sqrt{26}}cdot frac{sqrt{26}}{1}=5]
Откуда
[1+2operatorname{tg}alpha =1+2cdot 5=11]
Ответ: 11.
5. Тригонометрия на координатной сетке
Задачи, которые мы сейчас разберём, вполне могут встретиться в ОГЭ и даже ЕГЭ. Часто в них нет прямоугольного треугольника — есть лишь угол, в который этот треугольник предлагается вписать.
Для решения задач на координатной сетке достаточно посмотреть, через какие узлы сетки проходят интересующие нас лучи. И понять, какие из этих узлов имеет смысл соединить дополнительными построениями.
Звучит страшно, но на практике всё легко.:)
Задача 11. Найдите тангенс угла $ABC$, изображённого на координатной сетке:
Решение. Дополнительное построение: $AHbot BC$ — перпендикуляр из точки $A$ на луч $BC$.
Треугольник $BAH$ — прямоугольный, причём угол $ABC$ — один из его острых углов. Поэтому
[operatorname{tg}ABC=frac{AH}{BH}=frac{3}{4}=0,75]
Это и есть искомый тангенс.
Ответ: 0,75.
Ещё раз: важно, чтобы основание перпендикуляра попадало в узел сетки. Иначе нахождение длины катетов резко усложняется. Попробуйте сами:
Задача 12. ►
Найдите тангенс угла $ABC$, изображённого на координатной сетке:
Решение.
Дополнительное построение: $AHbot BC$ — перпендикуляр из точки $A$ к лучу $BC$.
Треугольник $BAH$ — прямоугольный с острым углом $ABC$. Поэтому
[operatorname{tg}ABC=frac{AH}{BH}=frac{2}{4}=frac{1}{2}]
Ответ: 0,5.
Разумеется, это были совсем простые задачи. Потому что один из лучей был параллелен линиям сетки.
Куда интереснее (и полезнее) рассмотреть ситуации, где лучи направлены под углом к сетке. Суть та же: ищем и соединяем узлы на лучах. Но тут уже нужна наблюдательность.
Задача 13. Найдите тангенс угла $MNK$, изображённого на координатной сетке:
Решение. Луч $KN$ содержит лишь две точки в узлах координатной сетки — собственно, $K$ и $N$. Понятно, что если продолжить луч за точку $K$, мы найдём ещё много таких точек, но будем решать задачу с тем, что есть.
Заметим, что прямая $MN$ наклонена к линиям сетки под углом 45° и образует диагонали квадратов. Это значит, что перпендикуляр к ней тоже будет наклонён под углом 45°.
Дополнительное построение: отрезок $KH$ — диагональ одного из квадратов сетки.
Очевидно, что угол $NHK$ прямой, поэтому треугольник $KHN$ прямоугольный и содержит искомый острый угол $MNK$. Находим тангенс:
[operatorname{tg}MNK=frac{HK}{HN}=frac{sqrt{2}}{2sqrt{2}}=frac{1}{2}=0,5]
Здесь мы предположили, что сторона квадрата сетки равна 1. Но с тем же успехом можно считать, что сторона квадрата $a$:
[operatorname{tg}MNK=frac{HK}{HN}=frac{asqrt{2}}{2asqrt{2}}=frac{1}{2}=0,5]
Ответ: 0,5.
Подобные задачи считаются довольно сложными. По статистике большинство выпускников 9 классов не способны их решать. Но вы-то теперь точно справитесь. Попробуйте:
Задача 14. ►
Найдите тангенс угла $DEF$, изображённого на координатной сетке:
Решение.
Дополнительное построение: отрезок $DH$.
Очевидно, $EH=DH$, угол $EHD$ прямой. Следовательно, треугольник $EDH$ — прямоугольный и равнобедренный. Поэтому $operatorname{tg}DEF=1$.
Либо можно посчитать «напролом», полагая, что сторона квадрата сетки равна $a$:
[operatorname{tg}DEF=frac{asqrt{10}}{asqrt{10}}=1]
Ответ: 1.
Вообще, поиск «правильных» узлов на координатной сетке — это своего рода искусство. И если углубляться в эту тему, то можно быстро выйти на «полуолимпиадные» задачи.
К тому же не существует «самого правильного» дополнительного построения. Задачу на координатной сетке всегда можно решить множеством различных способов. Так, в последнем примере можно было провести перпендикуляр вот так:
И даже так (хотя вряд ли этот способ можно назвать рациональным):
Во всех случаях ответ будет один и тот же. Поэтому не бойтесь экспериментировать. И переходите к следующему уроку — к действительно важным и полезным свойствам синусов, косинусов, тангенсов и котангенсов.:)
Смотрите также:
- Радианная и градусная мера угла

- Как быстро запомнить таблицу синусов и косинусов

- Сложные логарифмические неравенства

- Сложные выражения с дробями. Порядок действий

- Задача B5: площадь фигур с вершиной в начале координат

- Обход точек в стереометрии — 2

Запросы «sin» и «синус» перенаправляются сюда; у терминов sin и синус есть также другие значения.
Запрос «sec» перенаправляется сюда; см. также другие значения.

Рис. 1.
Графики тригонометрических функций: синуса, косинуса, тангенса, котангенса, секанса, косеканса
Тригонометри́ческие фу́нкции — элементарные функции[1], которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла дуги в круге). Эти функции нашли широкое применение в самых разных областях науки. По мере развития математики определение тригонометрических функций было расширено, в современном понимании их аргументом может быть произвольное вещественное или комплексное число.
Раздел математики, изучающий свойства тригонометрических функций, называется тригонометрией.
К тригонометрическим функциям традиционно причисляют:
- прямые тригонометрические функции:
- синус (
);
- косинус (
);
- производные тригонометрические функции:
- тангенс
;
- котангенс
;
- секанс
;
- косеканс
;
- обратные тригонометрические функции:
- арксинус, арккосинус и т. д.
В типографике литературы на разных языках сокращённое обозначение тригонометрических функций различно, например, в англоязычной литературе тангенс, котангенс и косеканс обозначаются 


Кроме этих шести широко известных тригонометрических функций, иногда в литературе используются некоторые редко используемые тригонометрические функции (версинус и т. д.).
Синус и косинус вещественного аргумента представляют собой периодические, непрерывные и бесконечно дифференцируемые вещественнозначные функции. Остальные четыре функции на вещественной оси также вещественнозначны, периодичны и бесконечно дифференцируемы, за исключением счётного числа разрывов второго рода: у тангенса и секанса в точках 

Графики тригонометрических функций показаны на рис. 1.
Способы определения[править | править код]
Определение для любых углов[править | править код]

Рис. 2.
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически[3]. В декартовой системе координат на плоскости построим окружность единичного радиуса (






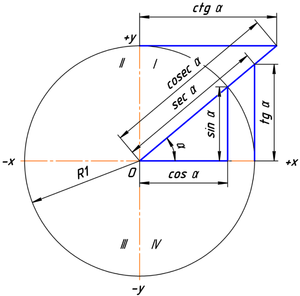
Синусом угла 






Косинусом угла 






Тангенсом угла 


Котангенсом угла 


Таким образом, определения тригонометрических функций выглядят следующим образом:
Нетрудно видеть, что такое определение также основывается на отношениях прямоугольного треугольника, с тем отличием, что учитывается знак (

В тригонометрии удобным оказывается вести счёт углов не в градусной мере, а в радианной. Так, угол в 






Наконец, определим тригонометрические функции вещественного числа 

Определение для острых углов[править | править код]

Рис. 4.
Тригонометрические функции острого угла

Определение тангенса. Марка СССР 1961 года
В геометрии тригонометрические функции острого угла определяются отношениями сторон прямоугольного треугольника[5]. Пусть 



Данное определение имеет некоторое методическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач о тупоугольных треугольниках. (См.: теорема синусов, теорема косинусов).
Определение как решений дифференциальных уравнений[править | править код]
Синус и косинус можно определить как единственные функции, вторые производные которых равны самим функциям, взятым со знаком минус:
То есть задать их как чётное (косинус) и нечётное (синус) решения дифференциального уравнения
с дополнительными условиями:


Определение как решений функциональных уравнений[править | править код]
Функции косинус и синус можно определить[7]
как решения (


при дополнительных условиях:




Определение через ряды[править | править код]
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу, и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:
Пользуясь этими формулами, а также равенствами 



где
— числа Бернулли,
— числа Эйлера.
Значения тригонометрических функций для некоторых углов[править | править код]
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («
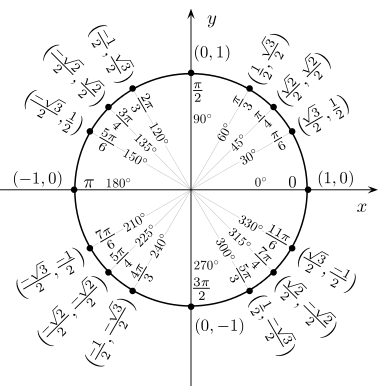
Значения косинуса и синуса на окружности
| Радианы | 
|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Значения тригонометрических функций нестандартных углов[править | править код]
| Радианы | 
|

|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
| Радианы | 
|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Значения тригонометрических функций для некоторых других углов
Свойства тригонометрических функций[править | править код]
Простейшие тождества[править | править код]
Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности (
Это соотношение называется основным тригонометрическим тождеством.
Разделив это уравнение на квадрат косинуса и синуса соответственно, получим:
Из определения тангенса и котангенса следует, что
Любую тригонометрическую функцию можно выразить через любую другую тригонометрическую функцию с тем же аргументом (с точностью до знака из-за неоднозначности раскрытия квадратного корня). Нижеприведённые формулы верны для 
| sin | cos | tg | ctg | sec | cosec | |
|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Непрерывность[править | править код]
Чётность[править | править код]
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность[править | править код]
Функции 




Формулы приведения[править | править код]
Формулами приведения называются формулы следующего вида:
Здесь 



или что то же самое:
Некоторые формулы приведения:

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Интересующие формулы приведения так же могут легко быть получены рассмотрением функций на единичной окружности.
Формулы сложения и вычитания[править | править код]
Значения тригонометрических функций суммы и разности двух углов:
Аналогичные формулы для суммы трёх углов:
Формулы для кратных углов[править | править код]
Формулы двойного угла:
Формулы тройного угла:
Прочие формулы для кратных углов:
следует из формулы дополнения и формулы Гаусса для гамма-функции.
Из формулы Муавра можно получить следующие общие выражения для кратных углов:
где ![[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26847bfc29bbeb4d6ef62ac3fd076378c0fd1db)


Формулы половинного угла:
Произведения[править | править код]
Формулы для произведений функций двух углов:
Аналогичные формулы для произведений синусов и косинусов трёх углов:
Формулы для произведений тангенсов и котангенсов трёх углов можно получить, поделив правые и левые части соответствующих равенств, представленных выше.
Степени[править | править код]

Иллюстрация равенства
Суммы[править | править код]
Существует представление:
где угол 
Универсальная тригонометрическая подстановка[править | править код]
Все тригонометрические функции можно выразить через тангенс половинного угла:






Исследование функций в математическом анализе[править | править код]
Разложение в бесконечные произведения[править | править код]
Тригонометрические функции могут быть представлены в виде бесконечного произведения многочленов:
Эти соотношения выполняются при любом значении 
Непрерывные дроби[править | править код]
Разложение тангенса в непрерывную дробь:
Производные и первообразные[править | править код]
Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:






Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом[8]:






Тригонометрические функции комплексного аргумента[править | править код]
Определение[править | править код]
Формула Эйлера:
Формула Эйлера позволяет определить тригонометрические функции от комплексных аргументов через экспоненту по аналогии с гиперболическими функциями, или (с помощью рядов) как аналитическое продолжение их вещественных аналогов:
где
Соответственно, для вещественного x:
Комплексные синус и косинус тесно связаны с гиперболическими функциями:
Большинство перечисленных выше свойств тригонометрических функций сохраняются и в комплексном случае. Некоторые дополнительные свойства:
- комплексные синус и косинус, в отличие от вещественных, могут принимать сколь угодно большие по модулю значения;
- все нули комплексных синуса и косинуса лежат на вещественной оси.
Комплексные графики[править | править код]
На следующих графиках изображена комплексная плоскость, а значения функций выделены цветом. Яркость отражает абсолютное значение (чёрный — ноль). Цвет изменяется от аргумента и угла согласно карте.
|
|
|
|
|
|
|

|

|

|

|

|

|
История названий[править | править код]
Линия синуса (линия 
Современные краткие обозначения 

Термины «тангенс» (лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке в его книге «Геометрия круглого» (Geometria rotundi, 1583).
Сам термин тригонометрические функции введён Клюгелем в 1770 году.
Позднее были введены и термины для обратных тригонометрических функций — арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс — с помощью добавления приставки «арк» (от лат. arcus — дуга), — Ж. Лагранжем и др.
См. также[править | править код]
- Гиперболические функции
- Интегральный синус
- Интегральный косинус
- Интегральный секанс
- Обратные тригонометрические функции
- Редко используемые тригонометрические функции
- Решение треугольников
- Синус-верзус
- Сферическая тригонометрия
- Тригонометрические тождества
- Тригонометрические функции от матрицы
- Тригонометрический ряд Фурье
- Функция Гудермана
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Эллиптические функции
Литература[править | править код]
- Бермант А. Ф., Люстерник Л. А. Тригонометрия. — М.: Наука, 1967.
- Тригонометрические функции — статья из Большой советской энциклопедии. — М.: Советская энциклопедия, 1977. — Т. 26. — С. 204—206.
- Бронштейн И. Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: М.: АСТ, 2006. — 509 с. — ISBN 5-17-009554-6 www.alleng.ru/d/math/math42.htm
- Двайт Г. Б. Тригонометрические функции // Таблицы интегралов и другие математические формулы. — 4-е изд. — М.: Наука, 1973. — С. 70—102.
- Кожеуров П. А. Тригонометрия. — М.: Физматгиз, 1963.
- Маркушевич А. И. Замечательные синусы. — М.: Наука, 1974.
- Математическая энциклопедия / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1984. — И. М. Виноградов. Тригонометрические функции // Математическая энциклопедия. — М.: Советская энциклопедия. — 1977—1985.
- Тригонометрические функции // Энциклопедический словарь юного математика / Ред. коллегия, Гнеденко Б. В. (гл. ред.), Савин А. П. и др. — М.: Педагогика, 1985 (1989). — С. 299—301—305. — 352 с., ил. — ISBN 5-7155-0218-7 (С. 342, 343 — таблицы тригонометрических функций 0°-90°, в том числе в радианах)
- Тригонометрические функции // Справочник по математике (для ср. уч. заведений) / Цыпкин А. Г., под ред. Степанова С. А. — 3-е изд. — М.: Наука, Гл. редакция физ.-мат. литературы, 1983. — С. 240—258. — 480 с.
Ссылки[править | править код]
- GonioLab — прояснённая единичная окружность, тригонометрические и гиперболические функции (Java Web Start)
- Weisstein, Eric W. Trigonometric Functions (англ.) на сайте Wolfram MathWorld.
- Онлайн калькулятор: вычисление значений тригонометрических функций (в том числе нахождение углов треугольника по сторонам)
- Интерактивная карта значений тригонометрических функций
- Тригонометрические таблицы (0° — 360°)
- «Синус и косинус — это проценты» — перевод статьи How To Learn Trigonometry Intuitively | BetterExplained (англ.)
Примечания[править | править код]
- ↑ Справочник: Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с. Архивная копия от 19 января 2015 на Wayback Machine относит их к специальным функциям.
- ↑ Знак математический. // Большая советская энциклопедия. 1-е изд. Т. 27. — М., 1933.
- ↑ Справочник по элементарной математике, 1978, с. 282—284.
- ↑ Шахмейстер А. Х. Определение основных тригонометрических функций // Тригонометрия : [рус.] : книга / А. Х. Шахмейстер; под ред. Б. Г. Зива. — 3-е изд., стереотипное. — М. : Издательство МЦНМО ; СПб. : «Петроглиф» : «Виктория плюс», 2013. — С. 11, 14, 18, 20. — 752 с. : илл. — (Математика. Элективные курсы). — 1500 экз. — ББК 22.141я71.6. — УДК 373.167.1:512(G). — ISBN 978-5-4439-0050-6. — ISBN 978-5-98712-042-2. — ISBN 978-5-91673-097-5.
- ↑ Справочник по элементарной математике, 1978, с. 271—272.
- ↑ Латинско-русский словарь. Дата обращения: 9 апреля 2023.
- ↑ Ильин В. А., Позняк Э. Г. Основы математического анализа. Ч. 1. — М.: Наука, 1998. — ISBN 5-02-015231-5.
- ↑ В формулах, содержащих логарифм в правой части равенств, константы интегрирования
, вообще говоря, различны для различных интервалов непрерывности.
Для удобства сразу же приведем таблицу с всеми тригонометрическими тождествами. Всегда удобно открыть формулы в одном месте, выбрать нужную и решить пример. После таблицы мы по отдельности рассмотрим каждую тригонометрическую формулу: обсудим ее вывод и порешаем примеры.
- Основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$ - Определение тангенса и котангенса через синус и косинус:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)};$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$ - Cвязь тангенса и котангенса:
$$tg(alpha)=frac{1}{ctg(alpha)};$$
$$tg(alpha)*ctg(alpha)=1;$$ - Тангенс через косинус. Котангенс через синус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$ctg(alpha)^2+1=frac{1}{sin(alpha)^2};$$ - Синус суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$ - Косинус суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$ - Тангенс суммы и разности:
$$tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};$$
$$tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};$$ - Котангенс суммы и разности:
$$сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};$$
$$сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};$$ - Двойной угол:
$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$ - Тройной угол:
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$ - Формулы половинного угла:
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$ - Понижение степени:
$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$ - Преобразование суммы и разности тригонометрических функций:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$ - Преобразование произведения тригонометрических функций:
$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$ - Формулы подстановки тангенса:
$$sin(alpha)=frac{2*tg(frac{alpha}{2})}{1+tg(frac{alpha}{2})^2};$$
$$cos(alpha)=frac{1-tg(frac{alpha}{2})^2}{1+tg(frac{alpha}{2})^2};$$
$$tg(alpha)=frac{2*tg(frac{alpha}{2})}{1-tg(frac{alpha}{2})^2};$$
$$ctg(alpha)=frac{1-tg(frac{alpha}{2})^2}{2*tg(frac{alpha}{2})};$$ - Формулы приведения можно найти в отдельной статье
Зачем нужны тригонометрические формулы?
Как видите, тригонометрических формул очень много. Тут еще и не все приведены. Но на ваше счастье, учить всю эту таблицу не нужно. Достаточно знать только основные: №1-6, 9. Остальные на ЕГЭ по профильной математике встречаются крайне редко, а если и попадутся, то, скорее всего, будут даны в справочных материалах.
Но для участия в олимпиадах или, если вы хотите поступать в сильный математический ВУЗ через вступительные экзамены, то вам может понадобиться вся таблица. По крайней мере, у вас точно должно быть представление о существовании таких формул, чтобы их вывести в случае необходимости. Да, большинство из них легко выводятся.
Тригонометрические формулы нужны, чтобы связать все тригонометрические функции между собой. Если вы знаете одну из функций, например, синус, то, используя эти формулы, можно легко найти оставшиеся три тригонометрические функции (косинус, тангенс и котангенс). Кроме этого тождества позволяют упростить выражение под тригонометрической функцией: например, выразить синус от двойного угла через комбинацию тригонометрических функций от одинарного угла, что бывает очень полезно при решении тригонометрических уравнений и неравенств.
Обсудим и порешаем примеры на все формулы из таблицы.
Основное тригонометрическое тождество
$$mathbf{sin(alpha)^2+cos(alpha)^2=1;}$$
Эту формулу можно считать главной и самой часто используемой в тригонометрии. Она выводится при помощи определения синуса и косинуса через прямоугольный треугольник и теоремы Пифагора. Не буду еще раз описывать вывод, с ним можно познакомиться в самой первой главе по тригонометрии.
При помощи основного тригонометрического тождества очень удобно искать значение синуса, если известен косинус и наоборот. Разберем пример:
Пример 1
Найдите (3sqrt{2}*sin(alpha)=?), если (cos(alpha)=frac{1}{3}) и (alphain(0;frac{pi}{2})). (ЕГЭ)
Чтобы найти значение выражения (3sqrt{2}*sin(alpha)) необходимо сначала найти значение синуса.
Формула, которая связывает и синус, и косинус – это основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$
Просто подставим в нее известное значение косинуса
$$sin(alpha)^2+left(frac{1}{3}right)^2=1;$$
$$sin(alpha)^2+frac{1}{9}=1;$$
$$sin(alpha)^2=1-frac{1}{9};$$
$$sin(alpha)^2=frac{8}{9};$$
$$sin(alpha)=pmsqrt{frac{8}{9}}=pmfrac{2sqrt{2}}{3};$$
Обратите внимание на знак (pm), отрицательное значение синуса нас тоже устраивает, так как при подстановке и возведении в квадрат знак минус исчезает.
В задании указано, что это пример из ЕГЭ первой части, значит должен быть только один ответ. Какое же значение синуса нам выбрать: положительное или отрицательное?
В этом нам поможет дополнительное условие на (alphain(0;frac{pi}{2})), что соответсвует первой четверти на тригонометрической окружности. Раз (alpha) лежит в первой четверти, то синус должен быть положительный. Выбираем положительное значение синуса:
$$sin(alpha)=frac{2sqrt{2}}{3};$$
И подставим найденное значение в искомое выражение:
$$3sqrt{2}*sin(alpha)=3sqrt{2}*frac{2sqrt{2}}{3}=4.$$
Ответ: (4.)
Аналогично по основному тригонометрическому тождеству можно находить значение косинуса, если известен синус.
Основные тригонометрическое тождество это ключ к решению более половины всех тригонометрических уравнений.
Основные связи тригонометрических функций
А как найти тангенс или котангенс, если нам, например, известен косинус? Посмотрите на формулы №2, для того, чтобы найти тангенс, нужно знать и косинус, и синус:
$$mathbf{tg(alpha)=frac{sin(alpha)}{cos(alpha)};}$$
$$mathbf{ctg(alpha)=frac{cos(alpha)}{sin(alpha)};}$$
Но зная косинус, мы легко можем найти синус по основному тригонометрическому тождеству, а потом уже найти тангенс.
Пример 2
Найдите (tg(alpha)) и (ctg(alpha)), если (cos(alpha)=frac{sqrt{10}}{10}) и (alpha in (frac{3pi}{2};2pi)).
Сначала находим значение синуса:
$$sin(alpha)^2+cos(alpha)^2=1;$$
$$sin(alpha)^2+left(frac{sqrt{10}}{10}right)^2=1;$$
$$sin(alpha)^2+frac{1}{10}=1;$$
$$sin(alpha)^2=1-frac{1}{10};$$
$$sin(alpha)^2=frac{9}{10};$$
$$sin(alpha)=pmsqrt{frac{9}{10}}=pmfrac{3}{sqrt{10}};$$
Так как по условию задачи (alpha in (frac{3pi}{2};2pi)), что соответсвует четвертой четверти на тригонометрической окружности, то (sin(alpha)<0). Выбираем отрицательное значение:
$$sin(alpha)=-frac{3}{sqrt{10}};$$
Теперь нам известны значения и косинуса, и синуса, можем найти тангенс:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)}=frac{-frac{3}{sqrt{10}}}{frac{sqrt{10}}{10}}=-frac{3}{sqrt{10}}*frac{10}{sqrt{10}}=-3;$$
Котангенс можно найти аналогично по формуле:
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$
Но поступим проще и воспользуемся тригонометрической формулой, связывающей тангенс с котангенсом:
$$mathbf{сtg(alpha)=frac{1}{tg(alpha)};}$$
$$сtg(alpha)=frac{1}{-3}=-frac{1}{3};$$
Ответ: (tg(alpha)=-3;) (ctg(alpha)=-frac{1}{3}.)
Как видите, чтобы найти тангенс или котангенс через косинус или синус, необходимо воспользоваться сразу двумя тригонометрическими формулами. Это не очень удобно, поэтому очень полезны тригонометрические формулы, связывающие тангенс с косинусом или котангенс с синусом напрямую:
$$mathbf{tg(alpha)^2+1=frac{1}{cos(alpha)^2};}$$
$$mathbf{ctg(alpha)^2+1=frac{1}{sin(alpha)^2};}$$
Вывод связи тангенса с косинусом и котангенса с синусом
Полезно знать, как они выводятся. Вывод, на самом деле, элементарный, с использованием основного тригонометрического тождества и определения тангенса через синус и косинус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$left(frac{sin(alpha)}{cos(alpha)}right)^2+1=frac{1}{cos(alpha)^2};$$
Приводим левую часть к общему знаменателю:
$$frac{sin(alpha)^2}{cos(alpha)^2}+frac{cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
$$frac{sin(alpha)^2+cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
В числителе у нас получилось основное тригонометрическое тождество:
$$frac{1}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
Получилось верное равенство – формула доказана. Аналогично доказывается формула для котангенса и синуса. (В качестве упражнения докажите ее сами).
Если решать пример №2 по этим формулам, то решение заметно сокращается:
$$tg(alpha)^2+1=frac{1}{left(frac{sqrt{10}}{10}right)^2};$$
$$tg(alpha)^2+1=10;$$
$$tg(alpha)^2=9;$$
$$tg(alpha)=pm3;$$
Так как (alpha in (frac{3pi}{2};2pi)), то тангенс будет отрицательным:
$$tg(alpha)=-3;$$
Формулы суммы и разности тригонометрических функций
- Синус суммы и разности:
$$mathbf{sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);}$$
$$mathbf{sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);}$$ - Косинус суммы и разности:
$$mathbf{cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);}$$
$$mathbf{cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);}$$ - Тангенс суммы и разности:
$$mathbf{tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};}$$
$$mathbf{tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};}$$ - Котангенс суммы и разности:
$$mathbf{сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};}$$
$$mathbf{сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};}$$
Формулы суммы разности тригонометрических функций попадаются в ЕГЭ по профильной математике в №12. В прошлые года эти формулы давались в справочные материалах и учить их было не обязательно. Тем не менее, я бы рекомендовал выучить хотя бы формулы суммы и разности для синуса и косинуса.
Это не очень удобно, но иногда формулы суммы разности используют для вывода формул приведения:
Пример 3
Упростить выражение (sin(frac{pi}{2}+alpha)).
Воспользуемся формулой синуса суммы:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(frac{pi}{2}+alpha)=sin(frac{pi}{2})*cos(alpha)+sin(alpha)*cos(frac{pi}{2})=$$
$$=1*cos(alpha)+sin(alpha)*0=cos(alpha);$$
Формулы суммы разности так же полезны, когда нужно посчитать значение тригонометрических функций некоторых нестандартных углов:
Пример 4
Найдите значение (sin(15^o)=?)
(15^o) нестандартный угол, вы его не найдете в тригонометрической таблице углов. Представим (15^o) в виде разности стандартных углов (15^o=45^o-30^o). И воспользуемся формулой синуса разности:
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(15^o)=sin(45^o-30^o)=sin(45^o)*cos(30^o)-sin(30^o)*cos(45^o)=$$
$$=frac{sqrt{2}}{2}*frac{sqrt{3}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
Вот мы наши синус (15^o). Получилось такое иррациональное некрасивое выражение, так и оставляем.
Ответ: (sin(15^o)=frac{sqrt{6}-sqrt{2}}{4}.)
Пример 5
Найдите значение (cos(75^o)=?)
(75^o) можно представить в виде суммы стандартных углов (75^o=30^o+45^o). Здесь воспользуемся формулой косинуса суммы:
$$cos(alpha+beta)=cos(30^o)*cos(45^o)-sin(30^0)*sin(45^0)=$$
$$=frac{sqrt{3}}{2}*frac{sqrt{2}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
У нас получился опять отвратительный ответ, но внимательный читатель заметит, что ответ такой же, как в предыдущем примере, это значит, что (cos(75^o)=sin(15^o)). Такой же вывод можно было бы сделать исходя из формул приведения и знания тригонометрической окружности.
Ответ: (cos(75^o)=frac{sqrt{6}-sqrt{2}}{4}.)
Мы не будем выводить эти формулы – это не самое приятное занятие. Их проще выучить, а вывод вам вряд ли когда-либо пригодится. Но сами формулы суммы и разности служат основой для доказательства других тригонометрических формул.
Формулы двойного угла
$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$
Формулы двойного угла для синуса, косинуса, тангенса и котангенса дают возможность выразить двойной угол (2alpha) через (alpha). Формулы для синуса и косинуса очень часто встречаются на ЕГЭ. Их обязательно нужно знать. Все они легко выводятся из формул синуса и косинуса суммы (формулы №5 и №6) :
$$cos(2alpha)=cos(alpha+alpha)=cos(alpha)*cos(alpha)-sin(alpha)*sin(alpha)=cos(alpha)^2-sin(alpha)^2;$$
Воспользовавшись основным тригонометрическим тождеством можно преобразовать эту формулу:
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=1-sin(alpha)^2-sin(alpha)^2=1-2sin(alpha)^2;$$
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=cos(alpha)^2-(1-cos(alpha)^2)=2cos(alpha)^2-1;$$
Синус двойного угла выводится аналогичным образом только с использованием формулы синуса суммы:
$$sin(2alpha)=sin(alpha)*cos(alpha)+sin(alpha)*cos(alpha)=2sin(alpha)cos(alpha);$$
Для вывода формул двойного угла для тангенса нам понадобится представить тангенс в виде отношения синуса к косинуса по определению и только что выведенные формулы синуса и косинуса двойного угла:
$$tg(2alpha)=frac{sin(2alpha)}{cos(2alpha)}=frac{2sin(alpha)cos(alpha)}{cos(alpha)^2-sin(alpha)^2}=frac{frac{2sin(alpha)cos(alpha)}{cos(alpha)^2}}{frac{cos(alpha)^2-sin(alpha)^2}{cos(alpha)^2}}=frac{frac{2sin(alpha)}{cos(alpha)}}{1-frac{sin(alpha)^2}{cos(alpha)^2}}=frac{2tg(alpha)}{1-tg(alpha)^2};$$
Котангенс двойного угла выводится абсолютно также:
$$сtg(2alpha)=frac{cos(2alpha)}{sin(2alpha)}=frac{cos(alpha)^2-sin(alpha)^2}{2sin(alpha)cos(alpha)}=frac{frac{cos(alpha)^2-sin(alpha)^2}{sin(alpha)^2}}{frac{2sin(alpha)cos(alpha)}{sin(alpha)^2}}=frac{frac{cos(alpha)^2}{sin(alpha)^2}-1}{frac{2cos(alpha)}{sin(alpha)}}=frac{ctg(alpha)^2-1}{2ctg(alpha)};$$
В первой части на ЕГЭ попадаются номера на преобразование тригонометрических выражений, где часто содержится двойной угол:
Пример 6
Найти значение (24cos(2alpha)=?), если (sin(alpha)=-0,2.)
Воспользуемся формулой косинуса двойного угла:
$$cos(2alpha)=1-2sin(alpha)^2;$$
$$24cos(2alpha)=24(1-2sin(alpha)^2)=24-48sin(alpha)^2=24-48*(-0,2)^2=24-48*0,04=22,08.$$
Пример 7
Найти значение (frac{10sin(6alpha)}{3cos(3alpha)}=?), если (sin(3alpha)=0,6.)
Используем синус двойного угла, для этого представим (6alpha=2*(3alpha)):
$$sin(6alpha)=sin(2*(3alpha))=2sin(3alpha)cos(3alpha);$$
$$frac{10sin(6alpha)}{3cos(3alpha)}=frac{10*2sin(3alpha)cos(3alpha)}{3cos(3alpha)}=frac{20sin(3alpha)}{3}=frac{20*0,6}{3}=frac{12}{3}=4.$$
Пример 8
Найти значение выражения (frac{12sin(11^o)cos(11^o)}{sin(22^o)}=?)
Замечаем, что (22^o=2*11^o) и воспользуемся синусом двойного угла:
$$frac{12sin(11^o)cos(11^o)}{sin(22^o)}=frac{12sin(11^o)cos(11^o)}{2sin(11^o)cos(11^o)}=frac{12}{2}=6.$$
Формулы тройного угла
Формулы тройного угла обычно попадаются на математических олимпиадах или вступительных экзаменах в математические ВУЗы. Учить их необязательно, но знать о существовании полезно, тем более, что они достаточно легко выводятся.
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$
Выведем эти формулы, использую формулы сложения. Начнем с косинуса тройного угла:
$$cos(3*alpha)=cos(2alpha+alpha)=cos(2alpha)*cos(alpha)-sin(2alpha)*sin(alpha)=$$
$$=(cos(alpha)^2-sin(alpha)^2)*cos(alpha)-2sin(alpha)*cos(alpha)*sin(alpha)=$$
$$=cos(alpha)^3-sin(alpha)^2*cos(alpha)-2sin(alpha)^2*cos(alpha)=$$
$$=cos(alpha)^3-3sin(alpha)^2*cos(alpha);$$
Если расписать (sin(alpha)^2=1-cos(alpha)^2), то получим еще один вариант формулы тройного угла:
$$cos(3*alpha)=cos(alpha)^3-3sin(alpha)^2*cos(alpha)=cos(alpha)^3-3(1-cos(alpha)^2)*cos(alpha)=$$
$$=4cos(alpha)^3-3cos(alpha);$$
Аналогично выводится формула синуса тройного угла:
$$sin(3alpha)=sin(2alpha+alpha)=sin(2alpha)*cos(alpha)+sin(alpha)*cos(2alpha)=$$
$$=2sin(alpha)*cos(alpha)*cos(alpha)+sin(alpha)*(cos(alpha)^2-sin(alpha)^2)=$$
$$=2sin(alpha)*cos(alpha)^2+sin(alpha)*cos(alpha)^2-sin(alpha)^3=3sin(alpha)*cos(alpha)^2-sin(alpha)^3;$$
Распишем по основному тригонометрическому тождеству (cos(alpha)^2=1-sin(alpha)^2) и подставим:
$$sin(3alpha)=3sin(alpha)*cos(alpha)^2-sin(alpha)^3=$$
$$=3sin(alpha)*(1-sin(alpha)^2)-sin(alpha)^3=3sin(alpha)-4sin(alpha)^3;$$
Для тангенса и котангенса формулы тройного угла здесь выводить не будем, так как они достаточно редки. Но в качестве упражнения можете сами выполнить вывод, представив тангенс или котангенс по определению: через отношение синуса тройного угла к косинусу тройного угла или наоборот соотвественно.
Формулы тройного угла обычно используются при преобразовании сложных тригонометрических выражений. Например, на вступительных экзаменах в МФТИ любят давать тригонометрические уравнения на тройной угол и больше.
Формулы половинного угла (двойного аргумента)
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$
Формулы половинного угла это по сути формулы обратные формулам двойного угла. Достаточно запомнить их элементарный вывод, тогда учить совсем необязательно. Здесь важный момент, что любой угол (alpha) всегда можно представить в виде удвоенного угла (frac{alpha}{2}):
$$alpha=2*frac{alpha}{2};$$
Выведем формулу синуса половинного угла, для этого нам понадобится формула косинуса двойного угла:
$$cos(alpha)=1-2*sin(frac{alpha}{2})^2;$$
Выразим отсюда (sin(frac{alpha}{2})):
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
Иногда эту формулу записывают без квадрата:
$$sin(frac{alpha}{2})=pmsqrt{frac{1-cos(alpha)}{2}};$$
Плюс минус возникает при избавлении от квадрата.
Вывод косинуса половинного угла тоже получается из формулы косинуса двойного угла:
$$cos(alpha)=2*cos(frac{alpha}{2})^2-1;$$
$$cos(frac{alpha}{2})^2=frac{cos(alpha)+1}{2};$$
$$cos(frac{alpha}{2})=pmsqrt{frac{cos(alpha)+1}{2}};$$
Доказательство формул половинного угла для тангенса и котангенса следует из выше доказанных формул:
$$tg(frac{alpha}{2})=frac{sin(frac{alpha}{2})}{cos(frac{alpha}{2})}=frac{pmsqrt{frac{1-cos(alpha)}{2}}}{pmsqrt{frac{cos(alpha)+1}{2}}}=sqrt{frac{frac{1-cos(alpha)}{2}}{frac{cos(alpha)+1}{2}}}=frac{1-cos(alpha)}{1+cos(alpha)};$$
Точно так же для котангенса:
$$сtg(frac{alpha}{2})=frac{cos(frac{alpha}{2})}{sin(frac{alpha}{2})}=frac{pmsqrt{frac{cos(alpha)+1}{2}}}{pmsqrt{frac{1-cos(alpha)}{2}}}=sqrt{frac{frac{cos(alpha)+1}{2}}{frac{1-cos(alpha)}{2}}}=frac{1+cos(alpha)}{1-cos(alpha)};$$
Пример 9
При помощи формул половинного угла можно, например, посчитать (cos(15^o)):
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$cos(15^o)^2=frac{1+cos(30^o)}{2}=frac{1+frac{sqrt{3}}{2}}{2}=frac{2+sqrt{3}}{4};$$
$$cos(15^o)=sqrt{frac{2+sqrt{3}}{4}}.$$
Кстати, формулы половинного угла справедливы не только в явном виде, когда аргумент правой части формулы (alpha), а левой (frac{alpha}{2}). Но и в неявном, достаточно, чтобы аргумент правой части был больше аргумента левой в два раза:
$$sin(5alpha)=pmsqrt{frac{1-cos(10alpha)}{2}};$$
Формулы понижения степени
$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$
Формулы понижения второй степени на самом деле дублируют формулы половинного угла.
Формулы понижения третей степени перестановкой слагаемых дублируют формулы тройного угла.
Преобразование суммы и разности тригонометрических функций:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$
Формулы для суммы и разности тригонометрических функций полезны, если необходимо превратить сумму двух функций в произведение. Они в основном используются в уравнениях и преобразованиях сложных выражений, когда необходимо слагаемые разложить на множители.
Для вывода формул суммы и разности синусов и косинусов нам понадобится пара трюков и формулы синуса и косинуса суммы и разности (тут можно запутаться, в названиях формул, будьте внимательны). Вывод получается не самый очевидный.
Обратите внимание, что любой угол (alpha) можно представить в таком странном виде:
$$alpha=frac{alpha}{2}+frac{alpha}{2}+frac{beta}{2}-frac{beta}{2}=frac{alpha+beta}{2}+frac{alpha-beta}{2};$$
Аналогично угол (beta):
$$beta=frac{alpha+beta}{2}-frac{alpha-beta}{2};$$
Эти странности нам понадобятся при выводе формул, просто обратите на них внимание.
А теперь перейдем непосредственно к выводу формулы суммы синусов двух углов. Для начала распишем угла (alpha) и (beta) по формулам выше:
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2}); qquad (*)$$
Теперь воспользуемся формулами синуса суммы и синуса разности:
$$sin(gamma+sigma)=sin(gamma)*cos(sigma)+sin(sigma)*cos(gamma);$$
$$sin(gamma-sigma)=sin(gamma)*cos(sigma)-sin(sigma)*cos(gamma);$$
Только у нас под синусами будут стоять не (gamma) и (sigma), а целые выражения.
Пусть:
$$gamma=frac{alpha+beta}{2};$$
$$sigma=frac{alpha-beta}{2};$$
Применим формулы синуса суммы и разности в (*):
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2})=$$
$$=left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})+sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)+$$
$$+left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})-sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)=$$
$$=2*sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2}); $$
В самом конце мы просто раскрыли большие скобки и привели подобные слагаемые.
Аналогично выводятся все остальные формулы.
Пример 10
Вычислить (sin(165)+sin(75)=?)
(165^o) и (75^o) это не табличные углы. Значения синусов этих углов мы не знаем. Для решения этого примера воспользуемся формулой суммы синусов:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(165^o)+sin(75^o)=2*sinleft(frac{165^o+75^o}{2}right)*cosleft(frac{165^o-75^o}{2}right)=$$
$$=2*sin(120^o)*cos(45^o)=2*frac{sqrt{3}}{2}*frac{sqrt{2}}{2}=frac{sqrt{6}}{2}.$$
Преобразование произведения тригонометрических функций
$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$
В некотором смысле формулы произведения синуса, косинуса, тангенса и котангенса являются обратными к тригонометрическим формулам суммы и разности тригонометрических функций. При помощи этих формул возможно перейти от произведения к сумме или разности.
Для вывода нам опять понадобятся формулы косинуса суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Сложим эти две формулы. Для этого складываем их левые части и приравниваем сумме правых частей:
$$cos(alpha+beta)+cos(alpha-beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha)+cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Приводим подобные слагаемые:
$$cos(alpha+beta)+cos(alpha-beta)=2*cos(alpha)*cos(beta);$$
Отсюда получаем:
$$cos(alpha)*cos(beta)=frac{1}{2}*(cos(alpha+beta)+cos(alpha-beta));$$
Формула произведения косинусов доказана.
Произведение синусов доказывается похожим образом. Для этого домножим формулу косинуса суммы слева и справа на ((-1)):
$$-cos(alpha+beta)=-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Косинус разности оставим без изменений:
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Сложим опять эти две формулы:
$$cos(alpha-beta)-cos(alpha+beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha)-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
$$cos(alpha-beta)-cos(alpha+beta)=2*sin(beta)*sin(alpha);$$
$$sin(beta)*sin(alpha)=frac{1}{2}*(cos(alpha-beta)-cos(alpha+beta));$$
Произведение синусов тоже доказано.
Для того, чтобы вывести формулу произведения синуса и косинуса, нам понадобятся формулы синуса суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
Сложим их:
$$sin(alpha+beta)+sin(alpha-beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha)+sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(alpha+beta)+sin(alpha-beta)=2*sin(alpha)*cos(beta);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$
Пример 11
Вычислить (sin(75^o)*cos(15^o)=?)
Воспользуемся формулой произведения синуса и косинуса:
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$
$$sin(75^o)*cos(15^o)=frac{1}{2}*(sin(75^o+15^o)+sin(75^o-15^o))=$$
$$=frac{1}{2}*(sin(90^o)+sin(60^o))=frac{1}{2}*(1+frac{sqrt{3}}{2})=frac{2+sqrt{3}}{4}.$$








































































![sin(nalpha)=sum_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}cos^{n-2k-1}alpha,sin^{2k+1}alpha,](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb020e5dfc3b2d5dfe1d1a0c571487ce387a8153)
![cos(nalpha)=sum_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}cos^{n-2k}alpha,sin^{2k}alpha,](https://wikimedia.org/api/rest_v1/media/math/render/svg/84f285d7cb530e87d8a9e33cff84fd4a4c9a8205)
![mathrm{tg}(nalpha)=frac{sin(nalpha)}{cos(nalpha)}=dfrac{displaystyle{sumlimits_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}mathrm{tg}^{2k+1}alpha}}{displaystyle{sumlimits_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}mathrm{tg}^{2k}alpha}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/8800a20a70495802fc2de287bb98d155e14720b1)
![mathrm{ctg}(nalpha)=frac{cos(nalpha)}{sin(nalpha)}=dfrac{displaystyle{sumlimits_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}mathrm{ctg}^{n-2k}alpha}}{displaystyle{sumlimits_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}mathrm{ctg}^{n-2k-1}alpha}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/90744f04ee2a1e34b1f0763e310c1c1d071f240d)