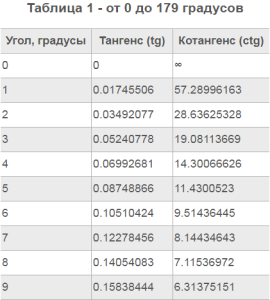
Полные таблицы косинусов и синусов (cos и sin), а также значений тангенсов (tg), котангенсов (ctg) – это мощный и полезный инструмент, помогающий решать множество задач, как теоретического, так и прикладного характера. В этой статье мы приведем некоторые главные таблицы значений тригонометрических функций (таблицу синусов, таблицу косинусов, таблицу тангенсов и котангенсов) для углов 0, 30, 45, 60, 90, …, 360 градусов (0, π6, π3, π2, … , 2π радиан). Также здесь будут встречаться отдельные таблицы Брадиса для синусов и косинусов, тангенсов и котангенсов с пояснением, как их использовать для нахождения значений основных тригонометрических функций.
Таблица основных тригонометрических функций для углов 0, 30, 45, 60, 90, …, 360 градусов
Исходя из определений синуса, косинуса, тангенса и котангенса можно найти значения этих функций для углов 0 и 90 градусов
sin 0=0, cos 0=1, tg 0=0, котангенс нуля – не определен,
sin 90°=1, cos 90°=0, сtg 90°=0, тангенс дявяноста градусов не определен.
Значения синусов, косинусов, тангенсов и котангенсов в курсе геометрии определяются как соотношения сторон прямоугольного треугольника, углы которого равны 30, 60 и 90 градусов, и также 45, 45 и 90 градусов.
Синус (син) – отношение противолежащего катета к гипотенузе.
Косинус (кос) – отношение прилежащего катета к гипотенузе.
Тангенс (танг) – отношение противолежащего катета к прилежащему.
Котангенс (котанг) – отношение прилежащего катета к противолежащему.
В соответствии с определениями находятся значения функций:
sin 30°=12, cos 30°=32, tg 30°=33, ctg 30°=3,sin 45°=22, cos 45°=22, tg 45°=1, ctg 45°=1,sin 60°=32, cos 45°=12, tg 45°=3, ctg 45°=33.
Сведем эти значения в таблицу и назовем ее таблицей основных значений косинуса и синуса, тангенса и котангенса.
| α° | 0 | 30 | 45 | 60 | 90 |
| sin α | 0 | 12 | 22 | 32 | 1 |
| cos α | 1 | 32 | 22 | 12 | 0 |
| tg α | 0 | 33 | 1 | 3 | не определен |
| ctg α | не определен | 3 | 1 | 33 | 0 |
| α, радиан | 0 | π6 | π4 | π3 | π2 |
Одно из важных свойств тригонометрических функций, представленное в таблице в тригонометрии и важное для изучения – периодичность. На основе этого свойства данную таблицу можно расширить,используя формулы приведения. Ниже представим расширенную таблицу значений основных тригонометрических функций для углов 0, 30, 60, … ,120, 135, 150, 180, … , 360 градусов ( 0 , π 6 , π 3 , π 2 , . . . , 2 π радиан).
| α° | 0 | 30 | 45 | 60 | 90 | 120 | 135 | 150 | 180 | 210 | 225 | 240 | 270 | 300 | 315 | 330 | 360 |
| sin α | 0 | 12 | 22 | 32 | 1 | 32 | 22 | 12 | 0 | -12 | -22 | -32 | -1 | -32 | -22 | -12 | 0 |
| cos α | 1 | 32 | 22 | 12 | 0 | -12 | -22 | -32 | -1 | -32 | -22 | -12 | 0 | 12 | 22 | 32 | 1 |
| tg α | 0 | 33 | 1 | 3 | – | -1 | -33 | 0 | 0 | 33 | 1 | 3 | – | -3 | -1 | 0 | |
| ctg α | – | 3 | 1 | 33 | 0 | -33 | -1 | -3 | – | 3 | 1 | 33 | 0 | -33 | -1 | -3 | – |
| α, радиан | 0 | π6 | π4 | π3 | π2 | 2π3 | 3π4 | 5π6 | π | 7π6 | 5π4 | 4π3 | 3π2 | 5π3 | 7π4 | 11π6 | 2π |
Периодичность синуса, косинуса, тангенса и котангенса позволяет расширять табличные значения углов сколько угодно. Значения, собранные в таблице, часто используются при решении задач (чаще всего), поэтому их рекомендуется запоминать и выучивать наизусть.
Как пользоваться таблицей основных значений тригонометрических функций
Принцип пользования таблицей значений тангенсов и котангенсов, а также синусов и косинусов, понятен на интуитивном уровне (но это не означает, что их не стоит изучать и заучивать). Пересечение строки и столбца дает значение функции для конкретного угла.
Нужно узнать, чему равен sin 7π6
Находим в таблице столбец, значение последней ячейки которого равно 7π6 радиан – то же самое, что 210 градусов. Затем выбираем сроку таблицы, в которой представлены значения синусов. На пересечении строки и столбца будем находить искомое значение:
sin 7π6=-12
Таблицы Брадиса
Таблица Брадиса позволяет вычислить значение синуса, косинуса, тангенса или котангенса с точностью до 4-х знаков после запятой без использования вычислительной техники (как и в решении предыдущего уравнения). Это своего рода замена инженерному калькулятору.
Владимир Модестович Брадис (1890 – 1975) – советский математик-педагог, с 1954 года член-корреспондент АПН СССР. Таблицы четырёхзначных логарифмов и натуральных тригонометрических величин, разработанные Брадисом, впервые вышли в 1921 году.
Сначала приведем таблицу Брадиса для синусов и косинусов. Она позволяет достаточно точно вычислять приближенные значения этих функций для углов, содержащих целое количество градусов и минут. В крайнем левом столбце таблицы представлены градусы, а в верхней строке – минуты. Отметим, что все значения углов таблицы Брадиса кратны шести минутам.
Таблица Брадиса для синусов и косинусов
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | cos | 1′ | 2′ | 3′ |
| 0.0000 | 90° | ||||||||||||||
| 0° | 0.0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0.0872 | 85° | 3 | 6 | 9 |
| 5° | 0.0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 82° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 0.1736 | 80° | 3 | 6 | 9 |
| 10° | 0.1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 77° | 3 | 6 | 9 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 0.2588 | 75° | 3 | 6 | 8 |
| 15° | 0.2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 74° | 3 | 6 | 8 |
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 72° | 3 | 6 | 8 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0.3420 | 70° | 3 | 5 | 8 |
| 20° | 0.3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0.4226 | 65° | 3 | 5 | 8 |
| 25° | 0.4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 63° | 3 | 5 | 8 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0.5000 | 60° | 3 | 5 | 8 |
| 30° | 0.5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 59° | 3 | 5 | 8 |
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0.5736 | 55° | 2 | 5 | 7 |
| 35° | 0.5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0.5878 | 54° | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52° | 2 | 5 | 7 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0.6428 | 50° | 2 | 4 | 7 |
| 40° | 0.6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 47° | 2 | 4 | 6 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 8909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0.7071 | 45° | 2 | 4 | 6 |
| 45° | 0.7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0.7660 | 40° | 2 | 4 | 6 |
| 50° | 0.7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 38° | 2 | 4 | 5 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 36° | 2 | 3 | 5 |
| 54° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0.8192 | 35° | 2 | 3 | 5 |
| 55° | 0.8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 34° | 2 | 3 | 5 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 32° | 2 | 3 | 5 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0.8660 | 30° | 1 | 3 | 4 |
| 60° | 0.8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| 61° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 27° | 1 | 3 | 4 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0.9063 | 25° | 1 | 3 | 4 |
| 65° | 0.9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9256 | 9272 | 22° | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9383 | 9391 | 0.9397 | 20° | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0.9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0.9659 | 15° | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0.9848 | 10° | 1 | 1 | 2 |
| 80° | 0.9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 5° | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0.9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0° | 0 | 0 | 0 |
| 90° | 1.0000 | ||||||||||||||
| sin | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | 1′ | 2′ | 3′ |
Для нахождения значений синусов и косинусов углов, не представленных в таблице, необходимо использовать поправки.
Теперь приведем таблицу Брадиса для тангенсов и котангенсов. Она содержит значения тангенсов углов от 0 до 76 градусов, и котангенсов углов от 14 до 90 градусов.
Таблица Брадиса для тангенса и котангенса
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | ctg | 1′ | 2′ | 3′ |
| 0 | 90° | ||||||||||||||
| 0° | 0,000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87° | 3 | 6 | 9 |
| 3° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86° | 3 | 6 | 9 |
| 4° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 0,0875 | 85° | 3 | 6 | 9 |
| 5° | 0,0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84° | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 83° | 3 | 6 | 9 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 82° | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 81° | 3 | 6 | 9 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0,1763 | 80° | 3 | 6 | 9 |
| 10° | 0,1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 79° | 3 | 6 | 9 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78° | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 77° | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76° | 3 | 6 | 9 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0,2679 | 75° | 3 | 6 | 9 |
| 15° | 0,2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 74° | 3 | 6 | 9 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 73° | 3 | 6 | 9 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 72° | 3 | 6 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71° | 3 | 6 | 10 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0,3640 | 70° | 3 | 7 | 10 |
| 20° | 0,3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69° | 3 | 7 | 10 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 68° | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67° | 3 | 7 | 10 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 66° | 3 | 7 | 10 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0,4663 | 65° | 4 | 7 | 11 |
| 25° | 0,4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 64° | 4 | 7 | 11 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63° | 4 | 7 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 62° | 4 | 7 | 11 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 61° | 4 | 8 | 11 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0,5774 | 60° | 4 | 8 | 12 |
| 30° | 0,5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 59° | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 58° | 4 | 8 | 12 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 57° | 4 | 8 | 12 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 56° | 4 | 8 | 13 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0,7002 | 55° | 4 | 9 | 13 |
| 35° | 0,7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54° | 4 | 8 | 13 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 53° | 5 | 9 | 14° |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52° | 5 | 9 | 14 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 51° | 5 | 9 | 14 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0,8391 | 50° | 5 | 10 | 15 |
| 40° | 0,8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0,8693 | 49° | 5 | 10 | 15 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 48° | 5 | 10 | 16 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 47° | 6 | 11 | 16 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0,9657 | 46° | 6 | 11 | 17 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1,0000 | 45° | 6 | 11 | 17 |
| 45° | 1,0000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 0355 | 44° | 6 | 12 | 18 |
| 46° | 0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 0724 | 43° | 6 | 12 | 18 |
| 47° | 0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 1106 | 42° | 6 | 13 | 19 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 41° | 7 | 13 | 20 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1,1918 | 40° | 7 | 14 | 21 |
| 50° | 1,1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 39° | 7 | 14 | 22 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 38° | 8 | 15 | 23 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 37° | 8 | 16 | 24 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 36° | 8 | 16 | 25 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1,4281 | 35° | 9 | 17 | 26 |
| 55° | 1,4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 34° | 9 | 18 | 27 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 33° | 10 | 19 | 29 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 32° | 10 | 20 | 30 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 31° | 11 | 21 | 32 |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1,7321 | 30° | 11 | 23 | 34 |
| 60° | 1,732 | 1,739 | 1,746 | 1,753 | 1,760 | 1,767 | 1,775 | 1,782 | 1,789 | 1,797 | 1,804 | 29° | 1 | 2 | 4 |
| 61° | 1,804 | 1,811 | 1,819 | 1,827 | 1,834 | 1,842 | 1,849 | 1,857 | 1,865 | 1,873 | 1,881 | 28° | 1 | 3 | 4 |
| 62° | 1,881 | 1,889 | 1,897 | 1,905 | 1,913 | 1,921 | 1,929 | 1,937 | 1,946 | 1,954 | 1,963 | 27° | 1 | 3 | 4 |
| 63° | 1,963 | 1,971 | 1,980 | 1,988 | 1,997 | 2,006 | 2,014 | 2,023 | 2,032 | 2,041 | 2,05 | 26° | 1 | 3 | 4 |
| 64° | 2,050 | 2,059 | 2,069 | 2,078 | 2,087 | 2,097 | 2,106 | 2,116 | 2,125 | 2,135 | 2,145 | 25° | 2 | 3 | 5 |
| 65° | 2,145 | 2,154 | 2,164 | 2,174 | 2,184 | 2,194 | 2,204 | 2,215 | 2,225 | 2,236 | 2,246 | 24° | 2 | 3 | 5 |
| 66° | 2,246 | 2,257 | 2,267 | 2,278 | 2,289 | 2,3 | 2,311 | 2,322 | 2,333 | 2,344 | 2,356 | 23° | 2 | 4 | 5 |
| 67° | 2,356 | 2,367 | 2,379 | 2,391 | 2,402 | 2,414 | 2,426 | 2,438 | 2,450 | 2,463 | 2,475 | 22° | 2 | 4 | 6 |
| 68° | 2,475 | 2,488 | 2,5 | 2,513 | 2,526 | 2,539 | 2,552 | 2,565 | 2,578 | 2,592 | 2,605 | 21° | 2 | 4 | 6 |
| 69° | 2,605 | 2,619 | 2,633 | 2,646 | 2,66 | 2,675 | 2,689 | 2,703 | 2,718 | 2,733 | 2,747 | 20° | 2 | 5 | 7 |
| 70° | 2,747 | 2,762 | 2,778 | 2,793 | 2,808 | 2,824 | 2,840 | 2,856 | 2,872 | 2,888 | 2,904 | 19° | 3 | 5 | 8 |
| 71° | 2,904 | 2,921 | 2,937 | 2,954 | 2,971 | 2,989 | 3,006 | 3,024 | 3,042 | 3,06 | 3,078 | 18° | 3 | 6 | 9 |
| 72° | 3,078 | 3,096 | 3,115 | 3,133 | 3,152 | 3,172 | 3,191 | 3,211 | 3,230 | 3,251 | 3,271 | 17° | 3 | 6 | 10 |
| 73° | 3,271 | 3,291 | 3,312 | 3,333 | 3,354 | 3,376 | 3 | 7 | 10 | ||||||
| 3,398 | 3,42 | 3,442 | 3,465 | 3,487 | 16° | 4 | 7 | 11 | |||||||
| 74° | 3,487 | 3,511 | 3,534 | 3,558 | 3,582 | 3,606 | 4 | 8 | 12 | ||||||
| 3,630 | 3,655 | 3,681 | 3,706 | 3,732 | 15° | 4 | 8 | 13 | |||||||
| 75° | 3,732 | 3,758 | 3,785 | 3,812 | 3,839 | 3,867 | 4 | 9 | 13 | ||||||
| 3,895 | 3,923 | 3,952 | 3,981 | 4,011 | 14° | 5 | 10 | 14 | |||||||
| tg | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | 1′ | 2′ | 3′ |
Как пользоваться таблицами Брадиса
Рассмотрим таблицу Брадиса для синусов и косинусов. Все, что относится к синусам, находится вверху и слева. Если нам нужны косинусы – смотрим на правую сторону внизу таблицы.
Для нахождения значений синуса угла нужно найти пересечение строки, содержащей в крайней левой ячейке необходимое количество градусов, и столбца, содержащего в верхней ячейке необходимое число минут.
Если точного значения угла нет в таблице Брадиса, прибегаем к помощи поправок. Поправки на одну, две и три минуты даны в крайних правых столбцах таблицы. Для нахождения значения синуса угла, которого нет в таблице, находим самое близкое к нему значение. После этого прибавляем или отнимаем поправку, соответствующую разнице между углами.
В случае, если мы ищем синус угла, который больше 90 градусов, сначала нужно воспользоваться формулами приведения, а уже потом – таблицей Брадиса.
Пусть нужно найти синус угла 17°44′. По таблице находим тождество синус 17°42′ и прибавляем к его значению поправку на две минуты:
17°44′-17°42’=2′ (необходимая поправка)sin 17°44’=0.3040+0.0006=0.3046
Принцип работы с косинусами, тангенсами и котангенсами аналогичен. Однако, важно помнить о знаке поправок.
При вычислении значений синусов поправка имеет положительный знак, а при вычислении косинусов поправку необходимо брать с отрицательным знаком.
В данной таблице приведены значения синусов и косинусов для углов от 0 до 359 градусов. Но если Вам нужно рассчитать значения тригонометрических функций
для более точных углов (с минутами и секундами) или углов больше 360 градусов или углов с отрицательными значениями (например 8° 5′ 53″
или -1775° 15′ 22″ ), то можно воспользоваться тригонометрическим калькулятором.
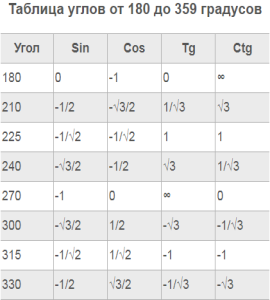
Таблица углов от 0 до 179 градусов
| Угол (градусы) | Синус (Sin) | Косинус (Cos) |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0.01745241 | 0.9998477 |
| 2 | 0.0348995 | 0.99939083 |
| 3 | 0.05233596 | 0.99862953 |
| 4 | 0.06975647 | 0.99756405 |
| 5 | 0.08715574 | 0.9961947 |
| 6 | 0.10452846 | 0.9945219 |
| 7 | 0.12186934 | 0.99254615 |
| 8 | 0.1391731 | 0.99026807 |
| 9 | 0.15643447 | 0.98768834 |
| 10 | 0.17364818 | 0.98480775 |
| 11 | 0.190809 | 0.98162718 |
| 12 | 0.20791169 | 0.9781476 |
| 13 | 0.22495105 | 0.97437006 |
| 14 | 0.2419219 | 0.97029573 |
| 15 | 0.25881905 | 0.96592583 |
| 16 | 0.27563736 | 0.9612617 |
| 17 | 0.2923717 | 0.95630476 |
| 18 | 0.30901699 | 0.95105652 |
| 19 | 0.32556815 | 0.94551858 |
| 20 | 0.34202014 | 0.93969262 |
| 21 | 0.35836795 | 0.93358043 |
| 22 | 0.37460659 | 0.92718385 |
| 23 | 0.39073113 | 0.92050485 |
| 24 | 0.40673664 | 0.91354546 |
| 25 | 0.42261826 | 0.90630779 |
| 26 | 0.43837115 | 0.89879405 |
| 27 | 0.4539905 | 0.89100652 |
| 28 | 0.46947156 | 0.88294759 |
| 29 | 0.48480962 | 0.87461971 |
| 30 | 0.5 | 0.8660254 |
| 31 | 0.51503807 | 0.8571673 |
| 32 | 0.52991926 | 0.8480481 |
| 33 | 0.54463904 | 0.83867057 |
| 34 | 0.5591929 | 0.82903757 |
| 35 | 0.57357644 | 0.81915204 |
| 36 | 0.58778525 | 0.80901699 |
| 37 | 0.60181502 | 0.79863551 |
| 38 | 0.61566148 | 0.78801075 |
| 39 | 0.62932039 | 0.77714596 |
| 40 | 0.64278761 | 0.76604444 |
| 41 | 0.65605903 | 0.75470958 |
| 42 | 0.66913061 | 0.74314483 |
| 43 | 0.68199836 | 0.7313537 |
| 44 | 0.69465837 | 0.7193398 |
| 45 | 0.70710678 | 0.70710678 |
| 46 | 0.7193398 | 0.69465837 |
| 47 | 0.7313537 | 0.68199836 |
| 48 | 0.74314483 | 0.66913061 |
| 49 | 0.75470958 | 0.65605903 |
| 50 | 0.76604444 | 0.64278761 |
| 51 | 0.77714596 | 0.62932039 |
| 52 | 0.78801075 | 0.61566148 |
| 53 | 0.79863551 | 0.60181502 |
| 54 | 0.80901699 | 0.58778525 |
| 55 | 0.81915204 | 0.57357644 |
| 56 | 0.82903757 | 0.5591929 |
| 57 | 0.83867057 | 0.54463904 |
| 58 | 0.8480481 | 0.52991926 |
| 59 | 0.8571673 | 0.51503807 |
| 60 | 0.8660254 | 0.5 |
| 61 | 0.87461971 | 0.48480962 |
| 62 | 0.88294759 | 0.46947156 |
| 63 | 0.89100652 | 0.4539905 |
| 64 | 0.89879405 | 0.43837115 |
| 65 | 0.90630779 | 0.42261826 |
| 66 | 0.91354546 | 0.40673664 |
| 67 | 0.92050485 | 0.39073113 |
| 68 | 0.92718385 | 0.37460659 |
| 69 | 0.93358043 | 0.35836795 |
| 70 | 0.93969262 | 0.34202014 |
| 71 | 0.94551858 | 0.32556815 |
| 72 | 0.95105652 | 0.30901699 |
| 73 | 0.95630476 | 0.2923717 |
| 74 | 0.9612617 | 0.27563736 |
| 75 | 0.96592583 | 0.25881905 |
| 76 | 0.97029573 | 0.2419219 |
| 77 | 0.97437006 | 0.22495105 |
| 78 | 0.9781476 | 0.20791169 |
| 79 | 0.98162718 | 0.190809 |
| 80 | 0.98480775 | 0.17364818 |
| 81 | 0.98768834 | 0.15643447 |
| 82 | 0.99026807 | 0.1391731 |
| 83 | 0.99254615 | 0.12186934 |
| 84 | 0.9945219 | 0.10452846 |
| 85 | 0.9961947 | 0.08715574 |
| 86 | 0.99756405 | 0.06975647 |
| 87 | 0.99862953 | 0.05233596 |
| 88 | 0.99939083 | 0.0348995 |
| 89 | 0.9998477 | 0.01745241 |
| 90 | 1 | 0 |
| 91 | 0.9998477 | -0.01745241 |
| 92 | 0.99939083 | -0.0348995 |
| 93 | 0.99862953 | -0.05233596 |
| 94 | 0.99756405 | -0.06975647 |
| 95 | 0.9961947 | -0.08715574 |
| 96 | 0.9945219 | -0.10452846 |
| 97 | 0.99254615 | -0.12186934 |
| 98 | 0.99026807 | -0.1391731 |
| 99 | 0.98768834 | -0.15643447 |
| 100 | 0.98480775 | -0.17364818 |
| 101 | 0.98162718 | -0.190809 |
| 102 | 0.9781476 | -0.20791169 |
| 103 | 0.97437006 | -0.22495105 |
| 104 | 0.97029573 | -0.2419219 |
| 105 | 0.96592583 | -0.25881905 |
| 106 | 0.9612617 | -0.27563736 |
| 107 | 0.95630476 | -0.2923717 |
| 108 | 0.95105652 | -0.30901699 |
| 109 | 0.94551858 | -0.32556815 |
| 110 | 0.93969262 | -0.34202014 |
| 111 | 0.93358043 | -0.35836795 |
| 112 | 0.92718385 | -0.37460659 |
| 113 | 0.92050485 | -0.39073113 |
| 114 | 0.91354546 | -0.40673664 |
| 115 | 0.90630779 | -0.42261826 |
| 116 | 0.89879405 | -0.43837115 |
| 117 | 0.89100652 | -0.4539905 |
| 118 | 0.88294759 | -0.46947156 |
| 119 | 0.87461971 | -0.48480962 |
| 120 | 0.8660254 | -0.5 |
| 121 | 0.8571673 | -0.51503807 |
| 122 | 0.8480481 | -0.52991926 |
| 123 | 0.83867057 | -0.54463904 |
| 124 | 0.82903757 | -0.5591929 |
| 125 | 0.81915204 | -0.57357644 |
| 126 | 0.80901699 | -0.58778525 |
| 127 | 0.79863551 | -0.60181502 |
| 128 | 0.78801075 | -0.61566148 |
| 129 | 0.77714596 | -0.62932039 |
| 130 | 0.76604444 | -0.64278761 |
| 131 | 0.75470958 | -0.65605903 |
| 132 | 0.74314483 | -0.66913061 |
| 133 | 0.7313537 | -0.68199836 |
| 134 | 0.7193398 | -0.69465837 |
| 135 | 0.70710678 | -0.70710678 |
| 136 | 0.69465837 | -0.7193398 |
| 137 | 0.68199836 | -0.7313537 |
| 138 | 0.66913061 | -0.74314483 |
| 139 | 0.65605903 | -0.75470958 |
| 140 | 0.64278761 | -0.76604444 |
| 141 | 0.62932039 | -0.77714596 |
| 142 | 0.61566148 | -0.78801075 |
| 143 | 0.60181502 | -0.79863551 |
| 144 | 0.58778525 | -0.80901699 |
| 145 | 0.57357644 | -0.81915204 |
| 146 | 0.5591929 | -0.82903757 |
| 147 | 0.54463904 | -0.83867057 |
| 148 | 0.52991926 | -0.8480481 |
| 149 | 0.51503807 | -0.8571673 |
| 150 | 0.5 | -0.8660254 |
| 151 | 0.48480962 | -0.87461971 |
| 152 | 0.46947156 | -0.88294759 |
| 153 | 0.4539905 | -0.89100652 |
| 154 | 0.43837115 | -0.89879405 |
| 155 | 0.42261826 | -0.90630779 |
| 156 | 0.40673664 | -0.91354546 |
| 157 | 0.39073113 | -0.92050485 |
| 158 | 0.37460659 | -0.92718385 |
| 159 | 0.35836795 | -0.93358043 |
| 160 | 0.34202014 | -0.93969262 |
| 161 | 0.32556815 | -0.94551858 |
| 162 | 0.30901699 | -0.95105652 |
| 163 | 0.2923717 | -0.95630476 |
| 164 | 0.27563736 | -0.9612617 |
| 165 | 0.25881905 | -0.96592583 |
| 166 | 0.2419219 | -0.97029573 |
| 167 | 0.22495105 | -0.97437006 |
| 168 | 0.20791169 | -0.9781476 |
| 169 | 0.190809 | -0.98162718 |
| 170 | 0.17364818 | -0.98480775 |
| 171 | 0.15643447 | -0.98768834 |
| 172 | 0.1391731 | -0.99026807 |
| 173 | 0.12186934 | -0.99254615 |
| 174 | 0.10452846 | -0.9945219 |
| 175 | 0.08715574 | -0.9961947 |
| 176 | 0.06975647 | -0.99756405 |
| 177 | 0.05233596 | -0.99862953 |
| 178 | 0.0348995 | -0.99939083 |
| 179 | 0.01745241 | -0.9998477 |
Таблица углов от 180 до 359 градусов
| Угол (градусы) | Синус (Sin) | Косинус (Cos) |
|---|---|---|
| 180 | 0 | -1 |
| 181 | -0.01745241 | -0.9998477 |
| 182 | -0.0348995 | -0.99939083 |
| 183 | -0.05233596 | -0.99862953 |
| 184 | -0.06975647 | -0.99756405 |
| 185 | -0.08715574 | -0.9961947 |
| 186 | -0.10452846 | -0.9945219 |
| 187 | -0.12186934 | -0.99254615 |
| 188 | -0.1391731 | -0.99026807 |
| 189 | -0.15643447 | -0.98768834 |
| 190 | -0.17364818 | -0.98480775 |
| 191 | -0.190809 | -0.98162718 |
| 192 | -0.20791169 | -0.9781476 |
| 193 | -0.22495105 | -0.97437006 |
| 194 | -0.2419219 | -0.97029573 |
| 195 | -0.25881905 | -0.96592583 |
| 196 | -0.27563736 | -0.9612617 |
| 197 | -0.2923717 | -0.95630476 |
| 198 | -0.30901699 | -0.95105652 |
| 199 | -0.32556815 | -0.94551858 |
| 200 | -0.34202014 | -0.93969262 |
| 201 | -0.35836795 | -0.93358043 |
| 202 | -0.37460659 | -0.92718385 |
| 203 | -0.39073113 | -0.92050485 |
| 204 | -0.40673664 | -0.91354546 |
| 205 | -0.42261826 | -0.90630779 |
| 206 | -0.43837115 | -0.89879405 |
| 207 | -0.4539905 | -0.89100652 |
| 208 | -0.46947156 | -0.88294759 |
| 209 | -0.48480962 | -0.87461971 |
| 210 | -0.5 | -0.8660254 |
| 211 | -0.51503807 | -0.8571673 |
| 212 | -0.52991926 | -0.8480481 |
| 213 | -0.54463904 | -0.83867057 |
| 214 | -0.5591929 | -0.82903757 |
| 215 | -0.57357644 | -0.81915204 |
| 216 | -0.58778525 | -0.80901699 |
| 217 | -0.60181502 | -0.79863551 |
| 218 | -0.61566148 | -0.78801075 |
| 219 | -0.62932039 | -0.77714596 |
| 220 | -0.64278761 | -0.76604444 |
| 221 | -0.65605903 | -0.75470958 |
| 222 | -0.66913061 | -0.74314483 |
| 223 | -0.68199836 | -0.7313537 |
| 224 | -0.69465837 | -0.7193398 |
| 225 | -0.70710678 | -0.70710678 |
| 226 | -0.7193398 | -0.69465837 |
| 227 | -0.7313537 | -0.68199836 |
| 228 | -0.74314483 | -0.66913061 |
| 229 | -0.75470958 | -0.65605903 |
| 230 | -0.76604444 | -0.64278761 |
| 231 | -0.77714596 | -0.62932039 |
| 232 | -0.78801075 | -0.61566148 |
| 233 | -0.79863551 | -0.60181502 |
| 234 | -0.80901699 | -0.58778525 |
| 235 | -0.81915204 | -0.57357644 |
| 236 | -0.82903757 | -0.5591929 |
| 237 | -0.83867057 | -0.54463904 |
| 238 | -0.8480481 | -0.52991926 |
| 239 | -0.8571673 | -0.51503807 |
| 240 | -0.8660254 | -0.5 |
| 241 | -0.87461971 | -0.48480962 |
| 242 | -0.88294759 | -0.46947156 |
| 243 | -0.89100652 | -0.4539905 |
| 244 | -0.89879405 | -0.43837115 |
| 245 | -0.90630779 | -0.42261826 |
| 246 | -0.91354546 | -0.40673664 |
| 247 | -0.92050485 | -0.39073113 |
| 248 | -0.92718385 | -0.37460659 |
| 249 | -0.93358043 | -0.35836795 |
| 250 | -0.93969262 | -0.34202014 |
| 251 | -0.94551858 | -0.32556815 |
| 252 | -0.95105652 | -0.30901699 |
| 253 | -0.95630476 | -0.2923717 |
| 254 | -0.9612617 | -0.27563736 |
| 255 | -0.96592583 | -0.25881905 |
| 256 | -0.97029573 | -0.2419219 |
| 257 | -0.97437006 | -0.22495105 |
| 258 | -0.9781476 | -0.20791169 |
| 259 | -0.98162718 | -0.190809 |
| 260 | -0.98480775 | -0.17364818 |
| 261 | -0.98768834 | -0.15643447 |
| 262 | -0.99026807 | -0.1391731 |
| 263 | -0.99254615 | -0.12186934 |
| 264 | -0.9945219 | -0.10452846 |
| 265 | -0.9961947 | -0.08715574 |
| 266 | -0.99756405 | -0.06975647 |
| 267 | -0.99862953 | -0.05233596 |
| 268 | -0.99939083 | -0.0348995 |
| 269 | -0.9998477 | -0.01745241 |
| 270 | -1 | 0 |
| 271 | -0.9998477 | 0.01745241 |
| 272 | -0.99939083 | 0.0348995 |
| 273 | -0.99862953 | 0.05233596 |
| 274 | -0.99756405 | 0.06975647 |
| 275 | -0.9961947 | 0.08715574 |
| 276 | -0.9945219 | 0.10452846 |
| 277 | -0.99254615 | 0.12186934 |
| 278 | -0.99026807 | 0.1391731 |
| 279 | -0.98768834 | 0.15643447 |
| 280 | -0.98480775 | 0.17364818 |
| 281 | -0.98162718 | 0.190809 |
| 282 | -0.9781476 | 0.20791169 |
| 283 | -0.97437006 | 0.22495105 |
| 284 | -0.97029573 | 0.2419219 |
| 285 | -0.96592583 | 0.25881905 |
| 286 | -0.9612617 | 0.27563736 |
| 287 | -0.95630476 | 0.2923717 |
| 288 | -0.95105652 | 0.30901699 |
| 289 | -0.94551858 | 0.32556815 |
| 290 | -0.93969262 | 0.34202014 |
| 291 | -0.93358043 | 0.35836795 |
| 292 | -0.92718385 | 0.37460659 |
| 293 | -0.92050485 | 0.39073113 |
| 294 | -0.91354546 | 0.40673664 |
| 295 | -0.90630779 | 0.42261826 |
| 296 | -0.89879405 | 0.43837115 |
| 297 | -0.89100652 | 0.4539905 |
| 298 | -0.88294759 | 0.46947156 |
| 299 | -0.87461971 | 0.48480962 |
| 300 | -0.8660254 | 0.5 |
| 301 | -0.8571673 | 0.51503807 |
| 302 | -0.8480481 | 0.52991926 |
| 303 | -0.83867057 | 0.54463904 |
| 304 | -0.82903757 | 0.5591929 |
| 305 | -0.81915204 | 0.57357644 |
| 306 | -0.80901699 | 0.58778525 |
| 307 | -0.79863551 | 0.60181502 |
| 308 | -0.78801075 | 0.61566148 |
| 309 | -0.77714596 | 0.62932039 |
| 310 | -0.76604444 | 0.64278761 |
| 311 | -0.75470958 | 0.65605903 |
| 312 | -0.74314483 | 0.66913061 |
| 313 | -0.7313537 | 0.68199836 |
| 314 | -0.7193398 | 0.69465837 |
| 315 | -0.70710678 | 0.70710678 |
| 316 | -0.69465837 | 0.7193398 |
| 317 | -0.68199836 | 0.7313537 |
| 318 | -0.66913061 | 0.74314483 |
| 319 | -0.65605903 | 0.75470958 |
| 320 | -0.64278761 | 0.76604444 |
| 321 | -0.62932039 | 0.77714596 |
| 322 | -0.61566148 | 0.78801075 |
| 323 | -0.60181502 | 0.79863551 |
| 324 | -0.58778525 | 0.80901699 |
| 325 | -0.57357644 | 0.81915204 |
| 326 | -0.5591929 | 0.82903757 |
| 327 | -0.54463904 | 0.83867057 |
| 328 | -0.52991926 | 0.8480481 |
| 329 | -0.51503807 | 0.8571673 |
| 330 | -0.5 | 0.8660254 |
| 331 | -0.48480962 | 0.87461971 |
| 332 | -0.46947156 | 0.88294759 |
| 333 | -0.4539905 | 0.89100652 |
| 334 | -0.43837115 | 0.89879405 |
| 335 | -0.42261826 | 0.90630779 |
| 336 | -0.40673664 | 0.91354546 |
| 337 | -0.39073113 | 0.92050485 |
| 338 | -0.37460659 | 0.92718385 |
| 339 | -0.35836795 | 0.93358043 |
| 340 | -0.34202014 | 0.93969262 |
| 341 | -0.32556815 | 0.94551858 |
| 342 | -0.30901699 | 0.95105652 |
| 343 | -0.2923717 | 0.95630476 |
| 344 | -0.27563736 | 0.9612617 |
| 345 | -0.25881905 | 0.96592583 |
| 346 | -0.2419219 | 0.97029573 |
| 347 | -0.22495105 | 0.97437006 |
| 348 | -0.20791169 | 0.9781476 |
| 349 | -0.190809 | 0.98162718 |
| 350 | -0.17364818 | 0.98480775 |
| 351 | -0.15643447 | 0.98768834 |
| 352 | -0.1391731 | 0.99026807 |
| 353 | -0.12186934 | 0.99254615 |
| 354 | -0.10452846 | 0.9945219 |
| 355 | -0.08715574 | 0.9961947 |
| 356 | -0.06975647 | 0.99756405 |
| 357 | -0.05233596 | 0.99862953 |
| 358 | -0.0348995 | 0.99939083 |
| 359 | -0.01745241 | 0.9998477 |
Другие таблицы
Таблица Брадиса
Таблица Брадиса необходима для вычислений, связанных со значениями тригонометрических функций. Обратите внимание, что здесь представлены усовершенствованные таблицы, значения которых основаны на современных (более точных) алгоритмах вычисления.
Таблица Брадиса для синуса и косинуса
Обратите внимание на то, что значения синусов и косинусов углов не может быть больше 1.
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 0.0000 | 90° | ||||||||||||||
| 0° | 0.0000 | 0.0017 | 0.0035 | 0.0052 | 0.0070 | 0.0087 | 0.0105 | 0.0122 | 0.0140 | 0.0157 | 0.0175 | 89° | 3 | 6 | 9 |
| 1° | 0.0175 | 0.0192 | 0.0209 | 0.0227 | 0.0244 | 0.0262 | 0.0279 | 0.0297 | 0.0314 | 0.0332 | 0.0349 | 88° | 3 | 6 | 9 |
| 2° | 0.0349 | 0.0366 | 0.0384 | 0.0401 | 0.0419 | 0.0436 | 0.0454 | 0.0471 | 0.0488 | 0.0506 | 0.0523 | 87° | 3 | 6 | 9 |
| 3° | 0.0523 | 0.0541 | 0.0558 | 0.0576 | 0.0593 | 0.0610 | 0.0628 | 0.0645 | 0.0663 | 0.0680 | 0.0698 | 86° | 3 | 6 | 9 |
| 4° | 0.0698 | 0.0715 | 0.0732 | 0.0750 | 0.0767 | 0.0785 | 0.0802 | 0.0819 | 0.0837 | 0.0854 | 0.0872 | 85° | 3 | 6 | 9 |
| 5° | 0.0872 | 0.0889 | 0.0906 | 0.0924 | 0.0941 | 0.0958 | 0.0976 | 0.0993 | 0.1011 | 0.1028 | 0.1045 | 84° | 3 | 6 | 9 |
| 6° | 0.1045 | 0.1063 | 0.1080 | 0.1097 | 0.1115 | 0.1132 | 0.1149 | 0.1167 | 0.1184 | 0.1201 | 0.1219 | 83° | 3 | 6 | 9 |
| 7° | 0.1219 | 0.1236 | 0.1253 | 0.1271 | 0.1288 | 0.1305 | 0.1323 | 0.1340 | 0.1357 | 0.1374 | 0.1392 | 82° | 3 | 6 | 9 |
| 8° | 0.1392 | 0.1409 | 0.1426 | 0.1444 | 0.1461 | 0.1478 | 0.1495 | 0.1513 | 0.1530 | 0.1547 | 0.1564 | 81° | 3 | 6 | 9 |
| 9° | 0.1564 | 0.1582 | 0.1599 | 0.1616 | 0.1633 | 0.1650 | 0.1668 | 0.1685 | 0.1702 | 0.1719 | 0.1736 | 80° | 3 | 6 | 9 |
| 10° | 0.1736 | 0.1754 | 0.1771 | 0.1788 | 0.1805 | 0.1822 | 0.1840 | 0.1857 | 0.1874 | 0.1891 | 0.1908 | 79° | 3 | 6 | 9 |
| 11° | 0.1908 | 0.1925 | 0.1942 | 0.1959 | 0.1977 | 0.1994 | 0.2011 | 0.2028 | 0.2045 | 0.2062 | 0.2079 | 78° | 3 | 6 | 9 |
| 12° | 0.2079 | 0.2096 | 0.2113 | 0.2130 | 0.2147 | 0.2164 | 0.2181 | 0.2198 | 0.2215 | 0.2233 | 0.2250 | 77° | 3 | 6 | 9 |
| 13° | 0.2250 | 0.2267 | 0.2284 | 0.2300 | 0.2317 | 0.2334 | 0.2351 | 0.2368 | 0.2385 | 0.2402 | 0.2419 | 76° | 3 | 6 | 9 |
| 14° | 0.2419 | 0.2436 | 0.2453 | 0.2470 | 0.2487 | 0.2504 | 0.2521 | 0.2538 | 0.2554 | 0.2571 | 0.2588 | 75° | 3 | 6 | 8 |
| 15° | 0.2588 | 0.2605 | 0.2622 | 0.2639 | 0.2656 | 0.2672 | 0.2689 | 0.2706 | 0.2723 | 0.2740 | 0.2756 | 74° | 3 | 6 | 8 |
| 16° | 0.2756 | 0.2773 | 0.2790 | 0.2807 | 0.2823 | 0.2840 | 0.2857 | 0.2874 | 0.2890 | 0.2907 | 0.2924 | 73° | 3 | 6 | 8 |
| 17° | 0.2924 | 0.2940 | 0.2957 | 0.2974 | 0.2990 | 0.3007 | 0.3024 | 0.3040 | 0.3057 | 0.3074 | 0.3090 | 72° | 3 | 6 | 8 |
| 18° | 0.3090 | 0.3107 | 0.3123 | 0.3140 | 0.3156 | 0.3173 | 0.3190 | 0.3206 | 0.3223 | 0.3239 | 0.3256 | 71° | 3 | 6 | 8 |
| 19° | 0.3256 | 0.3272 | 0.3289 | 0.3305 | 0.3322 | 0.3338 | 0.3355 | 0.3371 | 0.3387 | 0.3404 | 0.3420 | 70° | 3 | 6 | 8 |
| 20° | 0.3420 | 0.3437 | 0.3453 | 0.3469 | 0.3486 | 0.3502 | 0.3518 | 0.3535 | 0.3551 | 0.3567 | 0.3584 | 69° | 3 | 5 | 8 |
| 21° | 0.3584 | 0.3600 | 0.3616 | 0.3633 | 0.3649 | 0.3665 | 0.3681 | 0.3697 | 0.3714 | 0.3730 | 0.3746 | 68° | 3 | 5 | 8 |
| 22° | 0.3746 | 0.3762 | 0.3778 | 0.3795 | 0.3811 | 0.3827 | 0.3843 | 0.3859 | 0.3875 | 0.3891 | 0.3907 | 67° | 3 | 5 | 8 |
| 23° | 0.3907 | 0.3923 | 0.3939 | 0.3955 | 0.3971 | 0.3987 | 0.4003 | 0.4019 | 0.4035 | 0.4051 | 0.4067 | 66° | 3 | 5 | 8 |
| 24° | 0.4067 | 0.4083 | 0.4099 | 0.4115 | 0.4131 | 0.4147 | 0.4163 | 0.4179 | 0.4195 | 0.4210 | 0.4226 | 65° | 3 | 5 | 8 |
| 25° | 0.4226 | 0.4242 | 0.4258 | 0.4274 | 0.4289 | 0.4305 | 0.4321 | 0.4337 | 0.4352 | 0.4368 | 0.4384 | 64° | 3 | 5 | 8 |
| 26° | 0.4384 | 0.4399 | 0.4415 | 0.4431 | 0.4446 | 0.4462 | 0.4478 | 0.4493 | 0.4509 | 0.4524 | 0.4540 | 63° | 3 | 5 | 8 |
| 27° | 0.4540 | 0.4555 | 0.4571 | 0.4586 | 0.4602 | 0.4617 | 0.4633 | 0.4648 | 0.4664 | 0.4679 | 0.4695 | 62° | 3 | 5 | 8 |
| 28° | 0.4695 | 0.4710 | 0.4726 | 0.4741 | 0.4756 | 0.4772 | 0.4787 | 0.4802 | 0.4818 | 0.4833 | 0.4848 | 61° | 3 | 5 | 8 |
| 29° | 0.4848 | 0.4863 | 0.4879 | 0.4894 | 0.4909 | 0.4924 | 0.4939 | 0.4955 | 0.4970 | 0.4985 | 0.5000 | 60° | 3 | 5 | 8 |
| 30° | 0.5000 | 0.5015 | 0.5030 | 0.5045 | 0.5060 | 0.5075 | 0.5090 | 0.5105 | 0.5120 | 0.5135 | 0.5150 | 59° | 3 | 5 | 8 |
| 31° | 0.5150 | 0.5165 | 0.5180 | 0.5195 | 0.5210 | 0.5225 | 0.5240 | 0.5255 | 0.5270 | 0.5284 | 0.5299 | 58° | 2 | 5 | 7 |
| 32° | 0.5299 | 0.5314 | 0.5329 | 0.5344 | 0.5358 | 0.5373 | 0.5388 | 0.5402 | 0.5417 | 0.5432 | 0.5446 | 57° | 2 | 5 | 7 |
| 33° | 0.5446 | 0.5461 | 0.5476 | 0.5490 | 0.5505 | 0.5519 | 0.5534 | 0.5548 | 0.5563 | 0.5577 | 0.5592 | 56° | 2 | 5 | 7 |
| 34° | 0.5592 | 0.5606 | 0.5621 | 0.5635 | 0.5650 | 0.5664 | 0.5678 | 0.5693 | 0.5707 | 0.5721 | 0.5736 | 55° | 2 | 5 | 7 |
| 35° | 0.5736 | 0.5750 | 0.5764 | 0.5779 | 0.5793 | 0.5807 | 0.5821 | 0.5835 | 0.5850 | 0.5864 | 0.5878 | 54° | 2 | 5 | 7 |
| 36° | 0.5878 | 0.5892 | 0.5906 | 0.5920 | 0.5934 | 0.5948 | 0.5962 | 0.5976 | 0.5990 | 0.6004 | 0.6018 | 53° | 2 | 5 | 7 |
| 37° | 0.6018 | 0.6032 | 0.6046 | 0.6060 | 0.6074 | 0.6088 | 0.6101 | 0.6115 | 0.6129 | 0.6143 | 0.6157 | 52° | 2 | 5 | 7 |
| 38° | 0.6157 | 0.6170 | 0.6184 | 0.6198 | 0.6211 | 0.6225 | 0.6239 | 0.6252 | 0.6266 | 0.6280 | 0.6293 | 51° | 2 | 5 | 7 |
| 39° | 0.6293 | 0.6307 | 0.6320 | 0.6334 | 0.6347 | 0.6361 | 0.6374 | 0.6388 | 0.6401 | 0.6414 | 0.6428 | 50° | 2 | 5 | 7 |
| 40° | 0.6428 | 0.6441 | 0.6455 | 0.6468 | 0.6481 | 0.6494 | 0.6508 | 0.6521 | 0.6534 | 0.6547 | 0.6561 | 49° | 2 | 4 | 7 |
| 41° | 0.6561 | 0.6574 | 0.6587 | 0.6600 | 0.6613 | 0.6626 | 0.6639 | 0.6652 | 0.6665 | 0.6678 | 0.6691 | 48° | 2 | 4 | 7 |
| 42° | 0.6691 | 0.6704 | 0.6717 | 0.6730 | 0.6743 | 0.6756 | 0.6769 | 0.6782 | 0.6794 | 0.6807 | 0.6820 | 47° | 2 | 4 | 6 |
| 43° | 0.6820 | 0.6833 | 0.6845 | 0.6858 | 0.6871 | 0.6884 | 0.6896 | 0.6909 | 0.6921 | 0.6934 | 0.6947 | 46° | 2 | 4 | 6 |
| 44° | 0.6947 | 0.6959 | 0.6972 | 0.6984 | 0.6997 | 0.7009 | 0.7022 | 0.7034 | 0.7046 | 0.7059 | 0.7071 | 45° | 2 | 4 | 6 |
| 45° | 0.7071 | 0.7083 | 0.7096 | 0.7108 | 0.7120 | 0.7133 | 0.7145 | 0.7157 | 0.7169 | 0.7181 | 0.7193 | 44° | 2 | 4 | 6 |
| 46° | 0.7193 | 0.7206 | 0.7218 | 0.7230 | 0.7242 | 0.7254 | 0.7266 | 0.7278 | 0.7290 | 0.7302 | 0.7314 | 43° | 2 | 4 | 6 |
| 47° | 0.7314 | 0.7325 | 0.7337 | 0.7349 | 0.7361 | 0.7373 | 0.7385 | 0.7396 | 0.7408 | 0.7420 | 0.7431 | 42° | 2 | 4 | 6 |
| 48° | 0.7431 | 0.7443 | 0.7455 | 0.7466 | 0.7478 | 0.7490 | 0.7501 | 0.7513 | 0.7524 | 0.7536 | 0.7547 | 41° | 2 | 4 | 6 |
| 49° | 0.7547 | 0.7559 | 0.7570 | 0.7581 | 0.7593 | 0.7604 | 0.7615 | 0.7627 | 0.7638 | 0.7649 | 0.7660 | 40° | 2 | 4 | 6 |
| 50° | 0.7660 | 0.7672 | 0.7683 | 0.7694 | 0.7705 | 0.7716 | 0.7727 | 0.7738 | 0.7749 | 0.7760 | 0.7771 | 39° | 2 | 4 | 6 |
| 51° | 0.7771 | 0.7782 | 0.7793 | 0.7804 | 0.7815 | 0.7826 | 0.7837 | 0.7848 | 0.7859 | 0.7869 | 0.7880 | 38° | 2 | 4 | 5 |
| 52° | 0.7880 | 0.7891 | 0.7902 | 0.7912 | 0.7923 | 0.7934 | 0.7944 | 0.7955 | 0.7965 | 0.7976 | 0.7986 | 37° | 2 | 4 | 5 |
| 53° | 0.7986 | 0.7997 | 0.8007 | 0.8018 | 0.8028 | 0.8039 | 0.8049 | 0.8059 | 0.8070 | 0.8080 | 0.8090 | 36° | 2 | 3 | 5 |
| 54° | 0.8090 | 0.8100 | 0.8111 | 0.8121 | 0.8131 | 0.8141 | 0.8151 | 0.8161 | 0.8171 | 0.8181 | 0.8192 | 35° | 2 | 3 | 5 |
| 55° | 0.8192 | 0.8202 | 0.8211 | 0.8221 | 0.8231 | 0.8241 | 0.8251 | 0.8261 | 0.8271 | 0.8281 | 0.8290 | 34° | 2 | 3 | 5 |
| 56° | 0.8290 | 0.8300 | 0.8310 | 0.8320 | 0.8329 | 0.8339 | 0.8348 | 0.8358 | 0.8368 | 0.8377 | 0.8387 | 33° | 2 | 3 | 5 |
| 57° | 0.8387 | 0.8396 | 0.8406 | 0.8415 | 0.8425 | 0.8434 | 0.8443 | 0.8453 | 0.8462 | 0.8471 | 0.8480 | 32° | 2 | 3 | 5 |
| 58° | 0.8480 | 0.8490 | 0.8499 | 0.8508 | 0.8517 | 0.8526 | 0.8536 | 0.8545 | 0.8554 | 0.8563 | 0.8572 | 31° | 2 | 3 | 5 |
| 59° | 0.8572 | 0.8581 | 0.8590 | 0.8599 | 0.8607 | 0.8616 | 0.8625 | 0.8634 | 0.8643 | 0.8652 | 0.8660 | 30° | 1 | 3 | 4 |
| 60° | 0.8660 | 0.8669 | 0.8678 | 0.8686 | 0.8695 | 0.8704 | 0.8712 | 0.8721 | 0.8729 | 0.8738 | 0.8746 | 29° | 1 | 3 | 4 |
| 61° | 0.8746 | 0.8755 | 0.8763 | 0.8771 | 0.8780 | 0.8788 | 0.8796 | 0.8805 | 0.8813 | 0.8821 | 0.8829 | 28° | 1 | 3 | 4 |
| 62° | 0.8829 | 0.8838 | 0.8846 | 0.8854 | 0.8862 | 0.8870 | 0.8878 | 0.8886 | 0.8894 | 0.8902 | 0.8910 | 27° | 1 | 3 | 4 |
| 63° | 0.8910 | 0.8918 | 0.8926 | 0.8934 | 0.8942 | 0.8949 | 0.8957 | 0.8965 | 0.8973 | 0.8980 | 0.8988 | 26° | 1 | 3 | 4 |
| 64° | 0.8988 | 0.8996 | 0.9003 | 0.9011 | 0.9018 | 0.9026 | 0.9033 | 0.9041 | 0.9048 | 0.9056 | 0.9063 | 25° | 1 | 3 | 4 |
| 65° | 0.9063 | 0.9070 | 0.9078 | 0.9085 | 0.9092 | 0.9100 | 0.9107 | 0.9114 | 0.9121 | 0.9128 | 0.9135 | 24° | 1 | 2 | 4 |
| 66° | 0.9135 | 0.9143 | 0.9150 | 0.9157 | 0.9164 | 0.9171 | 0.9178 | 0.9184 | 0.9191 | 0.9198 | 0.9205 | 23° | 1 | 2 | 4 |
| 67° | 0.9205 | 0.9212 | 0.9219 | 0.9225 | 0.9232 | 0.9239 | 0.9245 | 0.9252 | 0.9259 | 0.9265 | 0.9272 | 22° | 1 | 2 | 3 |
| 68° | 0.9272 | 0.9278 | 0.9285 | 0.9291 | 0.9298 | 0.9304 | 0.9311 | 0.9317 | 0.9323 | 0.9330 | 0.9336 | 21° | 1 | 2 | 3 |
| 69° | 0.9336 | 0.9342 | 0.9348 | 0.9354 | 0.9361 | 0.9367 | 0.9373 | 0.9379 | 0.9385 | 0.9391 | 0.9397 | 20° | 1 | 2 | 3 |
| 70° | 0.9397 | 0.9403 | 0.9409 | 0.9415 | 0.9421 | 0.9426 | 0.9432 | 0.9438 | 0.9444 | 0.9449 | 0.9455 | 19° | 1 | 2 | 3 |
| 71° | 0.9455 | 0.9461 | 0.9466 | 0.9472 | 0.9478 | 0.9483 | 0.9489 | 0.9494 | 0.9500 | 0.9505 | 0.9511 | 18° | 1 | 2 | 3 |
| 72° | 0.9511 | 0.9516 | 0.9521 | 0.9527 | 0.9532 | 0.9537 | 0.9542 | 0.9548 | 0.9553 | 0.9558 | 0.9563 | 17° | 1 | 2 | 3 |
| 73° | 0.9563 | 0.9568 | 0.9573 | 0.9578 | 0.9583 | 0.9588 | 0.9593 | 0.9598 | 0.9603 | 0.9608 | 0.9613 | 16° | 1 | 2 | 3 |
| 74° | 0.9613 | 0.9617 | 0.9622 | 0.9627 | 0.9632 | 0.9636 | 0.9641 | 0.9646 | 0.9650 | 0.9655 | 0.9659 | 15° | 1 | 2 | 2 |
| 75° | 0.9659 | 0.9664 | 0.9668 | 0.9673 | 0.9677 | 0.9681 | 0.9686 | 0.9690 | 0.9694 | 0.9699 | 0.9703 | 14° | 1 | 2 | 2 |
| 76° | 0.9703 | 0.9707 | 0.9711 | 0.9715 | 0.9720 | 0.9724 | 0.9728 | 0.9732 | 0.9736 | 0.9740 | 0.9744 | 13° | 1 | 1 | 2 |
| 77° | 0.9744 | 0.9748 | 0.9751 | 0.9755 | 0.9759 | 0.9763 | 0.9767 | 0.9770 | 0.9774 | 0.9778 | 0.9781 | 12° | 1 | 1 | 2 |
| 78° | 0.9781 | 0.9785 | 0.9789 | 0.9792 | 0.9796 | 0.9799 | 0.9803 | 0.9806 | 0.9810 | 0.9813 | 0.9816 | 11° | 1 | 1 | 2 |
| 79° | 0.9816 | 0.9820 | 0.9823 | 0.9826 | 0.9829 | 0.9833 | 0.9836 | 0.9839 | 0.9842 | 0.9845 | 0.9848 | 10° | 1 | 1 | 2 |
| 80° | 0.9848 | 0.9851 | 0.9854 | 0.9857 | 0.9860 | 0.9863 | 0.9866 | 0.9869 | 0.9871 | 0.9874 | 0.9877 | 9° | 1 | 1 | 2 |
| 81° | 0.9877 | 0.9880 | 0.9882 | 0.9885 | 0.9888 | 0.9890 | 0.9893 | 0.9895 | 0.9898 | 0.9900 | 0.9903 | 8° | 0 | 1 | 1 |
| 82° | 0.9903 | 0.9905 | 0.9907 | 0.9910 | 0.9912 | 0.9914 | 0.9917 | 0.9919 | 0.9921 | 0.9923 | 0.9925 | 7° | 0 | 1 | 1 |
| 83° | 0.9925 | 0.9928 | 0.9930 | 0.9932 | 0.9934 | 0.9936 | 0.9938 | 0.9940 | 0.9942 | 0.9943 | 0.9945 | 6° | 0 | 1 | 1 |
| 84° | 0.9945 | 0.9947 | 0.9949 | 0.9951 | 0.9952 | 0.9954 | 0.9956 | 0.9957 | 0.9959 | 0.9960 | 0.9962 | 5° | 0 | 1 | 1 |
| 85° | 0.9962 | 0.9963 | 0.9965 | 0.9966 | 0.9968 | 0.9969 | 0.9971 | 0.9972 | 0.9973 | 0.9974 | 0.9976 | 4° | 0 | 1 | 1 |
| 86° | 0.9976 | 0.9977 | 0.9978 | 0.9979 | 0.9980 | 0.9981 | 0.9982 | 0.9983 | 0.9984 | 0.9985 | 0.9986 | 3° | 0 | 0 | 1 |
| 87° | 0.9986 | 0.9987 | 0.9988 | 0.9989 | 0.9990 | 0.9990 | 0.9991 | 0.9992 | 0.9993 | 0.9993 | 0.9994 | 2° | 0 | 0 | 0 |
| 88° | 0.9994 | 0.9995 | 0.9995 | 0.9996 | 0.9996 | 0.9997 | 0.9997 | 0.9997 | 0.9998 | 0.9998 | 0.9998 | 1° | 0 | 0 | 0 |
| 89° | 0.9998 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0° | 0 | 0 | 0 |
| 90° | 1.0000 | ||||||||||||||
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | 1′ | 2′ | 3′ |
Таблица Брадиса для тангенса и котангенса
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 0.0000 | 90° | ||||||||||||||
| 0° | 0.0000 | 0.0017 | 0.0035 | 0.0052 | 0.0070 | 0.0087 | 0.0105 | 0.0122 | 0.0140 | 0.0157 | 0.0175 | 89° | 3 | 6 | 9 |
| 1° | 0.0175 | 0.0192 | 0.0209 | 0.0227 | 0.0244 | 0.0262 | 0.0279 | 0.0297 | 0.0314 | 0.0332 | 0.0349 | 88° | 3 | 6 | 9 |
| 2° | 0.0349 | 0.0367 | 0.0384 | 0.0402 | 0.0419 | 0.0437 | 0.0454 | 0.0472 | 0.0489 | 0.0507 | 0.0524 | 87° | 3 | 6 | 9 |
| 3° | 0.0524 | 0.0542 | 0.0559 | 0.0577 | 0.0594 | 0.0612 | 0.0629 | 0.0647 | 0.0664 | 0.0682 | 0.0699 | 86° | 3 | 6 | 9 |
| 4° | 0.0699 | 0.0717 | 0.0734 | 0.0752 | 0.0769 | 0.0787 | 0.0805 | 0.0822 | 0.0840 | 0.0857 | 0.0875 | 85° | 3 | 6 | 9 |
| 5° | 0.0875 | 0.0892 | 0.0910 | 0.0928 | 0.0945 | 0.0963 | 0.0981 | 0.0998 | 0.1016 | 0.1033 | 0.1051 | 84° | 3 | 6 | 9 |
| 6° | 0.1051 | 0.1069 | 0.1086 | 0.1104 | 0.1122 | 0.1139 | 0.1157 | 0.1175 | 0.1192 | 0.1210 | 0.1228 | 83° | 3 | 6 | 9 |
| 7° | 0.1228 | 0.1246 | 0.1263 | 0.1281 | 0.1299 | 0.1317 | 0.1334 | 0.1352 | 0.1370 | 0.1388 | 0.1405 | 82° | 3 | 6 | 9 |
| 8° | 0.1405 | 0.1423 | 0.1441 | 0.1459 | 0.1477 | 0.1495 | 0.1512 | 0.1530 | 0.1548 | 0.1566 | 0.1584 | 81° | 3 | 6 | 9 |
| 9° | 0.1584 | 0.1602 | 0.1620 | 0.1638 | 0.1655 | 0.1673 | 0.1691 | 0.1709 | 0.1727 | 0.1745 | 0.1763 | 80° | 3 | 6 | 9 |
| 10° | 0.1763 | 0.1781 | 0.1799 | 0.1817 | 0.1835 | 0.1853 | 0.1871 | 0.1890 | 0.1908 | 0.1926 | 0.1944 | 79° | 3 | 6 | 9 |
| 11° | 0.1944 | 0.1962 | 0.1980 | 0.1998 | 0.2016 | 0.2035 | 0.2053 | 0.2071 | 0.2089 | 0.2107 | 0.2126 | 78° | 3 | 6 | 9 |
| 12° | 0.2126 | 0.2144 | 0.2162 | 0.2180 | 0.2199 | 0.2217 | 0.2235 | 0.2254 | 0.2272 | 0.2290 | 0.2309 | 77° | 3 | 6 | 9 |
| 13° | 0.2309 | 0.2327 | 0.2345 | 0.2364 | 0.2382 | 0.2401 | 0.2419 | 0.2438 | 0.2456 | 0.2475 | 0.2493 | 76° | 3 | 6 | 9 |
| 14° | 0.2493 | 0.2512 | 0.2530 | 0.2549 | 0.2568 | 0.2586 | 0.2605 | 0.2623 | 0.2642 | 0.2661 | 0.2679 | 75° | 3 | 6 | 9 |
| 15° | 0.2679 | 0.2698 | 0.2717 | 0.2736 | 0.2754 | 0.2773 | 0.2792 | 0.2811 | 0.2830 | 0.2849 | 0.2867 | 74° | 3 | 6 | 9 |
| 16° | 0.2867 | 0.2886 | 0.2905 | 0.2924 | 0.2943 | 0.2962 | 0.2981 | 0.3000 | 0.3019 | 0.3038 | 0.3057 | 73° | 3 | 6 | 9 |
| 17° | 0.3057 | 0.3076 | 0.3096 | 0.3115 | 0.3134 | 0.3153 | 0.3172 | 0.3191 | 0.3211 | 0.3230 | 0.3249 | 72° | 3 | 6 | 10 |
| 18° | 0.3249 | 0.3269 | 0.3288 | 0.3307 | 0.3327 | 0.3346 | 0.3365 | 0.3385 | 0.3404 | 0.3424 | 0.3443 | 71° | 3 | 6 | 10 |
| 19° | 0.3443 | 0.3463 | 0.3482 | 0.3502 | 0.3522 | 0.3541 | 0.3561 | 0.3581 | 0.3600 | 0.3620 | 0.3640 | 70° | 3 | 7 | 10 |
| 20° | 0.3640 | 0.3659 | 0.3679 | 0.3699 | 0.3719 | 0.3739 | 0.3759 | 0.3779 | 0.3799 | 0.3819 | 0.3839 | 69° | 3 | 7 | 10 |
| 21° | 0.3839 | 0.3859 | 0.3879 | 0.3899 | 0.3919 | 0.3939 | 0.3959 | 0.3979 | 0.4000 | 0.4020 | 0.4040 | 68° | 3 | 7 | 10 |
| 22° | 0.4040 | 0.4061 | 0.4081 | 0.4101 | 0.4122 | 0.4142 | 0.4163 | 0.4183 | 0.4204 | 0.4224 | 0.4245 | 67° | 3 | 7 | 10 |
| 23° | 0.4245 | 0.4265 | 0.4286 | 0.4307 | 0.4327 | 0.4348 | 0.4369 | 0.4390 | 0.4411 | 0.4431 | 0.4452 | 66° | 3 | 7 | 10 |
| 24° | 0.4452 | 0.4473 | 0.4494 | 0.4515 | 0.4536 | 0.4557 | 0.4578 | 0.4599 | 0.4621 | 0.4642 | 0.4663 | 65° | 3 | 7 | 10 |
| 25° | 0.4663 | 0.4684 | 0.4706 | 0.4727 | 0.4748 | 0.4770 | 0.4791 | 0.4813 | 0.4834 | 0.4856 | 0.4877 | 64° | 4 | 7 | 11 |
| 26° | 0.4877 | 0.4899 | 0.4921 | 0.4942 | 0.4964 | 0.4986 | 0.5008 | 0.5029 | 0.5051 | 0.5073 | 0.5095 | 63° | 4 | 7 | 11 |
| 27° | 0.5095 | 0.5117 | 0.5139 | 0.5161 | 0.5184 | 0.5206 | 0.5228 | 0.5250 | 0.5272 | 0.5295 | 0.5317 | 62° | 4 | 7 | 11 |
| 28° | 0.5317 | 0.5340 | 0.5362 | 0.5384 | 0.5407 | 0.5430 | 0.5452 | 0.5475 | 0.5498 | 0.5520 | 0.5543 | 61° | 4 | 7 | 11 |
| 29° | 0.5543 | 0.5566 | 0.5589 | 0.5612 | 0.5635 | 0.5658 | 0.5681 | 0.5704 | 0.5727 | 0.5750 | 0.5774 | 60° | 4 | 8 | 11 |
| 30° | 0.5774 | 0.5797 | 0.5820 | 0.5844 | 0.5867 | 0.5890 | 0.5914 | 0.5938 | 0.5961 | 0.5985 | 0.6009 | 59° | 4 | 8 | 12 |
| 31° | 0.6009 | 0.6032 | 0.6056 | 0.6080 | 0.6104 | 0.6128 | 0.6152 | 0.6176 | 0.6200 | 0.6224 | 0.6249 | 58° | 4 | 8 | 12 |
| 32° | 0.6249 | 0.6273 | 0.6297 | 0.6322 | 0.6346 | 0.6371 | 0.6395 | 0.6420 | 0.6445 | 0.6469 | 0.6494 | 57° | 4 | 8 | 12 |
| 33° | 0.6494 | 0.6519 | 0.6544 | 0.6569 | 0.6594 | 0.6619 | 0.6644 | 0.6669 | 0.6694 | 0.6720 | 0.6745 | 56° | 4 | 8 | 12 |
| 34° | 0.6745 | 0.6771 | 0.6796 | 0.6822 | 0.6847 | 0.6873 | 0.6899 | 0.6924 | 0.6950 | 0.6976 | 0.7002 | 55° | 4 | 8 | 13 |
| 35° | 0.7002 | 0.7028 | 0.7054 | 0.7080 | 0.7107 | 0.7133 | 0.7159 | 0.7186 | 0.7212 | 0.7239 | 0.7265 | 54° | 4 | 9 | 13 |
| 36° | 0.7265 | 0.7292 | 0.7319 | 0.7346 | 0.7373 | 0.7400 | 0.7427 | 0.7454 | 0.7481 | 0.7508 | 0.7536 | 53° | 4 | 9 | 13 |
| 37° | 0.7536 | 0.7563 | 0.7590 | 0.7618 | 0.7646 | 0.7673 | 0.7701 | 0.7729 | 0.7757 | 0.7785 | 0.7813 | 52° | 5 | 9 | 14 |
| 38° | 0.7813 | 0.7841 | 0.7869 | 0.7898 | 0.7926 | 0.7954 | 0.7983 | 0.8012 | 0.8040 | 0.8069 | 0.8098 | 51° | 5 | 9 | 14 |
| 39° | 0.8098 | 0.8127 | 0.8156 | 0.8185 | 0.8214 | 0.8243 | 0.8273 | 0.8302 | 0.8332 | 0.8361 | 0.8391 | 50° | 5 | 10 | 14 |
| 40° | 0.8391 | 0.8421 | 0.8451 | 0.8481 | 0.8511 | 0.8541 | 0.8571 | 0.8601 | 0.8632 | 0.8662 | 0.8693 | 49° | 5 | 10 | 15 |
| 41° | 0.8693 | 0.8724 | 0.8754 | 0.8785 | 0.8816 | 0.8847 | 0.8878 | 0.8910 | 0.8941 | 0.8972 | 0.9004 | 48° | 5 | 10 | 15 |
| 42° | 0.9004 | 0.9036 | 0.9067 | 0.9099 | 0.9131 | 0.9163 | 0.9195 | 0.9228 | 0.9260 | 0.9293 | 0.9325 | 47° | 5 | 11 | 16 |
| 43° | 0.9325 | 0.9358 | 0.9391 | 0.9424 | 0.9457 | 0.9490 | 0.9523 | 0.9556 | 0.9590 | 0.9623 | 0.9657 | 46° | 5 | 11 | 16 |
| 44° | 0.9657 | 0.9691 | 0.9725 | 0.9759 | 0.9793 | 0.9827 | 0.9861 | 0.9896 | 0.9930 | 0.9965 | 1.0000 | 45° | 6 | 11 | 17 |
| 45° | 1.0000 | 1.0035 | 1.0070 | 1.0105 | 1.0141 | 1.0176 | 1.0212 | 1.0247 | 1.0283 | 1.0319 | 1.0355 | 44° | 6 | 12 | 17 |
| 46° | 1.0355 | 1.0392 | 1.0428 | 1.0464 | 1.0501 | 1.0538 | 1.0575 | 1.0612 | 1.0649 | 1.0686 | 1.0724 | 43° | 6 | 12 | 18 |
| 47° | 1.0724 | 1.0761 | 1.0799 | 1.0837 | 1.0875 | 1.0913 | 1.0951 | 1.0990 | 1.1028 | 1.1067 | 1.1106 | 42° | 6 | 13 | 19 |
| 48° | 1.1106 | 1.1145 | 1.1184 | 1.1224 | 1.1263 | 1.1303 | 1.1343 | 1.1383 | 1.1423 | 1.1463 | 1.1504 | 41° | 6 | 13 | 20 |
| 49° | 1.1504 | 1.1544 | 1.1585 | 1.1626 | 1.1667 | 1.1708 | 1.1750 | 1.1792 | 1.1833 | 1.1875 | 1.1918 | 40° | 7 | 14 | 20 |
| 50° | 1.1918 | 1.1960 | 1.2002 | 1.2045 | 1.2088 | 1.2131 | 1.2174 | 1.2218 | 1.2261 | 1.2305 | 1.2349 | 39° | 7 | 14 | 21 |
| 51° | 1.2349 | 1.2393 | 1.2437 | 1.2482 | 1.2527 | 1.2572 | 1.2617 | 1.2662 | 1.2708 | 1.2753 | 1.2799 | 38° | 7 | 15 | 22 |
| 52° | 1.2799 | 1.2846 | 1.2892 | 1.2938 | 1.2985 | 1.3032 | 1.3079 | 1.3127 | 1.3175 | 1.3222 | 1.3270 | 37° | 8 | 15 | 23 |
| 53° | 1.3270 | 1.3319 | 1.3367 | 1.3416 | 1.3465 | 1.3514 | 1.3564 | 1.3613 | 1.3663 | 1.3713 | 1.3764 | 36° | 8 | 16 | 24 |
| 54° | 1.3764 | 1.3814 | 1.3865 | 1.3916 | 1.3968 | 1.4019 | 1.4071 | 1.4124 | 1.4176 | 1.4229 | 1.4281 | 35° | 8 | 17 | 25 |
| 55° | 1.4281 | 1.4335 | 1.4388 | 1.4442 | 1.4496 | 1.4550 | 1.4605 | 1.4659 | 1.4715 | 1.4770 | 1.4826 | 34° | 9 | 18 | 27 |
| 56° | 1.4826 | 1.4882 | 1.4938 | 1.4994 | 1.5051 | 1.5108 | 1.5166 | 1.5224 | 1.5282 | 1.5340 | 1.5399 | 33° | 9 | 19 | 28 |
| 57° | 1.5399 | 1.5458 | 1.5517 | 1.5577 | 1.5637 | 1.5697 | 1.5757 | 1.5818 | 1.5880 | 1.5941 | 1.6003 | 32° | 10 | 20 | 29 |
| 58° | 1.6003 | 1.6066 | 1.6128 | 1.6191 | 1.6255 | 1.6319 | 1.6383 | 1.6447 | 1.6512 | 1.6577 | 1.6643 | 31° | 10 | 21 | 31 |
| 59° | 1.6643 | 1.6709 | 1.6775 | 1.6842 | 1.6909 | 1.6977 | 1.7045 | 1.7113 | 1.7182 | 1.7251 | 1.7321 | 30° | 11 | 22 | 33 |
| 60° | 1.7321 | 1.7391 | 1.7461 | 1.7532 | 1.7603 | 1.7675 | 1.7747 | 1.7820 | 1.7893 | 1.7966 | 1.8040 | 29° | 12 | 23 | 35 |
| 61° | 1.8040 | 1.8115 | 1.8190 | 1.8265 | 1.8341 | 1.8418 | 1.8495 | 1.8572 | 1.8650 | 1.8728 | 1.8807 | 28° | 12 | 25 | 37 |
| 62° | 1.8807 | 1.8887 | 1.8967 | 1.9047 | 1.9128 | 1.9210 | 1.9292 | 1.9375 | 1.9458 | 1.9542 | 1.9626 | 27° | 13 | 26 | 40 |
| 63° | 1.9626 | 1.9711 | 1.9797 | 1.9883 | 1.9970 | 2.0057 | 2.0145 | 2.0233 | 2.0323 | 2.0413 | 2.0503 | 26° | 14 | 28 | 42 |
| 64° | 2.0503 | 2.0594 | 2.0686 | 2.0778 | 2.0872 | 2.0965 | 2.1060 | 2.1155 | 2.1251 | 2.1348 | 2.1445 | 25° | 15 | 30 | 45 |
| 65° | 2.1445 | 2.1543 | 2.1642 | 2.1742 | 2.1842 | 2.1943 | 2.2045 | 2.2148 | 2.2251 | 2.2355 | 2.2460 | 24° | 16 | 33 | 49 |
| 66° | 2.2460 | 2.2566 | 2.2673 | 2.2781 | 2.2889 | 2.2998 | 2.3109 | 2.3220 | 2.3332 | 2.3445 | 2.3559 | 23° | 18 | 35 | 53 |
| 67° | 2.3559 | 2.3673 | 2.3789 | 2.3906 | 2.4023 | 2.4142 | 2.4262 | 2.4383 | 2.4504 | 2.4627 | 2.4751 | 22° | 19 | 38 | 57 |
| 68° | 2.4751 | 2.4876 | 2.5002 | 2.5129 | 2.5257 | 2.5386 | 2.5517 | 2.5649 | 2.5782 | 2.5916 | 2.6051 | 21° | 21 | 42 | 62 |
| 69° | 2.6051 | 2.6187 | 2.6325 | 2.6464 | 2.6605 | 2.6746 | 2.6889 | 2.7034 | 2.7179 | 2.7326 | 2.7475 | 20° | 23 | 45 | 68 |
| 70° | 2.7475 | 2.7625 | 2.7776 | 2.7929 | 2.8083 | 2.8239 | 2.8397 | 2.8556 | 2.8716 | 2.8878 | 2.9042 | 19° | 25 | 50 | 75 |
| 71° | 2.9042 | 2.9208 | 2.9375 | 2.9544 | 2.9714 | 2.9887 | 3.0061 | 3.0237 | 3.0415 | 3.0595 | 3.0777 | 18° | 27 | 55 | 83 |
| 72° | 3.0777 | 3.0961 | 3.1146 | 3.1334 | 3.1524 | 3.1716 | 3.1910 | 3.2106 | 3.2305 | 3.2506 | 3.2709 | 17° | 30 | 61 | 92 |
| 73° | 3.2709 | 3.2914 | 3.3122 | 3.3332 | 3.3544 | 3.3759 | 3.3977 | 3.4197 | 3.4420 | 3.4646 | 3.4874 | 16° | 34 | 68 | 102 |
| 74° | 3.4874 | 3.5105 | 3.5339 | 3.5576 | 3.5816 | 3.6059 | 3.6305 | 3.6554 | 3.6806 | 3.7062 | 3.7321 | 15° | 38 | 77 | 115 |
| 75° | 3.7321 | 3.7583 | 3.7848 | 3.8118 | 3.8391 | 3.8667 | 3.8947 | 3.9232 | 3.9520 | 3.9812 | 4.0108 | 14° | 43 | 87 | 131 |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | 1′ | 2′ | 3′ |
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
Таблица синусов и косинусов может пригодится учащимся, студентам и инженерам для произведения тригонометрических расчетов. Она позволяет найти синус и косинус любого целого угла от 0 до 360 градусов.
Пользоваться таблицей очень просто – найдите нужный угол и в той же строке увидите синус и косинус этого угла. Для примера возьмем угол, равный 30 градусам. Найдя его в таблице мы увидим, что Cos(30) = 0,866025404, а Sin(30) = 0,5.
Для удобства вы можете воспользоваться поиском нужного угла, синуса или косинуса.
| Угол (градусы) | Косинус (Cos) | Синус (Sin) |
|---|---|---|
| 0° | 1 | 0 |
| 1° | 0,999847695 | 0,017452406 |
| 2° | 0,999390827 | 0,034899497 |
| 3° | 0,998629535 | 0,052335956 |
| 4° | 0,99756405 | 0,069756474 |
| 5° | 0,996194698 | 0,087155743 |
| 6° | 0,994521895 | 0,104528463 |
| 7° | 0,992546152 | 0,121869343 |
| 8° | 0,990268069 | 0,139173101 |
| 9° | 0,987688341 | 0,156434465 |
| 10° | 0,984807753 | 0,173648178 |
| 11° | 0,981627183 | 0,190808995 |
| 12° | 0,978147601 | 0,207911691 |
| 13° | 0,974370065 | 0,224951054 |
| 14° | 0,970295726 | 0,241921896 |
| 15° | 0,965925826 | 0,258819045 |
| 16° | 0,961261696 | 0,275637356 |
| 17° | 0,956304756 | 0,292371705 |
| 18° | 0,951056516 | 0,309016994 |
| 19° | 0,945518576 | 0,325568154 |
| 20° | 0,939692621 | 0,342020143 |
| 21° | 0,933580426 | 0,35836795 |
| 22° | 0,927183855 | 0,374606593 |
| 23° | 0,920504853 | 0,390731128 |
| 24° | 0,913545458 | 0,406736643 |
| 25° | 0,906307787 | 0,422618262 |
| 26° | 0,898794046 | 0,438371147 |
| 27° | 0,891006524 | 0,4539905 |
| 28° | 0,882947593 | 0,469471563 |
| 29° | 0,874619707 | 0,48480962 |
| 30° | 0,866025404 | 0,5 |
| 31° | 0,857167301 | 0,515038075 |
| 32° | 0,848048096 | 0,529919264 |
| 33° | 0,838670568 | 0,544639035 |
| 34° | 0,829037573 | 0,559192903 |
| 35° | 0,819152044 | 0,573576436 |
| 36° | 0,809016994 | 0,587785252 |
| 37° | 0,79863551 | 0,601815023 |
| 38° | 0,788010754 | 0,615661475 |
| 39° | 0,777145961 | 0,629320391 |
| 40° | 0,766044443 | 0,64278761 |
| 41° | 0,75470958 | 0,656059029 |
| 42° | 0,743144825 | 0,669130606 |
| 43° | 0,731353702 | 0,68199836 |
| 44° | 0,7193398 | 0,69465837 |
| 45° | 0,707106781 | 0,707106781 |
| 46° | 0,69465837 | 0,7193398 |
| 47° | 0,68199836 | 0,731353702 |
| 48° | 0,669130606 | 0,743144825 |
| 49° | 0,656059029 | 0,75470958 |
| 50° | 0,64278761 | 0,766044443 |
| 51° | 0,629320391 | 0,777145961 |
| 52° | 0,615661475 | 0,788010754 |
| 53° | 0,601815023 | 0,79863551 |
| 54° | 0,587785252 | 0,809016994 |
| 55° | 0,573576436 | 0,819152044 |
| 56° | 0,559192903 | 0,829037573 |
| 57° | 0,544639035 | 0,838670568 |
| 58° | 0,529919264 | 0,848048096 |
| 59° | 0,515038075 | 0,857167301 |
| 60° | 0,5 | 0,866025404 |
| 61° | 0,48480962 | 0,874619707 |
| 62° | 0,469471563 | 0,882947593 |
| 63° | 0,4539905 | 0,891006524 |
| 64° | 0,438371147 | 0,898794046 |
| 65° | 0,422618262 | 0,906307787 |
| 66° | 0,406736643 | 0,913545458 |
| 67° | 0,390731128 | 0,920504853 |
| 68° | 0,374606593 | 0,927183855 |
| 69° | 0,35836795 | 0,933580426 |
| 70° | 0,342020143 | 0,939692621 |
| 71° | 0,325568154 | 0,945518576 |
| 72° | 0,309016994 | 0,951056516 |
| 73° | 0,292371705 | 0,956304756 |
| 74° | 0,275637356 | 0,961261696 |
| 75° | 0,258819045 | 0,965925826 |
| 76° | 0,241921896 | 0,970295726 |
| 77° | 0,224951054 | 0,974370065 |
| 78° | 0,207911691 | 0,978147601 |
| 79° | 0,190808995 | 0,981627183 |
| 80° | 0,173648178 | 0,984807753 |
| 81° | 0,156434465 | 0,987688341 |
| 82° | 0,139173101 | 0,990268069 |
| 83° | 0,121869343 | 0,992546152 |
| 84° | 0,104528463 | 0,994521895 |
| 85° | 0,087155743 | 0,996194698 |
| 86° | 0,069756474 | 0,99756405 |
| 87° | 0,052335956 | 0,998629535 |
| 88° | 0,034899497 | 0,999390827 |
| 89° | 0,017452406 | 0,999847695 |
| 90° | 0 | 1 |
| 91° | -0,017452406 | 0,999847695 |
| 92° | -0,034899497 | 0,999390827 |
| 93° | -0,052335956 | 0,998629535 |
| 94° | -0,069756474 | 0,99756405 |
| 95° | -0,087155743 | 0,996194698 |
| 96° | -0,104528463 | 0,994521895 |
| 97° | -0,121869343 | 0,992546152 |
| 98° | -0,139173101 | 0,990268069 |
| 99° | -0,156434465 | 0,987688341 |
| 100° | -0,173648178 | 0,984807753 |
| 101° | -0,190808995 | 0,981627183 |
| 102° | -0,207911691 | 0,978147601 |
| 103° | -0,224951054 | 0,974370065 |
| 104° | -0,241921896 | 0,970295726 |
| 105° | -0,258819045 | 0,965925826 |
| 106° | -0,275637356 | 0,961261696 |
| 107° | -0,292371705 | 0,956304756 |
| 108° | -0,309016994 | 0,951056516 |
| 109° | -0,325568154 | 0,945518576 |
| 110° | -0,342020143 | 0,939692621 |
| 111° | -0,35836795 | 0,933580426 |
| 112° | -0,374606593 | 0,927183855 |
| 113° | -0,390731128 | 0,920504853 |
| 114° | -0,406736643 | 0,913545458 |
| 115° | -0,422618262 | 0,906307787 |
| 116° | -0,438371147 | 0,898794046 |
| 117° | -0,4539905 | 0,891006524 |
| 118° | -0,469471563 | 0,882947593 |
| 119° | -0,48480962 | 0,874619707 |
| 120° | -0,5 | 0,866025404 |
| 121° | -0,515038075 | 0,857167301 |
| 122° | -0,529919264 | 0,848048096 |
| 123° | -0,544639035 | 0,838670568 |
| 124° | -0,559192903 | 0,829037573 |
| 125° | -0,573576436 | 0,819152044 |
| 126° | -0,587785252 | 0,809016994 |
| 127° | -0,601815023 | 0,79863551 |
| 128° | -0,615661475 | 0,788010754 |
| 129° | -0,629320391 | 0,777145961 |
| 130° | -0,64278761 | 0,766044443 |
| 131° | -0,656059029 | 0,75470958 |
| 132° | -0,669130606 | 0,743144825 |
| 133° | -0,68199836 | 0,731353702 |
| 134° | -0,69465837 | 0,7193398 |
| 135° | -0,707106781 | 0,707106781 |
| 136° | -0,7193398 | 0,69465837 |
| 137° | -0,731353702 | 0,68199836 |
| 138° | -0,743144825 | 0,669130606 |
| 139° | -0,75470958 | 0,656059029 |
| 140° | -0,766044443 | 0,64278761 |
| 141° | -0,777145961 | 0,629320391 |
| 142° | -0,788010754 | 0,615661475 |
| 143° | -0,79863551 | 0,601815023 |
| 144° | -0,809016994 | 0,587785252 |
| 145° | -0,819152044 | 0,573576436 |
| 146° | -0,829037573 | 0,559192903 |
| 147° | -0,838670568 | 0,544639035 |
| 148° | -0,848048096 | 0,529919264 |
| 149° | -0,857167301 | 0,515038075 |
| 150° | -0,866025404 | 0,5 |
| 151° | -0,874619707 | 0,48480962 |
| 152° | -0,882947593 | 0,469471563 |
| 153° | -0,891006524 | 0,4539905 |
| 154° | -0,898794046 | 0,438371147 |
| 155° | -0,906307787 | 0,422618262 |
| 156° | -0,913545458 | 0,406736643 |
| 157° | -0,920504853 | 0,390731128 |
| 158° | -0,927183855 | 0,374606593 |
| 159° | -0,933580426 | 0,35836795 |
| 160° | -0,939692621 | 0,342020143 |
| 161° | -0,945518576 | 0,325568154 |
| 162° | -0,951056516 | 0,309016994 |
| 163° | -0,956304756 | 0,292371705 |
| 164° | -0,961261696 | 0,275637356 |
| 165° | -0,965925826 | 0,258819045 |
| 166° | -0,970295726 | 0,241921896 |
| 167° | -0,974370065 | 0,224951054 |
| 168° | -0,978147601 | 0,207911691 |
| 169° | -0,981627183 | 0,190808995 |
| 170° | -0,984807753 | 0,173648178 |
| 171° | -0,987688341 | 0,156434465 |
| 172° | -0,990268069 | 0,139173101 |
| 173° | -0,992546152 | 0,121869343 |
| 174° | -0,994521895 | 0,104528463 |
| 175° | -0,996194698 | 0,087155743 |
| 176° | -0,99756405 | 0,069756474 |
| 177° | -0,998629535 | 0,052335956 |
| 178° | -0,999390827 | 0,034899497 |
| 179° | -0,999847695 | 0,017452406 |
| 180° | -1 | 0 |
| 181° | -0,999847695 | -0,017452406 |
| 182° | -0,999390827 | -0,034899497 |
| 183° | -0,998629535 | -0,052335956 |
| 184° | -0,99756405 | -0,069756474 |
| 185° | -0,996194698 | -0,087155743 |
| 186° | -0,994521895 | -0,104528463 |
| 187° | -0,992546152 | -0,121869343 |
| 188° | -0,990268069 | -0,139173101 |
| 189° | -0,987688341 | -0,156434465 |
| 190° | -0,984807753 | -0,173648178 |
| 191° | -0,981627183 | -0,190808995 |
| 192° | -0,978147601 | -0,207911691 |
| 193° | -0,974370065 | -0,224951054 |
| 194° | -0,970295726 | -0,241921896 |
| 195° | -0,965925826 | -0,258819045 |
| 196° | -0,961261696 | -0,275637356 |
| 197° | -0,956304756 | -0,292371705 |
| 198° | -0,951056516 | -0,309016994 |
| 199° | -0,945518576 | -0,325568154 |
| 200° | -0,939692621 | -0,342020143 |
| 201° | -0,933580426 | -0,35836795 |
| 202° | -0,927183855 | -0,374606593 |
| 203° | -0,920504853 | -0,390731128 |
| 204° | -0,913545458 | -0,406736643 |
| 205° | -0,906307787 | -0,422618262 |
| 206° | -0,898794046 | -0,438371147 |
| 207° | -0,891006524 | -0,4539905 |
| 208° | -0,882947593 | -0,469471563 |
| 209° | -0,874619707 | -0,48480962 |
| 210° | -0,866025404 | -0,5 |
| 211° | -0,857167301 | -0,515038075 |
| 212° | -0,848048096 | -0,529919264 |
| 213° | -0,838670568 | -0,544639035 |
| 214° | -0,829037573 | -0,559192903 |
| 215° | -0,819152044 | -0,573576436 |
| 216° | -0,809016994 | -0,587785252 |
| 217° | -0,79863551 | -0,601815023 |
| 218° | -0,788010754 | -0,615661475 |
| 219° | -0,777145961 | -0,629320391 |
| 220° | -0,766044443 | -0,64278761 |
| 221° | -0,75470958 | -0,656059029 |
| 222° | -0,743144825 | -0,669130606 |
| 223° | -0,731353702 | -0,68199836 |
| 224° | -0,7193398 | -0,69465837 |
| 225° | -0,707106781 | -0,707106781 |
| 226° | -0,69465837 | -0,7193398 |
| 227° | -0,68199836 | -0,731353702 |
| 228° | -0,669130606 | -0,743144825 |
| 229° | -0,656059029 | -0,75470958 |
| 230° | -0,64278761 | -0,766044443 |
| 231° | -0,629320391 | -0,777145961 |
| 232° | -0,615661475 | -0,788010754 |
| 233° | -0,601815023 | -0,79863551 |
| 234° | -0,587785252 | -0,809016994 |
| 235° | -0,573576436 | -0,819152044 |
| 236° | -0,559192903 | -0,829037573 |
| 237° | -0,544639035 | -0,838670568 |
| 238° | -0,529919264 | -0,848048096 |
| 239° | -0,515038075 | -0,857167301 |
| 240° | -0,5 | -0,866025404 |
| 241° | -0,48480962 | -0,874619707 |
| 242° | -0,469471563 | -0,882947593 |
| 243° | -0,4539905 | -0,891006524 |
| 244° | -0,438371147 | -0,898794046 |
| 245° | -0,422618262 | -0,906307787 |
| 246° | -0,406736643 | -0,913545458 |
| 247° | -0,390731128 | -0,920504853 |
| 248° | -0,374606593 | -0,927183855 |
| 249° | -0,35836795 | -0,933580426 |
| 250° | -0,342020143 | -0,939692621 |
| 251° | -0,325568154 | -0,945518576 |
| 252° | -0,309016994 | -0,951056516 |
| 253° | -0,292371705 | -0,956304756 |
| 254° | -0,275637356 | -0,961261696 |
| 255° | -0,258819045 | -0,965925826 |
| 256° | -0,241921896 | -0,970295726 |
| 257° | -0,224951054 | -0,974370065 |
| 258° | -0,207911691 | -0,978147601 |
| 259° | -0,190808995 | -0,981627183 |
| 260° | -0,173648178 | -0,984807753 |
| 261° | -0,156434465 | -0,987688341 |
| 262° | -0,139173101 | -0,990268069 |
| 263° | -0,121869343 | -0,992546152 |
| 264° | -0,104528463 | -0,994521895 |
| 265° | -0,087155743 | -0,996194698 |
| 266° | -0,069756474 | -0,99756405 |
| 267° | -0,052335956 | -0,998629535 |
| 268° | -0,034899497 | -0,999390827 |
| 269° | -0,017452406 | -0,999847695 |
| 270° | 0 | -1 |
| 271° | 0,017452406 | -0,999847695 |
| 272° | 0,034899497 | -0,999390827 |
| 273° | 0,052335956 | -0,998629535 |
| 274° | 0,069756474 | -0,99756405 |
| 275° | 0,087155743 | -0,996194698 |
| 276° | 0,104528463 | -0,994521895 |
| 277° | 0,121869343 | -0,992546152 |
| 278° | 0,139173101 | -0,990268069 |
| 279° | 0,156434465 | -0,987688341 |
| 280° | 0,173648178 | -0,984807753 |
| 281° | 0,190808995 | -0,981627183 |
| 282° | 0,207911691 | -0,978147601 |
| 283° | 0,224951054 | -0,974370065 |
| 284° | 0,241921896 | -0,970295726 |
| 285° | 0,258819045 | -0,965925826 |
| 286° | 0,275637356 | -0,961261696 |
| 287° | 0,292371705 | -0,956304756 |
| 288° | 0,309016994 | -0,951056516 |
| 289° | 0,325568154 | -0,945518576 |
| 290° | 0,342020143 | -0,939692621 |
| 291° | 0,35836795 | -0,933580426 |
| 292° | 0,374606593 | -0,927183855 |
| 293° | 0,390731128 | -0,920504853 |
| 294° | 0,406736643 | -0,913545458 |
| 295° | 0,422618262 | -0,906307787 |
| 296° | 0,438371147 | -0,898794046 |
| 297° | 0,4539905 | -0,891006524 |
| 298° | 0,469471563 | -0,882947593 |
| 299° | 0,48480962 | -0,874619707 |
| 300° | 0,5 | -0,866025404 |
| 301° | 0,515038075 | -0,857167301 |
| 302° | 0,529919264 | -0,848048096 |
| 303° | 0,544639035 | -0,838670568 |
| 304° | 0,559192903 | -0,829037573 |
| 305° | 0,573576436 | -0,819152044 |
| 306° | 0,587785252 | -0,809016994 |
| 307° | 0,601815023 | -0,79863551 |
| 308° | 0,615661475 | -0,788010754 |
| 309° | 0,629320391 | -0,777145961 |
| 310° | 0,64278761 | -0,766044443 |
| 311° | 0,656059029 | -0,75470958 |
| 312° | 0,669130606 | -0,743144825 |
| 313° | 0,68199836 | -0,731353702 |
| 314° | 0,69465837 | -0,7193398 |
| 315° | 0,707106781 | -0,707106781 |
| 316° | 0,7193398 | -0,69465837 |
| 317° | 0,731353702 | -0,68199836 |
| 318° | 0,743144825 | -0,669130606 |
| 319° | 0,75470958 | -0,656059029 |
| 320° | 0,766044443 | -0,64278761 |
| 321° | 0,777145961 | -0,629320391 |
| 322° | 0,788010754 | -0,615661475 |
| 323° | 0,79863551 | -0,601815023 |
| 324° | 0,809016994 | -0,587785252 |
| 325° | 0,819152044 | -0,573576436 |
| 326° | 0,829037573 | -0,559192903 |
| 327° | 0,838670568 | -0,544639035 |
| 328° | 0,848048096 | -0,529919264 |
| 329° | 0,857167301 | -0,515038075 |
| 330° | 0,866025404 | -0,5 |
| 331° | 0,874619707 | -0,48480962 |
| 332° | 0,882947593 | -0,469471563 |
| 333° | 0,891006524 | -0,4539905 |
| 334° | 0,898794046 | -0,438371147 |
| 335° | 0,906307787 | -0,422618262 |
| 336° | 0,913545458 | -0,406736643 |
| 337° | 0,920504853 | -0,390731128 |
| 338° | 0,927183855 | -0,374606593 |
| 339° | 0,933580426 | -0,35836795 |
| 340° | 0,939692621 | -0,342020143 |
| 341° | 0,945518576 | -0,325568154 |
| 342° | 0,951056516 | -0,309016994 |
| 343° | 0,956304756 | -0,292371705 |
| 344° | 0,961261696 | -0,275637356 |
| 345° | 0,965925826 | -0,258819045 |
| 346° | 0,970295726 | -0,241921896 |
| 347° | 0,974370065 | -0,224951054 |
| 348° | 0,978147601 | -0,207911691 |
| 349° | 0,981627183 | -0,190808995 |
| 350° | 0,984807753 | -0,173648178 |
| 351° | 0,987688341 | -0,156434465 |
| 352° | 0,990268069 | -0,139173101 |
| 353° | 0,992546152 | -0,121869343 |
| 354° | 0,994521895 | -0,104528463 |
| 355° | 0,996194698 | -0,087155743 |
| 356° | 0,99756405 | -0,069756474 |
| 357° | 0,998629535 | -0,052335956 |
| 358° | 0,999390827 | -0,034899497 |
| 359° | 0,999847695 | -0,017452406 |
| 360° | 1 | 0 |
Часто используемые значения косинуса
Косинус 0 градусов = 1
Косинус 30 градусов = 0,866025404 = {dfrac {sqrt{3}}{2}}
Косинус 45 градусов = 0,707106781 = {dfrac {sqrt{2}}{2}}
Косинус 60 градусов = 0,5 = {dfrac {1}{2}}
Косинус 90 градусов = 0
Косинус 120 градусов = -0,5 = {-dfrac {1}{2}}
Косинус 135 градусов = -0,707106781 = {-dfrac {sqrt{3}}{2}}
Косинус 180 градусов = -1
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Тригонометрия в прямоугольном треугольнике
- Тригонометрический круг
- Основное тригонометрическое тождество
- Таблица значений тригонометрических функций
- Градусы и радианы
- Формулы приведения
- Теорема синусов
- Расширенная теорема синусов
- Теорема косинусов
- Тригонометрические уравнения (10-11 класс)
- Примеры решений заданий из ОГЭ
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник ABC, угол C равен 90°:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x, ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x, против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A. Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B) и на ось игрек (точка C).
Отрезок OB является проекцией отрезка OA на ось x, отрезок OC является проекцией отрезка OA на ось y.
Рассмотрим прямоугольный треугольник AOB:
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y. Точка B в этом случае будет иметь отрицательную координату по оси x. Косинус тупого угла отрицательный.
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x. (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y.
Координата по оси x – косинус угла, координата по оси y – синус угла.
Пример:
cos 150 ° = − 3 2
sin 150 ° = 1 2
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный.
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
| 0° | 30° | 45° | 60° | 90° | |
| sinα | 0 | 12 | 22 | 32 | 1 |
| cosα | 1 | 32 | 22 | 12 | 0 |
| tgα | 0 | 33 | 1 | 3 | нет |
| ctgα | нет | 3 | 1 | 33 | 0 |
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β:
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Скачать домашнее задание к уроку 1.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!