1. Формулы длины диагонали равнобедренной трапеции через ее стороны
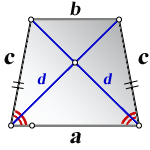
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
d – диагональ трапеции
Формула диагонали трапеции (d ):

2. Формулы длины диагонали равнобедренной трапеции по теореме косинусов
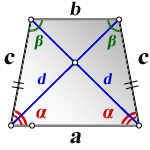
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α, β – углы трапеции
d – диагональ трапеции
Формулы диагонали трапеции (d ):
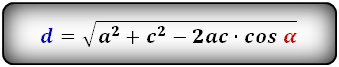
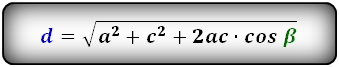
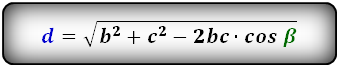
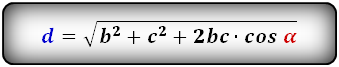
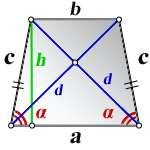
3. Формула длины диагонали равнобедренной трапеции
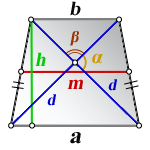
a – нижнее основание
b – верхнее основание
α, β – углы между диагоналями
h – высота трапеции
m – средняя линия трапеции
S – площадь трапеции
d – диагональ трапеции
Формулы диагонали трапеции (d ):

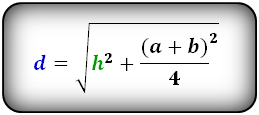
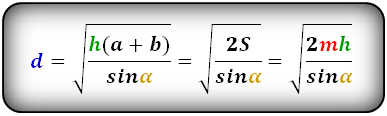
Справедливо для данного случая :
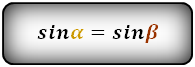
4. Формулы длины диагонали трапеции через высоту и стороны
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
h – высота трапеции
α – угол при нижнем основании
d – диагональ трапеции
Формулы диагонали трапеции (d ):
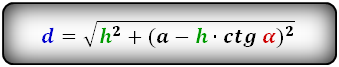
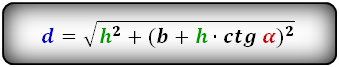

Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Найти длину диагонали трапеции
зная все четыре стороны
или две стороны и угол
или высоту, сторону и угол
или площадь, другую диагональ и угол
и еще много других формул.
1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны
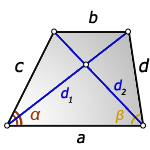
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции по теореме косинусов:
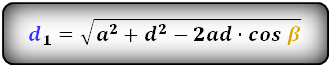
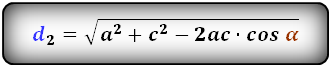
Формулы диагоналей трапеции через четыре стороны:
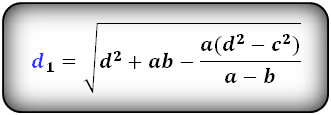

2. Формула длины диагоналей трапеции через высоту
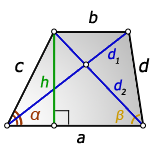
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
h – высота трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции через высоту:


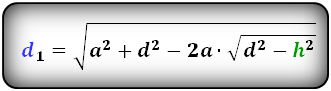
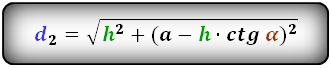


3. Формула длины диагонали трапеции через другую диагональ
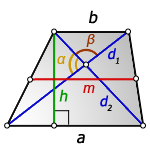
a – нижнее основание
b – верхнее основание
α, β – углы между диагоналями
h – высота трапеции
m – средняя линия трапеции
S – площадь трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции :
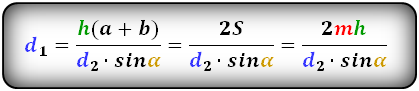
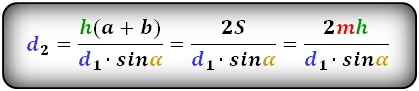
Справедливо для данного случая :
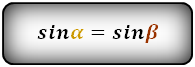
4. Формулы длины диагонали трапеции через сумму квадратов диагоналей
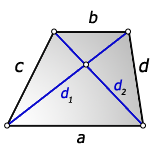
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
d1 , d2 – диагонали трапеции
Формула суммы квадратов диагоналей :
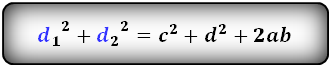
Формулы диагоналей трапеции :
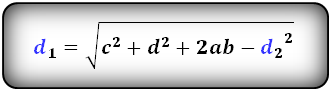
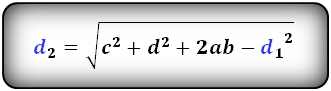
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула средней линии трапеции через основания (для всех видов трапеции)
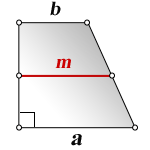
a – нижнее основание
b – верхнее основание
m – средняя линия
Формула средней линии, (m ):
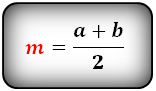
2. Формулы средней линии через основания, высоту и угол при нижнем основании
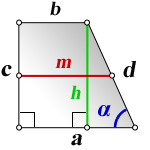
a, b – основания трапеции
c – боковая сторона под прямым углом к основаниям
d – боковая сторона
α – угол при основании
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
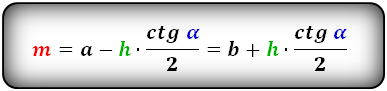
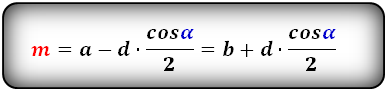
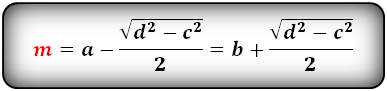
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
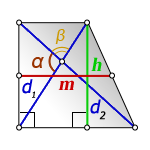
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
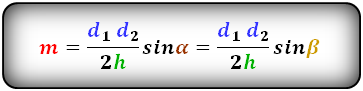
4. Формула средней линии трапеции через площадь и высоту (для всех видов трапеции)
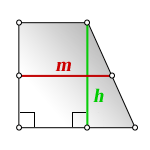
S – площадь трапеции
h – высота трапеции
m – средняя линия
Формула средней линии трапеции, (m ):
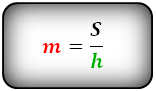
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула боковой стороны (с) прямоугольной трапеции через другие стороны и угол при нижнем основании
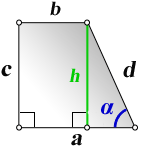
a – нижнее основание
b – верхнее основание
d – боковая сторона
α – угол при нижнем основании
h – высота трапеции
c – боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с) :

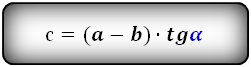
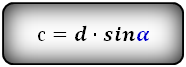
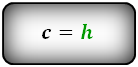
2. Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними
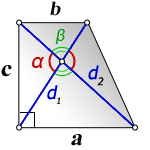
a – нижнее основание
b – верхнее основание
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
c – боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с):
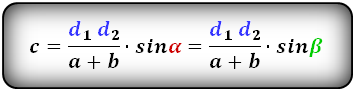
3. Формулы боковой стороны (с) прямоугольной трапеции через площадь
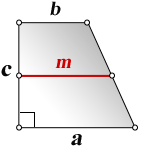
a – нижнее основание
b – верхнее основание
m – средняя линия трапеции
c – боковая сторона под прямым углом к основаниям
Формула длины боковой стороны (с) :
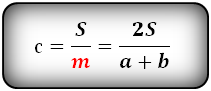
4. Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании
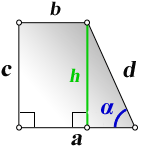
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
α – угол при нижнем основании
h – высота трапеции
d – боковая сторона
Формулы длины боковой стороны (d) :

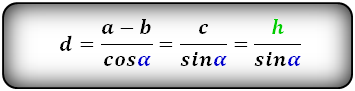
5. Формула боковой стороны (d) прямоугольной трапеции через площадь
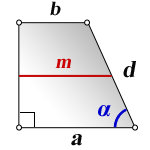
a – нижнее основание
b – верхнее основание
m – средняя линия трапеции
α – угол при нижнем основании
d – боковая сторона
Формула длины боковой стороны (d) :
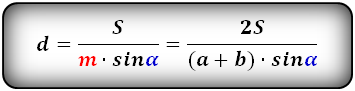
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула длины оснований прямоугольной трапеции через среднюю линию
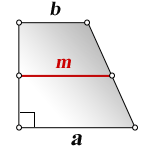
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины оснований :
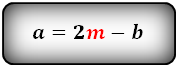
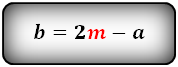
2. Формулы длины оснований через боковые стороны и угол при нижнем основании
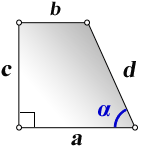
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α – угол при нижнем основании
Формулы длины оснований :
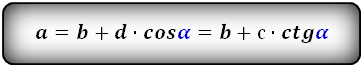
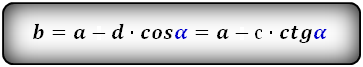
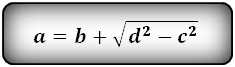

3. Формулы длины оснований трапеции через диагонали и угол между ними
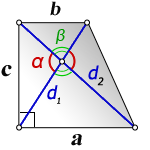
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
Формулы длины оснований :
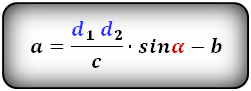
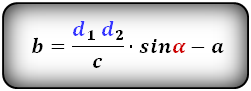
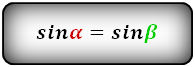
4. Формулы длины оснований трапеции через площадь
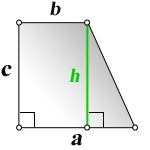
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
h – высота трапеции
Формулы длины оснований :
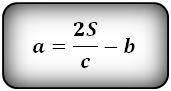
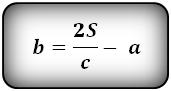
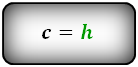
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула средней линии равнобедренной трапеции через основания
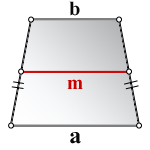
a – нижнее основание
b – верхнее основание
m – средняя линия
Формула средней линии, (m ):
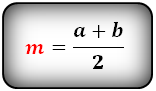
2. Формулы средней линии через основание, высоту и углы при нижнем основании
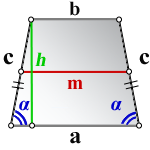
a – нижнее основание
b – верхнее основание
c – боковая сторона
α – угол при нижнем осровании
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
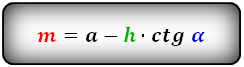
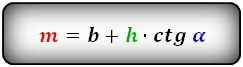
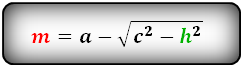
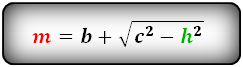
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
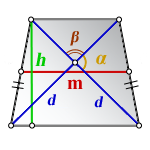
d – диагонали трапеции
α , β – углы между диагоналями
h – высота трапеции
m – средняя линия
Формула средней линии трапеции, (m ):
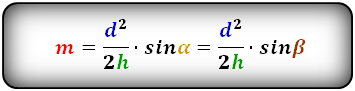
4. Формула средней линии трапеции через площадь и высоту
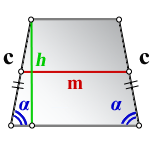
S – площадь трапеции
h – высота трапеции
α – угол при нижнем осровании
m – средняя линия
Формула средней линии трапеции, (m ):

Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула высоты равнобедренной трапеции через стороны и углы при основании
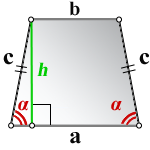
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α – угол при нижнем основании
h – высота трапеции
Формулы длины высоты, (h ):

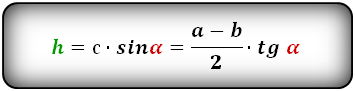
2. Формула высоты равнобедренной трапеции через диагонали и углы между ними
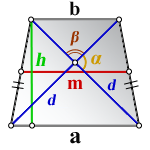
d – диагонали трапеции
α , β – углы между диагоналями
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
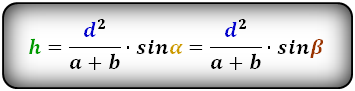
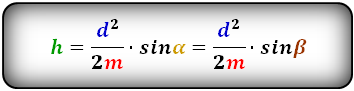
3. Формула высоты равнобедренной трапеции через площадь
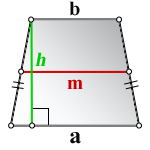
S – площадь трапеции
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
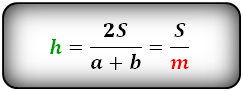
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула длины основания равнобедренной трапеции через среднюю линию
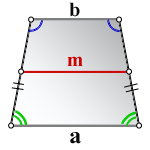
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины основания:
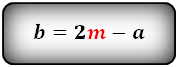
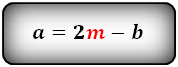
2. Формулы длины сторон через высоту и угол при нижнем основании
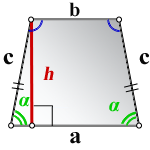
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α – угол при основании трапеции
h – высота трапеции
Формулы всех четырех сторон трапеции:
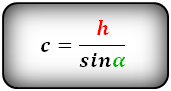
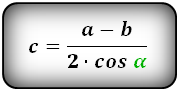
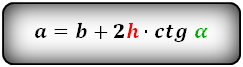
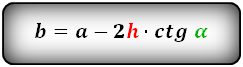
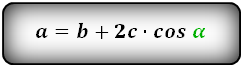
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
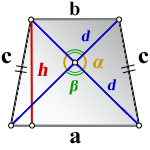
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
d – диагонали
α , β – углы между диагоналями
h – высота трапеции
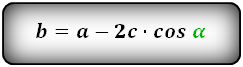
Формулы длины сторон трапеции:
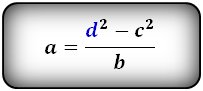
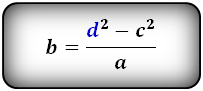

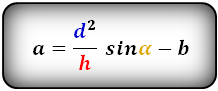
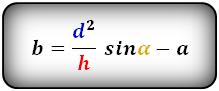
справедливо для данной ситуации:
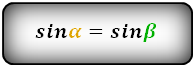
4. Формулы длины сторон равнобедренной трапеции через площадь
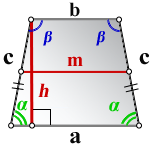
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α , β – углы при основаниях
m – средняя линия
h – средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
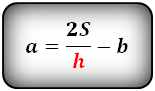
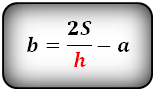
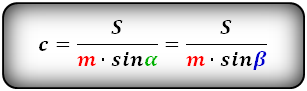

Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются – верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.
1. Формула высоты трапеции через стороны и углы при основании
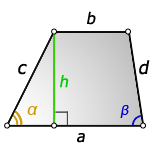
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
h – высота трапеции
Формулы длины высоты, (h ):
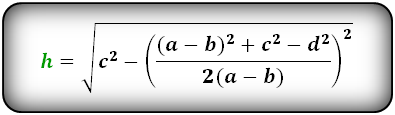
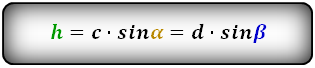
2. Формула высоты трапеции через диагонали и углы между ними
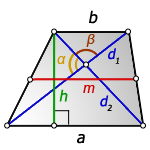
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
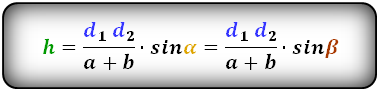
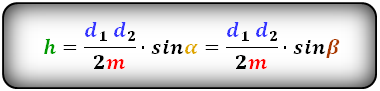
3. Формула высоты трапеции через площадь
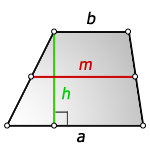
S – площадь трапеции
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
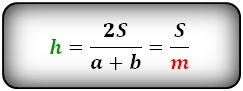
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются – верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции – отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.
1. Формула средней линии трапеции через основания
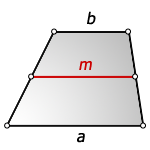
b – верхнее основание
a – нижнее основание
m– средняя линия
Формула средней линии, (m ):
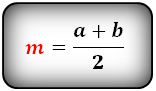
2. Формулы средней линии через основание, высоту и углы при нижнем основании
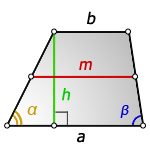
b – верхнее основание
a – нижнее основание
α, β – углы трапеции
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m):
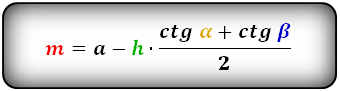
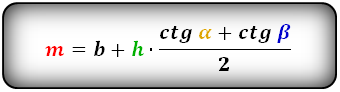
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
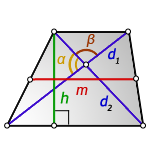
α, β – углы между диагоналями
d1 , d2 – диагонали трапеции
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
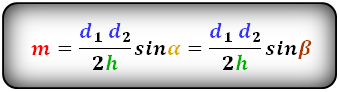
4. Формула средней линии трапеции через площадь и высоту
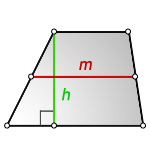
S – площадь трапеции
h – высота трапеции
m – средняя линия
Формула средней линии трапеции, (m):
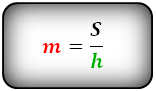
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула длины основания трапеции через среднюю линию
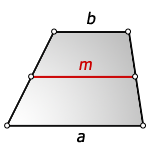
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины оснований :


2. Формулы длины сторон через высоту и углы при нижнем основании
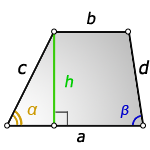
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
h – высота трапеции
Формулы всех четырех сторон трапеции:



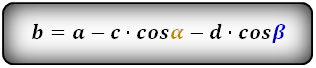
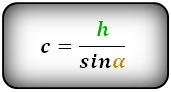
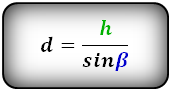
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
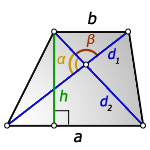
a – нижнее основание
b – верхнее основание
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
h – высота трапеции
Формулы длины сторон трапеции:
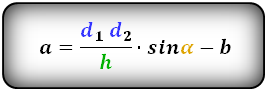
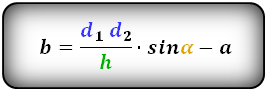
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Предмет: Геометрия,
автор: Алексей16567
Ответы
Автор ответа: fse13
0
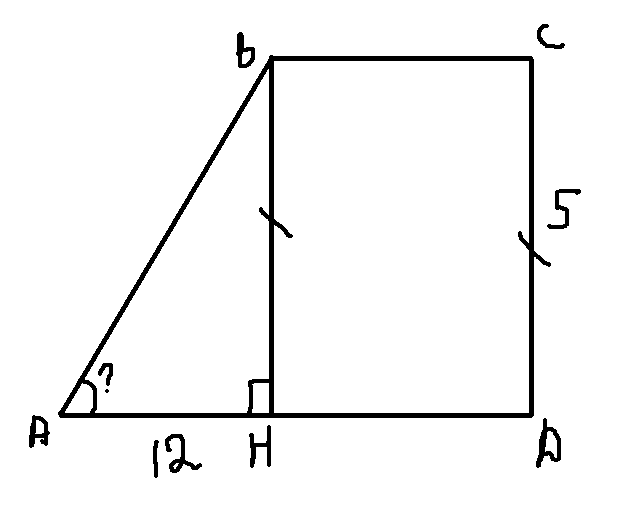
разность оснований в прям. трап. – это отрезок от основания высоты до острого угла.
т..к трап прям. то высота равна бок стороне = 5
Рассм. прям. тр-к ABH
AH=12
BH=5
AB=√12²+5²=√144+25=√169=13
SinA=BH/AB=5/13
CosA=AH/AB=12/13
tgA=BH/AH=5/12
Приложения:
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Химия,
автор: dadhayou
ДАЮ 70 БАЛЛОВ ТОЛЬКО БЫСТРО
1. Найти массу 0,896л сернистого газа So2
2. Найти массу кислорода, необходимого для сжигания 8г Ca.
5 лет назад
Предмет: Математика,
автор: dinara206021987
Помогите пожалуйста Математика 4 класс ❤
5 лет назад
Предмет: Математика,
автор: yudakov2006
1.УПРОСТИТЕ ВЫРАЖЕНИЕ. 6(3-0,5c)-2(0,8c-3)
5 лет назад
Предмет: Биология,
автор: Юленька117
У кроликов волнистая шерсть доминирует над гладкой. При скрещивании двух кроликов с волнистой шерстью в потомстве некоторые крольчата имели гладкую шерсть. Каковы генотипы родителей?
8 лет назад
Предмет: Алгебра,
автор: Nikita9595
решите уравнение:
sin(2x-п/3)+1=0
8 лет назад
![]()
Углы равнобедренной трапеции. Здравствуйте! В этой статье речь пойдёт о решении задач с трапецией. Данная группа заданий входит в состав экзамена, задачки простые. Будем вычислять углы трапеции, основания и высоты. Решение ряда задач сводится к решению прямоугольного треугольника, как говориться: куда мы без теоремы Пифагора, синуса и косинуса?
Работать будем с равнобедренной трапецией. У неё равны боковые стороны и углы при основаниях. О трапеции есть статья на блоге, посмотрите.

Отметим небольшой и важный нюанс, который в процессе решения самих заданий подробно расписывать не будем. Посмотрите, если у нас дано два основания, то большее основание высотами, опущенными к нему, разбивается на три отрезка – один равен меньшему основанию (это противолежащие стороны прямоугольника), два других равны друг другу (это катеты равных прямоугольных треугольников):

Простой пример: дано два основания равнобедренной трапеции 25 и 65. Большее основание разбивается на отрезки следующим образом:
![]()
*И ещё! В задачах не введены буквенные обозначения. Это сделано умышленно, чтобы не перегружать решение алгебраическими изысками. Согласен, что это математически неграмотно, но цель донести суть. А обозначения вершин и прочих элементов вы всегда можете сделать сами и записать математически корректное решение.
Рассмотрим задачи:

27439. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
Для того чтобы найти угол необходимо построить высоты. На эскизе обозначим данные в условии величины. Нижнее основание равно 65, высотами оно разбивается на отрезки 7, 51 и 7:

В прямоугольном треугольнике нам известна гипотенуза и катет, можем найти второй катет (высоту трапеции) и далее уже вычислить синус угла.
По теореме Пифагора указанный катет равен:
![]()
Таким образом:

Ответ: 0,96

27440. Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен 5/7. Найдите боковую сторону.
Построим высоты и отметим данные в условии величины, нижнее основание разбивается на отрезки 15, 43 и 15:

Ответ: 21

27441. Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен (2√10)/7. Найдите меньшее основание.
Построим высоты. Для того чтобы найти меньшее основание нам необходимо найти чему равен отрезок являющийся катетом в прямоугольном треугольнике (обозначен синим):

Можем вычислить высоту трапеции, а затем найти катет:

По теореме Пифагора вычисляем катет:

Таким образом, меньшее основание равно:
![]()
Ответ: 22

27442. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 5/11. Найдите высоту трапеции.
Построим высоты и отметим данные в условии величины. Нижнее основание разбивается на отрезки:

Что делать? Выражаем тангенс известного нам угла при основании в прямоугольном треугольнике:
![]()
Ответ: 10

27443. Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен 13/8. Найдите большее основание.
Строим высоты и вычисляем чему равен катет:

Таким образом большее основание будет равно:
![]()
Ответ: 71

27444. Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.
Строим высоты и отмечаем известные величины на эскизе. Нижнее основание разбивается на отрезки 35, 17, 35:

По определению тангенса:

Ответ: 0,4

77152. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
Построим эскиз, построим высоты и отметим известные величины, большее основание разбивается на отрезки 3, 6 и 3:

Выразим гипотенузу обозначенную как х через косинус:

Из основного тригонометрического тождества найдём cosα
![]()
Таким образом:

Ответ: 5

27818. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 500? Ответ дайте в градусах.

Из курса геометрии нам известно, что если имеем две параллельные прямые и секущую, что сумма внутренних односторонних углов равна 1800. В нашем случае это
![]()
C условии сказано, что разность противолежащих углов равна 500, то есть
![]()
Так как у равнобедренной трапеции углы при основании равны, то есть угол А равен углу В, то можем записать
![]()
Имеем два уравнения с двумя неизвестными, можем решить систему:

*Конечно, эту задачу можно было легко решить просто перебирая пары углов )

27833. В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 600. Найдите меньшее основание.

Построим высоты DE и CF:

Меньшее основание равно отрезку EF, так как DC и EF это противолежащие стороны прямоугольника. Отрезок EF мы можем найти если вычислим АЕ. Выразим этот катет прямоугольного треугольника ADE через функцию косинуса:

Так как AE=FB=5, то EF=25–5–5=15. Следовательно и DC=15.
Ответ: 15

27837. Основания равнобедренной трапеции равны 15 и 9, один из углов равен 450. Найдите высоту трапеции.

Из точек D и C опустим две высоты:

Как уже сказано выше они разбивают большее основание на три отрезка: один равен меньшему основанию, два других равны друг другу.
В данном случае они равны 3, 9 и 3 (в сумме 15). Кроме того, отметим что высотами отсекаются прямоугольные треугольники, причём они являются равнобедренными, так как углы при основании равны по 450. Отсюда следует, что высота трапеции будет равна 3.
Ответ: 3
На этом всё! Успеха вам!
С уважением, Александр.
P.S: Расскажите о сайте в социальных сетях!
В равнобокой трапеции ABCD AB = cd = 6 BC = 8 Ad = 12 найти синус косинус и тангенс угла A.
На этой странице находится вопрос В равнобокой трапеции ABCD AB = cd = 6 BC = 8 Ad = 12 найти синус косинус и тангенс угла A?. Здесь же – ответы на него,
и похожие вопросы в категории Геометрия, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 10 – 11 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.
Трапеция — геометрическая фигура представляет собой выпуклый четырехугольник с параллельными
противоположными сторонами. Они называются основаниями. Две другие стороны — боковые.
Трапеция, у которой они одинакового размера, называется равнобедренной. Если одна из боковых сторон
образует у основания угол в 90 градусов-прямоугольной.
Прямая линия, проведенная от одного основания
к другому, именуется высотой трапеции. Величина ее высчитывается делением суммы оснований на 2.
Диагонали — это отрезки, соединяющие противоположные углы фигуры. У равнобедренной трапеции
они равны по длине. Средняя линия-прямая, делящая пополам боковые стороны.
- Угол трапеции при основании через высоту и прилегающую
боковую сторону - Угол трапеции через нижнее основание, боковую сторону и
диагональ - Угол равнобедренной трапеции через нижнее основание,
среднию линию и боковую сторону - Угол равнобедренной трапеции через среднию линию, верхнее
основание и боковую сторону - Острый угол при нижнем основании прямоугольной трапеции
через высоту и два основания - Острый угол при нижнем основании прямоугольной трапеции
через два основания и боковую сторону
Угол трапеции при основании через высоту и прилегающую боковую сторону
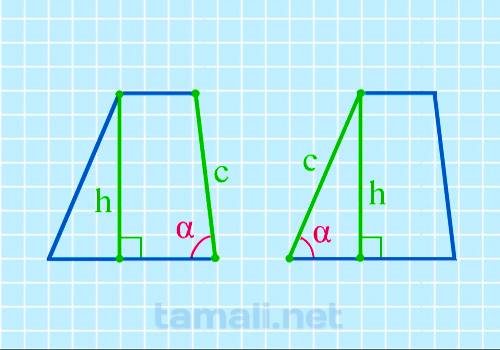
Введем обозначения: h-высота, с — боковая сторона. Угол трапеции α при основании вычисляется с
помощью формулы
sin α = h/с
где: h — высота трапеции, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Заменим буквенные обозначения условными цифрами. Пример: если высота равна
9см, боковая сторона-11см, получим: sin α = 9 / 11 = 0,818 , отсюда α =
55º. Указанное значение находим в таблице синусов. Данный показатель синуса угла соответствует
величине 55 градусов.
Через нижнее основание, среднию линию и боковую сторону в равнобедренной трапеции
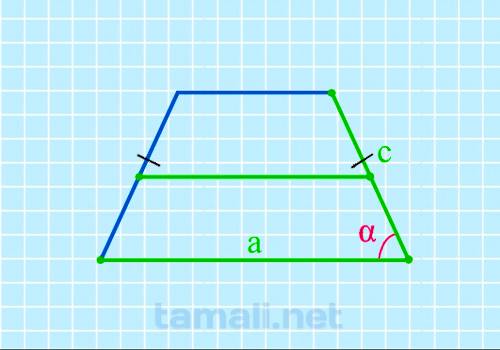
Угол равнобедренной трапеции через нижнее основание, среднюю линию и боковую сторону находится по
формуле:
cos α = (2a-2m) / 2c
где а — нижнее основание, m — средняя линия, с — боковая сторона.
Цифр после
запятой:
Результат в:
Пример.Заменим буквы условными цифровыми значениями. Если нижнее основание равно 8
см, средняя линия-6, а боковая сторона-4,8 см, то косинус угла равен 0,41666, что соответствует 65
градусам. cos α = (2 * 8 — 2 * 6) / 2 * 4,8 = 0, 41666, отсюда α =
65º. Равнобедренная трапеция — геометрическая фигура с нижними острыми углами. Это ее
особенность.
Угол трапеции, зная размер нижнего основания, боковой стороны и диагонали
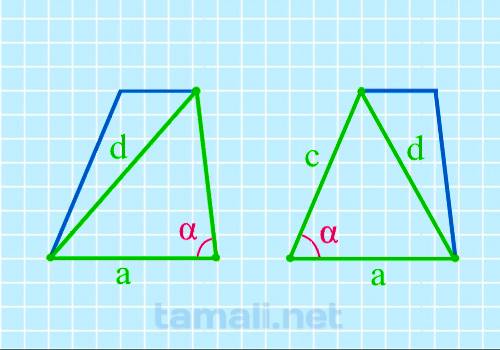
Если известны эти величины, воспользуемся формулой:
cos α= (a²+c²-d²) / 2ac
где а-нижнее основание, d-диагональ, с-боковая сторона.
Цифр после
запятой:
Результат в:
Пример. При условной величине нижнего основания 4 см, диагонали — 5.7 см,
боковой стороны — 4,4 см косинус равняется 0,081534, что соответствует углу 85 градусов по
таблице функций. cos α= (4² + 4,4² — 5,7²) / 2*4*4,4 = 0,081534,
отсюда α = 85º.
Через среднюю линию, верхнее основание и боковую сторону в равнобедренной трапеции
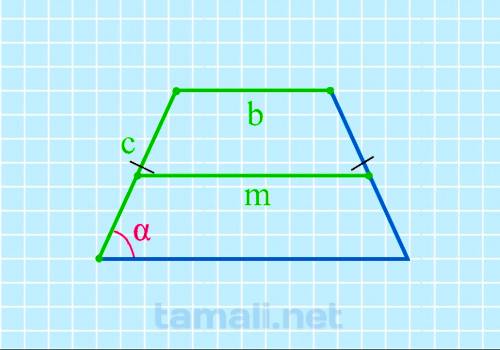
Нахождение угла равнобедренной трапеции через среднюю линию, верхнее основание и боковую сторону
выполняется по предложенной формуле:
cos α = (2m-2b) / 2c
где m — средняя линия, b — верхнее основание, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Введем условные цифровые значения. Допустим, что у равнобедренной трапеции
верхнее основание равно 4 см, средняя линия-6, боковая сторона-4 см. Косинус составляет 0,5.
Значение соответствует 60 градусам по таблице Брадиса. cos α = (2 * 6 — 2 * 4) / 2 * 4 = 0,5,
отсюда α = 60º
Вычисление острого угла при нижнем основании, если известны величины обоих оснований и боковой
стороны в прямоугольной трапеции
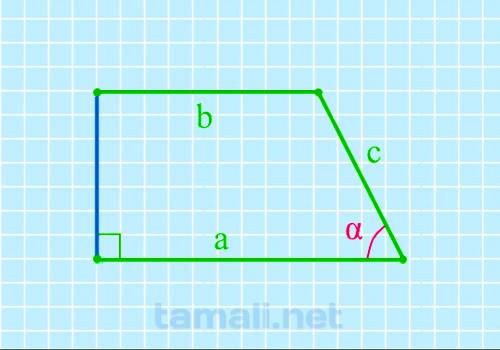
Находится по формуле
cos α = (a — b) / c
где a,b — основания, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Если буквенные выражения заменить условными цифровыми, получится наглядный
пример вычисления. Допустим, длина нижнего основания а 8 см, верхнего b-5,8 см, размер боковой
стороны с-4,8. Подставив в формулу цифровые значения, получим итог: косинус равен 0,45833.
Сравниваем показатель с таблицей вычисления Брадиса: он соответствует углу 63 градуса. cos α=(8 — 5,8) / 4,8 = 0,45833, отсюда α = 63º
Острый угол при нижнем основании, зная высоту и размеры двух оснований прямоугольной трапеции
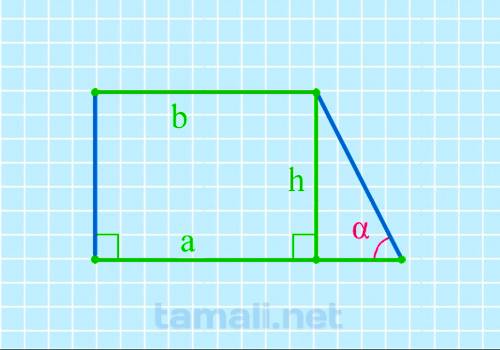
При известных указанных величинах воспользуемся следующей формулой:
tg(α) = h / (a-b)
где h — высота, a,b — верхнее и нижнее основания.
Цифр после
запятой:
Результат в:
Пример. Введя условные цифровые значения h = 15, a = 11, b = 10 получим tg(α) = 15 / (11-10) = 15. При вычислении получим значение тангенса: 15.
По таблице функций показатель соответствует 86 градусам.
Следует знать несколько закономерностей данной геометрической конструкции. У трапеции четыре угла,
общая сумма которых составляет 360 градусов.
Равнобедренная отличается двумя равными острыми, прилегающими к нижнему основанию, и тупыми
одинаковой величины-к верхнему. У прямоугольной трапеции два угла по 90 градусов, другие —
острый и тупой. Если он прилегает к нижнему основанию, величина такого угла определяется делением
высоты на разность между нижним и верхним основаниями. Угол трапеции при основании равен отношению
высоты к боковой стороне.
