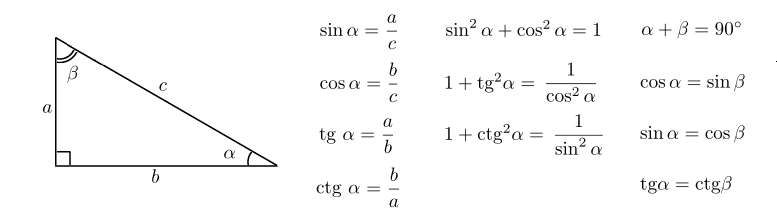Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?
Определение.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
 Например,
Например,
для угла A треугольника ABC
противолежащий катет — это BC.
Соответственно, синус угла A в треугольнике ABC — это
![]()
 Для угла B треугольника ABC
Для угла B треугольника ABC
противолежащим является катет AC.
Соответственно, синус угла B в треугольнике ABC
равен отношению AC к AB:
![]()
Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы. Длины отрезков выражаются положительными числами, поэтому синус угла треугольника также является положительным числом.
Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.
Вывод:
Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:
![]()
Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.
Например,
1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.
Тогда
![]()
2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.
Тогда
![]()
Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.
Угол A в обоих треугольниках одинаков.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Синус, косинус и тангенс острого угла прямоугольного треугольника
Рассмотрим прямоугольный треугольник АВС с прямым углом С:
Катет ВС этого треугольника является противолежащим углу А, а катет АС – прилежащим к этому углу.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Синус угла, который равен 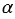 , обозначается символом
, обозначается символом 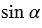 , читается: “синус альфа”.
, читается: “синус альфа”.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Косинус угла, который равен 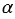 , обозначается символом
, обозначается символом 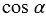 , читается: “косинус альфа”.
, читается: “косинус альфа”.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету. Тангенс угла, который равен 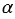 , обозначается символом
, обозначается символом 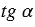 , читается: “тангенс альфа”.
, читается: “тангенс альфа”.
На рисунке
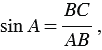 (1)
(1)
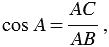 (2)
(2)
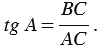 (3)
(3)
Из формул (1) и (2) получаем:
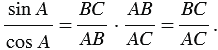
Сравнивая с формулой (3), находим:
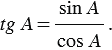 (4)
(4)
Получили, что тангенс угла равен отношению синуса к косинусу этого угла.
Докажем, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
Дано: 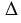 АВС,
АВС, 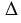 А1В1С1,
А1В1С1, 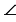 С =
С =  С1 = 900,
С1 = 900,  А =
А =  А1.
А1.
Доказать: sin A = sin A1, cos A = cos A1, tg A = tg A1.
Доказательство:
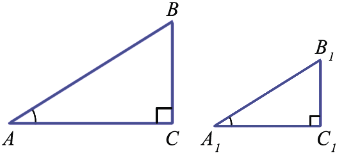
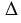 АВС
АВС 
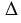 А1В1С1 по первому признаку подобия треугольников (т.к.
А1В1С1 по первому признаку подобия треугольников (т.к.  С =
С = 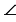 С1 = 900,
С1 = 900, 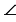 А =
А = 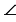 А1). Из подобия треугольников следует пропорциональность сходственных сторон, поэтому мы можем записать:
А1). Из подобия треугольников следует пропорциональность сходственных сторон, поэтому мы можем записать:
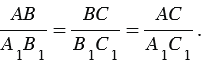
Из этих равенств следует, что 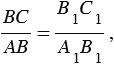 т.е. sin A = sin A1. Аналогично
т.е. sin A = sin A1. Аналогично 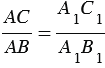 , т.е. cos A = cos A1, и
, т.е. cos A = cos A1, и 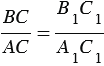 , т.е. tg A = tg A1, что и требовалось доказать.
, т.е. tg A = tg A1, что и требовалось доказать.
Мы получили, что синус, косинус и тангенс острого угла зависит только от величины этого угла.
Докажем основное тригонометрическое тождество:
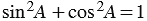
Из формул (1) и (2) получаем
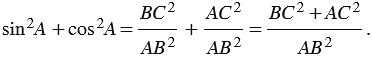
По теореме Пифагора 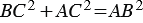 , поэтому
, поэтому 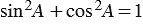 .
.
Советуем посмотреть:
Пропорциональные отрезки
Определение подобных треугольников
Отношение площадей подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Средняя линия треугольника
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
О подобии произвольных фигур
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 623,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 639,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 642,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1021,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 2,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1133,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1199,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1238,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1277,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Синусом угла в прямоугольном треугольнике называют отношение противолежащего катета к гипотенузе.
Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.
Для простоты запоминания можно дать такое определение: синус угла — это отношение дальнего от рассматриваемого угла катета к гипотенузе.
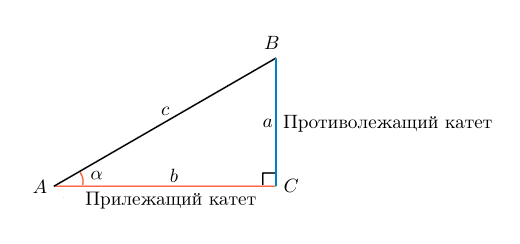
В случае с рисунком, описанным выше: sinα=acsinalpha=frac{a}{c}
В треугольнике, один из углов которого равен 90 градусам, известен катет при угле αalpha и равен он 3 см3text{ см}. Также дано произведение длин катетов и равно 12 см212text{ см}^2. Найдите синус угла αalpha.
Решение
Сначала нужно найти длину неизвестного нам катета. Для этого воспользуемся данным нам произведением. Обозначим неизвестный катет за xx. Тогда, по условию задачи:
3⋅x=123cdot x=12
x=123=4x=frac{12}{3}=4
a=x=4a=x=4
По теореме Пифагора найдем гипотенузу:
a2+b2=c2a^2+b^2=c^2
42+32=c24^2+3^2=c^2
25=c225=c^2
c=5c=5
sinα=ac=45=0.8sinalpha=frac{a}{c}=frac{4}{5}=0.8
Ответ
0.80.8
Вычислите синус 45 градусов.
Решение
Для этого воспользуемся тригонометрической таблицей углов. Находим, что:
sin45∘=π4=0.785sin 45^circ=frac{pi}{4}=0.785
Ответ
0.7850.785
Если в задаче известен косинус угла и нужно найти его синус, то наличие известных длин катетов и гипотенузы не обязательны. Достаточно просто воспользоваться основным тригонометрическим тождеством, которое имеет следующий вид:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
αalpha — любой угол.
Квадрат косинуса угла в треугольнике равен 0.8. Найдите синус данного угла.
Решение
Воспользуемся основным тригонометрическим тождеством:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
sin2α+0.8=1sin^2alpha+0.8=1
sin2α=0.2sin^2alpha=0.2
sinα=0.2sinalpha=sqrt{0.2}
sinα≈0.447sinalphaapprox0.447
Ответ
0.4470.447
Испытываете проблемы с вычислением синуса? Оформите задачу по математике на заказ у наших экспертов!
Тест по теме «Вычисление синуса»
Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачи по геометрии за 8 класс. Задачи на синус, косинус, тангенс острого угла прямоугольного треугольника, которые встречаются в 15 задании ОГЭ по математике.
Для начала введем понятия противолежащего и прилежащего катета.
Если катет находится напротив угла, относительно которого находится, то такой катет называется противолежащий. Если катет образует угол с гипотенузой, то катет называется прилежащим.
Определение синуса острого угла прямоугольного треугольника
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Запишем это определение по другому.
Выделенные буквы помогают определить, какой катет нам нужно взять. (сИнус – прОтиволежащий).
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Запишем это определение по другому.
Выделенные буквы помогают определить, какой катет нам нужно взять. (кОсинус – прИлежащий).
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему
Ниже приведу несколько типовых задач, на нахождение синуса, косинуса и тангенса острого угла прямоугольного треугольника:
Задача на нахождение синуса острого угла прямоугольного треугольника
Задача на нахождение косинуса острого угла прямоугольного треугольника
Задача на нахождение тангенса острого угла прямоугольного треугольника
Далее рассмотрим обратные задачи, где нужно будет составить соотношения для синуса, косинуса и тангенса острого угла прямоугольного треугольника и выразить неизвестную сторону.
Найдем сторону треугольника, зная синус острого угла прямоугольного треугольника
Найдем сторону треугольника, зная косинус острого угла прямоугольного треугольника
Найдем сторону треугольника, зная тангенс острого угла прямоугольного треугольника
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог
Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой нужной науки внесли ученые Ближнего Востока и Индии, которые придумали наиболее важные понятия, объяснили многие свойства, предложили варианты измерения и др.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии без таблиц и графиков.
Синус, косинус, тангенс и котангенс. Определения
Зачем разделять понятия синуса, косинуса, тангенса и котангенса?
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Что такое синус?
Синус угла (sin α) – это отношение противолежащего этому углу катета к гипотенузе.
Что такое косинус?
Косинус угла (cosα) – это отношение прилежащего катета к гипотенузе.
Что такое тангенс?
Тангенс угла (tg α) – это отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) – отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Синус и косинус можно представить через экспоненту (экспоненциальная функция).
Приведем иллюстрацию.

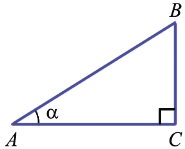
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Означения синуса, косинуса, тангенса и котангенса позволяют вычислять (находить) значения этих функций по известным длинам сторон треугольника.
Что и почему важно и принято помнить в ходе такого нахождения?
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тг и ктг – вся числовая прямая, то есть эти функции могут принимать любые значения.
Как найти синус? Для начала нужно определиться, какой перед нами треугольник: прямоугольный или произвольный. В первом случае можно использовать обычный тригонометрический метод, а во втором – теорему косинусов.
Как найти косинус? Соответственно, нам нужно знать значения прилежающего катета и гипотенузы.
Как найти тангенс? Если треугольник прямоугольный, то тангенс вычисляется при помощи значений противоположного катета и прилежащего (в уравнении нужно поделить одно на другое). Если речь идет о числах, тупых, развернутых углов и углов, превышающих 360 градусов, то тангенс определяется при помощи синуса и косинуса (посредством их отношения и деления).
Теорема синусов и косинусов используется для того чтобы искать элементы в произвольном треугольнике. Такой поиск используется часто.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность (круг) с центром в начале декартовой системы координат.

Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y).
Синус угла поворота α – это ордината точки A1(x , y). sin α=y
Косинус угла поворота α – это абсцисса точки A1(x , y). cos α=икс
Тангенс угла поворота α – это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx
Котанг угла поворота α – это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогична ситуация с котангенсом. Отличие состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Простое правило: синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)
Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)
При решении практических примеров не говорят “синус угла поворота α”. Слова “угол поворота” просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10π равен синусу угла поворота величиной 10π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности – точка A c координатами (1, 0).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t=y
Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t=x
Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α, cos α, tg α, ctg α – это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Синус, косинус, тангенс и котангенс – основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α=A1HOA1=y1=y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Синус, косинус, тангенс и котангенс: основные формулы