Задания
Версия для печати и копирования в MS Word
Тип 18 № 311914
i
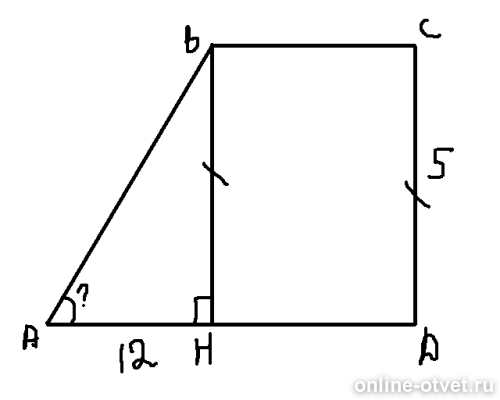
Найдите синус острого угла трапеции, изображённой на рисунке.
Спрятать решение
Решение.
Введем обозначения, как показано на рисунке и проведём высоту трапеции СH. В прямоугольном треугольнике BCH длины катетов равны 3 и 4, поэтому гипотенуза равна Следовательно, искомый синус острого угла B, равный отношению противолежащего углу катета CH к гипотенузе BC, равен
Ответ: 0,8.
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Спрятать решение
·
Помощь
focanean915
Вопрос по геометрии:
Помогите с задачей!!! Найдите Синус, Косинус и Тангенс острого угла прямоугольной трапеции, меньшая боковая сторона которой равна 5 см, а разность оснований-12 см?
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
ndfingh805
разность оснований в прям. трап. – это отрезок от основания высоты до острого угла.
т..к трап прям. то высота равна бок стороне = 5
Рассм. прям. тр-к ABH
AH=12
BH=5
AB=√12²+5²=√144+25=√169=13
SinA=BH/AB=5/13
CosA=AH/AB=12/13
tgA=BH/AH=5/12
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
ЗАДАЧА
Прежде чем приступить к решению задачи, мы:
– рассмотрим трапецию, вспомним ее основные характеристики;
– перенесем данные задачи на чертеж;
– внимательно прочитаем вопрос.
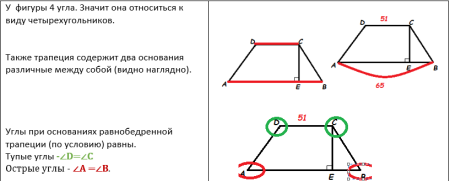
Как мы видим нам дана трапеция АВСD. Что мы знаем об этой фигуре? Давайте рассуждать:
По условию задачи СЕ- высота трапеции.
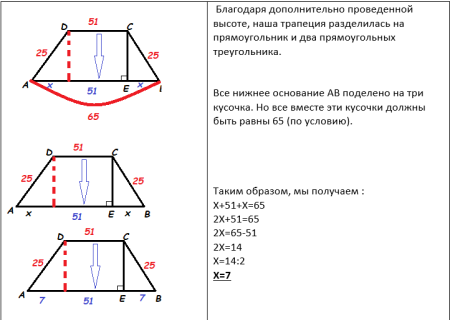
Проведем ещё одну высоту из точки D. Что нам это даст? Во- первых отметим ,что эти высоты равны друг другу. Во- вторых, построенная нами высота «отрезает» из нижнего основания кусочек равный 51. Наглядно это выглядит так;
Напомню, по условию, нам нужно найти синус острого угла трапеции. В нашей трапеции, как мы определили ранее, острые углы – А и В. Рассмотрим подробнее угол В в прямоугольном треугольнике СЕВ. Также вспомним, что синус острого угла – это отношение противоположного катета к гипотенузе прямоугольного ∆. Продолжение решения…..
Ученик
(228),
закрыт
6 лет назад
Ирка Багирка
Просветленный
(30770)
6 лет назад
Построим прямоугольную трапецию АВСD. Меньшее основание АВ, большее СD, угол А и угол D прямые. Проведем из угла В высоту ВН. Рассмотрим полученный треугольник ВСН. Угол ВНС = 90 градусов.
Катет ВН равен меньшей боковой стороне
ВН = АD = 5 см.
Катет СН равен разности оснований
СН = СD – АВ = 12 см.
По теореме Пифагора найдем гипотенузу
ВС = sqrt(ВН^2 + СН^2) =
sqrt(5^2 + 12^2) = sqrt(25 + 144) = sqrt 169 = 13 см.
sin ВСН = ВН/ВС = 5/13
соs ВСН = СН/ВС = 12/13
tg ВСН = ВН/СН = 5/12
В результате условия задачи будем рассматривать прямоугольный треугольник со сторонами a, являющимся катетом и равным 5 см, со вторым катетом b, который равен 12см. Гипотенуза c, длина которой пок анеизвестна.
Найдем c по теорме Пифагора:
с² = а² + b²
c² = 5² + 12²
c² = 25+144
c² = 169
c = √169
c=13 (см)
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
sin α = a/c = 5/13
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
cos α = b/c = 12/13
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
tg α = a/b = 5/12
Ответ: sin α = 5/13, cos α = 12/13, tg α = 5/12