Формулы половинного угла (аргумента) представляют собой противоположность формулам двойного угла , так как они выражают синус, косинус, тангенс и котангенс угла α2 при помощи тригонометрических функций угла α. В статье раскрыты формулы половинного угла и добавлены их доказательства с примерами решений.
Список формул половинного угла
Стандартные формулы половинного угла:
sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα
Формулы для sin и cos половинного угла справедливы при любом значении заданного угла α. Формулу для tg любого угла αопределяет tgα2, значение угла α≠π+2π·z при z равном любому целому числу ( выражение 1+cosα с таким же значением α не должно принимать значение 0). Формула ctg угла считается справедливой для любого угла α, где половинный угол имеет место быть, α≠2π·z.
Самые значимые формулы половинного угла для квадратов тригонометрических функций выводятся через положительное или отрицательное значение арифметического квадратного корня. Имеем формулы половинного угла:
sinα2=±1-cosα2, cosα2=±1+cosα2, tgα2=±1-cosα1+cosα, ctgα2=±1+cosα1-cosα
Знак «-» указывает, что тригонометрическая функция принадлежит определенной четверти угла α2.
Применим формулы на практике.
Доказательство формул половинного угла
Доказательство формул половинного угла основывается на формулах cos двойного угла cosα=1-2·sin2α2 и cosα=2·cos2α2-1. Упростив первое выражение по sin2α2, получим саму формулу половинного угла sin2α2=1-cosα2, второе выражение по cos2α2 получим cos2α2=1+cosα2.
Чтобы доказать формулы половинного угла для tg и ctg угла α2, необходимо применить основные тригонометрические тождества tgα2=sinα2cosα2 и ctgα2=cosα2sinα2, к ним необходимо добавить формулы половинного угла cos и sin, которые доказали выше. При подстановке получим выражения, имеющие вид:
tg2α2=sin2α2cos2α2=1-cosα21+cosα2=1-cosα1+cosα;ctg2α2=cos2α2sin2α2=1-cosα21+cosα2=1+cosα1-cosα;
Все формулы половинного угла были доказаны.
Примеры использования
Покажем применение формул половинного угла при решении примера.
Известно, что cos30°=32. Необходимо вычислить значение cos 15 градусов, используя формулы половинного угла.
Решение
Данный пример рассматривает применение формулы половинного угла для косинуса, имеющей вид cos2α2=1+cosα2.
Следуя из условия, подставляем числовые значения и получаем: cos215°=1+cos30°2=1+322=2+34. После получения значения косинуса 15 градусов, необходимо найти само значение косинуса. Для этого вспомним, что угол в 15 градусов принадлежит первой четверти. Там косинус угла имеет положительное значение ( чтобы вспомнить знаки тригонометрических функций, необходимо повторить теорию знаков синуса, косинуса, тангенса и котангенса по четвертям). Следуя из вышесказанного, имеем cos215°=2+34, тогда cos 15°=2+34=2+32. Ответ: cos 15°=2+32.
Применяя формулу половинного угла, стоит учитывать тот факт, что угол может быть не явного вида α2 и α, а потребует дальнейшего приведения к стандартному виду. Главное условие – нахождение аргумента в правой части формул половинного угла было в 2 раза больше, чем в левой. Иначе применение формулы будет невозможно.
Если формула позволит записывать данное равенство таким образом sin27α=1-cos14α2 или sin2 5α17=1-cos10α172, то формула будет применима.
Для правильного преобразования и применения формул половинного аргумента необходимо досконально изучить свойства тригонометрических функций. Не любое выражение поддается такому преобразованию в тригонометрии. Необходимо внимательно следить за значениями углов тригонометрических функций и их нахождение в четвертях для определения знака для выражения.
Все формулы половинного угла в тригонометрии:
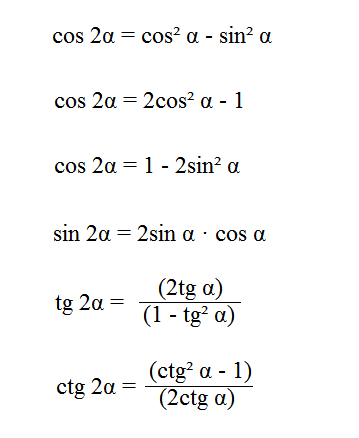
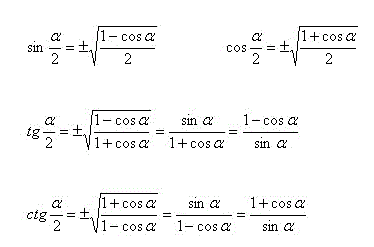
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Синус половинного угла
ОПРЕДЕЛЕНИЕ
Синус половинного угла выражается формулой, связывающей функцию угла (
alpha
) и функцию угла (
frac{alpha}{2}
) с формулой
(
sin frac{alpha}{2}=pm sqrt{frac{1-cos alpha}{2}}
)
Вывод формулы синуса с половинным углом
Вы можете получить эту формулу, используя формулу с двойным углом косинуса следующим образом:
(
cos alpha=cos left(2 cdot frac{alpha}{2}right)=1-2 sin ^{2} frac{alpha}{2}
)
отсюда
(
sin ^{2} frac{alpha}{2}=frac{1-cos alpha}{2}
)
Эта формула также называется формулой для снижения степени синуса.
Примеры решения проблем
ПРИМЕР 1
Рассчитать:
(
int_{0}^{frac{pi}{3}} 3 sin ^{2} frac{x}{2} d x
)
Чтобы вычислить этот интеграл, мы используем формулу полусинусоидального угла.
(
int_{0}^{frac{pi}{3}} 3 sin ^{2} frac{x}{2} d x=3 int_{0}^{frac{pi}{3}} frac{1-cos x}{2} d x=frac{3}{2}left(int_{0}^{frac{pi}{3}} d x-int_{0}^{frac{pi}{3}} cos x d xright) frac{3}{2}left(left.xright|_{0} ^{frac{pi}{3}}-sin left.xright|_{0} ^{frac{5}{3}}right)=frac{3}{2}left(frac{pi}{3}-0-sin frac{pi}{3}+sin 0right)=frac{3}{2}left(frac{pi}{3}-frac{sqrt{3}}{2}right)=frac{pi}{2}-frac{3 sqrt{3}}{4}
)
(
int_{0}^{frac{pi}{3}} 3 sin ^{2} frac{x}{2} d x=frac{pi}{2}-frac{3 sqrt{3}}{4}
)
ПРИМЕР 2
простить выражение
(
sin ^{2} frac{x}{2}-frac{1}{2} operatorname{tg} x sin x+frac{1}{2 cos x}
)
Чтобы упростить это выражение, мы будем использовать формулу для уменьшения степени синуса, а также представим касательную в виде (
operatorname{tg} x=frac{sin x}{cos }
):
(
sin ^{2} frac{x}{2}-frac{1}{2} operatorname{tg} x sin x+frac{1}{2 cos x}=frac{1-cos x}{2}-frac{1}{2} cdot frac{sin x}{cos x} cdot sin x+frac{1}{2 cos x}=frac{cos x-cos ^{2} x-sin ^{2} x+1}{2 cos x}=frac{cos x-1+1}{2 cos x}=frac{cos x}{2 cos x}=frac{1}{2}
)
(
sin ^{2} frac{x}{2}-frac{1}{2} operatorname{tg} x sin x+frac{1}{2 cos x}=frac{1}{2}
)
Формулы половинного угла (половинного аргумента) – это часть от всех основных тригонометрических формул. Они выражают функции синус, косинус, тангенс, котангенс угла `frac{alpha}2` через эти ж функции аргумента `alpha`. Они, можно сказать, противоположны формулам двойного угла. Ниже приведены все формулы половинных углов, их вывод, а также примеры решения задач с их использованием.
Список всех формул половинного угла
Их можно встретить записанными в двух видах. В первом каждая из тригонометрических функций выражается через радикал:
`sin frac alpha 2=pm sqrt{frac {1-cos alpha}2}`
`cos frac alpha 2=pm sqrt{frac {1+cos alpha}2}`
`tg frac alpha 2=pm sqrt{frac {1-cos alpha}{1+cos alpha}}=` `frac {sin alpha}{1+cos alpha}=frac {1-cos alpha}{sin alpha}`
`ctg frac alpha 2=pm sqrt{frac {1+cos alpha}{1-cos alpha}}=` `frac {sin alpha}{1-cos alpha}=frac {1+cos alpha}{sin alpha}`
Знак «+» или «-» перед корнями зависит от того, в какую из координатных четвертей попадает угол `frac{alpha}2`.
Во втором варианте имеем дело с квадратами тригонометрических функций половинного угла:
`sin^2 frac alpha 2=frac {1-cos alpha}2`
`cos^2 frac alpha 2=frac {1+cos alpha}2`
`tg^2 frac alpha 2=frac {1-cos alpha}{1+cos alpha}`
`ctg^2 frac alpha 2=frac {1+cos alpha}{1-cos alpha}`
Формула синуса и косинуса половинного угла имеет место при любом угле `alpha`.
Формула тангенса половинного угла справедлива для тех углов `alpha`, при которых определен `tg frac alpha 2`, то есть при ` alphanepi+2pi n, n in Z`.
Формула котангенса выполняется для тех `alpha`, при которых определен `ctg frac alpha 2`, то есть при ` alphane 2pi n, n in Z`.
С помощью следующего набора формул можно выразить каждую из тригонометрических функций угла `alpha` через тангенс половинного угла.
`sin alpha= frac{2tgfrac{alpha}{2}}{1 + tg^{2}frac{alpha}{2}},` ` alphane pi +2pi n, n in Z`
`cos alpha= frac{1 — tg^{2}frac{alpha}{2}}{1 + tg^{2}frac{alpha}{2}},` ` alpha ne pi +2pi n, n in Z`
`tg alpha= frac{2tgfrac{alpha}{2}}{1 — tg^{2}frac{alpha}{2}},` ` alpha ne pi +2pi n, n in Z,` ` alpha ne frac{pi}{2}+ pi n, n in Z`
`ctg alpha = frac{1 — tg^{2}frac{alpha}{2}}{2tgfrac{alpha}{2}},` ` alpha ne pi n, n in Z,` `alpha ne pi + 2pi n, n in Z`
Вывод формул половинного угла
Формула косинуса и синуса половинного угла выводится из формул косинуса двойного угла `cos 2alpha=1-2 sin^2 alpha` и `cos 2alpha=2 cos^2 alpha-1`. Запишем их в следующем виде: `cos alpha=1-2 sin^2 frac alpha 2` и `cos alpha=2 cos^2 frac alpha 2-1`. Выразив из первого равенства ` sin frac alpha 2` получим `sin frac alpha 2=pm sqrt{frac {1-cos alpha}2}`. Аналогично разрешив второе равенство относительно ` cos frac alpha 2` в результате будем иметь `cos frac alpha 2=pm sqrt{frac {1+cos alpha}2}`.
Формулы тангенса и котангенса половинного угла можно вывести, используя определения этих функций в виде `tg frac alpha 2=frac{sinfrac alpha 2}{cos frac alpha 2}` и `ctg frac alpha 2=frac{cos frac alpha 2}{sin frac alpha 2}`, а также две уже доказанные выше формулы для синуса и косинуса.
В результате будем иметь: `tg frac alpha 2=frac{sinfrac alpha 2}{cos frac alpha 2}=` `frac{pm sqrt{frac {1-cos alpha}2}}{pm sqrt{frac {1+cos alpha}2}}=` `pm sqrt{frac {1-cos alpha}{1+cos alpha}}` и `ctg frac alpha 2=frac{cosfrac alpha 2}{sin frac alpha 2}=` `frac{pm sqrt{frac {1+cos alpha}2}}{pm sqrt{frac {1-cos alpha}2}}=` `pm sqrt{frac {1+cos alpha}{1-cos alpha}}`.
Примеры использования при решении задач
Пример 1. Найти `cos 15^circ`, если известно, что `cos 30^circ=frac{sqrt3}2`.
Решение. Формула половинного угла для тригонометрической функции косинус имеет вид `cos^2 frac alpha 2=frac {1+cos alpha}2`. Подставив известные значения, имеем `cos^2 15^circ=frac {1+cos 30^circ}2=` `frac{1+frac{sqrt3}2}2=frac{2+sqrt3}4`. Имея значение `cos^2 15^circ`, найдем `cos 15^circ`. Поскольку угол 15 градусов лежит в первой координатной четверти, а косинус в этой четверти имеет знак «+», то `cos 15^circ=sqrt{frac{2+sqrt3}4}=` `frac{sqrt{2+sqrt3}}2`.
Ответ. `cos 15^circ=frac{sqrt{2+sqrt3}}2`.
Пример 2. Вычислить значение выражения `4cos frac {alpha}2+2cos alpha+5`, если `cos alpha=frac {1}8`.
Решение. Используя ту же формулу, что и в первом примере (`cos frac alpha 2=pm sqrt{frac {1+cos alpha}2}`) и известное значение косинуса, упростим выражение: `4sqrt{frac {1+cos alpha}2}+2cos alpha+5=4sqrt{frac {1+frac {1}8}2}+2 cdot frac {1}8+5=` `4sqrt{frac {9}16}+frac{1}4+5=8frac{1}4`.
Ответ. `4cos frac {alpha}2+2cos alpha+5=8frac{1}4`.
Еще несколько примеров с подробным объяснением посмотрите на видео:
В большинстве случаев формулы половинного угла используются при преобразовании тригонометрических выражений.
Материалы по теме:
- Тригонометрические формулы: косинус, синус и тангенс двойного угла
- Формулы понижения степени в тригонометрии: вывод и примеры
- Все формулы по тригонометрии
- Формулы приведения тригонометрических функций
![]() Загрузка…
Загрузка…
ВИДЕО УРОК
Синус, косинус, тангенс и котангенс половины угла.
Формулы деления аргумента пополам выражают тригонометрические функции
половинного аргумента α/2 через
тригонометрические функции аргумента α.
Синус половины
угла равен плюс или минус квадратному корню из полуразности между единицей и
косинусом целого числа.

Рассмотрим соотношения

В результате почленного вычитания получим:

откуда

ПРИМЕР:
Вычислите sin α/2, если
cos α = – 4/5 и 180° < α < 270°.
РЕШЕНИЕ:
По формуле

Находим

Учитывая, что sin α/2 ˃ 0 при
180°
< α < 270°, то есть
90° < α/2 < 135°, получим

ОТВЕТ:
sin
α/2 ≈ 0,948683.
ПРИМЕР:
Найдём sin 15° без таблицы:
РЕШЕНИЕ:

ОТВЕТ:

Косинус половины угла
равен плюс или минус квадратному корню из полусуммы единицы и косинуса целого
числа.

Складывая почленно равенства

будем иметь:

откуда

ПРИМЕР:
Найдём
sin
α/2, cos
α/2,
если
cos
α = 0,8
и
0 < α < π/2.
РЕШЕНИЕ:
Угол
α/2 находится в
I четверти, поэтому
sin α/2 ˃ 0, cos α/2 ˃ 0.

ОТВЕТ:
sin
α/2 ≈ 0,316,
cos
α/2 ≈ 0,949.
Тангенс половины угла равен плюс или минус корню квадратному из дроби,
числитель которой есть разность между единицей и косинусом целого угла, а
знаменатель есть сумма единицы и косинуса целого угла.

Разделим почленно равенство

на равенство

получим:

ПРИМЕР:
Найдём значение tg 112°30ʹ без
таблиц.
РЕШЕНИЕ:
ОТВЕТ:
tg 112°30ʹ = –1 – √͞͞͞͞͞2.
Котангенс половины угла равен плюс или минус корню квадратному из дроби,
числитель которой есть сумма между единицей и косинусом целого угла, а
знаменатель есть разность единицы и косинуса целого угла.
ПРИМЕР:
Дано: cos α = 49/81.
Найти: sin α/2, cos
α/2.
РЕШЕНИЕ:
Имеем:
ПРИМЕР:
Найти tg α/2, если
cos
α = 0,8
и
0 < α < π/2.
РЕШЕНИЕ:
По формуле
находим:
tg α/2 ˃
0, так как половина острого угла – угол острый, а тангенс острого угла
положительный.
Если
бы, например угол α находился в промежутке между 270° и 360°, то cos α был бы
так же положительным, но тангенс половины этого угла уже был бы отрицательным,
так как
135° < α/2
< 180°,
то есть подвижной радиус, соответствующий углу α/2, расположился бы во второй четверти, поэтому перед корнем в формуле
надо
взять знак минус.
Последний пример поясняет смысл двух знаков ± перед
радикалом в формулах
Знаки
плюс или минус берутся в соответствии с тем, в какой четверти расположится
подвижной радиус половины угла.
Если
же величина угла α, а
следовательно, и α/2 неизвестны, то перед радикалом ставим оба
знака.
Для
тангенса половинного угла можно вывести ещё две формулы.
Если в равенстве
помножить числитель и знаменатель правой части на 2 sin α/2, то получим:
Но
так как
2 sin2 α/2 = 1
– cos α, а
2 sin α/2 cos α/2 = sin α, то
Если же числитель и знаменатель правой части равенства
помножить
на 2 cos α/2, а
затем воспользоваться формулами
2 sin α/2 cos α/2 = sin α,
2 cos2 α/2 = 1
+ cos α
получим:
Применим полученные формулы к предыдущему примеру. Имеем: cos α = 0,8. Пусть угол α – острый. Тогда
откуда по формуле
находим:
По формуле
получим:
Пусть угол α заключён между 270° и 360°, тогда cos α = +0,8, но sin α = –0,6, и для tg α/2 получим:
по другой формуле:
Формулы
были
выведены из таких тождеств:
2 sin2 α/2 = 1
– cos α,
2 cos2 α/2 = 1
+ cos α.
Эти
тождества
1 – cos α = 2
sin2 α/2,
1 + cos α = 2
cos2 α/2.
полезно
помнить, так как ими часто приходится пользоваться при различных
преобразованиях. Эти формулы связывают тригонометрические функции углов, из
которых один вдвое больше другого.
ПРИМЕР:
Привести к простейшему
виду выражение
РЕШЕНИЕ:
Пользуясь формулой
1 + cos 2α = 2 cos2 α
имеем:
ПРИМЕР:
Привести к простейшему
виду выражение
РЕШЕНИЕ:
Пользуясь формулой
sin 2α = 2
sin α cos α
имеем:
ПРИМЕР:
Доказать справедливость
равенства
РЕШЕНИЕ:
Преобразуем левую часть:
а это – правая часть.
Аналогично можно вывести
формулы и для ctg α/2.
Выражение тригонометрических функций угла через тангенс половины этого угла.
Все тригонометрические функции любого угла выражаются
рационально (с
помощью действий сложения, вычитания, умножения, деления и возведения в целую
степень) через тангенс половины этого
угла.
Имеем:
sin α = 2 sin α/2 cos α/2.
Разделим правую часть на
sin2 α/2 + cos2 α/2,
получим:
Числитель и знаменатель правой части делим
на cos2 α/2, получим:
Точно
так же, разделив правую часть тождества
cos
α
= cos2 α/2 – sin2
α/2
на sin2 α/2 + cos2 α/2, получим:
Разделим числитель и знаменатель правой части
на cos2 α/2, будем иметь:
и, наконец,
Так как значения функций sес α и cosес α обратны
по величине соответственным значениям функций
cos α и sin α, то они также рационально
выражаются через tg α/2.
Задания к уроку 23
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 5. Периодичность тригонометрических функций
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований































