Как найти синус третьего угла треугольника

Синус угла в обычном треугольнике

Синус (sin) – это одна из прямых тригонометрических функций. Подробнее о ней можно узнать из нашей статьи Что такое синус.

Синус угла в прямоугольном треугольнике

Прежде чем выяснять, как найти синус угла, необходимо определиться с условными обозначениями. Пусть в прямоугольном треугольнике:

• α – острый угол, синус которого нужно найти;
• с – гипотенуза;
• b – прилежащий катет;
• a – противолежащий катет.

Тогда чтобы найти синус острого угла прямоугольного треугольника, достаточно посчитать соотношение длины противолежащего катета к длине гипотенузы: sin(α) = a/c. При этом стоит запомнить, что sin 90° всегда равен 1.

Синус угла в произвольном треугольнике

Находить синус угла в произвольном треугольнике проще всего с использованием теоремы косинусов (cos): квадрат длины любой стороны равен сумме квадратов длин двух других сторон за минусом их удвоенного произведения на косинус угла между ними.

a² = b² + c² – 2*b*c*cos(α)

Из данной формулы можно найти косинус: cos(α) = (b² + c² – a²)/(2*b*c)

А поскольку для одного и того же угла sin(α)² + cos(α)² = 1 и это константа, то можно вывести формулу для определения синуса:

Более детально нахождение синуса угла с использованием косинуса рассмотрено в нашей статье Как найти синус, если известен косинус.

Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

для угла A треугольника ABC

противолежащий катет — это BC.

Соответственно, синус угла A в треугольнике ABC — это

Для угла B треугольника ABC

противолежащим является катет AC.

Соответственно, синус угла B в треугольнике ABC

равен отношению AC к AB:

Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы. Длины отрезков выражаются положительными числами, поэтому синус угла треугольника также является положительным числом.

Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.

Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:

Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.

1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.

2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.

Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.

2
Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α). Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С) . А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С) ²).

Как найти синус угла в треугольнике? Не в прямоугольном, в любом

Если рассматриваемый треугольник является прямоугольным, то можно использовать базовое определение тригонометрической функции синуса для острых углов. По определению синусом угла называют соотношение длины катета, лежащего напротив этого угла, к длине гипотенузы этого треугольника. То есть, если катеты имеют длину А и В, а длина гипотенузы равна С, то синус угла α, лежащего напротив катета А, определяйте по формуле α=А/С, а синус угла β, лежащего напротив катета В – по формуле β=В/С. Синус третьего угла в прямоугольном треугольнике находить нет необходимости, так как угол, лежащий напротив гипотенузы всегда равен 90°, а его синус всегда равен единице.

2
Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α). Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С) . А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С) ²).

3
Воспользуйтесь для нахождения синуса угла двумя разными формулами расчета площади треугольника, в одной из которых задействованы только длины его сторон, а в другой – длины двух сторон и синус угла между ними. Так как результаты их будут равны, то из тождества можно выразить синус угла. Формула нахождения площади через длины сторон (формула Герона) выглядит так: S=¼*√((А+В+С) *(В+С-А) *(А+С-В) *(А+В-С)) . А вторую формулу можно написать так: S=А*В*sin(γ). Подставьте первую формулу во вторую и составьте формулу для синуса угла, лежащего напротив стороны С: sin(γ)= ¼*√((А+В+С) *(В+С-А) *(А+С-В) *(А+В-С) /(А*В)) . Синусы двух других углов можно найти по аналогичным формулам.

Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы

Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.

Синус, косинус, тангенс и котангенс. Определения

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Синус угла ( sin α ) – отношение противолежащего этому углу катета к гипотенузе.

Косинус угла ( cos α ) – отношение прилежащего катета к гипотенузе.

Тангенс угла ( t g α ) – отношение противолежащего катета к прилежащему.

Котангенс угла ( c t g α ) – отношение прилежащего катета к противолежащему.

Данные определения даны для острого угла прямоугольного треугольника!

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса – вся числовая прямая, то есть эти функции могут принимать любые значения.

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от – ∞ до + ∞ .

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.

Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).

Синус (sin) угла поворота

Синус угла поворота α – это ордината точки A 1 ( x , y ). sin α = y

Косинус угла поворота α – это абсцисса точки A 1 ( x , y ). cos α = х

Тангенс угла поворота α – это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x

Котангенс угла поворота α – это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , – 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

Синус и косинус определены для любых углов α .

Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )

Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )

При решении практических примеров не говорят “синус угла поворота α “. Слова “угол поворота” просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Начальная точка на окружности – точка A c координатами ( 1 , 0 ).

Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .

Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Синус (sin) числа t

Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t = y

Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t = x

Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).

Можно сказать, что sin α , cos α , t g α , c t g α – это функции угла альфа, или функции углового аргумента.

Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.

Основные функции тригонометрии

Синус, косинус, тангенс и котангенс – основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.

sin α = A 1 H O A 1 = y 1 = y

Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

[spoiler title=”источники:”]

http://sprashivalka.com/tqa/q/807447

http://zaochnik.com/spravochnik/matematika/trigonometrija/sinus-kosinus-tangens-i-kotangens/

[/spoiler]

Не надо считать по таблицам синусов. Тем более что счет по таблицам не дает абсолютной точности. Обозначим углы треугольника А, В и С. А длины сторон, противолежащие этим углам, как а, b и c. Уж очень подозрительно красивы величины синусов двух углов, sinA = 0,6 и sinB = 0,8. Попробуем взять квадраты этих величин. 0,6^2 + 0,8^2 = 0,36 + 0,64 = 1. Сумма квадратов этих величин равна 1. Что это напоминает? Теорему Пифагора для прямоугольного треугольника – квадрат гипотенузы равен сумме квадратов катетов. У нас длина гипотенузы равна 1 (максимальная длина, так как гипотенуза всегда длиннее катетов). Тогда 0,36 и 0,64 – это квадраты длин катетов. Сами катеты равны 0,6 и 0,8. А синусы равны отношению катетов к гипотенузе. Итак, треугольник будет прямоугольный. Третий угол С = 90°. А sin90° = 1.

Если бы синусы углов А и В были другими, то треугольник не был бы прямоугольным, но и эта задача тоже решается, но гораздо сложнее через арксинусы и арккосинусы.

Как найти синус угла по сторонам треугольника

Синус – это одна из базовых тригонометрических функций. Первоначально формула ее нахождения была выведена из соотношений длин сторон в прямоугольном треугольнике. Ниже приведены как эти базовые варианты нахождения синусов углов по длинам сторон треугольника, так и формулы для более сложных случаев с произвольными треугольниками.

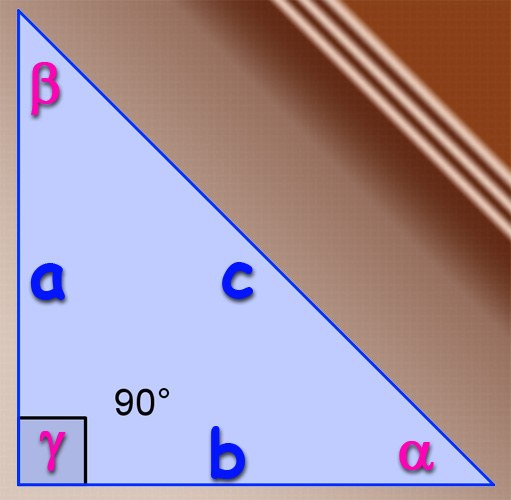
Инструкция

Если рассматриваемый треугольник является прямоугольным, то можно использовать базовое определение тригонометрической функции синуса для острых углов. По определению синусом угла называют соотношение длины катета, лежащего напротив этого угла, к длине гипотенузы этого треугольника. То есть, если катеты имеют длину А и В, а длина гипотенузы равна С, то синус угла α, лежащего напротив катета А, определяйте по формуле α=А/С, а синус угла β, лежащего напротив катета В – по формуле β=В/С. Синус третьего угла в прямоугольном треугольнике находить нет необходимости, так как угол, лежащий напротив гипотенузы всегда равен 90°, а его синус всегда равен единице.

Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α). Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С). А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С)²).

Воспользуйтесь для нахождения синуса угла двумя разными формулами расчета площади треугольника, в одной из которых задействованы только длины его сторон, а в другой – длины двух сторон и синус угла между ними. Так как результаты их будут равны, то из тождества можно выразить синус угла. Формула нахождения площади через длины сторон (формула Герона) выглядит так: S=¼*√((А+В+С)*(В+С-А)*(А+С-В)*(А+В-С)). А вторую формулу можно написать так: S=А*В*sin(γ). Подставьте первую формулу во вторую и составьте формулу для синуса угла, лежащего напротив стороны С: sin(γ)= ¼*√((А+В+С)*(В+С-А)*(А+С-В)*(А+В-С)/(А*В)). Синусы двух других углов можно найти по аналогичным формулам.

Видео по теме

Источники:

• треугольник синус

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?