Задание 16 в ОГЭ по математике это задачи на треугольники. У любого треугольника есть 6 элементов (3 стороны и 3 угла). Что связывает эти элементы между собой?
Для ответа на этот вопрос рассмотрим прямоугольный треугольник АВС с прямым углом С, катетами АС и ВС, гипотенузой АВ, и разберёмся, что значит противолежащий катет для острого угла А, прилежащий катет для острого угла А
Катет прямоугольного треугольника, который лежит напротив острого угла является противолежащим, т.е. для угла А противолежащим катетом является сторона ВС
Если же катет является стороной острого угла, то это прилежащий катет. Значит АС это прилежащий катет для острого угла А
А теперь попробуйте найти противолежащий и прилежащий катеты для острого угла B. Что поменялось?
ОПРЕДЕЛЕНИЯ синуса и косинуса острого угла.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего этому углу катета к гипотенузе
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего этому углу катета к гипотенузе
Запишем это “значками” для острого угла А. Вспомнив, что отношение записывается в виде дроби, и разобравшись с тем какой же катет прилежащий, а какой противолежащий получаем:
Сами значения синусов и косинусов для ВСЕХ углов это числовые коэффициенты, которые известны. Раньше эти коэффициенты можно было найти в таблицах Брадиса (небольшие книжечки)
Сейчас эти значения можно легко посчитать на калькуляторе (не возбраняется :)) НО вот для решения задач на экзамене все таки придется выучить значения синусов и косинусов “базовых” углов 30, 45 и 60 градусов.
Тогда получается, что стороны и углы треугольника можно связать через синусы или косинусы. Т.е. зная две стороны прямоугольного можно найти значения острых углов. Или зная сторону и угол, можно найти все остальные элементы прямоугольного треугольника.
ОСНОВНОЕ тригонометрическое тождество
Сумма квадрата синуса угла и квадрата косинуса того же угла равна 1
Это равенство позволяет переходить от синуса к косинусу, или от косинуса к синусу острого угла. Далее рассмотрим на примере задачи.
Немного разобравшись в понятиях синус и косинус можно решать задачи ОГЭ на эту тему.
Первая задача
Здесь достаточно знать определение синуса и делать простые вычисления.
Ответ: 0,36
Вторая задача
Перепишем условие
В этой задаче необходимо сделать переход от косинуса острого угла к синусу того же угла. Тогда пользуемся основным тригонометрическим тождеством, из которого выражаем синус через косинус:
подставляем значение косинуса из задания и считаем:
Нашли квадрат синуса. Значит с оговоркой, что угол острый, находим синус, извлекая корень из получившегося значения.
Ответ: 0,3
Завтра разберем задания связанные с теоремой синусов и теоремой косинусов произвольного треугольника.
Задания 16. Начало. Задачи на свойства треугольников можно посмотреть тут
Мне будет очень приятно, если вы поддержите лайком
Если есть задания, которые вы хотели бы разобрать, обязательно пишите в комментариях. На их основе смогу написать полезную статью 🙂
Спасибо.
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 233 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Источники:
Банк заданий ФИПИ.
В треугольнике ABC угол C прямой, BC = 8 , sin A = 0,4. Найдите AB.
Сторона равностороннего треугольника равна 10. Найдите его площадь, делённую на 
Периметр равностороннего треугольника равен 30. Найдите его площадь, делённую на
Высота равностороннего треугольника равна 10. Найдите его площадь, делённую на 
В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на
В треугольнике одна из сторон равна 10, другая равна 
а угол между ними равен 60°. Найдите площадь треугольника.
В треугольнике одна из сторон равна 10, другая равна 
а угол между ними равен 45°. Найдите площадь треугольника.
В треугольнике одна из сторон равна 10, другая равна а угол между ними равен 120°. Найдите площадь треугольника.
В треугольнике одна из сторон равна 10, другая равна а угол между ними равен 135°. Найдите площадь треугольника.
В треугольнике одна из сторон равна 10, другая равна 12, а угол между ними равен 30°. Найдите площадь треугольника.
В треугольнике одна из сторон равна 12, другая равна 16, а синус угла между ними равен 
Найдите площадь треугольника.
В треугольнике одна из сторон равна 12, другая равна 10, а косинус угла между ними равен 
Найдите площадь треугольника.
В треугольнике одна из сторон равна 12, другая равна 10, а тангенс угла между ними равен 
Найдите площадь треугольника.
Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
Периметр ромба равен 40, а один из углов равен 45°. Найдите площадь ромба, делённую на 
Периметр ромба равен 40, а один из углов равен 60°. Найдите площадь ромба, делённую на
Периметр ромба равен 24, а синус одного из углов равен 
Найдите площадь ромба.
Периметр ромба равен 24, а косинус одного из углов равен Найдите площадь ромба.
Периметр ромба равен 24, а тангенс одного из углов равен Найдите площадь ромба.
Всего: 233 1–20 | 21–40 | 41–60 | 61–80 …
Синус (sin) для острого угла рассматривается как отношение катета, который лежит напротив этого угла, к гипотенузе. Он является одной из тригонометрических функций, к которым еще относится косинус, тангенс и котангенс, а также секанс и косеканс.
Данная тригонометрическая функция, как и остальные, может рассматриваться для острых углов как соотношение сторон прямоугольного треугольника. Синусом (sin) угла принято
Леонард Эйлер
(04.04.1707 — 07.09.1783)
Швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.
называть ординату (координату по оси OY). Например:
Существует две наиболее распространенные единицы измерения углов. К ним относятся градусы и радианы. Перевести градусы в радианы достаточно просто. 360 градусов, то есть полный круг соответствует 2π радиану. Он считается положительным в том случае, если угол отсчитывается против часовой стрелки. Если же отсчитывать по часовой стрелке, тогда такой угол считается отрицательным: sin(-a) = sin a. Углы могут быть также и больше 360 градусов. К примеру, угол 740° — это два полных оборота плюс еще 20°. Так как мы, сделав несколько полных оборотов по окружности, возвращаемся на исходную точку, которая имеет те же координаты по оси Y. В тригонометрическом круге значение синуса повторяет свое значение каждые 360 градусов. Sin(а + 360°*n) = sin а, где n — целое число.
В общем история тригонометрии насчитывает два тысячелетия. Так как большинство математических соотношений невозможно было выразить при помощи обычных алгебраических операций, были введены тригонометрические функции, которые вначале оформлялись в виде таблиц. Упоминания о таких понятиях как «синус» и «косинус» в тригонометрических трактатах начинают появляться в индийских ученых ІV–V ст. В Х ст. арабские ученые владели понятиями «тангенс», возникло с потребностью гномики – учение о солнечных часах. В Европе первый трактат по тригонометрии «Пять книг о треугольнике всех видов», автором которого стал немецкий ученый Региомонтан (1436–1476), был опубликован в 1533 р. Современный вид тригонометрия приобрела в работах выдающегося математика, физика, астронома и механика Леонарда Эйлера. Математики Древней Индии синус называли словом «джива», что обозначало тетиву лука. В дальнейшем этот термин арабы превратили в «джиба». А тот в дальнейшем еще превратился в «джайо», более привычное для арабского языка слово, которое означает изгиб, складку одежды. Он же и соответствует латинскому слову sinus.
© 2007 — 2022 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель: Никитенко Евгений Игоревич
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены 
OBRAZOVALKA.COM
OBRAZOVALKA.COM — образовательный портал
Наш сайт это площадка для образовательных консультаций, вопросов и ответов для школьников и студентов .
На вопросы могут отвечать также любые пользователи, в том числе и педагоги.
Консультацию по вопросам и домашним заданиям может получить любой школьник или студент.
Задание:
Найдите синус, косинус и тангенс углов А и В треугольника АВС с прямым углом С, если: а) ВС=8, АВ=17; б) ВС=21, АС=20; в) ВС=1, АС=2; г)АС=24, АВ = 25.
Решение:
2
10 ответов:
2
0
Я так понял, что задача сводится к тому, что нам неизвестен угол треугольника, и нам нужно его найти.
Для того чтобы найти синус угла, а затем и сам угол в произвольном треугольнике, необходимо знать длины двух сторон: стороны, противолежащей искомому углу, и какой-либо другой стороны — и ещё величину угла, противолежащего этой последней стороне.
А затем нужно применить теорему синусов.
Обозначим искомый (неизвестный) угол как A, противолежащую сторону — a, другую известную сторону — b, известный противолежащий этой стороне угол — B.
По теореме синусов: a/sin(A) = b/sin(B).
Отсюда: sin(A) = a * sin(B)/b;
A = arcsin[a * sin(B)/b].
2
0
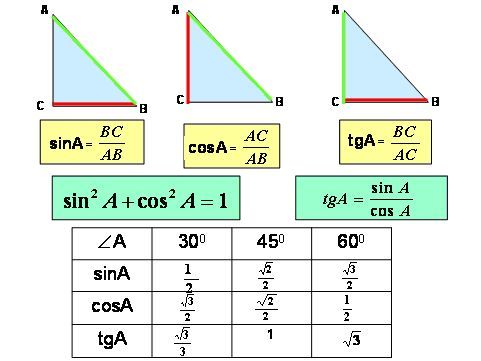
Для того, чтобы найти синус угла прямоугольного треугольника можно воспользоваться определением синуса. А синус — это отношение противолежащ. катета к гипотенузе. То есть синус угла А = ВС/АВ, где ВС — противол. катет, АВ — гипотенуза.
2
0
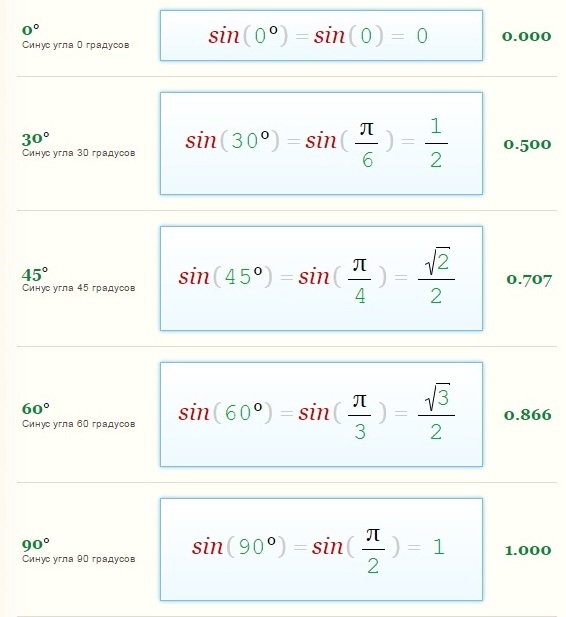
Для того, чтобы рассчитать синус угла в треугольнике, где один угол составляет 90 градусов, необходимо знать показатели двух сторон, а именно гипотенузы и катета, который не соприкасается с углом, то есть противолежащего.
1
0
Если известен угол треугольника, то можно воспользоваться специальным справочником и посмотреть там синус данного угла. Если же не известен угол, но то можно воспользоваться теоремой синусов. В частном случае, синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе.
1
0
Если величина угла неизвестна, то так: синус угла равен отношению длины противолежащей рассматриваемому углу стороны к диаметру описанной вокруг треугольника окружности. А как найти этот диаметр? Нужно найти центр описанной окружности. Для этого через середины любых двух сторон треугольника провести перпендикуляры. Точка пересечения этих перпендикуляров и есть центр описанной окружности. Расстояние от нее до любой вершины треугольника — радиус описанной окружности.
1
0
Чтобы ответить правильно на данный вопрос, нужно уточнить, синус угла в каком треугольнике нужно найти. Если этот треугольник произвольный, то это мы можем сделать только по теореме синусов (здесь см. исчерпывающий ответ Алекса).
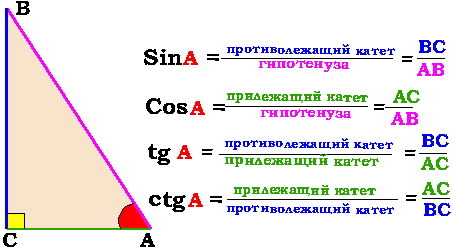
Если же нужно найти синус острого угла в прямоугольном треугольнике, то нужно воспользоваться определением синуса угла (как отношения противолежащего катета к гипотенузе). Тогда ответом будет: синус угла А = ВС/АВ, где ВС — противолежащий катет, АВ — гипотенуза.
1
0
В случае прямоугольного треугольника задача на нахождение синуса любого угла сводится всего лишь к вычислению отношения противолежащего от угла катета к гипотенузе — полученное значение и будет синусом. В произвольном треугольнике найти синус угла уже сложнее, но также возможно. Для этого надо хоть что-то знать из параметров треугольника. Например если известны три стороны треугольника, то углы находятся по теореме косинусов, а потом при желании легко находится синус уже найденного угла:
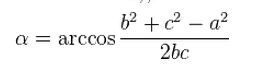
Так же синус любого угла можно найти если известны две стороны и угол между ними — по той же теореме косинусов находится третья сторона и далее как было описано.
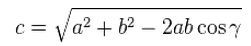
Если же угол находится не между известными сторонами в ход идет теорема синусов — находится второй угол не между сторонами и по свойству что сумма углов — 180 градусов находится третий угол:
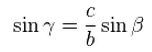
0
0
Давайте дадим определение, что же такое синус.
Синус угла (sin) в треугольнике — это отношение противолежащего катета к гипотенузе.
Так что найти синус угла довольно таки просто, если есть значение катета и гипотенузы.
0
0
Доброго времени суток.
Для нахождения синуса угла/углов прямоугольного треугольника можно воспользоваться двумя способами:
- первый из них — это взять транспортир и найти угол треугольника (сколько градусов), а затем уже по таблице найти синус данного угла;
- второй метод — это воспользоваться формулой нахождения синуса угла, который, как мы знаем, равен отношению противолежащего катета к гипотенузе.
Можно найти синус угла двумя способами и сравнить значения.
Все довольно просто.
0
0
Чтобы найти синус угла в любом треугольнике, необходимо воспользоваться формулами. Вот на этом рисунке показаны основные формулы, позволяющие рассчитывать синус угла в треугольнике:
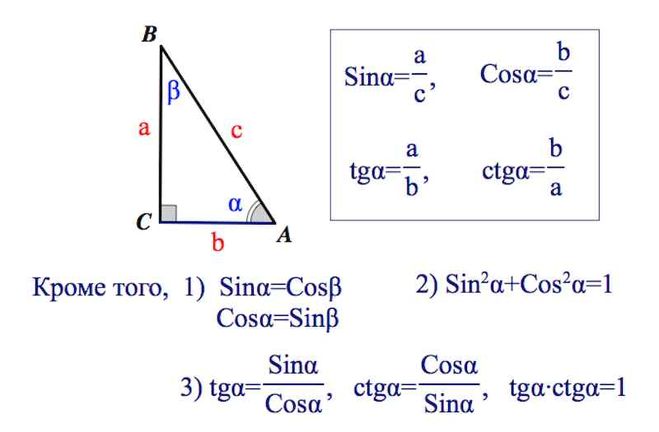
Воспользуйтесь этими формулами для рассчтеа.
Читайте также
Предположим, что Δ PMA вырожденный и все его точки слились в одну точку А (ну или почти слились, так что S ΔPMA → 0).
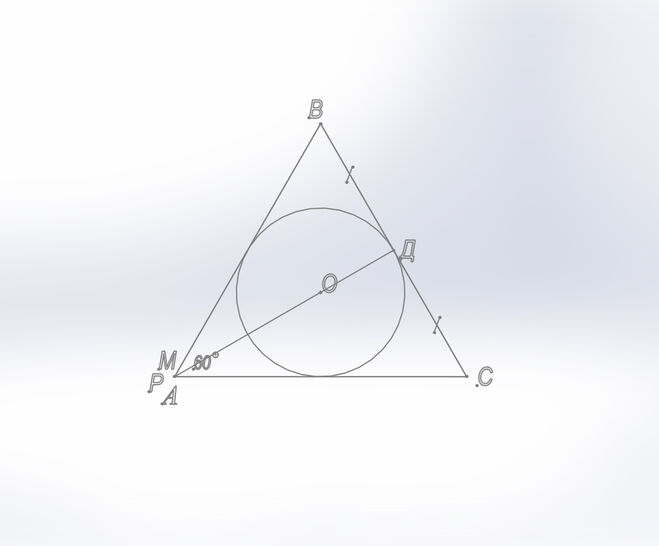
Тогда Δ ABC будет являться равносторонним.
S четырехугольника ВМРС = S ΔABC = √[p х ( p — a ) х ( p — b ) х ( p — c ) ] ` — формула Герона,
где
p — полупериметр, p = ( a + b + c ) / 2
a, b, с — длины сторон треугольника
Так как треугольник равносторонний, то формула Герона примет вид:
S четырехугольника ВМРС = SΔABC = а^2 х √3 / 4
S четырехугольника ВМРС = √108 х √3 / 4 = √324 / 4 = 4,5
Ps. не знаю зачем вспомнил формулу Герона, можно было бы и по обычной S = 0,5 х a х b х sin C. Стирать уже не хочу.
Ответ: площадь невыпуклого четырехугольника ВМРС равна 4,5.
У меня получился другой результат.
Обозначим угол между стороной а и основанием как х.
Площадь треугольника равна а*cos(x)*a*sin(x). Найдем на интервале от (0, п/2) максимум функции cos(x)*sin(x) = sin(2x)/2. Этот максимум достигается при 2х=п/2, т.е. при х=п/4=45 градусов. Третий угол такого треугольника — прямой, а основание равно а*sqrt(2).
Площадь правильного треугольника будет равна а*a*(squrt(2)/2)*(sq<wbr />urt(2)/2)=a*a*(2/4)=a<wbr />*a/2.
Площадь правильного треугольника со стороной а равна
a*a*sqrt(3)/2*(1/2)=<wbr />a*a*sqrt(3)/4, что примерно а*а*0.433 и меньше площади треугольника с углами 90, 45 и 45 градусов.
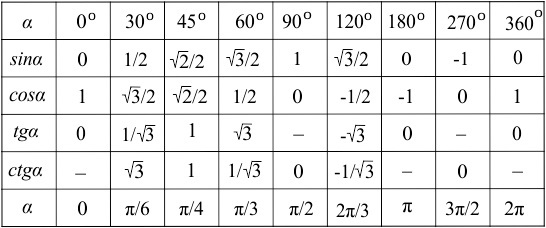
Для решения этой задачки (этого вопроса) можно использовать таблицу значений синуса. Эта табличка изучается в школе, она пропечатывается на многих современных тетрадях по математике и является допустимой, в том числе и на контрольных.
Находим слева sin, а сверху значение 270 градусов и видим на пересечении значение «-1».
Ответ: синус 270 градусов равен -1.
Для этого достаточно доказать либо равенства одного из острых углов в каждом треугольнике, либо равенство соотношений катетов в обоих треугольниках, либо равенство соотношений одного из катетов к гипотенузе.
Всё зависит от того, какие именно стороны заданы и какой именно угол надо найти.
Если известны два катета, то угол находится через тангенс или котангенс.
Если известны катет и гипотенуза, то угол ищем через синус или косинус.
Вспоминаем, что такое синус, косинус и тангенс в прямоугольном треугольнике.
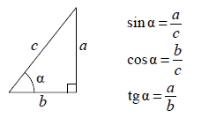Таким образом, синус и косинус задействуют гипотенузу, а тангенс – только катеты. Синус равен отношению противолежащего катета к гипотенузе; косинус – прилежащего к гипотенузе; тангенс – противолежащего катета к прилежащему.
Если на ОГЭ вы от волнения забудете, как находить косинус, синус и тангенс, загляните в справочные материалы на ваших листах с заданиями, там будут подсказки (в разделе геометрии).
В открытом банке заданий ФИПИ есть следующие задачи на эту тему, которые могут вам попасться на реальном экзамене в этом году.
Задания из банка ФИПИ с sin, cos, tg
Найти катет по известному синусу угла и гипотенузе
В треугольнике ABC угол C равен 90°, sinB=4/15, AB=45. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=45*4/15=12Ответ: 12
D8213E
В треугольнике ABC угол C равен 90°, sinB=7/12, AB=48. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=48*7/12=28Ответ: 28
B972FB
В треугольнике ABC угол C равен 90°, sinB=4/11, AB=55. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=55*4/11=20Ответ: 20
E65720
В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=51*5/17=15Ответ: 15
D893F0
В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=21*3/7=9Ответ: 9
6544F6
В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=18*4/9=8Ответ: 8
F6882F
В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=16*5/8=10Ответ: 10
564758
В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=10*3/5=6Ответ: 6
50A4DC
В треугольнике ABC угол C равен 90°, sinB=5/16, AB=80. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=80*5/16=25Ответ: 25
3D5005
В треугольнике ABC угол C равен 90°, sinB=7/20, AB=40. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=40*7/20=14Ответ: 14
14A018
Найти катет по известному косинусу и гипотенузе
В треугольнике ABC угол C равен 90°, cosB=2/5, AB=10. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=10*2/5=4Ответ: 4
1B8713
В треугольнике ABC угол C равен 90°, cosB=5/6, AB=18. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=18*5/6=15Ответ: 15
481278
В треугольнике ABC угол C равен 90°, cosB=4/7, AB=21. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=21*4/7=12Ответ: 12
D4E48F
В треугольнике ABC угол C равен 90°, cosB=3/8, AB=64. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=64*3/8=24Ответ: 24
3F99AC
В треугольнике ABC угол C равен 90°, cosB=7/9, AB=54. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=54*7/9=42Ответ: 42
915280
В треугольнике ABC угол C равен 90°, cosB=9/10, AB=60. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=60*9/10=54Ответ: 54
56F660
В треугольнике ABC угол C равен 90°, cosB=5/12, AB=60. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=60*5/12=25Ответ: 25
CA8E29
В треугольнике ABC угол C равен 90°, cosB=9/14, AB=42. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=42*9/14=27Ответ: 27
52D8C1
В треугольнике ABC угол C равен 90°, cosB=11/15, AB=75. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=75*11/15=55Ответ: 55
73E3A7
В треугольнике ABC угол C равен 90°, cosB=13/16, AB=96. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=96*13/16=78Ответ: 78
D8738D
Найти катет по известному катету и тангенсу
В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=12*3/4=9Ответ: 9
08FD08
В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=18*7/6=21Ответ: 21
1BBB13
В треугольнике ABC угол C равен 90°, tgB=9/7, BC=42. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=42*9/7=54Ответ: 54
14C45C
В треугольнике ABC угол C равен 90°, tgB=8/5, BC=20. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=20*8/5=32Ответ: 32
1DB806
В треугольнике ABC угол C равен 90°, tgB=11/8, BC=24. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=24*11/8=33Ответ: 33
EF04D8
В треугольнике ABC угол C равен 90°, tgB=5/9, BC=27. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=27*5/9=15Ответ: 15
A915AF
В треугольнике ABC угол C равен 90°, tgB=7/12, BC=48. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=48*7/12=28Ответ: 28
48CB65
В треугольнике ABC угол C равен 90°, tgB=4/7, BC=35. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=35*4/7=20Ответ: 20
1EB6B0
В треугольнике ABC угол C равен 90°, tgB=7/4, BC=36. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=36*7/4=63Ответ: 63
93C176
В треугольнике ABC угол C равен 90°, tgB=3/5, BC=30. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=30*3/5=18Ответ: 18
757BB5
Найти синус по косинусу и наоборот
В решении заданий такого типа используйте основное тригонометрическое тождество
sin2α + cos2α=1
Выражаем то, что нужно найти, и подставляем известные значения.
Синус острого угла А треугольника АВС равен $frac{sqrt{21}}5$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√21/5)2 = 1 – 21/25 = 1 – 0,84 = 0,16
cosA = 0,4Ответ: 0,4
99B7F9
Синус острого угла А треугольника АВС равен $frac{3sqrt{11}}{10}$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (3√11/10)2 = 1 – 99/100 = 0,01
cosA = 0,1Ответ: 0,1
E52F99
Синус острого угла А треугольника АВС равен $frac{sqrt{91}}{10}$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√91/10)2 = 1 – 91/100 = 0,09
cosA = 0,3Ответ: 0,3
5F0BC9
Синус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (2√6/5)2 = 1 – 24/25 = 1-0,96 = 0,04
cosA = 0,2Ответ: 0,2
DF0885
Синус острого угла A треугольника ABC равен $frac{3sqrt7}8$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (3√7/8)2 = 1 – 63/64 = 1-0,984375 = 0,015625
cosA = 0,125Ответ: 0,125
Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.
D56817
Синус острого угла A треугольника ABC равен 4/5 . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (4/5)2 = 1 – 16/25 = 1-0,64 = 0,36
cosA = 0,6Ответ: 0,6
F548B1
Синус острого угла A треугольника ABC равен $frac{sqrt7}4$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√7/4)2 = 1 – 7/16 = 1-0,4375 = 0,5625
cosA = 0,75Ответ: 0,75
F6FBB5
Синус острого угла A треугольника ABC равен 3/5 . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (3/5)2 = 1 – 9/25 = 1-0,36 = 0,64
cosA = 0,8Ответ: 0,8
4257EE
Синус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√19/10)2 = 1 – 19/100 = 1-0,19 = 0,81
cosA = 0,9Ответ: 0,9
DC7D62
Синус острого угла A треугольника ABC равен $frac{sqrt{15}}4$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√15/4)2 = 1 – 15/16 = 1-0,9375 = 0,0625
cosA = 0,25Ответ: 0,25
11D7EC
Косинус острого угла A треугольника ABC равен $frac{sqrt{21}}5$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√21/5)2 = 1 – 21/25 = 1-0,84 = 0,16
sinA = 0,4Ответ: 0,4
4BD96F
Косинус острого угла A треугольника ABC равен $frac{3sqrt{11}}{10}$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (3√11/10)2 = 1 – 99/100 = 1-0,99 = 0,01
sinA = 0,1Ответ: 0,1
EE565F
Косинус острого угла A треугольника ABC равен $frac{sqrt{91}}{10}$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√91/10)2 = 1 – 91/100 = 1-0,91 = 0,09
sinA = 0,3Ответ: 0,3
EE4155
Косинус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (2√6/5)2 = 1 – 24/25 = 1-0,96 = 0,04
sinA = 0,2Ответ: 0,2
2657CA
Косинус острого угла A треугольника ABC равен $frac{3sqrt7}8$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (3√7/8)2 = 1 – 63/64 = 1-0,984375 = 0,015625
sinA = 0,125Ответ: 0,125
Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.
857A3B
Косинус острого угла A треугольника ABC равен 4/5. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (4/5)2 = 1 – 16/25 = 1-0,64 = 0,36
sinA = 0,6Ответ: 0,6
588CA0
Косинус острого угла A треугольника ABC равен $frac{sqrt7}4$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√7/4)2 = 1 – 7/16 = 1-0,4375 = 0,5625
sinA = 0,75Ответ: 0,75
5AC6CD
Косинус острого угла A треугольника ABC равен 3/5. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (3/5)2 = 1 – 9/25 = 1-0,36 = 0,64
sinA = 0,8Ответ: 0,8
3B3235
Косинус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√19/10)2 = 1 – 19/100 = 1-0,19 = 0,81
sinA = 0,9Ответ: 0,9
4D93A9
Косинус острого угла A треугольника ABC равен $frac{sqrt{15}}4$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√15/4)2 = 1 – 15/16 = 1-0,9375 = 0,0625
sinA = 0,25Ответ: 0,25
A426BF
Найти площадь треугольника по двум сторонам и углу между ними
Вспоминаем формулу нахождения площади треугольника по двум сторонам и углу между ними:
S=1/2аb•sinγ, где а и b – стороны треугольника, γ – угол между ними.
Подставляем известные величины и считаем.
Формула так же есть в справочных материалах ОГЭ, на экзамене можете ими воспользоваться.
В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=6*10*1/3=20
Ответ: 20
D8DE10
В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=6*12*1/4=18
Ответ: 18
510B5D
В треугольнике ABC известно, что AB=20, BC=7, sin∠ABC=2/5. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=20*7*2/5=56
Ответ: 56
21430B
В треугольнике ABC известно, что AB=15, BC=8, sin∠ABC=5/6. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=15*8*5/6=100
Ответ: 100
770975
В треугольнике ABC известно, что AB=14, BC=5, sin∠ABC=6/7. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=14*5*6/7=60
Ответ: 60
845EFC
В треугольнике ABC известно, что AB=12, BC=20, sin∠ABC=5/8. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*20*5/8=150
Ответ: 150
34F484
В треугольнике ABC известно, что AB=12, BC=15, sin∠ABC=4/9. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*15*4/9=80
Ответ: 80
86F9F5
В треугольнике ABC известно, что AB=16, BC=25, sin∠ABC=3/10. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=16*25*3/10=120
Ответ: 120
6B1EDE
В треугольнике ABC известно, что AB=9, BC=16, sin∠ABC=7/12. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=9*16*7/12=84
Ответ: 84
521C5A
В треугольнике ABC известно, что AB=12, BC=10, sin∠ABC=8/15. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*10*8/15=64
Ответ: 64
3A3D0B
Найти косинус угла, если известны 3 стороны треугольника
Вспомним теорему косинусов.
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
а2 = b2 + с2 – 2bс • cosα
Нужно выразить косинус и подставить известные величины.
Эта формула так же будет у вас под рукой на экзамене в справочных материалах ОГЭ.
В треугольнике АВС известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
cosα = (82 +102 – 122) : 2*8*10 = 20/160 = 0,125Ответ: 0,125
40840C
В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+7^2-9^2}{2ast 5ast 7}$ = -7/70 = -0,1
Ответ: -0,1
112015
В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{3^2+8^2-7^2}{2ast 3ast 8}$= 24/48 = 0,5
Ответ: 0,5
6E8D8A
В треугольнике ABC известно, что AB=5, BC=10, AC=11. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+10^2-11^2}{2ast 5ast 10}$= 4/100 = 0,04
Ответ: 0,04
844A89
В треугольнике ABC известно, что AB=6, BC=7, AC=8. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{6^2+7^2-8^2}{2ast 6ast 7}$= 21/84 = 0,25
Ответ: 0,25
79B29A
В треугольнике ABC известно, что AB=5, BC=6, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+6^2-4^2}{2ast 5ast 6}$= 45/60 = 0,75
Ответ: 0,75
6557F1
В треугольнике ABC известно, что AB=6, BC=8, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{6^2+8^2-4^2}{2ast 6ast 8}$= 84/96
Ответ: 0,875
B5CF05
В треугольнике ABC известно, что AB=7, BC=8, AC=13. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{7^2+8^2-13^2}{2ast 7ast 8}$= -56/112 = -0,5
Ответ: -0,5
91941D
В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{8^2+10^2-14^2}{2ast 8ast 10}$= -32/160 = -0,2
Ответ: -0,2
755B8F
В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{2^2+3^2-4^2}{2ast 2ast 3}$= -3/12 = -0,25
Ответ: -0,25
05C64C
Найти синус по двум сторонам
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. И тот, и другой, известны. Подставляем и считаем.
В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/10 = 0,6
Ответ: 0,6
A67245
В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 4/5 = 0,8
Ответ: 0,8
46D9DF
В треугольнике ABC угол C равен 90°, AC=7, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 7/25 = 0,28
Ответ: 0,28
6DA700
В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 24/25 = 0,96
Ответ: 0,96
C7A2A0
В треугольнике ABC угол C равен 90°, AC=6, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/20 = 0,3
Ответ: 0,3
ED2D47
В треугольнике ABC угол C равен 90°, AC=11, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 11/20 = 0,55
Ответ: 0,55
F1D3F8
В треугольнике ABC угол C равен 90°, AC=8, AB=40. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 8/40 = 0,2
Ответ: 0,2
CDC6C7
В треугольнике ABC угол C равен 90°, AC=16, AB=40. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 16/40 = 0,4
Ответ: 0,4
20BC46
В треугольнике ABC угол C равен 90°, AC=9, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 9/25 = 0,36
Ответ: 0,36
E2F916
В треугольнике ABC угол C равен 90°, AC=13, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 13/20 = 0,65
Ответ: 0,65
2C2621
Найти косинус по двум сторонам треугольника
Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. Подставляем известные значения и считаем.
В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 8/10 = 0,8
Ответ: 0,8
36727A
В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 3/5 = 0,6
Ответ: 0,6
E4988D
В треугольнике ABC угол C равен 90°, BC=14, AB=50. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/50 = 0,28
Ответ: 0,28
B9AA7C
В треугольнике ABC угол C равен 90°, BC=72, AB=75. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 72/75 = 0,96
Ответ: 0,96
6E5515
В треугольнике ABC угол C равен 90°, BC=14, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/20 = 0,7
Ответ: 0,7
E812C8
В треугольнике ABC угол C равен 90°, BC=9, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 9/20 = 0,45
Ответ: 0,45
C759C5
В треугольнике ABC угол C равен 90°, BC=30, AB=40. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 30/40 = 0,75
Ответ: 0,75
8854A8
В треугольнике ABC угол C равен 90°, BC=26, AB=40. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 26/40 = 0,65
Ответ: 0,65
C5CD1E
В треугольнике ABC угол C равен 90°, BC=16, AB=25. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 16/25 = 0,64
Ответ: 0,64
C3A5F2
В треугольнике ABC угол C равен 90°, BC=7, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 7/20 = 0,35
Ответ: 0,35
D58395
Найти тангенс угла по двум катетам
Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Подставляем значения катетов и считаем.
В треугольнике ABC угол C равен 90°, BC=5, AC=2. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 2/5 = 0,4
Ответ: 0,4
98C7DF
В треугольнике ABC угол C равен 90°, BC=5, AC=3. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/5 = 0,6
Ответ: 0,6
22FD03
В треугольнике ABC угол C равен 90°, BC=10, AC=7. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 7/10 = 0,7
Ответ: 0,7
C18053
В треугольнике ABC угол C равен 90°, BC=10, AC=8. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 8/10 = 0,8
Ответ: 0,8
33DA26
В треугольнике ABC угол C равен 90°, BC=15, AC=3. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/15 = 0,2
Ответ: 0,2
DD620C
В треугольнике ABC угол C равен 90°, BC=9, AC=27. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 27/9 = 3
Ответ: 3
342F0C
В треугольнике ABC угол C равен 90°, BC=5, AC=20. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 20/5 = 4
Ответ: 4
B800B8
В треугольнике ABC угол C равен 90°, BC=3, AC=18. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 18/3 = 6
Ответ: 6
FF498A
В треугольнике ABC угол C равен 90°, BC=4, AC=28. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 28/4 = 7
Ответ: 7
C9E181
В треугольнике ABC угол C равен 90°, BC=7, AC=35. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 35/7 = 5
Ответ: 5
0663D4
© 2007 – 2023 Сообщество учителей-предметников “Учительский портал”
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены
