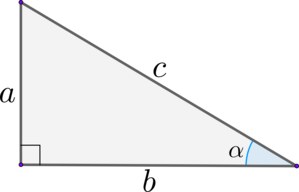
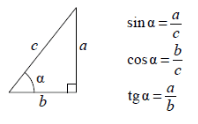Вспоминаем, что такое синус, косинус и тангенс в прямоугольном треугольнике.
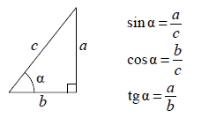
Если на ОГЭ вы от волнения забудете, как находить косинус, синус и тангенс, загляните в справочные материалы на ваших листах с заданиями, там будут подсказки (в разделе геометрии).
В открытом банке заданий ФИПИ есть следующие задачи на эту тему, которые могут вам попасться на реальном экзамене в этом году.
Задания из банка ФИПИ с sin, cos, tg
Найти катет по известному синусу угла и гипотенузе
В треугольнике ABC угол C равен 90°, sinB=4/15, AB=45. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=45*4/15=12Ответ: 12
D8213E
В треугольнике ABC угол C равен 90°, sinB=7/12, AB=48. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=48*7/12=28Ответ: 28
B972FB
В треугольнике ABC угол C равен 90°, sinB=4/11, AB=55. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=55*4/11=20Ответ: 20
E65720
В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=51*5/17=15Ответ: 15
D893F0
В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=21*3/7=9Ответ: 9
6544F6
В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=18*4/9=8Ответ: 8
F6882F
В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=16*5/8=10Ответ: 10
564758
В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=10*3/5=6Ответ: 6
50A4DC
В треугольнике ABC угол C равен 90°, sinB=5/16, AB=80. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=80*5/16=25Ответ: 25
3D5005
В треугольнике ABC угол C равен 90°, sinB=7/20, AB=40. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=40*7/20=14Ответ: 14
14A018
Найти катет по известному косинусу и гипотенузе
В треугольнике ABC угол C равен 90°, cosB=2/5, AB=10. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=10*2/5=4Ответ: 4
1B8713
В треугольнике ABC угол C равен 90°, cosB=5/6, AB=18. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=18*5/6=15Ответ: 15
481278
В треугольнике ABC угол C равен 90°, cosB=4/7, AB=21. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=21*4/7=12Ответ: 12
D4E48F
В треугольнике ABC угол C равен 90°, cosB=3/8, AB=64. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=64*3/8=24Ответ: 24
3F99AC
В треугольнике ABC угол C равен 90°, cosB=7/9, AB=54. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=54*7/9=42Ответ: 42
915280
В треугольнике ABC угол C равен 90°, cosB=9/10, AB=60. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=60*9/10=54Ответ: 54
56F660
В треугольнике ABC угол C равен 90°, cosB=5/12, AB=60. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=60*5/12=25Ответ: 25
CA8E29
В треугольнике ABC угол C равен 90°, cosB=9/14, AB=42. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=42*9/14=27Ответ: 27
52D8C1
В треугольнике ABC угол C равен 90°, cosB=11/15, AB=75. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=75*11/15=55Ответ: 55
73E3A7
В треугольнике ABC угол C равен 90°, cosB=13/16, AB=96. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=96*13/16=78Ответ: 78
D8738D
Найти катет по известному катету и тангенсу
В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=12*3/4=9Ответ: 9
08FD08
В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=18*7/6=21Ответ: 21
1BBB13
В треугольнике ABC угол C равен 90°, tgB=9/7, BC=42. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=42*9/7=54Ответ: 54
14C45C
В треугольнике ABC угол C равен 90°, tgB=8/5, BC=20. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=20*8/5=32Ответ: 32
1DB806
В треугольнике ABC угол C равен 90°, tgB=11/8, BC=24. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=24*11/8=33Ответ: 33
EF04D8
В треугольнике ABC угол C равен 90°, tgB=5/9, BC=27. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=27*5/9=15Ответ: 15
A915AF
В треугольнике ABC угол C равен 90°, tgB=7/12, BC=48. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=48*7/12=28Ответ: 28
48CB65
В треугольнике ABC угол C равен 90°, tgB=4/7, BC=35. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=35*4/7=20Ответ: 20
1EB6B0
В треугольнике ABC угол C равен 90°, tgB=7/4, BC=36. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=36*7/4=63Ответ: 63
93C176
В треугольнике ABC угол C равен 90°, tgB=3/5, BC=30. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=30*3/5=18Ответ: 18
757BB5
Найти синус по косинусу и наоборот
В решении заданий такого типа используйте основное тригонометрическое тождество
sin2α + cos2α=1
Выражаем то, что нужно найти, и подставляем известные значения.
Синус острого угла А треугольника АВС равен $frac{sqrt{21}}5$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√21/5)2 = 1 – 21/25 = 1 – 0,84 = 0,16
cosA = 0,4Ответ: 0,4
99B7F9
Синус острого угла А треугольника АВС равен $frac{3sqrt{11}}{10}$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (3√11/10)2 = 1 – 99/100 = 0,01
cosA = 0,1Ответ: 0,1
E52F99
Синус острого угла А треугольника АВС равен $frac{sqrt{91}}{10}$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√91/10)2 = 1 – 91/100 = 0,09
cosA = 0,3Ответ: 0,3
5F0BC9
Синус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (2√6/5)2 = 1 – 24/25 = 1-0,96 = 0,04
cosA = 0,2Ответ: 0,2
DF0885
Синус острого угла A треугольника ABC равен $frac{3sqrt7}8$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (3√7/8)2 = 1 – 63/64 = 1-0,984375 = 0,015625
cosA = 0,125Ответ: 0,125
Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.
D56817
Синус острого угла A треугольника ABC равен 4/5 . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (4/5)2 = 1 – 16/25 = 1-0,64 = 0,36
cosA = 0,6Ответ: 0,6
F548B1
Синус острого угла A треугольника ABC равен $frac{sqrt7}4$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√7/4)2 = 1 – 7/16 = 1-0,4375 = 0,5625
cosA = 0,75Ответ: 0,75
F6FBB5
Синус острого угла A треугольника ABC равен 3/5 . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (3/5)2 = 1 – 9/25 = 1-0,36 = 0,64
cosA = 0,8Ответ: 0,8
4257EE
Синус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√19/10)2 = 1 – 19/100 = 1-0,19 = 0,81
cosA = 0,9Ответ: 0,9
DC7D62
Синус острого угла A треугольника ABC равен $frac{sqrt{15}}4$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√15/4)2 = 1 – 15/16 = 1-0,9375 = 0,0625
cosA = 0,25Ответ: 0,25
11D7EC
Косинус острого угла A треугольника ABC равен $frac{sqrt{21}}5$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√21/5)2 = 1 – 21/25 = 1-0,84 = 0,16
sinA = 0,4Ответ: 0,4
4BD96F
Косинус острого угла A треугольника ABC равен $frac{3sqrt{11}}{10}$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (3√11/10)2 = 1 – 99/100 = 1-0,99 = 0,01
sinA = 0,1Ответ: 0,1
EE565F
Косинус острого угла A треугольника ABC равен $frac{sqrt{91}}{10}$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√91/10)2 = 1 – 91/100 = 1-0,91 = 0,09
sinA = 0,3Ответ: 0,3
EE4155
Косинус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (2√6/5)2 = 1 – 24/25 = 1-0,96 = 0,04
sinA = 0,2Ответ: 0,2
2657CA
Косинус острого угла A треугольника ABC равен $frac{3sqrt7}8$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (3√7/8)2 = 1 – 63/64 = 1-0,984375 = 0,015625
sinA = 0,125Ответ: 0,125
Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.
857A3B
Косинус острого угла A треугольника ABC равен 4/5. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (4/5)2 = 1 – 16/25 = 1-0,64 = 0,36
sinA = 0,6Ответ: 0,6
588CA0
Косинус острого угла A треугольника ABC равен $frac{sqrt7}4$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√7/4)2 = 1 – 7/16 = 1-0,4375 = 0,5625
sinA = 0,75Ответ: 0,75
5AC6CD
Косинус острого угла A треугольника ABC равен 3/5. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (3/5)2 = 1 – 9/25 = 1-0,36 = 0,64
sinA = 0,8Ответ: 0,8
3B3235
Косинус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√19/10)2 = 1 – 19/100 = 1-0,19 = 0,81
sinA = 0,9Ответ: 0,9
4D93A9
Косинус острого угла A треугольника ABC равен $frac{sqrt{15}}4$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√15/4)2 = 1 – 15/16 = 1-0,9375 = 0,0625
sinA = 0,25Ответ: 0,25
A426BF
Найти площадь треугольника по двум сторонам и углу между ними
Вспоминаем формулу нахождения площади треугольника по двум сторонам и углу между ними:
S=1/2аb•sinγ, где а и b – стороны треугольника, γ – угол между ними.
Подставляем известные величины и считаем.
Формула так же есть в справочных материалах ОГЭ, на экзамене можете ими воспользоваться.
В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=6*10*1/3=20
Ответ: 20
D8DE10
В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=6*12*1/4=18
Ответ: 18
510B5D
В треугольнике ABC известно, что AB=20, BC=7, sin∠ABC=2/5. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=20*7*2/5=56
Ответ: 56
21430B
В треугольнике ABC известно, что AB=15, BC=8, sin∠ABC=5/6. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=15*8*5/6=100
Ответ: 100
770975
В треугольнике ABC известно, что AB=14, BC=5, sin∠ABC=6/7. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=14*5*6/7=60
Ответ: 60
845EFC
В треугольнике ABC известно, что AB=12, BC=20, sin∠ABC=5/8. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*20*5/8=150
Ответ: 150
34F484
В треугольнике ABC известно, что AB=12, BC=15, sin∠ABC=4/9. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*15*4/9=80
Ответ: 80
86F9F5
В треугольнике ABC известно, что AB=16, BC=25, sin∠ABC=3/10. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=16*25*3/10=120
Ответ: 120
6B1EDE
В треугольнике ABC известно, что AB=9, BC=16, sin∠ABC=7/12. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=9*16*7/12=84
Ответ: 84
521C5A
В треугольнике ABC известно, что AB=12, BC=10, sin∠ABC=8/15. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*10*8/15=64
Ответ: 64
3A3D0B
Найти косинус угла, если известны 3 стороны треугольника

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
а2 = b2 + с2 – 2bс • cosα
Нужно выразить косинус и подставить известные величины.
Эта формула так же будет у вас под рукой на экзамене в справочных материалах ОГЭ.
В треугольнике АВС известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
cosα = (82 +102 – 122) : 2*8*10 = 20/160 = 0,125Ответ: 0,125
40840C
В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+7^2-9^2}{2ast 5ast 7}$ = -7/70 = -0,1
Ответ: -0,1
112015
В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{3^2+8^2-7^2}{2ast 3ast 8}$= 24/48 = 0,5
Ответ: 0,5
6E8D8A
В треугольнике ABC известно, что AB=5, BC=10, AC=11. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+10^2-11^2}{2ast 5ast 10}$= 4/100 = 0,04
Ответ: 0,04
844A89
В треугольнике ABC известно, что AB=6, BC=7, AC=8. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{6^2+7^2-8^2}{2ast 6ast 7}$= 21/84 = 0,25
Ответ: 0,25
79B29A
В треугольнике ABC известно, что AB=5, BC=6, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+6^2-4^2}{2ast 5ast 6}$= 45/60 = 0,75
Ответ: 0,75
6557F1
В треугольнике ABC известно, что AB=6, BC=8, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{6^2+8^2-4^2}{2ast 6ast 8}$= 84/96
Ответ: 0,875
B5CF05
В треугольнике ABC известно, что AB=7, BC=8, AC=13. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{7^2+8^2-13^2}{2ast 7ast 8}$= -56/112 = -0,5
Ответ: -0,5
91941D
В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{8^2+10^2-14^2}{2ast 8ast 10}$= -32/160 = -0,2
Ответ: -0,2
755B8F
В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{2^2+3^2-4^2}{2ast 2ast 3}$= -3/12 = -0,25
Ответ: -0,25
05C64C
Найти синус по двум сторонам
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. И тот, и другой, известны. Подставляем и считаем.
В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/10 = 0,6
Ответ: 0,6
A67245
В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 4/5 = 0,8
Ответ: 0,8
46D9DF
В треугольнике ABC угол C равен 90°, AC=7, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 7/25 = 0,28
Ответ: 0,28
6DA700
В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 24/25 = 0,96
Ответ: 0,96
C7A2A0
В треугольнике ABC угол C равен 90°, AC=6, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/20 = 0,3
Ответ: 0,3
ED2D47
В треугольнике ABC угол C равен 90°, AC=11, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 11/20 = 0,55
Ответ: 0,55
F1D3F8
В треугольнике ABC угол C равен 90°, AC=8, AB=40. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 8/40 = 0,2
Ответ: 0,2
CDC6C7
В треугольнике ABC угол C равен 90°, AC=16, AB=40. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 16/40 = 0,4
Ответ: 0,4
20BC46
В треугольнике ABC угол C равен 90°, AC=9, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 9/25 = 0,36
Ответ: 0,36
E2F916
В треугольнике ABC угол C равен 90°, AC=13, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 13/20 = 0,65
Ответ: 0,65
2C2621
Найти косинус по двум сторонам треугольника
Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. Подставляем известные значения и считаем.
В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 8/10 = 0,8
Ответ: 0,8
36727A
В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 3/5 = 0,6
Ответ: 0,6
E4988D
В треугольнике ABC угол C равен 90°, BC=14, AB=50. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/50 = 0,28
Ответ: 0,28
B9AA7C
В треугольнике ABC угол C равен 90°, BC=72, AB=75. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 72/75 = 0,96
Ответ: 0,96
6E5515
В треугольнике ABC угол C равен 90°, BC=14, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/20 = 0,7
Ответ: 0,7
E812C8
В треугольнике ABC угол C равен 90°, BC=9, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 9/20 = 0,45
Ответ: 0,45
C759C5
В треугольнике ABC угол C равен 90°, BC=30, AB=40. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 30/40 = 0,75
Ответ: 0,75
8854A8
В треугольнике ABC угол C равен 90°, BC=26, AB=40. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 26/40 = 0,65
Ответ: 0,65
C5CD1E
В треугольнике ABC угол C равен 90°, BC=16, AB=25. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 16/25 = 0,64
Ответ: 0,64
C3A5F2
В треугольнике ABC угол C равен 90°, BC=7, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 7/20 = 0,35
Ответ: 0,35
D58395
Найти тангенс угла по двум катетам
Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Подставляем значения катетов и считаем.
В треугольнике ABC угол C равен 90°, BC=5, AC=2. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 2/5 = 0,4
Ответ: 0,4
98C7DF
В треугольнике ABC угол C равен 90°, BC=5, AC=3. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/5 = 0,6
Ответ: 0,6
22FD03
В треугольнике ABC угол C равен 90°, BC=10, AC=7. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 7/10 = 0,7
Ответ: 0,7
C18053
В треугольнике ABC угол C равен 90°, BC=10, AC=8. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 8/10 = 0,8
Ответ: 0,8
33DA26
В треугольнике ABC угол C равен 90°, BC=15, AC=3. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/15 = 0,2
Ответ: 0,2
DD620C
В треугольнике ABC угол C равен 90°, BC=9, AC=27. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 27/9 = 3
Ответ: 3
342F0C
В треугольнике ABC угол C равен 90°, BC=5, AC=20. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 20/5 = 4
Ответ: 4
B800B8
В треугольнике ABC угол C равен 90°, BC=3, AC=18. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 18/3 = 6
Ответ: 6
FF498A
В треугольнике ABC угол C равен 90°, BC=4, AC=28. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 28/4 = 7
Ответ: 7
C9E181
В треугольнике ABC угол C равен 90°, BC=7, AC=35. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 35/7 = 5
Ответ: 5
0663D4
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 211 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Источники:
Банк заданий ФИПИ.
В треугольнике ABC угол C прямой, BC = 8 , sin A = 0,4. Найдите AB.
Сторона равностороннего треугольника равна 10. Найдите его площадь, делённую на
Периметр равностороннего треугольника равен 30. Найдите его площадь, делённую на
Высота равностороннего треугольника равна 10. Найдите его площадь, делённую на
В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на
В треугольнике одна из сторон равна 10, другая равна а угол между ними равен 60°. Найдите площадь треугольника.
В треугольнике одна из сторон равна 10, другая равна а угол между ними равен 45°. Найдите площадь треугольника.
В треугольнике одна из сторон равна 10, другая равна а угол между ними равен 120°. Найдите площадь треугольника.
В треугольнике одна из сторон равна 10, другая равна а угол между ними равен 135°. Найдите площадь треугольника.
В треугольнике одна из сторон равна 10, другая равна 12, а угол между ними равен 30°. Найдите площадь треугольника.
В треугольнике одна из сторон равна 12, другая равна 16, а синус угла между ними равен Найдите площадь треугольника.
В треугольнике одна из сторон равна 12, другая равна 10, а косинус угла между ними равен Найдите площадь треугольника.
В треугольнике одна из сторон равна 12, другая равна 10, а тангенс угла между ними равен Найдите площадь треугольника.
Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
Периметр ромба равен 40, а один из углов равен 45°. Найдите площадь ромба, делённую на
Периметр ромба равен 40, а один из углов равен 60°. Найдите площадь ромба, делённую на
Периметр ромба равен 24, а синус одного из углов равен Найдите площадь ромба.
Периметр ромба равен 24, а косинус одного из углов равен Найдите площадь ромба.
Периметр ромба равен 24, а тангенс одного из углов равен Найдите площадь ромба.
Всего: 211 1–20 | 21–40 | 41–60 | 61–80 …
6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Вычисление синуса, косинуса и тангенса угла треугольника
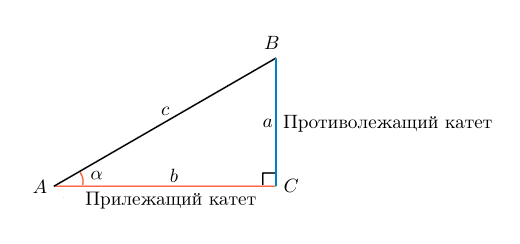
В прямоугольном треугольнике:
(blacktriangleright) Синус острого угла равен отношению противолежащего катета к гипотенузе: [{large{sin alpha =
dfrac{a}{c}}}]
(blacktriangleright) Косинус острого угла равен отношению прилежащего катета к гипотенузе: [{large{cos alpha =
dfrac{b}{c}}}]
(blacktriangleright) Тангенс острого угла равен отношению противолежащего катета к прилежащему: [{large{mathrm{tg}, alpha
= dfrac{a}{b}}}]
(blacktriangleright) Котангенс острого угла равен отношению прилежащего катета к противолежащему: [{large{mathrm{ctg},
alpha =dfrac{b}{a}}}]
Важные формулы:
[{large{begin{array}{|lcl|} hline sin^2 alpha+cos^2 alpha
=1&qquad& mathrm{tg}, alpha cdot mathrm{ctg}, alpha
=1\ &&\
mathrm{tg}, alpha=dfrac{sin alpha}{cos
alpha}&&mathrm{ctg}, alpha
=dfrac{cos alpha}{sin alpha}\&&\
hline
end{array}}}]
[begin{array}{|c|c|c|c|c|c|}
hline & phantom{000}, 0^circ phantom{000}& phantom{000},
30^circ phantom{000} &
phantom{000}, 45^circ phantom{000} & phantom{000}, 60^circ phantom{000}
& phantom{000}, 90^circ phantom{000}\[1ex]
hline sin & 0 ½&frac{sqrt2}2&frac{sqrt3}2 & 1\[1ex]
hline cos & 1 & frac{sqrt3}2&frac{sqrt2}2½ & 0\[1ex]
hline mathrm{tg} & 0 & frac{sqrt3}3&1&sqrt3 & text{не сущ.}\[1ex]
hline mathrm{ctg}& text{не сущ.} &sqrt3&1&frac{sqrt3}3 & 0\[1ex]
hline
end{array}]
Задание
1
#612
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 90^{circ}), (sin {angle BAC} = dfrac{2}{3}). Найдите (AC), если (AB = 6sqrt{5}).
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего этому углу катета к гипотенузе, тогда [dfrac{BC}{AB} = dfrac{2}{3}qquadRightarrowqquad BC = dfrac{2}{3}AB = 4sqrt{5}.]
По теореме Пифагора (AC^2 = AB^2 – BC^2 = 36cdot 5 – 16cdot 5 = 20cdot 5 = 10^2), тогда (AC = 10).
Ответ: 10
Задание
2
#2098
Уровень задания: Равен ЕГЭ
Дан прямоугольный треугольник (ABC), причем (angle C=90^circ). Известно, что (cos angle B=dfrac13), (AB=9). Найдите (BC).
По определению косинуса [cosangle B=dfrac{BC}{AB}=dfrac13 quad
Leftrightarrow quad BC=dfrac13cdot AB=dfrac13cdot 9=3]
Ответ: 3
Задание
3
#2099
Уровень задания: Равен ЕГЭ
Дан треугольник (ABC), причем (angle C=90^circ). Найдите длину его гипотенузы, если (AC=8, cos angle A=dfrac45).
По определению косинуса [cos angle A=dfrac{AC}{AB}=dfrac45
quad Leftrightarrow quad AB=ACcdot dfrac54=10]
Ответ: 10
Задание
4
#3320
Уровень задания: Равен ЕГЭ
Большее основание равнобедренной трапеции равно (34). Боковая сторона равна (14). Синус острого угла равен (dfrac{2sqrt{10}}7). Найдите меньшее основание.

Проведем (BHperp AD). Из (triangle ABH): [dfrac{2sqrt{10}}7=sinangle A=dfrac{BH}{AB}quadRightarrowquad
BH=4sqrt{10}] Тогда по теореме Пифагора [AH=sqrt{14^2-(4sqrt{10})^2}=6] Так как (AH=0,5(AD-BC)), то (BC=AD-2AH=34-12=22).
Ответ: 22
Задание
5
#3305
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (CH) – высота, (AB=13), (mathrm{tg},angle A=0,2). Найдите (AH).
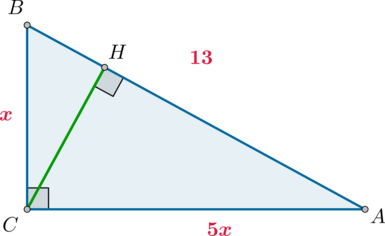
Так как по определению из (triangle ABC): [dfrac{BC}{AC}=mathrm{tg},angle A=dfrac 15] то можно принять (BC=x), (AC=5x). Следовательно, по теореме Пифагора [BC^2+AC^2=AB^2quadRightarrowquad x^2+(5x)^2=13^2quadRightarrowquad
x^2=dfrac{13}2] Из (triangle AHC): [cos angle A=dfrac{AH}{AC}] Из (triangle ABC): [cos angle A=dfrac{AC}{AB}] Следовательно: [dfrac{AH}{AC}=dfrac{AC}{AB}quadRightarrowquad
AH=dfrac{AC^2}{AB}=dfrac{(5x)^2}{13}=dfrac{25}2=12,5]
Ответ: 12,5
Задание
6
#3306
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (CH) – высота, (AB=26), (mathrm{tg},angle B=5). Найдите (AH).
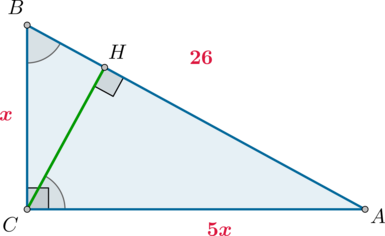
По определению из (triangle ABC): [dfrac{AC}{BC}=mathrm{tg},angle B=dfrac 51] Следовательно, можно принять (AC=5x), (BC=x). Тогда по теореме Пифагора (x^2+(5x)^2=26^2), откуда (x=sqrt{26}).
Тогда [sinangle B=dfrac{AC}{AB}=dfrac5{sqrt{26}}] По свойству прямоугольного треугольника (angle B=angle HCA). Следовательно, из (triangle HCA): [dfrac5{sqrt{26}}=sin angle HCA=dfrac{AH}{AC}quadRightarrowquad
AH=25]
Ответ: 25
Задание
7
#3307
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (AB=17), (mathrm{tg},angle A=0,25). Найдите высоту (CH).
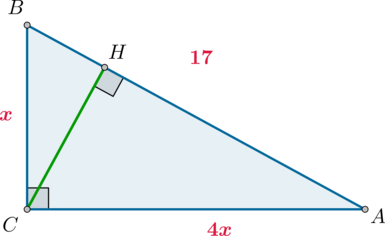
По определению из (triangle ABC): [dfrac{BC}{AC}=mathrm{tg},angle A=dfrac 14] Следовательно, можно принять (AC=4x), (BC=x). Тогда по теореме Пифагора (x^2+(4x)^2=17^2), откуда (x=sqrt{17}).
Так как площадь прямоугольного треугольника (ABC), с одной стороны, равна (0,5CHcdot AB), а с другой стороны, равна (0,5BCcdot AC), то [CHcdot AB=BCcdot ACquadRightarrowquad CH=dfrac{4x^2}{AB}=4]
Ответ: 4
Уметь оперативно и правильно решать задачи ЕГЭ на вычисление элементов многоугольника необходимо всем выпускникам вне зависимости от того, базовый или профильный уровень экзамена они сдают. Причем этой теме традиционно посвящается несколько заданий. Поэтому, если учащийся рассчитывает получить достойные баллы по итогам прохождения ЕГЭ, то ему обязательно стоит уделить внимание задачам, в которых требуется найти синус, косинус и тангенс угла треугольника.
Вместе с образовательным порталом «Школково» вы сможете восполнить пробелы в знаниях и отточить необходимый навык. Весь теоретический и практический материал составлен и изложен таким образом, чтобы все выпускники могли без особых затруднений справляться с задачами ЕГЭ, в которых требуется вычислить тангенс, синус или косинус угла треугольника.
Основные моменты
Первое, что нужно сделать при решении подобных задач в ЕГЭ, – вспомнить, что такое тангенс, косинус и синус угла треугольника. Далее рекомендуется следовать такому алгоритму:
- Выделяем треугольник, в который входит сторона или угол, который требуется найти.
- Определяем известные элементы и выявляем тригонометрическую функцию, которая их связывает.
- Записываем получившееся соотношение и применяем подходящую формулу.
Научившись правильно выполнять упражнения на вычисление элементов многоугольника, а также, например, по теме «Окружность, описанная около многоугольника», которые представлены в данном разделе образовательного портала «Школково», вы сможете закрепить материал и без труда справляться с подобными заданиями на аттестационном экзамене.

УСТАЛ? Просто отдохни

Если конкретно, то дело обстоит так. Косинус (cos) угла – это отношение прилежащего катета к гипотенузе. Cинус (sin) – это отношение противолежащего катета к гипотенузе. Тангенс угла tg(α) — есть отношение противолежащего катета a к прилежащему катету. И еще один лайфхак. Если вы вдруг прям забудете такие простые вещи, мало ли, тоже бывает, то как находить косинус, синус и тангенс, загляните в справочные материалы на ваших листах с заданиями, там будут подсказки (в разделе геометрии).
В открытом банке заданий ФИПИ есть следующие задачи на эту тему, которые могут вам попасться на реальном экзамене в этом году.
Задания из банка ФИПИ с sin, cos, tg
Найти катет по известному синусу угла и гипотенузе
В треугольнике ABC угол C равен 90°, sinB=4/15, AB=45. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=45*4/15=12Ответ: 12
D8213E
В треугольнике ABC угол C равен 90°, sinB=7/12, AB=48. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=48*7/12=28Ответ: 28
B972FB
В треугольнике ABC угол C равен 90°, sinB=4/11, AB=55. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=55*4/11=20Ответ: 20
E65720
В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=51*5/17=15Ответ: 15
D893F0
В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=21*3/7=9Ответ: 9
6544F6
В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=18*4/9=8Ответ: 8
F6882F
В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=16*5/8=10Ответ: 10
564758
В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=10*3/5=6Ответ: 6
50A4DC
В треугольнике ABC угол C равен 90°, sinB=5/16, AB=80. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=80*5/16=25Ответ: 25
3D5005
В треугольнике ABC угол C равен 90°, sinB=7/20, AB=40. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=40*7/20=14Ответ: 14
14A018
Найти катет по известному косинусу и гипотенузе
В треугольнике ABC угол C равен 90°, cosB=2/5, AB=10. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=10*2/5=4Ответ: 4
1B8713
В треугольнике ABC угол C равен 90°, cosB=5/6, AB=18. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=18*5/6=15Ответ: 15
481278
В треугольнике ABC угол C равен 90°, cosB=4/7, AB=21. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=21*4/7=12Ответ: 12
D4E48F
В треугольнике ABC угол C равен 90°, cosB=3/8, AB=64. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=64*3/8=24Ответ: 24
3F99AC
В треугольнике ABC угол C равен 90°, cosB=7/9, AB=54. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=54*7/9=42Ответ: 42
915280
В треугольнике ABC угол C равен 90°, cosB=9/10, AB=60. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=60*9/10=54Ответ: 54
56F660
В треугольнике ABC угол C равен 90°, cosB=5/12, AB=60. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=60*5/12=25Ответ: 25
CA8E29
В треугольнике ABC угол C равен 90°, cosB=9/14, AB=42. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=42*9/14=27Ответ: 27
52D8C1
В треугольнике ABC угол C равен 90°, cosB=11/15, AB=75. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=75*11/15=55Ответ: 55
73E3A7
В треугольнике ABC угол C равен 90°, cosB=13/16, AB=96. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=96*13/16=78Ответ: 78
D8738D
Найти катет по известному катету и тангенсу
В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=12*3/4=9Ответ: 9
08FD08
В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=18*7/6=21Ответ: 21
1BBB13
В треугольнике ABC угол C равен 90°, tgB=9/7, BC=42. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=42*9/7=54Ответ: 54
14C45C
В треугольнике ABC угол C равен 90°, tgB=8/5, BC=20. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=20*8/5=32Ответ: 32
1DB806
В треугольнике ABC угол C равен 90°, tgB=11/8, BC=24. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=24*11/8=33Ответ: 33
EF04D8
В треугольнике ABC угол C равен 90°, tgB=5/9, BC=27. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=27*5/9=15Ответ: 15
A915AF
В треугольнике ABC угол C равен 90°, tgB=7/12, BC=48. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=48*7/12=28Ответ: 28
48CB65
В треугольнике ABC угол C равен 90°, tgB=4/7, BC=35. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=35*4/7=20Ответ: 20
1EB6B0
В треугольнике ABC угол C равен 90°, tgB=7/4, BC=36. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=36*7/4=63Ответ: 63
93C176
В треугольнике ABC угол C равен 90°, tgB=3/5, BC=30. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=30*3/5=18Ответ: 18
757BB5
Найти синус по косинусу и наоборот
В решении заданий такого типа используйте основное тригонометрическое тождество
sin2α + cos2α=1
Выражаем то, что нужно найти, и подставляем известные значения.
Синус острого угла А треугольника АВС равен $frac{sqrt{21}}5$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√21/5)2 = 1 – 21/25 = 1 – 0,84 = 0,16
cosA = 0,4Ответ: 0,4
99B7F9
Синус острого угла А треугольника АВС равен $frac{3sqrt{11}}{10}$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (3√11/10)2 = 1 – 99/100 = 0,01
cosA = 0,1Ответ: 0,1
E52F99
Синус острого угла А треугольника АВС равен $frac{sqrt{91}}{10}$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√91/10)2 = 1 – 91/100 = 0,09
cosA = 0,3Ответ: 0,3
5F0BC9
Синус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (2√6/5)2 = 1 – 24/25 = 1-0,96 = 0,04
cosA = 0,2Ответ: 0,2
DF0885
Синус острого угла A треугольника ABC равен $frac{3sqrt7}8$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (3√7/8)2 = 1 – 63/64 = 1-0,984375 = 0,015625
cosA = 0,125Ответ: 0,125
Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.
D56817
Синус острого угла A треугольника ABC равен 4/5 . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (4/5)2 = 1 – 16/25 = 1-0,64 = 0,36
cosA = 0,6Ответ: 0,6
F548B1
Синус острого угла A треугольника ABC равен $frac{sqrt7}4$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√7/4)2 = 1 – 7/16 = 1-0,4375 = 0,5625
cosA = 0,75Ответ: 0,75
F6FBB5
Синус острого угла A треугольника ABC равен 3/5 . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (3/5)2 = 1 – 9/25 = 1-0,36 = 0,64
cosA = 0,8Ответ: 0,8
4257EE
Синус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√19/10)2 = 1 – 19/100 = 1-0,19 = 0,81
cosA = 0,9Ответ: 0,9
DC7D62
Синус острого угла A треугольника ABC равен $frac{sqrt{15}}4$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 – sin2A =1 – (√15/4)2 = 1 – 15/16 = 1-0,9375 = 0,0625
cosA = 0,25Ответ: 0,25
11D7EC
Косинус острого угла A треугольника ABC равен $frac{sqrt{21}}5$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√21/5)2 = 1 – 21/25 = 1-0,84 = 0,16
sinA = 0,4Ответ: 0,4
4BD96F
Косинус острого угла A треугольника ABC равен $frac{3sqrt{11}}{10}$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (3√11/10)2 = 1 – 99/100 = 1-0,99 = 0,01
sinA = 0,1Ответ: 0,1
EE565F
Косинус острого угла A треугольника ABC равен $frac{sqrt{91}}{10}$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√91/10)2 = 1 – 91/100 = 1-0,91 = 0,09
sinA = 0,3Ответ: 0,3
EE4155
Косинус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (2√6/5)2 = 1 – 24/25 = 1-0,96 = 0,04
sinA = 0,2Ответ: 0,2
2657CA
Косинус острого угла A треугольника ABC равен $frac{3sqrt7}8$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (3√7/8)2 = 1 – 63/64 = 1-0,984375 = 0,015625
sinA = 0,125Ответ: 0,125
Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.
857A3B
Косинус острого угла A треугольника ABC равен 4/5. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (4/5)2 = 1 – 16/25 = 1-0,64 = 0,36
sinA = 0,6Ответ: 0,6
588CA0
Косинус острого угла A треугольника ABC равен $frac{sqrt7}4$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√7/4)2 = 1 – 7/16 = 1-0,4375 = 0,5625
sinA = 0,75Ответ: 0,75
5AC6CD
Косинус острого угла A треугольника ABC равен 3/5. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (3/5)2 = 1 – 9/25 = 1-0,36 = 0,64
sinA = 0,8Ответ: 0,8
3B3235
Косинус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√19/10)2 = 1 – 19/100 = 1-0,19 = 0,81
sinA = 0,9Ответ: 0,9
4D93A9
Косинус острого угла A треугольника ABC равен $frac{sqrt{15}}4$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 – cos2A =1 – (√15/4)2 = 1 – 15/16 = 1-0,9375 = 0,0625
sinA = 0,25Ответ: 0,25
A426BF
Найти площадь треугольника по двум сторонам и углу между ними
Вспоминаем формулу нахождения площади треугольника по двум сторонам и углу между ними:
S=1/2аb•sinγ, где а и b – стороны треугольника, γ – угол между ними.
Подставляем известные величины и считаем.
Формула так же есть в справочных материалах ОГЭ, на экзамене можете ими воспользоваться.
В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=6*10*1/3=20
Ответ: 20
D8DE10
В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=6*12*1/4=18
Ответ: 18
510B5D
В треугольнике ABC известно, что AB=20, BC=7, sin∠ABC=2/5. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=20*7*2/5=56
Ответ: 56
21430B
В треугольнике ABC известно, что AB=15, BC=8, sin∠ABC=5/6. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=15*8*5/6=100
Ответ: 100
770975
В треугольнике ABC известно, что AB=14, BC=5, sin∠ABC=6/7. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=14*5*6/7=60
Ответ: 60
845EFC
В треугольнике ABC известно, что AB=12, BC=20, sin∠ABC=5/8. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*20*5/8=150
Ответ: 150
34F484
В треугольнике ABC известно, что AB=12, BC=15, sin∠ABC=4/9. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*15*4/9=80
Ответ: 80
86F9F5
В треугольнике ABC известно, что AB=16, BC=25, sin∠ABC=3/10. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=16*25*3/10=120
Ответ: 120
6B1EDE
В треугольнике ABC известно, что AB=9, BC=16, sin∠ABC=7/12. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=9*16*7/12=84
Ответ: 84
521C5A
В треугольнике ABC известно, что AB=12, BC=10, sin∠ABC=8/15. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*10*8/15=64
Ответ: 64
3A3D0B
Найти косинус угла, если известны 3 стороны треугольника

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
а2 = b2 + с2 – 2bс • cosα
Нужно выразить косинус и подставить известные величины.
Эта формула так же будет у вас под рукой на экзамене в справочных материалах ОГЭ.
В треугольнике АВС известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
cosα = (82 +102 + 122) : 2*8*10 = 164/160 = 1,025Ответ: 1,025
40840C
В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
112015
В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
6E8D8A
В треугольнике ABC известно, что AB=5, BC=10, AC=11. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
844A89
В треугольнике ABC известно, что AB=6, BC=7, AC=8. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
79B29A
В треугольнике ABC известно, что AB=5, BC=6, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
6557F1
В треугольнике ABC известно, что AB=6, BC=8, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
B5CF05
В треугольнике ABC известно, что AB=7, BC=8, AC=13. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
91941D
В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
755B8F
В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 – 2bс • cosα
2bс • cosα = b2 + с2 – а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
05C64C
Найти синус по двум сторонам
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. И тот, и другой, известны. Подставляем и считаем.
В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/10 = 0,6
Ответ: 0,6
A67245
В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 4/5 = 0,8
Ответ: 0,8
46D9DF
В треугольнике ABC угол C равен 90°, AC=7, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 7/25 = 0,28
Ответ: 0,28
6DA700
В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 24/25 = 0,96
Ответ: 0,96
C7A2A0
В треугольнике ABC угол C равен 90°, AC=6, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/20 = 0,3
Ответ: 0,3
ED2D47
В треугольнике ABC угол C равен 90°, AC=11, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 11/20 = 0,55
Ответ: 0,55
F1D3F8
В треугольнике ABC угол C равен 90°, AC=8, AB=40. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 8/40 = 0,2
Ответ: 0,2
CDC6C7
В треугольнике ABC угол C равен 90°, AC=16, AB=40. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 16/40 = 0,4
Ответ: 0,4
20BC46
В треугольнике ABC угол C равен 90°, AC=9, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 9/25 = 0,36
Ответ: 0,36
E2F916
В треугольнике ABC угол C равен 90°, AC=13, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 13/20 = 0,65
Ответ: 0,65
2C2621
Найти косинус по двум сторонам треугольника
Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. Подставляем известные значения и считаем.
В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 8/10 = 0,8
Ответ: 0,8
36727A
В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 3/5 = 0,6
Ответ: 0,6
E4988D
В треугольнике ABC угол C равен 90°, BC=14, AB=50. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/50 = 0,28
Ответ: 0,28
B9AA7C
В треугольнике ABC угол C равен 90°, BC=72, AB=75. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 72/75 = 0,96
Ответ: 0,96
6E5515
В треугольнике ABC угол C равен 90°, BC=14, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/20 = 0,7
Ответ: 0,7
E812C8
В треугольнике ABC угол C равен 90°, BC=9, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 9/20 = 0,45
Ответ: 0,45
C759C5
В треугольнике ABC угол C равен 90°, BC=30, AB=40. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 30/40 = 0,75
Ответ: 0,75
8854A8
В треугольнике ABC угол C равен 90°, BC=26, AB=40. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 26/40 = 0,65
Ответ: 0,65
C5CD1E
В треугольнике ABC угол C равен 90°, BC=16, AB=25. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 16/25 = 0,64
Ответ: 0,64
C3A5F2
В треугольнике ABC угол C равен 90°, BC=7, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 7/20 = 0,35
Ответ: 0,35
D58395
Найти тангенс угла по двум катетам
Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Подставляем значения катетов и считаем.
В треугольнике ABC угол C равен 90°, BC=5, AC=2. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 2/5 = 0,4
Ответ: 0,4
98C7DF
В треугольнике ABC угол C равен 90°, BC=5, AC=3. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/5 = 0,6
Ответ: 0,6
22FD03
В треугольнике ABC угол C равен 90°, BC=10, AC=7. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 7/10 = 0,7
Ответ: 0,7
C18053
В треугольнике ABC угол C равен 90°, BC=10, AC=8. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 8/10 = 0,8
Ответ: 0,8
33DA26
В треугольнике ABC угол C равен 90°, BC=15, AC=3. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/15 = 0,2
Ответ: 0,2
DD620C
В треугольнике ABC угол C равен 90°, BC=9, AC=27. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 27/9 = 3
Ответ: 3
342F0C
В треугольнике ABC угол C равен 90°, BC=5, AC=20. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 20/5 = 4
Ответ: 4
B800B8
В треугольнике ABC угол C равен 90°, BC=3, AC=18. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 18/3 = 6
Ответ: 6
FF498A
В треугольнике ABC угол C равен 90°, BC=4, AC=28. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 28/4 = 7
Ответ: 7
C9E181
В треугольнике ABC угол C равен 90°, BC=7, AC=35. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 35/7 = 5
Ответ: 5
0663D4
Задачи ОГЭ с развернутым ответом
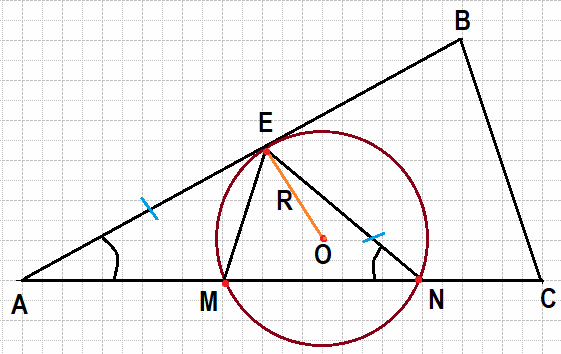
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 4 и 15 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{15}}4$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 4*15
АE = $sqrt{4ast15}$= $sqrt{60}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 – 2AE*AM*cos∠BAC
EM2 = $sqrt{60}$2 +42 – 2*$sqrt{60}$*4*$frac{sqrt{15}}4$= 60+16-2*$sqrt{60}$*$sqrt{15}$=76-2*30=16
EM = $sqrt{16}$ =4из той же теоремы найдем
EN2 = AE2+AN2 – 2AE*AN*cos∠BAC
EN2 = $sqrt{60}$2 +152 – 2*$sqrt{60}$*15*$frac{sqrt{15}}4$=60+225-($sqrt{900}$*15)/2=285-225=60
EN = $sqrt{60}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{60}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{15}}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{15}}4right)^2\sinangle ENA^2;=;1;-;frac{15}{16}\sinangle ENA^2;=;frac1{16}\sinangle ENA;=frac14\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2astsinangle;E;N;A};;=frac4{2ast{displaystylefrac14}}=8\\\\$
Ответ: 8
F41EBF
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 12 и 21 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt7}4$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 12*21
АE = $sqrt{12ast21}$= $sqrt{252}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 – 2AE*AM*cos∠BAC
EM2 = $sqrt{252}$2 +122 – 2*$sqrt{252}$*12*$frac{sqrt7}4$= 252+144-2*$sqrt{252}$*12*$frac{sqrt7}4$=396-252=$sqrt{144}$
EM = $sqrt{144}$ =12из той же теоремы найдем
EN2 = AE2+AN2 – 2AE*AN*cos∠BAC
EN2 = $sqrt{252}$2 +212 – 2*$sqrt{252}$*21*$frac{sqrt7}4$=252+441-441=252
EN = $sqrt{252}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{252}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt7}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt7}4right)^2\sinangle ENA^2;=;1;-;frac7{16}\sinangle ENA^2;=;frac9{16}\sinangle ENA^;=frac34\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac{12}{2{displaystylefrac34}}=frac{48}6=8$
Ответ: 8
23C5ED
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 8 и 30 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{15}}4$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 8*30
АE = $sqrt{8ast30}$= $sqrt{240}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 – 2AE*AM*cos∠BAC
EM2 = $sqrt{240}$2 +82 – 2*$sqrt{240}$*8*$frac{sqrt{15}}4$=240+64-240=64
EM = 8из той же теоремы найдем
EN2 = AE2+AN2 – 2AE*AN*cos∠BAC
EN2 = $sqrt{240}$2 +302 – 2*$sqrt{240}$*30*$frac{sqrt{15}}4$=240+900-900=240
EN = $sqrt{240}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{240}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{15}}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{15}}4right)^2\sinangle ENA^2;=;1;-;frac{15}{16}\sinangle ENA^2;=;frac1{16}\sinangle ENA;=frac14\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac8{2{displaystylefrac14}}=frac{32}2=16$
Ответ: 16
1D3A90
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 18 и 22 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{11}}6$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 18*22
АE = $sqrt{18ast22}$= $sqrt{396}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 – 2AE*AM*cos∠BAC
EM2 = $sqrt{396}$2 +182 – 2*$sqrt{396}$*18*$frac{sqrt{11}}6$=396+324-396=324
EM = 18из той же теоремы найдем
EN2 = AE2+AN2 – 2AE*AN*cos∠BAC
EN2 = $sqrt{396}$2 +222 – 2*$sqrt{396}$*22*$frac{sqrt{11}}6$=396+484-484=396
EN = $sqrt{396}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{396}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{11}}6right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{11}}6right)^2\sinangle ENA^2;=;1;-;frac{11}{36}\sinangle ENA^2;=;frac{25}{36}\sinangle ENA;=frac56\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac18{2{displaystylefrac56}}=frac{21.6}2=10.8$
Ответ: 10.8
35C690
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 18 и 40 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt5}3$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 18*40
АE = $sqrt{18ast40}$= $sqrt{720}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 – 2AE*AM*cos∠BAC
EM2 = $sqrt{720}$2 +182 – 2*$sqrt{720}$*18*$frac{sqrt{5}}3$=720+324-720=324
EM = 18из той же теоремы найдем
EN2 = AE2+AN2 – 2AE*AN*cos∠BAC
EN2 = $sqrt{720}$2 +402 – 2*$sqrt{720}$*40*$frac{sqrt{5}}3$=720+1600-1600=720
EN = $sqrt{720}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{720}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt5}3right)^2;=1\sinangle ENA^2=1-left(frac{sqrt5}3right)^2\sinangle ENA^2;=;1;-;frac59\sinangle ENA^2;=;frac49\sinangle ENA;=frac23\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac18{2{displaystylefrac23}}=frac{54}4=13.5$
Ответ: 13.5
CCD611
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 35 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{35}}6$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 9*35
АE = $sqrt{9ast35}$= $sqrt{315}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 – 2AE*AM*cos∠BAC
EM2 = $sqrt{315}$2 +92 – 2*$sqrt{315}$*9*$frac{sqrt{35}}6$=315+81-315=81
EM = 9из той же теоремы найдем
EN2 = AE2+AN2 – 2AE*AN*cos∠BAC
EN2 = $sqrt{315}$2 +352 – 2*$sqrt{315}$*35*$frac{sqrt{35}}6$=315+1225-1225=315
EN = $sqrt{315}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{315}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{35}}6right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{35}}6right)^2\sinangle ENA^2;=;1;-;frac{35}{36}\sinangle ENA^2;=;frac1{36}\sinangle ENA;=frac16\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac9{2{displaystylefrac16}}=frac{54}2=27$
Ответ: 27
65B0A0
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 12 и 45 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{15}}4$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 12*45
АE = $sqrt{12ast45}$= $sqrt{540}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 – 2AE*AM*cos∠BAC
EM2 = $sqrt{540}$2 +122 – 2*$sqrt{540}$*12*$frac{sqrt{15}}4$=540+144-540=144
EM = 12из той же теоремы найдем
EN2 = AE2+AN2 – 2AE*AN*cos∠BAC
EN2 = $sqrt{540}$2 +452 – 2*$sqrt{540}$*45*$frac{sqrt{15}}4$=540+2025-2025=540
EN = $sqrt{540}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{540}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{15}}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{15}}4right)^2\sinangle ENA^2;=;1;-;frac{15}{16}\sinangle ENA^2;=;frac1{16}\sinangle ENA;=frac14\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac{12}{2{displaystylefrac14}}=frac{48}2=24$
Ответ: 24
36C43D
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 32 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{2sqrt2}3$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 9*32
АE = $sqrt{9ast32}$= $sqrt{288}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 – 2AE*AM*cos∠BAC
EM2 = $sqrt{288}$2 +92 – 2*$sqrt{288}$*9*$frac{2sqrt2}3$=288+81-288=81
EM = 9из той же теоремы найдем
EN2 = AE2+AN2 – 2AE*AN*cos∠BAC
EN2 = $sqrt{288}$2 +322 – 2*$sqrt{288}$*32*$frac{2sqrt2}3$=288+1024-1024=288
EN = $sqrt{288}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{288}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{2sqrt2}3right)^2;=1\sinangle ENA^2=1-left(frac{2sqrt2}3right)^2\sinangle ENA^2;=;1;-;frac89\sinangle ENA^2;=;frac13\sinangle ENA;=frac13\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac9{2{displaystylefrac13}}=frac{27}2=13,5$
Ответ: 13,5
A077B6
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 24 и 42 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt7}4$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 24*42
АE = $sqrt{24ast42}$= $sqrt{1008}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 – 2AE*AM*cos∠BAC
EM2 = $sqrt{1008}$2 +242 – 2*$sqrt{1008}$*24*$frac{sqrt7}4$=1008+576-1008=576
EM = 24из той же теоремы найдем
EN2 = AE2+AN2 – 2AE*AN*cos∠BAC
EN2 = $sqrt{1008}$2 +422 – 2*$sqrt{1008}$*42*$frac{sqrt7}4$=1008+1764-1764=1008
EN = $sqrt{1008}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{1008}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt7}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt7}4right)^2\sinangle ENA^2;=;1;-;frac7{16}\sinangle ENA^2;=;frac9{16}\sinangle ENA;=frac34\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac{24}{2{displaystylefrac34}}=frac{96}3=32$
Ответ: 32
973563
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 36 и 44 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{11}}6$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 36*44
АE = $sqrt{36ast44}$= $sqrt{1584}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 – 2AE*AM*cos∠BAC
EM2 = $sqrt{1584}$2 +362 – 2*$sqrt{1584}$*36*$frac{sqrt11}6$=1584+1296-1584=1296
EM = 36из той же теоремы найдем
EN2 = AE2+AN2 – 2AE*AN*cos∠BAC
EN2 = $sqrt{1584}$2 +442 – 2*$sqrt{1584}$*44*$frac{sqrt11}6$=1584+1936-1936=1584
EN = $sqrt{1584}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{1584}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{11}}6right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{11}}6right)^2\sinangle ENA^2;=;1;-;frac{11}{36}\sinangle ENA^2;=;frac{25}{36}\sinangle ENA;=frac56\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac{36}{2{displaystylefrac56}}=frac{216}{10}=21.6$
Ответ: 21.6
A142B2
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 16 и 39 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{39}}8$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 16*39
АE = $sqrt{16ast39}$= $sqrt{624}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 – 2AE*AM*cos∠BAC
EM2 = $sqrt{624}$2 +162 – 2*$sqrt{624}$*16*$frac{sqrt{39}}8$=624+256-624=256
EM = 16из той же теоремы найдем
EN2 = AE2+AN2 – 2AE*AN*cos∠BAC
EN2 = $sqrt{624}$2 +392 – 2*$sqrt{624}$*39*$frac{sqrt{39}}8$=624+1521-1521=624
EN = $sqrt{624}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{624}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{39}}8right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{39}}8right)^2\sinangle ENA^2;=;1;-;frac{39}{64}\sinangle ENA^2;=;frac{25}{64}\sinangle ENA;=frac58\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac{39}{2{displaystylefrac58}}=frac{312}{10}=31.2$
Ответ: 31.2
553368
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{11}}6$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 9*11
АE = $sqrt{9ast11}$= 3$sqrt{11}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 – 2AE*AM*cos∠BAC
EM2 = 32$sqrt{11}$2 +92 – 2*3$sqrt{11}$*9*$frac{sqrt{11}}6$=9*11+81-11*9=81
EM = 9из той же теоремы найдем
EN2 = AE2+AN2 – 2AE*AN*cos∠BAC
EN2 = 32$sqrt{11}$2 +112 – 2*3$sqrt{11}$*11*$frac{sqrt{11}}6$=32$sqrt{11}$2 +121-121 = 32$sqrt{11}$2
EN = 3$sqrt{11}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = 3$sqrt{11}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle B;A;C^2+cosangle B;A;C^2=1\sinangle B;A;C^2=1-cosangle B;A;C^2\sinangle B;A;C^2=1-frac{sqrt{11}}6^2\sinangle B;A;C^2;=;1-frac{11}{36}\sinangle B;A;C^2;=frac{25}{36}\sinangle B;A;C;=;frac56\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2astsinangle;B;A;C};;=frac9{2ast{displaystylefrac56}}=5.4\\\\$
Ответ: 5.4
B83171
Синусом угла в прямоугольном треугольнике называют отношение противолежащего катета к гипотенузе.
Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.
Для простоты запоминания можно дать такое определение: синус угла — это отношение дальнего от рассматриваемого угла катета к гипотенузе.
В случае с рисунком, описанным выше: sinα=acsinalpha=frac{a}{c}
В треугольнике, один из углов которого равен 90 градусам, известен катет при угле αalpha и равен он 3 см3text{ см}. Также дано произведение длин катетов и равно 12 см212text{ см}^2. Найдите синус угла αalpha.
Решение
Сначала нужно найти длину неизвестного нам катета. Для этого воспользуемся данным нам произведением. Обозначим неизвестный катет за xx. Тогда, по условию задачи:
3⋅x=123cdot x=12
x=123=4x=frac{12}{3}=4
a=x=4a=x=4
По теореме Пифагора найдем гипотенузу:
a2+b2=c2a^2+b^2=c^2
42+32=c24^2+3^2=c^2
25=c225=c^2
c=5c=5
sinα=ac=45=0.8sinalpha=frac{a}{c}=frac{4}{5}=0.8
Ответ
0.80.8
Вычислите синус 45 градусов.
Решение
Для этого воспользуемся тригонометрической таблицей углов. Находим, что:
sin45∘=π4=0.785sin 45^circ=frac{pi}{4}=0.785
Ответ
0.7850.785
Если в задаче известен косинус угла и нужно найти его синус, то наличие известных длин катетов и гипотенузы не обязательны. Достаточно просто воспользоваться основным тригонометрическим тождеством, которое имеет следующий вид:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
αalpha — любой угол.
Квадрат косинуса угла в треугольнике равен 0.8. Найдите синус данного угла.
Решение
Воспользуемся основным тригонометрическим тождеством:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
sin2α+0.8=1sin^2alpha+0.8=1
sin2α=0.2sin^2alpha=0.2
sinα=0.2sinalpha=sqrt{0.2}
sinα≈0.447sinalphaapprox0.447
Ответ
0.4470.447
Испытываете проблемы с вычислением синуса? Оформите задачу по математике на заказ у наших экспертов!