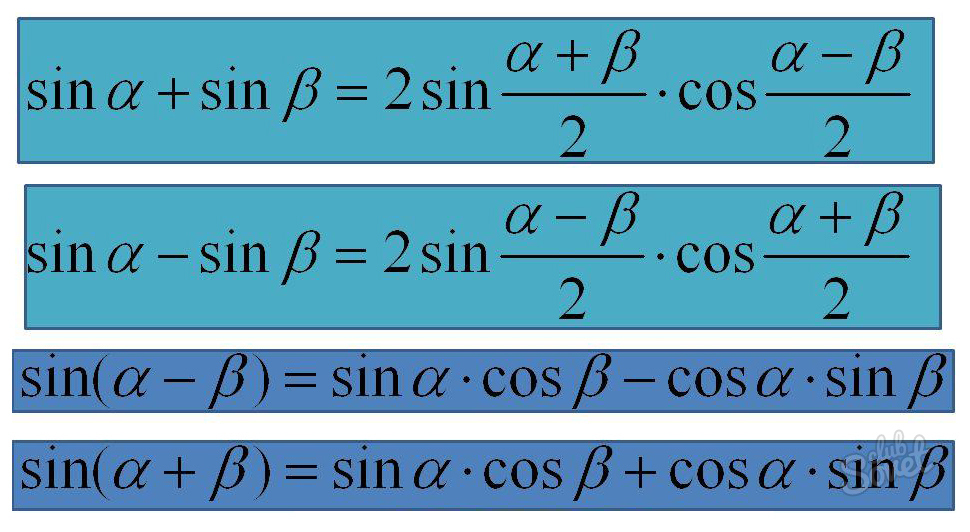В статье мы расскажем, как находить значения:
(cos300^°), (sin(-540^°)), (cos 510^°), (sin(-135^°))
и других тригонометрических выражений без тригонометрической таблицы.
Как вычисляются синусы и косинусы углов?
Чтобы вычислить косинус и синус некоторого угла нужно:
1. Отложить этот угол на тригонометрическом круге и определить какая точка соответствует этому углу;
2. Найти абсциссу и ординату этой точки. Косинус угла равен – абсциссе, а синус угла – ординате.
Предположим, стоит задача найти косинус и синус угла (30^°). Отложим на круге угол в (30^°) и найдем какая точка соответствует этому углу.
Если построить все точно, то видно, что абсцисса точки равна (0,866)… , что равно числу (frac{sqrt{3}}{2}) , а ордината равна (0,5), то есть (frac{1}{2}).

Получается, (cos 30^° = frac{sqrt{3}}{2}), а (sin30^° =frac{1}{2}).
Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:
В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».
Обычно на осях не отмечают (0,1); (0,2); (0,3) и т.д., а сразу наносят стандартные значения для синуса и косинуса: (±frac{1}{2}=±0,5); (±frac{sqrt{2}}{2} ≈±0,707); (±frac{sqrt{3}}{2} ≈±0,866).
Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.
Как отметить любой угол на тригонометрическом круге?
Для этого нужно знать несколько фактов:
- Начало отсчета находится в крайней правой точке окружности;
-
Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;
-
Градусная мера окружности равна (360^°), полуокружности (180^°), а четверти (90^°);
-
Углы в (0^°), (30^°), (45^°) и (60^°) выглядят так:


- Одна точка может соответствовать разным углам;
- Угол может быть больше (360^°). В этом случае он просто сделает полный оборот и пойдет дальше. Фактически, можно (360^°) просто отбросить и откладывать тот угол, который останется – в итоге вы всё равно окажетесь в той же точке.
Пример. Отметьте угол в (90^° ) и (-90^°).
Решение:

Пример. Отметьте угол в (225^° ) и (-135^°).
Решение: (225^°=180^°+45^°)
(-135^°=-90^°-45^°)

Пример. Отметьте угол в (420^° ) и (-390^°).
Решение: (420^°=360^°+60^°)
(-390^°=-360^°-30^°)


Задание 1. Отметьте на окружности точки соответствующие углам: (720^°), (225^°), (300^°), (870^°), (900^°), (-330^°), (-630^°), (-210^°).
Как находить синус и косинус любого угла?
Простой алгоритм:
- Начертите тригонометрический круг и оси косинусов и синусов (не обязательно рисовать прям аккуратно, как на картинке ниже, можно и некрасиво – главное не запутаться какая точка к какому значению относится).
- Отложите на круге угол, синус и косинус которого надо найти, и определите точку на круге, соответствующую этому углу.
- Найдите координаты точки, используя картинку ниже.

Пример. Вычислите (sin300^°) и (cos300^°) .
Решение: (300^°=360^°-60^°)

(cos 300^°=frac{1}{2}), (sin{300^°}=-frac{sqrt{3}}{2}).
Пример . Вычислите (sin(-540^°)) и (cos(-540^°)) .
Решение. (-540^°=-360^°-180^°).

(-540^°) на тригонометрическом круге совпадает с (-1) на оси косинусов. То есть, координаты этой точки: ((-1;0)). Значит, (cos(-540^°)=-1), а (sin(-540^° )=0).
Да, имея перед глазами тригонометрический круг, вычислять синусы и косинусы любых углов легко. Возможно, у вас возник вопрос: «а что делать, если круга нет? Как делать такие вычисления на ЕГЭ?». Ответ очевиден – нарисовать круг самому! Для этого надо понять, как располагаются значения на нем. Подробную методику того, как это делается я рассказывала в этой статье.
Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).

Примеры вычисления синуса и косинуса из ЕГЭ
В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.
Пример . Найдите значение выражения (-18sqrt{2}sin(-135^°)).
Решение. (-135^°=-90^°-45^°)

Получается (-18sqrt{2} sin(-135^° )=-18sqrt{2}cdot-frac{sqrt{2}}{2}=frac{18cdotsqrt{2}cdotsqrt{2}}{2}=9cdot 2=18.)
Ответ: (18).
Пример . Найдите значение выражения (54sqrt{3}cos(510^°)).
Решение. (510^°=360^°+150^°=360^°+180^°-30^°.)

(54sqrt{3}cos(510^°)=54sqrt{3}cdot(-frac{sqrt{3}}{2})=-frac{54cdot sqrt{3}cdot sqrt{3}}{2}=-27cdot 3=-81.)
Ответ: (-81).
Смотрите также:
Как найти тангенс и котангенс без тригонометрической таблицы? Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?
Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов
Как найти синус угла в треугольнике? Не в прямоугольном, в любом
Если рассматриваемый треугольник является прямоугольным, то можно использовать базовое определение тригонометрической функции синуса для острых углов. По определению синусом угла называют соотношение длины катета, лежащего напротив этого угла, к длине гипотенузы этого треугольника. То есть, если катеты имеют длину А и В, а длина гипотенузы равна С, то синус угла α, лежащего напротив катета А, определяйте по формуле α=А/С, а синус угла β, лежащего напротив катета В – по формуле β=В/С. Синус третьего угла в прямоугольном треугольнике находить нет необходимости, так как угол, лежащий напротив гипотенузы всегда равен 90°, а его синус всегда равен единице.
2
Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α). Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С) . А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С) ²).
3
Воспользуйтесь для нахождения синуса угла двумя разными формулами расчета площади треугольника, в одной из которых задействованы только длины его сторон, а в другой – длины двух сторон и синус угла между ними. Так как результаты их будут равны, то из тождества можно выразить синус угла. Формула нахождения площади через длины сторон (формула Герона) выглядит так: S=¼*√((А+В+С) *(В+С-А) *(А+С-В) *(А+В-С)) . А вторую формулу можно написать так: S=А*В*sin(γ). Подставьте первую формулу во вторую и составьте формулу для синуса угла, лежащего напротив стороны С: sin(γ)= ¼*√((А+В+С) *(В+С-А) *(А+С-В) *(А+В-С) /(А*В)) . Синусы двух других углов можно найти по аналогичным формулам.
Синус угла в обычном треугольнике
Синус (sin) – это одна из прямых тригонометрических функций. Подробнее о ней можно узнать из нашей статьи Что такое синус.
Синус угла в прямоугольном треугольнике
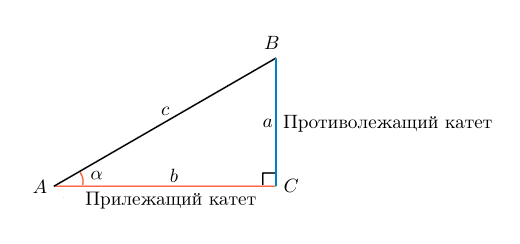
Прежде чем выяснять, как найти синус угла, необходимо определиться с условными обозначениями. Пусть в прямоугольном треугольнике:
- α – острый угол, синус которого нужно найти;
- с – гипотенуза;
- b – прилежащий катет;
- a – противолежащий катет.
Тогда чтобы найти синус острого угла прямоугольного треугольника, достаточно посчитать соотношение длины противолежащего катета к длине гипотенузы: sin(α) = a/c. При этом стоит запомнить, что sin 90° всегда равен 1.
Синус угла в произвольном треугольнике
Находить синус угла в произвольном треугольнике проще всего с использованием теоремы косинусов (cos): квадрат длины любой стороны равен сумме квадратов длин двух других сторон за минусом их удвоенного произведения на косинус угла между ними.
a² = b² + c² – 2*b*c*cos(α)
Из данной формулы можно найти косинус: cos(α) = (b² + c² – a²)/(2*b*c)
А поскольку для одного и того же угла sin(α)² + cos(α)² = 1 и это константа, то можно вывести формулу для определения синуса:
Более детально нахождение синуса угла с использованием косинуса рассмотрено в нашей статье Как найти синус, если известен косинус.
Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
для угла A треугольника ABC
противолежащий катет — это BC.
Соответственно, синус угла A в треугольнике ABC — это
Для угла B треугольника ABC
противолежащим является катет AC.
Соответственно, синус угла B в треугольнике ABC
равен отношению AC к AB:
Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы. Длины отрезков выражаются положительными числами, поэтому синус угла треугольника также является положительным числом.
Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.
Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:
Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.
1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.
2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.
Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.
2
Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α). Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С) . А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С) ²).
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии “на пальцах”.
Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
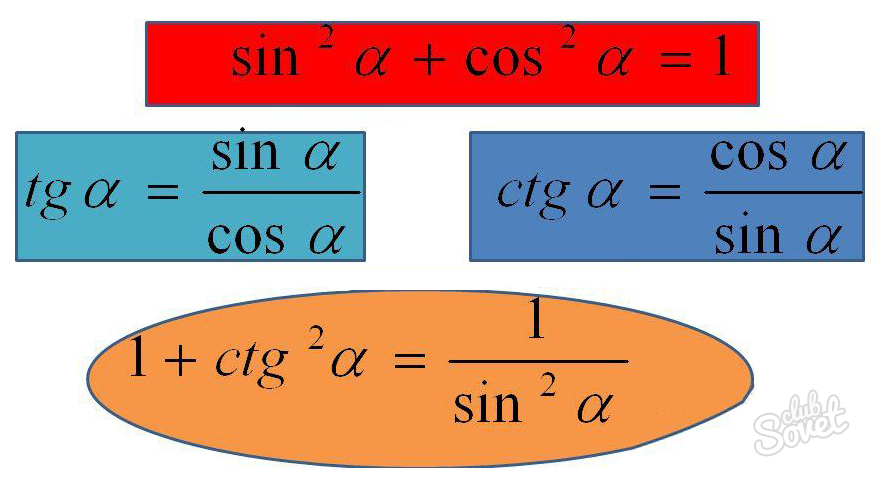
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
Или в виде формул:
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
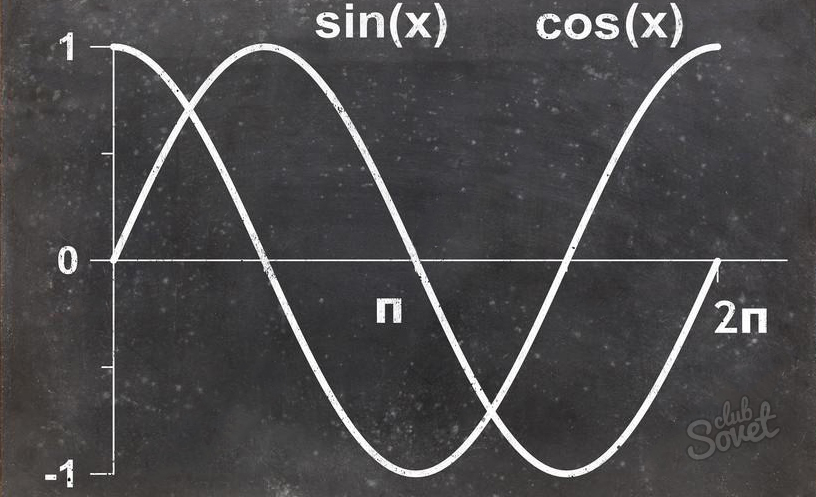
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
| 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|
| sin | 0 | 1 | √3 | – |
| ctg | – | √3 | 1 |
Принцип повтора знаков тригонометрических функцийУгол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны. Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно. Тригонометрический кругУглы в радианахДля математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π . Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций. [spoiler title=”источники:”] http://dudom.ru/kompjutery/sinus-ugla-v-obychnom-treugolnike/ http://matematika.club/articles/trigonometry/ [/spoiler] |
Можно найти Синус/косинус/тангенс острого угла (не зная градусов) не прямоугольного треугольника
Ученик
(96),
закрыт
1 год назад
Noname
Гений
(69596)
1 год назад
Есть теорема косинусов, которая работает для любого треугольника (в том числе для прямоугольного, тупоугольного, даже для вырожденного). По длинам трех сторон можно найти косинус угла.
Кстати, если вы попытаетесь применить ее в прямоугольном треугольнике, то получите теорему Пифагора (потому что т. Пифагора – частный случай теоремы косинусов).
Андрей Панарин
Искусственный Интеллект
(188109)
1 год назад
Всегда можно из одной вершины опустить высоту, которая поделит обычный треугольник на два прямоугольных. Затем рассчитать стороны нужного нам прямоугольного треугольника (того, в котором есть нужный нам угол) и по их соотношениям определить синус, косинус и тангенс нужного нам угла.
Синусом угла в прямоугольном треугольнике называют отношение противолежащего катета к гипотенузе.
Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.
Для простоты запоминания можно дать такое определение: синус угла — это отношение дальнего от рассматриваемого угла катета к гипотенузе.
В случае с рисунком, описанным выше: sinα=acsinalpha=frac{a}{c}
В треугольнике, один из углов которого равен 90 градусам, известен катет при угле αalpha и равен он 3 см3text{ см}. Также дано произведение длин катетов и равно 12 см212text{ см}^2. Найдите синус угла αalpha.
Решение
Сначала нужно найти длину неизвестного нам катета. Для этого воспользуемся данным нам произведением. Обозначим неизвестный катет за xx. Тогда, по условию задачи:
3⋅x=123cdot x=12
x=123=4x=frac{12}{3}=4
a=x=4a=x=4
По теореме Пифагора найдем гипотенузу:
a2+b2=c2a^2+b^2=c^2
42+32=c24^2+3^2=c^2
25=c225=c^2
c=5c=5
sinα=ac=45=0.8sinalpha=frac{a}{c}=frac{4}{5}=0.8
Ответ
0.80.8
Вычислите синус 45 градусов.
Решение
Для этого воспользуемся тригонометрической таблицей углов. Находим, что:
sin45∘=π4=0.785sin 45^circ=frac{pi}{4}=0.785
Ответ
0.7850.785
Если в задаче известен косинус угла и нужно найти его синус, то наличие известных длин катетов и гипотенузы не обязательны. Достаточно просто воспользоваться основным тригонометрическим тождеством, которое имеет следующий вид:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
αalpha — любой угол.
Квадрат косинуса угла в треугольнике равен 0.8. Найдите синус данного угла.
Решение
Воспользуемся основным тригонометрическим тождеством:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
sin2α+0.8=1sin^2alpha+0.8=1
sin2α=0.2sin^2alpha=0.2
sinα=0.2sinalpha=sqrt{0.2}
sinα≈0.447sinalphaapprox0.447
Ответ
0.4470.447
Испытываете проблемы с вычислением синуса? Оформите задачу по математике на заказ у наших экспертов!
Тест по теме «Вычисление синуса»
Как найти синус?
Решение многих как алгебраических, так и геометрических задач невозможно без использования такой тригонометрической функции как синус. Для нахождения величины синуса можно использовать как собственно определение функции, так и соотношения тождеств тригонометрии, формулы приведения, а также теорему синусов. С каждым из данных способов более подробно и познакомит данная статья.
1
Нахождение величины синуса по определению
Формулировка термина “синус” определяет данную тригонометрическую величину как соотношение определенных сторон прямоугольного треугольника – отношение катета, лежащего против искомого угла, к гипотенузе.
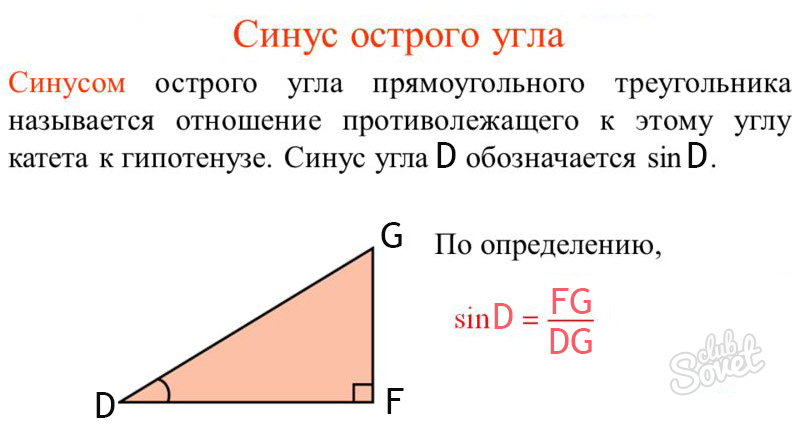
Рассмотрим ΔDFG, ∠DFG = 90°. Тогда:
- sinD = FG / DG,
- FG — противолежащий катет,
- DG — гипотенуза представленного треугольника.
2
Нахождение величины синуса через формулу теоремы синусов
Данная теорема является универсальной, т.к. позволяет установить соотношение между углами и сторонами не только прямоугольного, то и произвольного треугольника.
Рассмотрим ΔLMN,
- MN = l, NL = m, ML = n.
- ∠M = η, ∠N = μ, ∠L = γ.
Для произвольного треугольника ΔLMN верно соотношение l / sinL = m / sinM = n / sinN – каждая сторона треугольника пропорциональна синусу угла, напротив которого она располагается.
Обозначив радиус описанной около треугольника окружности через R, соотношение теоремы синусов справедливо в следующей форме:
l / sinL = m / sinM = n / sinN = 2R.
Из соотношения следует:
sinL = l / 2R,
sinM = m / 2R,
sinN = n / 2R.
3
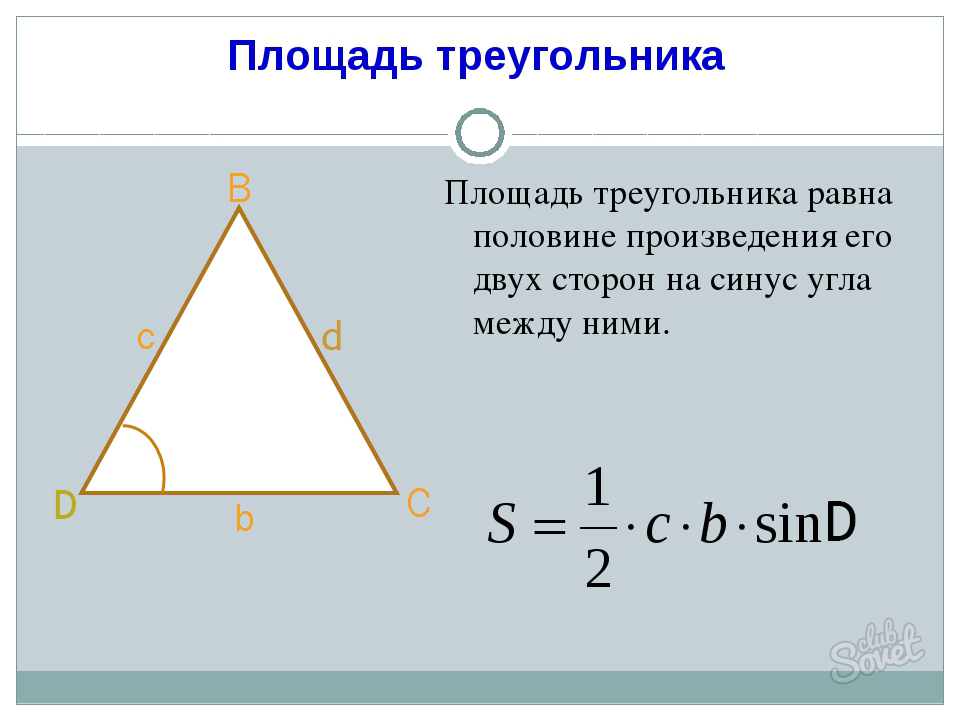
Нахождение величины синуса через площадь треугольника
Перед вами ΔDBC со сторонами
DB = c,
BC = d,
DC = b.
Для нахождения площади треугольника можно воспользоваться соотношением S = bc / 2sinD (или S = cd / 2sinB, или S = bd / 2sinC). Из этого следует, что:
- sinD = bc / 2S,
- sinB = cd / 2S,
- sinC = bd / 2S.
4
Нахождение величины синуса через тождества тригонометрии
Тождественные выражения справедливы для угла любой градусной меры.
- cos2φ + sin2φ = 1 ⇒ sin2φ = 1 — cos2φ ⇒ ΙsinφΙ = √ 1 — cos2φ ⇒ sinφ = ±√ 1 — cos2φ.
- tgφ = sinφ / cosφ ⇒ sinφ = cosφ * tgφ.
- ctgφ = cosφ / sinφ ⇒ sinφ = cosφ / ctgφ.
- 1/sin2φ = ctg2φ + 1 ⇒ sin2φ = 1 / (ctg2φ + 1) ⇒ ΙsinφΙ = 1 / √ctg2φ + 1 ⇒ sinφ = ± 1 / √ctg2φ + 1.
5
Нахождение величины синуса через формулы преобразования
- sin(η + μ) = sinη * cosμ + cosη * sinμ,
- sin(η – μ) = sinη * cosμ – cosη * sinμ,
- sinη + sinμ = 2sin((η + μ)/2) * cos((η – μ)/2),
- sinη – sinμ = 2cos((η + μ)/2) * sin((η – μ)/2)
- sinη * sinμ = (cos(η – μ) – cos(η + μ))/2,
- sinη = 2tg(η/2) / (1 + tg2(η/2)).
- sin2η =2sinη * cosη,
- sin3η =3sinη – 4sin3η.
6
Нахождение синуса угла – табличные величины
Воспользовавшись таблицей Брадиса, можно определить значение синуса для каждого угла в промежутке от 0° до 360°. Наиболее часто при решении задач школьного курса геометрии используются следующие табличные величины:
- sin0° = 0, sin90° = 1,
- sin30° = 1/2, sin180° = 0,
- sin60° = √3/2, sin270° = -1,
- sin45° = √2/2, sin360° = 0.