Как найти синус угла дифракционной решетки

Как определить угол дифракции

Световые волны отклоняются от своего прямолинейного пути при прохождении через малые отверстия или мимо таких же малых препятствий. Это явление возникает, когда размеры препятствий или отверстий сравнимы с длиной волны, и называется дифракцией. Задачи на определение угла отклонения света приходится решать чаще всего применительно к дифракционным решеткам – поверхностям, в которых чередуются прозрачные и непрозрачные участки одинаковых размеров.

Инструкция

Выясните период (d) дифракционной решетки – так называют суммарную ширину одной прозрачной (a) и одной непрозрачной (b) ее полос: d = a+b. Эту пару обычно называют одним штрихом решетки, а измеряют в количестве штрихов на один миллиметр. Например, дифракционная решетка может содержать 500 штрихов на 1 мм, и тогда d = 1/500.

Для вычислений имеет значение угол (α), под которым свет падает на дифракционную решетку. Он отсчитывается от нормали к поверхности решетки, а в формуле участвует синус этого угла. Если в исходных условиях задачи сказано, что свет падает по нормали (α=0), этой величиной можно пренебречь, так как sin(0°)=0.

Выясните длину волны (λ) падающего на дифракционную решетку света. Это одна из наиболее важных характеристик, определяющих угол дифракции. Нормальный солнечный свет содержит целый спектр длин волн, но в теоретических задачах и лабораторных работах, как правило, речь идет о точечном участке спектра – о «монохроматическом» свете. Видимой области соответствуют длины примерно от 380 до 740 нанометров. Например, один из оттенков зеленого цвета имеет длину волны, равную 550нм (λ=550).

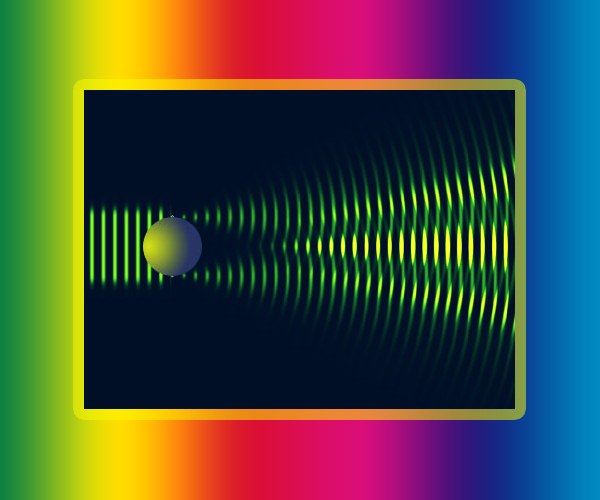
Прошедший через дифракционную решетку свет отклоняется на разные углы, образуя при этом неоднородную картину распределения с чередующимися максимумами и минимумами освещенности – дифракционный спектр. Каждому максимуму соответствует собственный угол дифракции. Выясните: угол которого максимума (k) требуется рассчитать. Отсчет ведется от нулевого – центрального – уровня. Например, условия могут требовать расчета искомой величины для второго (k=2) максимума дифракционного спектра.

Воспользуйтесь формулой, связывающей длину волны падающего на дифракционную решетку света с углом дифракции (φ) максимумов определенного порядка: d*(sin(φ)-sin(α)) = k*λ. Выведите из нее определение угла φ – у вас должно получиться такое равенство: φ = arcsin(sin(α)+(k*λ)/d). Подставьте определенные на предыдущих шагах значения в эту формулу и произведите расчеты.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Дифракционная
решётка —
оптический прибор, работающий по
принципу дифракции света,
представляет собой совокупность большого
числа регулярно расположенных штрихов
(щелей, выступов), нанесённых на некоторую
поверхность.

Виды
решёток

• Отражательные:
  Штрихи нанесены на зеркальную
  (металлическую) поверхность, и наблюдение
  ведется в отражённом свете

• Прозрачные:
  Штрихи нанесены на прозрачную поверхность
  (или вырезаются в виде щелей на
  непрозрачном экране), наблюдение ведется
  в проходящем свете.

Формулы

Расстояние,
через которое повторяются штрихи на
решётке, называют периодом дифракционной
решётки. Обозначают буквой d.

Если
известно число штрихов (N),
приходящихся на 1 мм решётки, то период
решётки находят по формуле: d =
1 / N мм.

Условия
интерференционных максимумов дифракционной
решётки, наблюдаемых под определёнными
углами, имеют вид:

где

d —
период решётки,

α —
угол максимума данного цвета,

k —
порядок максимума, то есть порядковый
номер максимума, отсчитанный от центра
картинки,

λ —
длина волны.

Дифракционная
решетка

Д
ифракция
на решетке происходит аналогично
дифракции на ще­ли. Однако при большом
числе близко расположенных параллель­ных
щелей дифракционные максимумы значительно
сужаются. Рас­стояние между
соответствующими точками соседних
щелей (или сумма ширины щели и промежутка
между щелями) называется постоянной,
или
периодом g
дифракционной
решетки. У хороших дифракционных решеток
число ще­лей на 1 мм достигает 1700.’

Если

α
макс — угол, определяющий направ­ление
на дифракционный ‘ максимум,

g
—
постоянная решетки,

— длина волны,

/
— расстояние от решетки до экрана,

а
—
расстояние до максимума к-го порядка,

то
в
соответствии
с рисунком

где
а
определяется
из условия tg
а
=
а/1.
Обратите
внимание:

1Синус
дифракционного угла пропорционален
длине волны. По­этому решетка в отличие
от призмы преломляет красный свет
сильнее
всего.

2
чем меньше постоянная решетки тем больше
угол дифракции при фиксированной длинны
волны

3
если постоянная дифракционной решетки
известна то по положению дифракционных
максимумов можно определить длину волны
света.

Уравнение,
описывающее дифракцию на решетке, можно
записать в виде:

m =
d
( sin
ф 
)

m-порядок
спектра

d-период
решётки

Для
того, чтобы в точке наблюдался
интерференционный максимум, разность
хода Δ между волнами, испущенными
соседними щелями, должна быть равна
целому числу длин волн:

Δ = d sin θm = mλ (m = 0, ±1, ±2, …).

Здесь d –
период решетки, m –
целое число, которое называется порядком
дифракционного максимума.
В тех точках экрана, для которых это
условие выполнено, располагаются так
называемые главные
максимумы дифракционной
картины.

В
фокальной плоскости линзы расстояние y_m от
максимума нулевого порядка (m = 0)
до максимума m-го
порядка при малых углах дифракции равно

где F –
фокусное расстояние.

В
оптическом диапазоне вследствие малости
длины волны размер зон Френеля оказывается
достаточно малым. Дифракционные явления
проявляются наиболее отчетливо, когда
на препятствии укладывается лишь
небольшое число зон:

Это
соотношение можно рассматривать
как критерий
наблюдения дифракции.
Если число зон Френеля, укладывающихся
на препятствии, становится очень большим,
дифракционные явления практически
незаметны:

Это
сильное неравенство определяет границу
применимости геометрической оптики.
Узкий пучок света, который в геометрической
оптике называется лучом, может быть
сформирован только при выполнении этого
условия. Таким образом, геометрическая
оптика является предельным случаем
волновой оптики.

34.
Поляризация
света – процесс упорядочения колебаний
вектора напряжённости электрического
поля световой волны при прохождении
света сквозь некоторые вещества (при
преломлении) или при отражении светового
потока.

Поляризатор
– вещество (или устройство) служащее
для преобразования естественного света
в плоскополяризованный.

Плоскость
поляризации – плоскость, проходящая
через направление колебаний светового
вектора плоскополяризованной волны и
направление распространения этой волны.

35.
Процессы
получения и преобразования поляризов.
света основаны на взаимодействиях света
с веществом, нарушающих осевую симметрию
светового луча. Для получения полностью
или частично поляризованного света
используется одно из трёх физ. явлений:
поляризация при отражении или преломлении
света на границе раздела двух изотропных
сред с разл. показателями преломления,
линейный дихроизм и двойное лучепреломление
.В первом случае анизотропия взаимодействия
света со средой определяется наличием
выделенной плоскости падения света и
различием коэф. отражения для компонент
светового луча, поляризованных параллельно
и перпендикулярно этой плоскости.

При
нормальном падении света на поверхность
раздела (когда положение плоскости
падения не определено) аксиальная
симметрия взаимодействия света со
средой не нарушается и поляризац.
преобразования светового пучка не
происходит. В соответствии с ф-лами
Френеля степень поляризации отражённой
и преломлённой компонент светового
пучка зависит от угла падения. Если
световой луч падает на границу раздела
под углом Брюстера (см. Брюстера закон),
то отражённый свет оказывается полностью
поляризованным. На этом основано действие
отражательных П. Осн. недостаток отражат.
П.- малость коэф. отражения – устраняется
при использовании многослойных
диэлектрич. покрытий (интерференционные
П.). Однако при этом сохраняются общие
для всех отражат. П. недостатки – сильная
зависимость степени поляризации от
угла падения (малая угл. апертура) и от
длины волны света (хроматизм).

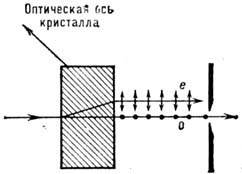
Рис.
Поляризация света с помощью двупреломляю-щего
кристалла: направления электрических
колебаний указаны стрелками (колебания
в плоскости рисунка) и точками
(перпендикулярно плоскости рисунка); о
и е – обыкновенный и необыкновенный
лучи.

36
. Закон
Брюстера — закон оптики, выражающий
связь показателя преломления с таким
углом, при котором свет, отражённый от
границы раздела, будет полностью
поляризованным в плоскости, перпендикулярной
плоскости падения, а преломлённый луч
частично поляризуется в плоскости
падения, причем поляризация преломленного
луча достигает наибольшего значения.
Легко установить, что в этом случае
отраженный и преломленный лучи взаимно
перпендикулярны. Соответствующий угол
называется углом Брюстера.

Это
явление оптики названо по имени
шотландского физика Дэвида Брюстера,
открывшего его в 1815 году.

Закон
Брюстера: , где n21 — показатель преломления
второй среды относительно первой, θBr —
угол падения (угол Брюстера).

При
отражении от одной пластинки под углом
Брюстера интенсивность линейно
поляризованного света очень мала (около
4 % от интенсивности падающего луча).
Поэтому для того, чтобы увеличить
интенсивность отраженного света (или
поляризовать свет, прошедший в стекло,
в плоскости, параллельной плоскости
падения) применяют несколько скрепленных
пластинок, сложенных в стопу — стопу
Столетова. Легко проследить по чертежу
происходящее. Пусть на верхнюю часть
стопы падает луч света. От первой пластины
будет отражаться полностью поляризованный
луч (около 4 % первоначальной интенсивности),
от второй пластины также отразится
полностью поляризованный луч (около
3,75 % первоначальной интенсивности) и
так далее. При этом луч, выходящий из
стопы снизу, будет все больше поляризоваться
в плоскости, параллельной плоскости
падения, по мере добавления пластин.

37.
Поляриза́тор — вещество, позволяющее
выделить из электромагнитной волны
(естественный свет является частным
случаем) часть, обладающую желаемой
поляризацией при пропускании его сквозь
или отражении от поверхности, получая
проекцию волны на плоскость поляризации.
Они используются в поляризацио́нных
фильтрах. В радиотехнике и в быту под
поляризатором понимается устройство
для преобразования вертикальной или
горизонтальной поляризации в круговую
(эллиптическую) или наоборот. В антеннах
в качестве поляризаторов используют
волноводы с вкрученными винтами.

Поляроид
— название синтетической пластиковой
плёнки, используемой для поляризации
света. Обычный свет превращается в
плоскополяризированный, проходя через
пластинки, сделанные из материала,
называемого поляроидом, или через
кристаллы кальцита (особая кристаллическая
форма CaCO3), расположенные таким образом,
что они образуют так называемую призму
Николя.

Пусть
на поляризатор (или анализатор) падает
линейно поляризованный свет с амплитудой
Е0. Амплитуда прошедшего света будет
равна Е=Е0сosj, а интенсивность I=I0сos2j.

Эта
формула выражает закон Малюса:

Интенсивность
линейно поляризованного света, прошедшего
анализатор, пропорциональна квадрату
косинуса угла j между плоскостью колебаний
падающего света и плоскостью анализатора.

38.
ФРЕНЕЛЯ
ФОРМУЛЫ – определяют отношения амплитуды,
фазы и состояния поляризации отражённой
и преломлённой световых волн, возникающих
при прохождении света через границу
раздела двух прозрачных диэлектриков,
к соответствующим характеристикам
падающей волны. Установлены О. Ж. Френелем
в 1823 на основе представлений об упругих
поперечных колебаниях эфира. Однако те
же самые соотношения – Ф. ф.- следуют в
результате строгого вывода из эл–магн.
теории света при решении ур-ний Максвелла.

39.
При падении на плоскую границу различают
две поляризации света. s-Поляризация —
это поляризация света, для которой
напряжённость электрического поля
электромагнитной волны перпендикулярна
плоскости падения (т.е. плоскости, в
которой лежат и падающий, и отражённый
луч). p-Поляризация — поляризация света,
для которой вектор напряжённости
электрического поля лежит в плоскости
падения.

Формулы
Френеля для s-поляризации и p-поляризации
различаются. Поскольку свет с разными
поляризациями по-разному отражается
от поверхности, то отражённый свет
всегда частично поляризован, даже если
падающий свет неполяризован. Угол
падения, при котором отражённый луч
полностью поляризован, называется углом
Брюстера; он зависит от отношения
показателей преломления сред, образующих
границу раздела.

40.
Нормальное
падение

При
нормальном падении

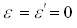
Тогда коэффициент отражения определяется
так:

(3.3.1)

Исходя
из выражения ( 3.2.12), получим коэффициент
пропускания:

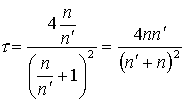
(3.3.2)

Если
граница раздела сред – стекло-воздух,
то ,

то есть при нормальном падении света
на стекло отражается около 4% энергии.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Что такое дифракционная решетка?

   Дифракционная решетка – это оптический прибор, который используется для изучения свойств света и создания спектров. Она состоит из множества параллельных узких щелей, которые расположены на определенном расстоянии друг от друга.

Когда свет проходит через решетку, он разделяется на несколько лучей, каждый из которых имеет свой угол дифракции. Это происходит из-за интерференции световых волн, проходящих через щели.

---

Полезные статьи:

Что такое спетрометр? Принцип работы

Интерферометры, виды, принцип работы

Все статьи

Дифракционная решетка это оптическая система, состоящая из множества параллельных щелей, расположенных на определенном расстоянии друг от друга. Она используется для разделения света на отдельные цвета и используется в оптических приборах, таких как спектроскопы и спектрофотометры.

Может использоваться для измерения длины волны света, определения дисперсии материала и исследования характеристик лазерного излучения. Она также может быть использована для создания цветных изображений и создания цветных фильтров.

Виды дифракционных решеток

Дифракционные решетки могут быть классифицированы по нескольким признакам, включая материал, форму, число щелей и ориентацию. Некоторые из наиболее распространенных видов дифракционных решеток включают:

• Кристаллические: используются кристаллы, такие как кварц или кристалл алмаза, которые имеют очень регулярную структуру.
• Стеклянные: изготавливаются из стекла, которое может быть отполировано до высокой степени гладкости.
• Металлические: решетки изготавливаются из металлов, таких как золото, серебро или медь.
• Пластиковые: решетки могут быть изготовлены из пластика, который имеет регулярную структуру, например, из поликарбоната или акрила.
• Полимерные: решетки изготавливаются из полимерных материалов, таких как поликарбонат или полистирол.
• Многощелевые: решетки имеют несколько щелей, которые могут быть расположены на разных расстояниях друг от друга.
• Однощелевые: имеют только одну щель.
• Круговые: имеют форму круга и используются для исследования поляризации света.
• Линейные: имеют форму линии и используются для изучения дифракции Френеля.

Каждый тип имеет свои преимущества и недостатки, которые зависят от конкретной области применения.

Характеристики и свойства дифракционной решетки

Длина дифракционной решетки

Длина дифракционной решетки – это расстояние между двумя соседними щелями в решетке. Она может быть разной в зависимости от типа решетки и ее назначения. Например, для обычных дифракционных решеток длина щелей обычно составляет от 100 до 200 микрометров.

Она может варьироваться в зависимости от ее конструкции и назначения. Некоторые из них могут иметь длину до нескольких метров, а другие – всего несколько сантиметров. В целом, длина является важным параметром, который влияет на точность и качество измерения света.

Длина волны дифракционной решётки определяется формулой Брэгга:

λ = d * sin(θ) / m,

• где λ – длина волны света,
• d – период дифракционной решётки,
• θ – угол дифракции,
• m – порядок дифракционного порядка.

Если мы знаем период дифракционной решётки, угол дифракции и порядок дифракционного максимума, то мы можем рассчитать длину волны света, которая будет соответствовать этому максимуму.

Период дифракционной решетки

Период дифракционной решетки – это расстояние между двумя соседними линиями решетки. Он определяет ширину спектра. Чем меньше период решетки, тем больше линий в спектре и тем шире спектр можно получить.

Однако, слишком маленький период может привести к тому, что линии будут слишком близко друг к другу, и их будет трудно различить. Поэтому, оптимальный период зависит от конкретной задачи и требований к спектру.

Максимум дифракционной решетки

Максимум дифракционной решетки – это угол, под которым свет максимально рассеивается при прохождении через решетку. Этот угол зависит от длины волны света и от расстояния между щелями. Чем больше расстояние между щелями, тем больше угол рассеяния.

Решетка может использоваться в различных областях, например, в оптике для создания лазерных лучей или в спектроскопии для анализа состава вещества.

Штрихи дифракционной решетки

Дифракционная решетка – это устройство, которое используется для получения дифракционных картин, которые являются результатом дифракции света на периодической структуре. Она состоит из множества параллельных линий, расположенных на определенном расстоянии друг от друга.

Штрихи дифракционной решетки представляют собой узкие линии, которые расположены на решетке. Они могут быть вертикальными, горизонтальными или наклонными. Они могут быть выполнены как на поверхности самой решетки, так и на ее обратной стороне.

Цель штрихов заключается в том, чтобы создать интерференционную картину, которая позволяет определить длину волны света. Чем более узкие штрихи используются, тем более точный результат можно получить.

Кроме того, штрихи дифракционной решетки могут быть использованы для измерения угла падения света на решетку. Это делается путем измерения расстояния между двумя соседними максимумами или минимумами.

Таким образом, штрихи играют важную роль в оптике и используются в различных научных и технических приложениях, таких как спектроскопия, лазерная техника и другие.

Порядок дифракционной решетки

Дифракционная решетка – это оптический элемент, который используется для дисперсии света и создания цветных изображений. Она состоит из множества параллельных и близко расположенных друг к другу штрихов или щелей. Порядок дифракционной решетки – это количество штрихов на единицу длины решетки.

Порядок дифракции – это порядок дифракционного максимума, который определяется расстоянием между соседними максимумами. Порядок дифракции обозначается буквой m и равен отношению расстояния между двумя максимумами к расстоянию между первым дифракционным максимумом и центральной линией.

Для расчета порядка необходимо знать длину волны света, угол падения света на решетку и угол дифракции. Формула для расчета порядка дифракции выглядит следующим образом:

m = sin(θ)/sin(θd),

• где θ – угол дифракции,
• θd – угол падения света,
• sin(θ) – синус угла дифракции,
• sin(θd) – синус угла падения света.

Порядок может быть положительным или отрицательным в зависимости от того, в какую сторону отклоняется свет при дифракции на решетке. Положительный порядок соответствует отклонению света вправо, а отрицательный – влево.

Спектр дифракционной решетки

Состоит из нескольких основных элементов:

1. Центральная полоса: Это самая яркая часть спектра, которая находится в центре. Она содержит все длины волн света, которые проходят через решетку без изменения своей частоты.

2. Краевые полосы: Они расположены по обе стороны от центральной полосы и содержат длины волн, которые были отклонены. Каждая краевая полоса соответствует определенной длине волны света.

3. Интерференционные полосы: Они появляются в спектре, когда свет проходит через дифракционную решетку несколько раз. Эти полосы имеют разную яркость и ширину в зависимости от угла падения света на решетку.

4. Полосы поглощения: Они возникают, когда свет взаимодействует с молекулами вещества, расположенного за решеткой. Эти полосы могут быть использованы для определения состава вещества.

В целом, спектр дифракционной решетки позволяет изучить свойства света и определить его частоту. Он широко используется в научных исследованиях, медицине, промышленности и других областях.

Угол дифракционной решетки

Угол дифракции – это угол между направлением распространения света и направлением, в котором свет отклоняется от своего первоначального направления. При прохождении через дифракционную решетку свет испытывает дифракцию на каждой из ее щелей, что приводит к отклонению света под углом, который зависит от длины волны света, ширины щелей и расстояния между ними.

Для расчета угла дифракции можно использовать формулу Брэгга-Френеля:

sin(θ) = λ/d * sin(φ/2),

• где θ – угол дифракции,
• λ – длина волны света,
• d – расстояние между щелями,
• φ – угол между нормалью к решетке и направлением распространения света.

Эта формула показывает, что угол дифракции зависит от длины волны, ширины щелей и угла между нормалью и направлением света. Чем больше расстояние между щелями и чем меньше ширина щелей, тем меньше угол дифракции.

Расстояние дифракционной решетки

Дифракционная решетка – это устройство, которое используется для разделения света на отдельные цвета или длины волн. Она состоит из множества параллельных узких линий, разделенных промежутками. Расстояние между линиями определяет частоту, на которую будет разбит свет.

Если расстояние между линиями меньше длины волны света, то свет будет разделен на отдельные цвета, каждый из которых будет иметь свою длину волны. Если же расстояние между линиями больше длины волны, то свет пройдет через решетку без изменения.

Таким образом, расстояние между линиями в дифракционной решетке является важным параметром, который определяет ее способность разделять свет на отдельные цвета.

Постоянная дифракционной решетки

Постоянная дифракционной решетки – это постоянная, которая определяет ее способность рассеивать свет. Формула для постоянной выглядит следующим образом:

d = λ/sin(θ),

• где d – постоянная дифракционной решетки,
• λ – длина волны света,
• θ – угол дифракции.

Плоская дифракционная решетка

Плоская дифракционная решетка представляет собой тонкую пластину, состоящую из множества параллельных линий, нанесенных на ее поверхность. Каждая линия имеет определенную ширину и угол наклона относительно нормали к поверхности решетки.

При прохождения света через плоскую дифракционную решетку, свет разделяется на различные цвета и напрвления. Это зависит от направления в зависимости от длины волнысвета и угла падения на решетку.

Это явление называется дифракцией Френеля и является результатом интеференции волн, которые отразились от каждой линии решетки.

Применения дифракционных решеток

Дифракционные решетки широко используются в различных областях науки и техники, включая:

• Оптика – используются для измерения длины волны света, определения дисперсии света и исследования других оптических явлений.
• Лазеры – для создания лазера с высокой стабильностью частоты и генерации узкополосного света.
• Астрономия – дифракция света от звездных объектов позволяет астрономам изучать структуру и свойства космических объектов.
• Медицина – анализ биологических образцов может использоваться для определения молекулярной структуры и состава клеток.
• Наука о материалах – дифракционное рассеяние света позволяет изучать структуру материалов и их свойства, такие как оптические и электронные свойства.
• Квантовая оптика – дифракция Френеля используется для генерации и управления фотонами в квантовых системах.
• Оптическая связь – элементы могут использоваться в качестве оптических фильтров и модуляторов для передачи данных в оптических системах связи.
• Оптический контроль – дифракционные методы используются для контроля качества поверхностей, измерения геометрических параметров и анализа других оптических сигналов.
• Оптика для медицины – элементы используются для диагностики и лечения офтальмологических заболеваний, таких как катаракта и глаукома.

Это только некоторые из областей применения. Они широко используются в научных исследованиях и технологиях, а также в повседневной жизни, например, в оптических приборах для просмотра изображений и в лазерных системах.

Производство дифракционных решеток

Дифракционные решетки могут быть изготовлены из различных материалов, включая кристаллы, стекло, металлы и другие материалы. Процесс производства включает в себя следующие этапы:

Подготовка материала 

Для изготовления дифракционной решетки необходимо выбрать подходящий материал, который должен иметь высокую прозрачность и однородность.

Формирование полос

На поверхность материала наносится тонкий слой материала, который будет использоваться для формирования полос. Этот слой может быть нанесен с помощью лазера, плазменного напыления или других методов.

Очистка поверхности

После нанесения слоя материала необходимо очистить поверхность от загрязнений и неровностей. Это можно сделать с помощью механической обработки или химических методов.

Обработка поверхности

На этом этапе происходит формирование полос с помощью лазерной обработки или плазменного напыления. В результате получаются узкие и параллельные полосы на поверхности материала.

Проверка качества

После формирования полос необходимо проверить качество. Это может быть сделано с помощью оптических методов, таких как измерение спектра или интерференционных картин.

В результате производства дифракционной решетки получается оптический элемент с высокой точностью и качеством, который может использоваться в различных оптических системах и устройствах.

Дифракция света.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: дифракция света, дифракционная решётка.

Если на пути волны возникает препятствие, то происходит дифракция – отклонение волны от прямолинейного распространения. Это отклонение не сводится к отражению или преломлению, а также искривлению хода лучей вследствие изменения показателя преломления среды.Дифракция состоит в том, что волна огибает край препятствия и заходит в область геометрической тени.

Пусть, например, плоская волна падает на экран с достаточно узкой щелью (рис. 1). На выходе из щели возникает расходящаяся волна, и эта расходимость усиливается с уменьшением ширины щели.

Рис. 1. Дифракция на щели

Вообще, дифракционные явления выражены тем отчётливей, чем мельче препятствие. Наиболее существенна дифракция в тех случаях, когда размер препятствия меньше или порядка длины волны. Именно такому условию должна удовлетворять ширина щели на рис. 1.

Дифракция, как и интерференция, свойственна всем видам волн – механическим и электромагнитным. Видимый свет есть частный случай электромагнитных волн; неудивительно поэтому, что можно наблюдать
дифракцию света.

Так, на рис. 2 изображена дифракционная картина, полученная в результате прохождения лазерного луча сквозь небольшое отверстие диаметром 0,2мм.

Рис. 2. Дифракция лазерного луча на отверстии

Мы видим, как и полагается, центральное яркое пятно; совсем далеко от пятна расположена тёмная область – геометрическая тень. Но вокруг центрального пятна – вместо чёткой границы света и тени! – идут чередующиеся светлые и тёмные кольца. Чем дальше от центра, тем менее яркими становятся светлые кольца; они постепенно исчезают в области тени.

Напоминает интерференцию, не правда ли? Это она и есть; данные кольца являются интерференционными максимумами и минимумами. Какие же волны тут интерферируют? Скоро мы разберёмся с этим вопросом, а заодно и выясним, почему вообще наблюдается дифракция.

Но прежде нельзя не упомянуть самый первый классический эксперимент по интерференции света – опыт Юнга, в котором существенно использовалось явление дифракции.

Опыт Юнга.

Всякий эксперимент с интерференцией света содержит некоторый способ получения двух когерентных световых волн. В опыте с зеркалами Френеля, как вы помните, когерентными источниками являлись два изображения одного и того же источника, полученные в обоих зеркалах.

Самая простая идея, которая возникла прежде всего, состояла в следующем. Давайте проколем в куске картона два отверстия и подставим под солнечные лучи. Эти отверстия будут когерентными вторичными источниками света, поскольку первичный источник один – Солнце. Следовательно, на экране в области перекрытия пучков, расходящихся от отверстий, мы должны увидеть интерференционную картину.

Такой опыт был поставлен задолго до Юнга итальянским учёным Франческо Гримальди (который открыл дифракцию света). Интерференции, однако, не наблюдалось. Почему же? Вопрос это не очень простой, и причина заключается в том, что Солнце – не точечный, а протяжённый источник света (угловой размер Солнца равен 30 угловым минутам). Солнечный диск состоит из множества точечных источников, каждый из которых даёт на экране свою интерференционную картину. Накладываясь, эти отдельные картины “смазывают” друг друга, и в результате на экране получается равномерная освещённость области перекрытия пучков.

Но если Солнце является чрезмерно “большим”, то нужно искусственно создать точечный первичный источник. С этой целью в опыте Юнга использовано маленькое предварительное отверстие (рис. 3).

Рис. 3. Схема опыта Юнга

Плоская волна падает на первое отверстие, и за отверстием возникает световой конус, расширяющийся вследствие дифракции. Он достигает следующих двух отверстий, которые становятся источниками двух когерентных световых конусов. Вот теперь – благодаря точечности первичного источника – в области перекрытия конусов будет наблюдаться интерференционная картина!

Томас Юнг осуществил этот эксперимент, измерил ширину интерференционных полос, вывел формулу и с помощью этой формулы впервые вычислил длины волн видимого света. Вот почему этот опыт вошёл в число самых знаменитых в истории физики.

Принцип Гюйгенса–Френеля.

Напомним формулировку принципа Гюйгенса: каждая точка, вовлечённая в волновой процесс, является источником вторичных сферических волн; эти волны распространяются от данной точки, как из центра, во все стороны и накладываются друг на друга.

Но возникает естественный вопрос: а что значит “накладываются”?

Гюйгенс свёл свой принцип к чисто геометрическому способу построения новой волновой поверхности как огибающей семейства сфер, расширяющихся от каждой точки исходной волновой поверхности. Вторичные волны Гюйгенса – это математические сферы, а не реальные волны; их суммарное действие проявляется только на огибающей, т. е. на новом положении волновой поверхности.

В таком виде принцип Гюйгенса не давал ответа на вопрос, почему в процессе распространения волны не возникает волна, идущая в обратном направлении. Не объяснёнными оставались и дифракционные явления.

Модификация принципа Гюйгенса состоялась лишь спустя 137 лет. Огюстен Френель заменил вспомогательные геометрические сферы Гюйгенса на реальные волны и предположил, что эти волны интерферируют друг с другом.

Принцип Гюйгенса–Френеля. Каждая точка волновой поверхности служит источником вторичных сферических волн. Все эти вторичные волны являются когерентными ввиду общности их происхождения от первичного источника (и, стало быть, могут интерферировать друг с другом); волновой процесс в окружающем пространстве есть результат интерференции вторичных волн.

Идея Френеля наполнила принцип Гюйгенса физическим смыслом. Вторичные волны, интерферируя, усиливают друг друга на огибающей своих волновых поверхностей в направлении “вперёд”, обеспечивая дальнейшее распространение волны. А в направлении “назад” происходит их интерференция с исходной волной, наблюдается взаимное гашение, и обратная волна не возникает.

В частности, свет распространяется там, где вторичные волны взаимно усиливаются. А в местах ослабления вторичных волн мы будем видеть тёмные участки пространства.

Принцип Гюйгенса–Френеля выражает важную физическую идею: волна, удалившись от своего источника, в дальнейшем “живёт своей жизнью” и уже никак от этого источника не зависит. Захватывая новые участки пространства, волна распространяется всё дальше и дальше вследствие интерференции вторичных волн, возбуждённых в различных точках пространства по мере прохождения волны.

Как принцип Гюйгенса–Френеля объясняет явление дифракции? Почему, например, происходит дифракция на отверстии? Дело в том, что из бесконечной плоской волновой поверхности падающей волны экранное отверстие вырезает лишь маленький светящийся диск, и последующее световое поле получается в результате интерференции волн вторичных источников, расположенных уже не на всей плоскости, а лишь на этом диске. Естественно, новые волновые поверхности теперь не будут плоскими; ход лучей искривляется, и волна начинает распространяться в разных направлениях, не совпадающих с первоначальным. Волна огибает края отверстия и проникает в область геометрической тени.

Вторичные волны, испущенные различными точками вырезанного светлого диска, интерферируют друг с другом. Результат интерференции определяется разностью фаз вторичных волн и зависит от угла отклонения лучей. В результате возникает чередование интерференционных максимумов и минимумов – что мы и видели на рис. 2.

Френель не только дополнил принцип Гюйгенса важной идеей когерентности и интерференции вторичных волн, но и придумал свой знаменитый метод решения дифракционных задач, основанный на построении так называемых зон Френеля. Изучение зон Френеля не входит в школьную программу – о них вы узнаете уже в вузовском курсе физики. Здесь мы упомянем лишь, что Френелю в рамках своей теории удалось дать объяснение нашего самого первого закона геометрической оптики – закона прямолинейного распространения света.

Дифракционная решётка.

Дифракционная решётка – это оптический прибор, позволяющий получать разложение света на спектральные составляющие и измерять длины волн. Дифракционные решётки бывают прозрачными и отражательными.

Мы рассмотрим прозрачную дифракционную решётку. Она состоит из большого числа щелей ширины , разделённых промежутками ширины (рис. 4). Свет проходит только сквозь щели; промежутки свет не пропускают. Величина называется периодом решётки.

Рис. 4. Дифракционная решётка

Дифракционная решётка изготавливается с помощью так называемой делительной машины, которая наносит штрихи на поверхность стекла или прозрачной плёнки. При этом штрихи оказываются непрозрачными промежутками, а нетронутые места служат щелями. Если, например, дифракционная решётка содержит 100 штрихов на миллиметр, то период такой решётки будет равен: d= 0,01 мм= 10 мкм.

Сперва мы посмотрим, как проходит сквозь решётку монохроматический свет, т. е. свет со строго определённой длиной волны. Отличным примером монохроматического света служит луч лазерной указки длина волны около 0,65 мкм).

На рис. 5 мы видим такой луч, падающий на одну из дифракционных решёток стандартного набора. Щели решётки расположены вертикально, и на экране за решёткой наблюдаются периодически расположенные вертикальные полосы.

Рис. 5. Дифракция лазерного луча на решётке

Как вы уже поняли, это интерференционная картина. Дифракционная решётка расщепляет падающую волну на множество когерентных пучков, которые распространяются по всем направлениям и интерферируют друг с другом. Поэтому на экране мы видим чередование максимумов и минимумов интерференции – светлых и тёмных полос.

Теория дифракционной решётки весьма сложна и во всей своей полноте оказывается далеко за рамками школьной программы. Вам следует знать лишь самые элементарные вещи, связанные с одной-единственной формулой; эта формула описывает положения максимумов освещённости экрана за дифракционной решёткой.

Итак, пусть на дифракционную решётку с периодом падает плоская монохроматическая волна (рис. 6). Длина волны равна .

Рис. 6. Дифракция на решётке

Для большей чёткости интерференционной картины можно поставить линзу между решёткой и экраном, а экран поместить в фокальной плоскости линзы. Тогда вторичные волны, идущие параллельно от различных щелей, соберутся в одной точке экрана (побочном фокусе линзы). Если же экран расположен достаточно далеко, то особой необходимости в линзе нет – лучи, приходящие в данную точку экрана от различных щелей, будут и так почти параллельны друг другу.

Рассмотрим вторичные волны, отклоняющиеся на угол .Разность хода между двумя волнами, идущими от соседних щелей, равна маленькому катету прямоугольного треугольника с гипотенузой ; или, что то же самое, эта разность хода равна катету треугольника . Но угол равен углу , поскольку это острые углы со взаимно перпендикулярными сторонами. Следовательно, наша разность хода равна .

Интерференционные максимумы наблюдаются в тех случаях, когда разность хода равна целому числу длин волн:

(1)

При выполнении этого условия все волны, приходящие в точку от различных щелей, будут складываться в фазе и усиливать друг друга. Линза при этом не вносит дополнительной разности хода – несмотря на то, что разные лучи проходят через линзу разными путями. Почему так получается? Мы не будем вдаваться в этот вопрос, поскольку его обсуждение выходит за рамки ЕГЭ по физике.

Формула (1) позволяет найти углы, задающие направления на максимумы:

. (2)

При получаем Это центральный максимум, или максимум нулевого порядка.Разность хода всех вторичных волн, идущих без отклонения, равна нулю, и в центральном максимуме они складываются с нулевым сдвигом фаз. Центральный максимум – это центр дифракционной картины, самый яркий из максимумов. Дифракционная картина на экране симметрична относительно центрального максимума.

При получаем угол:

.

Этот угол задаёт направления на максимумы первого порядка. Их два, и расположены они симметрично относительно центрального максимума. Яркость в максимумах первого порядка несколько меньше, чем в центральном максимуме.

Аналогично, при имеем угол:

.

Он задаёт направления на максимумы второго порядка. Их тоже два, и они также расположены симметрично относительно центрального максимума. Яркость в максимумах второго порядка несколько меньше, чем в максимумах первого порядка.

Примерная картина направлений на максимумы первых двух порядков показана на рис. 7.

Рис. 7. Максимумы первых двух порядков

Вообще, два симметричных максимума k-го порядка определяются углом:

. (3)

При небольших соответствующие углы обычно невелики. Например, при мкм и мкм максимумы первого порядка расположены под углом .Яркость максимумов k-го порядка постепенно убывает с ростом k. Сколько всего максимумов можно увидеть? На этот вопрос легко ответить с помощью формулы (2). Ведь синус не может быть больше единицы, поэтому:

.

Используя те же числовые данные, что и выше, получим: . Следовательно, наибольший возможный порядок максимума для данной решётки равен 15.

Посмотрите ещё раз на рис. 5. На экране мы видны 11 максимумов. Это центральный максимум, а также по два максимума первого, второго, третьего, четвёртого и пятого порядков.

С помощью дифракционной решётки можно измерить неизвестную длину волны. Направляем пучок света на решётку (период которой мы знаем), измеряем угол на максимум первого
порядка, пользуемся формулой (1) и получаем:

.

Дифракционная решётка как спектральный прибор.

Выше мы рассматривали дифракцию монохроматического света, каковым является лазерный луч. Часто приходится иметь дело с немонохроматическим излучением. Оно является смесью различных монохроматических волн, которые составляют спектр данного излучения. Например, белый свет – это смесь волн всего видимого диапазона, от красного до фиолетового.

Оптический прибор называется спектральным, если он позволяет раскладывать свет на монохроматические компоненты и тем самым исследовать спектральный состав излучения. Простейший спектральный прибор вам хорошо известен – это стеклянная призма. К числу спектральных приборов относится также и дифракционная решётка.

Предположим, что на дифракционную решётку падает белый свет. Давайте вернёмся к формуле (2) и подумаем, какие выводы из неё можно сделать.

Положение центрального максимума () не зависит от длины волны. В центре дифракционной картины сойдутся с нулевой разностью хода все монохроматические составляющие белого света. Поэтому в центральном максимуме мы увидим яркую белую полосу.

А вот положения максимумов порядка определяются длиной волны. Чем меньше , тем меньше угол для данного . Поэтому в максимуме k-го порядка монохроматические волны разделяются в пространстве: самой близкой к к центральному максимуму окажется фиолетовая полоса, самой далёкой – красная.

Следовательно, в каждом порядке белый свет раскладывается решёткой в спектр.
Максимумы первого порядка всех монохроматических компонент образуют спектр первого порядка; затем идут спектры второго, третьего и так далее порядков. Спектр каждого порядка имеет вид цветной полосы, в которой присутствуют все цвета радуги – от фиолетового до красного.

Дифракция белого света показана на рис. 8. Мы видим белую полосу в центральном максимуме, а по бокам – два спектра первого порядка. По мере возрастания угла отклонения цвет полос меняется от фиолетового к красному.

Рис. 8. Дифракция белого света на решётке

Но дифракционная решётка не только позволяет наблюдать спектры, т. е. проводить качественный анализ спектрального состава излучения. Важнейшим достоинством дифракционной решётки является возможность количественного анализа – как уже говорилось выше, мы с её помощью можем измерять длины волн. При этом измерительная процедура весьма проста: фактически она сводится к измерению угла направления на максимум.

Естественными примерами дифракционных решёток, встречающихся в природе, являются перья птиц, крылья бабочек, перламутровая поверхность морской раковины. Если, прищурившись, посмотреть на солнечный свет, то можно увидеть радужную окраску вокруг ресниц.Наши ресницы действуют в данном случае как прозрачная дифракционная решётка на рис. 6, а в качестве линзы выступает оптическая система роговицы и хрусталика.

Спектральное разложение белого света, даваемое дифракционной решёткой, проще всего наблюдать, глядя на обычный компакт-диск (рис. 9). Оказывается, дорожки на поверхности диска образуют отражательную дифракционную решётку!